Construction of a Time-Variant Integrated Drought Index Based on the GAMLSS Approach and Copula Function
Abstract
:1. Introduction
2. Study Area and Research Framework
2.1. Study Area and Data Sources
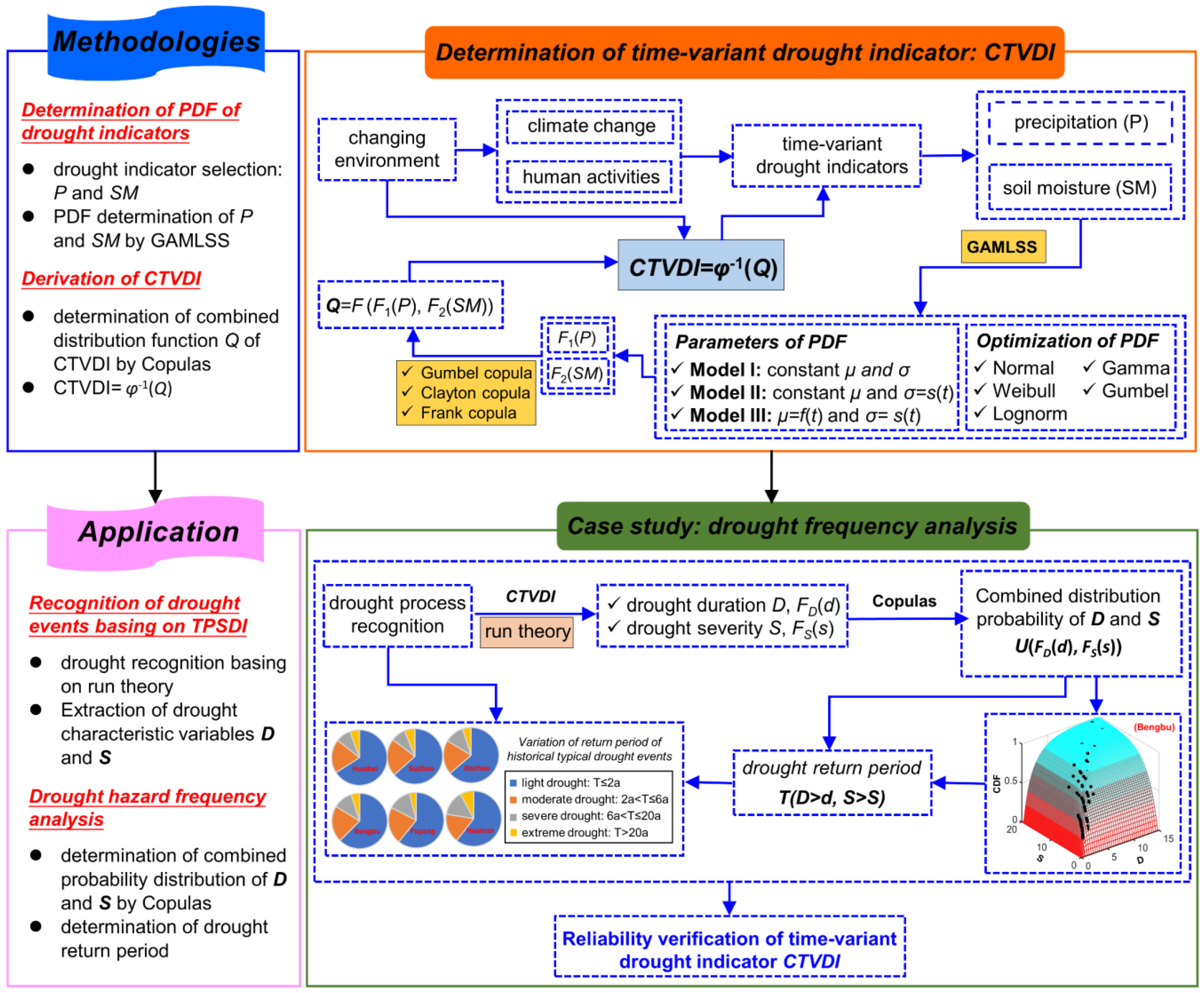
2.2. Research Framework
3. Methodologies
3.1. Generalized Additive Models for Location, Scale and Shape (GAMLSS) Method
3.1.1. Introduction to GAMLSS
3.1.2. Parameter Optimization of GAMLSS
3.2. Copula Function
3.3. Calculation Procedures of Integrated Index CTVDI
4. Results and Discussion
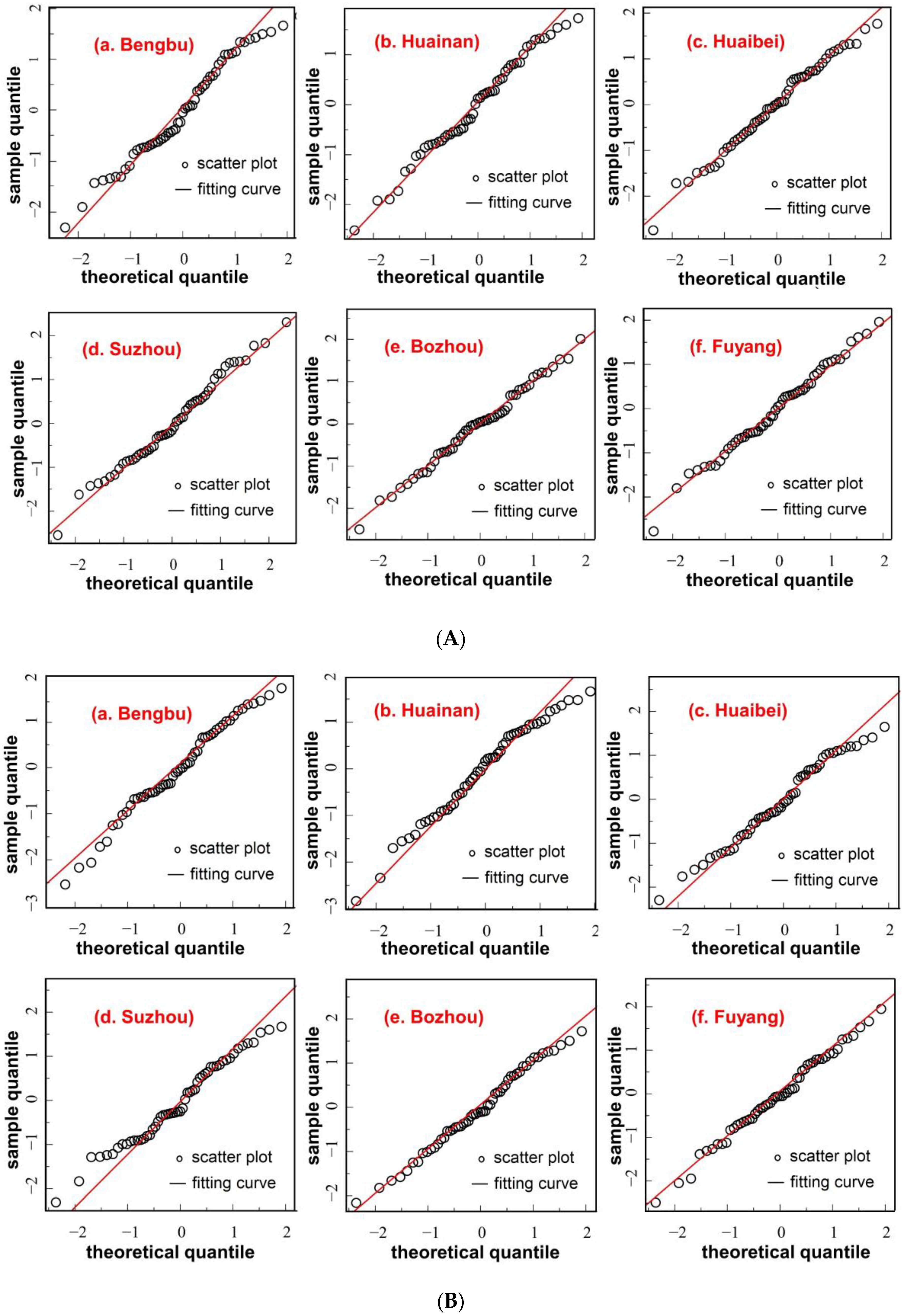
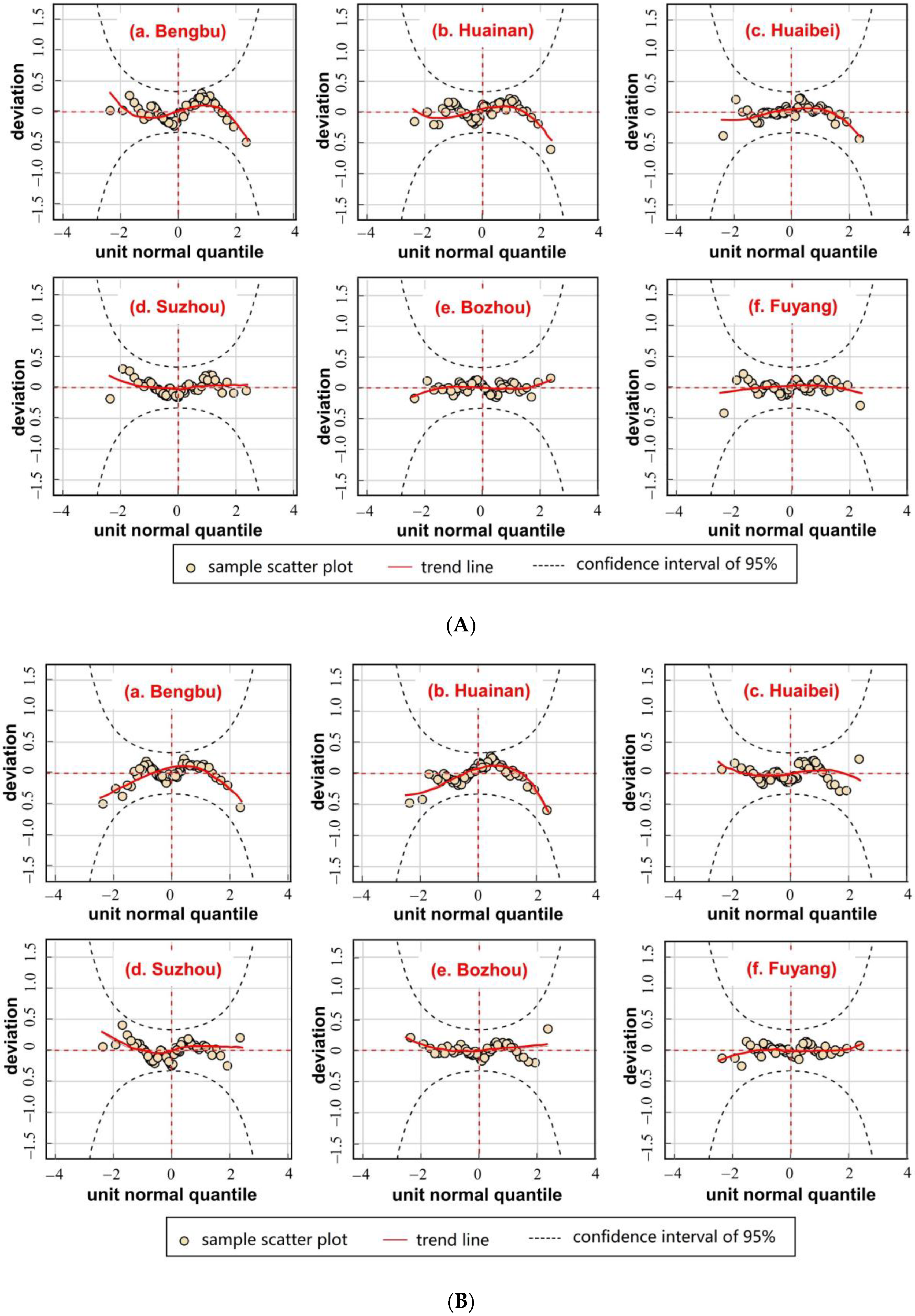
4.1. Performance Analysis of GAMLSS Model
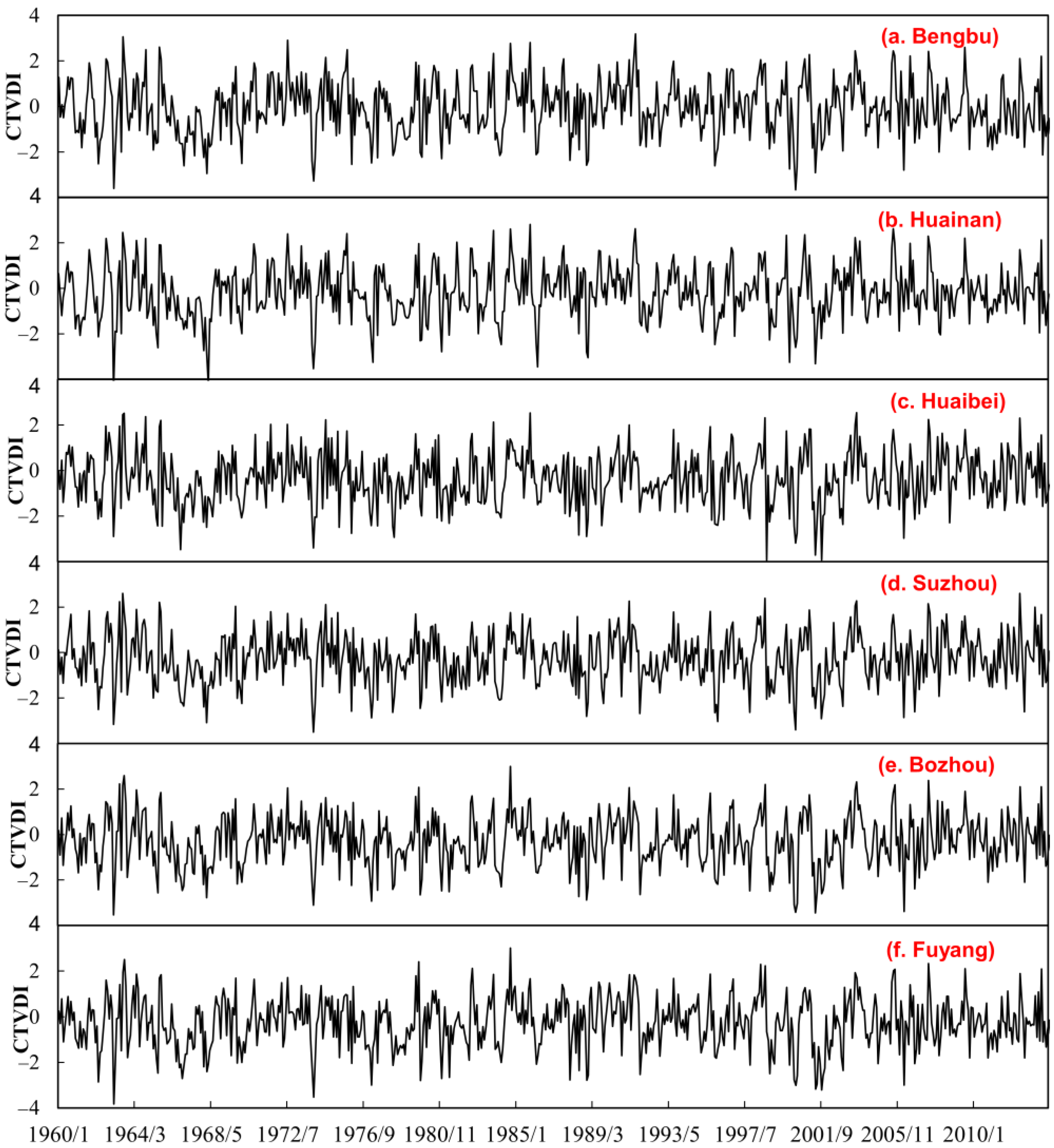
4.2. Derivation of CTVDI Series and Its Application in Drought Process Recognition
4.3. Drought Frequency and Return Period Determination Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, H.; Zhang, X.Y.; Liu, S.D. Risk assessment to China’s agricultural drought disaster in county unit. Nat. Hazards 2012, 61, 785–801. [Google Scholar]
- Jin, J.L.; Yang, Q.Q.; Zhou, Y.L.; Cui, Y.; Zhang, Y.L.; Jiang, S.M.; Zhang, M.; Yuan, X.C. Research progress on drought analysis technologies. J. North China Univ. Water Resour. Electr. Power Nat. Sci. Ed. 2016, 37, 1–15. (In Chinese) [Google Scholar]
- Wu, H.J.; Singh, X.L.S.V.P.; Feng, K.; Niu, J.P. Agricultural drought prediction based on conditional distributions of Vine Copulas. Water Resour. Res. 2021, 57, e2021WR029562. [Google Scholar] [CrossRef]
- Wang, S.T.; Cao, Z.; Luo, P.P.; Zhu, W. Spatiotemporal variations and climatological trends in precipitation indices in Shaanxi Province, China. Atmosphere 2022, 13, 744. [Google Scholar] [CrossRef]
- Cook, B.I.; Smerdon, J.E.; Seager, R.; Coats, S. Global warming and 21st century drying. Clim. Dyn. 2014, 43, 2607–2627. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Xu, H.T.; Li, Y.Y.; Wen, L.; Li, J.Q.; Lu, G.H.; Li, X.Y. Climate and drought risk regionalization in China based on probabilistic aridity and drought index. Sci. Total Environ. 2018, 612, 513–521. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, S.T.; Luo, P.P.; Xie, D.N.; Zhu, W. Watershed ecohydrological processes in a changing environment: Opportunities and challenges. Water 2022, 14, 1502. [Google Scholar] [CrossRef]
- Wu, J.J.; He, B.; Lü, A.F.; Zhou, L.; Liu, M.; Zhao, L. Quantitative assessment and spatial characteristic analysis of agricultural drought risk in China. Nat. Hazards 2013, 66, 155–166. [Google Scholar]
- Chang, J.X.; Guo, A.J.; Wang, Y.M.; Ha, Y.P.; Zhang, R.; Xue, L.; Tu, Z.Q. Reservoir operations to mitigate drought effects with a hedging policy triggered by the drought prevention limiting water level. Water Resour. Res. 2019, 55, 904–922. [Google Scholar] [CrossRef]
- Yuan, W.P.; Zhou, G.S. Theoretical study and research prospect on drought indices. Adv. Earth Sci. 2004, 19, 982–991. (In Chinese) [Google Scholar]
- Xiao, M.Z.; Zhang, Q.; Zhang, X.H. Spatial-temporal Patterns of Drought Risk across the Pearl River Basin. Acta Geogr. Sin. 2012, 67, 83–92. (In Chinese) [Google Scholar]
- Gao, X.N.; Xu, Q.Z.; Zong, J.X.; Xu, Y.Q. Temporal and spatial patterns of droughts based on standard precipitation index (SPI) in Liaoning Province in recent 54a. Ecol. Environ. Sci. 2015, 24, 1851–1857. (In Chinese) [Google Scholar]
- Adnan, S.; Ullah, K.; Li, S.L.; Gao, S.T.; Khan, A.H.; Mahmood, R. Comparison of various drought indices to monitor drought status in Pakistan. Clim. Dyn. 2018, 51, 1885–1899. [Google Scholar] [CrossRef]
- Rashid, M.M.; Beecham, S. Development of a non-stationary standardized precipitation index and its application to a south Australian climate. Sci. Total Environ. 2019, 657, 882–892. [Google Scholar] [CrossRef]
- Chang, W.J.; Liang, Z.M.; Ma, H.B. Construction of drought composite indicator based on principal component analysis and its application. Hydrology 2017, 37, 33–38. (In Chinese) [Google Scholar]
- Hu, N. Application of “intra-class-inter-class” comprehensive drought index in drought assessment of Liaoning Province. Water Resour. Plan. Des. 2019, 6, 56–59. (In Chinese) [Google Scholar]
- Shen, Z.X.; Zhang, Q.; Singh, V.P.; Sun, P.; Sun, C.Q.; Yu, H.Q. Agricultural drought monitoring across Inner Mongolia, China: Model development, spatiotemporal patterns and impacts. J. Hydrol. 2019, 571, 793–804. [Google Scholar] [CrossRef]
- Xie, P.; Chen, G.C.; Xia, J. Hydrological frequency calculation principle of inconsistent annual runoff series under change environments. Eng. J. Wuhan Univ. 2005, 38, 6–9. [Google Scholar]
- Song, S.B.; Singh, V.P. Frequency analysis of droughts using the Plackett copula and parameter estimation by genetic algorithm. Stoch. Environ. Res. Risk Assess. 2010, 24, 783–805. [Google Scholar] [CrossRef]
- Wang, S.T.; Luo, P.P.; Xu, C.Y.; Zhu, W.; Cao, Z.; Ly, S. Reconstruction of historical land use and urban flood simulation in Xi’an, Shannxi, China. Remote Sens. 2022, 14, 6067. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Cheng, D.D.; He, H.; Li, Y.; Zhou, J.H. Research progress of composite drought index. Water Resour. Prot. 2021, 37, 36–45. (In Chinese) [Google Scholar]
- Bai, X.; Wang, Y.M.; Jin, J.L.; Qi, X.M.; Wu, C.G. Precondition cloud and maximum entropy principle coupling model-based approach for the comprehensive assessment of drought risk. Sustainability 2018, 10, 3236. [Google Scholar] [CrossRef]
- Akantziliotou, K.; Rigby, R.A.; Stasinopoulos, D.M. The R implementation of generalized additive models for location, scale and shape. J. R. Stat. Soc. 2002, 54, 507–554. [Google Scholar]
- Stasinopoulos, D.M.; Rigby, R.A. Generalized additive models for location scale and shape (GAMLSS) in R. J. Stat. Softw. 2007, 23, 1–46. [Google Scholar] [CrossRef]
- Tang, S.M. Nonstationary Flood Frequency Analysis Based on Covariates. Master’s Dissertation, Tianjin University, Tianjin, China, 2016. (In Chinese). [Google Scholar]
- Mo, S.H.; Li, C.X.; Xing, H.; Jiang, K.X. GAMLSS model-based analysis on annual runoff in Xiaoli river basin. J. Basic Sci. Eng. 2022, 30, 40–49. (In Chinese) [Google Scholar]
- Rigby, R.A.; Stasinopoulos, D.M. A semi-parametric additive model for variance heterogeneity. Stat. Comput. 1996, 6, 57–65. [Google Scholar] [CrossRef]
- Chen, F.L.; Yang, K.; Cai, W.J.; Long, A.H.; He, X.L. Study on hydrological drought index based on GAMLSS: Taking Manas River Basin as an example. Geogr. Res. 2012, 61, 785–801. (In Chinese) [Google Scholar]
- Wang, Y.X. Driving Mechanism and Quantitative Assessment of Drought in Luanhe River Basin under Changing Environment. Master’s Dissertation, Tianjin University, Tianjin, China, 2017. (In Chinese). [Google Scholar]
- Shiau, J.T. Fitting drought duration and severity with two-dimensional copulas. Water Resour. Manag. 2006, 20, 795–815. [Google Scholar] [CrossRef]
- Wu, C.G.; Zhou, L.Y.; Zhang, L.B.; Jin, J.L.; Zhou, Y.L. Precondition cloud algorithm and Copula coupling model-based approach for drought hazard comprehensive assessment. Int. J. Disaster Risk Reduct. 2019, 38, 101220. [Google Scholar] [CrossRef]
- Genest, C.; Rwest, L.P. Statistical inference procedures for bivariate Archimedean copulas. J. Am. Stat. Assoc. 1993, 88, 1034–1043. [Google Scholar] [CrossRef]
- Li, Y.Y. Research on the Drought Assessment-Propagation-Driving-Prediction under the Climate and Land Use Cover Change Scenarios. Master’s Dissertation, Xi’an University of Technology, Xi’an, China, 2018. (In Chinese). [Google Scholar]
- Zhang, Y.; Huang, S.Z.; Huang, Q.; Li, P.; Ma, L. Construction and application of a new comprehensive drought index based on Copula function. J. Hydraul. Eng. 2018, 49, 703–714. (In Chinese) [Google Scholar]
- Zhou, Y.L.; Yuan, X.C.; Jin, J.L.; Li, J.Q.; Song, S.B. Regional hydrological drought frequency based on Copulas. Sci. Geogr. Sin. 2011, 31, 1383–1388. (In Chinese) [Google Scholar]
- Shiau, J.T.; Shen, H.W. Recurrence analysis of hydrologic drought of different severity. J. Water Resour. Plan. Manag. 2001, 127, 30–40. [Google Scholar] [CrossRef]
- Wen, K.G.; Zhai, W.Q. China Meteorological Disaster Statistics Manual: Anhui Edition; China Meteorological Press: Beijing, China, 2007. (In Chinese)
- Zhou, H.K.; Wu, J.J.; Li, X.H.; Liu, L.Z.; Yang, J.H.; Han, X.Y. Suitability of assimilated data-based standardized soil moisture index for agricultural drought monitoring. Acta Ecol. Sin. 2019, 39, 2191–2202. (In Chinese) [Google Scholar]
| Name | Determination of Distribution Parameters | |
|---|---|---|
| NO | ||
| LOGNO | ||
| WEI | ||
| GA | ||
| GU |
| Name | Type | Huaibei | Suzhou | Bozhou | Bengbu | Fuyang | Huainan | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P | SM | P | SM | P | SM | P | SM | P | SM | P | SM | ||
| Scenario 1: constant μ and σ | NO | 601 | 266 | 593 | 276 | 602 | 252 | 600 | 259 | 602 | 261 | 592 | 275 |
| LOGNO | 602 | 268 | 598 | 279 | 596 | 255 | 603 | 264 | 589 | 266 | 604 | 280 | |
| WEI | 598 | 262 | 591 | 273 | 596 | 247 | 596 | 247 | 595 | 251 | 589 | 259 | |
| GA | 597 | 267 | 592 | 278 | 594 | 254 | 597 | 262 | 590 | 265 | 592 | 278 | |
| GU | 614 | 263 | 606 | 274 | 625 | 248 | 613 | 246 | 625 | 251 | 604 | 257 | |
| Scenario 2: μ = f(t) and constant σ | NO | 602 | 257 | 595 | 263 | 603 | 246 | 601 | 259 | 603 | 256 | 593 | 271 |
| LOGNO | 603 | 259 | 599 | 266 | 596 | 249 | 604 | 264 | 589 | 261 | 603 | 276 | |
| WEI | 598 | 253 | 593 | 259 | 598 | 241 | 598 | 243 | 596 | 246 | 591 | 259 | |
| GA | 599 | 258 | 594 | 265 | 595 | 248 | 599 | 262 | 591 | 259 | 593 | 275 | |
| GU | 615 | 254 | 607 | 258 | 627 | 240 | 615 | 241 | 626 | 245 | 606 | 256 | |
| Scenario 3: μ = f(t) and σ = s(t) | NO | 604 | 259 | 597 | 264 | 604 | 248 | 601 | 257 | 605 | 257 | 592 | 271 |
| LOGNO | 602 | 261 | 595 | 268 | 597 | 251 | 597 | 262 | 590 | 262 | 601 | 277 | |
| WEI | 599 | 254 | 594 | 259 | 598 | 242 | 596 | 245 | 597 | 247 | 586 | 256 | |
| GA | 599 | 260 | 593 | 267 | 595 | 250 | 595 | 261 | 592 | 260 | 585 | 275 | |
| GU | 617 | 254 | 609 | 260 | 624 | 242 | 613 | 243 | 627 | 246 | 603 | 254 | |
| City | Name | Type | Distribution Parameter | Residual Distribution Parameter | ||||
|---|---|---|---|---|---|---|---|---|
| AV | VA | SC | KC | FC | ||||
| Huaibei | P | GA | μ = exp(4.7862) | 0.0018 | 1.0192 | −0.2744 | 2.5630 | 0.9929 |
| σ = exp(−0.7287) | ||||||||
| SM | WEI | μ = exp(3.6082 − 0.0018·t) | −0.0019 | 1.0158 | 0.0465 | 2.4647 | 0.9922 | |
| σ = exp(2.8581) | ||||||||
| Suzhou | P | WEI | μ = exp(4.9376) | 0.0003 | 1.0013 | 0.1000 | 2.5842 | 0.9938 |
| σ = exp(0.9520) | ||||||||
| SM | GU | μ = (36.8974 − 0.0835·t) | 0.0005 | 0.9956 | 0.1559 | 2.4970 | 0.9908 | |
| σ = exp(0.7262) | ||||||||
| Bozhou | P | GA | μ = exp(4.7933) | 0.0000 | 1.0185 | −0.0009 | 2.8585 | 0.9966 |
| σ = exp(−0.7785) | ||||||||
| SM | GU | μ = (34.7393 − 0.0484·t) | 0.0007 | 0.9987 | 0.1415 | 2.6827 | 0.9953 | |
| σ = exp(−0.5639) | ||||||||
| Bengbu | P | GA | μ = (4.6641 − 0.0053·t) | 0.0054 | 1.0252 | −0.0231 | 2.0978 | 0.9879 |
| σ = exp(−0.4236 − 0.0146·t) | ||||||||
| SM | GU | μ = (38.3270 − 0.0394·t) | −0.0063 | 1.0873 | −0.3833 | 2.7571 | 0.9889 | |
| σ = exp(0.5237) | ||||||||
| Fuyang | P | LOGNO | μ = 4.6452 | 0.0000 | 1.0185 | −0.1165 | 2.7462 | 0.9946 |
| σ = exp(− 0.7432) | ||||||||
| SM | GU | μ = 36.1412 − 0.0461·t | −0.0005 | 1.0271 | −0.0491 | 2.8125 | 0.9968 | |
| σ = exp(0.5921) | ||||||||
| Huainan | P | GA | μ = exp(4.5209 + 0.0065·t) | 0.0061 | 1.0253 | −0.1981 | 2.3835 | 0.9901 |
| σ = exp(−0.3317 − 0.0162·t) | ||||||||
| SM | GU | μ = 37.1387 − 0.0348·t | −0.0109 | 1.1009 | −0.4277 | 2.5492 | 0.9872 | |
| σ = exp(0.2777 + 0.0122·t ) | ||||||||
| Name | Type | Huaibei | Suzhou | Bozhou | Bengbu | Fuyang | Huainan | Average |
|---|---|---|---|---|---|---|---|---|
| P and CTVDI | LCC | 0.68 | 0.72 | 0.73 | 0.77 | 0.75 | 0.74 | 0.73 |
| KCC | 0.68 | 0.67 | 0.71 | 0.79 | 0.68 | 0.73 | 0.71 | |
| SM and CTVDI | LCC | 0.83 | 0.82 | 0.92 | 0.91 | 0.88 | 0.85 | 0.87 |
| KCC | 0.73 | 0.71 | 0.87 | 0.82 | 0.76 | 0.77 | 0.78 |
| Name | Huaibei | Suzhou | Bozhou | Bengbu | Fuyang | Huainan |
|---|---|---|---|---|---|---|
| Drought event amount | 91 | 82 | 80 | 80 | 74 | 76 |
| Average of drought duration (month) | 3.1 | 3.04 | 3.19 | 2.53 | 3.23 | 2.88 |
| Average of non-drought duration (month) | 4.13 | 4.37 | 4.93 | 5.86 | 5.04 | 6.13 |
| Maximum of drought duration (month) | 16 | 12 | 14 | 13 | 14 | 9 |
| Average of drought severity | 4.22 | 4.05 | 4.26 | 3.57 | 4.4 | 3.98 |
| Maximum of drought severity | 20.89 | 15.57 | 18.61 | 18.95 | 18.43 | 15.94 |
| Kendall correlation coefficient of drought duration and severity | 0.78 | 0.72 | 0.77 | 0.7 | 0.73 | 0.74 |
| City | T ≤ 2a (Light Drought) | 2a < T ≤ 6a (Moderate Drought) | 6a < T ≤ 20a (Severe Drought) | T > 20a (Extreme Drought) | Total Amount |
|---|---|---|---|---|---|
| Huaibei | 60 | 18 | 8 | 5 | 91 |
| Suzhou | 52 | 18 | 7 | 5 | 82 |
| Bozhou | 51 | 16 | 9 | 4 | 80 |
| Bengbu | 50 | 17 | 9 | 4 | 80 |
| Fuyang | 46 | 16 | 11 | 6 | 79 |
| Huainan | 45 | 15 | 8 | 3 | 71 |
| City | No. | Time of Drought Event | Drought Duration /Month | Drought Severity | Joint Frequency | Return Period /Year |
|---|---|---|---|---|---|---|
| Huaibei | 1 | August 1966–June 1967 | 11 | 17.56 | 0.0094 | 64.2 |
| 2 | November 1967–July 1968 | 9 | 14.19 | 0.0239 | 25.2 | |
| 3 | October 1991–January 1993 | 16 | 14.08 | 0.0038 | 160.1 | |
| 4 | September 1998–September 1999 | 12 | 13.23 | 0.0152 | 39.6 | |
| 5 | March 2001–November 2001 | 9 | 18.43 | 0.0074 | 81.2 | |
| Suzhou | 1 | May 1966–January 1967 | 9 | 13.78 | 0.0183 | 34.2 |
| 2 | September 1967–July 1968 | 11 | 15.57 | 0.0088 | 70.3 | |
| 3 | January 1978–December 1978 | 12 | 10.46 | 0.0074 | 87.9 | |
| 4 | March 1981–April 1982 | 12 | 13.54 | 0.0215 | 28.7 | |
| 5 | March 2001–November 2001 | 9 | 14.95 | 0.0133 | 47.5 | |
| Bozhou | 1 | May 1966–June 1967 | 14 | 18.62 | 0.0056 | 121.6 |
| 2 | March 1978–January 1979 | 11 | 12.17 | 0.0202 | 33.5 | |
| 3 | October 1991–August 1992 | 11 | 11.51 | 0.0203 | 33.3 | |
| 4 | March 2001–November 2001 | 9 | 18.26 | 0.0084 | 80.3 | |
| Bengbu | 1 | May 1966–June 1967 | 13 | 18.95 | 0.0044 | 157.9 |
| 2 | November 1967–June 1968 | 8 | 13.62 | 0.0206 | 34.3 | |
| 3 | March 1978–March 1979 | 13 | 15.55 | 0.0064 | 109.9 | |
| 4 | October 2010–June 2011 | 9 | 11.25 | 0.0253 | 27.6 | |
| Fuyang | 1 | December 1960–July 1961 | 8 | 11.05 | 0.0275 | 27.3 |
| 2 | October 1967–May 1968 | 8 | 15.94 | 0.0072 | 104.3 | |
| 3 | August 1978–March 1979 | 8 | 7.62 | 0.0304 | 24.7 | |
| 4 | November 1983–May 1984 | 7 | 11.11 | 0.0363 | 20.7 | |
| 5 | October 1991–June 1992 | 9 | 11.04 | 0.0168 | 44.7 | |
| 6 | March 2001–November 2001 | 9 | 12.98 | 0.0153 | 50.4 | |
| Huainan | 1 | May 1966–June 1967 | 14 | 20.89 | 0.0051 | 136.1 |
| 2 | February 1978–March 1979 | 13 | 15.6 | 0.0087 | 79.1 | |
| 3 | March 2001–November 2001 | 9 | 20.49 | 0.0077 | 89.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, X.; Jin, J.; Wu, C.; Zhou, Y.; Zhang, L.; Cui, Y.; Tong, F. Construction of a Time-Variant Integrated Drought Index Based on the GAMLSS Approach and Copula Function. Water 2023, 15, 1653. https://doi.org/10.3390/w15091653
Bai X, Jin J, Wu C, Zhou Y, Zhang L, Cui Y, Tong F. Construction of a Time-Variant Integrated Drought Index Based on the GAMLSS Approach and Copula Function. Water. 2023; 15(9):1653. https://doi.org/10.3390/w15091653
Chicago/Turabian StyleBai, Xia, Juliang Jin, Chengguo Wu, Yuliang Zhou, Libing Zhang, Yi Cui, and Fang Tong. 2023. "Construction of a Time-Variant Integrated Drought Index Based on the GAMLSS Approach and Copula Function" Water 15, no. 9: 1653. https://doi.org/10.3390/w15091653
APA StyleBai, X., Jin, J., Wu, C., Zhou, Y., Zhang, L., Cui, Y., & Tong, F. (2023). Construction of a Time-Variant Integrated Drought Index Based on the GAMLSS Approach and Copula Function. Water, 15(9), 1653. https://doi.org/10.3390/w15091653








