Exploring Multiscale Variability in Groundwater Quality: A Comparative Analysis of Spatial and Temporal Patterns via Clustering
Abstract
:1. Introduction
2. Materials and Methods
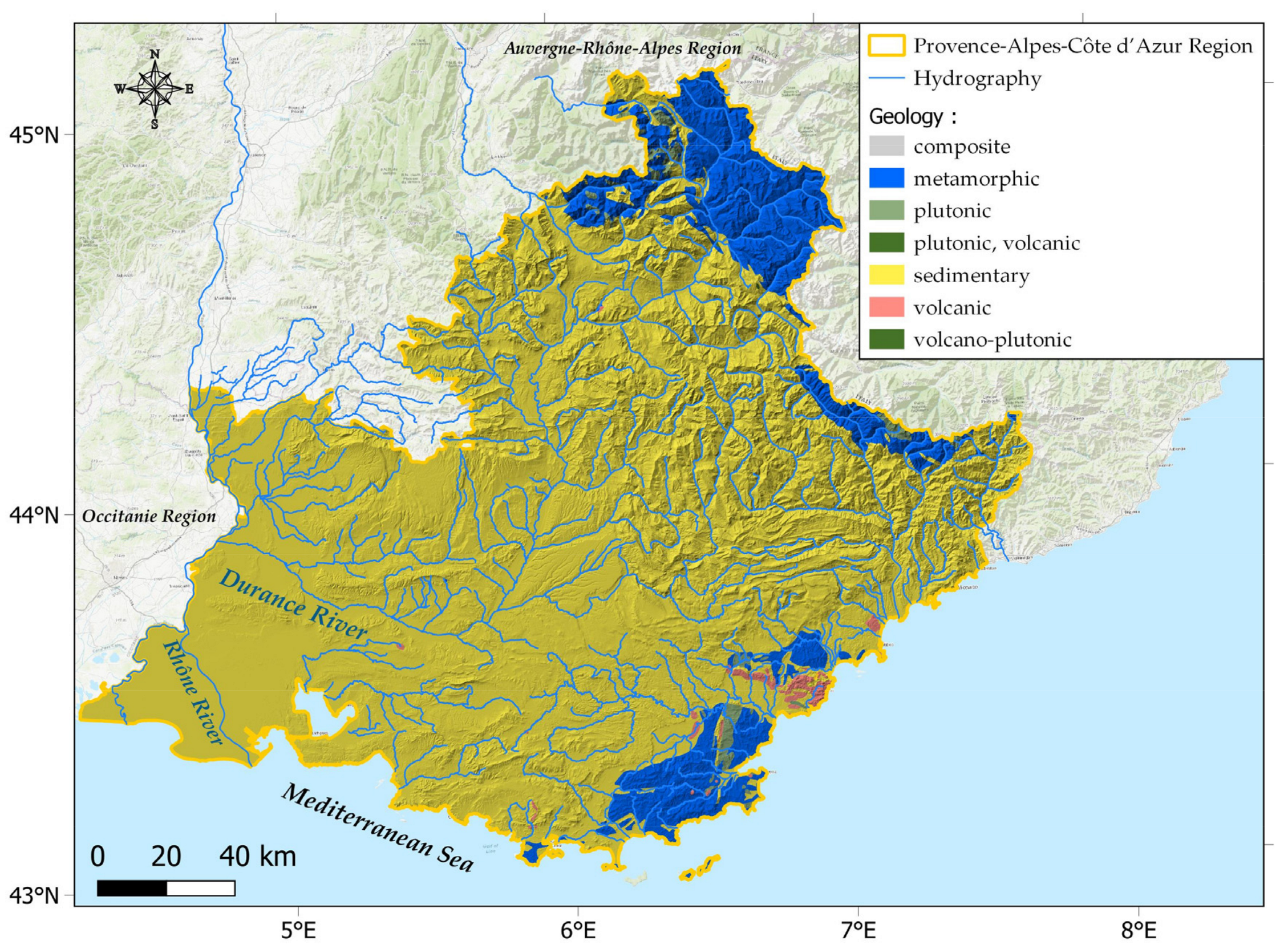
2.1. Study Location
2.2. Data Sources and Processing
2.3. Data Treatement and Multivariate Statististical Analysis
2.3.1. Log Transformation
2.3.2. Principal Component Analysis (PCA)
2.3.3. Hierarchical Clustering
2.3.4. Spatial and Temporal Variability
2.3.5. Kriging
3. Results
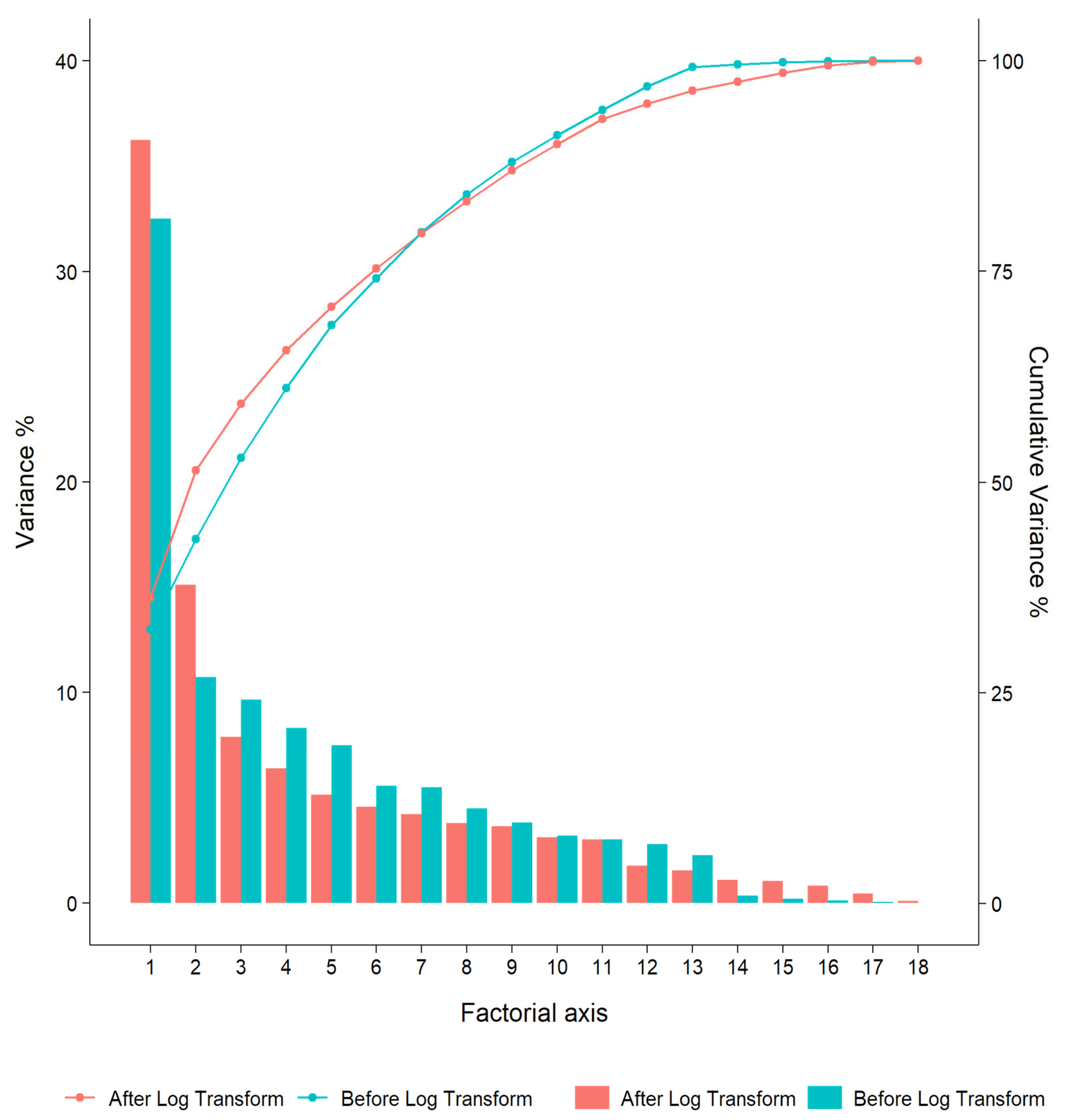
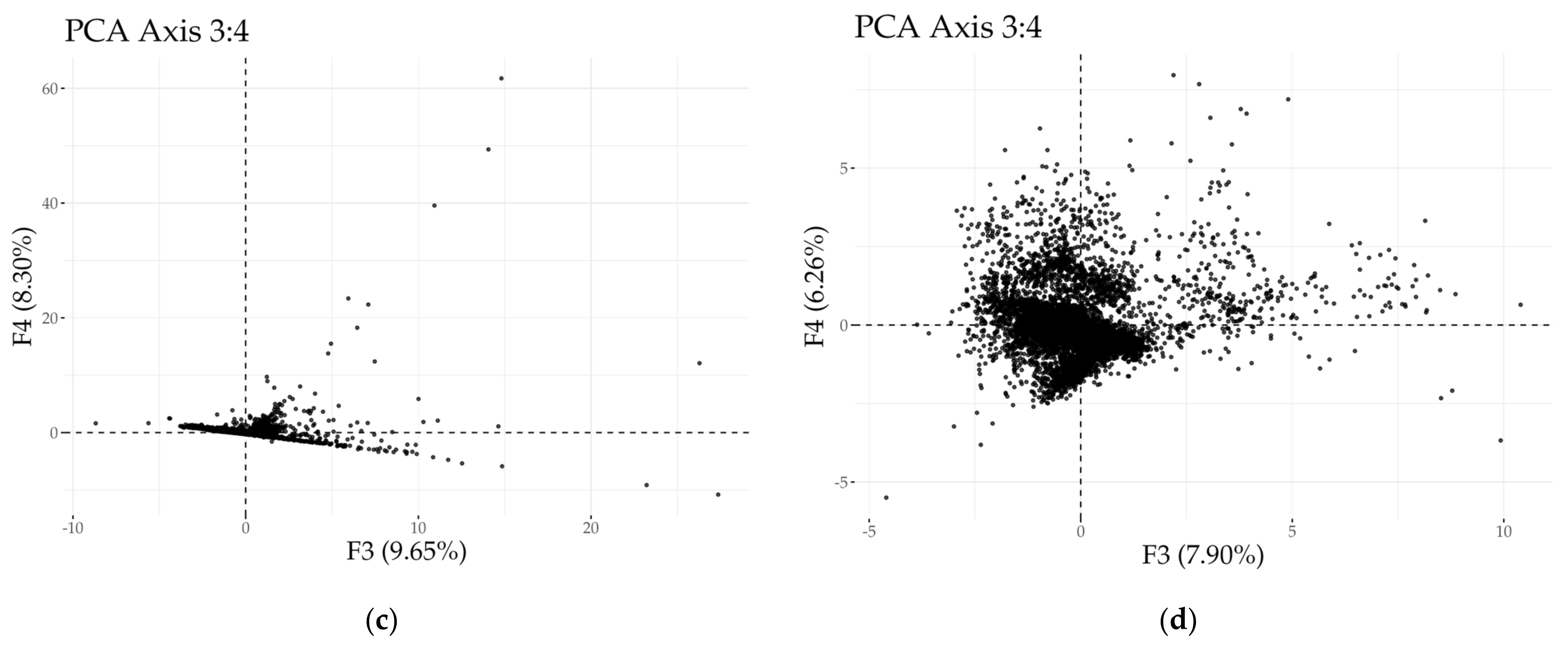
3.1. Achieving a Symmetrical Data Distribution
3.2. PCA Results: General Chemistry and Spatial Distribution of Groundwater
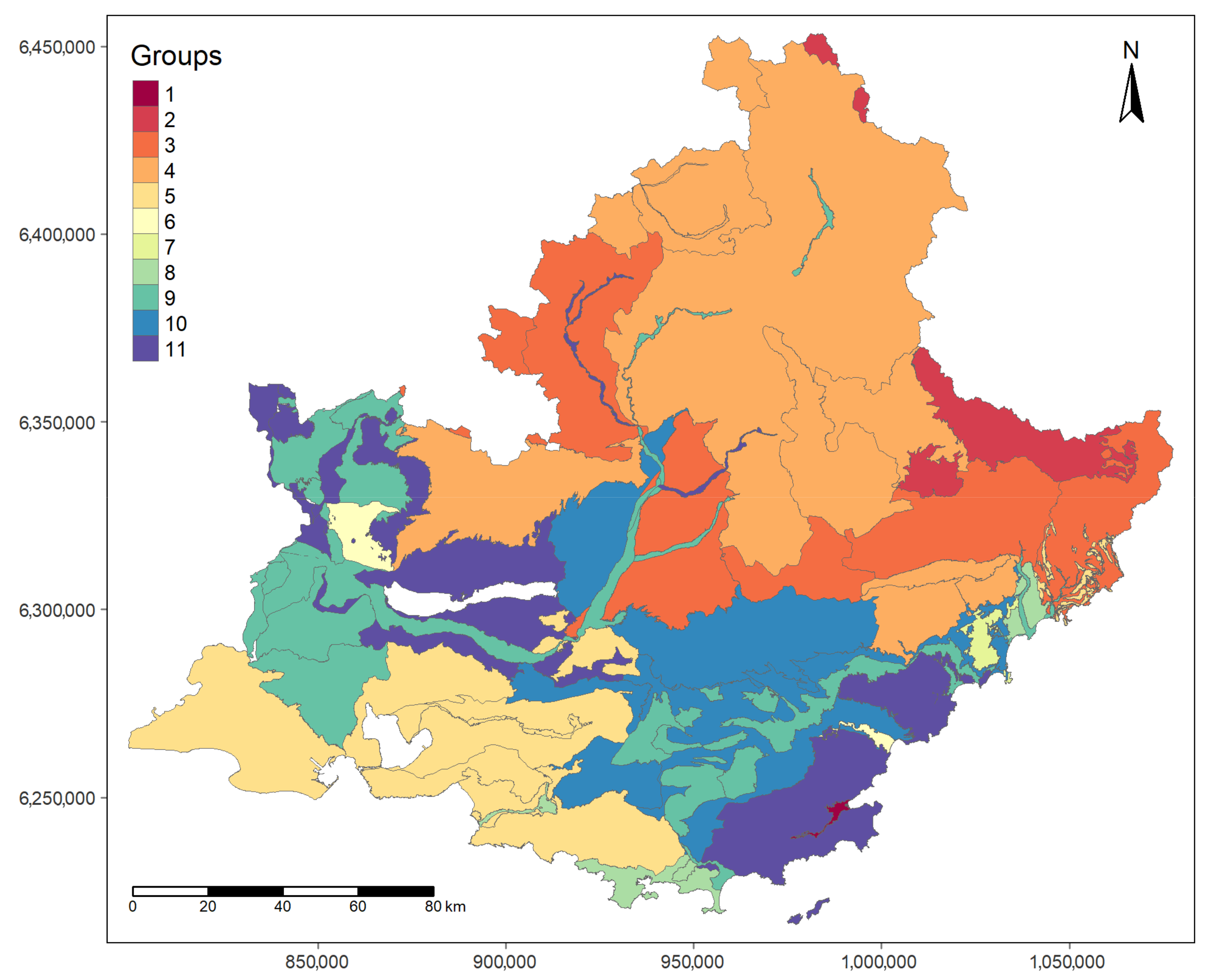
3.3. AHC Results: Grouping Groundwater Bodies Using AHC
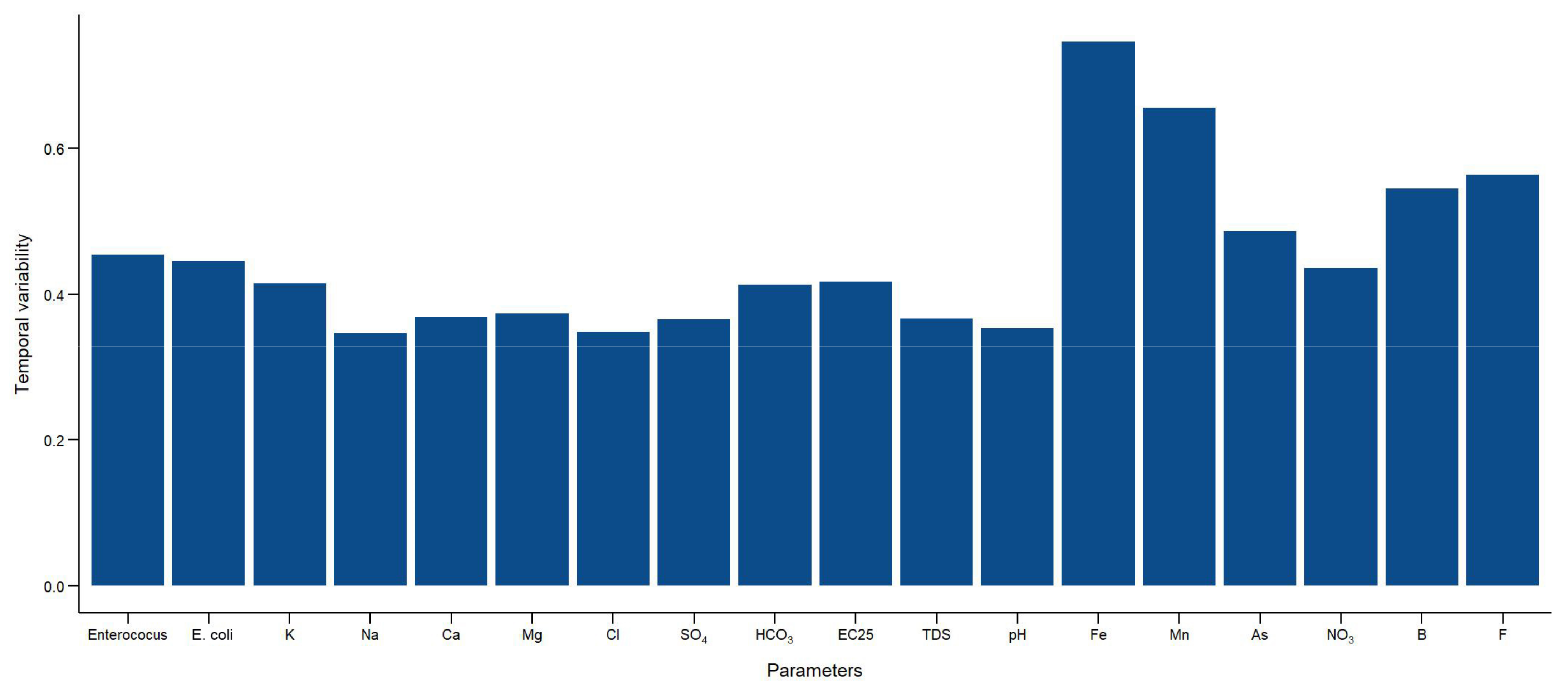
3.4. Spatial and Temporal Variability
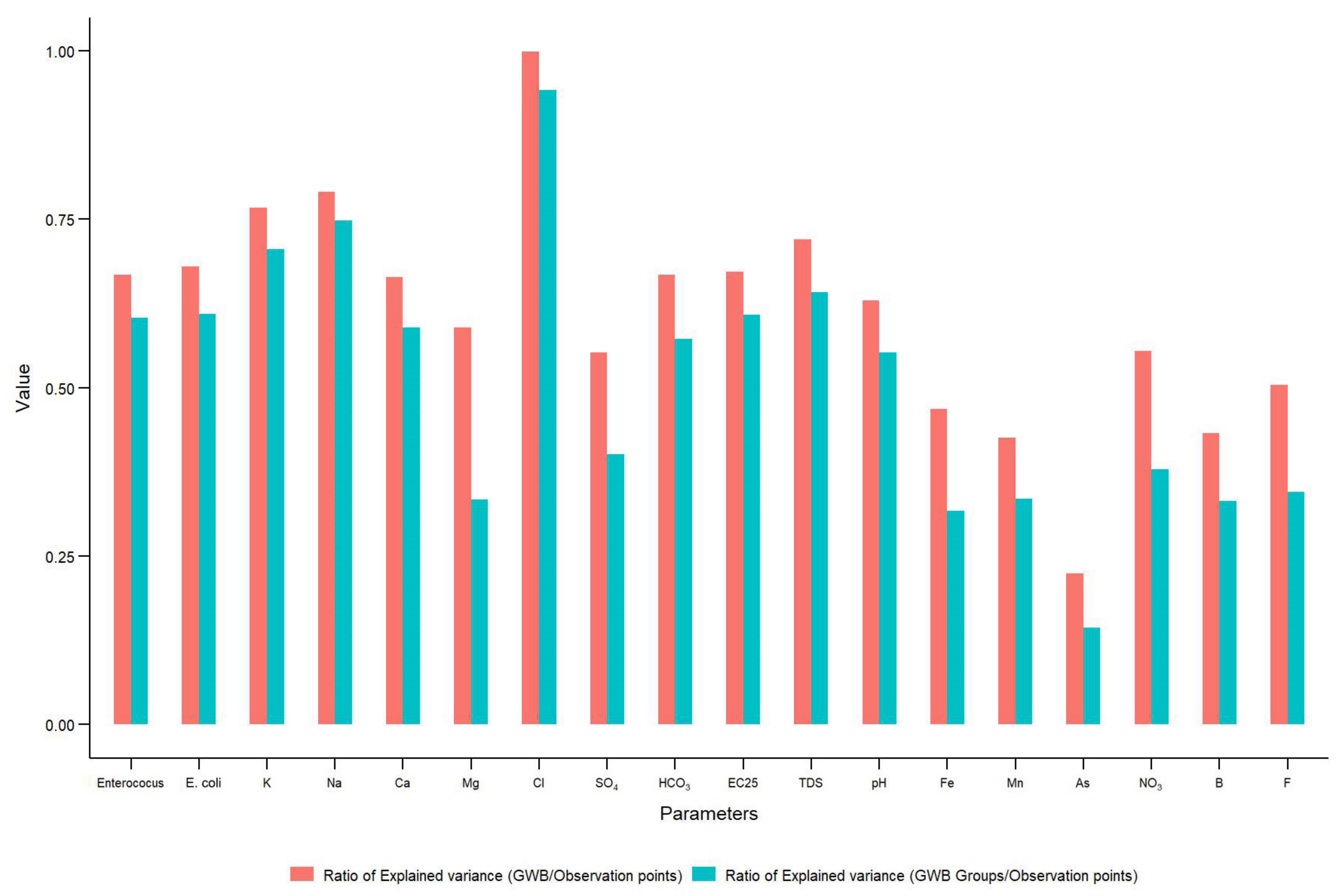
3.5. Determining the Proper Scaling of Groundwater Water Quality
4. Discussion
4.1. Processes of Acquisition of Water Characteristics
4.2. A Relevant and Efficient Grouping of GWBs
4.3. Methodological Contributions
- The log transformation to the data greatly reduces the problem of data non-normality and improves the statistical properties of the dataset, thus enhancing the robustness and reliability of subsequent analyses.
- It also mitigates the effects of outliers without eliminating the information they convey. The integrity of the dataset is thus preserved for analysis.
- The quantification of the loss of information that accompanies the clustering allows the effectiveness of the method to be measured.
- However, the proposed method has certain limitations. In particular, at this stage, the analysis is carried out parameter by parameter, which does not take into account the interrelations between several parameters. A more integrated approach, which could be based on principal components rather than on parameters, could be developed, but it would go beyond the scope of our study. It should be noted, however, that this approach is implicitly supported by the generation of GWB groups, as the classification process takes into account the relationships between different groundwater quality parameters.
- The method applied here is currently being applied in parallel in other French administrative regions and should be the subject of further advances. Whether the groundwater conditions are similar or quite different, there is no reason why the analysis should not be similar to the one conducted here. This method is flexible and applicable to various geological contexts and hydrogeological conditions. The applicability depends on the availability of a statistically significant number of samples per observation point and per GWB. Interpretation will, of course, be guided by the specificities of the region under consideration in terms of geological formations, land use patterns, and possible sources of contamination.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jakeman, A.J.; Barreteau, O.; Hunt, R.J.; Rinaudo, J.-D.; Ross, A.; Arshad, M.; Hamilton, S. Integrated Groundwater Management: An Overview of Concepts and Challenges. In Integrated Groundwater Management; Springer: Berlin/Heidelberg, Germany, 2016; pp. 3–20. [Google Scholar]
- Priyan, K. Issues and Challenges of Groundwater and Surface Water Management in Semi-Arid Regions. In Groundwater Resources Development and Planning in the Semi-Arid Region; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1–17. [Google Scholar]
- Syafiuddin, A.; Boopathy, R.; Hadibarata, T. Challenges and Solutions for Sustainable Groundwater Usage: Pollution Control and Integrated Management. Curr. Pollut. Rep. 2020, 6, 310–327. [Google Scholar] [CrossRef]
- Foster, S. Global Policy Overview of Groundwater in Urban Development—A Tale of 10 Cities! Water 2020, 12, 456. [Google Scholar] [CrossRef]
- Closas, A.; Villholth, K.G. Groundwater Governance: Addressing Core Concepts and Challenges. WIREs Water 2020, 7, e1392. [Google Scholar] [CrossRef]
- Walker, D.B.; Baumgartner, D.J.; Gerba, C.P.; Fitzsimmons, K. Surface Water Pollution. In Environmental and Pollution Science; Elsevier: Amsterdam, The Netherlands, 2019; pp. 261–292. [Google Scholar]
- Li, P.; Karunanidhi, D.; Subramani, T.; Srinivasamoorthy, K. Sources and Consequences of Groundwater Contamination. Arch. Environ. Contam. Toxicol. 2021, 80, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Daly, D. Groundwater—The ’hidden Resource’. In Proceedings of the Biology and Environment: Proceedings of the Royal Irish Academy; Royal Irish Academy: Dublin, Ireland, 2009; Volume 109, pp. 221–236. [Google Scholar]
- Koundouri, P. Current Issues in the Economics of Groundwater Resource Management. J. Econ. Surv. 2004, 18, 703–740. [Google Scholar] [CrossRef]
- Kemper, K.E. Groundwater—From Development to Management. Hydrogeol. J. 2004, 12, 3–5. [Google Scholar] [CrossRef]
- Ortiz-Letechipia, J.; González-Trinidad, J.; Júnez-Ferreira, H.E.; Bautista-Capetillo, C.; Dávila-Hernández, S. Evaluation of Groundwater Quality for Human Consumption and Irrigation in Relation to Arsenic Concentration in Flow Systems in a Semi-Arid Mexican Region. Int. J. Environ. Res. Public Health 2021, 18, 8045. [Google Scholar] [CrossRef] [PubMed]
- Chave, P. The EU Water Framework Directive; IWA Publishing: London, UK, 2001; ISBN 1900222124. [Google Scholar]
- Kallis, G.; Butler, D. The EU Water Framework Directive: Measures and Implications. Water Policy 2001, 3, 125–142. [Google Scholar] [CrossRef]
- European Commission. Directive 2014/80/EU Amending Annex II to Directive 2006/ 118/EC of the European Parliament and of the Council on the Protection of Groundwater Against Pollution and Deterioration. Off. J. Eur. Union 2014, L182, 52–55. [Google Scholar]
- European Commission. Directive 2006/118/EC of the European Parliament and of the Council of 12 December 2006 on the Protection of Groundwater against Pollution and Deterioration. Off. J. Eur. Union 2006, 19–31. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=celex%3A32006L0118 (accessed on 21 January 2023).
- European Commission. Directive 2000/60/EC of the European Parliament and of the Council of 23 October 2000 Establishing a Framework for Community Action in the Field of Water Policy. Off. J. Eur. Communities 2000, L327, 1–72. [Google Scholar]
- Brugeron, A. Cartographie et Systèmes d’Information Géographique Pour La Gestion Des Ressources En Eau Souterraine; HAL: Paris, France, 2012. [Google Scholar]
- Pouey, J.; Galey, C.; Chesneau, J.; Jones, G.; Franques, N.; Beaudeau, P. EpiGEH, groupe des référents régionaux; Mouly, D. Implementation of a National Waterborne Disease Outbreak Surveillance System: Overview and Preliminary Results, France, 2010 to 2019. Eurosurveillance 2021, 26, 2001466. [Google Scholar] [CrossRef] [PubMed]
- Beaudeau, P.; Pascal, M.; Mouly, D.; Galey, C.; Thomas, O. Health Risks Associated with Drinking Water in a Context of Climate Change in France: A Review of Surveillance Requirements. J. Water Clim. Chang. 2011, 2, 230–246. [Google Scholar] [CrossRef]
- Tiouiouine, A.; Jabrane, M.; Kacimi, I.; Morarech, M.; Bouramtane, T.; Bahaj, T.; Yameogo, S.; Rezende-Filho, A.T.; Dassonville, F.; Moulin, M.; et al. Determining the Relevant Scale to Analyze the Quality of Regional Groundwater Resources While Combining Groundwater Bodies, Physicochemical and Biological Databases in Southeastern France. Water 2020, 12, 3476. [Google Scholar] [CrossRef]
- Jabrane, M.; Touiouine, A.; Bouabdli, A.; Chakiri, S.; Mohsine, I.; Valles, V.; Barbiero, L. Data Conditioning Modes for the Study of Groundwater Resource Quality Using a Large Physico-Chemical and Bacteriological Database, Occitanie Region, France. Water 2023, 15, 84. [Google Scholar] [CrossRef]
- Tiouiouine, A.; Yameogo, S.; Valles, V.; Barbiero, L.; Dassonville, F.; Moulin, M.; Bouramtane, T.; Bahaj, T.; Morarech, M.; Kacimi, I. Dimension Reduction and Analysis of a 10-Year Physicochemical and Biological Water Database Applied to Water Resources Intended for Human Consumption in the Provence-Alpes-Cote d’azur Region, France. Water 2020, 12, 525. [Google Scholar] [CrossRef]
- Ozer, D.J. Correlation and the Coefficient of Determination. Psychol. Bull. 1985, 97, 307. [Google Scholar] [CrossRef]
- St, L.; Wold, S. Analysis of Variance (ANOVA). Chemom. Intell. Lab. Syst. 1989, 6, 259–272. [Google Scholar]
- Psomas, A.; Bariamis, G.; Roy, S.; Rouillard, J.; Stein, U. Comparative Study on Quantitative and Chemical Status of Groundwater Bodies: Study of the Impacts of Pressures on Groundwater in Europe, Service Contract, 315/B2020/EEA.58185; EEA: Copenhagen, Denmark, 2021. [Google Scholar]
- Maréchal, J.-C.; Rouillard, J. Groundwater in France: Resources, Use and Management Issues. In Sustainable Groundwater Management: A Comparative Analysis of French and Australian Policies and Implications to Other Countries; Springer: Berlin/Heidelberg, Germany, 2020; pp. 17–45. [Google Scholar]
- Masses d’eau Souterraines-Métropole-Version État Des Lieux 2019. Available online: https://geo.data.gouv.fr/fr/datasets/1a983edfe5ea441fef359a652e98217c9c3ce3c6 (accessed on 20 March 2021).
- Ringnér, M. What Is Principal Component Analysis? Nat. Biotechnol. 2008, 26, 303–304. [Google Scholar] [CrossRef]
- Madhulatha, T.S. An Overview on Clustering Methods. arXiv 2012, arXiv:1205.1117. [Google Scholar] [CrossRef]
- Cousineau, D.; Chartier, S. Outliers Detection and Treatment: A Review. Int. J. Psychol. Res. 2010, 3, 58–67. [Google Scholar] [CrossRef]
- Pearson, K. On Lines and Planes of Closest Fit to Systems of Points in Space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Helena, B.; Pardo, R.; Vega, M.; Barrado, E.; Fernandez, J.M.; Fernandez, L. Temporal Evolution of Groundwater Composition in an Alluvial Aquifer (Pisuerga River, Spain) by Principal Component Analysis. Water Res. 2000, 34, 807–816. [Google Scholar] [CrossRef]
- Rezende-Filho, A.T.; Valles, V.; Furian, S.; Oliveira, C.M.S.C.; Ouardi, J.; Barbiero, L. Impacts of Lithological and Anthropogenic Factors Affecting Water Chemistry in the Upper Paraguay River Basin. J. Environ. Qual. 2015, 44, 1832–1842. [Google Scholar] [CrossRef] [PubMed]
- Day, W.H.E.; Edelsbrunner, H. Efficient Algorithms for Agglomerative Hierarchical Clustering Methods. J. Classif. 1984, 1, 7–24. [Google Scholar] [CrossRef]
- Bouguettaya, A.; Yu, Q.; Liu, X.; Zhou, X.; Song, A. Efficient Agglomerative Hierarchical Clustering. Expert Syst. Appl. 2015, 42, 2785–2797. [Google Scholar] [CrossRef]
- Owamah, H.I. A Comprehensive Assessment of Groundwater Quality for Drinking Purpose in a Nigerian Rural Niger Delta Community. Groundw. Sustain. Dev. 2020, 10, 100286. [Google Scholar] [CrossRef]
- Miles, J. R-Squared, Adjusted R-Squared. In Encyclopedia of Statistics in Behavioral Science; R Foundation for Statistical Computing: Vienna, Austria, 2005; ISBN 9780470013199. [Google Scholar]
- Achen, C.H. What Does “Explained Variance“ Explain?: Reply. Political Anal. 1990, 2, 173–184. [Google Scholar] [CrossRef]
- Cressie, N. The Origins of Kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Barbel-Périneau, A.; Barbiero, L.; Danquigny, C.; Emblanch, C.; Mazzilli, N.; Babic, M.; Simler, R.; Valles, V. Karst Flow Processes Explored through Analysis of Long-Term Unsaturated-Zone Discharge Hydrochemistry: A 10-Year Study in Rustrel, France. Hydrogeol. J. 2019, 27, 1711–1723. [Google Scholar] [CrossRef]
- Rezende Filho, A.T.; Furian, S.; Victoria, R.L.; Mascré, C.; Valles, V.; Barbiero, L. Hydrochemical Variability at the Upper Paraguay Basin and Pantanal Wetland. Hydrol. Earth Syst. Sci. 2012, 16, 2723–2737. [Google Scholar] [CrossRef]
- Batiot, C.; Emblanch, C.; Blavoux, B. Total Organic Carbon (TOC) and Magnesium (Mg2+): Two Complementary Tracers of Residence Time in Karstic Systems. Comptes Rendus Geosci. 2003, 335, 205–214. [Google Scholar] [CrossRef]
- Moral, F.; Cruz-Sanjulián, J.J.; Olías, M. Geochemical Evolution of Groundwater in the Carbonate Aquifers of Sierra de Segura (Betic Cordillera, Southern Spain). J. Hydrol. 2008, 360, 281–296. [Google Scholar] [CrossRef]


| F1 | F2 | F3 | F4 | F5 | |
|---|---|---|---|---|---|
| Enterococcus | 0.035 | 0.800 | −0.299 | −0.241 | 0.208 |
| E. coli | 0.052 | 0.799 | −0.283 | −0.244 | 0.219 |
| K | 0.727 | 0.336 | 0.230 | 0.002 | −0.267 |
| Na | 0.721 | 0.392 | 0.202 | 0.019 | −0.305 |
| Ca | 0.829 | −0.283 | −0.299 | −0.002 | 0.094 |
| Mg | 0.723 | −0.015 | −0.061 | 0.116 | 0.051 |
| Cl | 0.751 | 0.344 | 0.161 | −0.006 | −0.292 |
| SO4 | 0.729 | 0.238 | 0.144 | 0.042 | −0.067 |
| HCO3 | 0.676 | −0.420 | −0.402 | 0.011 | 0.128 |
| EC25 | 0.779 | −0.129 | −0.215 | 0.066 | −0.012 |
| TDS | 0.912 | −0.226 | −0.249 | 0.045 | 0.060 |
| pH | −0.378 | 0.531 | −0.189 | −0.224 | −0.151 |
| Fe | 0.070 | 0.423 | −0.109 | 0.663 | −0.167 |
| Mn | 0.117 | 0.380 | −0.017 | 0.541 | 0.524 |
| As | −0.199 | 0.074 | 0.619 | 0.229 | 0.219 |
| NO3 | 0.531 | −0.200 | 0.245 | −0.185 | 0.079 |
| B | 0.554 | 0.048 | 0.285 | −0.196 | 0.254 |
| F | 0.522 | 0.055 | 0.415 | −0.277 | 0.325 |
| Parameter | Nugget | Spherical Semi-Variance | Lag | % Nugget Effect | ANOVA R2 |
|---|---|---|---|---|---|
| Enterococcus | 0.28 | 0.12 | 4000 | 70.0 | 0.546 |
| E. coli | 0.3 | 0.22 | 3000 | 57.7 | 0.555 |
| EC25 | 0.007 | 0.042 | 62,000 | 14.3 | 0.654 |
| Na | 0.08 | 0.36 | 150,000 | 18.2 | 0.583 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohsine, I.; Kacimi, I.; Abraham, S.; Valles, V.; Barbiero, L.; Dassonville, F.; Bahaj, T.; Kassou, N.; Touiouine, A.; Jabrane, M.; et al. Exploring Multiscale Variability in Groundwater Quality: A Comparative Analysis of Spatial and Temporal Patterns via Clustering. Water 2023, 15, 1603. https://doi.org/10.3390/w15081603
Mohsine I, Kacimi I, Abraham S, Valles V, Barbiero L, Dassonville F, Bahaj T, Kassou N, Touiouine A, Jabrane M, et al. Exploring Multiscale Variability in Groundwater Quality: A Comparative Analysis of Spatial and Temporal Patterns via Clustering. Water. 2023; 15(8):1603. https://doi.org/10.3390/w15081603
Chicago/Turabian StyleMohsine, Ismail, Ilias Kacimi, Shiny Abraham, Vincent Valles, Laurent Barbiero, Fabrice Dassonville, Tarik Bahaj, Nadia Kassou, Abdessamad Touiouine, Meryem Jabrane, and et al. 2023. "Exploring Multiscale Variability in Groundwater Quality: A Comparative Analysis of Spatial and Temporal Patterns via Clustering" Water 15, no. 8: 1603. https://doi.org/10.3390/w15081603






