1. Introduction
Water resource availability is directly connected to the sustainability and development of human society and ecosystems [
1,
2,
3]. Due to limited water supplies and pressure from increasing water consumption, water resources are becoming scarcer, especially in arid and semi-arid environments [
4,
5,
6,
7,
8,
9]. As a result, hydrological patterns, particularly in these climatic zones, are likely to be affected. Therefore, these regions are likely to face the greatest pressure in freshwater supply and management [
10,
11,
12,
13]. In addition, there is an urgent need to characterize the rapid response of runoff to extreme precipitation events that are becoming more frequent in arid and semi-arid and Mediterranean regions [
14,
15], as they often generate extremely damaging flash floods and inundations [
16,
17,
18]. Since accurate simulations of flow are possible in arid and semi-arid regions, effective water resource management and flood warning require accurate and precise simulations of streamflow [
19,
20,
21,
22,
23,
24,
25].
Hydrological modeling in semi-arid areas is strongly influenced by alternating seasons [
26,
27]. These studies have shown that the flow regime of rivers in these contexts is largely influenced by a highly variable distribution of precipitation during the seasons; i.e., maximum flows are generally observed in winter, autumn, and sometimes spring, while low-flow periods are most often marked during the dry period of the year, namely“summer”. During the last decades, hydrological modeling has undergone a long process of improvement through the development of advanced models that differ in terms of temporal classification of space and processes and integrate the complexity of the system in hydrological simulations. In addition, modeling has become one of the main tools for water resources management since extreme events (floods and droughts) are more devastating and threaten the population worldwide [
28,
29,
30,
31,
32]. It is noteworthy that the improvement of the performance of flow simulations in semi-arid regions is necessary, and this can only be done through the implementation of models more suitable for these areas, especially the discrete, semi-distributed, and global conceptual models that are most used in hydrological studies due to their adaptability to different climatic contexts [
33,
34,
35]. This applicability usually differs from one climate to another, and even within the same climate, one can sometimes have very different results from one period to another [
36,
37,
38,
39,
40,
41,
42,
43,
44,
45]. Conceptual hydrological models offer several advantages in terms of applicability, especially in developing country basins that are characterized by data scarcity [
46,
47,
48]. Among their advantages are the reduced number of data inputs and consequently a reduced number of calibrated parameters of hydrological models. This is known to be effective for avoiding overparameterization risk and reducing the model uncertainty issue [
49]. Based on these advantages, the applicability of these conceptual models to a wide range of watersheds around the world can be easily justified.
In this study, a comparative hydrological modeling approach was adopted through the use of two models with different levels of sophistication: the distributed model (ATHYS) [
50] and the lumped model (GR4J) developed by CEMAGREF [
51]. The ATHYS model was based on a variety of production and transfer methods. The runoff from each grid cell was computed using a reservoir model, and the runoff volume was routed to the outlet using a lag and route routing method to obtain the hydrograph and volume of the discharge. The main advantage of the GR4J model is that it does not require a comprehensive description of the watershed and its continuous functioning, ensuring throughout the year a complete accounting of the water entering and leaving the basin and monitoring the overall humidity level [
52]. The input data are precipitation and evapotranspiration, which are simple measurements with few parameters to be adjusted.
The region of Souss-Massa (southwest Morocco), including the Aguenza watershed, which is the subject of this study, presents a great constraint, that could be a limiting factor if not a brake of its development: the problem of floods and inundations. Indeed, this watershed is one of the Moroccan watersheds that contain a large number of sites threatened by floods. The latter sometimes disrupts the economic activities of this basin and causes considerable damage to the basic infrastructures and also to agricultural production, which is the main source for most inhabitants in these regions [
53]. During this study, two modeling approaches were used to understand better the hydrological behavior of the Aguenza watershed. The first approach consists of using daily data to carry out continuous modeling that allows us to better analyze the fast-evolution inflows after the rainstorms. Generally, this approach is considered the most appropriate since it takes into account for each event the previous rainfall (previous 10 days) in determining the parameters. Furthermore, continuous hydrological models are considered the most appropriate for estimating initial conditions [
54,
55]. In this sense, the continuous approach has some disadvantages concerning the data series used; i.e., it needs to provide long precipitation time series and, in some cases, other data such as evapotranspiration, temperature, relative soil moisture, etc. [
56]. The continuous mode simulation uses two conceptual rainfall-runoff models that differ in terms of spatialization to test their influence on the quality of results. The second phase of this study consisted of using the most important historical flood events that occurred in the Aguenza watershed either in autumn or winter between 1984 and 2014 in order to elaborate an event-based modeling (time step = 60 min). Indeed, ten of the most intense rainfall-runoff events (maximum rainfall intensity reaching in the studied basin a value of 13.20 mm·h
−1) were used to study and simulate the hydrological behavior of the Aguenza watershed, in particular the flood-generation process.
The main objectives of the present study are the following: (1) comparing distributed and lumped models to evaluate the utility of using a spatially distributed modeling approach for correctly reproducing the Aguenza streamflow continuously at daily time steps and (2) using the event-based mode to characterize the flood-generation process by simulating historical rainfall-runoff events. Our findings are expected to provide water managers with valuable information for better water resource management and subsequently for establishing preventive measures.
2. Materials and Methods
2.1. Study Area
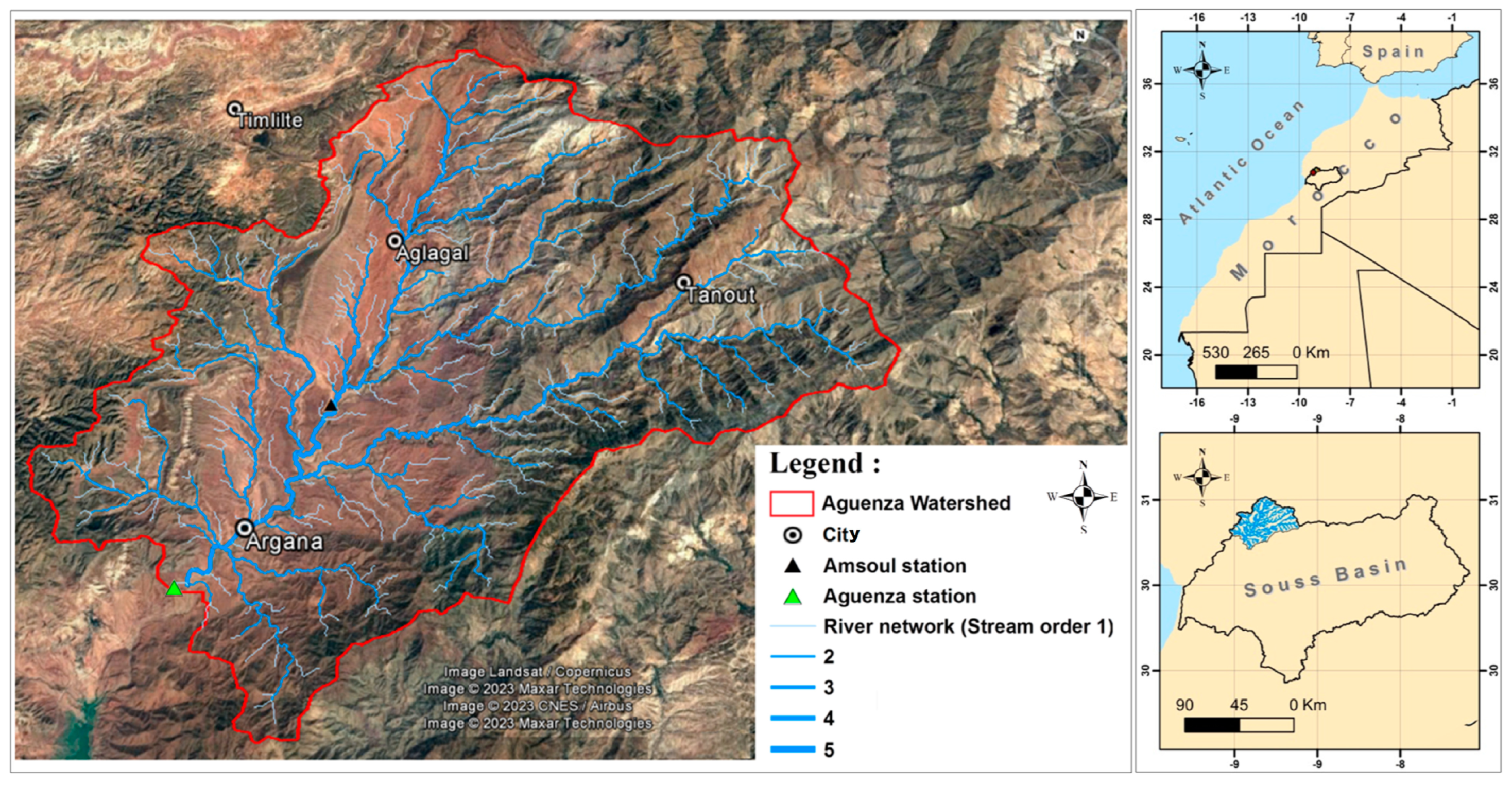
The general context of the study is part of a comprehensive framework that includes the full extent of the land affected by the flood problem, namely the Souss Plain that is part of the large Souss-Massa Basin. The origin of floods comes from the various tributaries of the Souss Basin, which have violent and irregular floods. Therefore, it is the Souss Basin and more precisely the station of the Aguenza watershed that is the subject of this study. The Aguenza watershed covers an area of 1162 km
2 (
Figure 1). The Anti-Atlas Mountains from the southern part and the High-Atlas Mountains, which constitute the eastern and northern parts of the watershed, delimit it. In terms of climate, the river is dominated by arid to semi-arid climates, with the heaviest precipitation falling on the upper Atlas outcrops [
57]. The mean annual precipitation varies from 280 mm in the Anti-Atlas downstream part to 600 mm, which is observed in the High Atlas Mountains upstream part.
2.2. Data Processing
2.2.1. Geographic Data
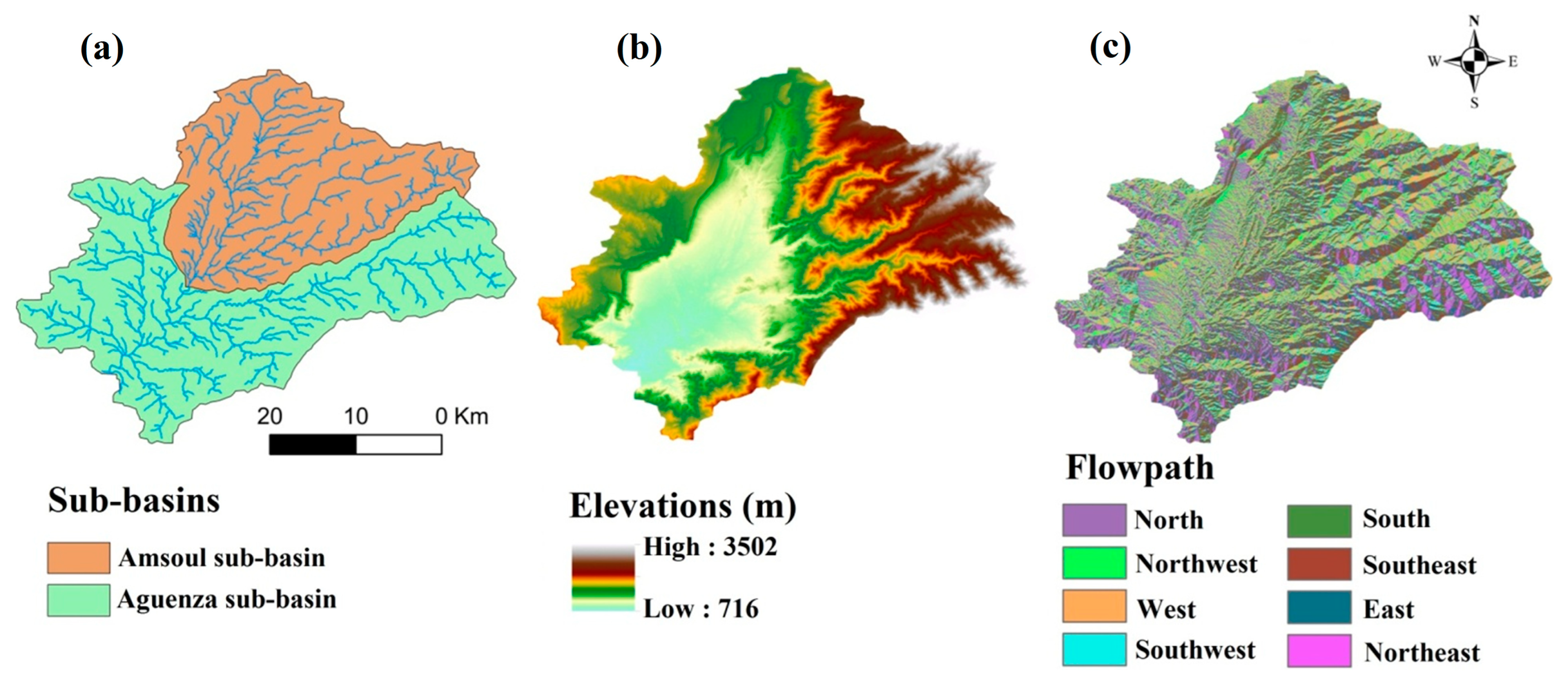
The digital elevation model (DEM) is a set of altimetric points (three coordinates: x, y, and z). The assembly of these points makes it possible to reconstitute the topography of the site; note that, in this study, a DEM with a high resolution of 12.5 m was used. The software then processes these data to obtain the hydrographic network, the sub-watersheds, the drainage directions, etc. (
Figure 2). In addition, to have correct results, it is necessary to make some corrections, especially for the drainage files (depression and loop correction).
2.2.2. Meteorological Data
In this study, daily precipitation, temperature, and evapotranspiration (from 1 January 1982 to 31 December 2011) were obtained for two meteorological stations (Aguenza and Amsoul), and flow data series were obtained for one flow gauge (Aguenza: from 1 January 2000 to 31 December 2011). It is also important to note that the hydro-meteorological data were obtained on an hourly time step to perform an event study focusing on the ten most significant flood events that occurred in the Aguenza watershed between the years 1984 and 2014.
The Aguenza watershed is characterized by a rainy season and a hot and dry summer with an average of 271.34 mm/year (1982–2011). Two seasons can be distinguished: the rainy season (October to April) with irregular rainfall and the dry season (May to September) where precipitation is relatively low (
Figure 3). The temperature regime is characterized by strong annual amplitudes that accentuate the phenomenon of evapotranspiration. The annual evaporation is 2279 mm. Evaporation is highest in July (360 mm) and lowest in December and January (46 mm).
2.3. ATHYS Platform
ATHYS is a rainfall-runoff modeling platform developed by the Research Institute for Development (IRD) in Montpellier, France; it consists of four modules: (i) MERCEDES (Regular Square Elementary Mesh for the Study of Superficial Flows); (ii) VISHYR (Visualization of Hydrological data); (iii) VICAIR (Visualization of Raster Maps and Images); and (iv) SPATIAL: spatial interpolation platform [
58]. MERCEDES is based on the spatial discretization of the basin in regular square meshes, which makes it possible to take into account the spatial variability of the main factors that determine the flows [
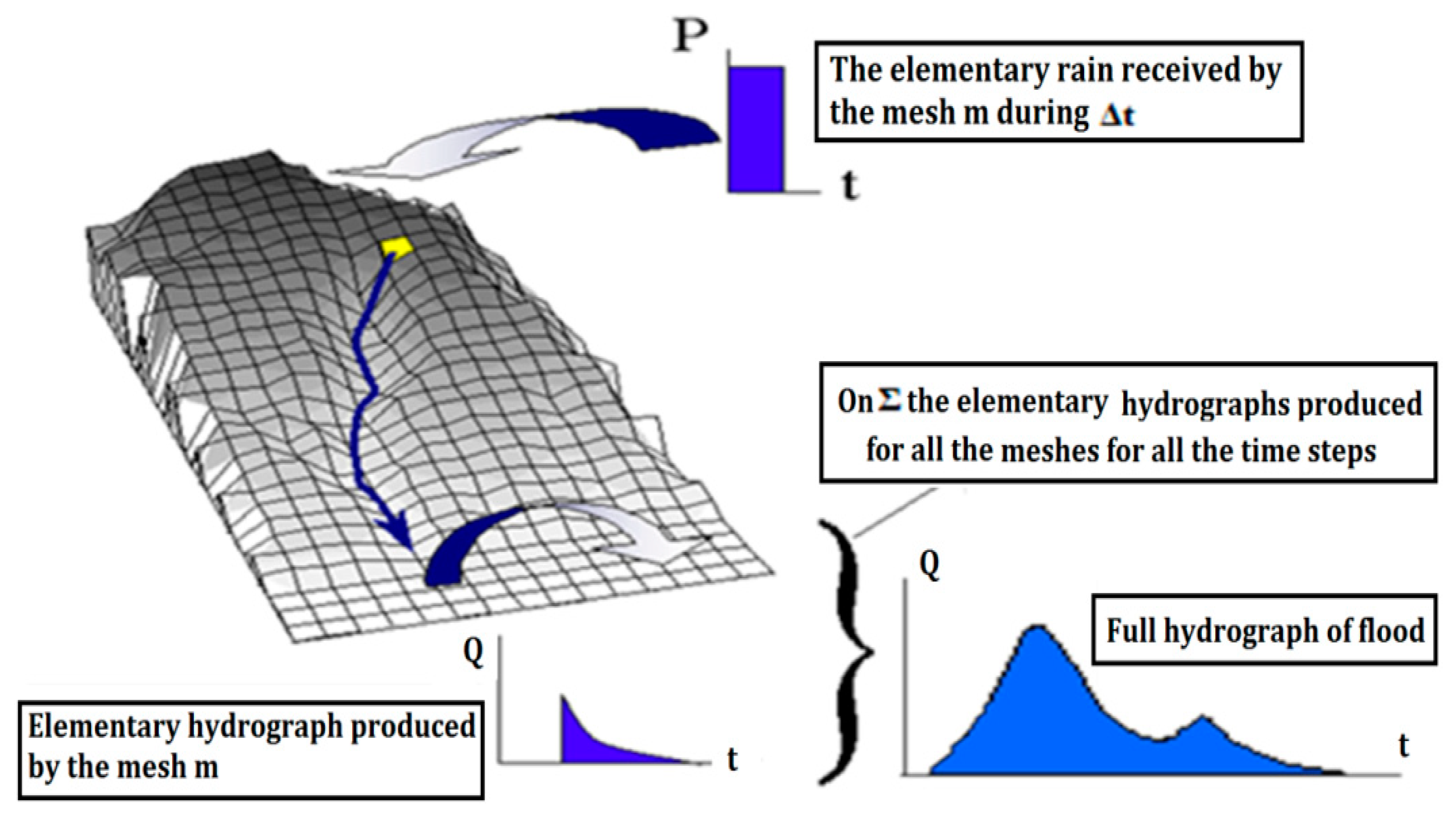
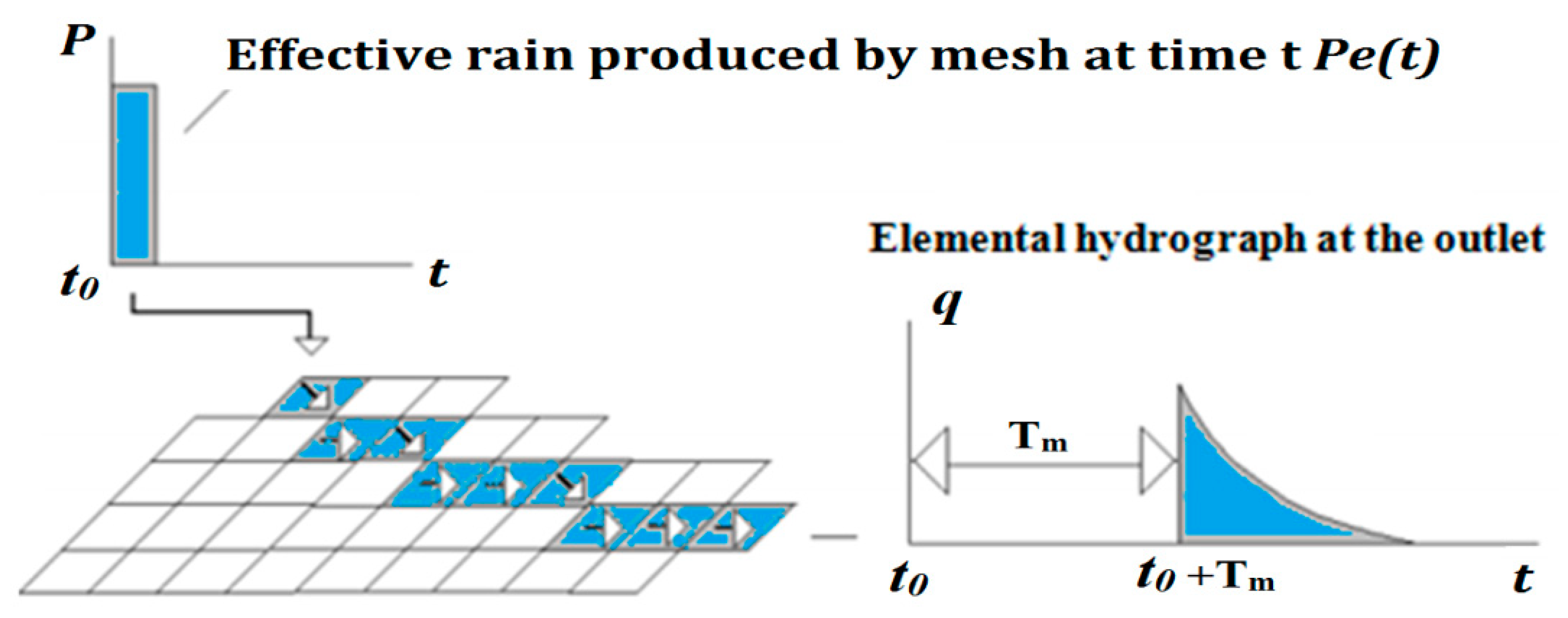
59]; the main interest of this free software is the possibility to spatialized the rainfall–runoff transformation. Indeed, the model uses a DEM as input to calculate the runoff mesh by mesh. This principle is combined with a spatialization of rainfall data, which allows large catchments to account for spatial variation of rainfall intensities. The flow generated for a rainy event (rainfall–runoff transformation) is calculated in three steps (
Figure 4):
For each mesh, the production model is used to estimate the amount of rain that contributes to runoff;
The transfer model calculates the hydrograph produced by each mesh at the outlet of the catchment. This calculation is made from the result obtained by applying the production function;
The inputs of each mesh are summed to obtain the total flow at the outlet.
From the input data (DEM, drainage file, and precipitation), the ATHYS hydrological model allows to definition of the streamflow at the daily and hourly time step in various points of the catchment.
The software offers several production and transfer models. The following choices were made.
2.3.1. Production Function “SCS”
The U.S. Department of Agriculture Soil Conservation Service (USDA-SCS) model [
60] was selected as a production function to estimate the precipitation amounts that contribute to the runoff generation. This function was extensively used in successively applied in a semi-arid environment, including the Moroccan basins [
19,
20,
33,
61,
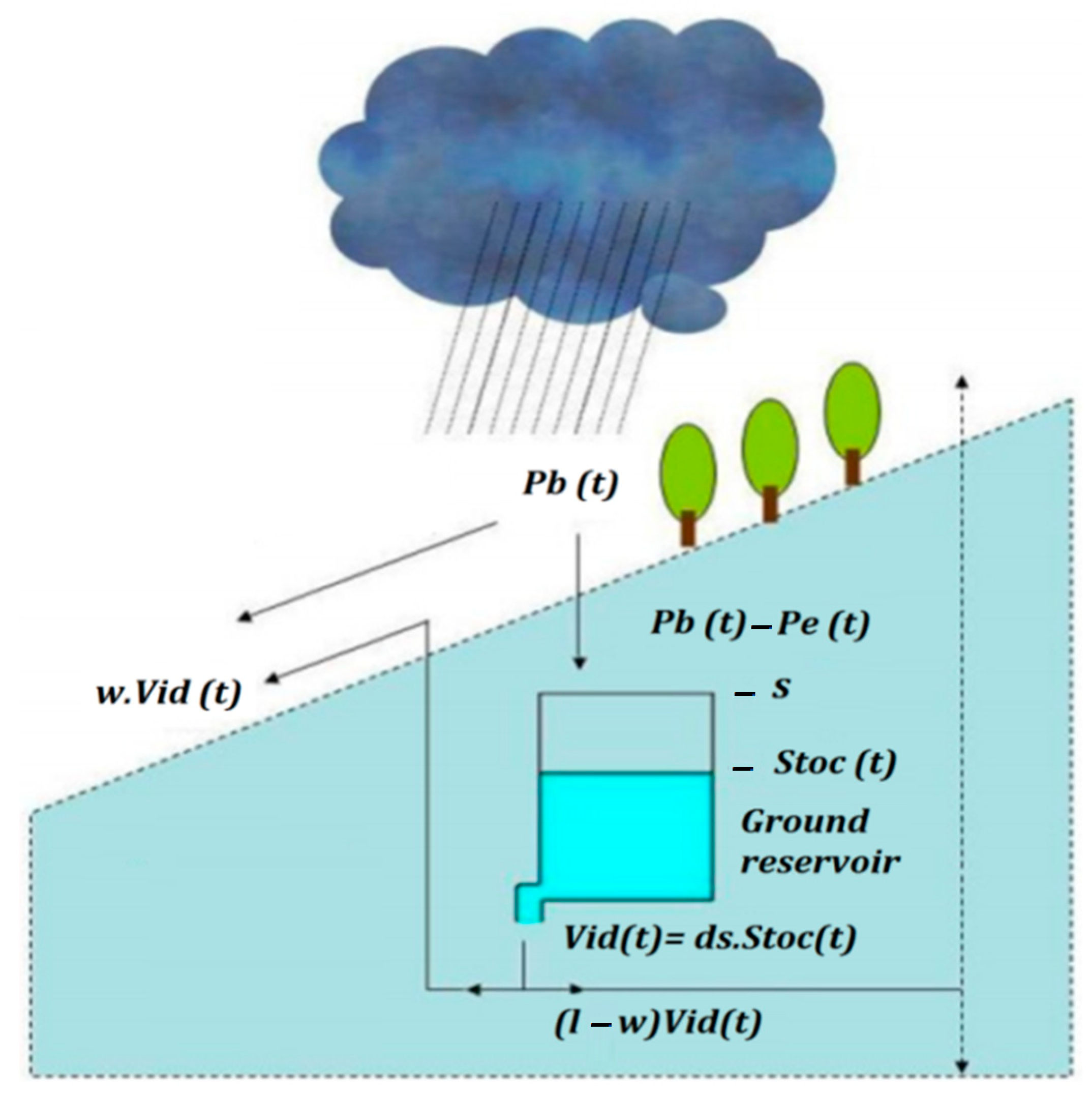
62]. The SCS principle of functioning is illustrated in
Figure 5. For each square mesh of the watershed discretization, a ground tank is associated. The capacity of this soil reservoir defines the initial water deficit of the mesh: this parameter is denoted as S (mm). It is the function of the initial water content in the soil and the maximum storage capacity of local water when the soils are dry, or at least, very little moist. This parameter constitutes the initial condition of the model and is variable from one event to another. The SCS model is particularly sensitive to the capacity of this soil reservoir [
57,
63].
The SCS method is the most commonly used and is capable of fitting different types of flooding processes [
60]. The version used in this study is composed of three parameters:
S (mm) represents the total capacity of the ground tank, and this capacity depends on many characteristics of the soil (depth, heterogeneity, porosity, hydraulic conductivity, a dip of the subsoil, etc.);
ds (d−1) is the proportional emptying at the level of the reservoir by deep percolation, evaporation, sub-surface flow, etc.;
ω (dimensionless) represents the fraction of drainage, which participates in the runoff in the form of exfiltration.
2.3.2. Transfer Function “Lag and Route”
The choice of the lag and route model is explained by the desire to obtain both global modelings in the contribution of different parameters (losses, runoff, etc.) and precision by choosing to know this contribution for each mesh independently of the others (
Figure 6).
Moreover, in this model, all parameters are constant over time. This function consisted of the two following parameters:
V0 (m/s) is the maximum velocity reached at the outlet during the event. This model calculates a transfer time Tm that designates the time elapsed between the rain falling on the mesh m and the start of the passage of the event in the outlet. It is calculated from the position of the mesh and the outlet (length Lm between mesh and outlet), the drainage pattern, and the speed V0;
K0 (dimensionless) is called the damping parameter. It is connected to the damping time Km by the following relationship:
2.4. GR4J Model
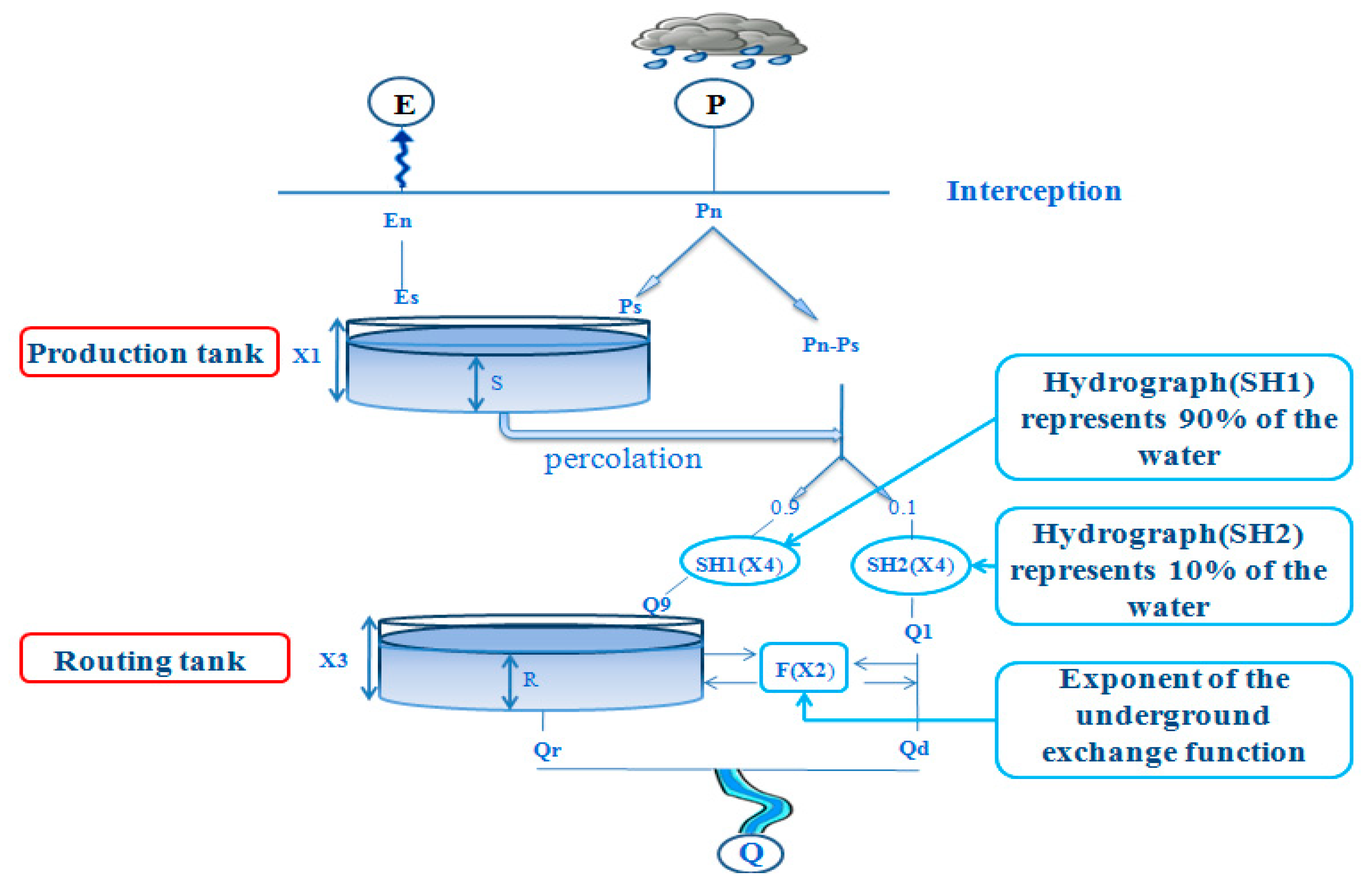
The GR4J model is a four-parameter rainfall–runoff transformation model [
51]. The version used was developed by Perrin in 2002 and improved by Perrin and his team in 2003. The GR4J model is characterized by a structure with two associated tanks (
Figure 7): the first tank is a production tank, and the second is a routing tank; these are linked to unit hydrographs (SH1 and SH2) to obtain finally a simulated flow (expressed in mm) as an output of the model. This model also allows monitoring of the pond’s moisture status to take into account previous conditions and ensure continuous operation [
64].
The GR4J model is a global model with four parameters, and these parameters are as follows:
X1: Maximum capacity of the production tank (in mm);
X2: Coefficient of the underground exchange function (in mm);
X3: Maximum capacity of the routing tank (in mm);
X4: Base time of the unit hydrograph (days);
Input data: Daily precipitation and evapotranspiration (mm/d);
Data produced average daily flow (mm/d).
2.5. Performance Criteria
The performance criteria of a hydrological model can be based on mere visual appreciation or based on statistical calculations known as objective functions to standardize the comparison between the result of the simulation or forecast and observations [
65]. The identification of the parameter values of the hydrological model, depending on the objective function used, quantifies the difference between the observed and simulated variables. The most commonly used objective function in hydrology is the Nash–Sutcliffe criterion (NSE), and closer the latter is to 1, the closer the simulation is to the observation [
66]:
The determination coefficient (R
2) was also used in this study. This criterion varies between 0 and 1 (a value of 1 indicates that the simulation is identical to the observation). The mathematical equation describing this criterion is as follows:
However, the RMSE-observations standard deviation ratio (RSR) is also used to evaluate the performance of the model. The use of this standard deviation (SD) of the observed data allows the normalization of the RMSE criterion. It is frequently used to measure the differences between the values predicted by a model and the observed values [
67,
68,
69]. Its range varies from 0 to infinity, while a value of 0 is a perfect score. It is given as follows:
To evaluate further model simulations in terms of error quantification, another performance criterion was selected to know better the tendency of the model to underestimate or overestimate streamflow. This criterion is the bias error (PBIAS), which varies between −∞ and +∞, with a value of 0 for an unbiased model. Generally, the hydrological model underestimates flows when the value of this criterion is positive, but negative values indicate an overestimation of flows [
70]. The descriptive equation for this criterion is written as follows:
where Q
obs,i; Q
calc,i; and Q
obs,m present the observed and simulated flows over a time step and the average of the observed flows, respectively. These functions compare the model simulation on the n-time step with the mean of the observations taken as a reference model.
4. Discussion
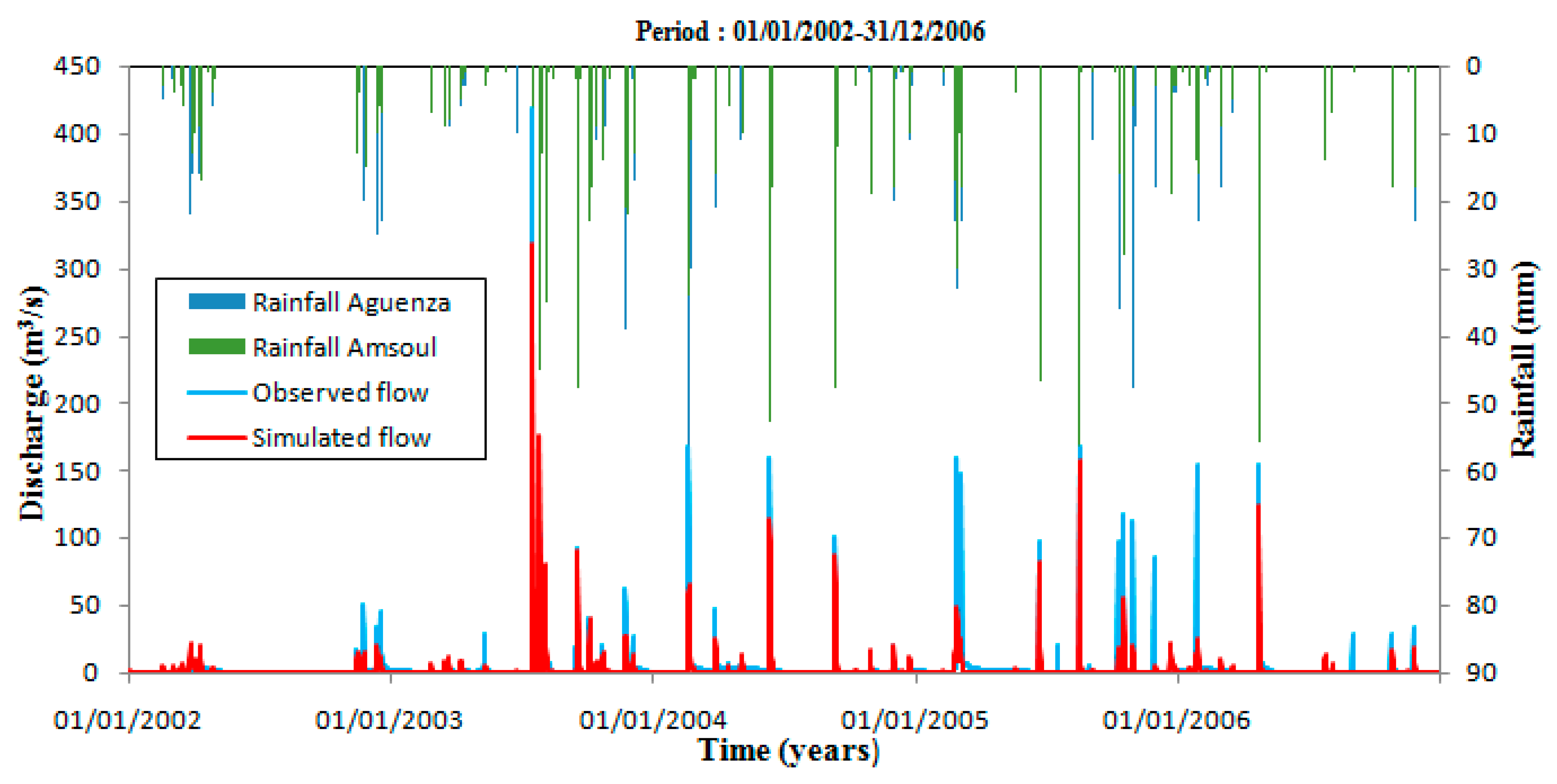
The estimation of streamflow in the data-scarce Aguenza watershed was made using two models with different characteristics: the conceptual and lumped model GR4J, which does not take into consideration the spatial variability of the hydrological processes, and the spatially distributed model ATHYS, which estimates the water level on each mesh by taking into account the spatial organization of various factors influencing streamflow generation.
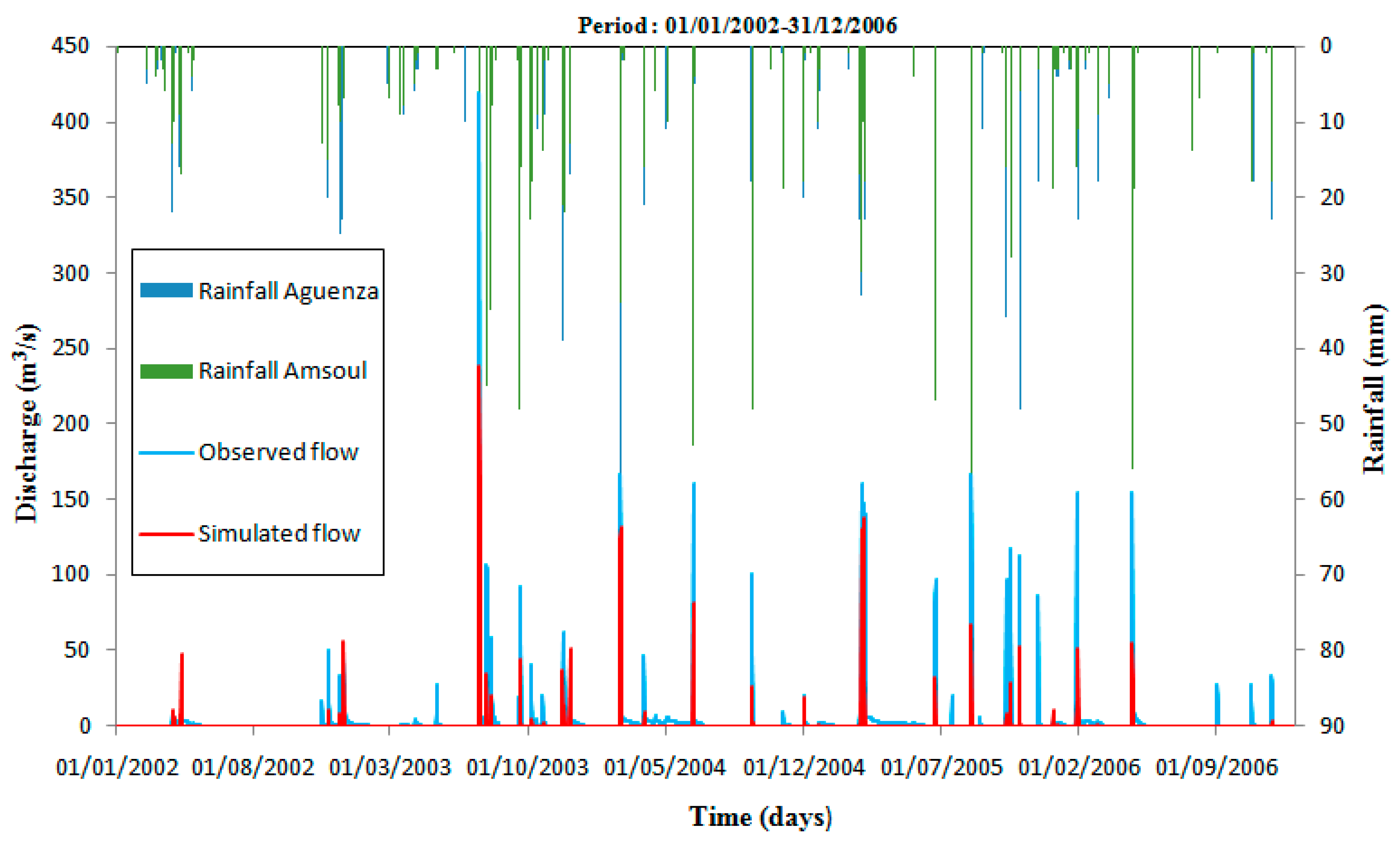
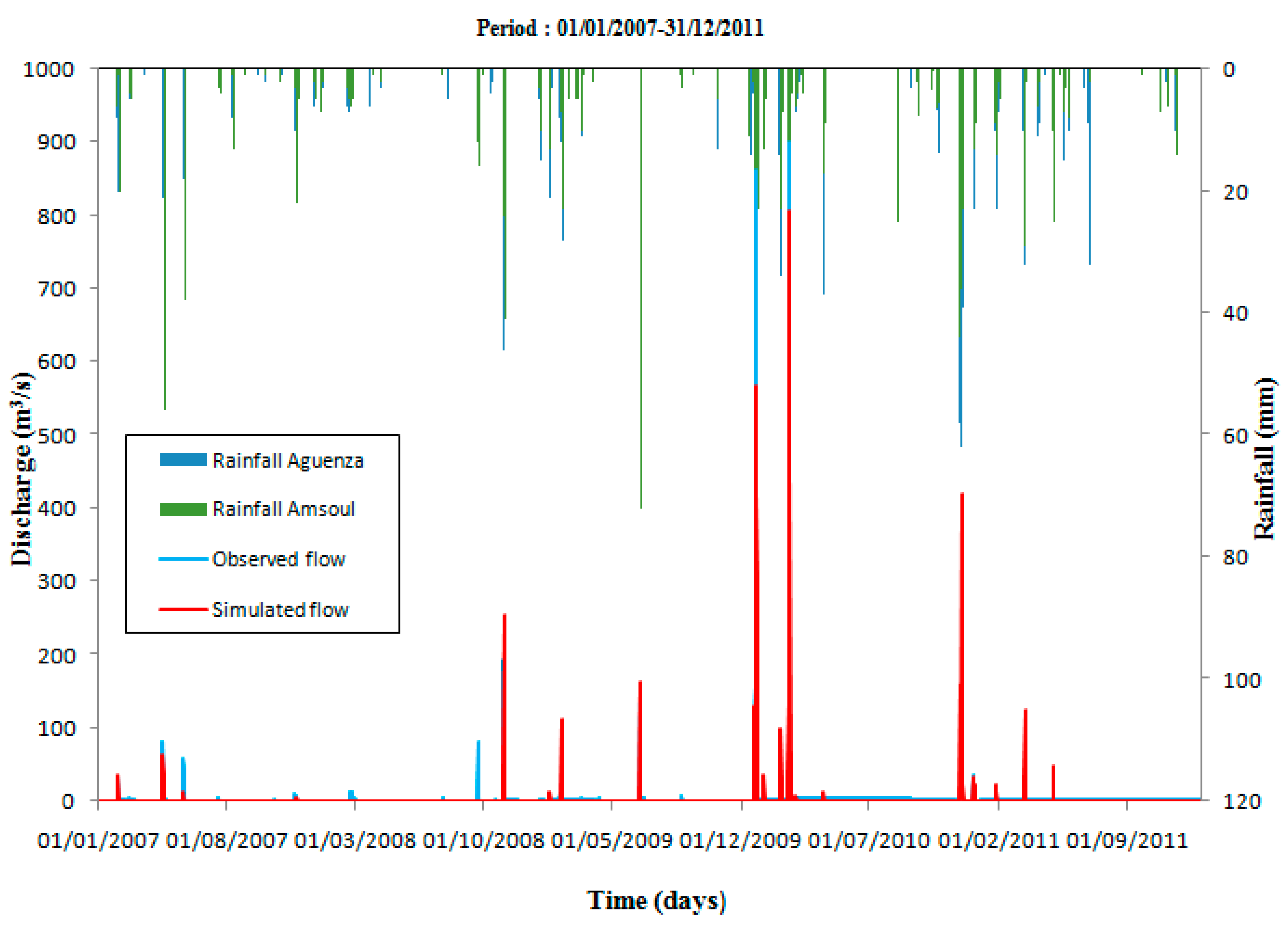
The results obtained after the implementation of the two hydrological models mentioned above in the Aguenza watershed confirm that the inclusion of spatial information improves the modeling results, particularly for the calibration period, where the use of ATHYS led to an improvement of 8%, 6%, and 45.2% in the values of NSE, RSR, and PBIAS, respectively, compared to GR4J. Additionally, during the validation process, the use of the spatially distributed model ATHYS resulted in a remarkable increase in model performance, with NSE values improving by 6% and errors estimated by the RSR and PBIAS criteria minimized by 4% and 8.9%. These findings demonstrate the benefit of using a distributed approach in the estimation of flows in the studied watershed. The validation results obtained using the two models on the Aguenza watershed are satisfactory (NSE > 0.5), indicating that these models are suitable for use in semi-arid areas, specifically in the southwest of Morocco, where the Aguenza watershed is located.
The GR4J model and the coupled SCS-LR model tend to underestimate flows in the studied watershed. In general, the underestimation or overestimation of peak flows is closely related to land use, soil type, and saturation, especially in arid and semi-arid areas [
11,
20,
21,
77,
78,
79,
80]. In these environments, the rainfall–runoff transformation primarily depends on the soil saturation condition where, for example, during the dry period, the first rain events seep through the previous layer and do not transform into surface runoff. It should also be noted that the most recent layer of the geology of the Aguenza watershed is formed mainly by dolomitic limestones and fine sandstones, forming the most erosion-resistant soils [
81], as these types of soils allow better infiltration of surface water and subsequently influence the underestimation of peak flows in karstic basins [
77,
82,
83]; this is confirmed by the very important value of the parameter of a total capacity of the ground reservoir (S = 110 mm); therefore, a great quantity of precipitation is lost by infiltration, causing the underestimation of the peaks of flow during the hydrological modeling of the basins of karstic and rural nature.
Nevertheless, this ATHYS model has a very important advantage because it allows the good reproduction of low flows, which have a very important impact on the hydrological cycle, and it also allows the consideration of the water exchanges between the surface and the underground, which reduces greatly the significant underestimation of the peak flows during hydrological modeling of the karst areas.
Event-based models have several advantages over continuous models and are often preferred for real-time and operational applications [
56]. They require only event-scale data and avoid the use of full-time series, and they consider only event-scale flood processes. In this study, event-based modeling is elaborated to allow the simulation of the rainfall–runoff relationship to simulate the hydrologic behavior of the Aguenza watershed for a specific operating mode. In general, flood events are used without considering the specification of the history of previous conditions.
The results obtained for 70% of the events selected for calibration and validation have a quality between good and very good, which shows the applicability of the coupled model SCS-LR in the Aguenza watershed. It should be noted that the underestimation of point flows in all events is mainly due to the karstic and rural nature of the studied watershed [
81]. Nevertheless, the rise time in the simulated hydrographs is higher than those of the observed hydrographs, which is mainly due to the difficulties encountered in accessing data related to the hydrodynamic properties of the soils; this condition and the simplicity and applicability of the empirical SCS model in semi-arid areas [
20,
84,
85] were among the main conditions for the implementation of the SCS model that does not take into consideration the state of soil moisture before each rainfall event and subsequent influences on the simulation of the rise times.
Finally, it is important to note the importance of this study regarding knowing the evolution of floods and the resulting volumes after a rain event for better management of water resources in areas with a semi-arid climate that is characterized by a non-linear relationship between the volumes of water runoff and rainfall [
85]. The reservoirs of these areas strongly influence the amount of water runoff, especially after a long period of absence or low precipitation in semi-arid basins of karst nature such as the Aguenza Basin which is the subject of this study, and all these factors generally make the simulation of flows more and more complicated in watersheds with arid and semi-arid climates [
86,
87,
88,
89].
5. Conclusions
This work focused on rainfall-flow modeling using two different models: one the global “GR4J” and the other the discretized “ATHYS”. The first phase aimed to study the influence of the spatialization of the watersheds on the modeling results through the use of two hydrological models with different characteristics, and the second phase consisted of using the ATHYS model to simulate the flows by applying the event-based approach and to study the main floods that occurred between 1984 and 2014 in the Aguenza watershed.
The obtained results from the comparative study of lumped and distributed models show the importance of taking into account the hydrological processes since, after the use of the discretized model “ATHYS”, remarkable improvements were observed in the general aspect of the resulting hydrographs. This improvement was also confirmed based on the performance criteria; as an example, the value of NSE during the calibration process increased successively by 8%, and the errors were minimized by 45.2% according to the PBIAS criterion when applying the SCS-LR model instead of the GR4J model. In this context, it is necessary to understand the importance of taking into account the hydrological processes during the modeling to obtain realistic results close to the reality of the watersheds. The validation results of the two hydrological models are satisfactory (average of NSE = 0.55), which confirms their applicability in the semi-arid context.
In this study, an event-mode model was also developed to allow the simulation of the rainfall–runoff relationship to simulate the hydrological behavior of the Aguenza watershed for a specific operating mode. In general, flood events are used without considering the specification of the history of previous conditions. The results obtained by applying the ATHYS model in event mode are interesting and give appreciable results, namely that the values of the NSE criterion obtained for the calibration procedure vary between 0.60 and 0.83 as the maximum value. During the validation procedure, although the observed contrast in the quality of the results is remarkable, the average value of the NSE (average NSE = 0.60) shows that the validation was well done, and this confirms the first results obtained by the ATHYS and GR4J models in continuous mode.
By comparing and analyzing the results and simulations, decision-makers can understand the hydrological behavior in the considered watershed to better specify the limits of this study, to allow an evaluation of the availability and/or access to data to find much more relevant simulation results in the future, and also to increase the relevance and applicability of other hydrological models with different characteristics.