Sustainability Analysis of the Water Environment Carrying Capacity of Harbin City Based on an Optimized Set Pair Analysis Posture-Deviation Coefficient Method Evaluation Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.3. Methods
2.3.1. Relationship between System Methods
2.3.2. Calculating Optimization Index Weights
2.3.3. Calculating Evaluation Linkage
2.3.4. Calculating Set-to-Potential Eigenvalues
2.3.5. Determination of Rank by the Partial Coefficient Method
2.3.6. Comparative Test of Applicability by the Confidence Criterion Judging Method
3. Results and Discussion
3.1. Load Factor Values and Evaluation Index Weights
3.2. Eigenvalue and Evaluation Result Level
3.3. Support and Judgment Level
3.4. Confidence Method for the Comparison Test Optimization Model
3.5. Sustainability Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Duan, C.; Liu, C.; Chen, X.; Liu, W.; Zheng, H. Discussion on the Concept and Research Methods of Regional Water Resources Carrying Capacity. Acta Geogr. Sin. 2010, 65, 82–90. [Google Scholar]
- Wang, S.; Zou, L.X.; Li, H.B.; Zheng, K.K.; Wang, Y.; Zheng, G.C.; Li, J. Full-scale membrane bioreactor process WWTPs in East Taihu basin: Wastewater characteristics, energy consumption and sustainability. Sci. Total Environ. 2020, 723, 137983. [Google Scholar] [CrossRef]
- Yang, Q.C.; Wang, H.; Mu, H.K.; Luo, J.N.; Bao, X.H.; Bian, J.M.; Martin, J.D. Risk assessment of water resources and environmental carrying capacity in Yinchuan city. Hum. Ecol. Risk Assess. 2019, 25, 120–131. [Google Scholar] [CrossRef]
- Zhu, L.J.; Li, X.C.; Bai, Y.R.; Yi, T.L.; Yao, L.Q. Evaluation of water resources carrying capacity and its obstruction factor Analysis: A case study of hubei province, China. Water 2019, 11, 2573. [Google Scholar] [CrossRef]
- Bian, D.H.; Yang, X.H.; Wu, F.F.; Babuna, P.; Luo, Y.K.; Wang, B.; Chen, Y.J. A three-stage hybrid model investigating regional evaluation, pattern analysis and obstruction factor analysis for water resource spatial equilibrium in China. J. Clean. Prod. 2022, 331, 129940. [Google Scholar] [CrossRef]
- Chi, M.B.; Zhang, D.S.; Fan, G.W.; Zhang, W.; Liu, H.L. Prediction of water resource carrying capacity by the analytic hierarchy process-fuzzy discrimination method in a mining area. Ecol. Indic. 2019, 96, 647–655. [Google Scholar] [CrossRef]
- Wang, W.; Zeng, W. Optimizing the Regional Industrial Structure Based on the Environmental Carrying Capacity: An Inexact fuzzy Multi-Objective Programming Model. Sustainability 2013, 5, 5391. [Google Scholar] [CrossRef]
- Chen, H.S. The Establishment and Application of Environment Sustainability Evaluation Indicators for Ecotourism Environments. Sustainability 2015, 7, 727. [Google Scholar] [CrossRef]
- Wang, W.; Sun, Y.; Wu, J. Environmental Warning System Based on the DPSIR Model: A Practical and Concise Method for Environmental Assessment. Sustainability 2018, 10, 1728. [Google Scholar] [CrossRef]
- Wang, H.R.; Gong, S.X.; Deng, C.Y.; Yang, B.; Zuo, P. Research on water resources carrying capacity based on five-element connection number. J. Northwest Univ. 2019, 49, 211–218. [Google Scholar]
- Ye, F.; Jin, J.L.; Fang, G.H. Evaluation of water resources carrying capacity of Hefei City based on set pair analysis connection number. J. Water Resour. Eng. 2020, 31, 85–90. [Google Scholar]
- Liu, Y.H.; Li, Y.B.; Liang, X.Y.; Ran, C.H. Study on water resource carrying capacity evaluation and change in China. Resour. Environ. Yangtze Basin 2019, 28, 1080–1091. [Google Scholar]
- Davies, E.G.R.; Simonovic, S.P. Global water resources modeling with an integrated model of the social–economic–environmental system. Adv. Water Resour. 2011, 34, 684–700. [Google Scholar] [CrossRef]
- Paredes-Arquiola, J.; Andreu-Alvarez, J.; Martin-Monerris, M.; Solera, A. Water quantity and quality models applied to the Jucar River basin, Spain. Water Resour. Manag. 2010, 24, 2759–2779. [Google Scholar] [CrossRef]
- Langsdale, S.; Beall, A.; Carmichael, J.; Cohen, S.; Forster, C. An exploration of water resources futures under climate change using system dynamics modeling. Integr. Assess. 2007, 7, 51–79. [Google Scholar]
- Almendinger, J.E.; Ulrich, J.S. Use of SWAT to Estimate Spatial Scaling of Phosphorus Export Coefficients and Load Reductions Due to Agricultural BMPS. J. Am. Water Resour. Assoc. 2017, 53, 547–561. [Google Scholar] [CrossRef]
- Dai, M.; Wang, L.; Wei, X. Spatial differentiation of water resources carrying capacity in Guangxi based on entropy weight fuzzy comprehensive evaluation model. Soil Water Conserv. Res. 2016, 23, 193–199. [Google Scholar]
- Gao, J. The evaluation of water resources carrying capacity in Hohhot based on fuzzy analysis method. Inner Mong. Water Conserv. 2020, 4, 13–15. [Google Scholar]
- Guo, Y.; Wang, R.; Tong, Z.J.; Liu, X.P.; Zhang, J.Q. Dynamic evaluation and regionalization of maize drought vulnerability in the midwest of Jilin Province. Sustainability 2019, 11, 4234. [Google Scholar] [CrossRef]
- Jago-on, K.A.B.; Kaneko, S.; Fujikura, R.; Fujiwara, A.; Imai, T.; Matsumoto, T.; Zhang, J.Y.; Tanikawa, H.; Tanaka, K.; Lee, B.; et al. Urbanization and subsurface environmental issues: An attempt at DPSIR model application in Asian cities. Sci. Total Environ. 2009, 407, 3089–3104. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhou, J.Q.; Loaiciga, H.; Guo, H.C.; Hong, S. A DPSIR model for ecological security assessment through indicator screening: A case study at Dianchi Lake in China. PLoS ONE 2015, 10, e0131732. [Google Scholar] [CrossRef]
- Beltaos, S. Threshold between mechanical and thermal breakup of river ice cover. Cold Reg. Sci. Technol. 2003, 37, 1–13. [Google Scholar] [CrossRef]
- Yang, H.M.; Zhao, K.Q. The calculation and application of partial connection numbers. CAAI Trans. Intell. Syst. 2019, 14, 865–876. [Google Scholar]
- Wang, T.Y.; Du, C.; Nie, T.Z.; Sun, Z.Y.; Zhu, S.J.; Feng, C.X.; Dai, C.L.; Chu, L.L.; Liu, Y.; Liang, Q.Z. Spatiotemporal Analysis of Maize Water Requirement in the Heilongjiang Province of China during 1960–2015. Water 2020, 12, 2472. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, C.L.; Shi, W.L.; Fu, Y.C. Quantitative evaluation and optimized utilization of water resources-water environment carrying capacity based on naturebased solutions. J. Hydrol. 2019, 568, 96–107. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Drake, S.; Lü, H.S.; Xia, J. Analysis of Temporal and Spatial Differences in Eco-environmental Carrying Capacity Related to Water in the Haihe River Basins, China. Water Resour. Manag. 2010, 24, 1089–1105. [Google Scholar] [CrossRef]
- Miao, H.C.; Li, D.L.; Zuo, Q.T.; Yu, L.; Fei, X.X.; Hao, L.G. A scenario-based optimization model for planning sustainable water-resources process management under uncertainty. Processes 2019, 7, 312. [Google Scholar] [CrossRef]
- Beltaos, S. Hydro-climatic impacts on the ice cover of the lower Peace River. Hydrol. Process. 2008, 22, 3252–3263. [Google Scholar] [CrossRef]
- Song, X.M.; Kong, F.Z.; Zhan, C.S. Assessment of Water Resources Carrying Capacity in Tianjin City of China. Water Resour. Manag. 2011, 25, 857–873. [Google Scholar] [CrossRef]
- Klavins, M.; Briede, A.; Rodinov, V. Long term changes in ice and discharge regime of rivers in the Baltic region in relation to climatic variability. Clim. Chang. 2009, 95, 485–498. [Google Scholar] [CrossRef]
- Sagin, J.; Van Der Sanden, J.J.; Evans, E.; McKay, H.; Das, A.; Lindenschmidt, K.-E. Monitoring the freeze-up and ice cover progression of the Slave River. Can. J. Civ. Eng. 2015, 42, 609–621. [Google Scholar]
- Yang, J.F.; Lei, K.; Khu, S.; Meng, W. Assessment of Water Resources Carrying Capacity for Sustainable Development Based on A System Dynamics Model: A Case Study of Tieling City, China. Water Resour. Manag. 2014, 29, 885–899. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, B.; Zhang, W.G.; Jin, G.; Li, Z.H. Assessing the Regional Spatio-temporal Pattern of Water Stress: A Case Study in Zhangye City of China. Phys. Chem. Earth 2015, 1, 2–9. [Google Scholar] [CrossRef]
- Li, Z.L.; Shao, Q.X.; Xu, Z.X.; Cai, X.T. Analysis of Parameter Uncertainty in Semi-distributed Hydrological Models Using Bootstrap Method: A Case Study of Swat Model Applied to Yingluoxia Watershed in Northwest China. J. Hydrol. 2010, 385, 76–83. [Google Scholar] [CrossRef]
- Yang, J.F.; Lei, K.; Khu, S.; Meng, W.; Qiao, F. Assessment of water environmental carrying capacity for sustainable development using a coupled system dynamics approach applied to the Tieling of the Liao River Basin, China. Environ. Earth Sci. 2015, 73, 5173–5183. [Google Scholar] [CrossRef]
- Park, H.; Yoshikawa, Y.; Oshima, K.; Kim, Y.; Ngo-Duc, T.; Kimball, J.S.; Yang, D. Quantification of Warming Climate-Induced Changes in Terrestrial Arctic River Ice Thickness and Phenology. J. Clim. 2016, 29, 1733–1754. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, W.X.; Zhao, Y.; Song, W.B. Development tendency analysis and evaluation of the water ecological carrying capacity in the Siping area of Jilin Province in China based on system dynamics and analytic hierarchy process. Ecol. Modell. 2014, 275, 9–21. [Google Scholar] [CrossRef]
- Wang, Q.; Li, S.Q.; Li, R.R. Evaluating water resource sustainability in Beijing, China: Combining PSR model and matter-element extension method. J. Clean. Prod. 2019, 206, 171–179. [Google Scholar] [CrossRef]
- Zhang, S.H.; Xiang, M.S.; Yang, J.S.; Fan, W.W.; Yi, Y.J. Distributed hierarchical evaluation and carrying capacity models for water resources based on optimal water cycle theory. Ecol. Indic. 2019, 101, 432–443. [Google Scholar] [CrossRef]
- Gu, H.M.; Jia, L.; Jiang, X.H.; Xu, J.X.; Dong, G.T. Evaluation of water resources bearing capacity based on entropy-weight and matter-element assessment methods in midstream of Heihe River. J. Irrig. Drain Eng. 2016, 35, 87–92. [Google Scholar]
- Mashaly, A.F.; Fernald, A.G. Identifying Capabilities and Potentials of System Dynamics in Hydrology and Water Resources as a Promising Modeling Approach for Water Management. Water 2020, 12, 1432. [Google Scholar] [CrossRef]
- Barati, A.A.; Azadi, H.; Scheffran, J. A system dynamics model of smart groundwater governance. Agric. Water Manag. 2019, 221, 502–518. [Google Scholar] [CrossRef]
- Vieira, E.D.; Sandoval-Solis, S. Water resources sustainability index for a water-stressed basin in Brazil. J. Hydrol. Reg. Stud. 2018, 19, 97–109. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Li, W.C.; Wang, X.; Cui, T.T.; Cheng, Z.H.; Wang, S. Study on Water Resources Carrying Capacity in Ningxia Based on Principal Component Analysis and Factor Analysis. J. Hydrol. 2017, 37, 64–72. [Google Scholar]
- Panno, A.; Carrus, G.; Lafortezza, R.; Mariani, L.; Sanesi, G. Nature-based solutions to promote human resilience and wellbeing in cities during increasingly hot summers. Environ. Res. 2017, 159, 249–256. [Google Scholar] [CrossRef] [PubMed]
- Morris, R.L.; Konlechner, T.M.; Ghisalberti, M.; Swearer, S.E. From grey to green: Efficacy of eco-engineering solutions for nature-based coastal defence. Glob. Chang. Biol. 2018, 24, 1827–1842. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, S.; Pusch, M.T. Estimating the recreational carrying capacity of a lowland river section. Water Sci. Technol. 2012, 66, 2033–2039. [Google Scholar] [CrossRef]
- Lin, L.; Liu, Y.; Chen, J.N.; Zhang, T.Z.; Zeng, S.Y. Comparative analysis of environmental carrying capacity of the Bohai Sea Rim area in China. J. Environ. Monit. 2011, 13, 3178–3184. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Bian, J.M.; Wan, H.L. Hydrochemical appraisal of groundwater quality and pollution source analysis of oil field area: A case study in Daqing City, China. Environ. Sci. Pollut. Res. 2021, 28, 18667–18685. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.B.; Xu, D.S.; Liu, L.L. Construction of Regional Informatization Ecological Environment Based on the Entropy Weight Modified AHP Hierarchy Model. Sustain. Comput. Inform. Syst. 2019, 18, 2210–5379. [Google Scholar] [CrossRef]
- Dai, D.; Sun, M.D.; Xu, X.Q.; Lei, K. Assessment of the water resource carrying capacity based on the ecological footprint: A case study in zhangjiakou city, North China. Environ. Sci. Pollut. Res. 2019, 26, 11000–11011. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Zhou, M.; Lv, J.; Chen, K. Trends in global research in forest carbon sequestration: A bibliometric analysis. J. Clean. Prod. 2020, 252, 119908. [Google Scholar] [CrossRef]
- Li, Z.; Jin, J.L.; Cui, Y.; Zhou, R.X.; Ning, S.W.; Zhou, Y.L.; Zhou, L.G. Evaluation method of regional water resources carrying capacity based on semipartial connection number and dynamic subtraction set pair potential. J. Lake Sci. 2022, 34, 1656–1669. [Google Scholar]
- Jin, J.L.; Chen, P.F.; Chen, M.L.; Li, J.Q.; Xu, X.Y.; Chang, T. Bibliometric analysis of research progress on water resources carrying capacity based on knowledge map. Water Resour. Prot. 2019, 35, 14. [Google Scholar]
- Li, C.; Li, H.J.; Feng, S.D.; Liu, X.Y.; Guo, S. A study on the spatiotemporal characteristics and change trend of the atmospheric environmental carrying capacity in the Jing-Jin-Ji region, China. J. Clean. Prod. 2019, 211, 27–35. [Google Scholar] [CrossRef]
- Meng, C.; Wang, X.; Li, Y. An optimization model for water management based on water resources and environmental carrying capacities: A case study of the yinma river basin, northeast China. Water 2018, 10, 565. [Google Scholar] [CrossRef]
- Secinaro, S.; Brescia, V.; Calandra, D.; Biancone, P. Employing bibliometric analysis to identify suitable business models for electric cars. J. Clean. Prod. 2020, 264, 121503. [Google Scholar] [CrossRef]
- Yang, Y.F.; Wang, H.R.; Zhou, J.W.; Yan, J.W. Evaluation Model of Water Resources Carrying Capacity Based on Set Pair Potential and Partial Connection Number. Adv. Eng. Sci. 2021, 53, 99–105. [Google Scholar]
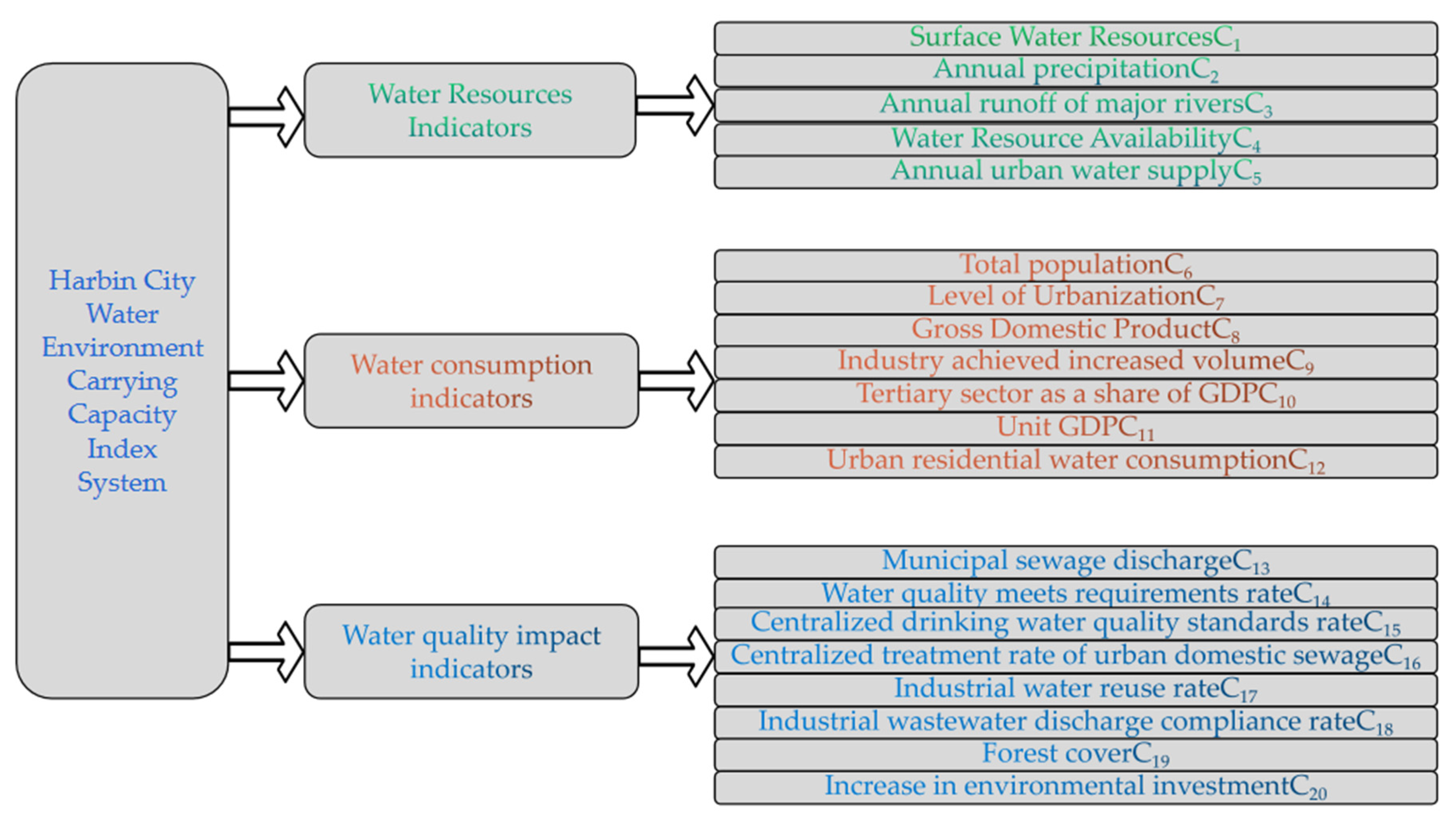





| Evaluation Indicators | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 |
| Loadable | ≥100 | ≥600 | ≥200 | ≥40 | ≤45,000 | ≤800 | ≤50 | ≤8000 | ≤1000 | ≥50 |
| Criticality | [70, 100) | [300, 600) | [100, 200) | [20, 40) | (45,000, 60,000] | (800, 1000] | (50, 80] | (8000, 20,000] | (1000, 1400] | [20, 50) |
| Overloading | <70 | <300 | <100 | <20 | >60,000 | >1000 | >80 | >20,000 | >1400 | <20 |
| Evaluation Indicators | C11 | C12 | C13 | C14 | C15 | C16 | C17 | C18 | C19 | C20 |
| Loadable | ≤66 | ≤10,000 | ≤5000 | ≥80 | ≥90 | ≥80 | ≥80 | ≥95 | ≥40 | ≥80 |
| Criticality | (66, 248] | (10,000, 40,000] | (5000, 7500] | [60, 80) | [70, 90) | [50, 90) | [50, 80) | [90, 95) | [25, 40) | [50, 80) |
| Overloading | >248 | >40,000 | >7500 | <60 | <70 | <50 | <50 | <90 | <25 | <50 |
| Posture | SE | Grade |
|---|---|---|
| Same posture | [1.0, 1.4] | Positive Level 1 |
| Favoring the same dynamics | (1.4, 1.8] | Bias positive Level 2 |
| Parity posture | (1.8, 2.2] | Positive Level 2 |
| Favoring the opposite dynamics | (2.2, 2.6] | Bias negative Level 2 |
| Opposite posture | (2.6, 3.0] | Positive Level 3 |
| Evaluation Indicators | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 |
| AHP weights | 0.07 | 0.073 | 0.06 | 0.083 | 0.093 | 0.063 | 0.063 | 0.03 | 0.037 | 0.07 |
| PP-AHP weights | 0.026 | 0.026 | 0.024 | 0.026 | 0.055 | 0.02 | 0.103 | 0.04 | 0.049 | 0.017 |
| Evaluation Indicators | C11 | C12 | C13 | C14 | C15 | C16 | C17 | C18 | C19 | C20 |
| AHP weights | 0.017 | 0.03 | 0.02 | 0.057 | 0.057 | 0.057 | 0.037 | 0.057 | 0.03 | 0.02 |
| PP-AHP weights | 0.049 | 0.019 | 0.027 | 0.064 | 0.103 | 0.059 | 0.099 | 0.1 | 0.061 | 0.037 |
| Year | Number of Contacts | SE | Grade |
|---|---|---|---|
| 2006 | 0.262 + 0.612I + 0.126J | 1.863503737 | Positive Level 2 |
| 2007 | 0.284 + 0.617I + 0.099J | 1.814117478 | Positive Level 2 |
| 2008 | 0.28 + 0.621I + 0.099J | 1.819802604 | Positive Level 2 |
| 2009 | 0.281 + 0.606I + 0.113J | 1.83159522 | Positive Level 2 |
| 2010 | 0.325 + 0.60I + 0.074J | 1.748237038 | Bias Positive Level 2 |
| 2011 | 0.316 + 0.59I + 0.094J | 1.77808089 | Bias Positive Level 2 |
| 2012 | 0.323 + 0.589I + 0.088J | 1.764297458 | Bias Positive Level 2 |
| 2013 | 0.333 + 0.602I + 0.065J | 1.732201156 | Bias Positive Level 2 |
| 2014 | 0.348 + 0.593I + 0.059J | 1.710318666 | Bias Positive Level 2 |
| 2015 | 0.327 + 0.608I + 0.065J | 1.738912508 | Bias Positive Level 2 |
| 2016 | 0.36 + 0.576I + 0.064J | 1.704757847 | Bias Positive Level 2 |
| 2017 | 0.36 + 0.606I + 0.034J | 1.674201471 | Bias Positive Level 2 |
| 2018 | 0.306 + 0.457I + 0.236J | 1.930387368 | Positive Level 2 |
| 2019 | 0.267 + 0.453I + 0.281J | 2.013888289 | Positive Level 2 |
| 2020 | 0.293 + 0.52I + 0.187J | 1.893646336 | Positive Level 2 |
| Method | Year | Support Level | Grade | ||
|---|---|---|---|---|---|
| Level 1 | Level 2 | Level 3 | |||
| First order | 2006 | 0.445690966 | 0.933965553 | 0.22989635 | 2 |
| 2007 | 0.479182183 | 0.947210296 | 0.183612738 | 2 | |
| 2008 | 0.472278472 | 0.947783832 | 0.18493421 | 2 | |
| 2009 | 0.473093116 | 0.938308666 | 0.207653618 | 2 | |
| 2010 | 0.536515722 | 0.95642926 | 0.139262856 | 2 | |
| 2011 | 0.521495012 | 0.943821035 | 0.174818609 | 2 | |
| 2012 | 0.532262532 | 0.946631328 | 0.164181644 | 2 | |
| 2013 | 0.547253568 | 0.961164842 | 0.12383843 | 2 | |
| 2014 | 0.567672216 | 0.963445389 | 0.111866509 | 2 | |
| 2015 | 0.538977957 | 0.961906958 | 0.124534978 | 2 | |
| 2016 | 0.581114654 | 0.957289482 | 0.122448582 | 2 | |
| 2017 | 0.58593583 | 0.978848992 | 0.066787571 | 2 | |
| 2018 | 0.48946241 | 0.815112985 | 0.392355718 | 2 | |
| 2019 | 0.434585901 | 0.790495727 | 0.453868044 | 2 | |
| 2020 | 0.480836552 | 0.872908538 | 0.324489281 | 2 | |
| Second order | 2006 | 0.479041394 | 0.933965553 | 0.281177525 | 2 |
| 2007 | 0.505602875 | 0.947210296 | 0.231292506 | 2 | |
| 2008 | 0.498563731 | 0.947783832 | 0.231492137 | 2 | |
| 2009 | 0.503851796 | 0.938308666 | 0.260084547 | 2 | |
| 2010 | 0.557345763 | 0.95642926 | 0.186141878 | 2 | |
| 2011 | 0.548491921 | 0.943821035 | 0.22972998 | 2 | |
| 2012 | 0.557678475 | 0.946631328 | 0.218335674 | 2 | |
| 2013 | 0.565671295 | 0.961164842 | 0.167645603 | 2 | |
| 2014 | 0.58459616 | 0.963445389 | 0.155331083 | 2 | |
| 2015 | 0.557239545 | 0.961906958 | 0.166971138 | 2 | |
| 2016 | 0.600423385 | 0.957289482 | 0.173020616 | 2 | |
| 2017 | 0.595634964 | 0.978848992 | 0.095156117 | 2 | |
| 2018 | 0.578882899 | 0.815112985 | 0.503330198 | 2 | |
| 2019 | 0.539906487 | 0.790495727 | 0.554760073 | 2 | |
| 2020 | 0.542379123 | 0.872908538 | 0.410366993 | 2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, N.; Yao, Z.; Xie, Y.; Wang, T.; Yang, J.; Li, X.; Fu, Q. Sustainability Analysis of the Water Environment Carrying Capacity of Harbin City Based on an Optimized Set Pair Analysis Posture-Deviation Coefficient Method Evaluation Model. Water 2023, 15, 1575. https://doi.org/10.3390/w15081575
Sun N, Yao Z, Xie Y, Wang T, Yang J, Li X, Fu Q. Sustainability Analysis of the Water Environment Carrying Capacity of Harbin City Based on an Optimized Set Pair Analysis Posture-Deviation Coefficient Method Evaluation Model. Water. 2023; 15(8):1575. https://doi.org/10.3390/w15081575
Chicago/Turabian StyleSun, Nan, Zhongbao Yao, Yunpeng Xie, Tianyi Wang, Jinzhao Yang, Xinyu Li, and Qiang Fu. 2023. "Sustainability Analysis of the Water Environment Carrying Capacity of Harbin City Based on an Optimized Set Pair Analysis Posture-Deviation Coefficient Method Evaluation Model" Water 15, no. 8: 1575. https://doi.org/10.3390/w15081575
APA StyleSun, N., Yao, Z., Xie, Y., Wang, T., Yang, J., Li, X., & Fu, Q. (2023). Sustainability Analysis of the Water Environment Carrying Capacity of Harbin City Based on an Optimized Set Pair Analysis Posture-Deviation Coefficient Method Evaluation Model. Water, 15(8), 1575. https://doi.org/10.3390/w15081575






