Inflow Prediction of Centralized Reservoir for the Operation of Pump Station in Urban Drainage Systems Using Improved Multilayer Perceptron Using Existing Optimizers Combined with Metaheuristic Optimization Algorithms
Abstract
:1. Introduction
2. Methodologies
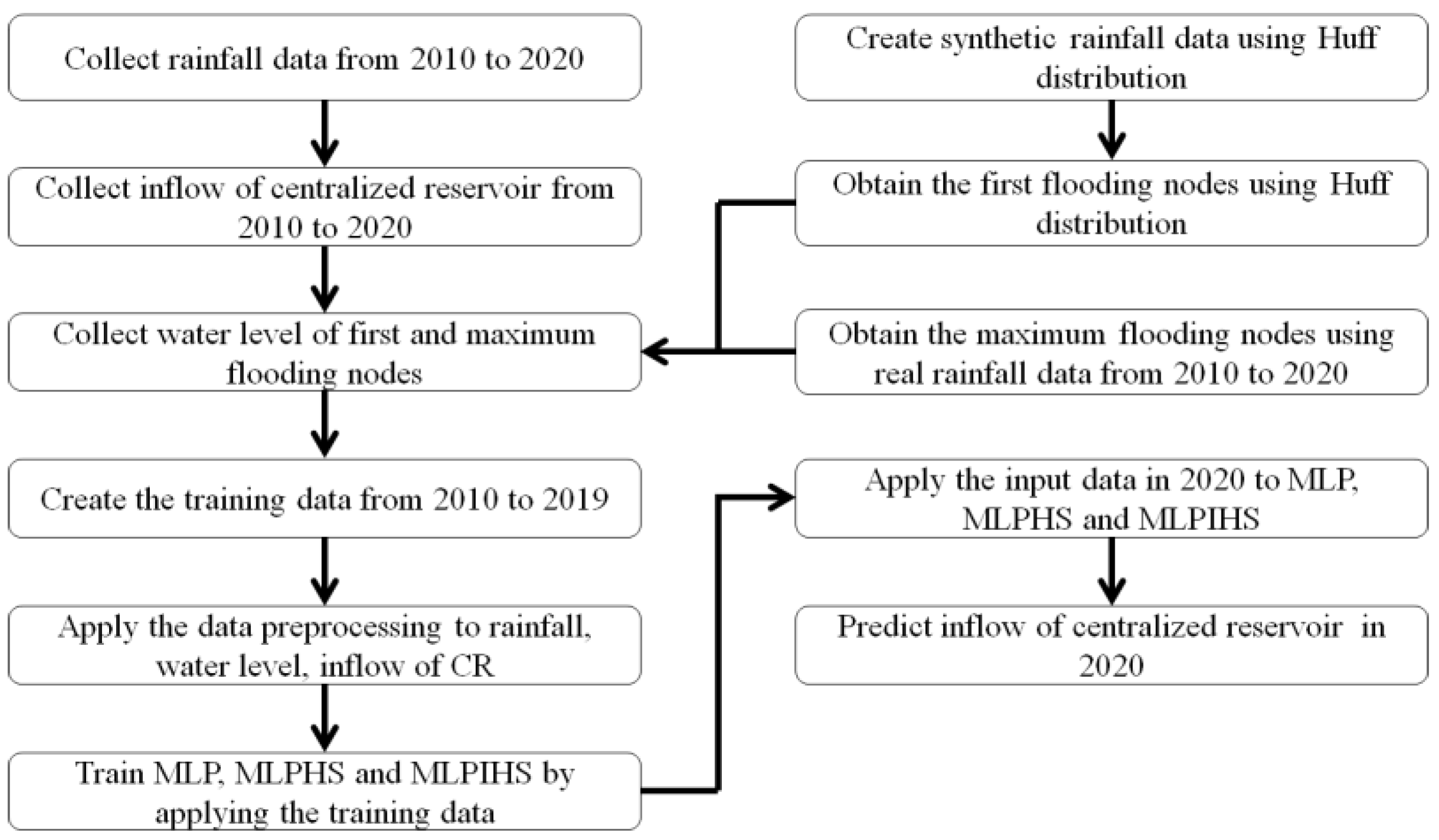
2.1. Overview
2.2. Preparation of Training Data
2.2.1. Correlation Analysis
2.2.2. Normalization of Training Data
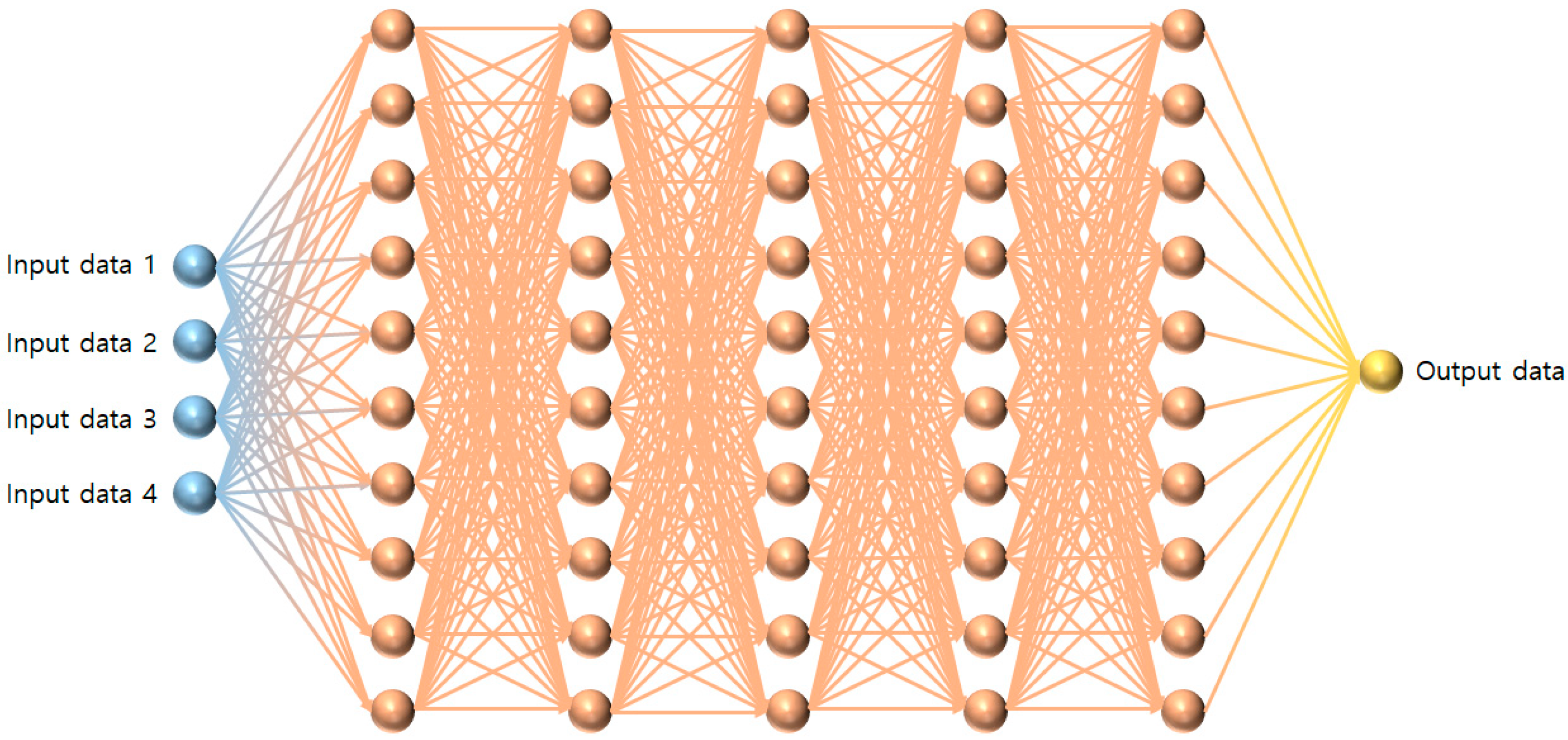
2.3. MLP Combined with IHS
2.3.1. Existing Optimizers in MLP
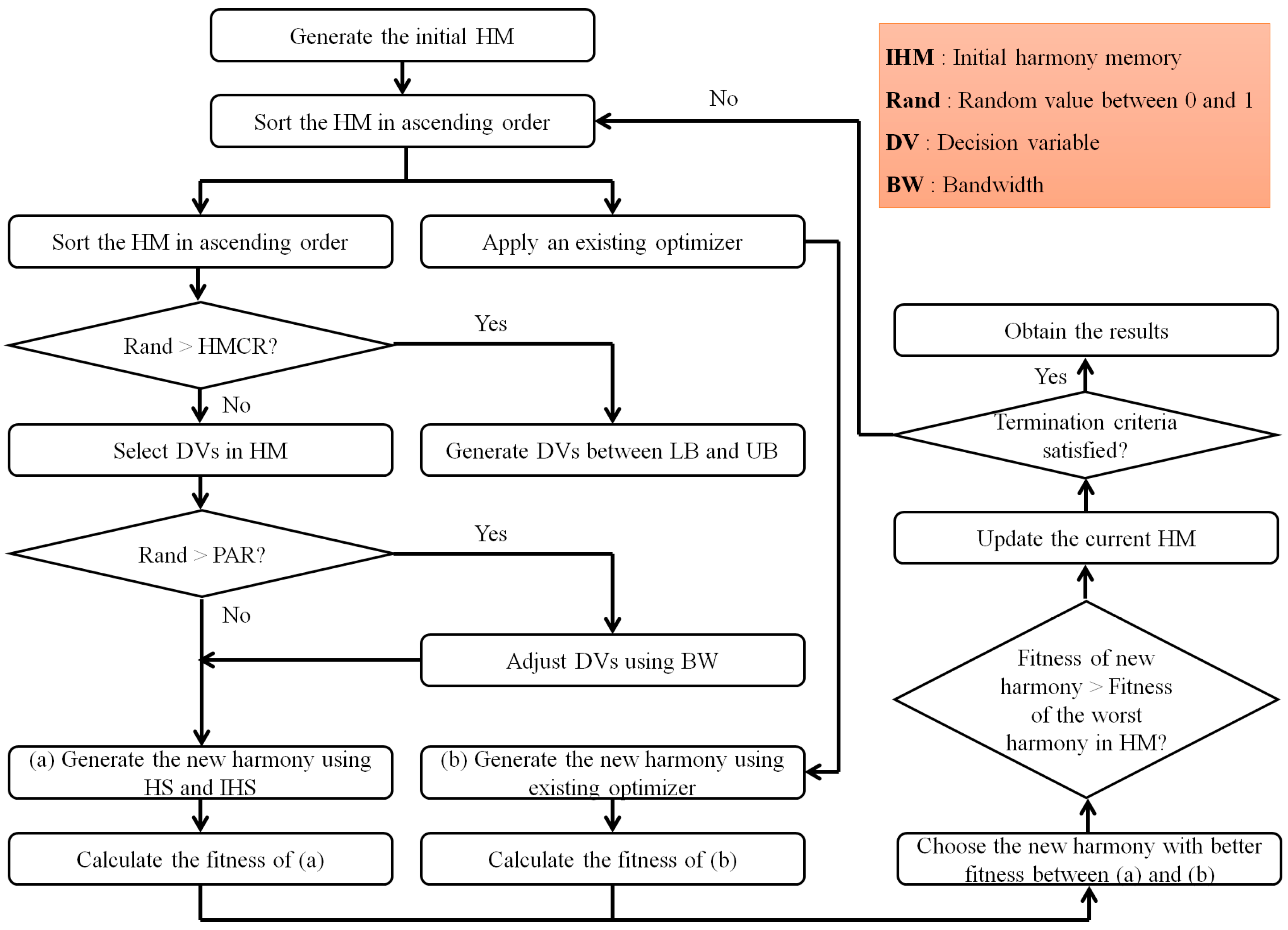
2.3.2. IHS
- Step 1. Create initial solutions based on the range of decision variables and generate the HMS.
- Step 2. Sort the HM in HMS based on the value of the objective function.
- Step 3(a). Select decision variables in the existing HM when HMCR is applied.
- Step 3(b). Adjust new decision variables based on BW when PAR is applied.
- Step 4. Create a new solution using the decision variables created in Steps 3(a) and 3(b).
- Step 5. Compare the new solution with the worst solution in the existing HM to decide whether it should be replaced.
- Step 6. Repeat Steps 2 to 5 until the termination criteria is satisfied.
2.3.3. Combined Optimizer Using Metaheuristic Optimization in MLP
2.4. Selection of Monitoring Nodes
2.4.1. Selection of Maximum Flooding Nodes
2.4.2. Selection of First Flooding Nodes
3. Application and Results
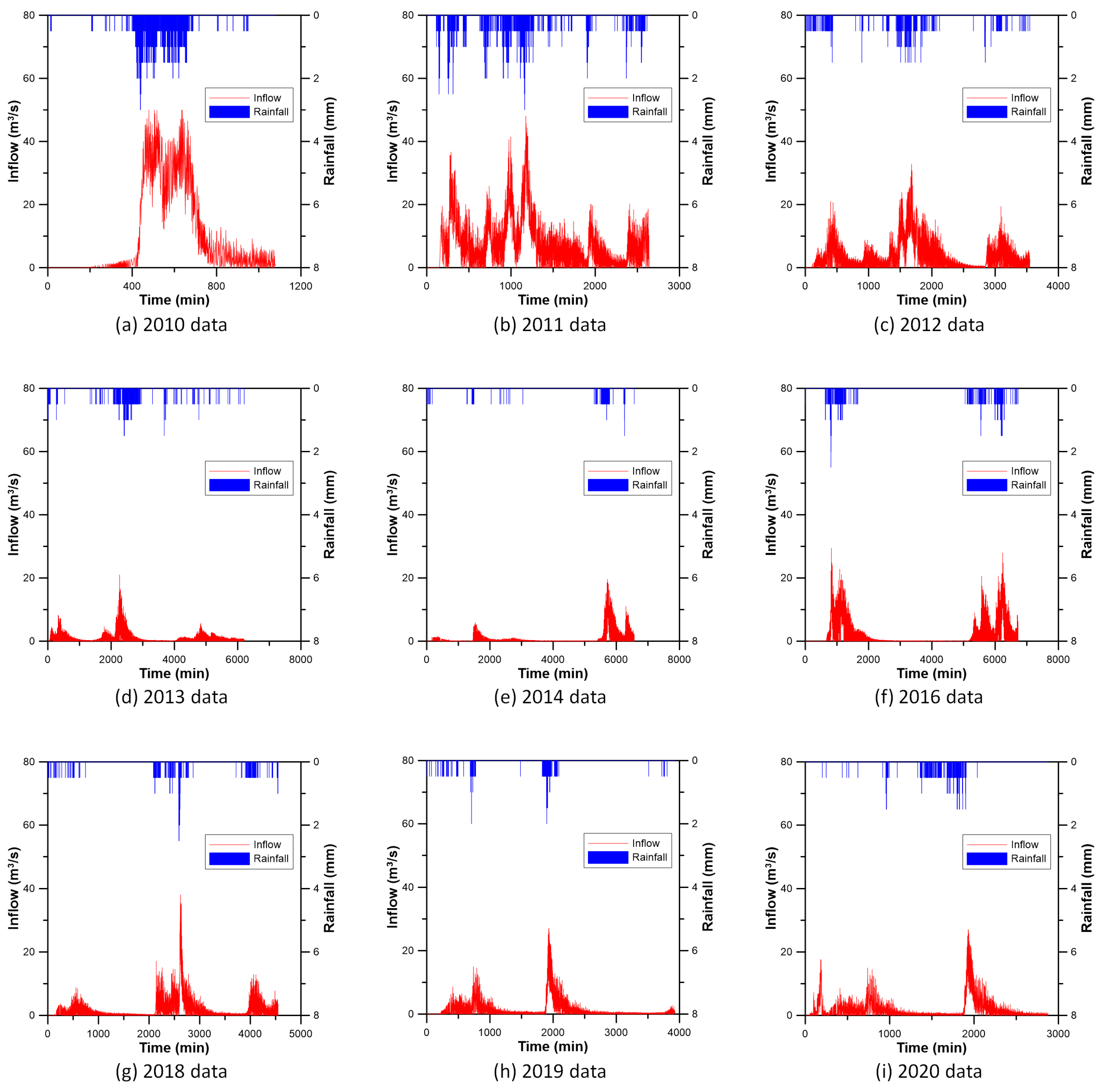
3.1. Study Area
3.2. Preparation of Data for Inflow Prediction of CR
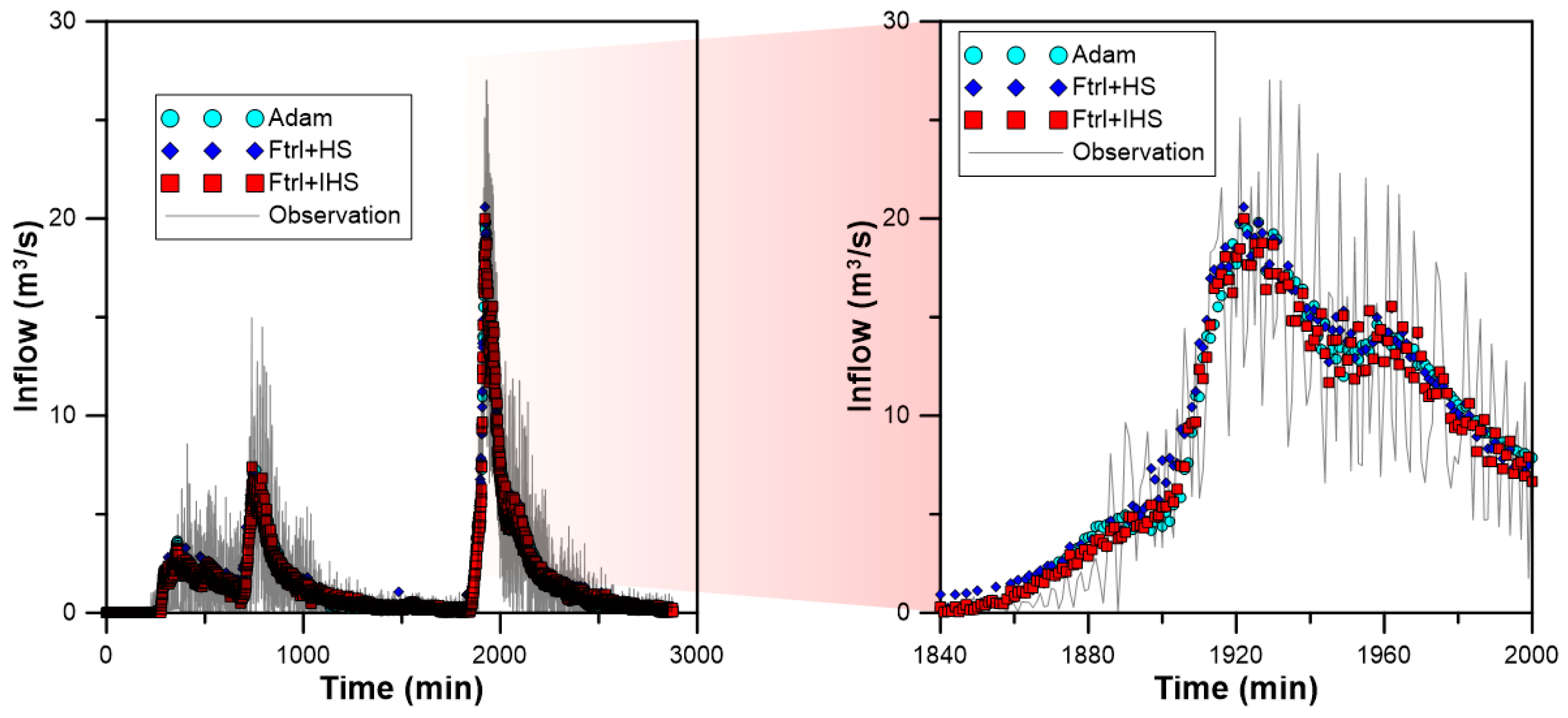
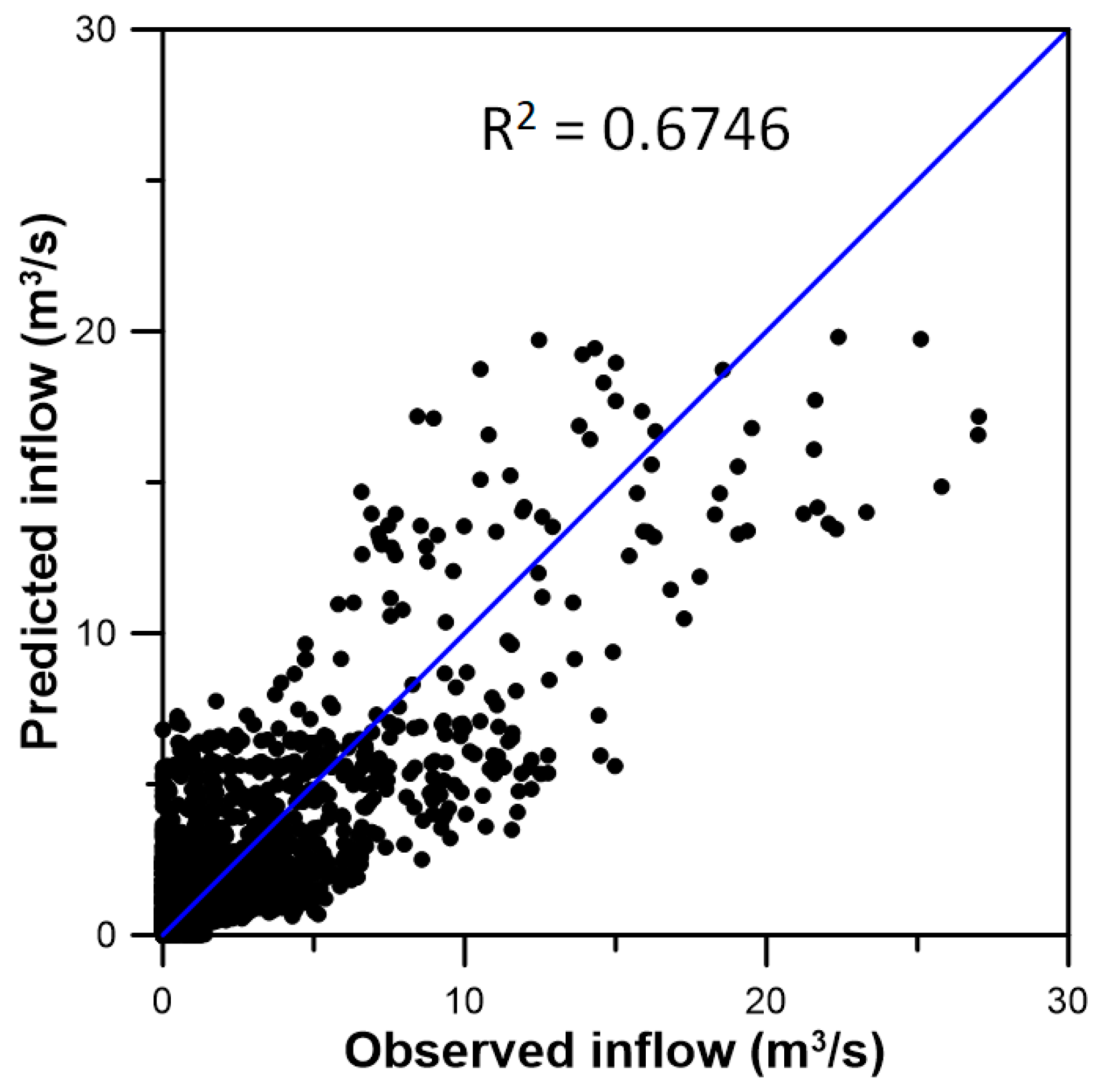
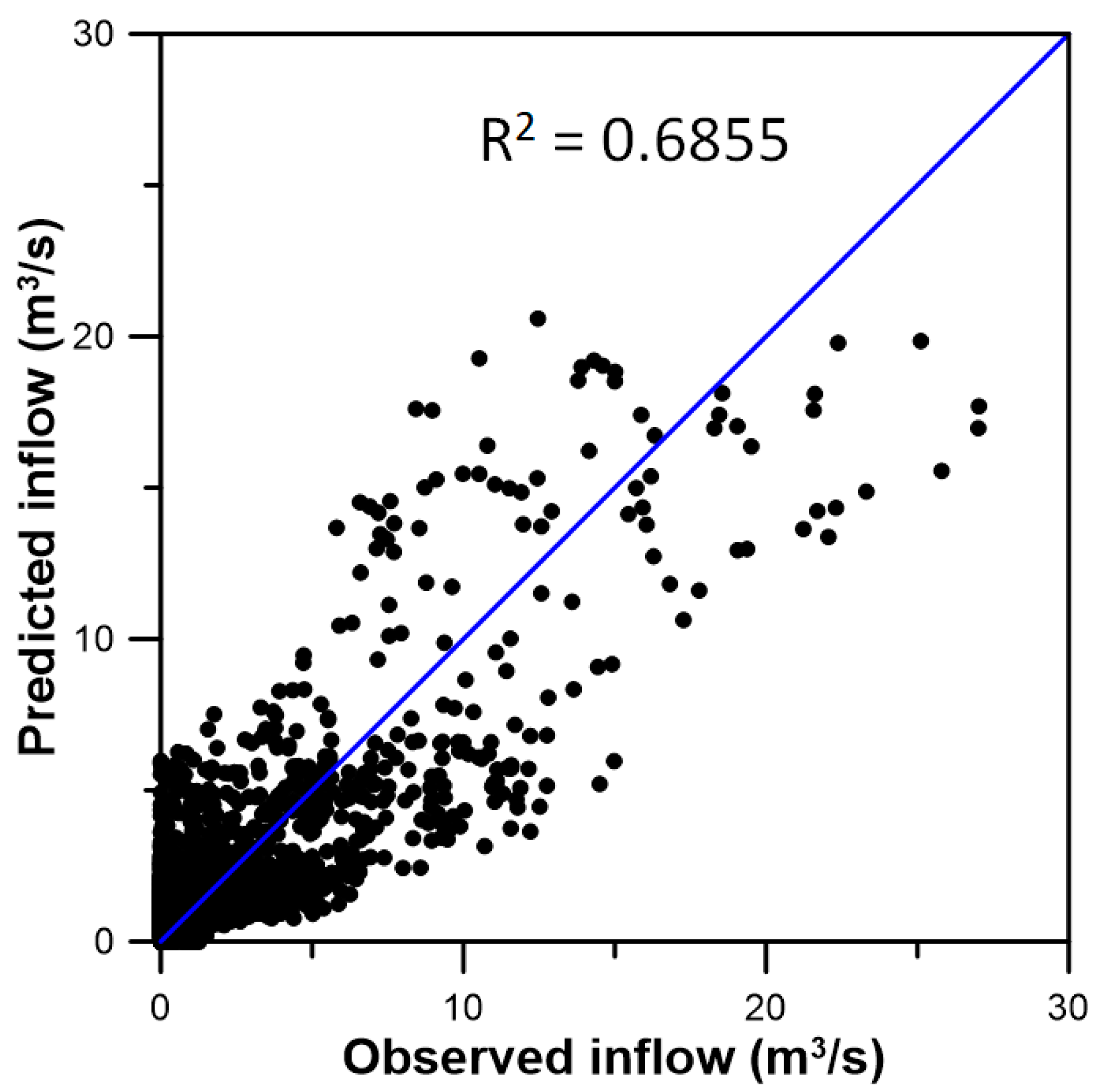
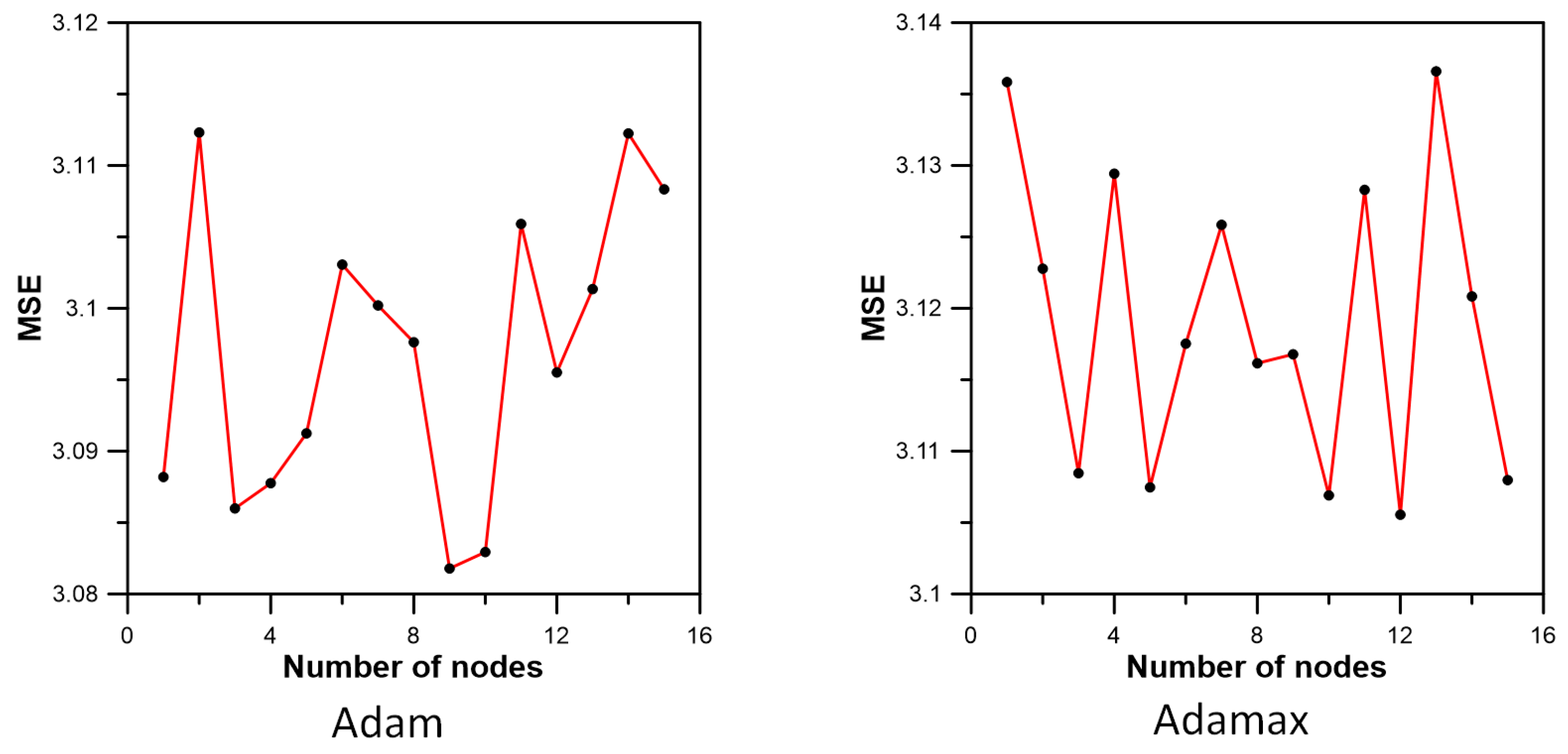
3.3. Inflow Prediction Using MLPIHS
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CR | Centralized reservoir |
| DR | Decentralized reservoir |
| UDS | Urban drainage system |
| MLP | Multilayer perceptron |
| ANN | Artificial neural network |
| RNN | Recurrent neural network |
| CNN | Convolutional neural network |
| LSTM | Long short-term memory |
| GRU | Gated recurrent unit |
| GA | Genetic algorithm |
| PSO | Particle swarm optimization |
| HS | Harmony search |
| IHS | Improved harmony search |
| RCGA | Real-coded genetic algorithm |
| MLPHS | MLP using new optimizer combined with HS |
| MLPIHS | MLP using new optimizer combined with IHS |
| GD | Gradient descent |
| SGD | Stochastic gradient descent |
| NAG | Nesterov accelerated gradient |
| Adagrad | Adaptive gradient |
| RMSprop | Root mean squared propagation |
| AdaDelta | Adaptive delta |
| Adam | Adaptive moment |
| Nadam | Nesterov accelerated adaptive moment |
| HMS | Harmony memory size |
| HMCR | Harmony memory considering rate |
| PAR | Pitch adjusting rate |
| BW | Bandwidth |
| HM | Harmony memory |
| SWMM | Storm water management model |
| MSE | Mean square error |
| MAE | Mean absolute error |
References
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Minsky, M.; Papert, S. Perceptrons; MIT Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Worland, S.C.; Steinschneider, S.; Asquith, W.; Knight, R.; Wieczorek, M. Prediction and inference of flow duration curves using multioutput neural networks. Water Resour. Res. 2019, 55, 6850–6868. [Google Scholar] [CrossRef] [Green Version]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef]
- Bui, Q.T.; Nguyen, Q.H.; Nguyen, X.L.; Pham, V.D.; Nguyen, H.D.; Pham, V.M. Verification of novel integrations of swarm intelligence algorithms into deep learning neural network for flood susceptibility mapping. J. Hydrol. 2020, 581, 124379. [Google Scholar] [CrossRef]
- Shamshirband, S.; Hashemi, S.; Salimi, H.; Samadianfard, S.; Asadi, E.; Shadkani, S.; Kargar, K.; Mosavi, A.; Nabipour, N.; Chau, K.W. Predicting standardized streamflow index for hydrological drought using machine learning models. Eng. Appl. Comput. Fluid Mech. 2020, 14, 339–350. [Google Scholar] [CrossRef]
- Tao, H.; Al-Khafaji, Z.S.; Qi, C.; Zounemat-Kermani, M.; Kisi, O.; Tiyasha, T.; Chau, K.; Nourani, V.; Melesse, A.M.; Elhakeem, M.; et al. Artificial intelligence models for suspended river sediment prediction: State-of-the art, modeling framework appraisal, and proposed future research directions. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1585–1612. [Google Scholar] [CrossRef]
- Singh, V.K.; Panda, K.C.; Sagar, A.; Al-Ansari, N.; Duan, H.F.; Paramaguru, P.K.; Vishwakarma, D.K.; Kumar, A.; Kumar, D.; Kashyap, P.S.; et al. Novel Genetic Algorithm (GA) based hybrid machine learning-pedotransfer Function (ML-PTF) for prediction of spatial pattern of saturated hydraulic conductivity. Eng. Appl. Comput. Fluid Mech. 2022, 16, 1082–1099. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Dorigo, M. Optimization, Learning and Natural Algorithms. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 1992. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Srinivasulu, S.; Jain, A. A comparative analysis of training methods for artificial neural network rainfall–runoff models. Appl. Soft Comput. 2006, 6, 295–306. [Google Scholar] [CrossRef]
- Nasseri, M.; Asghari, K.; Abedini, M.J. Optimized scenario for rainfall forecasting using genetic algorithm coupled with artificial neural network. Expert Syst. Appl. 2008, 35, 1415–1421. [Google Scholar] [CrossRef]
- Sedki, A.; Ouazar, D.; El Mazoudi, E. Evolving neural network using real coded genetic algorithm for daily rainfall–runoff forecasting. Expert Syst. Appl. 2009, 36, 4523–4527. [Google Scholar] [CrossRef]
- Yeo, W.K.; Seo, Y.M.; Lee, S.Y.; Jee, H.K. Study on water stage prediction using hybrid model of artificial neural network and genetic algorithm. J. Korea Water Resour. Assoc. 2010, 43, 721–731. [Google Scholar]
- Lee, W.J.; Lee, E.H. Runoff prediction based on the discharge of pump stations in an urban stream using a modified multi-layer perceptron combined with meta-heuristic optimization. Water 2022, 14, 99. [Google Scholar] [CrossRef]
- Google Research. Tensorflow Serving. 2016. Available online: www.tensorflow.org/tfx/guide/serving?hl=ko (accessed on 10 January 2023).
- Minns, A.W.; Hall, M.J. Artificial neural networks as rainfall-runoff models. Hydrol. Sci. J. 1996, 41, 399–417. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency. Storm Water Management Model User’s Manual Version 5.0; EPA: Washington DC, USA, 2010. [Google Scholar]
- Lee, E.H.; Lee, Y.S.; Joo, J.G.; Jung, D.; Kim, J.H. Investigating the impact of proactive pump operation and capacity expansion on urban drainage system resilience. J. Water Resour. Plan. Manag. 2017, 143, 04017024. [Google Scholar] [CrossRef]
- Huff, F.A. Time distribution of rainfall in heavy storms. Water Resour. Res. 1967, 3, 1007–1019. [Google Scholar] [CrossRef]
- Yoon, Y.N.; Jung, J.H.; Ryu, J.H. Introduction of design flood estimation. J. Korea Water Resour. Assoc. 2013, 46, 55–68. [Google Scholar]









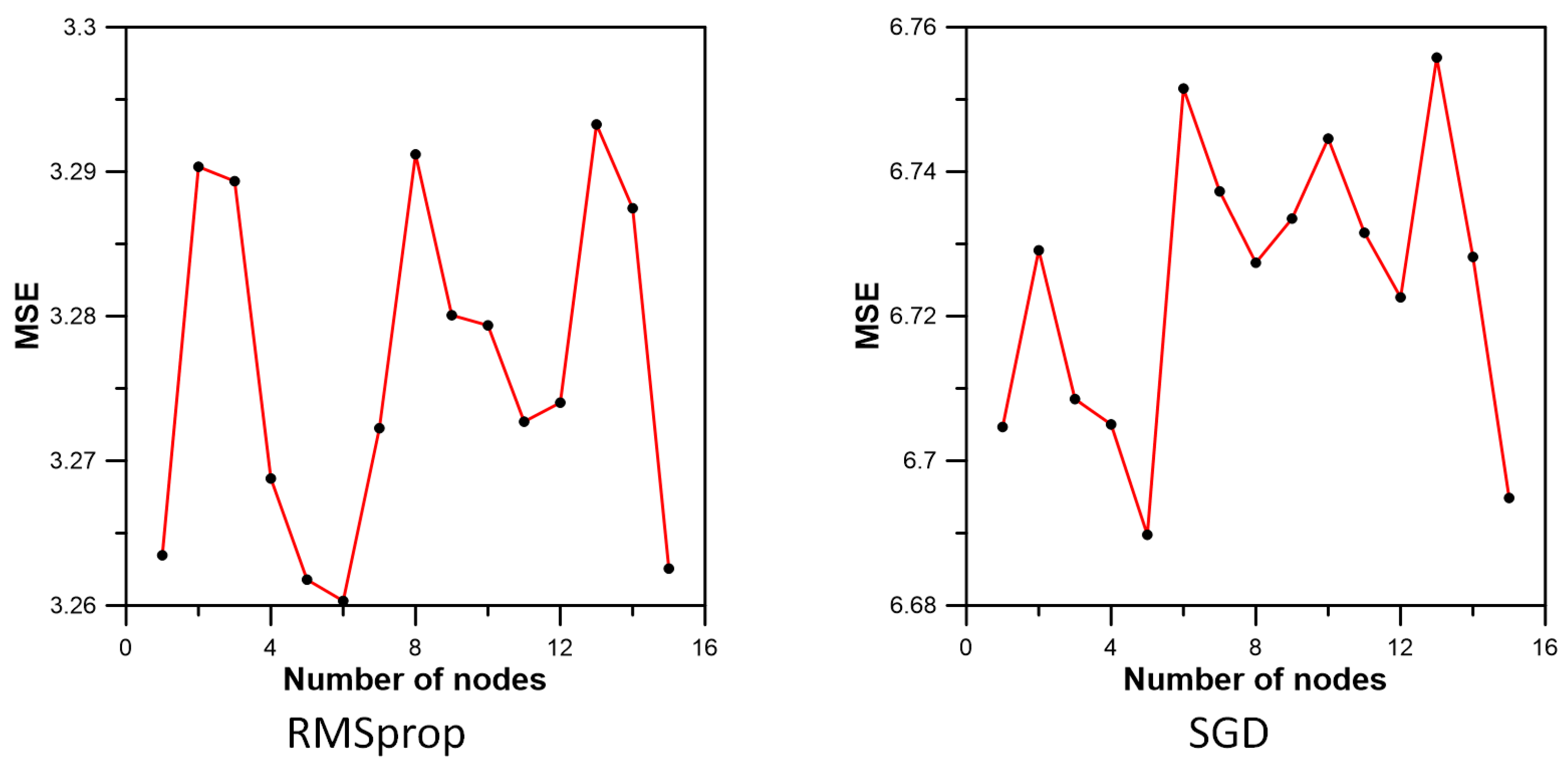
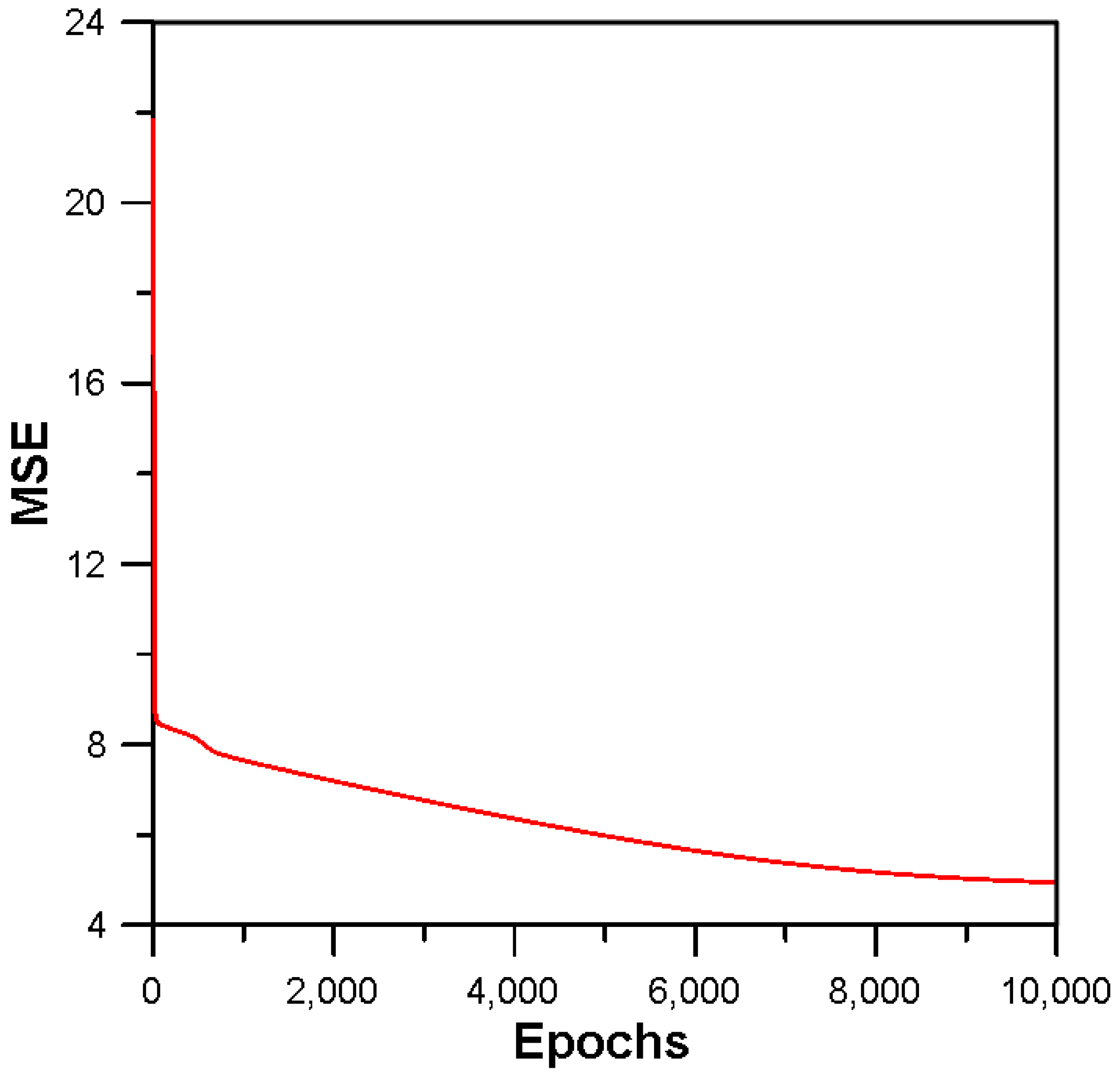
| Optimizers | Description |
|---|---|
| Adadelta | Update the learning rate using a Hessian matrix and exponential average |
| Adagrad | Use a flexible learning rate based on the learning process |
| Adam | Combine momentum and RMSporp |
| Adamax | Apply a new infinity norm |
| Ftrl | Normalize the follow the leader by considering gradient (leader) with the smallest loss |
| Nadam | Combine Nesterov accelerated gradient and RMSprop |
| RMSprop | Improve learning stopping using an exponential average |
| SGD | Select randomly from the entire data set |
| Rainfall Events | 2010 | 2011 | 2012 | 2013 | 2014 | 2016 | 2018 | 2019 |
|---|---|---|---|---|---|---|---|---|
| Maximum flooding nodes | 550 | 550 | 550 | 550 | 550 | 550 | 550 | 550 |
| Duration (m) | 30 | 60 | 90 |
|---|---|---|---|
| First flooding nodes | 560 | 560 | 575 |
| Data Type | Monitoring Node (550) | Monitoring Node (560) | Monitoring Node (575) | Rainfall Data |
|---|---|---|---|---|
| Lag time (min) | 15 | 14 | 13 | 17 |
| Correlation coefficient | 0.813 | 0.949 | 0.952 | 0.747 |
| Method | Adadelta | Adagrad | Adam | Adamax | Ftrl | Nadam | RMSprop | SGD |
|---|---|---|---|---|---|---|---|---|
| MSE | 4.312000 | 5.970060 | 3.082933 | 3.106901 | 11.978707 | 3.199255 | 3.261781 | 6.689764 |
| MAE | 1.285771 | 1.261158 | 1.021378 | 1.024476 | 1.635111 | 1.036619 | 1.085643 | 1.443204 |
| Method | Adadelta +HS | Adagrad +HS | Adam +HS | Adamax +HS | Ftrl +HS | Nadam +HS | RMSprop +HS | SGD +HS |
| MSE | 3.199255 | 3.088522 | 3.071538 | 3.078417 | 2.936929 | 3.137013 | 3.034306 | 4.901860 |
| MAE | 1.036619 | 1.028809 | 1.018922 | 1.025179 | 1.001793 | 1.044988 | 1.015344 | 1.304466 |
| Method | Adadelta +IHS | Adagrad +IHS | Adam +IHS | Adamax +IHS | Ftrl +IHS | Nadam +IHS | RMSprop +IHS | SGD +IHS |
| MSE | 3.029370 | 2.984212 | 3.047000 | 3.046682 | 2.930192 | 3.119831 | 3.020394 | 3.247332 |
| MAE | 1.017907 | 1.020483 | 1.030821 | 1.024705 | 0.989532 | 1.037507 | 1.000169 | 1.177632 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, E.H. Inflow Prediction of Centralized Reservoir for the Operation of Pump Station in Urban Drainage Systems Using Improved Multilayer Perceptron Using Existing Optimizers Combined with Metaheuristic Optimization Algorithms. Water 2023, 15, 1543. https://doi.org/10.3390/w15081543
Lee EH. Inflow Prediction of Centralized Reservoir for the Operation of Pump Station in Urban Drainage Systems Using Improved Multilayer Perceptron Using Existing Optimizers Combined with Metaheuristic Optimization Algorithms. Water. 2023; 15(8):1543. https://doi.org/10.3390/w15081543
Chicago/Turabian StyleLee, Eui Hoon. 2023. "Inflow Prediction of Centralized Reservoir for the Operation of Pump Station in Urban Drainage Systems Using Improved Multilayer Perceptron Using Existing Optimizers Combined with Metaheuristic Optimization Algorithms" Water 15, no. 8: 1543. https://doi.org/10.3390/w15081543






