Estimation of Global Water Quality in Four Municipal Wastewater Treatment Plants over Time Based on Statistical Methods
Abstract
:1. Introduction
- (1)
- Reduction of dimensionality of the data. This can be useful when the initial data contain a large number of variables and are therefore difficult to visualize or analyze.
- (2)
- Derivation/extraction of new features or elements from the original data that are more insightful or understandable than the original ones.
- (3)
- Visualization of high-dimensional data in two or three dimensions that may not have been visible in the initial high-dimensional space.
- (4)
- Reduction of the impact of noise or measurement errors on data.
- (5)
- Reduction of the impact of multicollinearity in the analysis by identifying the most important characteristics or components.
- (1)
- Difficulty in interpreting the resulting principal components, which are not always easy to understand or describe in terms of the original characteristics.
- (2)
- Loss of information when choosing a subset of the most crucial features or components to reduce the dimensionality of the data.
- (3)
- Difficulty in identifying the most crucial features due to distortion of the covariance matrix by outliers.
- (4)
- Difficulty in scaling: although PCA assumes that the data are scaled and centralized, some resulting principal components may not correctly represent the underlying patterns in the data if the data are not correctly scaled.
- (5)
2. Materials and Methods
2.1. Study Area Sites
2.2. Parameters Monitored
2.3. Descriptive Statistics
2.4. Correlation Analysis
2.5. Wastewater Quality Index Calculations
3. Results
3.1. Temporal Evolution of Influent and Effluent Qualities
3.2. Multivariate Statistical Analysis Approach
3.3. Approach to Statistical Modeling
3.4. Assessment and Verification of Model Quality
- Predictedi = values of predicted parameter
- Calculatedi = values of measured parameter
- N = Total number of samples
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Margenat, A.; Matamoros, V.; Diez, S.; Canameras, N.; Comas, J.; Bayona, J.M. Occurrence of chemical contaminants in peri-urban agricultural irrigation waters and assessment of their phytotoxicity and crop productivity. J. Sci. Total Environ. 2017, 599–600, 1140–1148. [Google Scholar] [CrossRef] [PubMed]
- Archer, E.; Petrie, B.; Kasprzyk-Hordern, B.; Wolfaardt, G. The fate of pharmaceuticals and personal care products (PPCPs), Endocrine Disrupting Contaminants (EDCs), Metabolites and illicit drugs in a WWTW and environmental waters. Chemosphere 2017, 174, 437–446. [Google Scholar] [CrossRef]
- Rivera-Utrilla, J.; Sánchez-Polo, M.; Ferro-García, M.A.; Prados-Joya, G.; Ocampo-Pérez, R. Pharmaceuticals as emerging contaminants and their removal from water. A review. Chemosphere 2013, 93, 1268–1287. [Google Scholar] [CrossRef] [PubMed]
- Saleh, I.A.; Zouari, N.; Al-Ghouti, M.A. Removal of pesticides from water and wastewater: Chemical. physical and biological treatment approaches. Environ. Technol. Innov. 2020, 19, 101026. [Google Scholar] [CrossRef]
- Rout, P.R.; Zhang, T.C.; Bhunia, P.; Surampalli, R.Y. Treatment technologies for emerging contaminants in wastewater treatment plants: A review. Sci. Total Environ. 2021, 753, 141990. [Google Scholar] [CrossRef] [PubMed]
- Soto-Verjel, J.; Maturana, A.Y.; Villamizar, S.E. Advanced catalytic oxidation coupled to biological systems to treat pesticide contaminated water: A review on technological trends and future challenges. Water Sci. Technol. 2022, 85, 1263–1294. [Google Scholar] [CrossRef]
- Avella, A.C.; Görner, T.; Yvon, J.; Chappe, P.; Guinot-Thomas, P.; De Donato, P. A combined approach for a better understanding of wastewater treatment plants operation: Statistical analysis of monitoring database and sludge and sludge physico-chemical characterization. Water Res. 2011, 45, 981–992. [Google Scholar] [CrossRef]
- Lefkir, A.; Maachou, R.; Bermad, A.; Khouider, A. Factorization of physico chemical parameters of activated sludge process using the principal component analysis. Desalination Water Treat. 2016, 57, 20292–20297. [Google Scholar] [CrossRef]
- Tchobanoglous, G.; Burton, F.L. Wastewater engineering. Management 1991, 7, 4. [Google Scholar]
- Boyacioglu, H. Development of a water quality index based on a European classification scheme. Water SA 2007, 33, 101–106. [Google Scholar] [CrossRef] [Green Version]
- Rosen, C.; Lennox, J. Multivariate and multiscale monitoring of wastewater treatment operation. Water Res. 2001, 35, 3402–3410. [Google Scholar] [CrossRef]
- Aguado, D.; Rosen, C. Multivariate statistical monitoring of continuous wastewater treatment plants. Eng. Appl. Artif. Intell. 2008, 21, 1080–1091. [Google Scholar] [CrossRef]
- Singh, K.P.; Malik, A.; Mohan, D.; Sinha, S.; Singh, V.K. Chemometric data analysis of pollutants in wastewaterda case study. Anal. Chim. Acta 2005, 532, 15–25. [Google Scholar] [CrossRef]
- Zhang, Z.; Tao, F.; Du, J.; Shi, P.; Yu, D.; Meng, Y.; Sun, Y. Surface water quality and its control in a river with intensive human impacts- a case study of the Xiangjiang River, China. J. Environ. Manag. 2010, 91, 2483–2490. [Google Scholar] [CrossRef] [PubMed]
- Ouali, A.; Azri, C.; Medhioub, K.; Ghrabi, A. Descriptive and multivariable analysis of the physico-chemical and biological parameters of Sfax wastewater treatment plant. Desalination 2009, 246, 496–505. [Google Scholar] [CrossRef]
- Wuderlin, D.A.; Diaz, M.D.P.; Amé, M.V.; Pesce, S.F.; Hued, A.C.; Bistoni, M.L.A. Pattern recognition techniques for the evaluation of spatial and temporal variations in water quality, A case study: SuquÍa river basin (Cordoba-Argentina). Water Res. 2001, 35, 2881–2894. [Google Scholar]
- Kaiser, H.F. The varimax criteria for analytical rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Cloutier, V.; Lefebvre, R.; Therrien, R.; Savard, M.M. Multivariate statistical analysis of geochemical data as indicative of the hydrogeochemical evolution of groundwater in a sedimentary rock aquifer system. J. Hydrol. 2008, 353, 294–313. [Google Scholar] [CrossRef]
- Qasaimeh, A.; Al-Ghazawi, Z. Regression modeling for rapid prediction of wastewater BOD. Desalin. Water Treat. 2020, 201, 165–172. [Google Scholar] [CrossRef]
- Sharma, P.; Sood, S.; Mishra, S.K. Development of multiple linear regression model for biochemical oxygen demand (BOD) removal efficiency of different sewage treatment technologies in Delhi, India. Sustain. Water Resour. Manag. 2020, 6, 29. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning, 1st ed.; Springer Texts in Statistics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Phil. Trans. R. Soc. A 2016, 374, 20150202. [Google Scholar] [CrossRef] [Green Version]
- Johnstone, I.M.; Titterington, D.M. Statistical challenges of high-dimensional data. Phil. Trans. R. Soc. A 2009, 367, 4237–4253. [Google Scholar] [CrossRef] [Green Version]
- Rastogi, G.K.; Sinha, D. A novel approach to water quality management through correlation study. J. Environ. Res. Dev. 2011, 5, 1029–1035. [Google Scholar]
- Lebart, L.; Morineau, A.; Fenelon, J.P. Traitement des données statistiques (methodes et programmes); Dunod Editeur: Malakoff, Paris, 1979; 510p. [Google Scholar]
- Gallagher, N.B.; Wise, B.M.; Butler, S.W.; White, D.D.; Barna, G.G. Development and Benchmarking of Multivariate Statistical Process Control Tools for a Semiconductor Etch Process: Improving Robustness through Model Updating. IFAC Symp. Ser. 1997, 30, 79–84. [Google Scholar] [CrossRef] [Green Version]
- Bayo, J.; Lopez-Castellanos, J. Principal factor and hierarchical cluster analyses for the performance assessment of an urban wastewater treatment plant in the Southeast of Spain. Chemosphere 2016, 155, 152–162. [Google Scholar] [CrossRef] [PubMed]
- Costa, J.; Alves, M.; Ferreira, E. Principal component analysis and quantitative image analysis to predict effects of toxics in anaerobic granular sludge. Bioresour. Technol. 2009, 100, 1180–1185. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Durmusoglu, E.; Yilmaz, C. Evaluation and temporal variation of raw and pretreated leachate quality from an active solid waste landfill. Water. Air. Soil Pollut. 2006, 171, 359–382. [Google Scholar] [CrossRef]
- Goode, C.; LeRoy, J.; Allen, D. Multivariate statistical analysis of a high rate biofilm process treating kraft mill bleach plant effluent. Water Sci. Technol. 2007, 55, 47–55. [Google Scholar] [CrossRef]
- Platikanov, S.; Rodriguez-Mozaz, S.; Huerta, B.; Barcelo, D.; Cros, J.; Batle, M.; Poch, G.; Tauler, R. Chemometrics quality assessment of wastewater treatment plant effluents using physicochemical parameters and UV absorption measurements. J. Environ. Manag. 2014, 140, 33–44. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, Z.; Wu, G.; Wu, Q.; Zhang, F.; Niu, Z.; Hu, H.-Y. Characteristics of water quality of municipal wastewater treatment plants in China: Implications for resources utilization and management. J. Clean. Prod. 2016, 131, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Tomita, R.K.; Park, S.W.; Sotomayor, O.A. Analysis of activated sludge process using statistical tools—A PCA approach. Chem. Eng. J. 2002, 90, 283–290. [Google Scholar] [CrossRef]
- Wallace, J.; Champagne, P.; Hall, G. Multivariate statistical analysis of water chemistry conditions in three wastewater stabilization ponds with algae blooms and pH fluctuations. Water Res. 2016, 96, 155–165. [Google Scholar] [CrossRef] [PubMed]
- Bordalo, A.A.; Teixeira, R.; Wiebe, W.J. A water quality index applied to an international shared river basin: The case of the Douro River. Environ. Manag. 2006, 38, 910–920. [Google Scholar] [CrossRef] [PubMed]
- Uddin, M.G.; Nash, S.; Olbert, A.I. A review of water quality index models and their use for assessing surface water quality. Ecol. Indic. 2021, 122, 107218. [Google Scholar] [CrossRef]
- APHA (American Public Health Association). Standard methods for examination of water and wastewater. In Anales de Hidrología Médica, 23rd ed.; Universidad Complutense de Madrid: Washington, DC, USA, 2012. [Google Scholar]
- Association of Official Analytical Chemists. Official Methods of Analysis of AOAC International, 16th ed.; AOAC International: Gaithersburg, MD, USA, 2019. [Google Scholar]
- Bharti, N.; Katyal, D. Water quality indices used for surface water vulnerability assessment. Int. J. Environ. Sci. 2011, 2, 154. [Google Scholar]
- Pearson, K. On lines and planes of closet fit to systems of points in space. Philos. Mag. 1901, 2, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Chong, I.-G.; Jun, C.-H. Performance of some variable selection methods when multicollinearity is present. Chemom. Intell. Lab. Syst. 2005, 78, 103–112. [Google Scholar] [CrossRef]
- Mamun, M.; Kim, J.Y.; An, K.G. Multivariate Statistical Analysis of Water Quality and Trophic State in an Artificial Dam Reservoir. Water 2021, 13, 186. [Google Scholar] [CrossRef]
- CCME. Canadian Water Quality Guidelines for the Protection of Aquatic Life: CCME Water Quality Index. Canadian Environmental Quality Guideline; Canadian Council of Ministers of the Environment: Winnipeg, MB, USA, 2001. [Google Scholar]
- Lumb, A.; Halliwell, D.; Sharma, T. Application of CCME Water Quality Index to monitor water quality: A case study of the Mackenzie River basin. Canada. Environ. Monit. Assess. 2006, 113, 411–429. [Google Scholar] [CrossRef]
- De Rosemond, S.; Duro, D.C.; Dube, M. Comparative analysis of regional water quality in Canada using the Water Quality Index. Environ. Monit. Assess. 2009, 156, 223–240. [Google Scholar] [CrossRef] [PubMed]
- Hurley, T.; Sadiq, R.; Mazumder, A. Adaptation and evaluation of the Canadian Council of Ministers of the Environment Water Quality Index (CCME WQI) for use as an effective tool to characterize drinking source water quality. Water Res. 2012, 46, 3544–3552. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.A.; Paterson, R.; Khan, H. Modification and application of the Canadian Council of Ministers of the environment water quality index for the communication of drinking water quality data in Newfoundland and Labrador. Water Qual. Res. J. Can. 2004, 39, 285–293. [Google Scholar] [CrossRef] [Green Version]
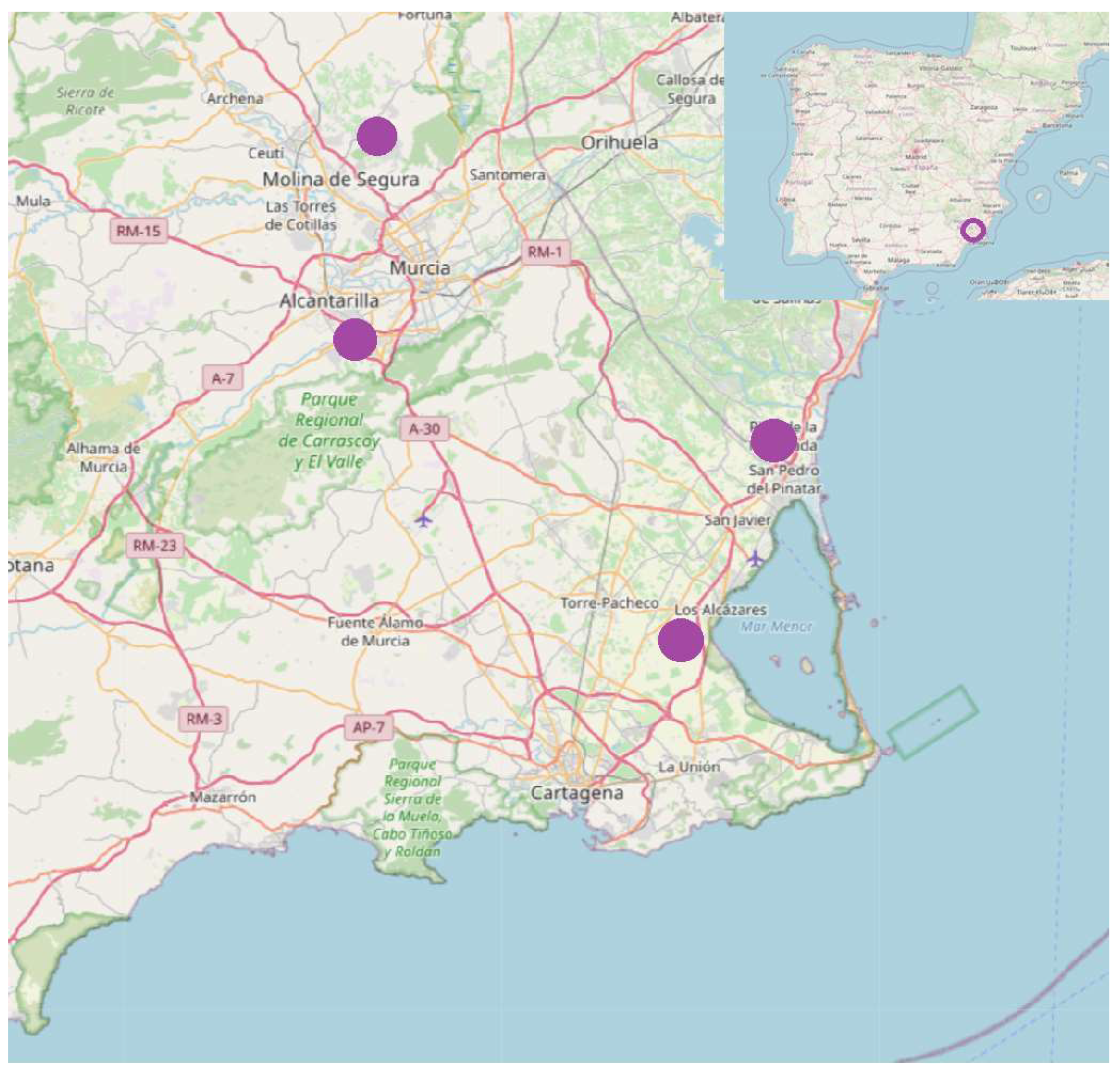
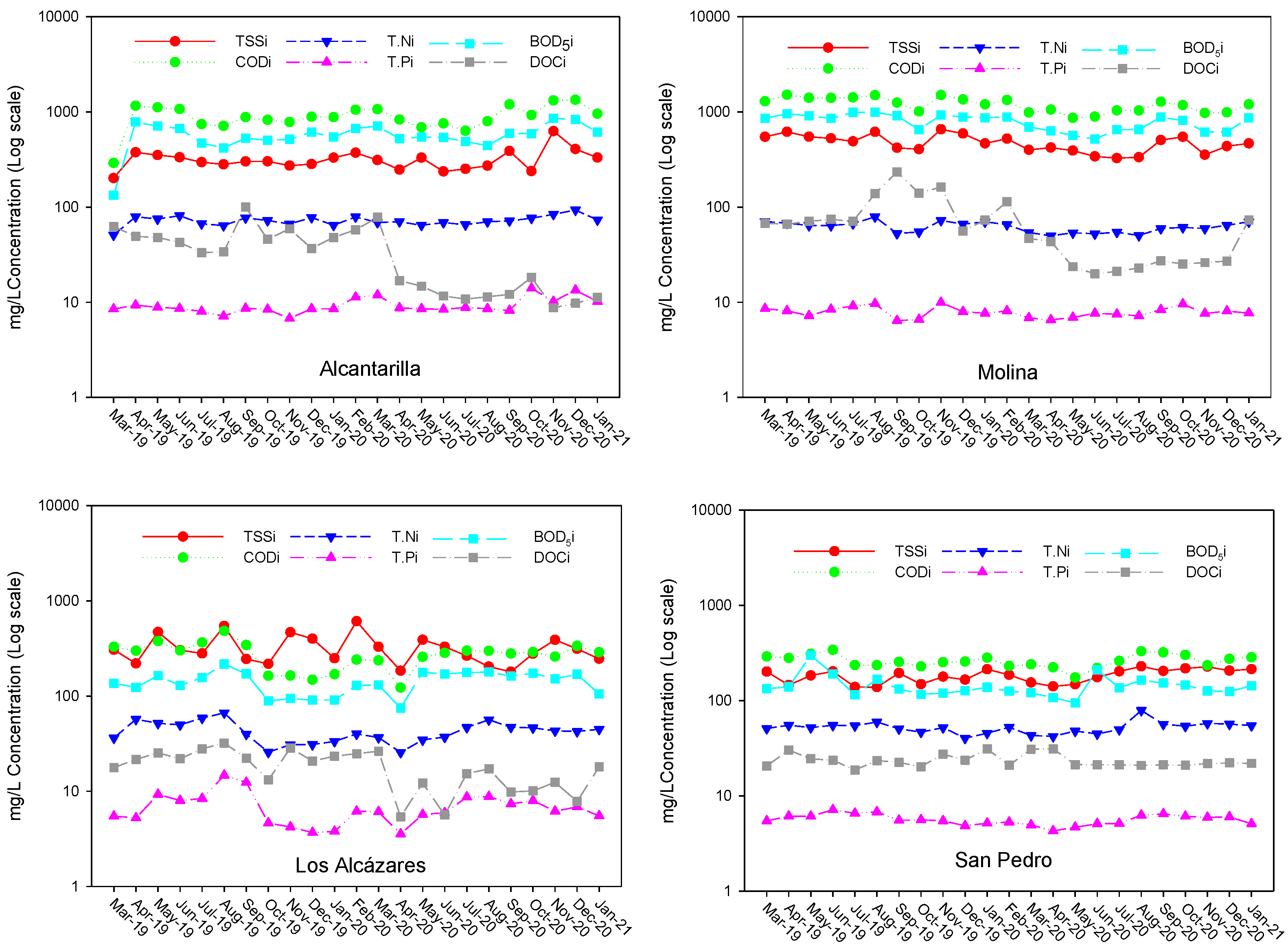
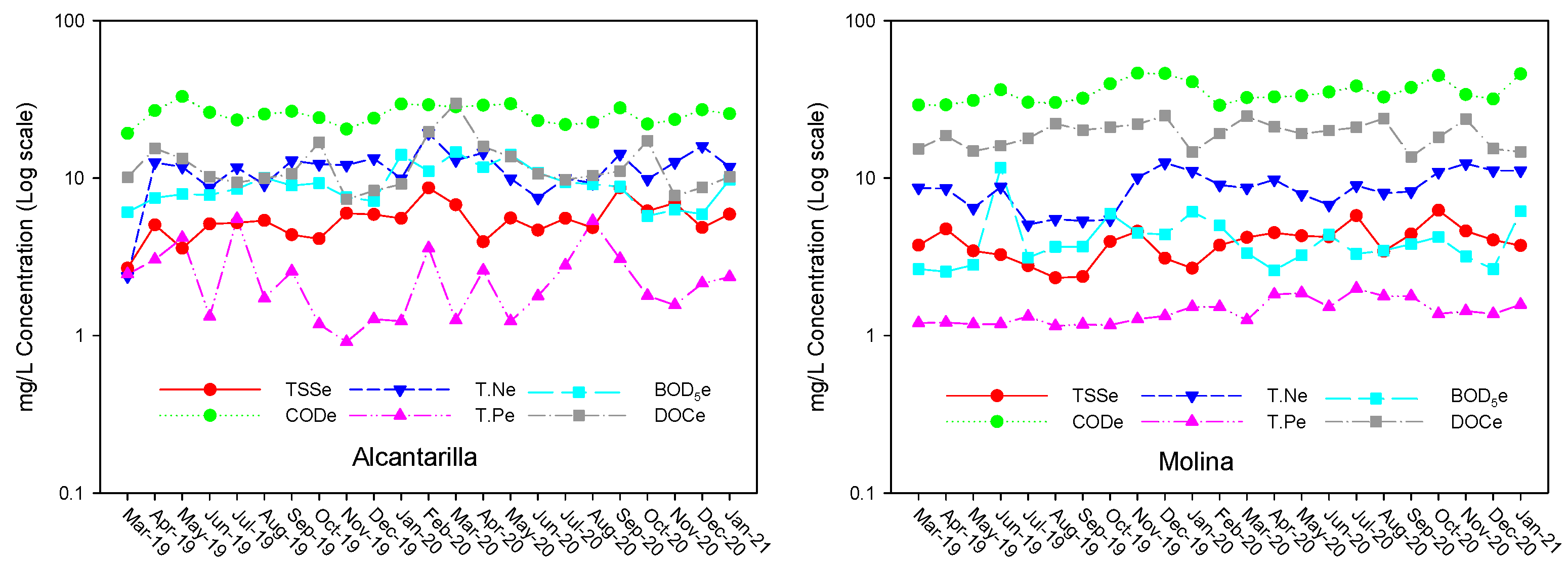
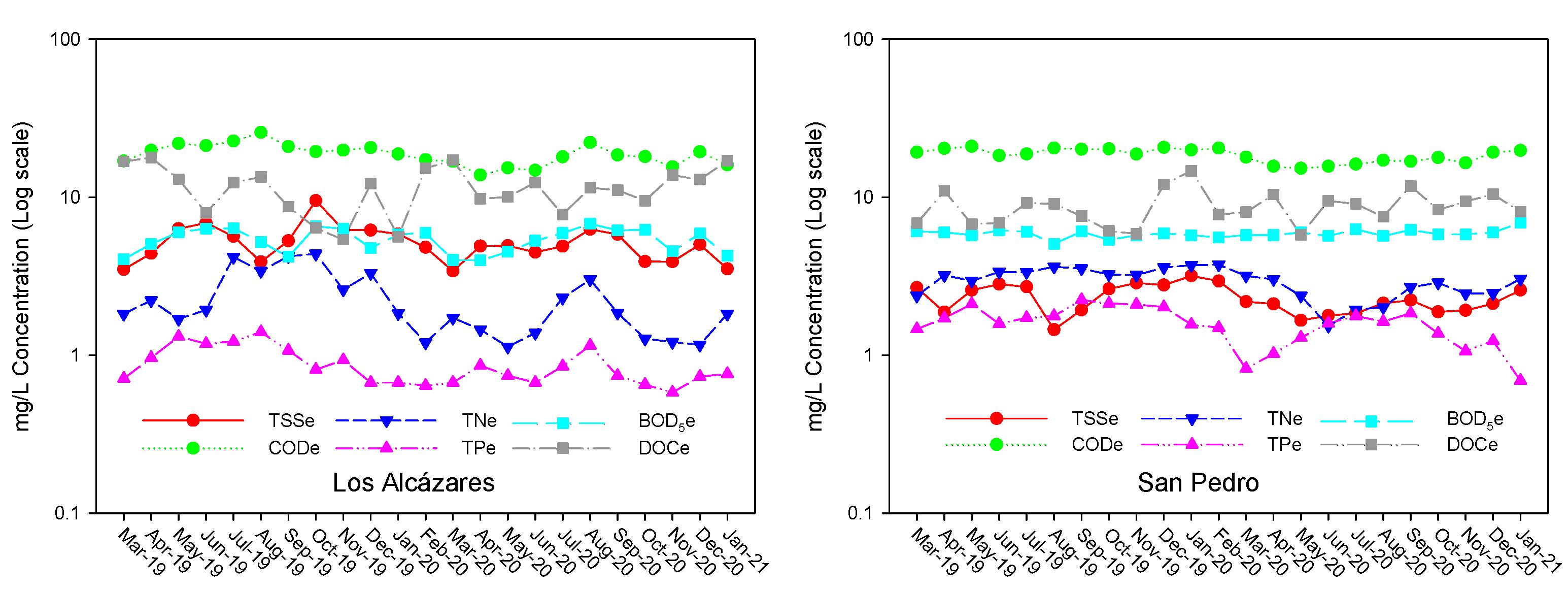


| Flow Rate in Million Gallons Day (mgd) | |||||
|---|---|---|---|---|---|
| WWTP (*) | Population Served | Design Flow | Flow Treated | Effluent Uses | Technology Used (**) |
| AL | 41,966 | 3 | 1.5 | Irrigation | CAS + DS + C + F + SF + UV |
| MO | 69,785 | 6 | 4 | Irrigation & Public domain | CAS + EA + C + F + SF + UV |
| LZ | 16,891 | 5 | 1.5 | Irrigation | CAS + EA + C + F + SF + UV |
| SP | 26,152 | 4.4 | 2 | Public domain | CAS + MBR + UV |
| WWQI | ||||
|---|---|---|---|---|
| Excellent | Good | Fair | Marginal | Poor |
| 95–100 | 80–94 | 65–79 | 45–64 | 0–44 |
| Very close to natural or pristine levels | Rarely depart from natural or desirable levels | Sometimes depart from natural or desirable levels | Often depart from natural or desirable levels | Quality is almost always threatened or impaired |
| WWTP | Influent | Effluent | ||
| Score | Category | Score | Category | |
| AL | 45–60 | Marginal | 95–100 | Excellent |
| MO | 44–60 | Marginal | 96–100 | Excellent |
| LZ | 45–60 | Marginal | 97–100 | Excellent |
| SP | 45–60 | Marginal | 98–100 | Excellent |
| AL | Principal Component a | MO | Principal Component b | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PC1 | PC2 | PC3 | PC4 | PC5 | PC1 | PC2 | PC3 | PC4 | PC5 | ||
| pHi | −0.56 | 0.45 | 0.79 | ||||||||
| ECi | −0.78 | 0.84 | |||||||||
| TSSi | 0.69 | 0.90 | |||||||||
| CODi | 0.92 | 0.86 | |||||||||
| TNi | 0.88 | 0.89 | |||||||||
| TPi | 0.69 | 0.83 | |||||||||
| BODi | 0.91 | 0.85 | |||||||||
| DOCi | 0.88 | 0.68 | |||||||||
| pHe | -0.85 | 0.77 | 0.47 | ||||||||
| ECe | −0.44 | 0.49 | −0.45 | −0.44 | −0.44 | 0.81 | |||||
| TSSe | 0.50 | −0.76 | |||||||||
| CODe | 0.42 | 0.71 | 0.78 | ||||||||
| TNe | 0.73 | −0.76 | |||||||||
| TPe | 0.55 | 0.70 | |||||||||
| BODe | 0.90 | 0.53 | |||||||||
| DOCe | 0.68 | 0.42 | 0.48 | ||||||||
| Eigenv | 6.18 | 2.37 | 1.73 | 1.50 | 1.27 | 5.19 | 2.87 | 2.29 | 1.76 | 1.43 | |
| Var (%) | 34.32 | 13.17 | 9.61 | 8.32 | 7.03 | 28.82 | 15.93 | 12.73 | 9.79 | 7.93 | |
| Cum (%) | 34.32 | 47.49 | 57.10 | 65.41 | 72.44 | 28.82 | 44.75 | 57.48 | 67.27 | 75.20 | |
| LZ | Principal Component c | SP | Principal Component d | ||||||||
| PC1 | PC2 | PC3 | PC4 | PC5 | PC1 | PC2 | PC3 | PC4 | PC5 | ||
| pHi | 0.90 | 0.90 | |||||||||
| ECi | −0.66 | 0.94 | |||||||||
| TSSi | 0.86 | 0.56 | 0.56 | ||||||||
| CODi | 0.77 | 0.86 | |||||||||
| TNi | 0.63 | 0.68 | 0.76 | ||||||||
| TPi | 0.74 | −0.45 | 0.78 | ||||||||
| BODi | 0.91 | 0.61 | |||||||||
| DOCi | 0.65 | 0.64 | −0.57 | 0.54 | |||||||
| pHe | 0.95 | 0.86 | |||||||||
| ECe | −0.83 | 0.93 | |||||||||
| TSSe | 0.86 | 0.59 | |||||||||
| CODe | 0.68 | −0.69 | 0.48 | ||||||||
| TNe | 0.55 | −0.60 | −0.68 | ||||||||
| TPe | 0.70 | 0.60 | |||||||||
| BODe | 0.83 | −0.65 | |||||||||
| DOCe | −0.77 | 0.68 | |||||||||
| Eigenv | 6.62 | 3.17 | 1.82 | 1.69 | 1.31 | 3.85 | 3.17 | 2.31 | 2.09 | 1.42 | |
| Var (%) | 36.79 | 17.58 | 10.13 | 9.36 | 7.29 | 21.39 | 17.62 | 12.82 | 11.61 | 7.87 | |
| Cum (%) | 36.79 | 54.37 | 64.50 | 73.86 | 81.15 | 21.39 | 39.01 | 51.83 | 63.44 | 71.31 | |
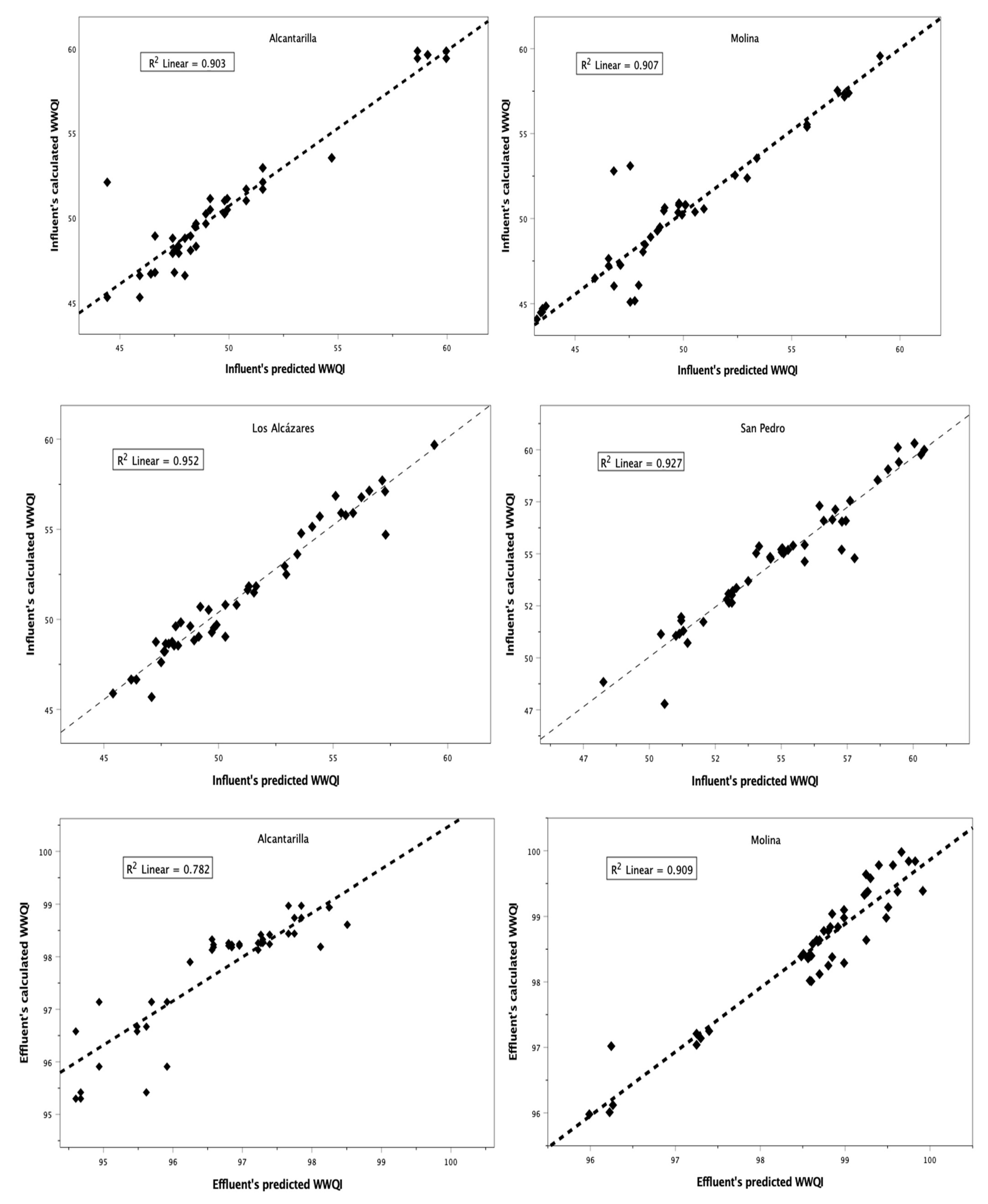
| WWTP | Numerical Expression | R2 | RMSE | |
|---|---|---|---|---|
| Data | ||||
| Train | Train | Test | ||
| AL | 0.903 | 2.15 | 7.06 | |
| 0.907 | 1.20 | 1.36 | ||
| MO | 0.952 | 0.67 | 2.20 | |
| 0.927 | 0.04 | 0.17 | ||
| LZ | 0.782 | 0.24 | 3.29 | |
| 0.909 | 0.05 | 0.29 | ||
| SP | 0.816 | 0.20 | 0.68 | |
| 0.979 | 0.01 | 0.02 | ||
| GL * | 0.810 | 0.84 | 1.51 | |
| 0.743 | 0.08 | 0.10 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Aatik, A.; Navarro, J.M.; Martínez, R.; Vela, N. Estimation of Global Water Quality in Four Municipal Wastewater Treatment Plants over Time Based on Statistical Methods. Water 2023, 15, 1520. https://doi.org/10.3390/w15081520
El Aatik A, Navarro JM, Martínez R, Vela N. Estimation of Global Water Quality in Four Municipal Wastewater Treatment Plants over Time Based on Statistical Methods. Water. 2023; 15(8):1520. https://doi.org/10.3390/w15081520
Chicago/Turabian StyleEl Aatik, Abderrazak, Juan Miguel Navarro, Ramón Martínez, and Nuria Vela. 2023. "Estimation of Global Water Quality in Four Municipal Wastewater Treatment Plants over Time Based on Statistical Methods" Water 15, no. 8: 1520. https://doi.org/10.3390/w15081520
APA StyleEl Aatik, A., Navarro, J. M., Martínez, R., & Vela, N. (2023). Estimation of Global Water Quality in Four Municipal Wastewater Treatment Plants over Time Based on Statistical Methods. Water, 15(8), 1520. https://doi.org/10.3390/w15081520








