Comparing Single and Multiple Imputation Approaches for Missing Values in Univariate and Multivariate Water Level Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Missing Data Mechanisms
2.2.1. Missing Completely at Random
2.2.2. Missing at Random
2.2.3. Missing Not at Random
2.3. Imputation Methods for Univariate and Multivariate Data
2.3.1. Imputation Methods for Univariate Water Level Time Series Data
Kalman Smoothing Method
Seasonal Decomposition Method
Random Method
2.3.2. Imputation Methods for Multivariate Water Level
k Nearest Neighbour Method
Predictive Mean Matching Method
Random Forests Method
2.4. Evaluation Metrics
3. Results
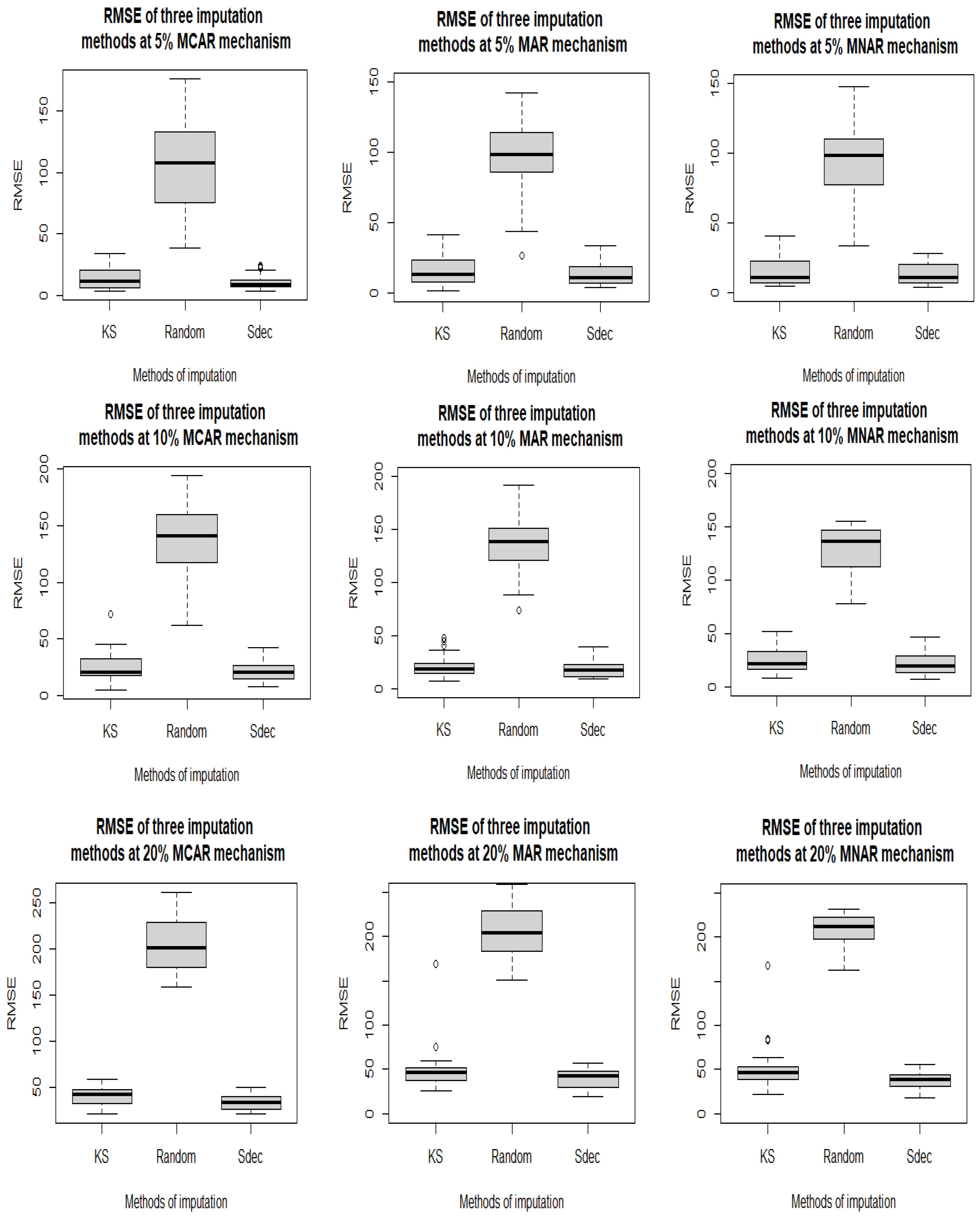
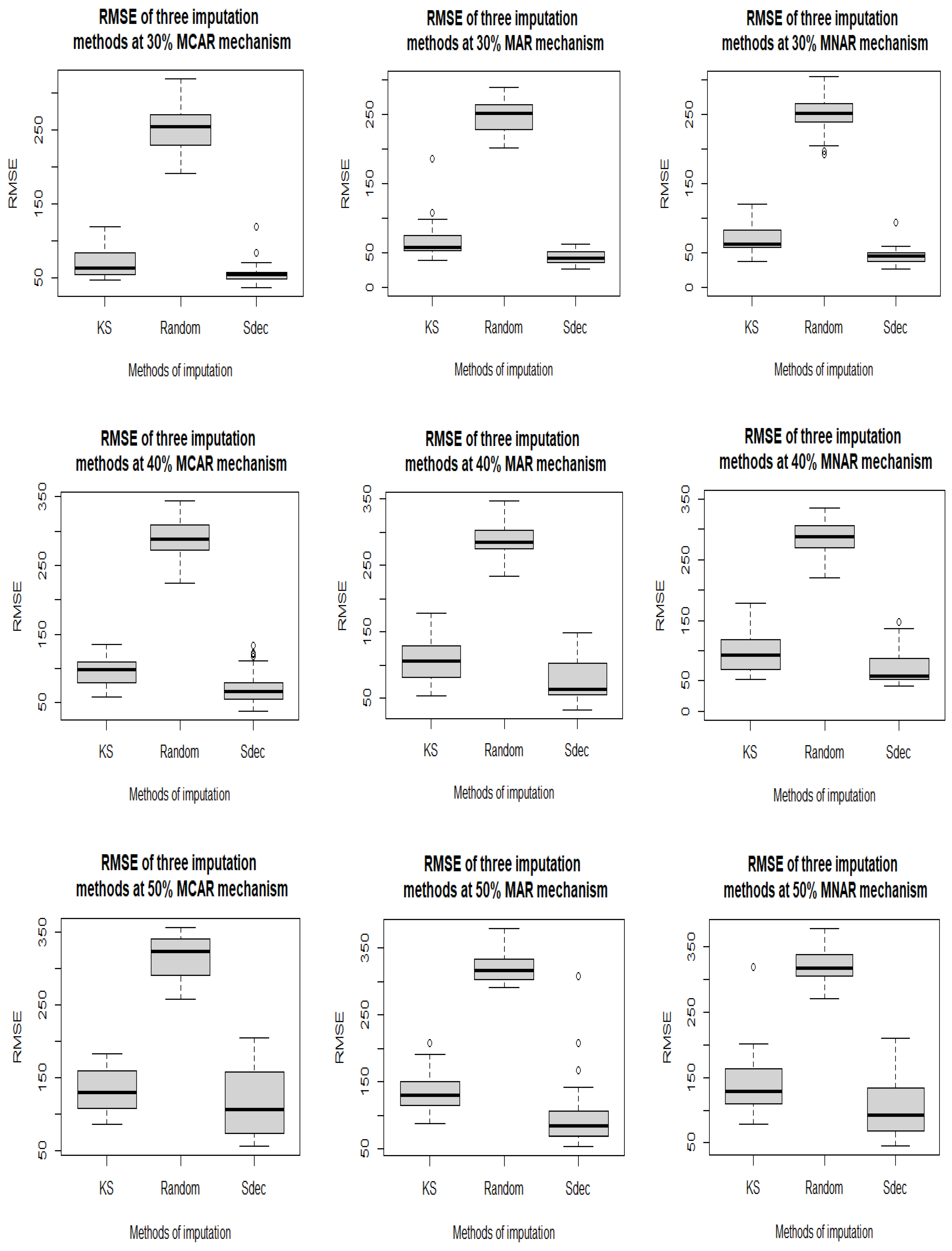
3.1. Univariate Water Level Imputation
3.2. Multivariate Water Level Imputation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| Abbreviation | Meaning |
| Missing data mechanisms | |
| MCAR | Missing completely at random |
| MAR | Missing at random |
| MNAR | Missing not at random |
| Imputation methods | |
| KS | Kalman smoothing |
| Sdec | Seasonal decomposition |
| PMM | Predictive mean matching |
| kNN | k nearest neighbour |
| RF | Random forest |
| MF | missForest |
| Evaluation metrics | |
| RMSE | Root mean square error |
| MAPE | Mean absolute percentage error |
References
- Phan, T.-T.-H.; Nguyen, X.H. Combining statistical machine learning models with ARIMA for water level forecasting: The case of the Red river. Adv. Water Res. 2020, 142, 103656. [Google Scholar] [CrossRef]
- Water Level. Available online: https://www.qmul.ac.uk/chesswatch/water-quality-sensors/water-level/ (accessed on 5 November 2022).
- Khalifeloo, M.H.; Mohammad, M.; Heydari, M. Multiple imputation for hydrological missing data by using a regression method (Klang River Basin). Int. J. Res. Eng. Technol. 2015, 4, 519–524. [Google Scholar]
- Elshorbagy, A.; Simonovic, S.; Panu, U. Estimation of missing streamflow data using principles of chaos theory. J. Hydrol. 2002, 255, 123–133. [Google Scholar] [CrossRef]
- Ramirez, S.G.; Williams, G.P.; Jones, N.L. Groundwater level data imputation using machine learning and remote earth observations using inductive bias. Remote Sens. 2022, 14, 5509. [Google Scholar] [CrossRef]
- Little, R.J.A. Missing-data adjustments in large surveys. J. Bus. Econ. Stat. 1988, 6, 287–296. [Google Scholar] [CrossRef]
- Zhang, Y.; Thorburn, P.J. Handling missing data in near real-time environmental monitoring: A system and a review of selected methods. Fut. Generat. Comput. Syst. 2022, 128, 63–72. [Google Scholar] [CrossRef]
- Twala, B. An empirical comparison of techniques for handling incomplete data using decision trees. Appl. Artific. Intellig. 2009, 23, 373–405. [Google Scholar]
- Regonda, S.K.; Seo, D.-J.; Lawrence, B.; Brown, J.D.; Demargne, J. Short-term ensemble streamflow forecasting using operationally-produced single-valued streamflow forecasts—A Hydrologic Model Output Statistics (HMOS) approach. J. Hydrol. 2013, 497, 80–96. [Google Scholar] [CrossRef]
- Gao, Y.; Merz, C.; Lischeid, G.; Schneider, M. A review on missing hydrological data processing. Environ. Earth Sci. 2018, 77, 47. [Google Scholar] [CrossRef]
- Plaia, A.; Bondì, A.L. Single imputation method of missing values in environmental pollution datasets. Atmosp. Environ. 2006, 40, 7316–7330. [Google Scholar] [CrossRef]
- Guzman, J.A.; Moriasi, D.; Chu, M.; Starks, P.; Steiner, J.; Gowda, P. A tool for mapping and spatio-temporal analysis of hydrological data. Environ. Model. Softw. 2013, 48, 163–170. [Google Scholar] [CrossRef]
- Ekeu-wei, I.T.; Blackburn, G.A.; Pedruco, P. Infilling Missing Data in Hydrology: Solutions Using Satellite Radar Altimetry and Multiple Imputation for Data-Sparse Regions. Water 2018, 10, 1483. [Google Scholar] [CrossRef] [Green Version]
- Chung, S.Y.; Venkatramanan, S.; Elzain, H.E.; Selvam, S.; Prasanna, M.V. Supplement of missing data in groundwater-level variations of peak type using geostatistical methods. In GIS and Geostatistical Techniques for Groundwater Science, 1st ed.; Venkatramanan, S., Prasanna, M.V., Chung, S.Y., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 33–41. [Google Scholar] [CrossRef]
- Zhang, Y.; Thorburn, P.J.; Xiang, W.; Fitch, P. SSIM—A deep learning approach for recovering missing time series sensor data. IEEE Internet Things J. 2019, 6, 6618–6628. [Google Scholar] [CrossRef]
- Gires, A.; Tchiguirinskaia, I.; Schertzer, D. Infilling missing data of binary geophysical fields using scale invariant properties through an application to imperviousness in urban areas. Hydrol. Sci. J. 2021, 66, 1197–1210. [Google Scholar] [CrossRef]
- Norazian, M.N.; Shukri, Y.A.; Azam, R.N.; Al Bakri, A.M.M. Estimation of missing values in air pollution data using single imputation techniques. Sci. Asia 2008, 34, 341–345. [Google Scholar] [CrossRef]
- Kang, H. The prevention and handling of the missing data. Korean J. Anesthesiol. 2013, 64, 402–406. [Google Scholar] [CrossRef] [Green Version]
- Soley-Bori, M. (Boston University, Boston, United States); Dealing with Missing Data: Key Assumptions and Methods for Applied Analysis. 2013. Available online: https://www.bu.edu/sph/files/2014/05/Marina-tech-report.pdf (accessed on 22 October 2021).
- Peugh, J.L.; Enders, C.K. Missing data in educational research: A review of reporting practices and suggestions for improvement. Rev. Educ. Res. 2004, 74, 525–556. [Google Scholar] [CrossRef]
- Cool, A.L. (Texas A&M University, Texas, United States) A Review of Methods for Dealing with Missing Data. 2000. Available online: https://files.eric.ed.gov/fulltext/ED438311.pdf (accessed on 2 December 2022).
- Enders, C.K. Applied Missing Data Analysis, 1st ed.; Guilford Press: New York, NY, USA, 2010. [Google Scholar]
- Graham, J.W.; Hofer, S.M. Multiple imputation in multivariate research. In Modeling Longitudinal and Multilevel Data: Practical Issues, Applied Approaches, and Specific Examples; Little, T.D., Schnabel, K.U., Baumert, J., Eds.; Lawrence Erlbaum Associates Publishers: Hillsdale, NJ, USA, 2000; pp. 201–218. [Google Scholar]
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Arnab, R. Survey Sampling Theory and Applications, 1st ed.; Academic Press: London, UK, 2017. [Google Scholar]
- Zhang, Z. Missing data imputation: Focusing on single imputation. Ann. Translat. Med. 2016, 4, 1–9. [Google Scholar] [CrossRef]
- Saunders, J.A.; Morrow-Howell, N.; Spitznagel, E.; Doré, P.; Proctor, E.K.; Pescarino, R. Imputing missing data: A comparison of methods for social work researchers. Soc. Work Res. 2006, 30, 19–31. [Google Scholar] [CrossRef]
- Rubin, D.B. Multiple imputations in sample surveys: A phenomenological Bayesian approach to nonresponse (with discussion). In Proceedings of the American Statistical Association, Alexandria, VA, USA, 8–10 March 1978; Available online: http://www.asasrms.org/Proceedings/papers/1978_004.pdf (accessed on 1 December 2022).
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Moritz, S.; Bartz-Beielstein, T. imputeTS: Time series missing value imputation in R. R. J. 2017, 9, 207–218. Available online: https://cran.r-project.org/web/packages/imputeTS/vignettes/imputeTS-Time-Series-Missing-Value-Imputation-in-R.pdf (accessed on 28 October 2021). [CrossRef] [Green Version]
- Wijesekara, W.; Liyanage, L. Comparison of Imputation Methods for Missing Values in Air Pollution Data: Case Study on Sydney Air Quality Index. In Proceedings of the Advances in Information and Communication, Future of Information and Communication Conference (FICC), San Francisco, CA, USA, 5–6 March 2020. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Moritz, S.; Zaefferer, M.; Stork, J.; Bartz-Beielstein, T.; Bartz-Beielstein, T. Data Preprocessing: A New Algorithm for Univariate Imputation Designed Specifically for Industrial Needs. In Proceedings of the Workshop on Computational Intelligence, Dortmund, Germany, 24–25 November 2016. [Google Scholar]
- Demirhan, H.; Renwick, Z. Missing value imputation for short to mid-term horizontal solar irradiance data. Appl. Energy 2018, 225, 998–1012. [Google Scholar] [CrossRef]
- Afrifa-Yamoah, E.; Mueller, U.A.; Taylor, S.M.; Fisher, A.J. Missing data imputation of high-resolution temporal climate time series data. Meteor. Appl. 2020, 27, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Moritz, S.; Sardá, A.; Bartz-Beielstein, T.; Zaefferer, M.; Stork, J. Comparison of different methods for univariate time series imputation in R. arXiv 2015. [Google Scholar] [CrossRef]
- Jadhav, A.; Pramod, D.; Ramanathan, K. Comparison of performance of data imputation methods for numeric dataset. Appl. Artif. Intel. 2019, 33, 913–933. [Google Scholar] [CrossRef]
- Alsaber, A.; Al-Herz, A.; Pan, J.; AL-Sultan, A.T.; Mishra, D.; KRRD Group. Handling missing data in a rheumatoid arthritis registry using random forest approach. Int. J. Rheum. Dis. 2021, 24, 1282–1293. [Google Scholar]
- Alsaber, A.; Pan, J.; Al-Hurban, A. Handling complex missing data using random forest approach for an air quality monitoring dataset: A case study of Kuwait environmental data (2012 to 2018). Int. J. Environ. Res. Public Health 2021, 18, 1333. [Google Scholar] [CrossRef]
- Ben Aissia, M.A.; Chebana, F.; Ouarda, T.B.M.J. Multivariate missing data in hydrology—Review and applications. Adv. Water Res. 2017, 110, 299–309. [Google Scholar] [CrossRef] [Green Version]
- Hamzah, F.B.; Hamzah, F.M.; Razali, S.F.M.; Samad, H. A comparison of multiple imputation methods for recovering missing data in hydrological studies. Civil Eng. J. 2021, 7, 1608–1619. [Google Scholar] [CrossRef]
- Hamzah, F.B.; Hamzah, F.M.; Razali, S.F.M.; El-Shafie, A. Multiple imputations by chained equations for recovering missing daily streamflow observations: A case study of Langat River basin in Malaysia. Hydrol. Sci. 2022, 67, 137–149. [Google Scholar] [CrossRef]
- Oyerinde, G.T.; Lawin, A.E.; Adeyeri, O.E. Multi-variate infilling of missing daily discharge data on the Niger basin. Water Pract. Techno. 2021, 16, 961–979. [Google Scholar] [CrossRef]
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Santos, M.S.; Pereira, R.C.; Costa, A.F.; Soares, J.P.; Santos, J.; Abreu, P.H. Generating Synthetic Missing Data: A Review by Missing Mechanism. IEEE Access 2019, 7, 11651–11667. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter. In Technical Report TR 95–041; Department of Computer Science, University of North Carolina: Chapel Hill, NC, USA, 1995. [Google Scholar]
- Maybeck, P.S. Chapter 1 Introduction. In Stochastic Models Estimation and Control (Mathematics in Science and Engineering); Maybeck, P.S., Ed.; Academic Press: London, UK, 1979; pp. 1–24. [Google Scholar]
- Durbin, J.; Koopman, S.J. Time Series Analysis by State Space Methods, 2nd ed.; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Fulton, C.T. Sectoral Prices and Price-Setting. Ph.D Thesis, University of Oregon, Eugene, OR, USA, 2016. [Google Scholar]
- Cleveland, R.B.; Cleveland, W.S.; McRee, J.E.; Terpenning, I. STL: A seasonal-trend decomposition procedure based on loess. J. Off. Stat. 1990, 6, 3–33. [Google Scholar]
- Eskelson, B.N.; Temesgen, H.; Lemay, V.; Barrett, T.M.; Crookston, N.L.; Hudak, A.T. The roles of nearest neighbor methods in imputing missing data in forest inventory and monitoring databases. Scand. J. For. Res. 2009, 24, 235–246. [Google Scholar] [CrossRef] [Green Version]
- Kowarik, A.; Templ, M. Imputation with the R Package VIM. J. Stat. Softw. 2016, 74, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Shao, J. Nearest neighbor imputation for survey data. J. Off. Stats. 2000, 16, 113–131. [Google Scholar]
- Gower, J.C. A general coefficient of similarity and some of its properties. Biometrics 1971, 27, 857–871. [Google Scholar] [CrossRef]
- Rubin, D.B. Statistical matching and file concatenation with adjusted weights and multiple imputations. J. Bus. Econ. Stats. 1986, 4, 87–94. [Google Scholar] [CrossRef]
- van Buuren, S.; Groothuis-Oudshoorn, K. mice: Multivariate Imputation by Chained Equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Introduction to Random Forest in Machine Learning. Available online: https://www.section.io/engineering-education/introduction-to-random-forest-in-machine-learning/ (accessed on 2 November 2022).
- Stekhoven, D.J.; Buehlmann, P. MissForest-nonparametric missing value imputation for mixed-type data. Bioinformatics 2012, 28, 112–118. [Google Scholar] [CrossRef] [Green Version]
- Doove, L.L.; Van Buuren, S.; Dusseldorp, E. Recursive partitioning for missing data imputation in the presence of interaction effects. Comput. Stats. Data Anal. 2014, 72, 92–104. [Google Scholar] [CrossRef]
- Hong, S.; Lynn, H. Accuracy of random-forest-based imputation of missing data in the presence of non-normality, non-linearity, and interaction. BMC Med. Res. Methodol. 2020, 20, 199. [Google Scholar] [CrossRef] [PubMed]
- Tang, F.; Ishwaran, H. Random forest missing data algorithms. statistical analysis data mining. ASA Data Sci. J. 2017, 10, 363–377. [Google Scholar] [CrossRef]
- Ramosaj, B.; Pauly, M. Predicting missing values: A comparative study on nonparametric approaches for imputation. Computing 2019, 34, 1741–1764. [Google Scholar] [CrossRef]
- Solaro, N.; Barbiero, A.; Manzi, G.; Ferrari, P.A. A simulation comparison of imputation methods for quantitative data in the presence of multiple data patterns. J. Stats. Comput. Sim. 2018, 88, 588–619. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Devel. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean absolute percentage error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef] [Green Version]
- Boehmke, B.; Greenwell, B.M. Hands-On Machine Learning with R, 1st ed.; CRC Press: New York, NY, USA, 2019. [Google Scholar] [CrossRef]
- Muinonen, E.; Maltamo, M.; Hyppänen, H.; Vainikainen, V. Forest stand characteristics estimation using a most similar neighbor approach and image spatial structure information. Remote Sens. Environ. 2001, 78, 223–228. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Nelson, M.D.; Wendt, D.G. Stratified estimation of forest area using satellite imagery, inventory data, and the k-nearest neighbors technique. Remote Sens. Environ. 2002, 82, 457–468. [Google Scholar] [CrossRef]
- Clavel, J.; Merceron, G.; Escarguel, G. Missing data estimation in morphometrics: How much is too much? Syst. Biol. 2014, 63, 203–218. [Google Scholar] [CrossRef]
- Madley-Dowd, P.; Hughes, R.; Tilling, K.; Heron, J. The proportion of missing data should not be used to guide decisions on multiple imputation. J. Clin. Epidem. 2019, 110, 63–73. [Google Scholar] [CrossRef] [PubMed] [Green Version]
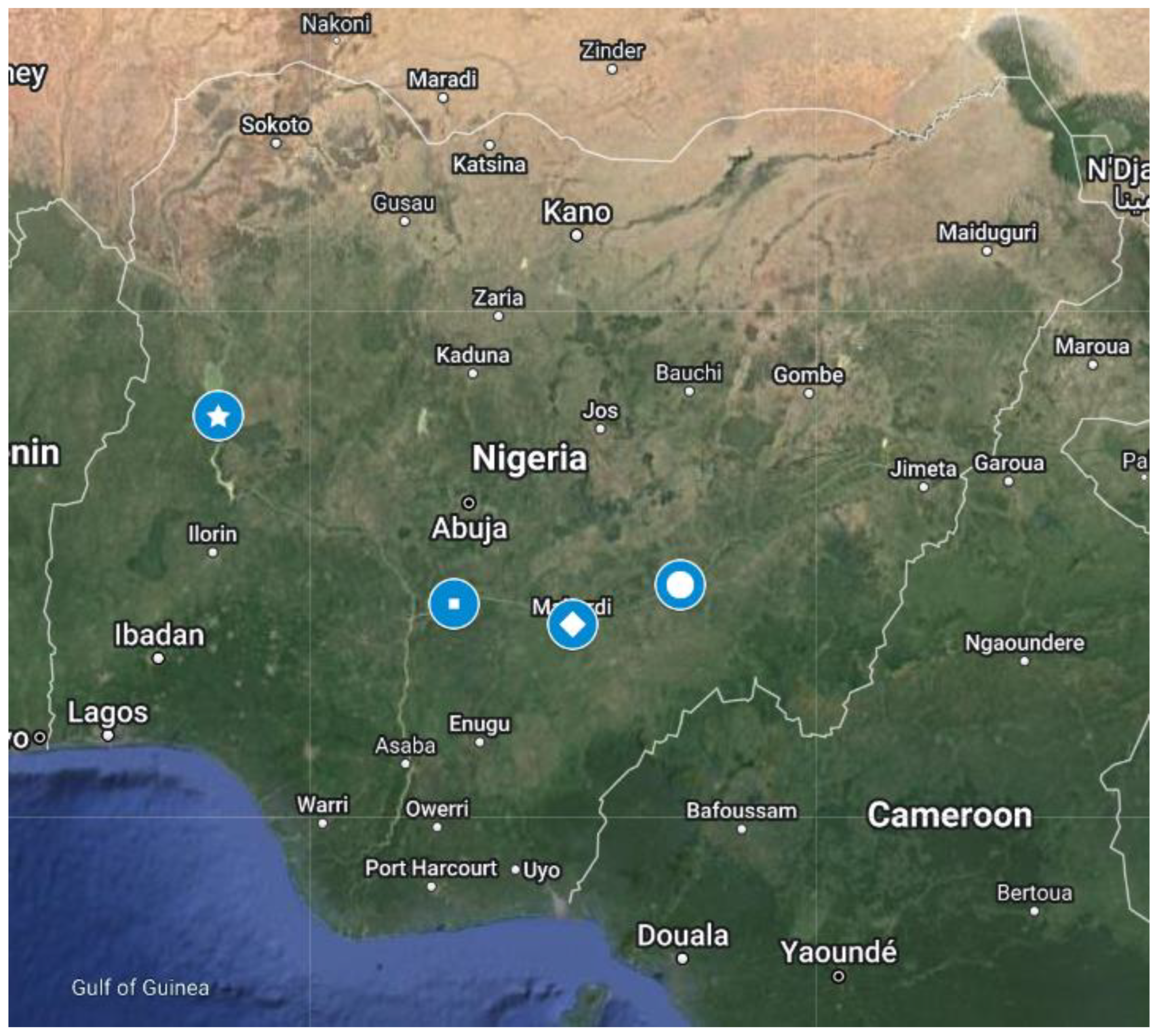
| Water Station | State | River | Established (Year) | Time (Month) | Latitude (Degrees) | Longitude (Degrees) |
|---|---|---|---|---|---|---|
| Kainji | Niger | Niger | 1980 | 2010–2016 | 10.0300 | 4.6000 |
| Ibi | Taraba | Benue | 1980 | 2011–2016 | 8.1800 | 9.7200 |
| Makurdi | Benue | Benue | 2010 | 2011–2016 | 7.7500 | 8.5300 |
| Umaisha | Nasarawa | Benue | 1980 | 2011–2016 | 7.9800 | 7.2000 |
| % Missing | Method | MCAR | RMSE MAR | MNAR | |||
|---|---|---|---|---|---|---|---|
| 5 | KS | 13.61 | (8.94) | 16.35 | (11.68) | 15.61 | (10.80) |
| Random | 102.60 | (35.74) | 96.28 | (27.07) | 92.76 | (27.84) | |
| Sdec | 10.46 | (5.96) | 13.53 | (7.98) | 13.76 | (7.60) | |
| 10 | KS | 25.36 | (13.49) | 22.44 | (11.62) | 25.42 | (12.60) |
| Random | 140.93 | (30.51) | 135.77 | (26.30) | 130.60 | (22.46) | |
| Sdec | 21.22 | (8.83) | 19.12 | (8.46) | 22.33 | (12.05) | |
| 20 | KS | 42.00 | (10.59) | 49.71 | (24.94) | 50.41 | (26.27) |
| Random | 204.30 | (28.58) | 205.60 | (30.97) | 209.40 | (21.59) | |
| Sdec | 34.73 | (8.24) | 39.06 | (10.78) | 37.77 | (9.13) | |
| 30 | KS | 69.53 | (20.06) | 67.12 | (28.94) | 68.04 | (17.96) |
| Random | 253.00 | (33.19) | 247.70 | (23.02) | 248.50 | (27.11) | |
| Sdec | 54.99 | (16.06) | 44.02 | (10.26) | 45.90 | (12.76) | |
| 40 | KS | 96.19 | (21.31) | 108.53 | (32.82) | 97.17 | (29.80) |
| Random | 287.70 | (25.80) | 287.20 | (25.45) | 286.60 | (27.53) | |
| Sdec | 73.24 | (25.38) | 75.16 | (32.89) | 71.58 | (28.49) | |
| 50 | KS | 134.41 | (29.58) | 134.38 | (29.17) | 141.40 | (46.30) |
| Random | 318.10 | (27.76) | 320.50 | (23.43) | 319.90 | (25.10) | |
| Sdec | 112.91 | (44.28) | 97.97 | (52.64) | 102.70 | (41.57) | |
| % Missing | Method | MCAR | MAPE × 103 MAR | MNAR | |||
|---|---|---|---|---|---|---|---|
| 5 | KS | 0.18 | (0.13) | 0.19 | (0.09) | 0.19 | (0.13) |
| Random | 1.27 | (0.44) | 1.08 | (0.35) | 1.23 | (0.52) | |
| Sdec | 0.16 | (0.10) | 0.18 | (0.09) | 0.17 | (0.12) | |
| 10 | KS | 0.39 | (0.16) | 0.38 | (0.15) | 0.35 | (0.16) |
| Random | 2.45 | (0.72) | 2.87 | (0.64) | 2.65 | (0.64) | |
| Sdec | 0.36 | (0.14) | 0.33 | (0.13) | 0.33 | (0.14) | |
| 20 | KS | 1.02 | (0.41) | 1.05 | (0.36) | 0.90 | (0.33) |
| Random | 5.56 | (1.02) | 5.40 | (0.95) | 5.91 | (0.92) | |
| Sdec | 0.79 | (0.23) | 0.83 | (0.20) | 0.76 | (0.20) | |
| 30 | KS | 1.90 | (0.56) | 2.11 | (1.25) | 1.85 | (0.63) |
| Random | 7.98 | (1.21) | 7.56 | (1.54) | 8.36 | (0.98) | |
| Sdec | 1.41 | (0.71) | 1.46 | (0.51) | 1.35 | (0.27) | |
| 40 | KS | 3.27 | (0.65) | 3.19 | (1.51) | 3.39 | (0.88) |
| Random | 11.01 | (1.10) | 11.01 | (1.34) | 10.91 | (1.28) | |
| Sdec | 2.52 | (1.31) | 2.36 | (1.17) | 2.29 | (1.03) | |
| 50 | KS | 5.25 | (1.71) | 4.70 | (0.99) | 5.47 | (1.09) |
| Random | 11.07 | (1.11) | 13.01 | (1.34) | 13.91 | (1.28) | |
| Sdec | 4.32 | (1.96) | 3.87 | (1.76) | 4.14 | (1.60) | |
| % Missing | Method | MCAR | MAR | MNAR | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ibi | Makurdi | Umaisha | Ibi | Makurdi | Umaisha | Ibi | Makurdi | Umaisha | ||
| 10 | RF | 22.51 | 21.24 | 50.24 | 21.02 | 26.02 | 53.51 | 25.80 | 31.33 | 66.74 |
| kNN | 17.17 | 16.22 | 36.61 | 19.55 | 15.39 | 42.42 | 19.11 | 19.47 | 48.17 | |
| MF | 14.60 | 19.24 | 37.71 | 17.25 | 19.13 | 35.06 | 20.18 | 19.67 | 54.26 | |
| PMM | 25.98 | 24.21 | 47.57 | 26.71 | 25.95 | 55.31 | 26.35 | 24.96 | 58.47 | |
| 20 | RF | 36.81 | 36.56 | 81.04 | 34.71 | 34.15 | 85.84 | 39.21 | 32.43 | 76.44 |
| kNN | 23.84 | 25.51 | 73.77 | 28.48 | 24.92 | 64.24 | 32.97 | 33.66 | 70.32 | |
| MF | 26.76 | 28.60 | 62.10 | 25.00 | 28.30 | 56.36 | 28.22 | 32.90 | 76.22 | |
| PMM | 33.16 | 39.17 | 67.82 | 34.28 | 38.65 | 87.78 | 41.99 | 41.25 | 94.16 | |
| 30 | RF | 45.66 | 47.17 | 99.47 | 44.66 | 43.07 | 100.85 | 49.17 | 43.93 | 106.59 |
| kNN | 31.86 | 36.19 | 79.21 | 33.11 | 37.80 | 74.05 | 38.69 | 38.79 | 83.80 | |
| MF | 33.19 | 39.19 | 85.16 | 38.45 | 35.64 | 94.59 | 39.62 | 39.89 | 91.93 | |
| PMM | 42.01 | 49.13 | 103.32 | 42.58 | 44.98 | 97.24 | 51.59 | 48.11 | 115.20 | |
| 40 | RF | 49.67 | 56.49 | 123.15 | 51.36 | 54.03 | 118.37 | 50.94 | 56.74 | 129.32 |
| kNN | 36.40 | 46.46 | 94.26 | 41.16 | 43.94 | 92.94 | 43.67 | 46.00 | 97.40 | |
| MF | 39.69 | 46.75 | 101.41 | 36.90 | 43.16 | 98.50 | 46.99 | 46.30 | 102.40 | |
| PMM | 57.15 | 61.82 | 127.80 | 48.60 | 63.14 | 117.17 | 58.36 | 55.54 | 129.24 | |
| 50 | RF | 59.70 | 64.19 | 136.39 | 62.00 | 62.59 | 139.55 | 56.40 | 58.46 | 147.40 |
| kNN | 44.69 | 48.28 | 109.82 | 45.45 | 51.10 | 117.73 | 49.19 | 54.01 | 111.92 | |
| MF | 45.76 | 52.00 | 106.10 | 49.49 | 46.83 | 106.82 | 49.75 | 53.94 | 111.39 | |
| PMM | 61.52 | 69.37 | 140.91 | 57.11 | 67.09 | 150.09 | 66.30 | 69.90 | 134.70 | |
| % Missing | Method | MCAR | MAR | MNAR | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ibi | Makurdi | Umaisha | Ibi | Makurdi | Umaisha | Ibi | Makurdi | Umaisha | ||
| 10 | RF | 0.0092 | 0.0062 | 0.0287 | 0.0079 | 0.0081 | 0.0526 | 0.0073 | 0.0070 | 0.0229 |
| kNN | 0.0062 | 0.0045 | 0.0348 | 0.0075 | 0.0041 | 0.0320 | 0.0055 | 0.0045 | 0.0181 | |
| MF | 0.0050 | 0.0054 | 0.0206 | 0.0062 | 0.0057 | 0.0249 | 0.0054 | 0.0043 | 0.0168 | |
| PMM | 0.0094 | 0.0065 | 0.0617 | 0.0111 | 0.0073 | 0.0407 | 0.0060 | 0.0050 | 0.0143 | |
| 20 | RF | 0.0178 | 0.0131 | 0.0877 | 0.0169 | 0.0123 | 0.1907 | 0.0143 | 0.0079 | 0.0232 |
| kNN | 0.0118 | 0.0094 | 0.0925 | 0.0138 | 0.0087 | 0.0902 | 0.0134 | 0.0104 | 0.0336 | |
| MF | 0.0105 | 0.0103 | 0.0507 | 0.0119 | 0.0109 | 0.0610 | 0.0115 | 0.0099 | 0.0273 | |
| PMM | 0.0159 | 0.0155 | 0.1973 | 0.0173 | 0.0133 | 0.1089 | 0.0171 | 0.0122 | 0.0401 | |
| 30 | RF | 0.0255 | 0.0210 | 0.1192 | 0.0266 | 0.0181 | 0.1654 | 0.0228 | 0.0161 | 0.0556 |
| kNN | 0.0177 | 0.0154 | 0.0967 | 0.0178 | 0.0172 | 0.1260 | 0.0174 | 0.0148 | 0.0396 | |
| MF | 0.0206 | 0.0170 | 0.1554 | 0.0230 | 0.0159 | 0.1524 | 0.0191 | 0.0145 | 0.0465 | |
| PMM | 0.0225 | 0.0224 | 0.2060 | 0.0257 | 0.0215 | 0.1519 | 0.0233 | 0.0179 | 0.0927 | |
| 40 | RF | 0.0337 | 0.0271 | 0.1634 | 0.0357 | 0.0270 | 0.2377 | 0.0292 | 0.0242 | 0.0793 |
| kNN | 0.0239 | 0.0225 | 0.1347 | 0.0282 | 0.0218 | 0.1942 | 0.0233 | 0.0197 | 0.0863 | |
| MF | 0.0279 | 0.0238 | 0.1616 | 0.0224 | 0.0218 | 0.2269 | 0.0253 | 0.0195 | 0.0800 | |
| PMM | 0.0388 | 0.0342 | 0.1859 | 0.0330 | 0.0345 | 0.2118 | 0.0352 | 0.0239 | 0.1587 | |
| 50 | RF | 0.0422 | 0.0358 | 0.2513 | 0.0452 | 0.0351 | 0.2330 | 0.0347 | 0.0275 | 0.1258 |
| kNN | 0.0346 | 0.0251 | 0.1972 | 0.0344 | 0.0286 | 0.2434 | 0.0293 | 0.0257 | 0.1129 | |
| MF | 0.0326 | 0.0298 | 0.2098 | 0.0393 | 0.0252 | 0.1895 | 0.0315 | 0.0260 | 0.1061 | |
| PMM | 0.0505 | 0.0425 | 0.3913 | 0.0398 | 0.0376 | 0.2812 | 0.0435 | 0.0344 | 0.1089 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Umar, N.; Gray, A. Comparing Single and Multiple Imputation Approaches for Missing Values in Univariate and Multivariate Water Level Data. Water 2023, 15, 1519. https://doi.org/10.3390/w15081519
Umar N, Gray A. Comparing Single and Multiple Imputation Approaches for Missing Values in Univariate and Multivariate Water Level Data. Water. 2023; 15(8):1519. https://doi.org/10.3390/w15081519
Chicago/Turabian StyleUmar, Nura, and Alison Gray. 2023. "Comparing Single and Multiple Imputation Approaches for Missing Values in Univariate and Multivariate Water Level Data" Water 15, no. 8: 1519. https://doi.org/10.3390/w15081519





