Risk Assessment Model for the Renewal of Water Distribution Networks: A Practical Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Phase 1—Probability of Failure in the Pipe
2.2. Phase 2—Assessment of the Degree of Impact
2.2.1. Potable Water Quality
2.2.2. Pipe Replacement Cost
2.3. Phase 3—Risk of Failure
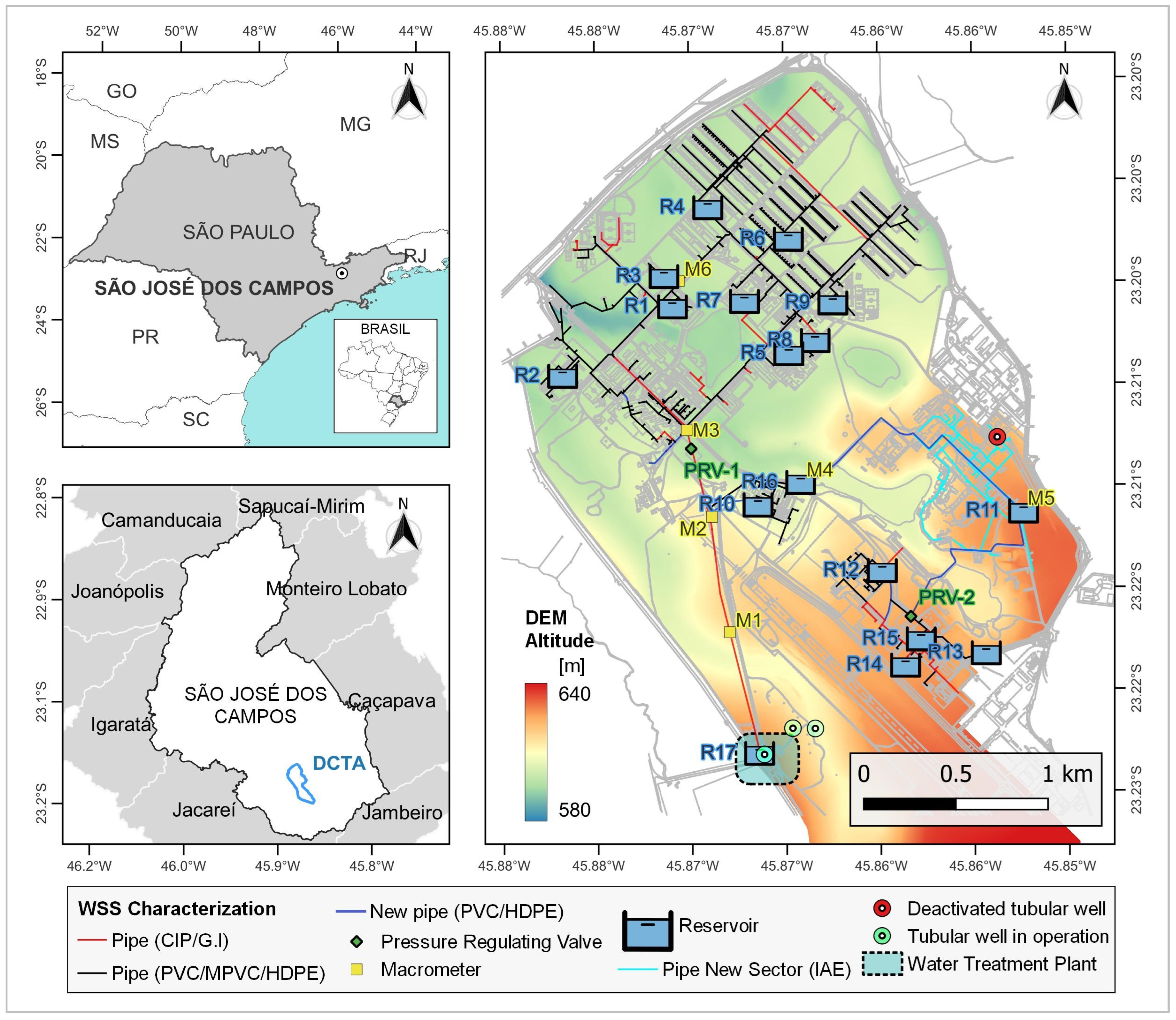
3. Case Study
4. Results
4.1. Phase 1—Probability of Failure
4.2. Phase 2—Assessment of the Degree of Impact
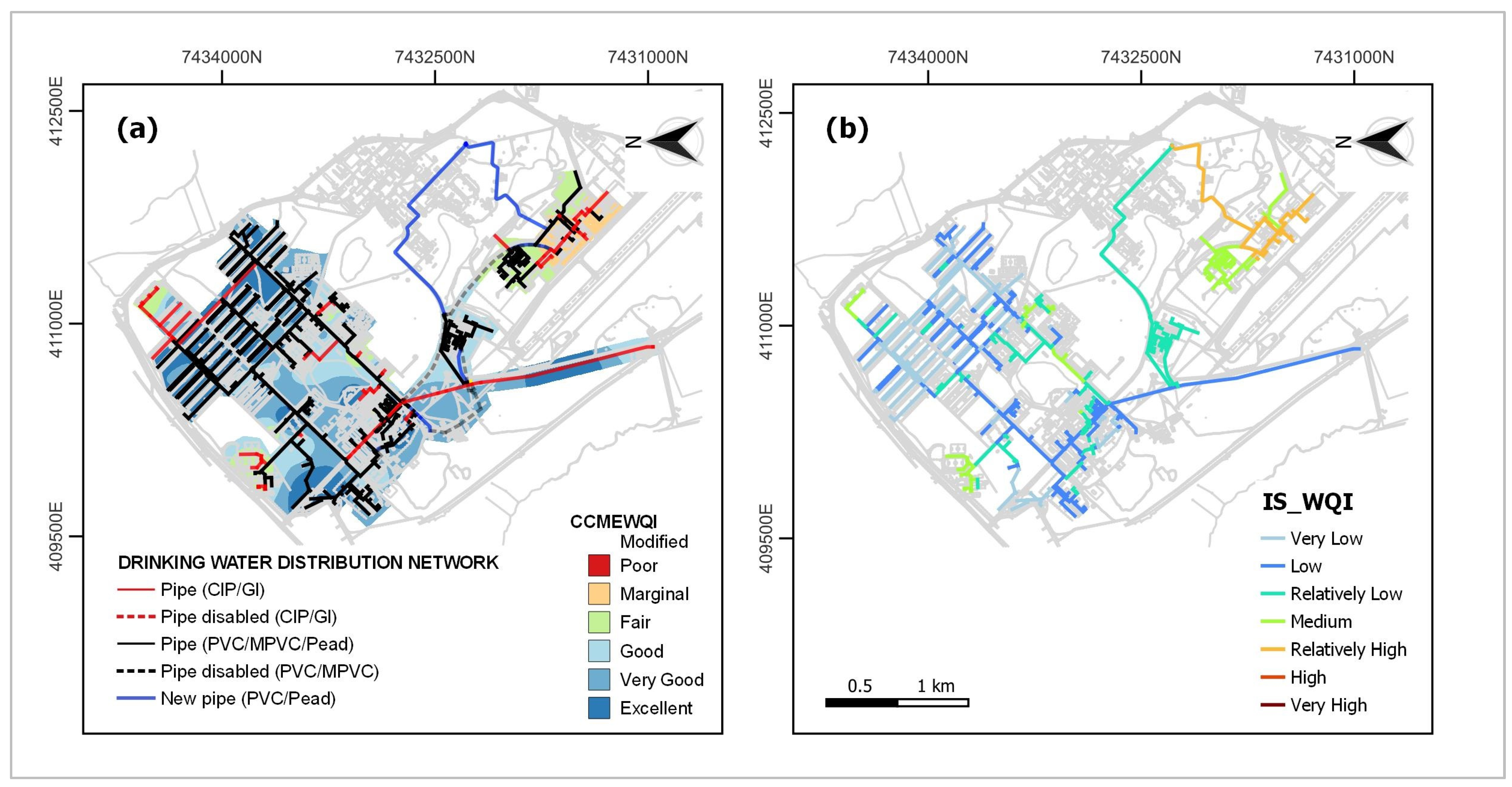
4.2.1. Potable Water Quality
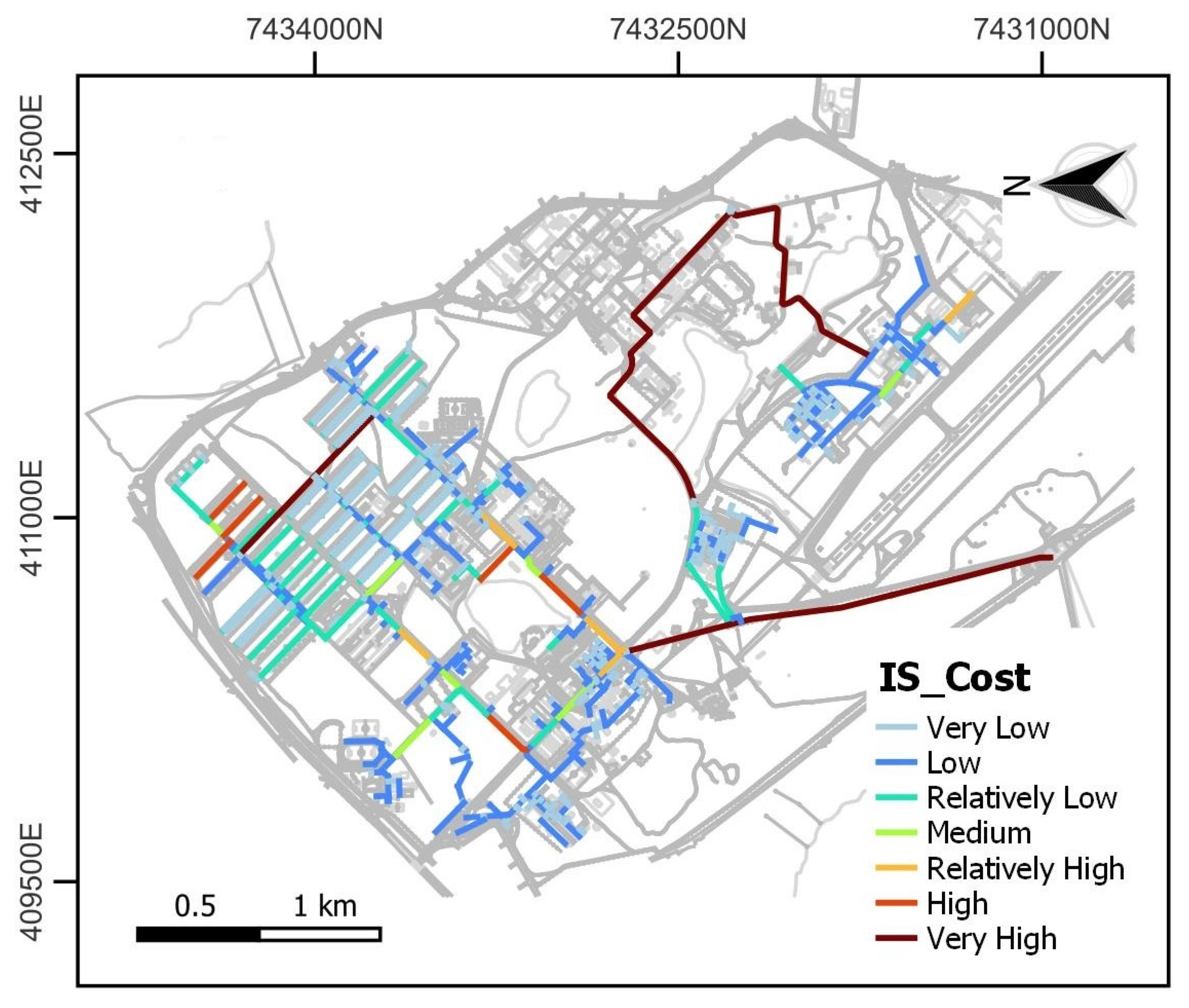
4.2.2. Pipe Replacement Cost
4.3. Phase 3—Risk of Failure
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kabir, G.; Tesfamariam, S.; Francisque, A.; Sadiq, R. Evaluating Risk of Water Mains Failure Using a Bayesian Belief Network Model. Eur. J. Oper. Res. 2015, 240, 220–234. [Google Scholar] [CrossRef]
- Gilbert, T.; James, P.; Smith, L.; Barr, S.; Morley, J. Topological Integration of BIM and Geospatial Water Utility Networks across the Building Envelope. Comput. Environ. Urban Syst. 2021, 86, 101570. [Google Scholar] [CrossRef]
- Minaei, A.; Haghighi, A.; Ghafouri, H.R. Computer-Aided Decision-Making Model for Multiphase Upgrading of Aged Water Distribution Mains. J. Water Resour. Plan. Manag. 2019, 145, 04019008. [Google Scholar] [CrossRef]
- Li, Z.; Liu, H.; Zhang, C.; Fu, G. Generative Adversarial Networks for Detecting Contamination Events in Water Distribution Systems Using Multi-Parameter, Multi-Site Water Quality Monitoring. Environ. Sci. Ecotechnol. 2023, 14, 100231. [Google Scholar] [CrossRef] [PubMed]
- Bakhtiari, P.H.; Nikoo, M.R.; Gandomi, A.H. Chapter 4—Evolutionary Computation Techniques for Optimal Response Actions against Water Distribution Networks Contamination. In Comprehensive Metaheuristics; Mirjalili, S., Gandomi, A.H., Eds.; Academic Press: Cambridge, MA, USA, 2023; pp. 65–84. ISBN 978-0-323-91781-0. [Google Scholar]
- Vishwakarma, A.; Sinha, S.K. Sinha Development of a Risk Modeling Framework for Water Pipeline Renewal Prioritization. Pipelines 2022, 2022, 61–69. [Google Scholar]
- Abd Rahman, N.; Muhammad, N.S.; Wan Mohtar, W.H.M. Evolution of Research on Water Leakage Control Strategies: Where Are We Now? Urban Water J. 2018, 15, 812–826. [Google Scholar] [CrossRef]
- Salehi, S.; Jalili Ghazizadeh, M.; Tabesh, M.; Valadi, S.; Salamati Nia, S.P. A Risk Component-Based Model to Determine Pipes Renewal Strategies in Water Distribution Networks. Struct. Infrastruct. Eng. 2021, 17, 1338–1359. [Google Scholar] [CrossRef]
- Wilson, D.; Filion, Y.; Moore, I. State-of-the-Art Review of Water Pipe Failure Prediction Models and Applicability to Large-Diameter Mains. Urban Water J. 2017, 14, 173–184. [Google Scholar] [CrossRef]
- Scheidegger, A.; Leitao, J.P.; Scholten, L. Statistical Failure Models for Water Distribution Pipes–A Review from a Unified Perspective. Water Res. 2015, 83, 237–247. [Google Scholar] [CrossRef] [PubMed]
- Robles-Velasco, A.; Cortés, P.; Muñuzuri, J.; Onieva, L. Prediction of Pipe Failures in Water Supply Networks Using Logistic Regression and Support Vector Classification. Reliab. Eng. Syst. Saf. 2020, 196, 106754. [Google Scholar] [CrossRef]
- Rifaai, T.M.; Abokifa, A.A.; Sela, L. Integrated Approach for Pipe Failure Prediction and Condition Scoring in Water Infrastructure Systems. Reliab. Eng. Syst. Saf. 2022, 220, 108271. [Google Scholar] [CrossRef]
- Jyrkama, M.I.; Pandey, M.D.; Li, M. Estimating Degradation Growth Rate and Time of Component Replacement from Limited Inspection Data Using Mixed-Effects Modelling. Nucl. Eng. Des. 2022, 388, 111618. [Google Scholar] [CrossRef]
- Kettler, A.J.; Goulter, I.C. An Analysis of Pipe Breakage in Urban Water Distribution Networks. Can. J. Civ. Eng. 1985, 12, 286–293. [Google Scholar] [CrossRef]
- Noori, A.; Bonakdari, H.; Hassaninia, M.; Morovati, K.; Khorshidi, I.; Noori, A.; Gharabaghi, B. A Reliable GIS-Based FAHP-FTOPSIS Model to Prioritize Urban Water Supply Management Scenarios: A Case Study in Semi-Arid Climate. Sustain. Cities Soc. 2022, 81, 103846. [Google Scholar] [CrossRef]
- Dawood, T.; Elwakil, E.; Novoa, H.M.; Delgado, J.F.G. Ensemble Intelligent Systems for Predicting Water Network Condition Index. Sustain. Cities Soc. 2021, 73, 103104. [Google Scholar] [CrossRef]
- Ostfeld, A. Water Distribution Networks. Intelligent Monitoring, Control, and Security of Critical Infrastructure Systems; Kyriakides, E., Polycarpou, M., Eds.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2015; Volume 565, ISBN 978-3-662-44159-6. [Google Scholar]
- Alves, D.; Blesa, J.; Duviella, E.; Rajaoarisoa, L. Leak Detection in Water Distribution Networks Based on Water Demand Analysis. IFAC-Pap. 2022, 55, 679–684. [Google Scholar] [CrossRef]
- Sitaropoulos, K.; Salamone, S.; Sela, L. Frequency-Based Leak Signature Investigation Using Acoustic Sensors in Urban Water Distribution Networks. Adv. Eng. Inform. 2023, 55, 101905. [Google Scholar] [CrossRef]
- Zhang, B.; Wan, W. A Transient-Features-Based Diagnostic Method of Multi Incipient Cracks in Pipeline Systems. Int. J. Press. Vessel. Pip. 2022, 199, 104701. [Google Scholar] [CrossRef]
- Xue, Y.; Yue, L.; Ding, R.; Zhu, S.; Liu, C.; Li, Y. Influencing Mechanisms of Gas Bubbles on Propagation Characteristics of Leakage Acoustic Waves in Gas-Liquid Two-Phase Flow. Ocean. Eng. 2023, 273, 114027. [Google Scholar] [CrossRef]
- Wan, W.; Chen, X.; Zhang, B.; Lian, J. Transient Simulation and Diagnosis of Partial Blockage in Long-Distance Water Supply Pipeline Systems. J. Pipeline Syst. Eng. Pract. 2021, 12, 04021016. Available online: https://ascelibrary.org/doi/10.1061/%28ASCE%29PS.1949-1204.0000562 (accessed on 19 March 2023). [CrossRef]
- Ana, E.V.; Bauwens, W. Modeling the Structural Deterioration of Urban Drainage Pipes: The State-of-the-Art in Statistical Methods. Urban Water J. 2010, 7, 47–59. [Google Scholar] [CrossRef]
- Shahata, K.; Zayed, T. Data Acquisition and Analysis for Water Main Rehabilitation Techniques. Struct. Infrastruct. Eng. 2012, 8, 1054–1066. [Google Scholar] [CrossRef]
- Martins, A.; Leitão, J.P.; Amado, C. Comparative Study of Three Stochastic Models for Prediction of Pipe Failures in Water Supply Systems. J. Infrastruct. Syst. 2013, 19, 442–450. [Google Scholar] [CrossRef]
- Osman, H.; Bainbridge, K. Comparison of Statistical Deterioration Models for Water Distribution Networks. J. Perform. Constr. Facil. 2011, 25, 259–266. [Google Scholar] [CrossRef]
- Tscheikner-Gratl, F.; Sitzenfrei, R.; Rauch, W.; Kleidorfer, M. Enhancement of Limited Water Supply Network Data for Deterioration Modelling and Determination of Rehabilitation Rate. Struct. Infrastruct. Eng. 2016, 12, 366–380. [Google Scholar] [CrossRef]
- Kabir, G.; Sadiq, R.; Tesfamariam, S. A Review of Multi-Criteria Decision-Making Methods for Infrastructure Management. Struct. Infrastruct. Eng. 2014, 10, 1176–1210. [Google Scholar] [CrossRef]
- Marques, J.; Cunha, M. Upgrading Water Distribution Networks to Work under Uncertain Conditions. Water Supply 2020, 20, 878–888. [Google Scholar] [CrossRef] [Green Version]
- Salehi, S.; Jalili Ghazizadeh, M.; Tabesh, M. A Comprehensive Criteria-Based Multi-Attribute Decision-Making Model for Rehabilitation of Water Distribution Systems. Struct. Infrastruct. Eng. 2018, 14, 743–765. [Google Scholar] [CrossRef]
- Trojan, F.; Morais, D.C. Prioritising Alternatives for Maintenance of Water Distribution Networks: A Group Decision Approach. Water SA 2012, 38, 555–564. [Google Scholar] [CrossRef] [Green Version]
- Tscheikner-Gratl, F.; Egger, P.; Rauch, W.; Kleidorfer, M. Comparison of Multi-Criteria Decision Support Methods for Integrated Rehabilitation Prioritization. Water 2017, 9, 68. [Google Scholar] [CrossRef] [Green Version]
- Christodoulou, S.; Deligianni, A.; Aslani, P.; Agathokleous, A. Risk-Based Asset Management of Water Piping Networks Using Neurofuzzy Systems. Comput. Environ. Urban Syst. 2009, 33, 138–149. [Google Scholar] [CrossRef]
- Devera, J. Risk Assessment Model for Pipe Rehabilitation and Replacement in a Water Distribuition System. Master’s Theses, California Polytechnic State University, San Luis Obispo, CA, USA, 2013. [Google Scholar] [CrossRef] [Green Version]
- Cortez, H. A Risk Analysis Model for the Maintenance and Rehabilitation of Pipes in a Water Distribution System: A Statistical Approach. Master’s Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2015. [Google Scholar] [CrossRef]
- D’Ercole, M.; Righetti, M.; Raspati, G.S.; Bertola, P.; Maria Ugarelli, R. Rehabilitation Planning of Water Distribution Network through a Reliability—Based Risk Assessment. Water 2018, 10, 277. [Google Scholar] [CrossRef] [Green Version]
- Salehi, S.; Tabesh, M.; Jalili Ghazizadeh, M. HRDM Method for Rehabilitation of Pipes in Water Distribution Networks with Inaccurate Operational-Failure Data. J. Water Resour. Plan. Manag. 2018, 144, 04018053. [Google Scholar] [CrossRef]
- Grigg, N.S.; Fontane, D.G.; Van Zyl, J. Water Distribution System Risk Tool for Investment Planning; Water Research Foundation: Denver, CO, USA, 2013. [Google Scholar]
- AWWA (American Water Works Association). Rehabilitation of Water Mains-M28; AWWA: Denver, CO, USA, 2014. [Google Scholar]
- Harvey, R.; McBean, E.A.; Gharabaghi, B. Predicting the Timing of Water Main Failure Using Artificial Neural Networks. J. Water Resour. Plan. Manag. 2014, 140, 425–434. Available online: https://ascelibrary.org/doi/10.1061/%28ASCE%29WR.1943-5452.0000354 (accessed on 22 November 2022). [CrossRef]
- St. Clair, A.M.; Sinha, S.K. Development of a Fuzzy Inference Performance Index for Ferrous Drinking Water Pipelines. J. Pipeline Syst. Eng. Pract. 2014, 5, 04014003. [Google Scholar] [CrossRef]
- Kutyłowska, M. Neural Network Approach for Failure Rate Prediction. Eng. Fail. Anal. 2015, 47, 41–48. [Google Scholar] [CrossRef]
- Marzouk, M.; Osama, A. Fuzzy-Based Methodology for Integrated Infrastructure Asset Management. Int. J. Comput. Intell. Syst. 2017, 10, 745–759. [Google Scholar] [CrossRef] [Green Version]
- Winkler, D.; Haltmeier, M.; Kleidorfer, M.; Rauch, W.; Tscheikner-Gratl, F. Pipe Failure Modelling for Water Distribution Networks Using Boosted Decision Trees. Struct. Infrastruct. Eng. 2018, 14, 1402–1411. [Google Scholar] [CrossRef] [Green Version]
- Phan, H.C.; Dhar, A.S.; Hu, G.; Sadiq, R. Managing Water Main Breaks in Distribution Networks––A Risk-Based Decision Making. Reliab. Eng. Syst. Saf. 2019, 191, 106581. [Google Scholar] [CrossRef]
- Boryczko, K.; Piegdoń, I.; Szpak, D.; Żywiec, J. Risk Assessment of Lack of Water Supply Using the Hydraulic Model of the Water Supply. Resources 2021, 10, 43. [Google Scholar] [CrossRef]
- Raspati, G.S.; Bruaset, S.; Bosco, C.; Mushom, L.; Johannessen, B.; Ugarelli, R. A Risk-Based Approach in Rehabilitation of Water Distribution Networks. Int. J. Environ. Res. Public Health 2022, 19, 1594. [Google Scholar] [CrossRef] [PubMed]
- Dandy, G.C.; Engelhardt, M.O. Multi-Objective Trade-Offs between Cost and Reliability in the Replacement of Water Mains. J. Water Resour. Plan. Manag. 2006, 132, 79–88. [Google Scholar] [CrossRef]
- Francisque, A.; Rodriguez, M.J.; Sadiq, R.; Miranda, L.F.; Proulx, F. Prioritizing Monitoring Locations in a Water Distribution Network: A Fuzzy Risk Approach. J. Water Supply Res. Technol.—AQUA 2009, 58, 488–509. [Google Scholar] [CrossRef]
- Rajani, B.; Kleiner, Y. Towards Pro-Active Rehabilitation Planning of Water Supply Systems. In Proceedings of the International Conference on Computer Rehabilitation of Water Networks-CARE-W, Dresden, Germany, 1 November 2002. [Google Scholar]
- Yamijala, S.; Guikema, S.D.; Brumbelow, K. Statistical Models for the Analysis of Water Distribution System Pipe Break Data. Reliab. Eng. Syst. Saf. 2009, 94, 282–293. [Google Scholar] [CrossRef]
- Sadiq, R.; Kleiner, Y.; Rajani, B. Water Quality Failures in Distribution Networks—Risk Analysis Using Fuzzy Logic and Evidential Reasoning. Risk Anal. Int. J. 2007, 27, 1381–1394. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Wang, L.; Shi, W.; Li, C.; Wei, G. Motion Adsorption Characteristics of Particulate Matter in Water Supply Network. Water 2022, 14, 3550. [Google Scholar] [CrossRef]
- Desta, W.M.; Feyessa, F.F.; Debela, S.K. Modeling and Optimization of Pressure and Water Age for Evaluation of Urban Water Distribution Systems Performance. Heliyon 2022, 8, e11257. [Google Scholar] [CrossRef]
- Martínez, F.A.; Lerma, N.; Redhisp Group. “QGISRed v.0.15” QGIS Plugin. Institute of Water and Environmental Engineering Technical University of Valencia: València, Spain, March 2022. Available online: Https://Github.Com/Neslerel/QGISRed/Releases/Tag/v0.15 (accessed on 25 April 2022).
- Rossman, L.A. EPANET 2.0-Manual Do Usuário (Tradução e Adaptação); Tradução: Heber Pimentel GOMES e Moisés Menezes SALVINO; Laboratório de Eficiência Energética e Hidraúlica em Saneamento, Universidade Federal da Paraíba (UFPB); United States Environmental Protection Agency (EPA): Cincinati, OH, USA, 2009.
- NBR 12218; Projeto de Rede de Distribuição de Água Para Abastecimento Público—Procedimento. Associação Brasileira de Normas Técnicas (ABNT): Rio de Janeiro, Brazil, 2017.
- Netto, A.; Fernández, M.F. y Manual de Hidráulica; Editora Blucher: São Paulo, Brazil, 2018; ISBN 978-85-212-0889-1. [Google Scholar]
- Haider, H.; Alkhowaiter, M.H.; Shafiquzzaman, M.; AlSaleem, S.S.; Almoshaogeh, M.; Alharbi, F. Spatiotemporal Water Quality Variations in Smaller Water Supply Systems: Using Modified CCME WQI from Groundwater Source to Distribution Networks Spatiotemporal Water Quality Variations in Smaller Water Supply Systems: Using Modified CCME WQI from Groundwater Source to Distribution Networks. Water 2019, 11, 1884. [Google Scholar] [CrossRef] [Green Version]
- Giustolisi, O.; Laucelli, D.; Savic, D.A. Development of Rehabilitation Plans for Water Mains Replacement Considering Risk and Cost-Benefit Assessment. Civ. Eng. Environ. Syst. 2006, 23, 175–190. [Google Scholar] [CrossRef]
- Rogers, P.D.; Grigg, N.S. Failure Assessment Modeling to Prioritize Water Pipe Renewal: Two Case Studies. J. Infrastruct. Syst. 2009, 15, 162–171. [Google Scholar] [CrossRef]
- SABESP. Banco de Preços de Obras e Serviços de Engenharia; SABESP: São Paulo, Brazil, 2022. [Google Scholar]
- Okabe, M.; Ito, K. Color Universal Design (Cud)-How to Make Figures and Presentations That Are Friendly to Colorblind People. Retrieved April. 2008, 21, 2017. [Google Scholar]
- Gomes, H.P. Sistemas de Abastecimento de Água: Dimensionamento Econômico e Operação de Redes e Elevatórias, 3rd ed.; Editora Universitária-UFPB: João Pessoa, Brazil, 2009; ISBN 978-85-7745-349-8. [Google Scholar]
- Tsutiya, M.T. Abastecimento de Água, 3rd ed.; Departamento de Engenharia Hidráulica e Sanitária da Escola Politécnica da Universidade de São Paulo: São Paulo, Brazil, 2006; ISBN 85-900823-6-9. [Google Scholar]
- Tesfamariam, S.; Rajani, B.; Sadiq, R. Consideration of Uncertainties to Estimate Structural Capacity of Ageing Cast Iron Water Mains—A Possibilistic Approach. Can. J. Civ. Eng 2006, 33, 1050–1064. [Google Scholar] [CrossRef] [Green Version]
- Najafi, M.; Kulandaivel, G. Pipeline Condition Prediction Using Neural Network Models. In Pipelines 2005: Optimizing Pipeline Design, Operations, and Maintenance in Today’s Economy; ASCE: Reston, VA, USA, 2005; pp. 767–781. [Google Scholar]
- Loucks, D.P. Water Resource Systems Models: Their Role in Planning. J. Water Resour. Plan. Manag. 1992, 118, 214–223. [Google Scholar] [CrossRef]
- Boulos, P.F.; Jacobsen, L.B.; Heath, J.E.; Kamojjala, S.R.I. Real-time Modeling of Water Distribution Systems: A Case Study. Journal-American Water Works Assoc. 2014, 106, E391–E401. [Google Scholar] [CrossRef]
- Walski, T.M. Case Study: Pipe Network Model Calibration Issues. J. Water Resour. Plan. Manag. 1986, 112, 238–249. [Google Scholar] [CrossRef]
- Shamir, U.; Howard, C.D. Engineering Analysis of Water-Distribution Systems. J. Am. Water Works Assoc. 1977, 69, 510–514. [Google Scholar] [CrossRef]
- Lingireddy, S.; Ormsbee, L.E.; Wood, D.J. Calibration of Hydraulic Network Models. Water Encycl. 2005, 3, 313–320. [Google Scholar]
- Haider, H.; Sadiq, R.; Tesfamariam, S. Risk-Based Framework for Improving Customer Satisfaction through System Reliability in Small-Sized to Medium-Sized Water Utilities. J. Manag. Eng. 2016, 32, 04016008. [Google Scholar] [CrossRef]
- Haider, H.; Haydar, S.; Sajid, M.; Tesfamariam, S.; Sadiq, R. Framework for Optimizing Chlorine Dose in Small- to Medium-Sized Water Distribution Systems: A Case of a Residential Neighbourhood in Lahore, Pakistan. Water SA 2015, 41, 614–623. [Google Scholar] [CrossRef]
- Bi, S.; Wang, L.; Li, Y.; Zhang, Z.; Wang, Z.; Ding, X.; Zhou, J. A Comprehensive Method for Water Environment Assessment Considering Trends of Water Quality. Adv. Civ. Eng. 2021, 2021, 5548113. [Google Scholar] [CrossRef]
- Duan, W.; Maskey, S.; Chaffe, P.L.B.; Luo, P.; He, B.; Wu, Y.; Hou, J. Recent Advancement in Remote Sensing Technology for Hydrology Analysis and Water Resources Management. Remote Sens. 2021, 13, 1097. [Google Scholar] [CrossRef]
- Fatima, S.U.; Khan, M.A.; Alamgir, A.; Mahmood, N.; Sulman, N. Multivariate and Spatial Methods-Based Water Quality Assessment of Chu Tran Valley, Gilgit Baltistan. Appl. Water Sci. 2022, 12, 129. [Google Scholar] [CrossRef]
- Elumalai, V.; Brindha, K.; Sithole, B.; Lakshmanan, E. Spatial Interpolation Methods and Geostatistics for Mapping Groundwater Contamination in a Coastal Area. Environ. Sci. Pollut. Res. 2017, 24, 11601–11617. [Google Scholar] [CrossRef]
- Elubid, B.A.; Huang, T.; Ahmed, E.H.; Zhao, J.; Elhag, K.M.; Abbass, W.; Babiker, M.M. Geospatial Distributions of Groundwater Quality in Gedaref State Using Geographic Information System (GIS) and Drinking Water Quality Index (DWQI) Geospatial Distributions of Groundwater Quality in Gedaref State Using Geographic Information System (GIS) and Drinking Water Quality Index (DWQI). Int. J. Environ. Res. Public. Health 2019, 16, 731. [Google Scholar] [CrossRef] [Green Version]
- Haldar, K.; Kujawa-Roeleveld, K.; Dey, P.; Bosu, S.; Datta, D.K.; Rijnaarts, H.H.M. Spatio-Temporal Variations in Chemical-Physical Water Quality Parameters Influencing Water Reuse for Irrigated Agriculture in Tropical Urbanized Deltas. Sci. Total Environ. 2020, 708, 134559. [Google Scholar] [CrossRef]
- García-Ávila, F.; Zhindón-Arévalo, C.; Valdiviezo-Gonzales, L.; Cadme-Galabay, M.; Gutiérrez-Ortega, H.; del Pino, L.F. A Comparative Study of Water Quality Using Two Quality Indices and a Risk Index in a Drinking Water Distribution Network. Environ. Technol. Rev. 2022, 11, 49–61. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Olbert, A.I. A Review of Water Quality Index Models and Their Use for Assessing Surface Water Quality. Ecol. Indic. 2021, 122, 107218. [Google Scholar] [CrossRef]
- Ministerio de La Protección Social y Ministerio de Ambiente, Vivienda y Desarrollo Territorial de Colombia. Resolución 2115 de 2007. Características, Instrumentos Básicos y Frecuencias Del Sistema de Control y Vigilancia Para La Calidad Del Agua Para Consumo Humano; MPS/MAVDT: Bogotá Colombia, 2007. [Google Scholar]
- García-Ubaque, C.A.; García-Ubaque, J.C.; Rodríguez-Miranda, J.P.; Pacheco-García, R.; García-Vaca, M.C. Limitations of the Water Quality Risk Index as an Estimator of Quality for Human Consumption. Rev. Salud Pública 2018, 20, 204–207. [Google Scholar] [CrossRef]
- Duarte-Jaramillo, L.; Mendoza-Atencio, M.A.; Jaramillo-Colorado, B.E.; González-Álvarez, Á. Water Quality in the Municipalities of Sincerín and Gambote, Bolívar, Colombia (2017–2018). Rev. Fac. Ing. Univ. Antioquia 2022, 103, 77–87. [Google Scholar] [CrossRef]
- Canadian Council of Ministers of the Environment (CCME). Canadian Water Quality Guidelines for the Protection of Aquatic Life: Quality Index, User’s Manual—2017 Update. In Canadian Environmental Quality Guidelines; CCME: Winnipeg, Canadian, 1999; Available online: https://ccme.ca/en/res/wqimanualen.pdf (accessed on 23 September 2022).
- WHO. Guidelines for Drinking-Water Quality, 4th ed.; Incorporating the 1st Addendum; Library Cataloguing-in-Publication Data; World Health Organization: Geneva, Switzerland, 2017; ISBN 978-92-4-154995-0.
- Brasil. Ministério da Saúde. Portaria GM/MS no 888, de 04 de maio de 2021. Altera o Anexo XX da Portaria de Consolidação GM/MS no 5, de 28 de Setembro de 2017, Para Dispor Sobre os Procedimentos de Controle e de Vigilância da Qualidade da água para Consumo Humano e seu Padrão de Potabilidade. Diário Oficial União. 2021; p. 127. Available online: https://www.in.gov.br/web/dou (accessed on 23 September 2022).
- Kilgour, B.W.; Francis, A.P.; Mercier, V. Reducing the Sensitivity of the Water Quality Index to Episodic Events. Water Qual. Res. J. Can. 2013, 48, 1–13. [Google Scholar] [CrossRef]
- Nistor, M.M.; Rahardjo, H.; Satyanaga, A.; Hao, K.Z.; Xiaosheng, Q.; Sham, A.W.L. Investigation of Groundwater Table Distribution Using Borehole Piezometer Data Interpolation: Case Study of Singapore. Eng. Geol. 2020, 271, 105590. [Google Scholar] [CrossRef]
- Gotway, C.A.; Ferguson, R.B.; Hergert, G.W.; Peterson, T.A. Comparison of Kriging and Inverse-Distance Methods for Mapping Soil Parameters. Soil Sci. Soc. Am. J. 1996, 60, 1237–1247. [Google Scholar] [CrossRef]

| Year | Authors | Risk 1 | Pipes Renewal Planning 2 | |
|---|---|---|---|---|
| Cat. | No. Criteria | |||
| 2013 | Devera [34] | PFC | M, H, EC, O, E, S | 10 |
| 2014 | Harvey et al. [40] | PFP | M, O | 5 |
| St. Clair and Sinha [41] | PFC | M, H, EC, O, QS | 14 | |
| 2015 | Kutyłowska [42] | PFP | M | 4 |
| 2017 | Marzouk and Osama [43] | PFC | M, H, EC, O, P | 11 |
| 2018 | Winkler et al. [44] | PFP | M, H, O, SL | 10 |
| D’Ercole et al. [36] | PFC | H, O | 3 | |
| Salehi et al. [37] | PFP | M, H | 6 | |
| 2019 | Phan et al. [45] | PFC | M, EC, O, E | 6 |
| 2021 | Salehi et al. [8] 3 | PFC | M, H, EC, P, S, QS | 19 |
| Boryczko et al. [46] | PFC | O, S | 2 | |
| 2022 | Raspati et al. [47] | PFC | M, H, EC, O | 8 |
| Pipe Design Parameters (PDPs) | Risk Level and Corresponding Failure Probability Score (FPSi) | |||||||
|---|---|---|---|---|---|---|---|---|
| V. Low | Low | R. Low | Medium | R. High | High | V. High | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| Hydraulic 1 | Pmin (m.w.c) 2 | 25 | 25–22 | 22–19 | 19–16 | 16–13 | 13–10 | <10 |
| Pmax (m.w.c) 2 | 25 | 25–30 | 30–35 | 35–40 | 40–45 | 45–50 | >50 | |
| Vmin (m/s) 3 | 1–0.9 | 0.9–0.8 | 0.8–0.7 | 0.7–0.6 | 0.6–0.5 | 0.5–0.4 | <0.4 | |
| Vmax (m/s) 3 | 0.9–1 | 1–1.1 | 1.1–1.2 | 1.2–1.3 | 1.3–1.4 | 1.4–1.5 | >1.5 | |
| Flow rate (L/s) | <0.8 | 0.8–21.6 | 21.6–42.5 | 42.5–63.3 | 63.3–84.2 | 84.2–105 | >105 | |
| Mechanical | Length (m) | <10 | 10–108 | 108–206 | 206–304 | 304–402 | 402–500 | >500 |
| Stiffness Ø (mm) | ≥300 | 300–250 | 250–200 | 200–150 | 150–100 | 100–50 | ≤50 | |
| Impact Criteria | Risk Level and Corresponding Impact Score (ISWQI) | ||||||
|---|---|---|---|---|---|---|---|
| V. Low | Low | R. Low | Medium | R. High | High | V. High | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Water Quality Index CCME WQIPipe [59] | 100–95 | 94–89 | 88–80 | 79–65 | 64–45 | 44–25 | 24–0 |
| Diameter (mm) | Abbreviation 1 | Price Per Linear Meter 2 | Pricing Source 3 | |||
|---|---|---|---|---|---|---|
| Material | Labor | Total | Material | Labor | ||
| 50 | G.I | BRL 97.53 | BRL 24.18 | BRL 121.71 | HM01210 | 70,080,034 |
| 100 | BRL 184.20 | BRL 28.19 | BRL 212.39 | HM01213 | 70,080,035 | |
| 100 | CIP | BRL 342.25 | BRL 28.19 | BRL 370.44 | HM04118 | 70,080,035 |
| 200 | BRL 441.19 | BRL 39.29 | BRL 480.48 | HM04105 | 70,080,035 | |
| 300 | BRL 656.56 | BRL 52.80 | BRL 709.36 | HM04107 | 70,080,039 | |
| 50 | BRL 97.53 | BRL 24.18 | BRL 121.71 | HM01210 | 70,080,034 | |
| 60 | BRL 150.09 | BRL 24.18 | BRL 174.27 | HM01211 | 70,080,034 | |
| 85 | BRL 331.56 | BRL 24.18 | BRL 355.74 | HM04129 | 70,080,034 | |
| 125 | HDPE | BRL 94.47 | BRL 26.23 | BRL 120.70 | HM02085 | 70,140,034 |
| 90 | BRL 64.19 | BRL 26.23 | BRL 90.42 | HM02093 | 70,140,034 | |
| 100 | MPVC | BRL 103.41 | BRL 18.62 | BRL 122.03 | HM01930 | 70,080,003 |
| 125 | BRL 103.41 | BRL 18.62 | BRL 122.03 | HM01930 | 70,080,003 | |
| 150 | BRL 182.55 | BRL 21.63 | BRL 204.18 | HM01931 | 70,080,004 | |
| 200 | BRL 323.24 | BRL 23.43 | BRL 346.67 | HM01932 | 70,080,005 | |
| 100 | PVC | BRL 90.32 | BRL 18.62 | BRL 108.94 | HM01914 | 70,080,003 |
| 110 | BRL 90.32 | BRL 18.62 | BRL 108.94 | HM01914 | 70,080,003 | |
| 160 | BRL 130.20 | BRL 21.63 | BRL 151.83 | HM07154 | 70,080,004 | |
| 200 | BRL 215.85 | BRL 23.43 | BRL 239.28 | HM07155 | 70,080,005 | |
| 25 | BRL 4.76 | BRL 2.41 | BRL 7.17 | HM01612 | 70,080,067 | |
| 32 | BRL 9.53 | BRL 9.66 | BRL 19.19 | HM01613 | 70,080,023 | |
| 40 | BRL 16.55 | BRL 13.72 | BRL 30.27 | HM01614 | 70,080,012 | |
| 50 | BRL 19.02 | BRL 16.80 | BRL 35.82 | HM01615 | 70,080,001 | |
| 60 | BRL 25.84 | BRL 16.80 | BRL 42.64 | HM01915 | 70,080,001 | |
| 75 | BRL 51.64 | BRL 17.39 | BRL 69.03 | HM01617 | 70,080,002 | |
| 85 | BRL 55.30 | BRL 17.39 | BRL 72.69 | HM01916 | 70,080,002 | |
| 50 | PVC SSR | BRL 25.84 | BRL 16.80 | BRL 42.64 | HM01915 | 70,080,001 |
| 75 | BRL 55.30 | BRL 17.39 | BRL 72.69 | HM01916 | 70,080,002 | |
| Impact Criteria | Risk Level and Corresponding Impact Score (ISCOST) | |||||||
|---|---|---|---|---|---|---|---|---|
| V. Low | Low | R. Low | Medium | R. High | High | V. High | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| Financial | Cost Range (1.000 × BRL) | 0–2 | 2–19 | 19–36 | 36–53 | 53–70 | 70–87 | >87 |
| TFPS | Total Failure Probability Score | ||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ISTotal | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | |
| Total Impact Score | 2 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 44 | 46 | 48 | 50 | 52 | 54 | 56 | 58 | 60 | 62 | 64 | 66 | 68 | 70 | 72 | 74 | 76 | 78 | 80 | 82 | 84 | 86 | 88 | 90 | 92 | 94 | 96 | 98 |
| 3 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 | 63 | 66 | 69 | 72 | 75 | 78 | 81 | 84 | 87 | 90 | 93 | 96 | 99 | 102 | 105 | 108 | 111 | 114 | 117 | 120 | 123 | 126 | 129 | 132 | 135 | 138 | 141 | 144 | 147 | |
| 4 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 | 84 | 88 | 92 | 96 | 100 | 104 | 108 | 112 | 116 | 120 | 124 | 128 | 132 | 136 | 140 | 144 | 148 | 152 | 156 | 160 | 164 | 168 | 172 | 176 | 180 | 184 | 188 | 192 | 196 | |
| 5 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 | 105 | 110 | 115 | 120 | 125 | 130 | 135 | 140 | 145 | 150 | 155 | 160 | 165 | 170 | 175 | 180 | 185 | 190 | 195 | 200 | 205 | 210 | 215 | 220 | 225 | 230 | 235 | 240 | 245 | |
| 6 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 | 126 | 132 | 138 | 144 | 150 | 156 | 162 | 168 | 174 | 180 | 186 | 192 | 198 | 204 | 210 | 216 | 222 | 228 | 234 | 240 | 246 | 252 | 258 | 264 | 270 | 276 | 282 | 288 | 294 | |
| 7 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 | 147 | 154 | 161 | 168 | 175 | 182 | 189 | 196 | 203 | 210 | 217 | 224 | 231 | 238 | 245 | 252 | 259 | 266 | 273 | 280 | 287 | 294 | 301 | 308 | 315 | 322 | 329 | 336 | 343 | |
| 8 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 | 168 | 176 | 184 | 192 | 200 | 208 | 216 | 224 | 232 | 240 | 248 | 256 | 264 | 272 | 280 | 288 | 296 | 304 | 312 | 320 | 328 | 336 | 344 | 352 | 360 | 368 | 376 | 384 | 392 | |
| 9 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 | 189 | 198 | 207 | 216 | 225 | 234 | 243 | 252 | 261 | 270 | 279 | 288 | 297 | 306 | 315 | 324 | 333 | 342 | 351 | 360 | 369 | 378 | 387 | 396 | 405 | 414 | 423 | 432 | 441 | |
| 10 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 | 210 | 220 | 230 | 240 | 250 | 260 | 270 | 280 | 290 | 300 | 310 | 320 | 330 | 340 | 350 | 360 | 370 | 380 | 390 | 400 | 410 | 420 | 430 | 440 | 450 | 460 | 470 | 480 | 490 | |
| 11 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 | 231 | 242 | 253 | 264 | 275 | 286 | 297 | 308 | 319 | 330 | 341 | 352 | 363 | 374 | 385 | 396 | 407 | 418 | 429 | 440 | 451 | 462 | 473 | 484 | 495 | 506 | 517 | 528 | 539 | |
| 12 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 | 252 | 264 | 276 | 288 | 300 | 312 | 324 | 336 | 348 | 360 | 372 | 384 | 396 | 408 | 420 | 432 | 444 | 456 | 468 | 480 | 492 | 504 | 516 | 528 | 540 | 552 | 564 | 576 | 588 | |
| 13 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 | 273 | 286 | 299 | 312 | 325 | 338 | 351 | 364 | 377 | 390 | 403 | 416 | 429 | 442 | 455 | 468 | 481 | 494 | 507 | 520 | 533 | 546 | 559 | 572 | 585 | 598 | 611 | 624 | 637 | |
| 14 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 | 294 | 308 | 322 | 336 | 350 | 364 | 378 | 392 | 406 | 420 | 434 | 448 | 462 | 476 | 490 | 504 | 518 | 532 | 546 | 560 | 574 | 588 | 602 | 616 | 630 | 644 | 658 | 672 | 686 | |
| RFS Value | Color 1 | Failure Risk Level | Suggested Action 2 | |
|---|---|---|---|---|
| RGB | Description | |||
| ≤69 | (0, 158, 15) | Green | Low | A |
| 70 to 184 | (86, 180, 233) | Blue | Medium | B |
| 185 to 396 | (240, 228, 66) | Yellow | High | C |
| ≥400 | (230, 159, 0) | Orange | Very High | D |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nunes, R.; Arraut, E.; Pimentel, M. Risk Assessment Model for the Renewal of Water Distribution Networks: A Practical Approach. Water 2023, 15, 1509. https://doi.org/10.3390/w15081509
Nunes R, Arraut E, Pimentel M. Risk Assessment Model for the Renewal of Water Distribution Networks: A Practical Approach. Water. 2023; 15(8):1509. https://doi.org/10.3390/w15081509
Chicago/Turabian StyleNunes, Rodrigo, Eduardo Arraut, and Marcio Pimentel. 2023. "Risk Assessment Model for the Renewal of Water Distribution Networks: A Practical Approach" Water 15, no. 8: 1509. https://doi.org/10.3390/w15081509
APA StyleNunes, R., Arraut, E., & Pimentel, M. (2023). Risk Assessment Model for the Renewal of Water Distribution Networks: A Practical Approach. Water, 15(8), 1509. https://doi.org/10.3390/w15081509








