An Assessment Model for the Erosion Occurrence of Gap-Graded Sand-Gravel Soils under Variable Seepage Direction
Abstract
:1. Introduction
2. Prediction of Critical Seepage Velocity for Erosion Occurrence under Variable Seepage Direction
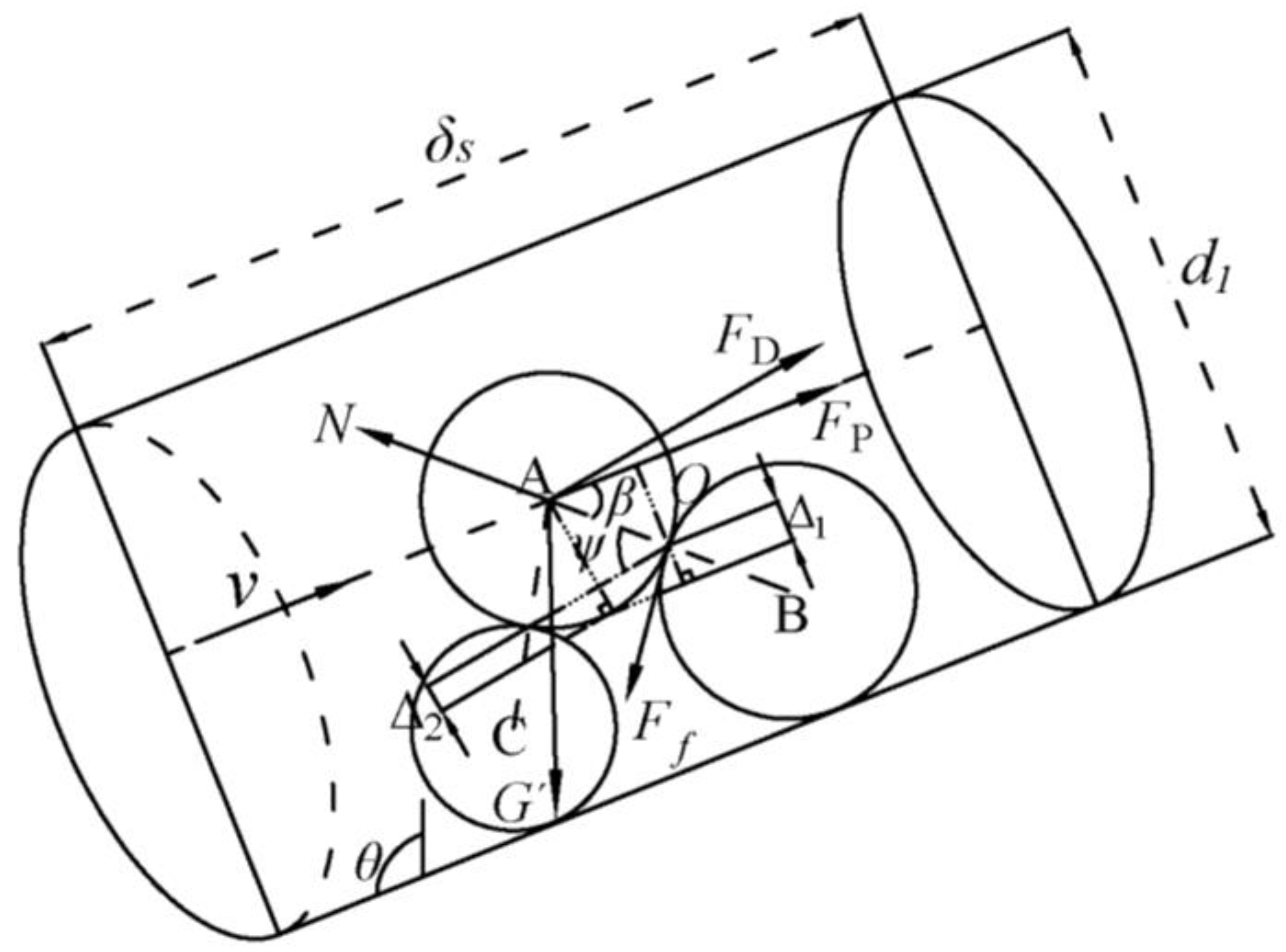
2.1. Force Analysis of Movable Particles
2.2. Analysis of the Relative Exposure Degree and Relative Hidden Degree
2.3. Critical Seepage Velocity for Particle Initiation
3. Simulation of Erosion Occurrence under Variable Seepage Direction
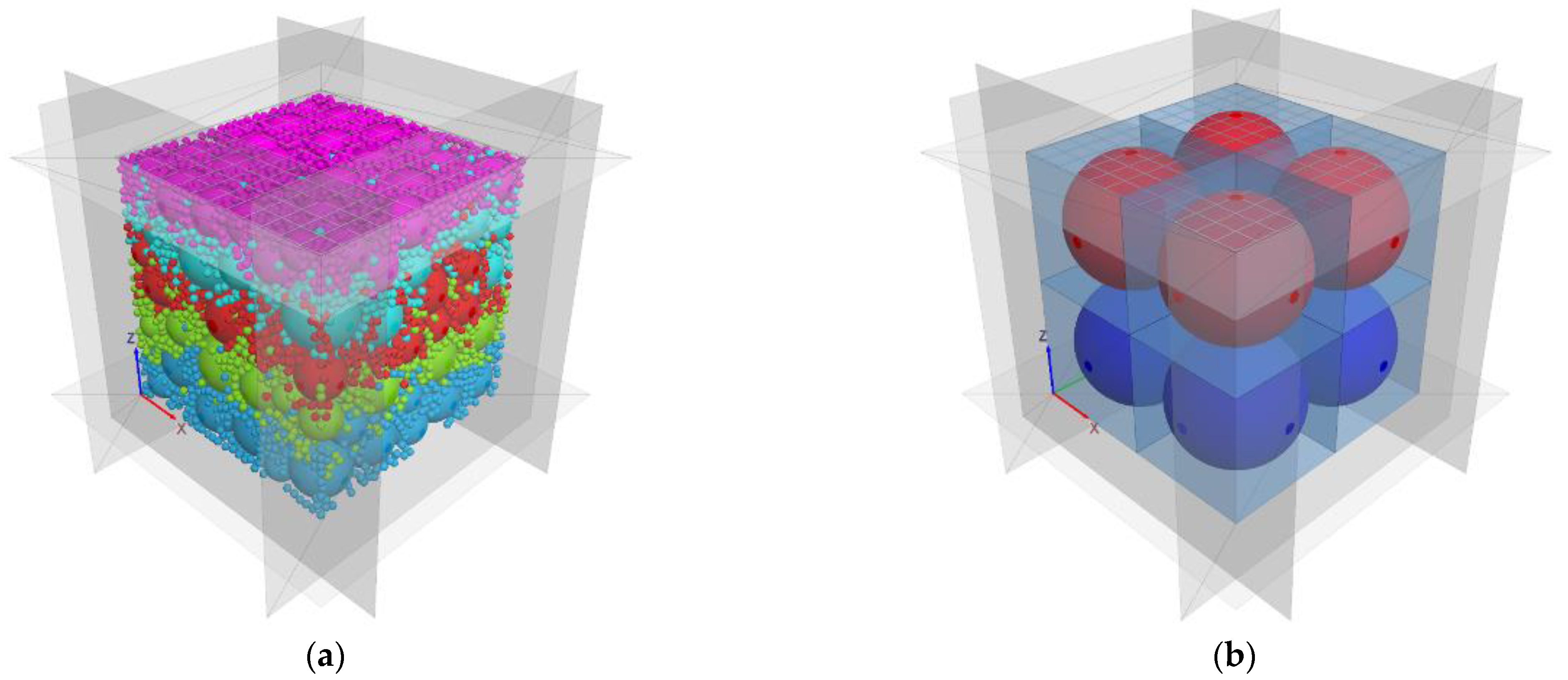
3.1. Numerical Model
3.2. Erosion Simulation Test
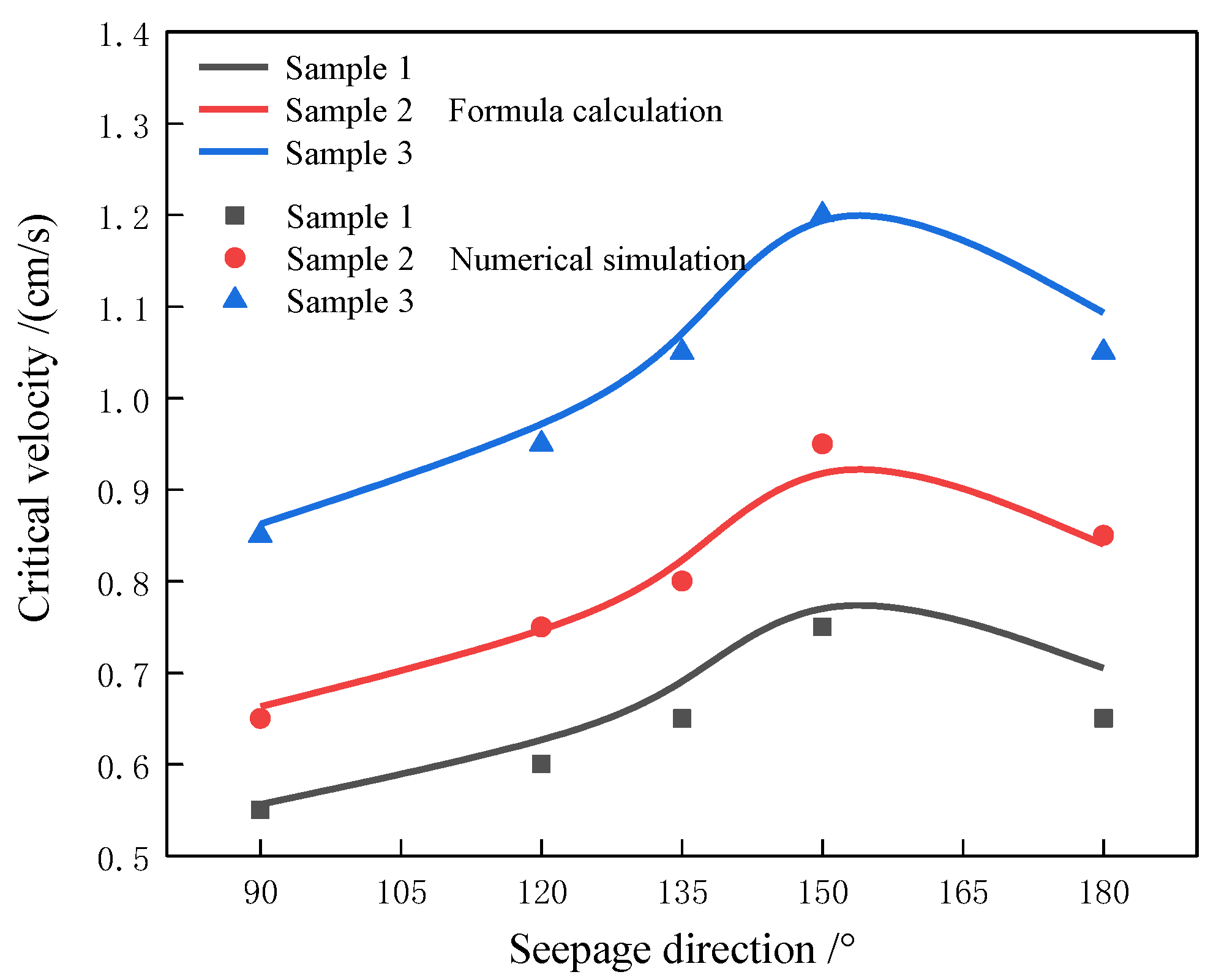
4. Verification of Existing Test Data
5. Analysis of the Differences in Particle Initiation Conditions
5.1. Seepage Direction
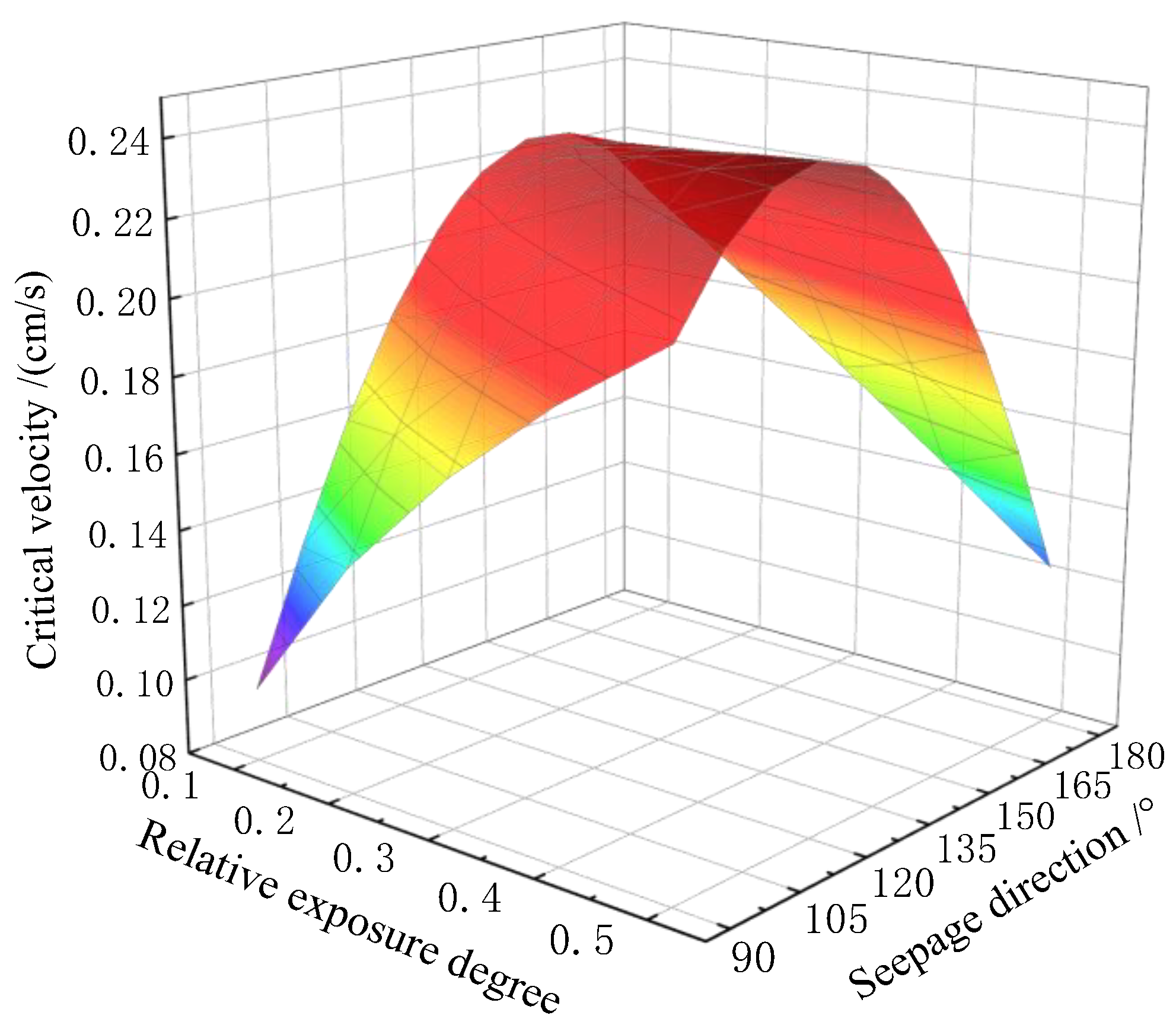
5.2. The Relative Exposure Degree and the Relative Hidden Degree
6. Conclusions
- The model comprehensively considered the effects of the seepage direction and the relative position of particles. Based on the rolling theory of soil particles, the formula for calculating the critical velocity of particles under the variable seepage condition was derived. Further, the hydraulic conditions of seepage erosion in different directions were verified using discrete element numerical simulation and existing test data, which created conditions for subsequent application to two-dimensional seepage.
- In the analysis of the influencing factors, the relative hidden degree was positively correlated with the critical hydraulic conditions of particle initiation, while the relative exposure degree and the seepage direction interact and jointly influence each other. Different from the existing conclusions, the effect of seepage direction on the critical hydraulic conditions was not linear; however, the critical velocity showed a trend of increasing and then decreasing with the increase in seepage direction, due to the influence of relative exposure. Meanwhile, the critical velocity also showed a trend of increasing and then decreasing with the increase in relative exposure in different seepage directions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Foster, M.; Fell, R.; Spannagle, M. The statistics of embankment dam failures and accidents. Can. Geotech. J. 2000, 37, 1000–1024. [Google Scholar] [CrossRef]
- Zhou, H.-B.; Cai, L.-B.; Gao, W.-j. Statistical analysis of the accidents of foundation pit of the urban mass rail transit station. Hydrogeol. Eng. Geol. 2009, 36, 67–71. [Google Scholar] [CrossRef]
- Zheng, G.; Zhu, H.-H.; Liu, X.-R.; Yang, G.-H. Control of safety of deep excavations and underground engineering and its impact on surrounding environment. China Civ. Eng. J. 2016, 49, 1–24. [Google Scholar] [CrossRef]
- Moffat, R.; Herrera, P. Hydromechanical model for internal erosion and its relationship with the stress transmitted by the finer soil fraction. Acta Geotech. 2015, 10, 643–650. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Yang, X.; Zhang, A.; Yu, M. Monte Carlo simulations of deformation behaviour of unbound granular materials based on a real aggregate library. Int. J. Pavement Eng. 2023, 24, 2165650. [Google Scholar] [CrossRef]
- Li, J.; Bi, W.; Yao, Y.; Liu, Z. State-of-the-Art Review of Utilization of Microbial-Induced Calcite Precipitation for Improving Moisture-Dependent Properties of Unsaturated Soils. Appl. Sci. 2023, 13, 2502. [Google Scholar] [CrossRef]
- Kezdi, A. Soil Physics: Selected Topics-Developments in Geotechnical Engineering; Elsevier: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Kenney, T.; Lau, D. Internal stability of granular filters: Reply. Can. Geotech. J. 1986, 23, 420–423. [Google Scholar] [CrossRef]
- Aberg, B. Washout of grains from filtered sand and gravel materials. J. Geotech. Eng. 1993, 119, 36–53. [Google Scholar] [CrossRef]
- Liu, Z.-Y.; Miao, T.-D. Assessment for the noncohesive piping-typed soils. Yantu Lixue/Rock Soil Mech. 2004, 25, 1072–1076. [Google Scholar] [CrossRef]
- Li, H.; Zhu, H.; Wei, X.; Liu, B.; Shao, M. Soil erosion leads to degradation of hydraulic properties in the agricultural region of Northeast China. Agric. Ecosyst. Environ. 2021, 314, 107388. [Google Scholar] [CrossRef]
- Parhizkar, M.; Shabanpour, M.; Lucas-Borja, M.E.; Zema, D.A.; Li, S.; Tanaka, N.; Cerdà, A. Effects of length and application rate of rice straw mulch on surface runoff and soil loss under laboratory simulated rainfall. Int. J. Sediment Res. 2021, 36, 468–478. [Google Scholar] [CrossRef]
- Kudai, K.; Sassa, S.; Yang, S.; Takada, K. Influence of soil and hydraulic conditions on the processes of internal erosion, cavity formation and collapse behind coastal structures. Coast. Eng. 2021, 170, 104013. [Google Scholar] [CrossRef]
- Liu, J. The Stability and Control of Seepage of Soil; China Water&Power Press: Beijing, China, 1992. [Google Scholar]
- Fleshman, M.S.; Rice, J.D. Laboratory Modeling of the Mechanisms of Piping Erosion Initiation. J. Geotech. Geoenvironmental Eng. 2014, 140, 04014017. [Google Scholar] [CrossRef]
- Ojha, C.S.P.; Singh, V.P.; Adrian, D.D. Determination of Critical Head in Soil Piping. J. Hydraul. Eng. 2003, 129, 511–518. [Google Scholar] [CrossRef]
- Okeke, A.C.-U.; Wang, F. Critical hydraulic gradients for seepage-induced failure of landslide dams. Geoenvironmental Disasters 2016, 3, 9. [Google Scholar] [CrossRef] [Green Version]
- Skempton, A.W.; Brogan, J.M. Experiments on piping in sandy gravels. Géotechnique 1994, 44, 449–460. [Google Scholar] [CrossRef]
- Wan, C.F.; Fell, R. Assessing the Potential of Internal Instability and Suffusion in Embankment Dams and Their Foundations. J. Geotech. Geoenvironmental Eng. 2008, 134, 401–407. [Google Scholar] [CrossRef]
- Ahlinhan, M.F.; Achmus, M. Experimental Investigation of Critical Hydraulic Gradients for Unstable Soils. In Scour and Erosion; ASCE: San Francisco, CA, USA, 2010; pp. 599–608. [Google Scholar]
- Prasomsri, J.; Shire, T.; Takahashi, A. Effect of fines content on onset of internal instability and suffusion of sand mixtures. Geotech. Lett. 2021, 11, 209–214. [Google Scholar] [CrossRef]
- Wang, P.; Ge, Y.; Wang, T.; Liu, Q.-w.; Song, S.-x. CFD-DEM modelling of suffusion in multi-layer soils with different fines contents and impermeable zones. J. Zhejiang Univ. Sci. A 2023, 24, 6–19. [Google Scholar] [CrossRef]
- Indraratna, B.; Radampola, S. Analysis of Critical Hydraulic Gradient for Particle Movement in Filtration. J. Geotech. Geoenvironmental Eng. 2002, 128, 347–350. [Google Scholar] [CrossRef]
- Xu, B.-q.; Chen, J.-s.; Liang, Y. Damage Test of Fine Sand Piping and Seepage Deformation Analysis. Water Resour. Power 2012, 30, 66–69. [Google Scholar] [CrossRef]
- Zhang, C.-H.; Ji, E.-Y.; Wang, B.-T. Research on a Critical Hydraulic Gradient of Piping in Noncohesive Soils. Adv. Civ. Eng. 2021, 2021, 6217101. [Google Scholar] [CrossRef]
- Huang, Z.; Bai, Y.; Xu, H.; Cao, Y.; Hu, X. A Theoretical Model to Predict the Critical Hydraulic Gradient for Soil Particle Movement under Two-Dimensional Seepage Flow. Water 2017, 9, 828. [Google Scholar] [CrossRef] [Green Version]
- Richards, K.S.; Reddy, K.R. True Triaxial Piping Test Apparatus for Evaluation of Piping Potential in Earth Structures. Geotech. Test. J. 2009, 33, 83–95. [Google Scholar] [CrossRef]
- Liang, Y.; Yeh, T.-C.J.; Ma, C.; Zhang, Q.; Yang, D.; Hao, Y. Experimental investigation of internal erosion behaviours in inclined seepage flow. Hydrol. Process. 2020, 34, 5315–5326. [Google Scholar] [CrossRef]
- Indraratna, B.; Vafai, F. Analytical Model for Particle Migration within Base Soil-Filter System. J. Geotech. Geoenvironmental Eng. 1997, 123, 100–109. [Google Scholar] [CrossRef]
- Kovács, G. Seepage Hydraulics; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands, 1981. [Google Scholar]
- Choi, S.-U.; Kwak, S. Theoretical and probabilistic analyses of incipient motion of sediment particles. KSCE J. Civ. Eng. 2001, 5, 59–65. [Google Scholar] [CrossRef]
- Wang, M.-N.; Jiang, Y.-T.; Yu, L.; Dong, Y.-C.; Duan, R.-Y. Analytical solution of startup critical hydraulic gradient of fine particles migration in sandy soil. Yantu Lixue/Rock Soil Mech. 2020, 41, 2515–2524. [Google Scholar] [CrossRef]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1973. [Google Scholar]
- Yang, F.-G.; Liu, X.-N.; Huang, E.; Yang, K.-J.; Cao, S.-Y. Study on the incipient velocity of Tangjiashan Barrier lake downstream area sediment. Sichuan Daxue Xuebao (Gongcheng Kexue Ban)/J. Sichuan Univ. (Eng. Sci. Ed.) 2009, 41, 84–89. [Google Scholar]
- Zhou, S.; Zhang, G.-g.; Liang, Z.-x.; Xing, R. Incipient velocity of non-cohesive uniform sediment on slopes. J. Sediment Res. 2015, 4, 7–13. [Google Scholar] [CrossRef]
- Felice, R.D. The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
- Itasca. Particle Flow Code, Version 5.0 User Manuals; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2018. [Google Scholar]
- Jiang, M.J.; Konrad, J.M.; Leroueil, S. An efficient technique for generating homogeneous specimens for DEM studies. Comput. Geotech. 2003, 30, 579–597. [Google Scholar] [CrossRef]
- Wu, M.-X.; Gao, G.-Y.; Yang, J.-X.; Zhan, Z.-G. A method of predicting critical gradient for piping of sand and gravel soils. Yantu Lixue/Rock Soil Mech. 2019, 40, 861–870. [Google Scholar] [CrossRef]
- Zhou, X.-j.; Jie, Y.-x.; Li, G.-x. Numerical simulation of the developing course of piping. Comput. Geotech. 2012, 44, 104–108. [Google Scholar] [CrossRef]





| Model | Parameter Type | Value |
|---|---|---|
| Particle model | Fine particle diameter/mm | 0.6 |
| Coarse particle diameter/mm | 2.0~5.0 | |
| Particle density/(kg/m3) | 2650 | |
| Friction coefficient | 0.5 | |
| Effective modulus/Pa | 1 × 109 | |
| Normal-to-shear stiffness ratio | 1.25 | |
| Initial porosity | 0.3 | |
| Fluid model | Fluid density/(kg/m3) | 1000 |
| Dynamic viscosity/() | 0.001 |
| Sample | Direction of Seepage/° | Calculation Results/(cm/s) | Simulation Results/(cm/s) |
|---|---|---|---|
| Sample 1 | 90 | 0.557 | 0.55 |
| 120 | 0.622 | 0.60 | |
| 135 | 0.678 | 0.65 | |
| 150 | 0.815 | 0.75 | |
| 180 | 0.706 | 0.65 | |
| Sample 2 | 90 | 0.664 | 0.65 |
| 120 | 0.742 | 0.75 | |
| 135 | 0.808 | 0.80 | |
| 150 | 0.971 | 0.95 | |
| 180 | 0.841 | 0.85 | |
| Sample 3 | 90 | 0.864 | 0.85 |
| 120 | 0.965 | 0.95 | |
| 135 | 1.050 | 1.05 | |
| 150 | 1.263 | 1.20 | |
| 180 | 1.094 | 1.05 |
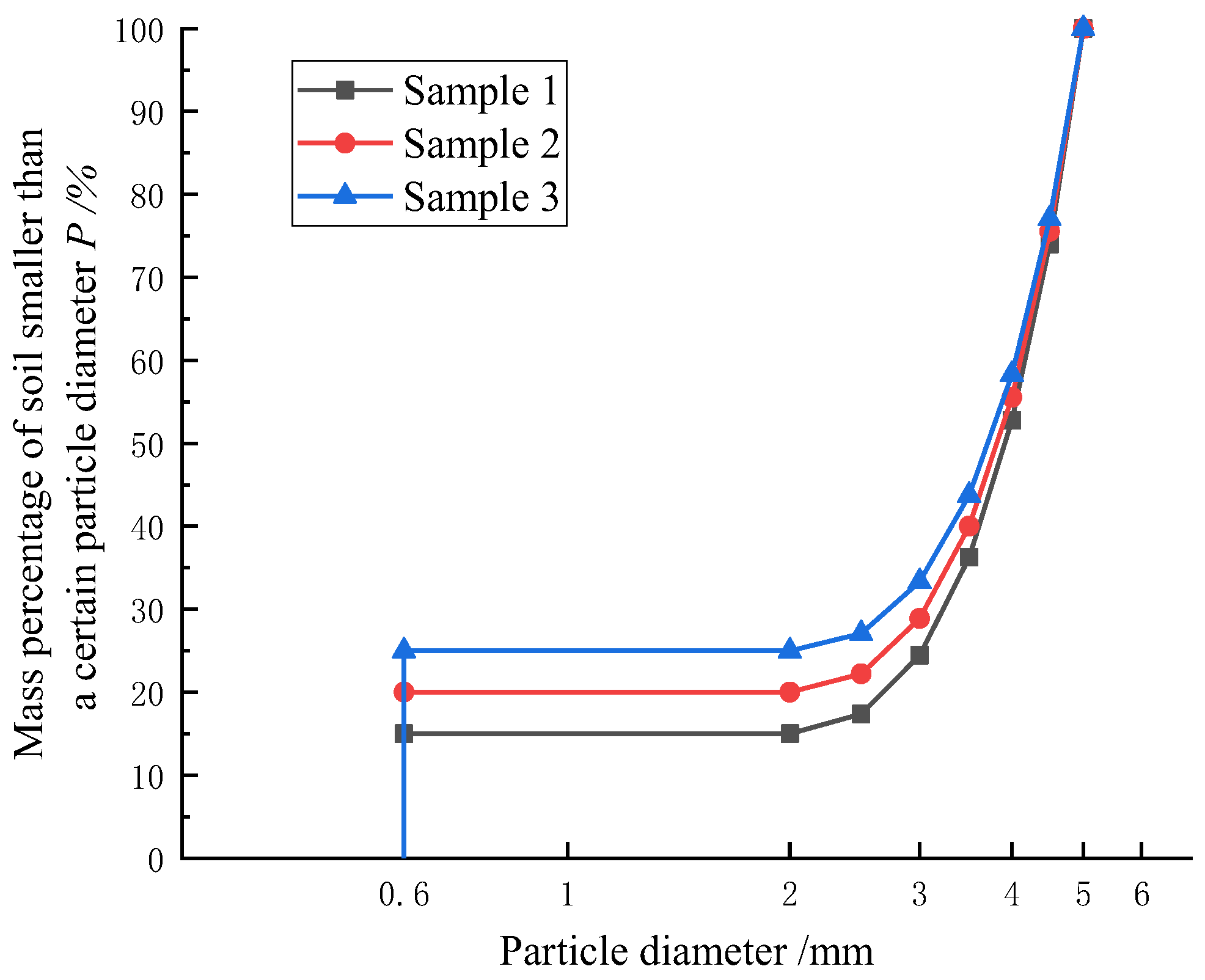
| Sample | Initial Relative Density | Natural Void Ratio e | Limiting Particle Diameter xa [9]/mm | Effective Particle Diameter of Skeletal Particles Dh/mm | Porosity of the Hypothetical Soil na | Minimum Pore Diameter d1/mm | Particle Diameter d |
|---|---|---|---|---|---|---|---|
| A | - | 0.52 | 1.000 | 3.235 | 0.44 | 0.568 | |
| B | - | 0.59 | 0.431 | 2.488 | 0.43 | 0.417 | |
| E1 | 0.5 | 0.62 | 0.537 | 1.279 | 0.47 | 0.500 | |
| 0.6 | 0.60 | 0.46 | 0.486 | ||||
| 0.85 | 0.55 | 0.44 | 0.452 | ||||
| E2 | 0.41 | 0.55 | 0.439 | 1.191 | 0.46 | 0.443 | |
| 0.5 | 0.52 | 0.45 | 0.427 | ||||
| 0.85 | 0.41 | 0.41 | 0.361 | ||||
| E3 | 0.75 | 0.52 | 0.96 | 2.166 | 0.44 | 0.386 | |
| 0.95 | 0.46 | 0.42 | 0.355 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Zhao, Y.; Liu, N.; Gao, X. An Assessment Model for the Erosion Occurrence of Gap-Graded Sand-Gravel Soils under Variable Seepage Direction. Water 2023, 15, 1487. https://doi.org/10.3390/w15081487
Li D, Zhao Y, Liu N, Gao X. An Assessment Model for the Erosion Occurrence of Gap-Graded Sand-Gravel Soils under Variable Seepage Direction. Water. 2023; 15(8):1487. https://doi.org/10.3390/w15081487
Chicago/Turabian StyleLi, Da, Yaowei Zhao, Ningyi Liu, and Xiaojuan Gao. 2023. "An Assessment Model for the Erosion Occurrence of Gap-Graded Sand-Gravel Soils under Variable Seepage Direction" Water 15, no. 8: 1487. https://doi.org/10.3390/w15081487





