Assessment of Water Conservation Services Based on the Method of Integrating Hydrological Observation Data According to Different Ecosystem Types and Regions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Technical Framework
2.3. Data Sources and Processing
2.3.1. Ecosystem Types Data
2.3.2. Determine Runoff Index by Ecosystem Type and Hydrological Soil Group (HSG)
2.3.3. Hydrological Station Data and Processing
2.3.4. Precipitation Data and Interpolation
2.3.5. Evapotranspiration Data and Processing
2.4. Methods
2.4.1. Runoff Depth Calculation
2.4.2. Water Conservation Calculation
2.4.3. Runoff Coefficient Calculation
2.4.4. Trend Analysis Method
3. Results
3.1. Change in Runoff Depth
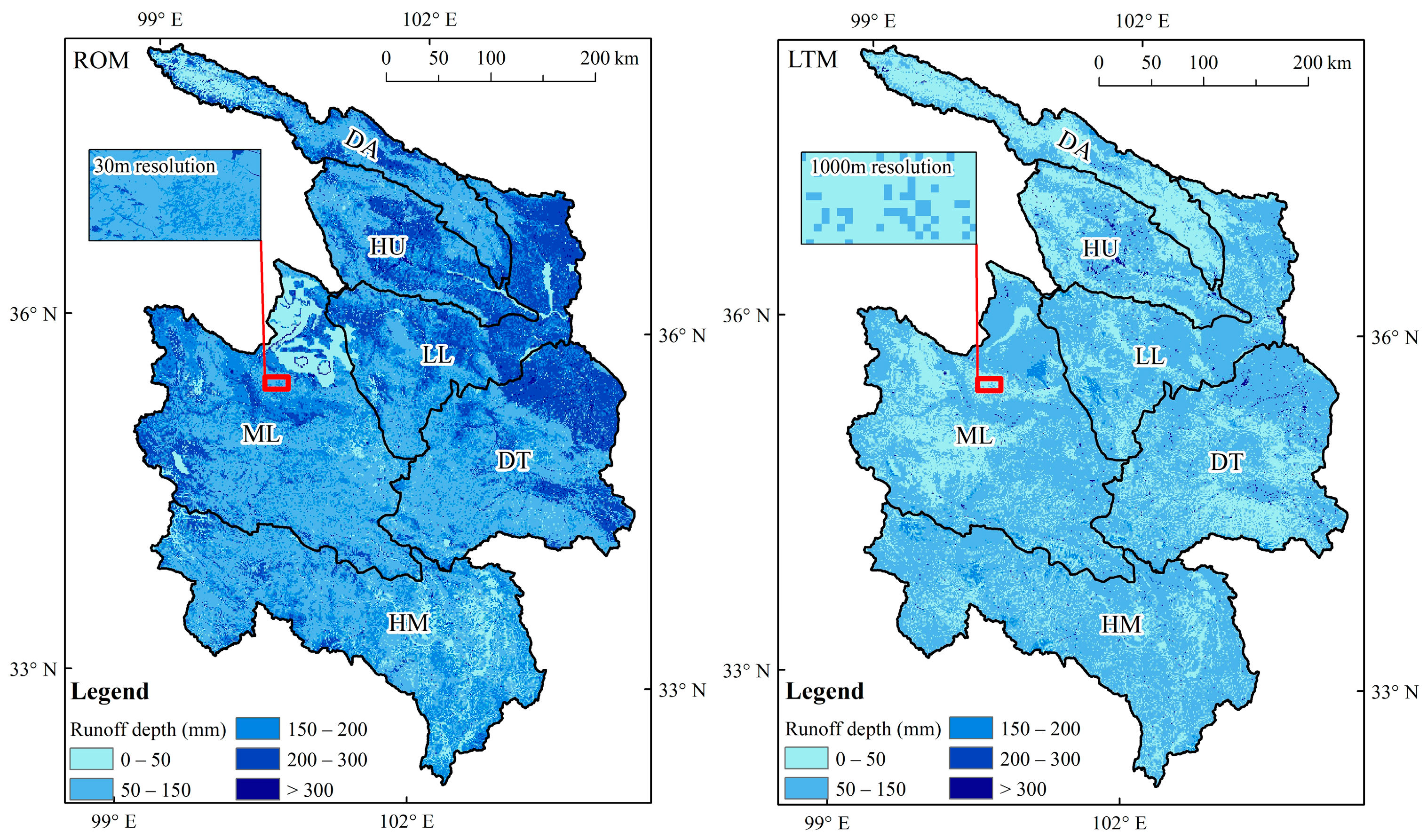
3.1.1. Spatial Variation
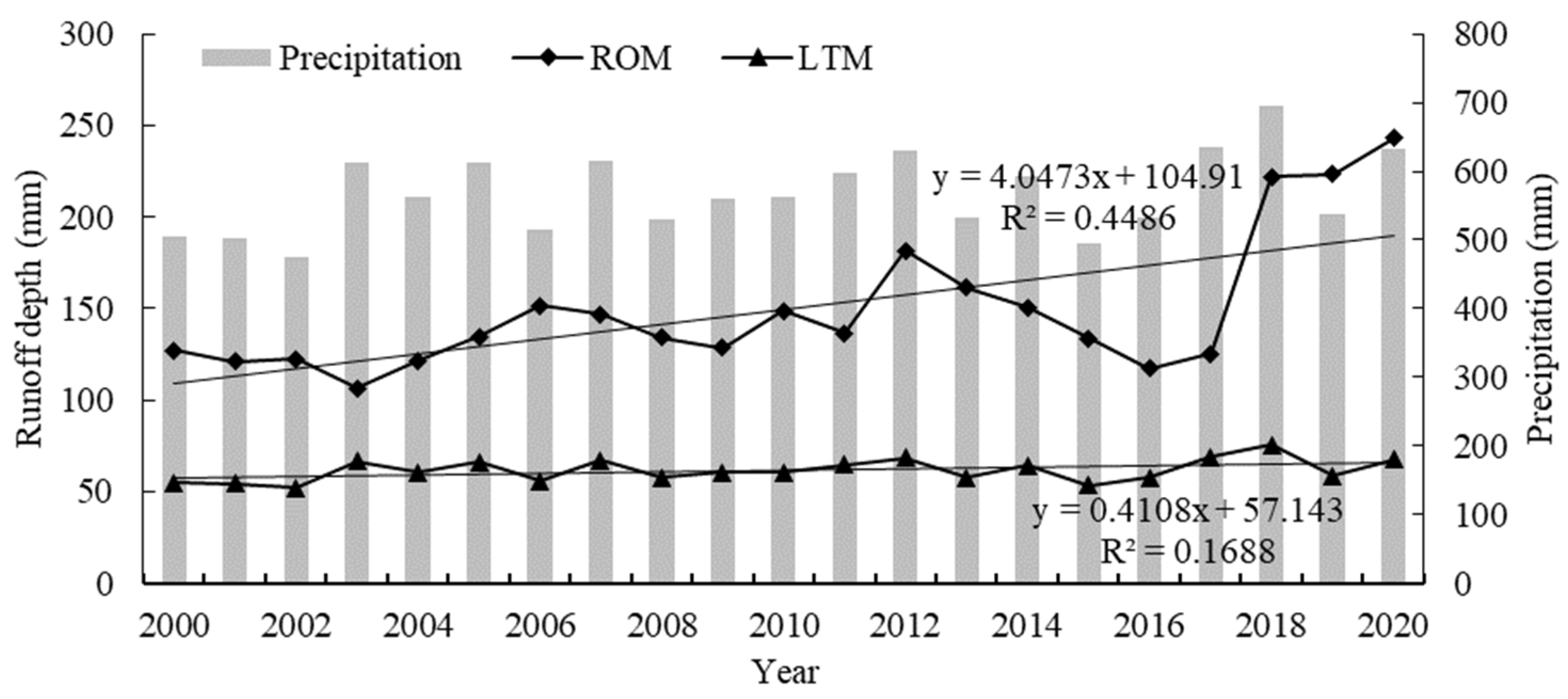
3.1.2. Time Variation
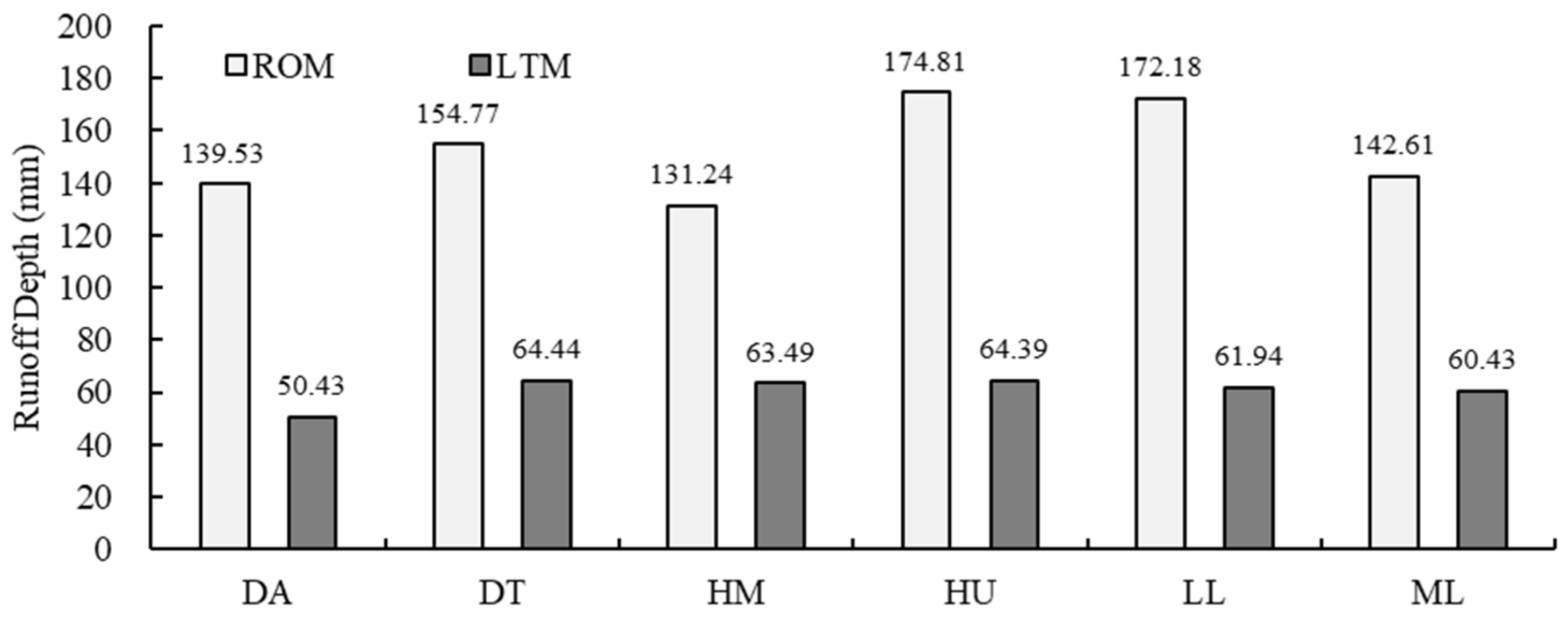
3.1.3. Sub-Watershed Comparison
3.2. Change in Water Conservation
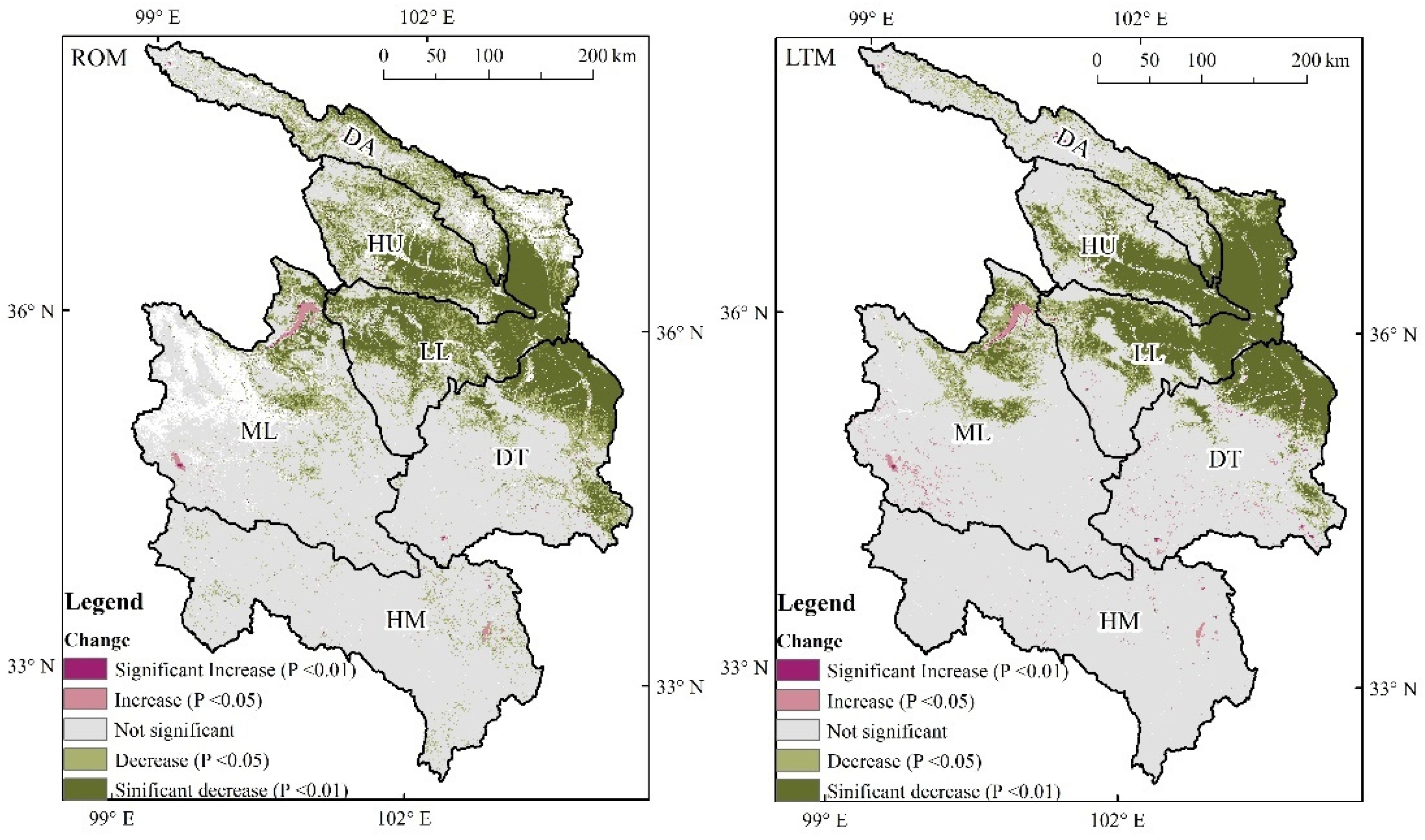
3.2.1. Spatial Variation
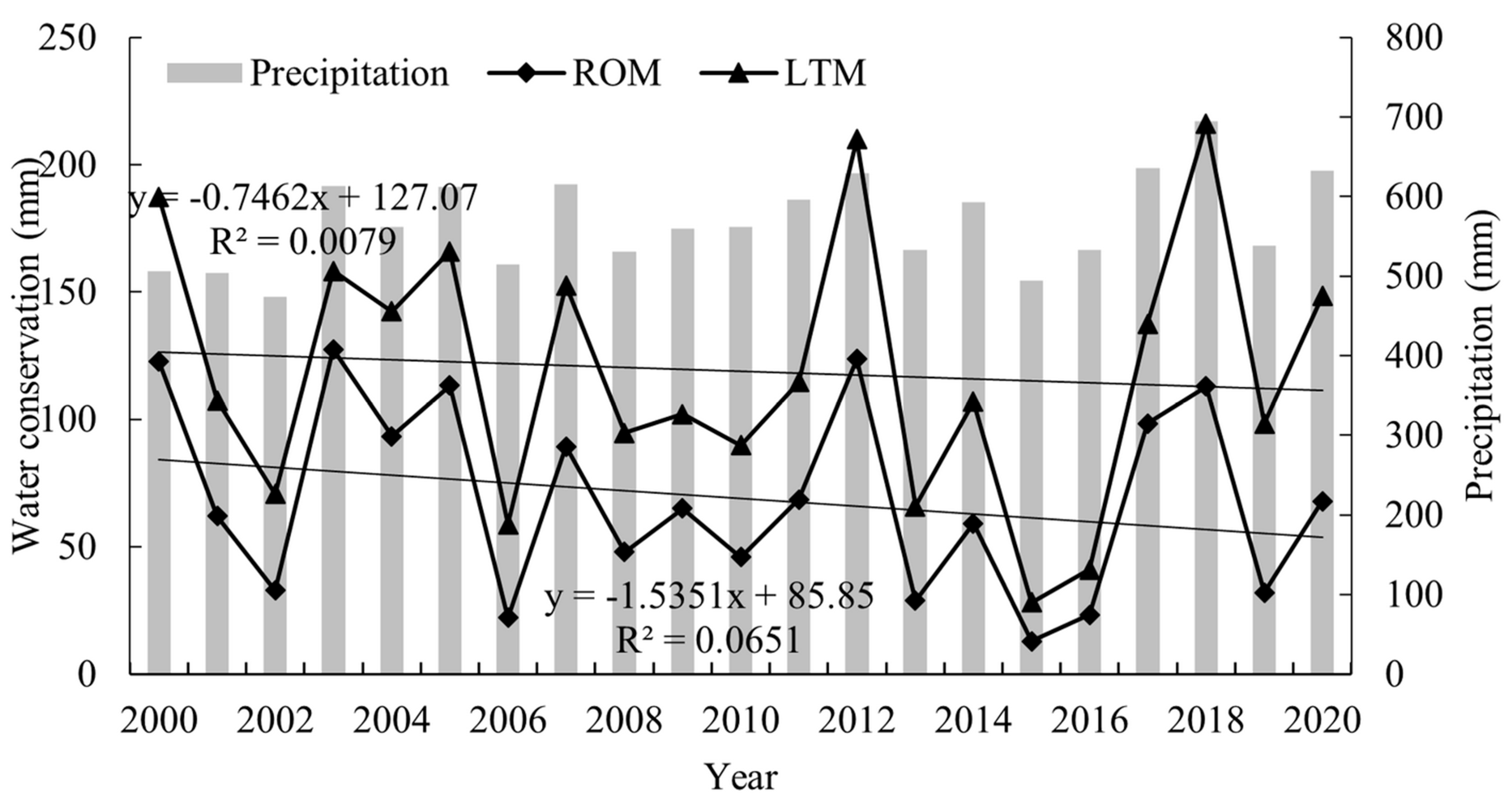
3.2.2. Time Variation
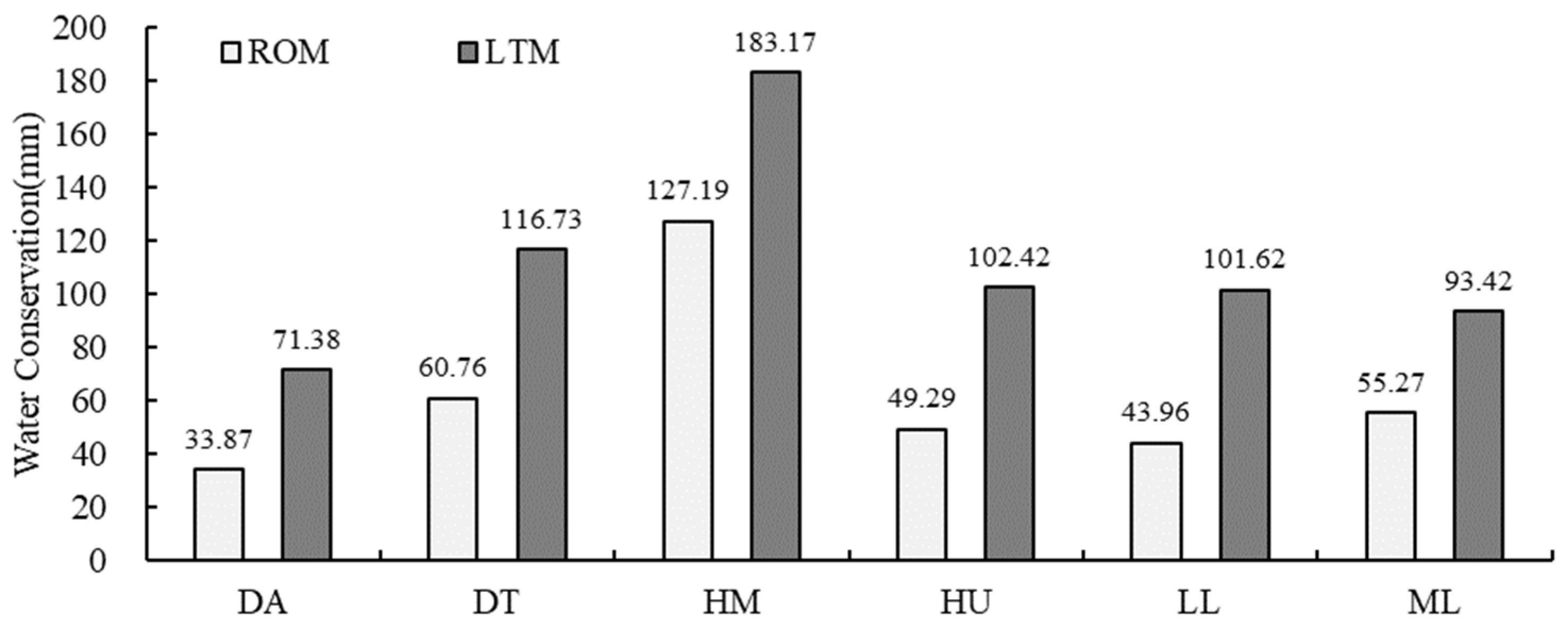
3.2.3. Sub-Watershed Comparison
3.3. Characteristics of Runoff Coefficient
3.3.1. Spatial Characteristics
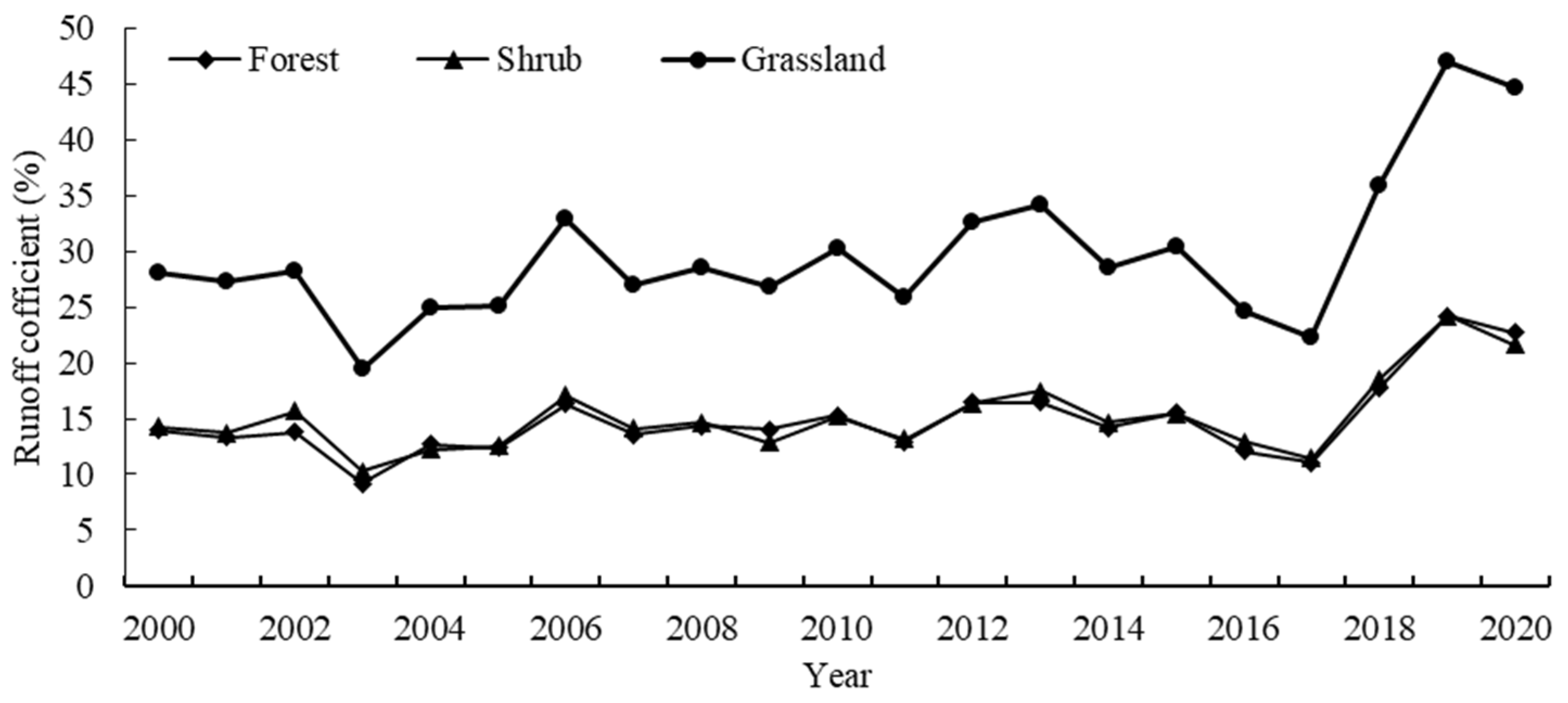
3.3.2. Time Characteristics
3.3.3. Sub-Watershed Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Renard, K.G.; Foster, G.R.; Weesies, G.A. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE), 1st ed.; U.S. Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1997; Volume 404. [Google Scholar]
- Fryrear, D.W.; Bilbro, J.D.; Saleh, A.; Schomberg, H.; Stout, J.E.; Zobeck, T.M. RWEQ: Improved wind erosion technology. J. Soil Water Conserv. 2000, 55, 183–189. [Google Scholar]
- Lu, Y.; Hu, J.; Sun, F.; Zhang, L.W. Water retention and hydrological regulation: Harmony but not the same in terrestrial hydrological ecosystem services. Acta Ecol. Sin. 2015, 35, 5191–5196. [Google Scholar]
- Xi, Q.J.; Zhong, H.; Wang, T.; He, T.; Gao, H.; Xia, J.; Wang-Erlandsson, L.; Tang, Q.; Liu, J. Spatio-temporal variation of gray-green-blue storage capacity in nine major basins of China. Chin. Sci. Bull.-Chin. 2021, 66, 4437–4448. [Google Scholar] [CrossRef]
- Wang, Y.F.; Ye, A.Z.; Qiao, F.; Li, Z.S.; Miu, C.Y.; Di, Z.H.; Gong, W. Review on connotation and estimation method of water conservation. South-North Water Transf. Water Sci. Technol. 2021, 19, 1041–1071. [Google Scholar]
- Gao, H.K.; Liu, J.G.; Gao, G.Y. Ecological and hydrological perspectives of the water retention concept. Acta Geogr. Sin. 2023, 78, 139–148. [Google Scholar]
- Sun, G.; Zhang, L.; Wang, Y.H. On accurately defining and quantifying the water retention services of forests. Acta Ecol. Sin. 2023, 43, 9–25. [Google Scholar]
- Wei, P.R.; Chen, S.Y.; Wu, M.H.; Deng, Y.F.; Xu, H.J.; Jia, Y.L.; Liu, F. Using the InVEST Model to Assess the Impacts of Climate and Land Use Changes on Water Yield in the Upstream Regions of the Shule River Basin. Water 2021, 13, 1250. [Google Scholar] [CrossRef]
- Daneshi, A.; Brouwer, R.; Najafinejad, A.; Panahi, M.; Zarandian, A.; Maghsood, F.F. Modeling the impacts of climate and land use change on water security in a semi-arid forested watershed using InVEST. J. Hydrol. 2021, 593, 18. [Google Scholar] [CrossRef]
- Lu, W.; Xia, W.; Shoemaker, C.A. Surrogate Global Optimization for Identifying Cost-Effective Green Infrastructure for Urban Flood Control with a Computationally Expensive Inundation Model. Water Resour. Res. 2022, 58, 23. [Google Scholar] [CrossRef]
- Zheng, H.; Li, Y.F.; Robinson, B.E.; Liu, G.; Ma, D.C.; Wang, F.C.; Lu, F.; Ouyang, Z.Y.; Daily, G.C. Using ecosystem service trade-offs to inform water conservation policies and management practices. Front. Ecol. Environ. 2016, 14, 527–532. [Google Scholar] [CrossRef]
- Ouyang, Z.Y.; Zheng, H.; Xiao, Y.; Polasky, S.; Liu, J.G.; Xu, W.H.; Wang, Q.; Zhang, L.; Xiao, Y.; Rao, E.M.; et al. Improvements in ecosystem services from investments in natural capital. Science 2016, 352, 1455–1459. [Google Scholar] [CrossRef]
- Gong, S.; Xiao, Y.; Zheng, H.; Xiao, Y.; Ouyang, Z.Y. Spatial patterns of ecosystem water conservation in China and its impact factors analysis. Acta Ecol. Sin. 2017, 37, 2455–2462. [Google Scholar]
- Wu, X.; Shi, W.J.; Tao, F.L. Estimations of forest water retention across China from an observation site-scale to a national-scale. Ecol. Indic. 2021, 132, 10. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, S.; Li, Q.; Xie, G.D. Spatio-temporal changes of water conservation service in the Beijing-Tianjin sandstorm source control project area. Acta Ecol. Sin. 2021, 41, 7530–7541. [Google Scholar]
- Reid, W.V.; Mooney, H.A.; Cropper, A.; Capistrano, D.; Chopra, K. Ecosystems and Human Well-Being—Synthesis: A Report of the Millennium Ecosystem Assessment, 1st ed.; Island Press: Washington, DC, USA, 2005. [Google Scholar]
- Agudelo, C.A.R.; Bustos, S.L.H.; Moreno, C.A.P. Modeling interactions among multiple ecosystem services. A critical review—ScienceDirect. Ecol. Model. 2020, 429, 22. [Google Scholar] [CrossRef]
- Hasan, S.S.; Zhen, L.; Miah, M.G.; Ahamed, T.; Samie, A. Impact of land use change on ecosystem services: A review. Environ. Dev. 2020, 34, 100527. [Google Scholar] [CrossRef]
- GB/T 38582-2020; Specification for Evaluation of Forest Ecosystem Service Function. National Forestry and Grassland Administration: Beijing, China, 2020. Available online: http://www.forestry.gov.cn/chinagreen/49/20210903/151956149968742.html (accessed on 2 March 2020).
- HJ 1173-2021; Technical Specifications for Investigation and Assessment of National Ecological Status—Ecosystem Service Assessment. Ministry of Ecology and Environment, PRC: Beijing, China, 2021. Available online: https://www.mee.gov.cn/ywgz/fgbz/bz/bzwb/stzl/202106/t20210615_839011.shtml (accessed on 6 August 2021).
- Wang, Q.; Ouyang, Z.Y. Eeo-Environment Investigation and Assessment from 2000 to 2010 with Remote Sensing of China, 1st ed.; Science Press: Beijing, China, 2014. [Google Scholar]
- Guidelines for Evaluating the Carrying Capacity of Resources and Environment and the Suitability of Land and Space Development (for Trial). Available online: http://www.gov.cn/zhengce/zhengceku/2020-01/22/content_5471523.htm (accessed on 19 January 2020).
- Technical Guide for Delimitation of Ecological Protection Red Line. Available online: https://www.mee.gov.cn/gkml/hbb/bwj/201505/t20150518_301834.htm (accessed on 8 May 2015).
- Gao, J.X.; Zou, C.X.; Zhang, K.; Xu, M.J.; Wang, Y. The establishment of Chinese ecological conservation redline and insights into improving international protected areas. J. Environ. Manag. 2020, 264, 110505. [Google Scholar] [CrossRef]
- Bedient, P.; Huber, W.; Vieux, B. Hydrology and Floodplain Analysis, 6th ed.; Pearson Publishing: Boston, MA, USA, 2013. [Google Scholar]
- Birkinshaw, S.J.; O’Donnell, G.; Glenis, V.; Kilsby, C. Improved hydrological modeling of urban catchments using runoff coefficients. J. Hydrol. 2021, 594, 125884. [Google Scholar] [CrossRef]
- Yin, H.L.; Zhao, Z.C.; Wang, R.Q.; Xu, Z.X.; Li, H.Z. Determination of urban runoff coefficient using time series inverse modeling. J. Hydrodyn. 2017, 29, 898–901. [Google Scholar] [CrossRef]
- Sajjad, R.U.; Kim, K.J.; Memon, S.; Sukhbaatar, C.; Paule, M.C.; Lee, B.Y.; Lee, C.H. Characterization of Stormwater Runoff from a Light Rail Transit Area. Water Environ. Res. 2015, 87, 813–822. [Google Scholar] [CrossRef] [PubMed]
- Maetens, W.; Poesen, J.; Vanmaercke, M. How effective are soil conservation techniques in reducing plot runoff and soil loss in Europe and the Mediterranean? Earth-Sci. Rev. 2012, 115, 21–36. [Google Scholar] [CrossRef]
- Sadeghi, S.H.R.; Gholami, L.; Sharifi, E.; Darvishan, A.K.; Homaee, M. Scale effect on runoff and soil loss control using rice straw mulch under laboratory conditions. Solid Earth 2015, 6, 1–8. [Google Scholar] [CrossRef]
- Fang, N.F.; Shi, Z.H.; Li, L.; Guo, Z.L.; Liu, Q.J.; Ai, L. The effects of rainfall regimes and land use changes on runoff and soil loss in a small mountainous watershed. Catena 2012, 99, 1–8. [Google Scholar] [CrossRef]
- Merten, G.H.; Araujo, A.G.; Biscaia, R.C.M.; Biscaia, R.C.M.; Barbosa, G.M.C.; Conte, O. No-till surface runoff and soil losses in southern Brazil. Soil Tillage Res. 2015, 152, 85–93. [Google Scholar] [CrossRef]
- Zheng, H.Y.; Miao, C.Y.; Zhang, G.H.; Li, X.Y.; Wang, S.; Wu, J.W.; Gou, J.J. Is the runoff coefficient increasing or decreasing after ecological restoration on China’s Loess Plateau? Int. Soil Water Conserv. Res. 2021, 9, 333–343. [Google Scholar] [CrossRef]
- Zeng, Z.Y.; Tang, G.Q.; Hong, Y.; Zeng, C.; Yang, Y. Development of an NRCS curve number global dataset using the latest geospatial remote sensing data for worldwide hydrologic applications. Remote Sens. Lett. 2017, 8, 528–536. [Google Scholar] [CrossRef]
- Xiong, J.H.; Yin, J.B.; Guo, S.L.; He, S.K.; Chen, J.; Abhishek. Annual runoff coefficient variation in a changing environment: A global perspective. Environ. Res. Lett. 2022, 17, 12. [Google Scholar] [CrossRef]
- Veerkamp, C.J.; Loreti, M.; Benavidez, R.; Jackson, B.; Schipper, A.M. Comparing three spatial modeling tools for assessing urban ecosystem services. Ecosyst. Serv. 2023, 59, 12. [Google Scholar] [CrossRef]
- Machado, R.E.; Cardoso, T.O.; Mortene, M.H. Determination of runoff coefficient (C) in catchments based on analysis of precipitation and flow events. Int. Soil Water Conserv. Res. 2022, 10, 208–216. [Google Scholar] [CrossRef]
- Shen, Y.P. National 1:250,000 Three-Level River Basin Data Set. Available online: www.ncdc.ac.cn (accessed on 23 January 2019).
- HJ 1166-2021; Technical Specifications for Investigation and Assessment of National Ecological Status—Remote Sensing Interpretation and Field Verification of Ecosystem. Ministry of Ecology and Environment, PRC: Beijing, China, 2021. Available online: https://www.mee.gov.cn/ywgz/fgbz/bz/bzwb/stzl/202106/t20210615_838997.shtml (accessed on 6 August 2021).
- Liu, J.Y.; Kuang, W.H.; Zhang, Z.X.; Xu, X.L.; Qin, Y.W.; Ning, J.; Zhou, W.C.; Zhang, S.W.; Li, R.D.; Yan, C.Z.; et al. Spatiotemporal characteristics, patterns, and causes of land-use changes in China since the late 1980s. J. Geogr. Sci. 2014, 24, 195–210. [Google Scholar] [CrossRef]
- Chu, X.Y.; Wang, Y.J.; Wang, Y.Q.; Cheng, C.; Xia, Y.P.; Wu, Y.; Chen, L. Runoff generation characteristics on three time scales for typical stands in Jinyun Mountain, Chongqing City. J. Beijing For. Univ. 2008, 30, 103–108. [Google Scholar]
- Kong, W.J.; Zhou, B.Z.; Fu, M.Y.; Li, Z.C.; Xie, J.Z.; Wu, M. Effects of different land-use on characteristics of soil and water conservation. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2009, 33, 57–61. [Google Scholar]
- Wang, X.D.; Zhang, H.J.; Cheng, J.H.; Sun, Y.H. Characteristics of Runoff on Forest Vegetation Slopes in Three Gorges Area. Res. Soil Water Conserv. 2008, 15, 1–3. [Google Scholar]
- Chen, B.; Wang, M.; Yao, H.E.; Hou, J.J.; Mao, Y.Q. Analysis of monitoring results of water and soil conservation monitoring points in the runoff area of Tangyu River basin from 2017 to 2019. Soil Water Conserv. China 2021, 5, 55–57. [Google Scholar]
- Feng, W.F.; Wang, Z.Q.; Shan, Y.X.; Li, Y.F.; Du, W.Z. Study on Variation of Runoff of Typical Forestland in Southern Mountain of Henan Province. J. Henan For. Sci. Technol. 2009, 29, 16–20. [Google Scholar]
- Zhu, Y.Q.; Zhao, Z.B.; Qi, G.P. Effects of Vegetation Types and Rainfall Regimes on Slope Erosion and Sediment Yield in Loess Hilly and Gully Region. J. Soil Water Conserv. 2019, 33, 9–16. [Google Scholar]
- Dong, H.B.; Zhang, J.J.; Zhang, B.; Zhang, R.; Zhou, X.X. Research on Rain-runoff Relationship in Different Land Use Types on the Loess Area in Western Shanxi Province. J. Arid Land Resour. Environ. 2009, 23, 110–116. [Google Scholar]
- Duan, W.B.; Liu, S.C. Analysis on Runoff and Sediment Yields of Water Conservation Forests in Lianhua Lake Reservoir Area. J. Soil Water Conserv. 2006, 20, 12–15. [Google Scholar]
- Song, J.H. Study on Forest Hydrological and Ecological Functions of Jinyun Mountain in Chongqing. Ph.D. Thesis, Beijing Forestry University, Beijing, China, 2008. [Google Scholar]
- Li, J.Y.; Miao, X.X.; Wang, Y.X.; Yu, D.M.; Zhang, X.Y.; Hu, X.S.; Xu, T.; Shen, Z.Y.; Liu, C.Y.; Yan, C.; et al. The Characteristics of Runoff and Sediment Yield on Slope Surface under Different Herbs and Slope Shapes in Loess Regions of Xining Basin. J. Salt Lake Res. 2022, 30, 33–45. [Google Scholar]
- Wei, X.P.; Xie, S.Y.; Zhang, Z.W.; Chen, Z.X. Characteristics of surface soil erosion of karst valley in different land use types at Nanping in Chongqing. Trans. Chin. Soc. Agric. Eng. 2011, 27, 42–46. [Google Scholar]
- Li, M.; Song, X.Y.; Shen, B.; Li, H.Y.; Meng, C.X. Influence of vegetation change on producing runoff and sediment in gully region of Loess Plateau. J. Northwest Sci-Tech Univ. AgricuUAure For. (Nat. Sci. Ed.) 2006, 34, 117–120. [Google Scholar]
- Zhang, Y.F.; Wang, X.P.; Hu, R.; Pan, Y.X.; Raradeloc, M. Rainfall partitioning into throughfall, stemflow and interception loss by two xerophytic shrubs within a rain-fed re-vegetated desert ecosystem, northwestern China. J. Hydrol. 2015, 527, 1084–1095. [Google Scholar] [CrossRef]
- Liu, Y.J.; Yang, J.; Hu, J.M.; Tang, C.J.; Zheng, H.J. Characteristics of the surface—Subsurface flow generation and sediment yield to the rainfall regime and land-cover by long-term in-situ observation in the red soil region, Southern China. J. Hydrol. 2016, 539, 457–467. [Google Scholar] [CrossRef]
- Annual Hydrological Report of P.R. China. Hydrological Data of Yellow River Basin; Hydrology Department of the Ministry of Water Resources of the People’s Republic of China Press: Beijing, China, 2001–2021.
- Mu, Q.Z.; Zhao, M.S.; Running, S.W. MODIS Global Terrestrial Evapotranspiration (ET) Product (NASA MOD16A2/A3) Collection 5. NASA Headquarters. Numerical Terradynamic Simulation Group Publications. 268. 2013. Available online: https://scholarworks.umt.edu/ntsg_pubs/268 (accessed on 8 November 2019).
- Kendall, M.G. Rank Correlation Methods, 1st ed.; Oxford University Press: Oxford, UK, 1948. [Google Scholar]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]






| Ecosystem Types | Literature | Rc (%) | Rit |
|---|---|---|---|
| Broadleaf forest | [41,42,43,44,45] | 3.33 | 1.55 |
| Coniferous forest | [13,42,46,47,48] | 2.15 | 1.00 |
| Mixed forest | [45,49] | 2.4 | 1.12 |
| Sparse forest | [47,50] | 16.02 | 7.45 |
| Broadleaf shrub | [41,46] | 3.58 | 1.67 |
| Coniferous shrub | [46] | 3.41 | 1.59 |
| Open shrublands | [47,50] | 16.02 | 7.45 |
| Marshy grassland | [48] | 9.11 | 4.24 |
| Steppe | [44,46,50] | 12.34 | 5.74 |
| Tussock | [47,51] | 10.18 | 4.73 |
| Sparse grassland | [47,50] | 16.02 | 7.45 |
| Marsh * | - | 0 | 0 |
| Lakes * | - | 0 | 0 |
| River * | - | 0 | 0 |
| Farmland | [52] | 49.69 | 23.11 |
| Plantation | [41,42,43,44,45,46,47,48,49,50] | 4.62 | 2.15 |
| Settlement | [26] | 90 | 41.86 |
| Urban green space | [41,42,43,44,45,46,47,48,49,50,51,52] | 7.91 | 3.68 |
| Industrial, mining and transportation | [26] | 73.33 | 34.11 |
| Desert * | [53] | 30 | 13.95 |
| Glacier/Permanent snow cover | - | 0 | 0 |
| Bare soil | [54] | 25 | 11.63 |
| Ecosystem Types | CNA | CNB | CNC | CND | Ris (A) | Ris (B) | Ris (C) | Ris (D) |
|---|---|---|---|---|---|---|---|---|
| Broadleaf forest | 36 | 62 | 75 | 81 | 1.00 | 1.72 | 2.08 | 2.25 |
| Coniferous forest | 37 | 62 | 75 | 81 | 1.00 | 1.68 | 2.03 | 2.19 |
| Mixed forest | 38 | 62 | 75 | 81 | 1.00 | 1.63 | 1.97 | 2.13 |
| Sparse forest | 72 | 82 | 83 | 87 | 1.00 | 1.14 | 1.15 | 1.21 |
| Broadleaf shrub | 45 | 65 | 75 | 80 | 1.00 | 1.44 | 1.67 | 1.78 |
| Coniferous shrub | 49 | 69 | 79 | 84 | 1.00 | 1.41 | 1.61 | 1.71 |
| Open shrublands | 72 | 82 | 83 | 87 | 1.00 | 1.14 | 1.15 | 1.21 |
| Marshy grassland | 49 | 69 | 79 | 84 | 1.00 | 1.41 | 1.61 | 1.71 |
| Steppe | 49 | 69 | 79 | 84 | 1.00 | 1.41 | 1.61 | 1.71 |
| Tussock | 49 | 69 | 79 | 84 | 1.00 | 1.41 | 1.61 | 1.71 |
| Sparse grassland | 72 | 82 | 83 | 87 | 1.00 | 1.14 | 1.15 | 1.21 |
| Marsh | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Lakes | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| River | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Farmland | 67 | 78 | 85 | 89 | 1.00 | 1.16 | 1.27 | 1.33 |
| Plantation | 52 | 69 | 79 | 84 | 1.00 | 1.33 | 1.52 | 1.62 |
| Settlement | 80 | 85 | 90 | 95 | 1.00 | 1.06 | 1.13 | 1.19 |
| Urban green space | 52 | 70 | 79 | 84 | 1.00 | 1.35 | 1.52 | 1.62 |
| Industrial, mining, and transportation | 80 | 85 | 90 | 95 | 1.00 | 1.06 | 1.13 | 1.19 |
| Desert | 72 | 82 | 83 | 87 | 1.00 | 1.14 | 1.15 | 1.21 |
| Glacier/permanent snow cover | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Bare soil | 72 | 82 | 83 | 87 | 1.00 | 1.14 | 1.15 | 1.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, J.; Hou, P.; Zhang, W.; Chen, Y.; Jin, D.; Gao, H.; Zhu, H.; Yang, M. Assessment of Water Conservation Services Based on the Method of Integrating Hydrological Observation Data According to Different Ecosystem Types and Regions. Water 2023, 15, 1475. https://doi.org/10.3390/w15081475
Zhai J, Hou P, Zhang W, Chen Y, Jin D, Gao H, Zhu H, Yang M. Assessment of Water Conservation Services Based on the Method of Integrating Hydrological Observation Data According to Different Ecosystem Types and Regions. Water. 2023; 15(8):1475. https://doi.org/10.3390/w15081475
Chicago/Turabian StyleZhai, Jun, Peng Hou, Wenguo Zhang, Yan Chen, Diandian Jin, Haifeng Gao, Hanshou Zhu, and Min Yang. 2023. "Assessment of Water Conservation Services Based on the Method of Integrating Hydrological Observation Data According to Different Ecosystem Types and Regions" Water 15, no. 8: 1475. https://doi.org/10.3390/w15081475






