Data Modeling of Sewage Treatment Plant Based on Long Short-Term Memory with Multilayer Perceptron Network
Abstract
:1. Introduction
2. Methodology
2.1. The Setup of the Studied WWTP
2.2. Dataset and Preprocessing
- In the case of data missing due to failure in sensor communication, the previous value before the missing data will be used.
- In this WWTP setup, the sampling interval of the sensor is one minute, and in most of the time, the data value does not vary obviously within this interval. Therefore, in order to improve the learning efficiency, the mean value of the data within one hour is taken as the sampling point; in this way, there are 24 samples per day that will be recorded.
- For the fan operation status, the on status corresponds to the value 1, and the off status is 0.
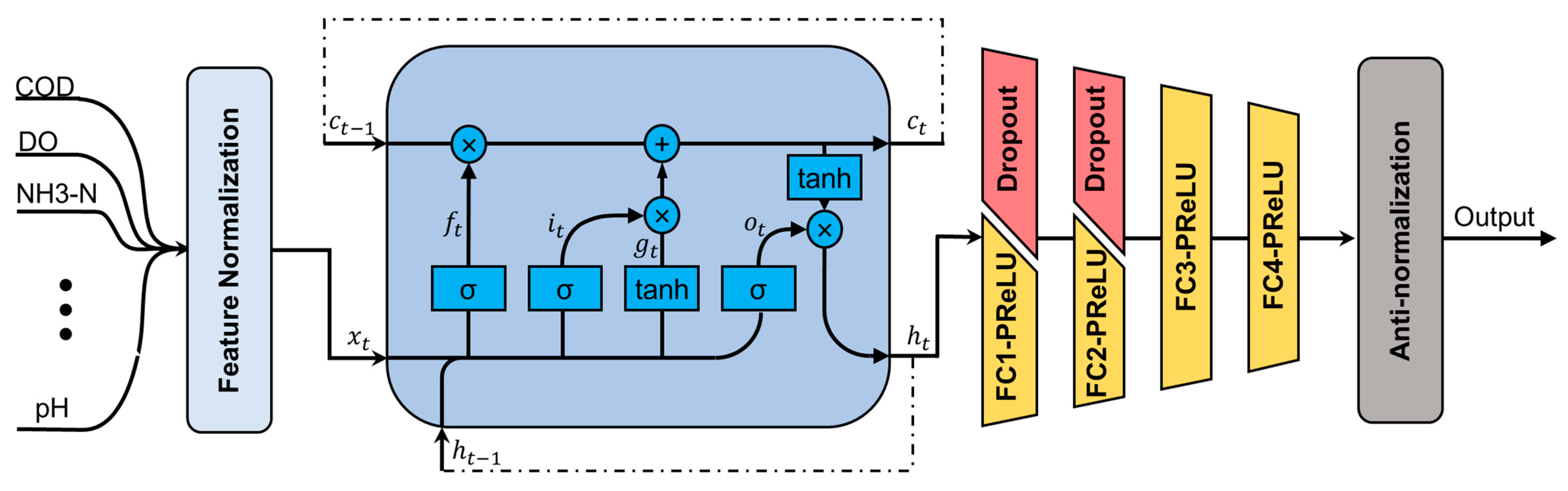
3. The LMPNet Model
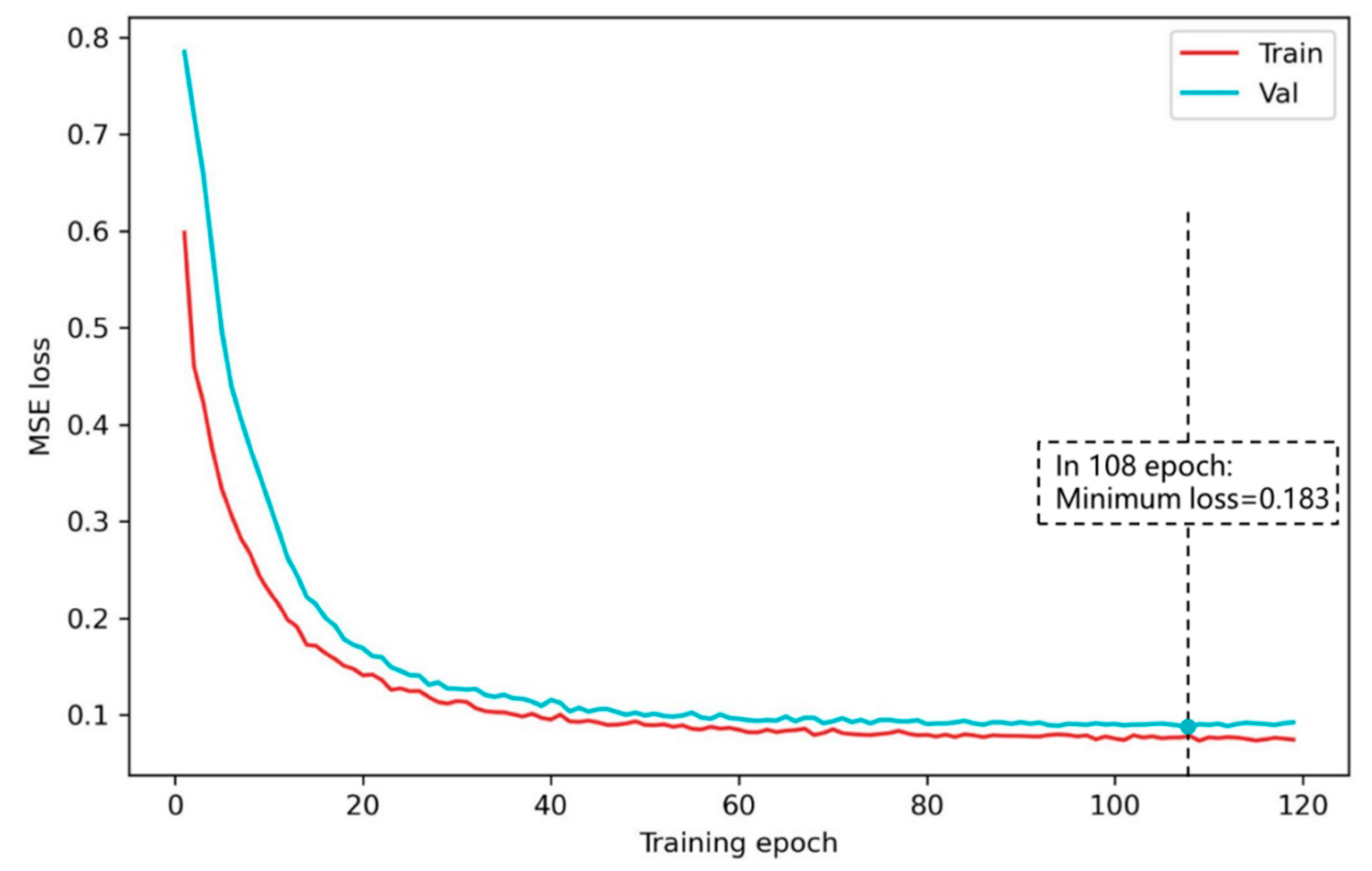
3.1. The Hyperparameters Selection
3.2. The Structure of the LMPNet
3.3. Performance Evaluation
3.4. Model Lifelong Learning
4. Experimental Results and Discussion
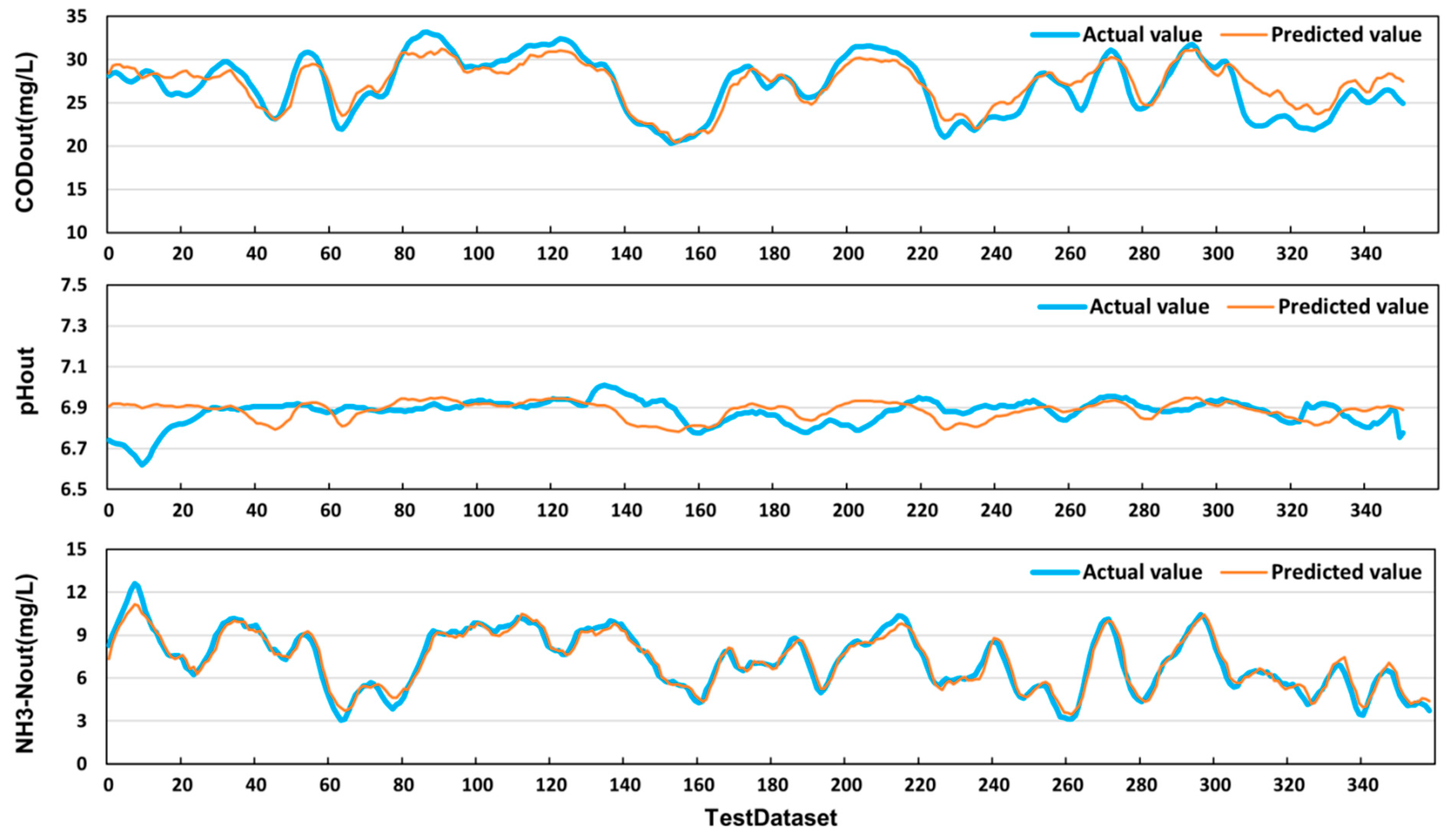
4.1. Output Water Quality Prediction with LMPNet
4.2. The Ablation of the Input Water Quality Characteristics
4.3. Influence of Different Time Delays on Prediction
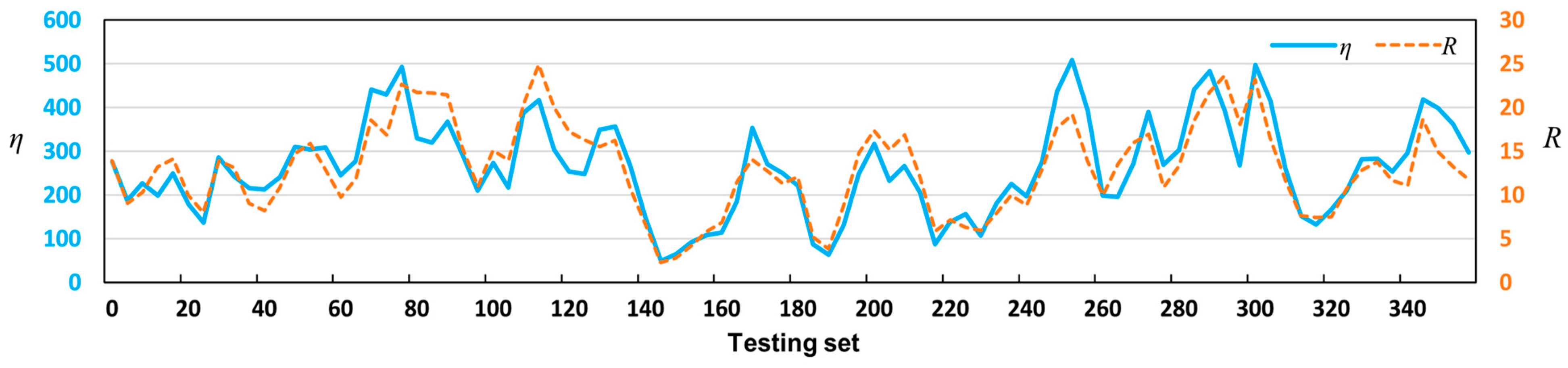
4.4. Energy Efficiency Analysis for Wastewater Purification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Geissen, V.; Mol, H.; Klumpp, E.; Umlauf, G.; Nadal, M.; van der Ploeg, M.; van de Zee, S.E.A.T.M.; Ritsema, C.J. Emerging Pollutants in the Environment: A Challenge for Water Resource Management. Int. Soil Water Conserv. Res. 2015, 3, 57–65. [Google Scholar] [CrossRef]
- Crini, G.; Lichtfouse, E. Advantages and Disadvantages of Techniques Used for Wastewater Treatment. Environ. Chem. Lett. 2019, 17, 145–155. [Google Scholar] [CrossRef]
- Wang, G.; Li, J.; Sun, W.; Xue, B.; Yinglan, A.; Liu, T. Non-Point Source Pollution Risks in a Drinking Water Protection Zone Based on Remote Sensing Data Embedded within a Nutrient Budget Model. Water Res. 2019, 157, 238–246. [Google Scholar] [CrossRef]
- Li, W.; Li, L.; Qiu, G. Energy Consumption and Economic Cost of Typical Wastewater Treatment Systems in Shenzhen, China. J. Clean. Prod. 2017, 163, S374–S378. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, G.; Tian, H. Current State of Sewage Treatment in China. Water Res. 2014, 66, 85–98. [Google Scholar] [CrossRef] [PubMed]
- Garrido-Baserba, M.; Corominas, L.; Cortés, U.; Rosso, D.; Poch, M. The Fourth-Revolution in the Water Sector Encounters the Digital Revolution. Environ. Sci. Technol. 2020, 54, 4698–4705. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.; Shukla, S.; Wadhvani, R. Dynamic Selection of Normalization Techniques Using Data Complexity Measures. Expert Syst. Appl. 2018, 106, 252–262. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, J.; Liu, Q.; Tillotson, M.R.; Guan, D.; Hubacek, K. Physical and Virtual Water Transfers for Regional Water Stress Alleviation in China. Proc. Natl. Acad. Sci. USA 2015, 112, 1031–1035. [Google Scholar] [CrossRef] [Green Version]
- Matheri, A.N.; Ntuli, F.; Ngila, J.C.; Seodigeng, T.; Zvinowanda, C. Performance Prediction of Trace Metals and Cod in Wastewater Treatment Using Artificial Neural Network. Comput. Chem. Eng. 2021, 149, 107308. [Google Scholar] [CrossRef]
- Han, H.; Liu, Z.; Hou, Y.; Qiao, J. Data-Driven Multiobjective Predictive Control for Wastewater Treatment Process. IEEE Trans. Ind. Inf. 2020, 16, 2767–2775. [Google Scholar] [CrossRef]
- Farhi, N.; Kohen, E.; Mamane, H.; Shavitt, Y. Prediction of Wastewater Treatment Quality Using LSTM Neural Network. Environ. Technol. Innov. 2021, 23, 101632. [Google Scholar] [CrossRef]
- Jawad, J.; Hawari, A.H.; Javaid Zaidi, S. Artificial Neural Network Modeling of Wastewater Treatment and Desalination Using Membrane Processes: A Review. Chem. Eng. J. 2021, 419, 129540. [Google Scholar] [CrossRef]
- Jones, R.A.; Lee, G.F. Recent Advances in Assessing Impact of Phosphorus Loads on Eutrophication-Related Water Quality. Water Res. 1982, 16, 503–515. [Google Scholar] [CrossRef]
- Barker, P.S.; Dold, P.L. General Model for Biological Nutrient Removal Activated-Sludge Systems: Model Presentation. Water Environ. Res. 1997, 69, 969–984. [Google Scholar] [CrossRef]
- Bunce, J.T.; Ndam, E.; Ofiteru, I.D.; Moore, A.; Graham, D.W. A Review of Phosphorus Removal Technologies and Their Applicability to Small-Scale Domestic Wastewater Treatment Systems. Front. Environ. Sci. 2018, 6, 8. [Google Scholar] [CrossRef] [Green Version]
- Yaqub, M.; Asif, H.; Kim, S.; Lee, W. Modeling of a Full-Scale Sewage Treatment Plant to Predict the Nutrient Removal Efficiency Using a Long Short-Term Memory (LSTM) Neural Network. J. Water Process Eng. 2020, 37, 101388. [Google Scholar] [CrossRef]
- Nancharaiah, Y.V.; Venkata Mohan, S.; Lens, P.N.L. Recent Advances in Nutrient Removal and Recovery in Biological and Bioelectrochemical Systems. Bioresour. Technol. 2016, 215, 173–185. [Google Scholar] [CrossRef]
- Yan, T.; Ye, Y.; Ma, H.; Zhang, Y.; Guo, W.; Du, B.; Wei, Q.; Wei, D.; Ngo, H.H. A Critical Review on Membrane Hybrid System for Nutrient Recovery from Wastewater. Chem. Eng. J. 2018, 348, 143–156. [Google Scholar] [CrossRef]
- Shen, Y.; Yang, D.; Wu, Y.; Zhang, H.; Zhang, X. Operation Mode of a Step-Feed Anoxic/Oxic Process with Distribution of Carbon Source from Anaerobic Zone on Nutrient Removal and Microbial Properties. Sci. Rep. 2019, 9, 1153. [Google Scholar] [CrossRef] [Green Version]
- Ge, S.; Zhu, Y.; Lu, C.; Wang, S.; Peng, Y. Full-Scale Demonstration of Step Feed Concept for Improving an Anaerobic/Anoxic/Aerobic Nutrient Removal Process. Bioresour. Technol. 2012, 120, 305–313. [Google Scholar] [CrossRef]
- Jeppsson, U.; Pons, M.-N.; Nopens, I.; Alex, J.; Copp, J.B.; Gernaey, K.V.; Rosen, C.; Steyer, J.-P.; Vanrolleghem, P.A. Benchmark Simulation Model No 2: General Protocol and Exploratory Case Studies. Water Sci. Technol. 2007, 56, 67–78. [Google Scholar] [CrossRef]
- Alex, J.; Benedetti, L.; Copp, J.; Gernaey, K.V.; Jeppsson, U.; Nopens, I.; Pons, M.N.; Steyer, J.P.; Vanrolleghem, P. Benchmark Simulation Model No. 1 (BSM1); IWA Publishing: London, UK, 2018; 58p. [Google Scholar]
- Fang, F.; Ni, B.; Li, W.; Sheng, G.; Yu, H. A Simulation-Based Integrated Approach to Optimize the Biological Nutrient Removal Process in a Full-Scale Wastewater Treatment Plant. Chem. Eng. J. 2011, 174, 635–643. [Google Scholar] [CrossRef]
- Cheng, T.; Harrou, F.; Kadri, F.; Sun, Y.; Leiknes, T. Forecasting of Wastewater Treatment Plant Key Features Using Deep Learning-Based Models: A Case Study. IEEE Access 2020, 8, 184475–184485. [Google Scholar] [CrossRef]
- Mohammad, A.T.; Al-Obaidi, M.A.; Hameed, E.M.; Basheer, B.N.; Mujtaba, I.M. Modelling the Chlorophenol Removal from Wastewater via Reverse Osmosis Process Using a Multilayer Artificial Neural Network with Genetic Algorithm. J. Water Process Eng. 2020, 33, 100993. [Google Scholar] [CrossRef]
- Irfan, M.; Waqas, S.; Arshad, U.; Khan, J.A.; Legutko, S.; Kruszelnicka, I.; Ginter-Kramarczyk, D.; Rahman, S.; Skrzypczak, A. Response Surface Methodology and Artificial Neural Network Modelling of Membrane Rotating Biological Contactors for Wastewater Treatment. Materials 2022, 15, 1932. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.; Yang, J.; Zhong, N.; Tu, X.; Jia, J.; Wang, J. Tackling Environmental Challenges in Pollution Controls Using Artificial Intelligence: A Review. Sci. Total Environ. 2020, 699, 134279. [Google Scholar] [CrossRef]
- Han, H.-G.; Qiao, J.-F.; Chen, Q.-L. Model Predictive Control of Dissolved Oxygen Concentration Based on a Self-Organizing RBF Neural Network. Control. Eng. Pract. 2012, 20, 465–476. [Google Scholar] [CrossRef]
- Suryawan, I.W.K.; Prajati, G.; Afifah, A.S.; Apritama, M.R. NH3-N and COD Reduction in Endek (Balinese Textile) Wastewater by Activated Sludge under Different DO Condition with Ozone Pretreatment. Walailak J. Sci. Technol. 2021, 18, 6. [Google Scholar] [CrossRef]
- Vijayabhanu, R.; Radha, V. Statistical Normalization Techniques for the Prediction of COD Level for an Anaerobic Wastewater Treatment Plant. In Proceedings of the Second International Conference on Computational Science, Engineering and Information Technology—CCSEIT’12, Coimbatore, India, 26–28 October 2012; pp. 232–236. [Google Scholar]
- Mu, Y.; Liu, X.; Wang, L. A Pearson’s Correlation Coefficient Based Decision Tree and Its Parallel Implementation. Inf. Sci. 2018, 435, 40–58. [Google Scholar] [CrossRef]
- Young, S.R.; Rose, D.C.; Karnowski, T.P.; Lim, S.-H.; Patton, R.M. Optimizing Deep Learning Hyper-Parameters through an Evolutionary Algorithm. In Proceedings of the Workshop on Machine Learning in High-Performance Computing Environments, Austin, TX, USA, 15 November 2015; pp. 1–5. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- He, T.; Zhang, Z.; Zhang, H.; Zhang, Z.; Xie, J.; Li, M. Bag of Tricks for Image Classification with Convolutional Neural Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 558–567. [Google Scholar]
- Leshno, M.; Lin, V.Y.; Pinkus, A.; Schocken, S. Multilayer Feedforward Networks with a Nonpolynomial Activation Function Can Approximate Any Function. Neural Netw. 1993, 6, 861–867. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Yan, W.; Xu, R.; Wang, K.; Di, T.; Jiang, Z. Soft Sensor Modeling Method Based on Semisupervised Deep Learning and Its Application to Wastewater Treatment Plant. Ind. Eng. Chem. Res. 2020, 59, 4589–4601. [Google Scholar] [CrossRef]
- Zhang, D. A Coefficient of Determination for Generalized Linear Models. Am. Stat. 2017, 71, 310–316. [Google Scholar] [CrossRef]
- Liu, Y.; Su, Y.; Liu, A.-A.; Schiele, B.; Sun, Q. Mnemonics Training: Multi-Class Incremental Learning Without Forgetting. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 12242–12251. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]

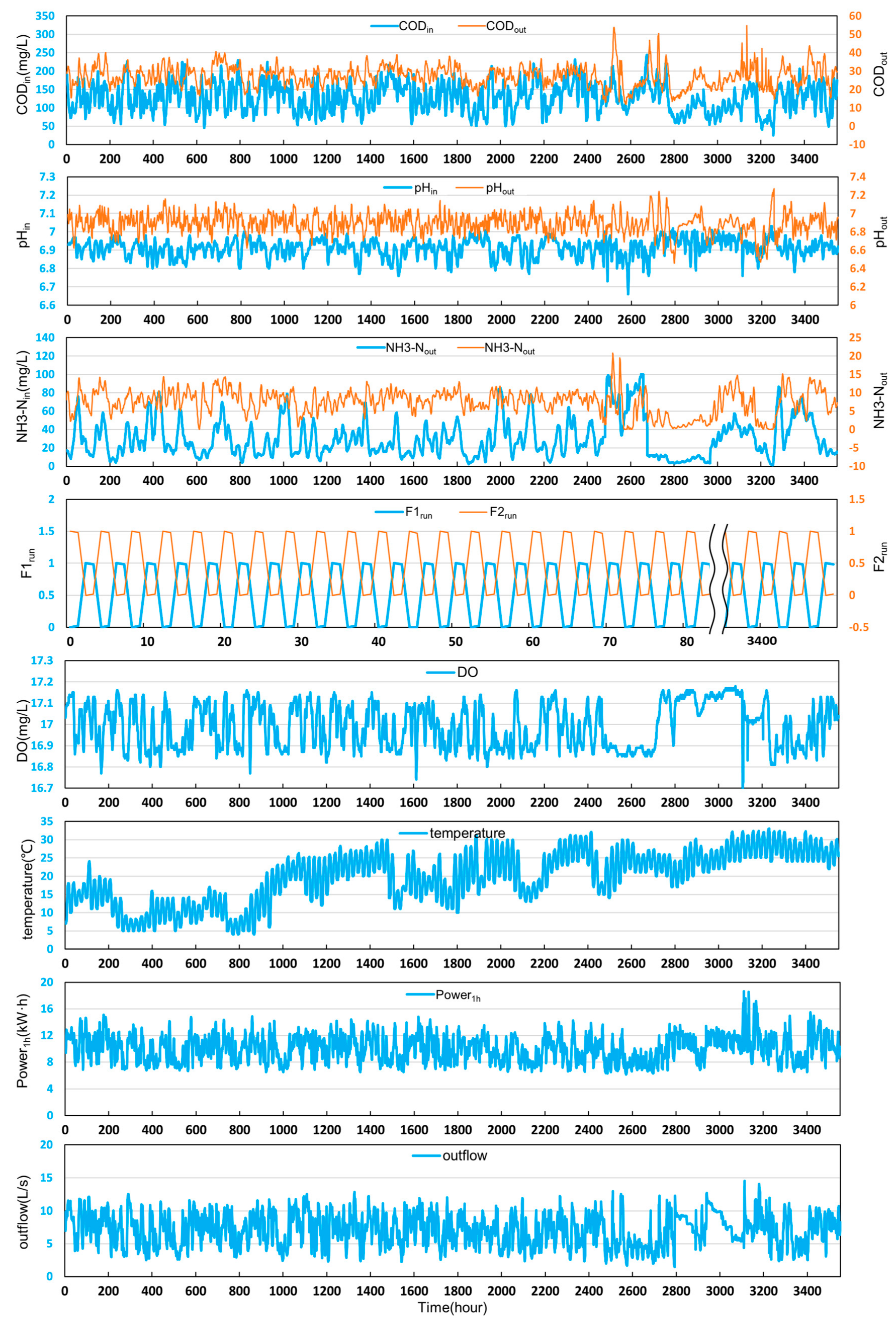



| Water Characteristics and Operating Parameters | ||||
|---|---|---|---|---|
| Variables | Units | Statistics | ||
| Range | Mean | Std | ||
| CODin | mg/L | 53.2–231.6 | 131.6 | 41.5 |
| CODout | mg/L | 14.8–33.16 | 27.0 | 3.5 |
| NH3-Nin | mg/L | 27.5–14.2 | 27.5 | 14.2 |
| NH3-Nout | mg/L | 0.9–10.4 | 7.2 | 2.1 |
| pHin | – | 6.7–7.0 | 6.9 | 0.05 |
| pHout | – | 6.7–7.0 | 6.9 | 0.05 |
| DO | mg/L | 16.3–17.1 | 17 | 0.1 |
| temperature | °C | 25–34.3 | 29.2 | 2.9 |
| Power1h | kW·h | 6.9–15.4 | 10.2 | 1.9 |
| outflow | L/s | 2.5–12.7 | 7.4 | 2.3 |
| F1run | – | 0–1 | 0.52 | 0.48 |
| F2run | – | 0–1 | 0.52 | 0.48 |
| Hyperparameters | Optimum Values |
|---|---|
| Batch size | 512 |
| Dropout rate | 0.5 |
| Epoch | 120 |
| Optimizer | Adam |
| Learning rate | 0.0003 |
| Weight decay | 0.0001 |
| Train and validation set split ratio | 0.8 |
| Loss function | MSELoss |
| Predicted Water Quality Parameters | ||||||
|---|---|---|---|---|---|---|
| CODout | pHout | NH3-Nout | ||||
| Δt (hour) | MAE | MSE | MAE | MSE | MAE | MSE |
| 6 | 1.299 | 2.440 | 0.053 | 0.005 | 0.761 | 0.958 |
| 8 | 1.143 | 1.936 | 0.055 | 0.006 | 0.645 | 0.671 |
| 10 | 1.306 | 2.584 | 0.054 | 0.005 | 0.698 | 0.800 |
| 12 | 1.67 | 4.346 | 0.051 | 0.005 | 0.905 | 1.388 |
| 14 | 1.992 | 6.146 | 0.046 | 0.004 | 1.116 | 2.086 |
| 16 | 2.342 | 8.287 | 0.038 | 0.003 | 1.415 | 3.075 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Wu, N.; Zou, Q.; Zou, H.; Zhu, L.; Wei, J.; Huang, H. Data Modeling of Sewage Treatment Plant Based on Long Short-Term Memory with Multilayer Perceptron Network. Water 2023, 15, 1472. https://doi.org/10.3390/w15081472
Wei Z, Wu N, Zou Q, Zou H, Zhu L, Wei J, Huang H. Data Modeling of Sewage Treatment Plant Based on Long Short-Term Memory with Multilayer Perceptron Network. Water. 2023; 15(8):1472. https://doi.org/10.3390/w15081472
Chicago/Turabian StyleWei, Zhengxi, Ning Wu, Qingchuan Zou, Huanxin Zou, Liucun Zhu, Jinzhan Wei, and Hong Huang. 2023. "Data Modeling of Sewage Treatment Plant Based on Long Short-Term Memory with Multilayer Perceptron Network" Water 15, no. 8: 1472. https://doi.org/10.3390/w15081472
APA StyleWei, Z., Wu, N., Zou, Q., Zou, H., Zhu, L., Wei, J., & Huang, H. (2023). Data Modeling of Sewage Treatment Plant Based on Long Short-Term Memory with Multilayer Perceptron Network. Water, 15(8), 1472. https://doi.org/10.3390/w15081472






