Prediction of Sediment Yields Using a Data-Driven Radial M5 Tree Model
Abstract
:1. Introduction
Literature Review
2. Materials and Methods
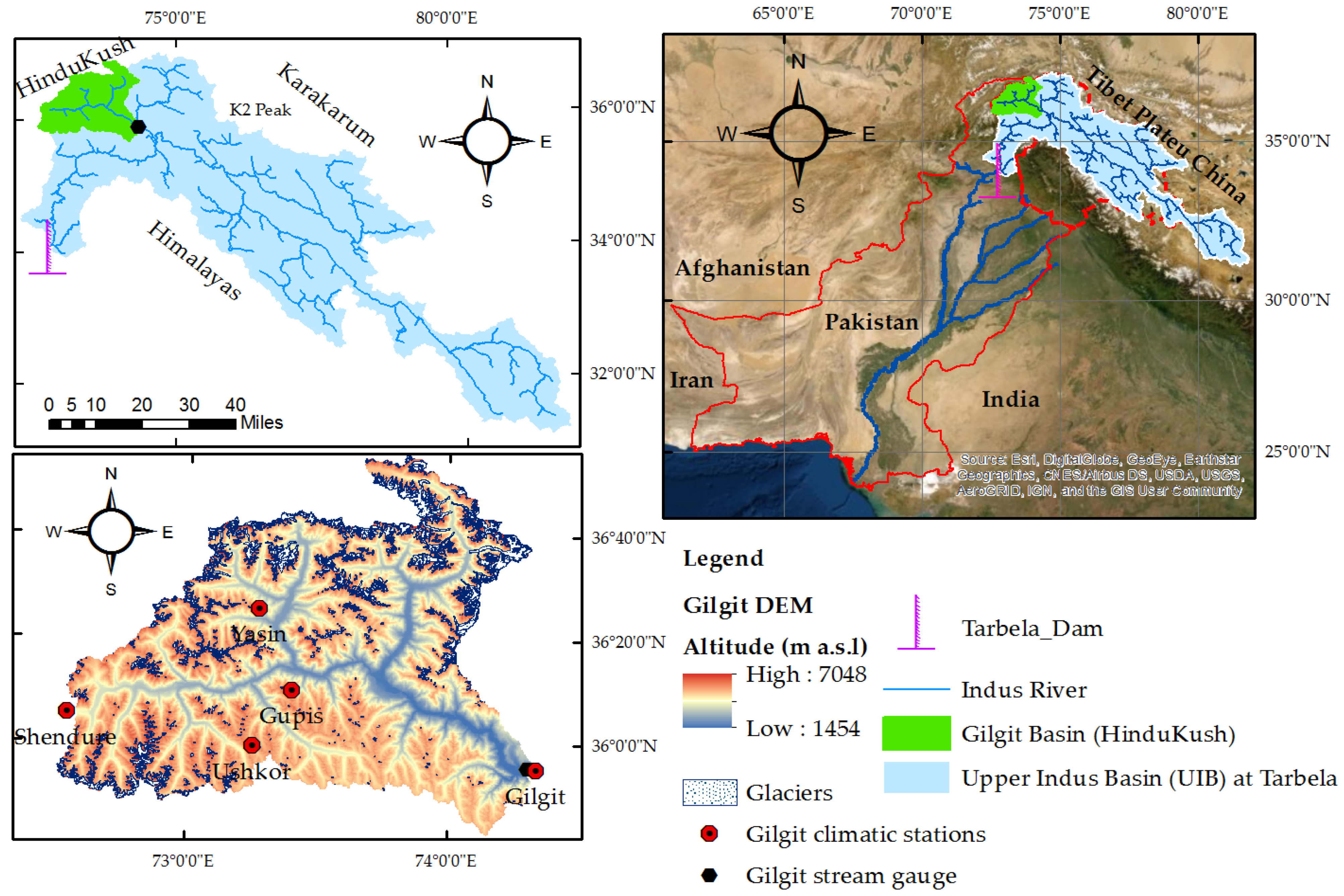
2.1. Study Area
| Variable | Data Source | Interval | Period | Source |
|---|---|---|---|---|
| Q * | Mean daily discharge (m3/s) | Daily | 1981–2010 | Water and Power Development Authority (WAPDA), Pakistan |
| SSC * | Suspended sediment concentration (mg/L) | Intermittent weekdays | 1981–2010 | Water and Power Development Authority (WAPDA), Pakistan |
| SCF | Snow cover fractions calculated from MODIS satellite data ranging from 0 to 1 | Weekly | 2000–2010 | https://nsidc.org/data/MOD10A2 accessed on 24 April 2020 |
| T | Daily maximum, minimum and mean basin air temperature for a grid of 5 × 5 km in size (°C) | Daily | 1981–2010 | [59,60] |
| P | Daily mean rainfall (mm/day) on a grid of 5 × 5 km in size | Daily | 1981–2010 | [59,60] |
| Evap | Daily mean evapotranspiration (mm/day) on a grid of 5 × 5 km in size | Daily | 1981–2010 | [59,60] |
| Input Variable | Description (Basin Average) | Log Q (m3/Day) | log SSY (tons/Day) | SCA (Fractions) | Tavg (°C) | P (mm) | Evap (mm/Day) |
|---|---|---|---|---|---|---|---|
| log Q | Logarithm of discharge | 1.000 | |||||
| log SSY | Logarithm of sediment yields | 0.870 | 1.000 | ||||
| SCA | Snow cover area | −0.850 | −0.740 | 1.000 | |||
| Tavg. | Temperature | 0.870 | 0.790 | −0.880 | 1.000 | ||
| P | Effective rainfall | 0.160 | 0.150 | 0.090 | 0.100 | 1.000 | |
| Evap. | Evapotranspiration | 0.860 | 0.810 | −0.820 | 0.930 | 0.060 | 1.000 |
2.2. Snow cover Estimation Using the Temperature Index Snow Model
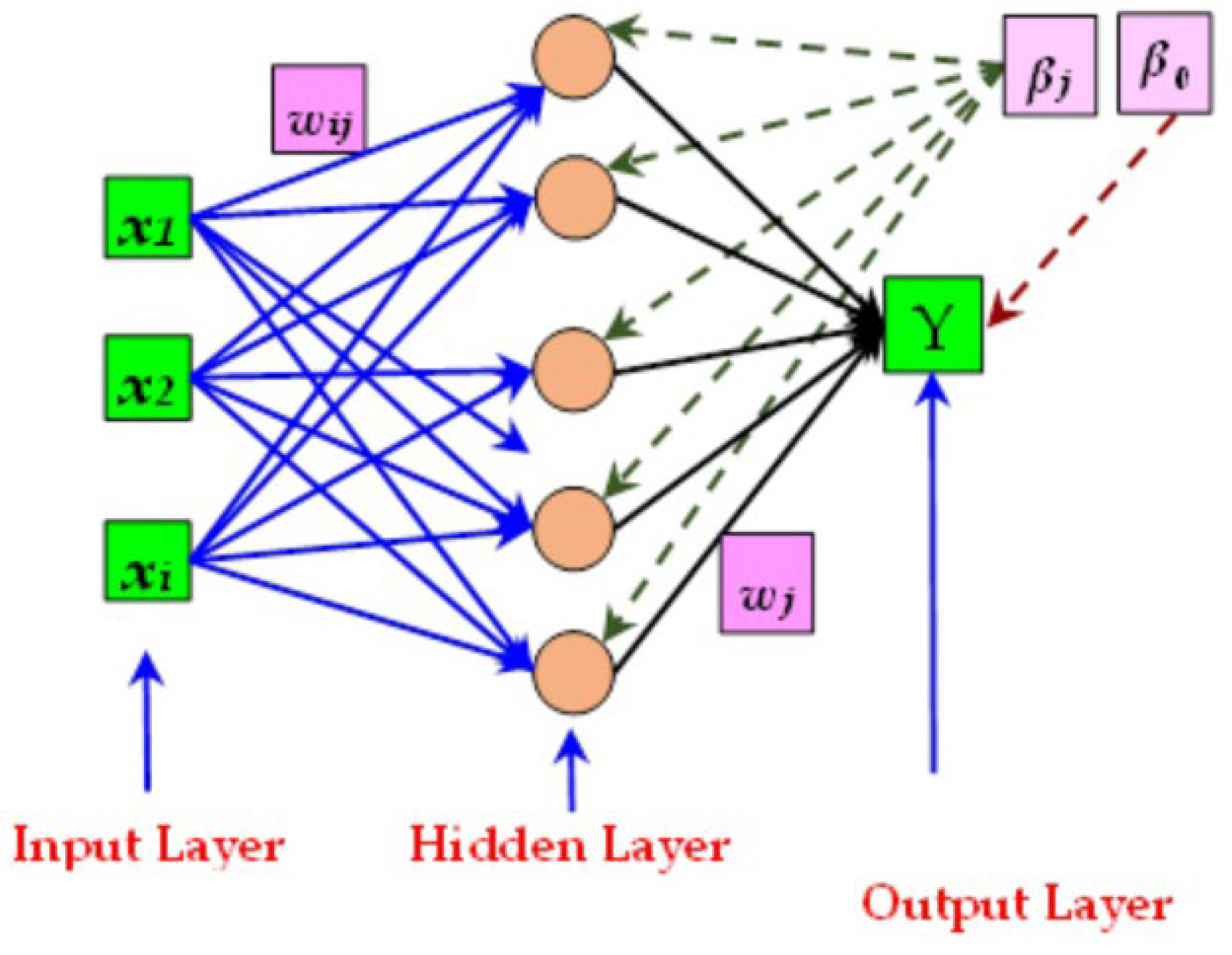
2.3. Artificial Neural Networks
2.4. Multivariate Adaptive Regression Splines (MARS)
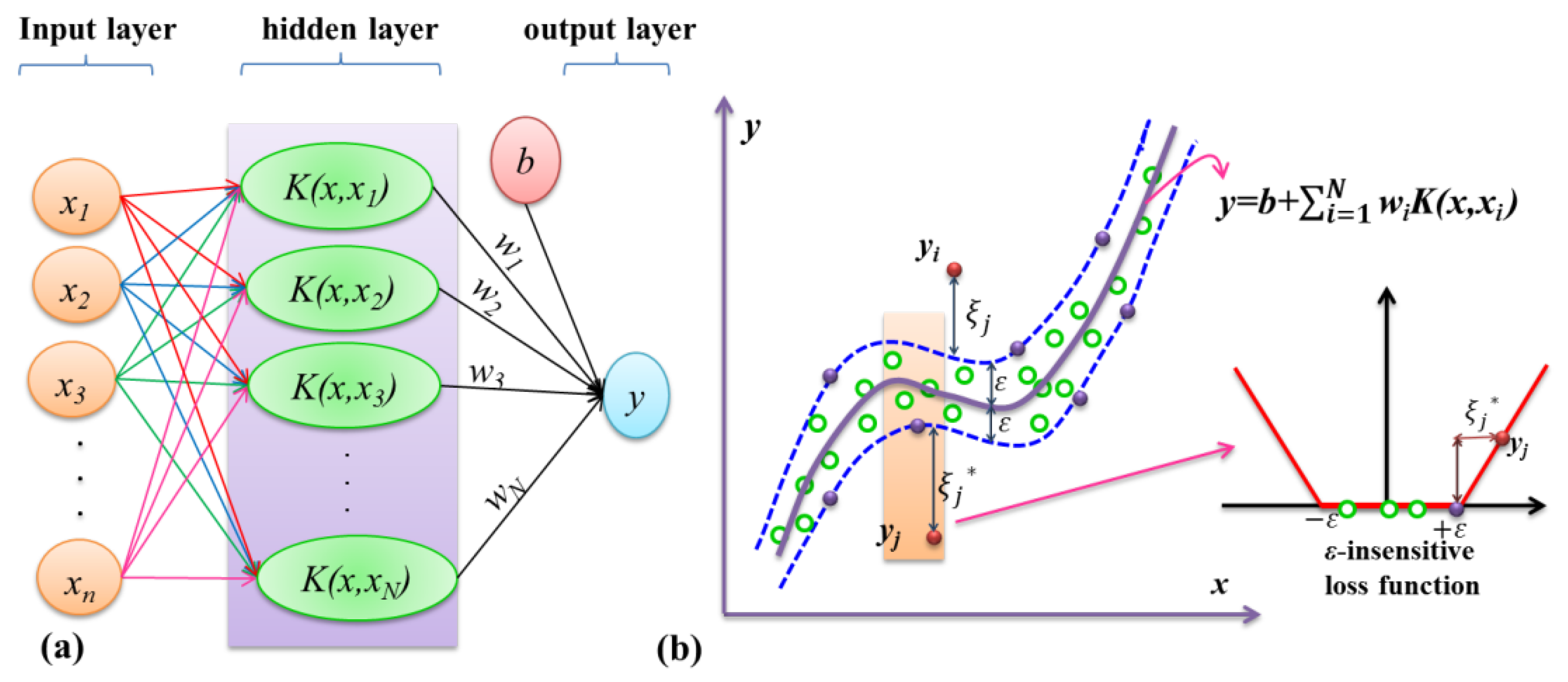
2.5. Support Vector Regression
2.6. Response Surface Method (RSM)
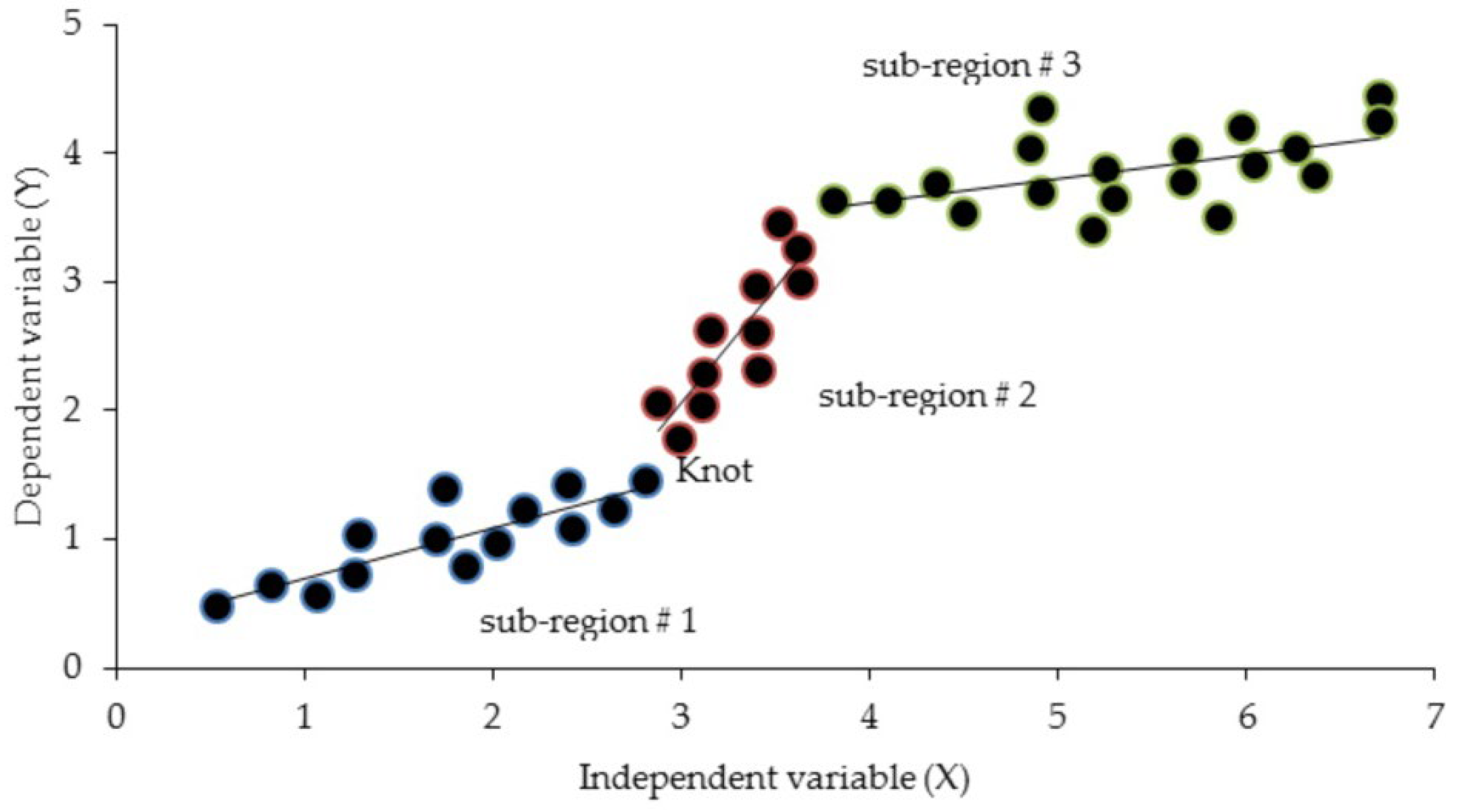
2.7. M5Tree Model

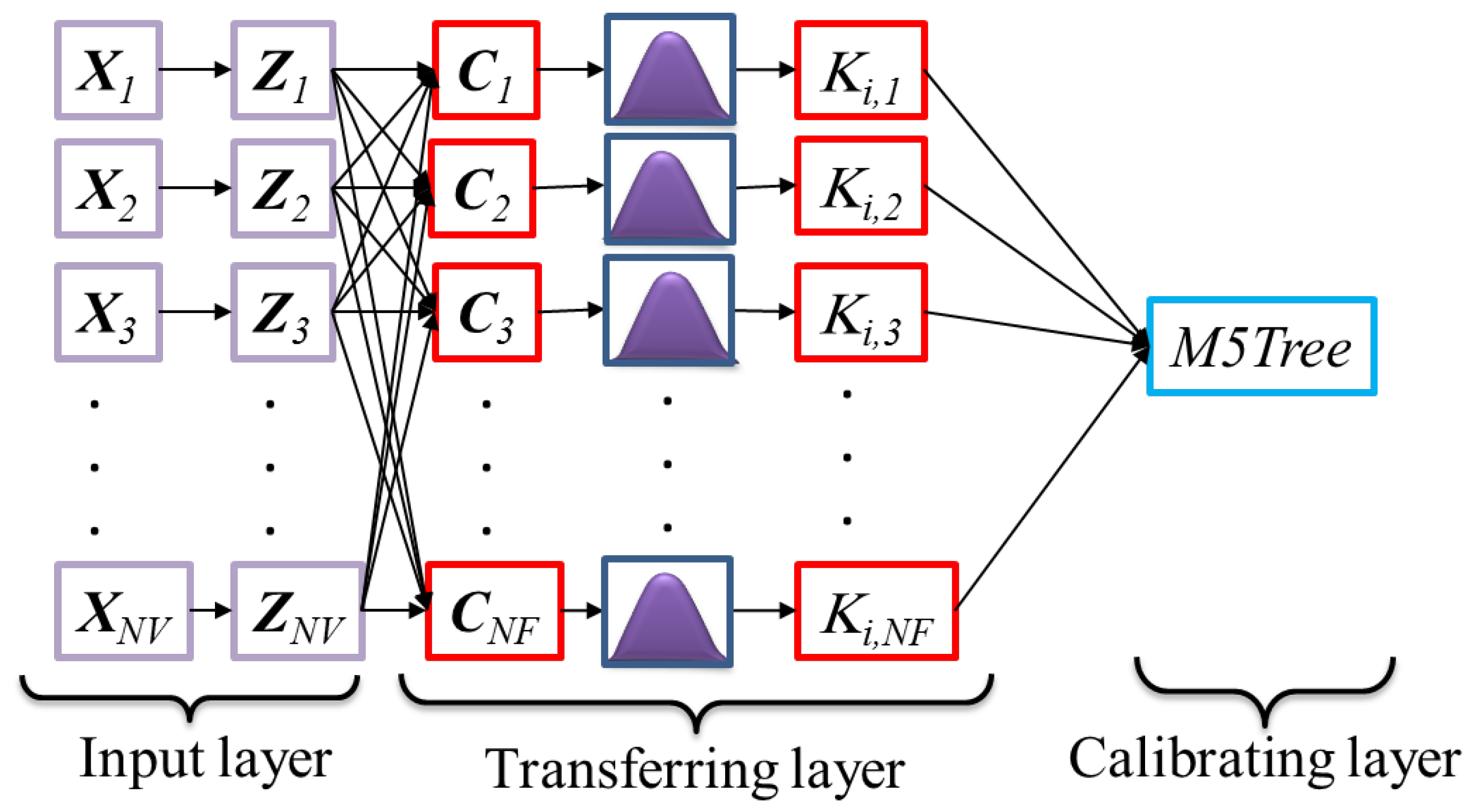
2.8. Radial M5Tree Model
- Creation of a randomly selected center point of RBF datasets.
- Transformation of input datasets of layer 1 into a radial space using Equation (21) on the basis of the RBF center point as follows:
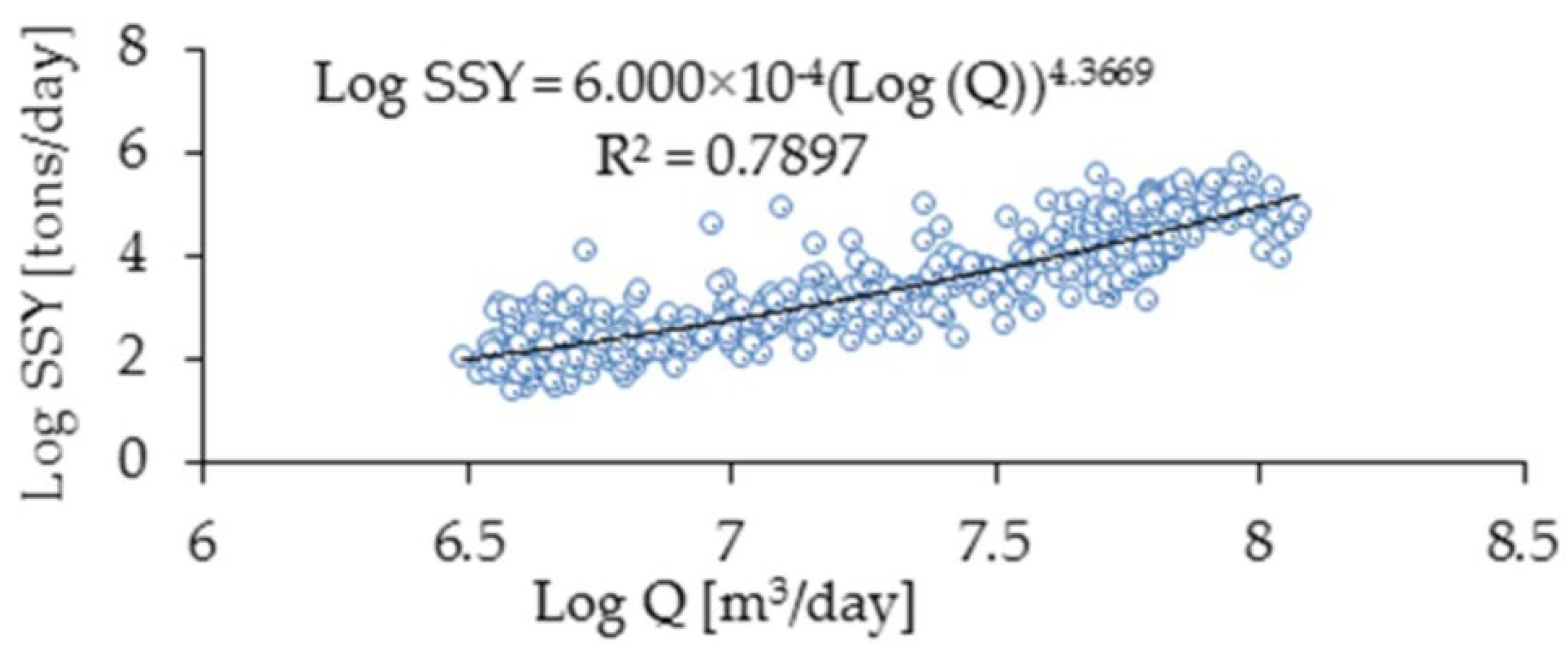
2.9. Sediment Rating Curve (SRC)
2.10. Performance Metrics for Model Evaluation
2.11. Application of the ANN, MARS, SVR, M5Tree, RM5Tree and RSM Models
- (a)
- Flows:
- (b)
- Snow cover area and flows:
- (c)
- Flow, snow cover area and effective rainfall:
- (d)
- Flow, snow cover area, temperature and evapotranspiration:
- (e)
- Mean basin air temperature:
- (f)
- Flow, snow cover area, temperature, rainfall and evapotranspiration:
3. Results and Discussions
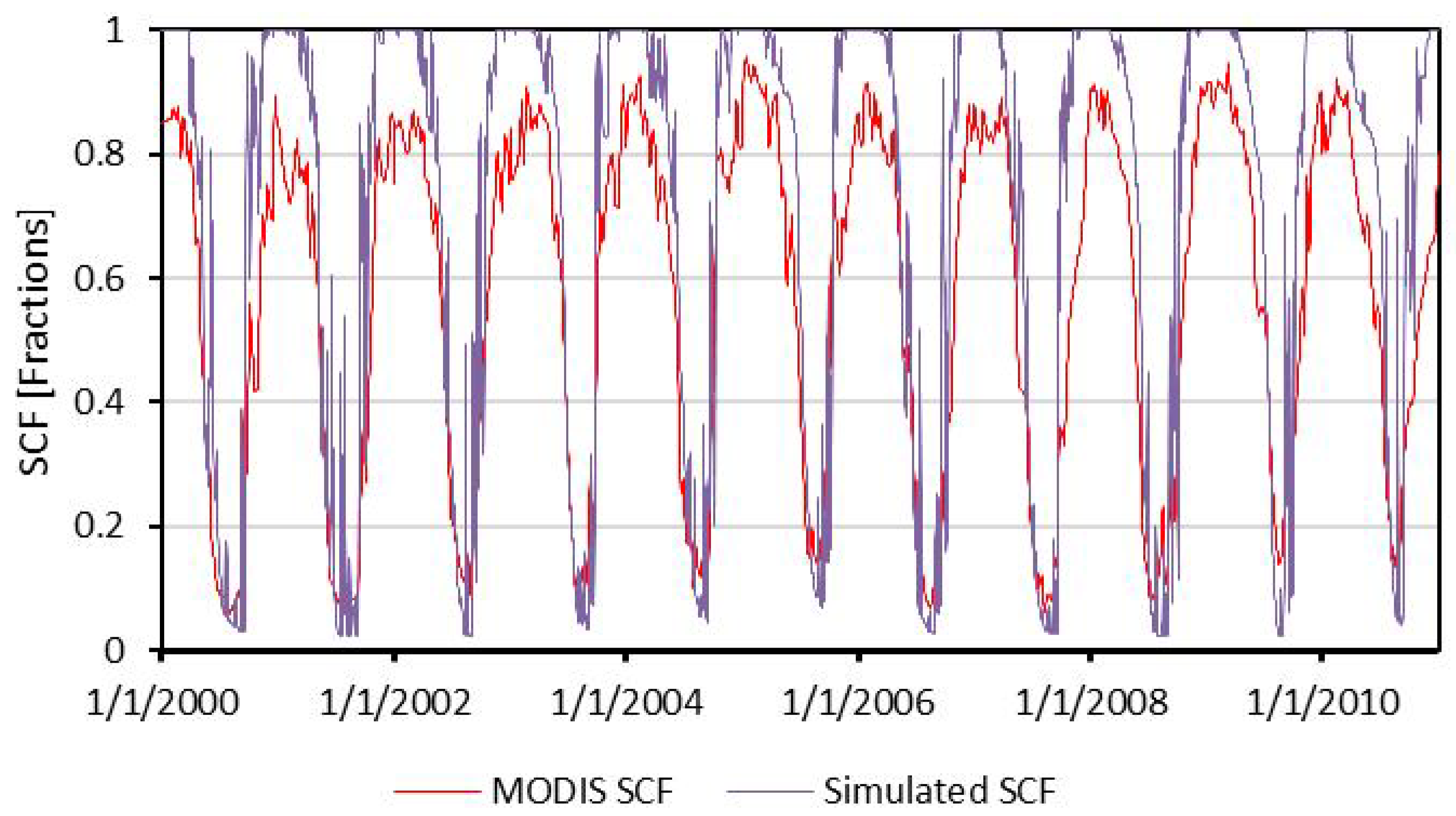
3.1. Simulation Results of Snow Melting and Snow Cover Area
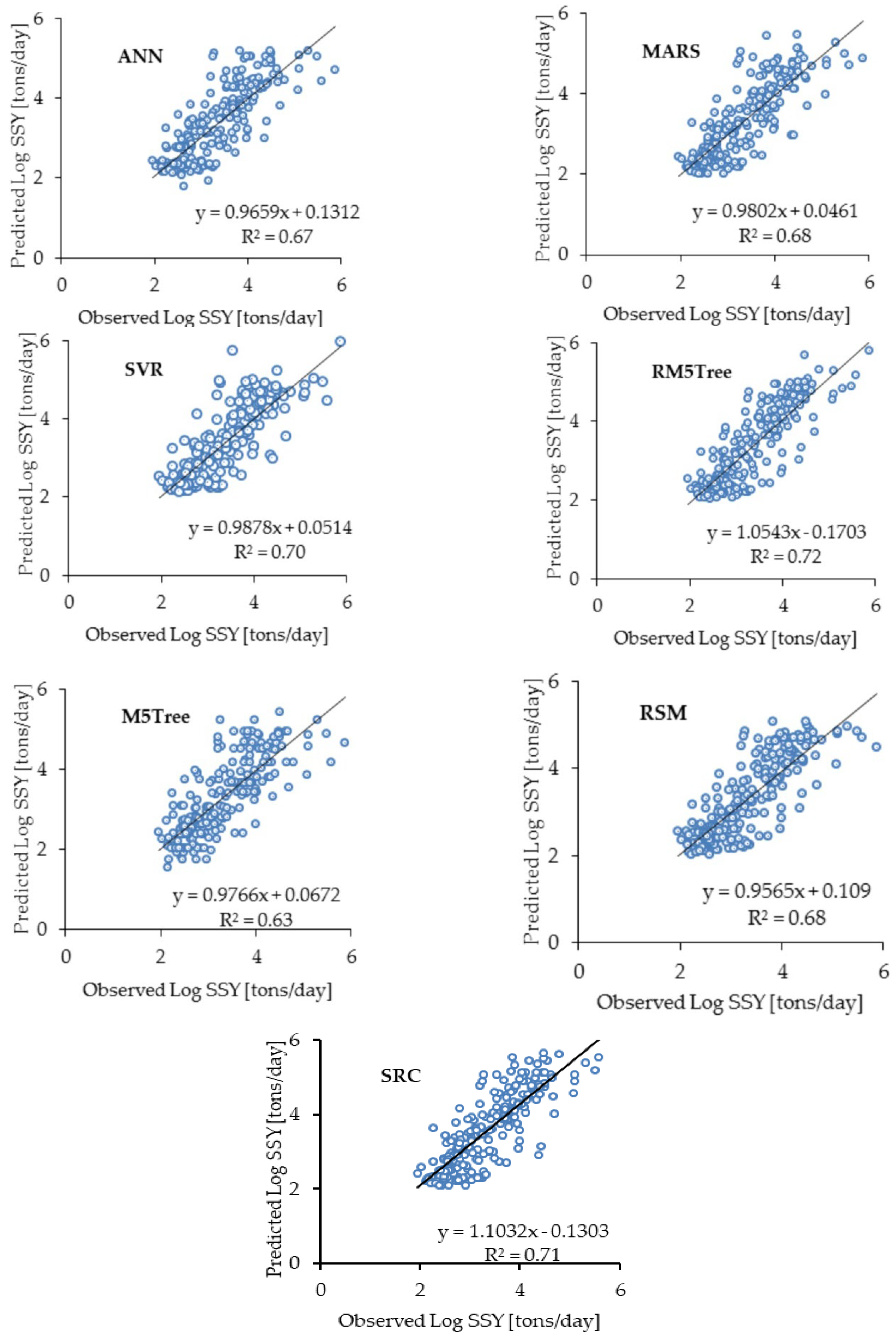
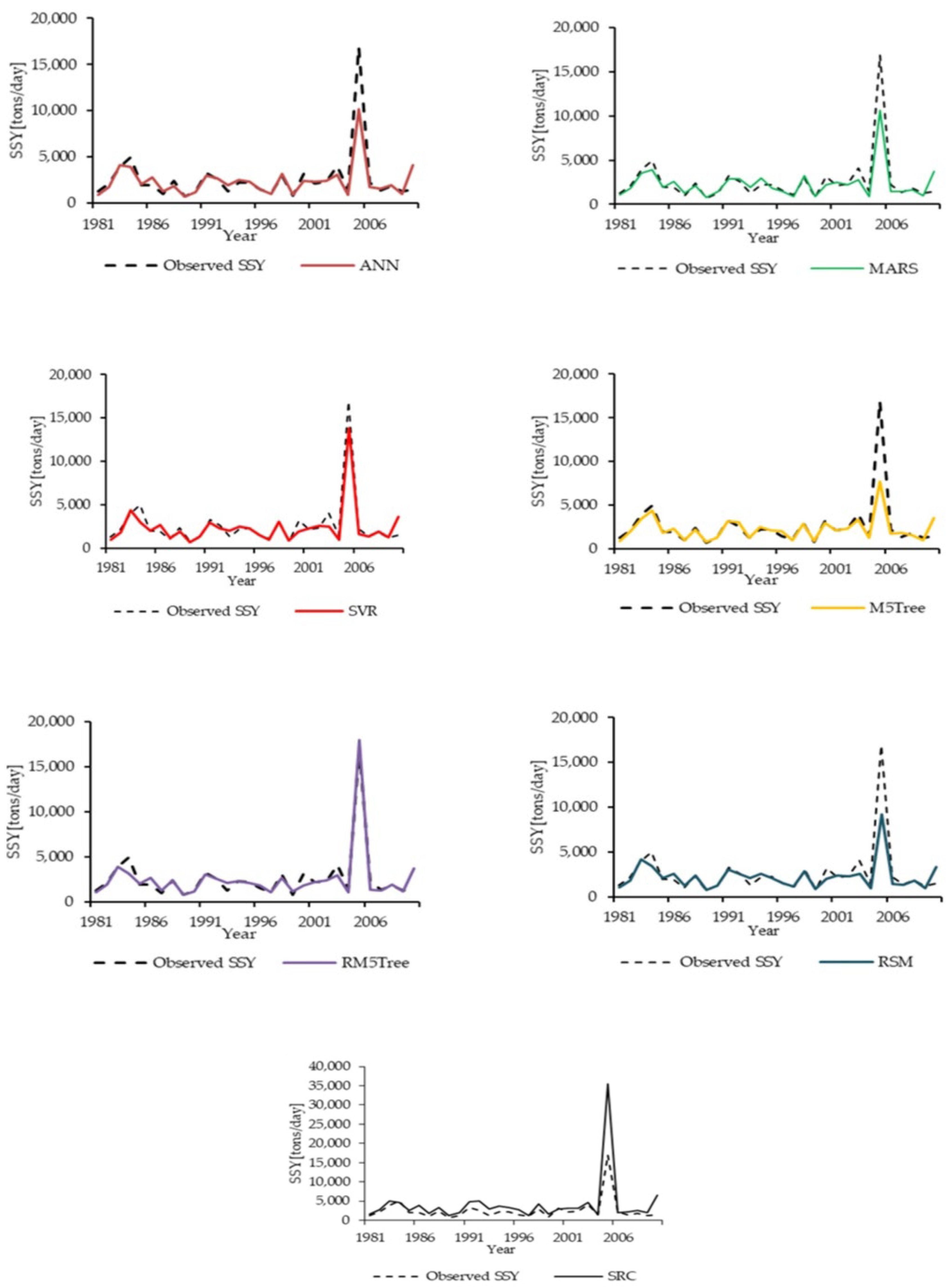
3.2. Comparison of the ANN, MARS, SVR, M5Tree, RM5Tree, RSM and SRC Models
3.3. Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Foster, G.R.; Meyer, L.D. A Closed-Form Soil Erosion Equation for Upland Areas. In Sedimentation Symposium; Einstein, H.A., Shen, H.W., Eds.; Colorado State University: Fort Collins, CO, USA, 1972; pp. 12–19. [Google Scholar]
- Knack, I.M.; Shen, H.T. A numerical model for sediment transport and bed change with river ice. J. Hydraul. Res. 2018, 56, 844–856. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Muhammad Adnan, R. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Hussan, W.U.; Shahzad, M.K.; Seidel, F.; Nestmann, F. Application of Soft Computing Models with Input Vectors of Snow Cover Area in Addition to Hydro-Climatic Data to Predict the Sediment Loads. Water 2020, 12, 1481. [Google Scholar] [CrossRef]
- Gomez, B. Bedload transport. Earth Sci. Rev. 1991, 31, 89–132. [Google Scholar] [CrossRef]
- Parsons, A.J.; Cooper, J.; Wainwright, J. What is suspended sediment? Earth Surf. Process. Landforms 2015, 40, 1417–1420. [Google Scholar] [CrossRef] [Green Version]
- Hussan, W.U.; Shahzad, M.K.; Seidel, F.; Costa, A.; Nestmann, F. Comparative Assessment of Spatial Variability and Trends of Flows and Sediments under the Impact of Climate Change in the Upper Indus Basin. Water 2020, 12, 730. [Google Scholar] [CrossRef] [Green Version]
- Kemp, P.; Sear, D.; Collins, A.; Naden, P.; Jones, I. The impacts of fine sediment on riverine fish. Hydrol. Process. 2011, 25, 1800–1821. [Google Scholar] [CrossRef]
- Mohammadi, B.; Guan, Y.; Moazenzadeh, R.; Safari, M.J.S. Implementation of hybrid particle swarm optimization-differential evolution algorithms coupled with multi-layer perceptron for suspended sediment load estimation. Catena 2021, 198, 105024. [Google Scholar] [CrossRef]
- Jiang, B.; Liu, H.; Xing, Q.; Cai, J.; Zheng, X.; Li, L.; Liu, S.; Zheng, Z.; Xu, H.; Meng, L. Evaluating traditional empirical models and BPNN models in monitoring the concentrations of chlorophyll-A and total suspended particulate of eutrophic and turbid waters. Water 2021, 13, 650. [Google Scholar] [CrossRef]
- Bashar, K.E.; ElTahir, E.O.; Fattah, S.A.; Ali, A.S.; Osman, M. Nile Basin Reservoir Sedimentation Prediction and Mitigation. Nile Basin Capacity Building Network Cairo Egypt. 2010. Available online: https://www.nbcbn.com/ctrl/images/img/uploads/4427_31104551.pdf (accessed on 4 March 2023).
- Ghernaout, R.; Remini, B. Impact of suspended sediment load on the silting of SMBA reservoir (Algeria). Environ. Earth Sci. 2014, 72, 915–929. [Google Scholar] [CrossRef]
- Wisser, D.; Frolking, S.; Hagen, S.; Bierkens, M.F.P. Beyond peak reservoir storage? A global estimate of declining water storage capacity in large reservoirs. Water Resour. Res. 2013, 49, 5732–5739. [Google Scholar] [CrossRef] [Green Version]
- Khan, N.M.; Tingsanchali, T. Optimization and simulation of reservoir operation with sediment evacuation: A case study of the Tarbela Dam, Pakistan. Hydrol. Process. 2009, 23, 730–747. [Google Scholar] [CrossRef]
- Ackers, J.; Hieatt, M.; Molyneux, J.D. Mangla reservoir, Pakistan—Approaching 50 years of service. Dams Reserv. 2016, 26, 68–83. [Google Scholar] [CrossRef]
- Adnan, R.M.; Yaseen, Z.M.; Heddam, S.; Shahid, S.; Sadeghi-Niaraki, A.; Kisi, O. Predictability performance enhancement for suspended sediment in rivers: Inspection of newly developed hybrid adaptive neuro-fuzzy system model. Int. J. Sediment Res. 2022, 37, 383–398. [Google Scholar] [CrossRef]
- Muhammad, R.; Zhongmin, A.; Kulwinder, L.; Parmar, S.; Soni, K.; Kisi, O.; Adnan, R.M. Modeling monthly streamflow in mountainous basin by MARS, GMDH-NN and DENFIS using hydroclimatic data. Neural Comput. Appl. 2020, 33, 2853–2871. [Google Scholar]
- Ahmad, N. Water Resources of Pakistan and Their Utilization; Shahid Nazir: Lahore, Pakistan, 1993; Available online: http://catalogue.nust.edu.pk/cgi-bin/koha/opac-detail.pl?biblionumber=695 (accessed on 21 May 2020).
- Pakistan Water Sector Strategy. In Executive Summary; Report; Ministry of Water and Power, Office of the Chief Engineering Advisor/Chairman Federal Flood Commission, Government of Pakistan: Islamabad, Pakistan, 2002; Volume 1.
- Faran Ali, K.; de Boer, D.H. Factors controlling specific sediment yield in the upper Indus River basin, Northern Pakistan. Hydrol. Process. 2008, 22, 3102–3114. [Google Scholar] [CrossRef]
- Chen, X.Y.; Chau, K.W. A Hybrid Double Feedforward Neural Network for Suspended Sediment Load Estimation. Water Resour. Manag. 2016, 30, 2179–2194. [Google Scholar] [CrossRef]
- Jain, S.K. Development of Integrated Sediment Rating Curves Using ANNs. J. Hydraul. Eng. 2001, 127, 30–37. [Google Scholar] [CrossRef]
- Kerem Cigizoglu, H.; Kisi, Ö. Methods to improve the neural network performance in suspended sediment estimation. J. Hydrol. 2006, 317, 221–238. [Google Scholar] [CrossRef]
- Rajaee, T.; Mirbagheri, S.A.; Zounemat-Kermani, M.; Nourani, V. Daily suspended sediment concentration simulation using ANN and neuro-fuzzy models. Sci. Total Environ. 2009, 407, 4916–4927. [Google Scholar] [CrossRef]
- Melesse, A.M.; Ahmad, S.; McClain, M.E.; Wang, X.; Lim, Y.H. Suspended sediment load prediction of river systems: An artificial neural network approach. Agric. Water Manag. 2011, 98, 855–866. [Google Scholar] [CrossRef]
- Taşar, B.; Kaya, Y.; Varçin, H.; Üneş, F.; Demirci, M. Forecasting of Suspended Sediment in Rivers Using Artificial Neural Networks Approach. Int. J. Adv. Eng. Res. Sci. 2017, 4, 79–84. [Google Scholar] [CrossRef]
- Kumar, D.; Pandey, A.; Sharma, N.; Flügel, W.-A. Modeling Suspended Sediment Using Artificial Neural Networks and TRMM-3B42 Version 7 Rainfall Dataset. J. Hydrol. Eng. 2015, 20, C4014007. [Google Scholar] [CrossRef]
- Cobaner, M.; Unal, B.; Kisi, O. Suspended sediment concentration estimation by an adaptive neuro-fuzzy and neural network approaches using hydro-meteorological data. J. Hydrol. 2009, 367, 52–61. [Google Scholar] [CrossRef]
- Kisi, O.; Haktanir, T.; Ardiclioglu, M.; Ozturk, O.; Yalcin, E.; Uludag, S. Adaptive neuro-fuzzy computing technique for suspended sediment estimation. Adv. Eng. Softw. 2009, 40, 438–444. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J. River suspended sediment estimation by climatic variables implication: Comparative study among soft computing techniques. Comput. Geosci. 2012, 43, 73–82. [Google Scholar] [CrossRef]
- Emamgholizadeh, S.; Demneh, R. The comparison of artificial intelligence models for the estimation of daily suspended sediment load: A case study on Telar and Kasilian Rivers in Iran. Water Sci. Technol. Water Supply 2018, 19, 165–178. [Google Scholar] [CrossRef] [Green Version]
- Cimen, M. Estimation of daily suspended sediments using support vector machines. Hydrol. Sci. J. 2008, 53, 656–666. [Google Scholar] [CrossRef]
- Buyukyildiz, M.; Kumcu, S.Y. An Estimation of the Suspended Sediment Load Using Adaptive Network Based Fuzzy Inference System, Support Vector Machine and Artificial Neural Network Models. Water Resour. Manag. 2017, 31, 1343–1359. [Google Scholar] [CrossRef]
- Kakaei Lafdani, E.; Moghaddam Nia, A.; Ahmadi, A. Daily suspended sediment load prediction using artificial neural networks and support vector machines. J. Hydrol. 2013, 478, 50–62. [Google Scholar] [CrossRef]
- Noori, R.; Ghiasi, B.; Salehi, S.; Esmaeili Bidhendi, M.; Raeisi, A.; Partani, S.; Meysami, R.; Mahdian, M.; Hosseinzadeh, M.; Abolfathi, S. An efficient data driven-based model for prediction of the total sediment load in rivers. Hydrology 2022, 9, 36. [Google Scholar] [CrossRef]
- Rajaee, T. Wavelet and ANN combination model for prediction of daily suspended sediment load in rivers. Sci. Total Environ. 2011, 409, 2917–2928. [Google Scholar] [CrossRef] [PubMed]
- Olyaie, E.; Banejad, H.; Chau, K.-W.; Melesse, A.M. A comparison of various artificial intelligence approaches performance for estimating suspended sediment load of river systems: A case study in United States. Environ. Monit. Assess. 2015, 187, 189. [Google Scholar] [CrossRef]
- Khosravi, K.; Rezaie, F.; Cooper, J.R.; Kalantari, Z.; Abolfathi, S.; Hatamiafkoueieh, J. Soil water erosion susceptibility assessment using deep learning algorithms. J. Hydrol. 2023, 618, 129229. [Google Scholar] [CrossRef]
- Nourani, V.; Andalib, G. Daily and Monthly Suspended Sediment Load Predictions Using Wavelet Based Artificial Intelligence Approaches. J. Mt. Sci. 2015, 12, 85–100. [Google Scholar] [CrossRef]
- Alizamir, M.; Kisi, O.; Adnan, R.M.; Kuriqi, A. Modelling reference evapotranspiration by combining neuro-fuzzy and evolutionary strategies. Acta Geophys. 2020, 68, 1113–1126. [Google Scholar] [CrossRef]
- Mostafa, R.R.; Kisi, O.; Adnan, R.M.; Sadeghifar, T.; Kuriqi, A. Modeling Potential Evapotranspiration by Improved Machine Learning Methods Using Limited Climatic Data. Water 2023, 15, 486. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Mostafa, R.R.; Chen, Z.; Parmar, K.S.; Kisi, O.; Zounemat-Kermani, M. Water Temperature Prediction Using Improved Deep Learning Methods through Reptile Search Algorithm and Weighted Mean of Vectors Optimizer. J. Mar. Sci. Eng. 2023, 11, 259. [Google Scholar] [CrossRef]
- Hild, C.; Bozdogan, H. The use of information-based model evaluation criteria in the GMDH algorithm. Syst. Anal. Model. Simul. 1995, 20, 29–50. [Google Scholar]
- Ivakhnenko, A.G. The Group Method of Data of Handling; A rival of the method of stochastic approximation. Sov. Autom. Control 1968, 1, 43–55. [Google Scholar]
- Yeganeh-Bakhtiary, A.; Eyvazoghli, H.; Shabakhty, N.; Kamranzad, B.; Abolfathi, S. Machine Learning as a Downscaling Approach for Prediction of Wind Characteristics under Future Climate Change Scenarios. Complexity 2022, 13, 8451812. [Google Scholar] [CrossRef]
- Abolfathi, S.; Yeganeh-Bakhtiary, A.; Hamze-Ziabari, S.M.; Borzooei, S. Wave runup prediction using M5′ model tree algorithm. Ocean Eng. 2016, 112, 76–81. [Google Scholar] [CrossRef]
- Rahgoshay, M.; Feiznia, S.; Arian, M.; Hashemi, S.A.A. Simulation of daily suspended sediment load using an improved model of support vector machine and genetic algorithms and particle swarm. Arab. J. Geosci. 2019, 12, 277. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Kisi, O.; Shiri, J. Evaluating the performance of four different heuristic approaches with Gamma test for daily suspended sediment concentration modeling. Environ. Sci. Pollut. Res. Int. 2019, 26, 22670–22687. [Google Scholar] [CrossRef] [PubMed]
- Adnan, R.M.; Liang, Z.; Trajkovic, S.; Zounemat-Kermani, M.; Li, B.; Kisi, O. Daily streamflow prediction using optimally pruned extreme learning machine. J. Hydrol. 2019, 577, 123981. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; El-Shafie, A.; Zounemat-Kermani, M.; Kisi, O. Prediction of Suspended Sediment Load Using Data-Driven Models. Water 2019, 11, 2060. [Google Scholar] [CrossRef] [Green Version]
- Yilmaz, B.; Aras, E.; Nacar, S.; Kankal, M. Estimating suspended sediment load with multivariate adaptive regression spline, teaching-learning based optimization, and artificial bee colony models. Sci. Total Environ. 2018, 639, 826–840. [Google Scholar] [CrossRef]
- Chachi, J.; Taheri, S.M.; Pazhand, H.R. Suspended load estimation using L1-fuzzy regression, L2-fuzzy regression and MARS-fuzzy regression models. Hydrol. Sci. J. 2016, 61, 1489–1502. [Google Scholar] [CrossRef] [Green Version]
- Janga Reddy, M.; Ghimire, B. Use of Model Tree and Gene Expression Programming to Predict the Suspended Sediment Load in Rivers. J. Intell. Syst. 2009, 18, 211–228. [Google Scholar] [CrossRef]
- Goyal, M.K. Modeling of Sediment Yield Prediction Using M5 Model Tree Algorithm and Wavelet Regression. Water Resour. Manag. 2014, 28, 1991–2003. [Google Scholar] [CrossRef]
- Senthil Kumar, A.R.; Ojha, C.S.P.; Goyal, M.K.; Singh, R.D.; Swamee, P.K. Modeling of Suspended Sediment Concentration at Kasol in India Using ANN, Fuzzy Logic, and Decision Tree Algorithms. J. Hydrol. Eng. 2012, 17, 394–404. [Google Scholar] [CrossRef]
- Tao, H.; Keshtegar, B.; Yaseen, Z.M. The feasibility of integrative radial basis M5Tree predictive model for river suspended sediment load simulation. Water Resour. Manag. 2019, 33, 4471–4490. [Google Scholar] [CrossRef]
- Tahir, A.A.; Chevallier, P.; Arnaud, Y.; Neppel, L.; Ahmad, B. Modeling snowmelt-runoff under climate scenarios in the Hunza River basin, Karakoram Range, Northern Pakistan. J. Hydrol. 2011, 409, 104–117. [Google Scholar] [CrossRef]
- Adnan, M.; Nabi, G.; Saleem Poomee, M.; Ashraf, A. Snowmelt runoff prediction under changing climate in the Himalayan cryosphere: A case of Gilgit River Basin. Geosci. Front. 2017, 8, 941–949. [Google Scholar] [CrossRef] [Green Version]
- Immerzeel, W.W.; Wanders, N.; Lutz, A.F.; Shea, J.M.; Bierkens, M.F.P. Reconciling high-altitude precipitation in the upper Indus basin with glacier mass balances and runoff. Hydrol. Earth Syst. Sci. 2015, 19, 4673–4687. [Google Scholar] [CrossRef] [Green Version]
- Lutz, A.F.; Immerzeel, W.W. HI-AWARE Reference Climate Dataset for the Indus, Ganges and Brahmaputra River Basins; Future Water Report 146; CRDI: Wageningen, The Netherlands, 2015; Available online: https://www.futurewater.eu/wp-content/uploads/2015/10/Report_IGB_historical_climate_dataset.pdf (accessed on 21 May 2020).
- Shahin, M.A.; Maier, H.R.; Jaksa, M.B. Data Division for Developing Neural Networks Applied to Geotechnical Engineering. J. Comput. Civ. Eng. 2004, 18, 105–114. [Google Scholar] [CrossRef]
- Hewitt, K. The Karakoram Anomaly? Glacier Expansion and the ‘Elevation Effect’, Karakoram Himalaya. Mt. Res. Dev. 2005, 25, 332–340. [Google Scholar] [CrossRef] [Green Version]
- Hewitt, K. Tributary glacier surges: An exceptional concentration at Panmah Glacier, Karakoram Himalaya. J. Glaciol. 2007, 53, 181–188. [Google Scholar] [CrossRef] [Green Version]
- Winiger, M.; Gumpert, M.; Yamout, H. Karakorum-Hindukush-western Himalaya: Assessing high-altitude water resources. Hydrol. Process. 2005, 19, 2329–2338. [Google Scholar] [CrossRef]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Costa, A.; Molnar, P.; Stutenbecker, L.; Bakker, M.; Silva, T.A.; Schlunegger, F.; Lane, S.N.; Loizeau, J.-L.; Girardclos, S. Temperature signal in suspended sediment export from an Alpine catchment. Hydrol. Earth Syst. Sci. 2018, 22, 509–528. [Google Scholar] [CrossRef] [Green Version]
- Govindaraju, R.S. Artificial Neural Networks in Hydrology. I: Preliminary Concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar]
- Govindaraju, R.S. Artificial Neural Networks in Hydrology. II: Hydrologic Applications. J. Hydrol. Eng. 2000, 5, 124–137. [Google Scholar]
- Haykin, S.S. Neural Networks. A Comprehensive Foundation/Simon Haykin, 2nd ed.; Prentice Hall: London, UK; Upper Saddle River, NJ, USA, 1999; ISBN 0132733501. [Google Scholar]
- Muhammad Adnan, R.; Yuan, X.; Kisi, O.; Yuan, Y.; Tayyab, M.; Lei, X. Application of soft computing models in streamflow forecasting. In Proceedings of the Institution of Civil Engineers-Water Management; Thomas Telford Ltd.: London, UK, 2019; Volume 172, pp. 123–134. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation: Parallel Distributed Processing: Explorations in the Microstructure of Cognition; Rumelhart, D.E., McClelland, J.L., PDP Research Group, Eds.; MIT Press: Cambridge, MA, USA, 1986; Volume 1, pp. 318–362. ISBN 0-262-68053-X. [Google Scholar]
- Minns, A.W.; Hall, M.J. Artificial neural networks as rainfall-runoff models. Hydrol. Sci. J. 1996, 41, 399–417. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Ewees, A.A.; Parmar, K.S.; Yaseen, Z.M.; Shahid, S.; Kisi, O. The Viability of Extended Marine Predators Algorithm-Based Artificial Neural Networks for Streamflow Prediction. Appl. Soft Comput. 2022, 131, 109739. [Google Scholar] [CrossRef]
- Kisi, O.; Keshtegar, B.; Zounemat-Kermani, M.; Heddam, S.; Trung, N.-T. Modeling reference evapotranspiration using a novel regression-based method: Radial Basis M5 Model Tree. Theor. Appl. Climatol. 2021, 145, 639–659. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Heddam, S.; Zounemat-Kermani, M.; Kisi, O.; Li, B. Least square support vector machine and multivariate adaptive regression splines for streamflow prediction in mountainous basin using hydro-meteorological data as inputs. J. Hydrol. 2020, 586, 124371. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Gan, Y. Comparison of six different soft computing methods in modeling evaporation in different climates. Hydrol. Earth Syst. Sci. Discuss. 2016, 1–51. [Google Scholar] [CrossRef]
- Jalali-Heravi, M.; Asadollahi-Baboli, M.; Mani-Varnosfaderani, A. Shuffling multivariate adaptive regression splines and adaptive neuro-fuzzy inference system as tools for QSAR study of SARS inhibitors. J. Pharm. Biomed. Anal. 2009, 50, 853–860. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, L.; Xiao, M. A new hybrid reliability-based design optimization method under random and interval uncertainties. Int. J. Numer. Methods Eng. 2020, 121, 4435–4457. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, L.; Xiao, M. Maximizing natural frequencies of inhomogeneous cellular structures by kriging-assisted multiscale topology optimization. Comput. Struct. 2020, 230, 106197. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T.C. Evaluating seismic liquefaction potential using multivariate adaptive regression splines and logistic regression. Geomech. Eng. 2016, 10, 269–284. [Google Scholar] [CrossRef]
- Keshtegar, B.; Mert, C.; Kisi, O. Comparison of four heuristic regression techniques in solar radiation modeling: Kriging Method VS RSM, Mars and M5 Model Tree. Renew. Sustain. Energy Rev. 2018, 81, 330–341. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Xiao, M.; Zhang, J.; Gao, L. A system active learning Kriging method for system reliability-based design optimization with a multiple response model. Reliab. Eng. Syst. Saf. 2020, 199, 106935. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, M.; Gao, L.; Chu, S. Probability and interval hybrid reliability analysis based on adaptive local approximation of projection outlines using support vector machine. Comput. Aided Civ. Infrastruct. Eng. 2019, 34, 991–1009. [Google Scholar] [CrossRef]
- Xiao, M.; Gao, L.; Xiong, H.; Luo, Z. An efficient method for reliability analysis under epistemic uncertainty based on evidence theory and support vector regression. J. Eng. Des. 2015, 26, 340–364. [Google Scholar] [CrossRef]
- Fink, O.; Zio, E.; Weidmann, U. Predicting component reliability and level of degradation with complex-valued neural networks. Reliab. Eng. Syst. Saf. 2014, 121, 198–206. [Google Scholar] [CrossRef] [Green Version]
- Gunn, S.R. Support Vector Machines for Classification and Regression; ISIS Technical Report; University of Southampton: Southampton, UK, 1998; Volume 14, pp. 5–16. [Google Scholar]
- Alamoudi, M.; Taylan, O.; Keshtegar, B.; Abusurrah, M.; Balubaid, M. Modeling sulphur dioxide (SO2) quality levels of Jeddah City using machine learning approaches with meteorological and chemical factors. Sustainability 2022, 14, 16291. [Google Scholar] [CrossRef]
- Hill, W.J.; Hunter, W.G. A review of response surface methodology: A literature survey. Technometrics 1966, 8, 571. [Google Scholar] [CrossRef]
- Gunst, R.F. Response surface methodology: Process and product optimization using designed experiments. Technometrics 1996, 38, 284–286. [Google Scholar] [CrossRef]
- Keshtegar, B.; El Amine Ben Seghier, M. Modified response surface method basis harmony search to predict the burst pressure of corroded pipelines. Eng. Fail. Anal. 2018, 89, 177–199. [Google Scholar] [CrossRef]
- Keshtegar, B.; Heddam, S. Modeling daily dissolved oxygen concentration using modified response surface method and artificial neural network: A comparative study. Neural Comput. Appl. 2017, 30, 2995–3006. [Google Scholar] [CrossRef]
- Ahmadi, A.A.; Arabbeiki, M.; Ali, H.M.; Goodarzi, M.; Safaei, M.R. Configuration and optimization of a minichannel using water–alumina nanofluid by non-dominated sorting genetic algorithm and response surface method. Nanomaterials 2020, 10, 901. [Google Scholar] [CrossRef]
- Keshtegar, B.; Kisi, O. Modified response-surface method: New approach for modeling pan evaporation. J. Hydrol. Eng. 2017, 22, 04017045. [Google Scholar] [CrossRef]
- Keshtegar, B.; Bagheri, M.; Fei, C.-W.; Lu, C.; Taylan, O.; Thai, D.-K. Multi-extremum-modified response basis model for nonlinear response prediction of Dynamic Turbine Blisk. Eng. Comput. 2021, 38, 1243–1254. [Google Scholar] [CrossRef]
- Lu, C.; Fei, C.-W.; Liu, H.-T.; Li, H.; An, L.-Q. Moving extremum surrogate modeling strategy for dynamic reliability estimation of turbine blisk with multi-physics fields. Aerosp. Sci. Technol. 2020, 106, 106112. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Xue, Y. M5 model trees and neural networks: Application to flood forecasting in the upper reach of the Huai River in China. J. Hydrol. Eng. 2004, 9, 491–501. [Google Scholar] [CrossRef]
- Adnan, R.M.; Petroselli, A.; Heddam, S.; Santos, C.A.G.; Kisi, O. Short term rainfall-runoff modelling using several machine learning methods and a conceptual event-based model. Stoch. Environ. Res. Risk Assess. 2021, 35, 597–616. [Google Scholar] [CrossRef]
- Rahimikhoob, A. Comparison of M5 model tree and Artificial Neural Network’s methodologies in modelling daily reference evapotranspiration from NOAA satellite images. Water Resour. Manag. 2016, 30, 3063–3075. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Keshtegar, B.; Kisi, O.; Scholz, M. Towards a comprehensive assessment of statistical versus soft computing models in hydrology: Application to monthly pan evaporation prediction. Water 2021, 13, 2451. [Google Scholar] [CrossRef]
- Chen, S.; Cowan, C.F.N.; Grant, P.M. Orthogonal least squares learning algorithm for radial basis function networks. IEEE Trans. Neural Netw. 1991, 2, 302–309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, J.; Xiao, M.; Gao, L.; Chu, S. A combined projection-outline-based Active Learning Kriging and adaptive importance sampling method for hybrid reliability analysis with small failure probabilities. Comput. Methods Appl. Mech. Eng. 2019, 344, 13–33. [Google Scholar] [CrossRef]
- Keshtegar, B.; Kisi, O. RM5Tree: Radial Basis M5 model tree for accurate structural reliability analysis. Reliab. Eng. Syst. Saf. 2018, 180, 49–61. [Google Scholar] [CrossRef]
- Tahir, A.A.; Hakeem, S.A.; Hu, T.; Hayat, H.; Yasir, M. Simulation of snowmelt-runoff under climate change scenarios in a data-scarce mountain environment. Int. J. Digit. Earth 2019, 12, 910–930. [Google Scholar] [CrossRef]
- Hayat, H.; Akbar, T.; Tahir, A.; Hassan, Q.; Dewan, A.; Irshad, M. Simulating Current and Future River-Flows in the Karakoram and Himalayan Regions of Pakistan Using Snowmelt-Runoff Model and RCP Scenarios. Water 2019, 11, 761. [Google Scholar] [CrossRef] [Green Version]
- Lutz, A.F.; Immerzeel, W.W.; Kraaijenbrink, P.D.A.; Shrestha, A.B.; Bierkens, M.F.P. Climate Change Impacts on the Upper Indus Hydrology: Sources, Shifts and Extremes. PLoS ONE 2016, 11, e0165630. [Google Scholar] [CrossRef] [Green Version]
- Adnan, M.; Nabi, G.; Kang, S.; Zhang, G.; Adnan, R.M.; Anjum, M.N.; Iqbal, M.; Ali, A.F. Snowmelt Runoff Modelling under Projected Climate Change Patterns in the Gilgit River Basin of Northern Pakistan. Pol. J. Environ. Stud. 2017, 26, 525–542. [Google Scholar] [CrossRef]
- Tao, H.; Al-Khafaji, Z.S.; Qi, C.; Zounemat-Kermani, M.; Kisi, O.; Tiyasha, T.; Chau, K.-W.; Nourani, V.; Melesse, A.M.; Elhakeem, M.; et al. Artificial intelligence models for suspended river sediment prediction: State-of-the art, modeling framework appraisal, and proposed future research directions. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1585–1612. [Google Scholar] [CrossRef]
- Kisi, O.; Heddam, S.; Keshtegar, B.; Piri, J.; Adnan, R. Predicting daily streamflow in a cold climate using a novel data mining technique: Radial M5 Model Tree. Water 2022, 14, 1449. [Google Scholar] [CrossRef]


| ksnow = 4.2 mm/Day/°C | ||
|---|---|---|
| Calibration Period (2000–2007) | Validation Period (2008–2010) | |
| R2 | 0.90 | 0.90 |
| MAPE | 0.12 | 0.10 |
| RMSE | 0.15 | 0.15 |
| Scenarios | Model Inputs | R2 | RMSE | MAPE (%) | |||
|---|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | Training | Testing | ||
| S1 | Qt, Qt−1 − Qt−4 | 0.86 | 0.62 | 0.40 | 0.61 | 9.89 | 12.90 |
| S2 | SCAt, SCAt−2, Qt | 0.86 | 0.67 | 0.40 | 0.54 | 9.94 | 12.45 |
| S3 | SCAt, SCAt−4, Qt, Rt−1 | 0.86 | 0.64 | 0.40 | 0.58 | 9.83 | 12.74 |
| S4 | SCAt, SCAt−4, Qt, Evapt−1, Tt−1 | 0.85 | 0.64 | 0.40 | 0.57 | 9.93 | 13.17 |
| S5 | SCAt, Qt, Qt−1, Tt−1, Evapt−1 | 0.86 | 0.64 | 0.40 | 0.60 | 9.68 | 14.21 |
| S6 | Tt − Tt−4 | 0.81 | 0.60 | 0.46 | 0.61 | 11.49 | 14.14 |
| S7 | SCAt, Evapt−1, Qt, Rt−1, Tt | 0.86 | 0.64 | 0.40 | 0.60 | 13.17 | 9.83 |
| S8 | SCAt, Qt, Evapt−1, Rt−1, Tt−1 | 0.86 | 0.65 | 0.40 | 0.57 | 9.80 | 12.71 |
| Scenarios | Model Inputs | R2 | RMSE | MAPE (%) | |||
|---|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | Training | Testing | ||
| S1 | Qt, Qt−1 − Qt−4 | 0.84 | 0.64 | 0.42 | 0.58 | 10.69 | 12.97 |
| S2 | SCAt, SCAt−2, Qt | 0.82 | 0.67 | 0.44 | 0.54 | 10.65 | 12.03 |
| S3 | SCAt, SCAt−4, Qt, Rt−1 | 0.83 | 0.68 | 0.44 | 0.53 | 10.79 | 11.71 |
| S4 | SCAt, SCAt−4, Qt, Evapt−1, Tt−1 | 0.85 | 0.64 | 0.40 | 0.55 | 10.03 | 12.21 |
| S5 | SCAt, Qt, Qt−1, Tt−1, Evapt−1 | 0.84 | 0.66 | 0.42 | 0.55 | 10.38 | 12.24 |
| S6 | Tt − Tt−4 | 0.77 | 0.56 | 0.51 | 0.60 | 12.64 | 13.74 |
| S7 | SCAt, Evapt−1, Qt, Rt−1, Tt | 0.86 | 0.64 | 0.40 | 0.57 | 9.91 | 12.49 |
| S8 | SCAt, Qt, Evapt−1, Rt−1, Tt−1 | 0.84 | 0.65 | 0.42 | 0.54 | 10.33 | 12.04 |
| Scenarios | Model Inputs | R2 | RMSE | MAPE (%) | |||
|---|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | Training | Testing | ||
| S1 | Qt, Qt−1 − Qt−4 | 0.82 | 0.69 | 0.45 | 0.53 | 10.79 | 11.94 |
| S2 | SCAt, SCAt−2, Qt | 0.86 | 0.69 | 0.40 | 0.57 | 9.37 | 11.80 |
| S3 | SCAt, SCAt−4, Qt, Rt−1 | 0.83 | 0.69 | 0.43 | 0.51 | 10.35 | 11.30 |
| S4 | SCAt, SCAt−4, Qt, Evapt−1, Tt−1 | 0.84 | 0.70 | 0.42 | 0.51 | 9.81 | 10.92 |
| S5 | SCAt, Qt, Qt−1, Tt−1, Evapt−1 | 0.85 | 0.62 | 0.41 | 0.60 | 9.76 | 12.38 |
| S6 | Tt − Tt-4 | 0.84 | 0.53 | 0.42 | 0.67 | 8.93 | 13.54 |
| S7 | SCAt, Evapt−1, Qt, Rt−1, Tt | 0.85 | 0.69 | 0.41 | 0.55 | 9.81 | 11.93 |
| S8 | SCAt, Qt, Evapt−1, Rt−1, Tt−1 | 0.85 | 0.68 | 0.41 | 0.53 | 9.72 | 11.16 |
| Scenarios | Model Inputs | R2 | RMSE | MAPE (%) | |||
|---|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | Training | Testing | ||
| S1 | Qt, Qt−1 − Qt−4 | 0.94 | 0.62 | 0.25 | 0.64 | 5.02 | 15.13 |
| S2 | SCAt, SCAt−2, Qt | 0.95 | 0.63 | 0.24 | 0.59 | 4.71 | 14.07 |
| S3 | SCAt, SCAt−4, Qt, Rt−1 | 0.95 | 0.52 | 0.24 | 0.72 | 5.08 | 16.06 |
| S4 | SCAt, SCAt−4, Qt, Evapt−1, Tt−1 | 0.95 | 0.56 | 0.23 | 0.65 | 5.11 | 15.64 |
| S5 | SCAt, Qt, Qt−1, Tt−1, Evapt−1 | 0.96 | 0.59 | 0.21 | 0.63 | 4.66 | 15.14 |
| S6 | Tt − Tt−4 | 0.96 | 0.50 | 0.21 | 0.72 | 4.73 | 17.16 |
| S7 | SCAt, Evapt−1, Qt, Rt−1, Tt | 0.95 | 0.57 | 0.23 | 0.67 | 4.90 | 16.36 |
| S8 | SCAt, Qt, Evapt−1, Rt−1, Tt−1 | 0.95 | 0.59 | 0.22 | 0.65 | 4.81 | 15.08 |
| Scenarios | Model Inputs | R2 | RMSE | MAPE (%) | |||
|---|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | Training | Testing | ||
| S1 | Qt, Qt−1 − Qt−4 | 0.81 | 0.71 | 0.46 | 0.53 | 11.08 | 11.85 |
| S2 | SCAt, SCAt−2, Qt | 0.83 | 0.70 | 0.44 | 0.52 | 10.73 | 11.70 |
| S3 | SCAt, SCAt−4, Qt, Rt−1 | 0.81 | 0.70 | 0.47 | 0.52 | 11.47 | 12.00 |
| S4 | SCAt, SCAt−4, Qt, Evapt−1, Tt−1 | 0.83 | 0.71 | 0.44 | 0.51 | 10.75 | 11.76 |
| S5 | SCAt, Qt, Qt−1, Tt−1, Evapt−1 | 0.82 | 0.72 | 0.44 | 0.52 | 10.69 | 12.03 |
| S6 | Tt − Tt−4 | 0.76 | 0.60 | 0.51 | 0.58 | 12.92 | 13.67 |
| S7 | SCAt, Evapt−1, Qt, Rt−1, Tt | 0.83 | 0.71 | 0.44 | 0.54 | 10.66 | 12.36 |
| S8 | SCAt, Qt, Evapt−1, Rt−1, Tt−1 | 0.83 | 0.72 | 0.44 | 0.51 | 10.76 | 11.99 |
| Scenarios | Model Inputs | R2 | RMSE | MAPE (%) | |||
|---|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | Training | Testing | ||
| S1 | Qt, Qt−1 − Qt−4 | 0.82 | 0.66 | 0.45 | 0.59 | 10.90 | 13.07 |
| S2 | SCAt, SCAt−2, Qt | 0.83 | 0.66 | 0.43 | 0.55 | 10.56 | 12.36 |
| S3 | SCAt, SCAt−4, Qt, Rt−1, | 0.83 | 0.65 | 0.44 | 0.55 | 10.68 | 12.10 |
| S4 | SCAt, SCAt−4, Qt, Evapt−1, Tt−1 | 0.83 | 0.66 | 0.43 | 0.54 | 10.46 | 12.22 |
| S5 | SCAt, Qt, Qt−1, Tt−1, Evapt−1 | 0.84 | 0.67 | 0.42 | 0.53 | 10.46 | 11.75 |
| S6 | Tt − Tt−4 | 0.77 | 0.58 | 0.50 | 0.60 | 12.54 | 14.08 |
| S7 | SCAt, Evapt−1, Qt, Rt−1, Tt | 0.84 | 0.68 | 0.42 | 0.53 | 10.38 | 12.00 |
| S8 | SCAt, Qt, Evapt−1, Rt−1, Tt−1 | 0.84 | 0.68 | 0.42 | 0.51 | 10.42 | 11.72 |
| Models | Results for Training Period | Results for Testing Period | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | MAPE (%) | R2 | RMSE | MAPE (%) | |
| SRC | 0.80 | 0.49 | 13.29 | 0.71 | 0.60 | 13.82 |
| ANN | 0.86 | 0.40 | 9.94 | 0.67 | 0.54 | 12.45 |
| MARS | 0.83 | 0.44 | 10.79 | 0.68 | 0.53 | 11.71 |
| SVR | 0.84 | 0.42 | 9.81 | 0.70 | 0.51 | 10.92 |
| M5Tree | 0.95 | 0.24 | 4.71 | 0.63 | 0.59 | 14.07 |
| RM5Tree | 0.83 | 0.44 | 10.76 | 0.72 | 0.51 | 11.99 |
| RSM | 0.84 | 0.42 | 10.42 | 0.68 | 0.51 | 11.72 |
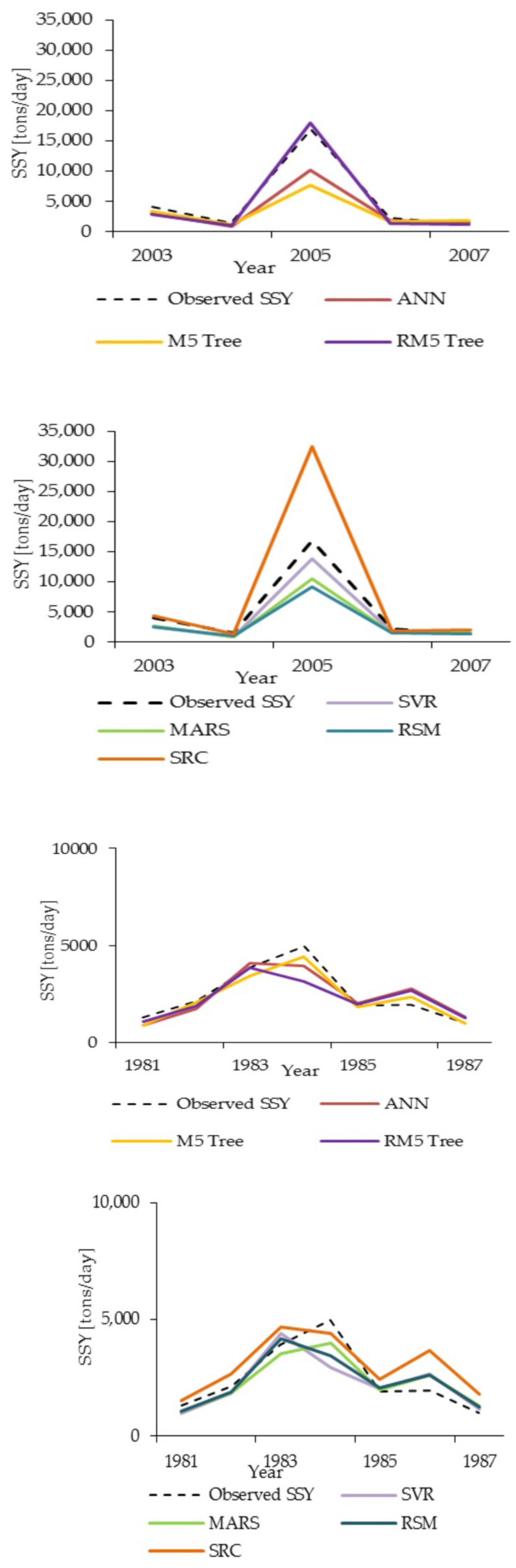
| Year | Peaks > 3200 [tons/Day] | ANN [tons/Day] | MARS [tons/Day] | SVR [tons/Day] | M5Tree [tons/Day] | RM5Tree [tons/Day] | RSM [tons/Day] | SRC [tons/Day] |
|---|---|---|---|---|---|---|---|---|
| 1983 | 3901 | 4092 (95.09) | 3603 (89.81) | 4376 (93.07) | 3432 (87.99) | 3861 (98.99) | 4163 (93.28) | 5008 (71.62) |
| 1984 | 4955 | 3945 (79.61) | 3960 (79.93) | 2937 (74.46) | 4410 (89.01) | 3135 (63.28) | 3428 (69.19) | 4704 (94.93) |
| 1991 | 3256 | 3013 (92.52) | 2917 (89.57) | 2916 (96.80) | 3140 (96.43) | 3024 (92.87) | 3022 (92.80) | 4806 (52.40) |
| 2003 | 4057 | 3085 (76.03) | 2741 (67.57) | 2516 (81.56) | 3332 (82.12) | 2904 (71.57) | 2568 (63.29) | 4732 (83.38) |
| 2005 | 16,898 | 10,113 (59.85) | 10,585 (62.4) | 13,794 (63.60) | 7678 (45.44) | 17,961 (93.71) | 9184 (54.35) | 35,507 (10.12) |
| Mean (Relative Accuracy %) | 6613 | 4849 (80.62) | 4741 (77.86) | 5308 (81.90) | 4398 (80.20) | 6177 (84.10) | 4473 (74.58) | 10,951 (62.49) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keshtegar, B.; Piri, J.; Hussan, W.U.; Ikram, K.; Yaseen, M.; Kisi, O.; Adnan, R.M.; Adnan, M.; Waseem, M. Prediction of Sediment Yields Using a Data-Driven Radial M5 Tree Model. Water 2023, 15, 1437. https://doi.org/10.3390/w15071437
Keshtegar B, Piri J, Hussan WU, Ikram K, Yaseen M, Kisi O, Adnan RM, Adnan M, Waseem M. Prediction of Sediment Yields Using a Data-Driven Radial M5 Tree Model. Water. 2023; 15(7):1437. https://doi.org/10.3390/w15071437
Chicago/Turabian StyleKeshtegar, Behrooz, Jamshid Piri, Waqas Ul Hussan, Kamran Ikram, Muhammad Yaseen, Ozgur Kisi, Rana Muhammad Adnan, Muhammad Adnan, and Muhammad Waseem. 2023. "Prediction of Sediment Yields Using a Data-Driven Radial M5 Tree Model" Water 15, no. 7: 1437. https://doi.org/10.3390/w15071437






