Streamflow Simulation with High-Resolution WRF Input Variables Based on the CNN-LSTM Hybrid Model and Gamma Test
Abstract
:1. Introduction
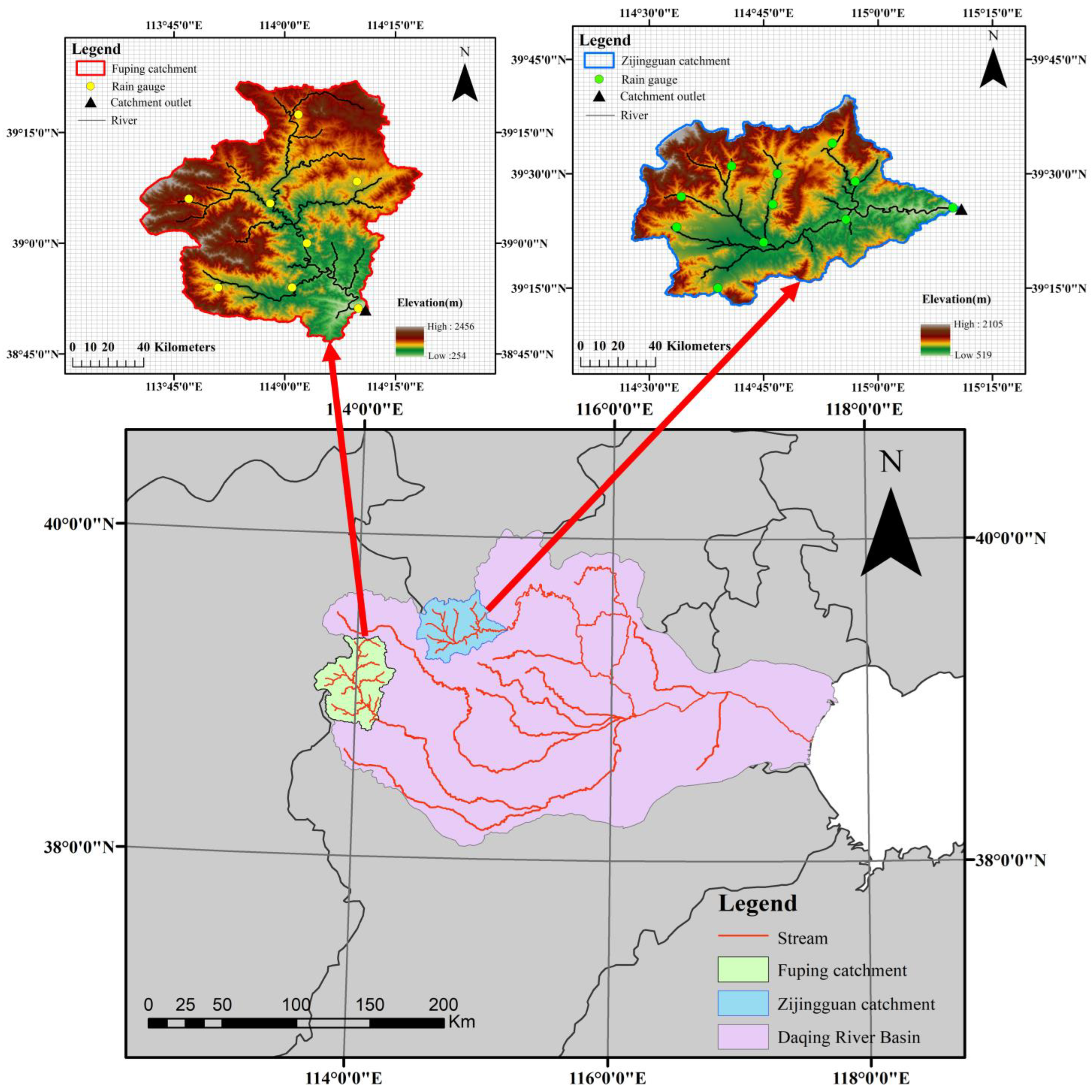
2. Study Area
3. Methodology
3.1. Weather Research and Forecasting Model (WRF)
3.2. Gamma Test
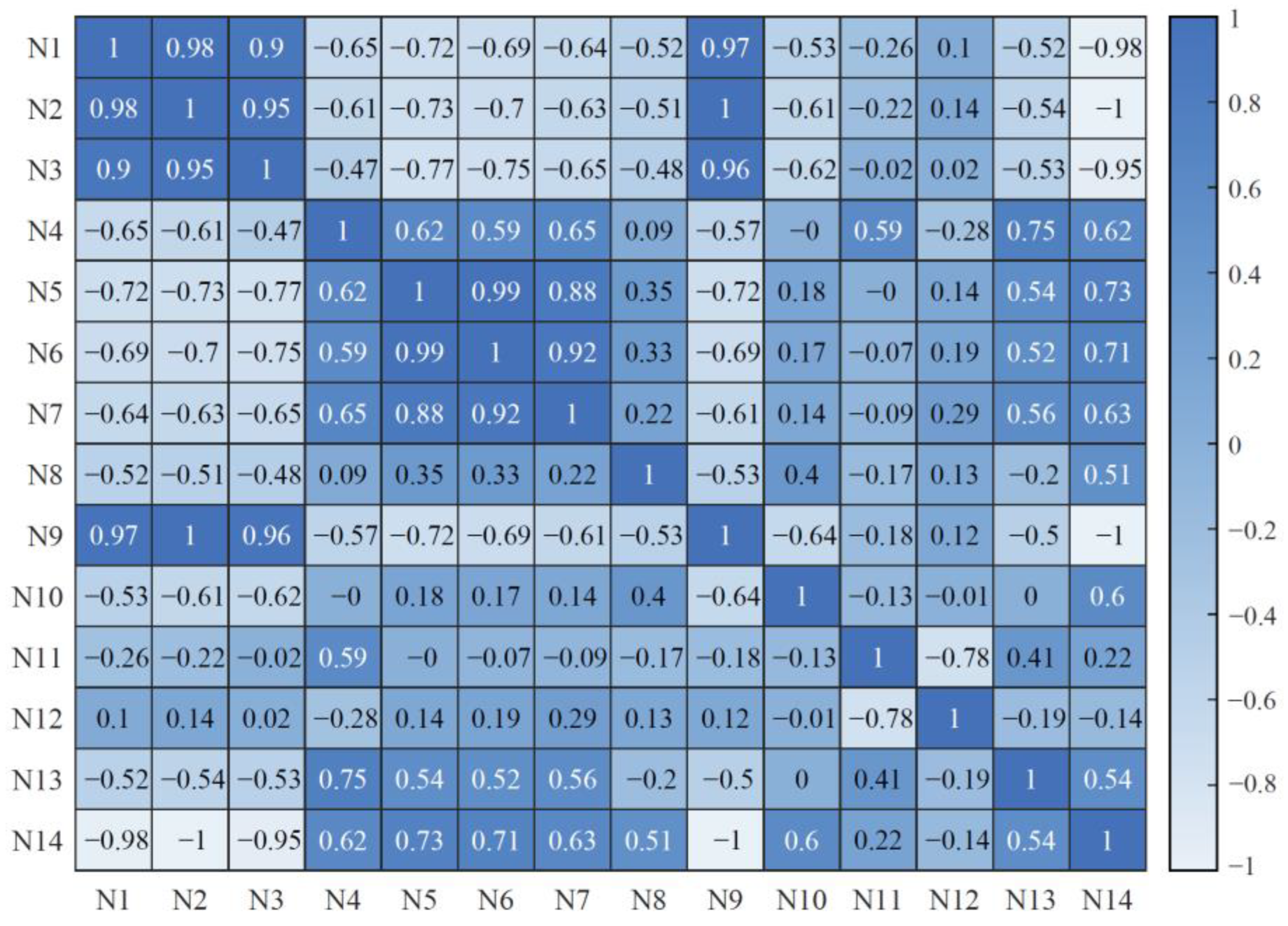
- Selecting variables which have significant spatial variabilities or have significant impacts on the runoff generation in the spatial dimension, i.e., taking the time series mean value of the runoff generation (i.e., variable 15 + 16) in each grid as the output, and the time series average values of other meteorological variables in each grid as the inputs, and then applying the Gamma test to select the most important variables in the spatial dimension;
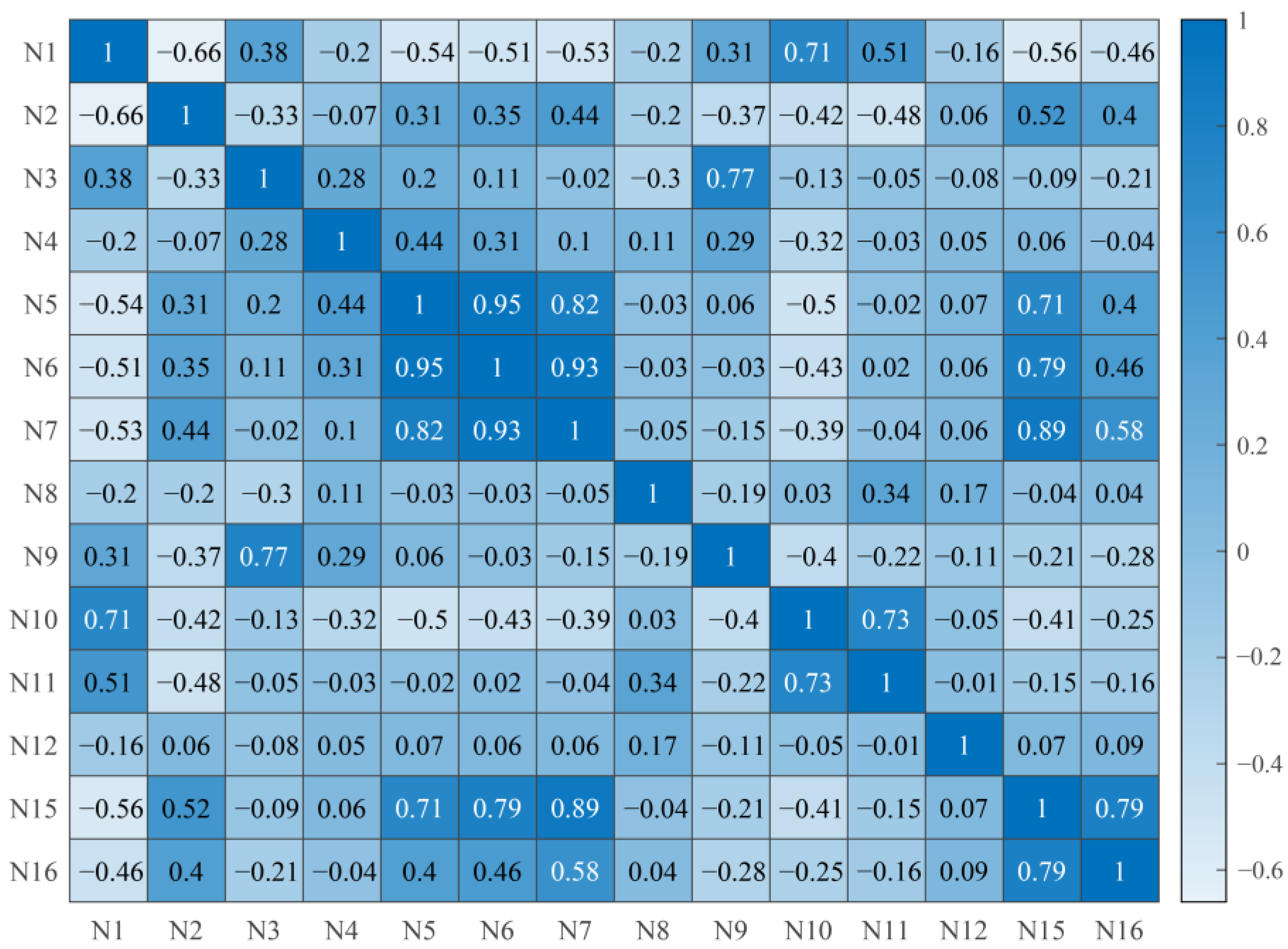
- Selecting variables which have significant temporal variabilities or have significant impacts on the runoff generation in the temporal dimension, i.e., taking the average areal values of each variable in each day as the inputs, and the daily streamflow at the outlet of the catchment as the output, and then applying Gamma test to select the most important variables in the temporal dimension.
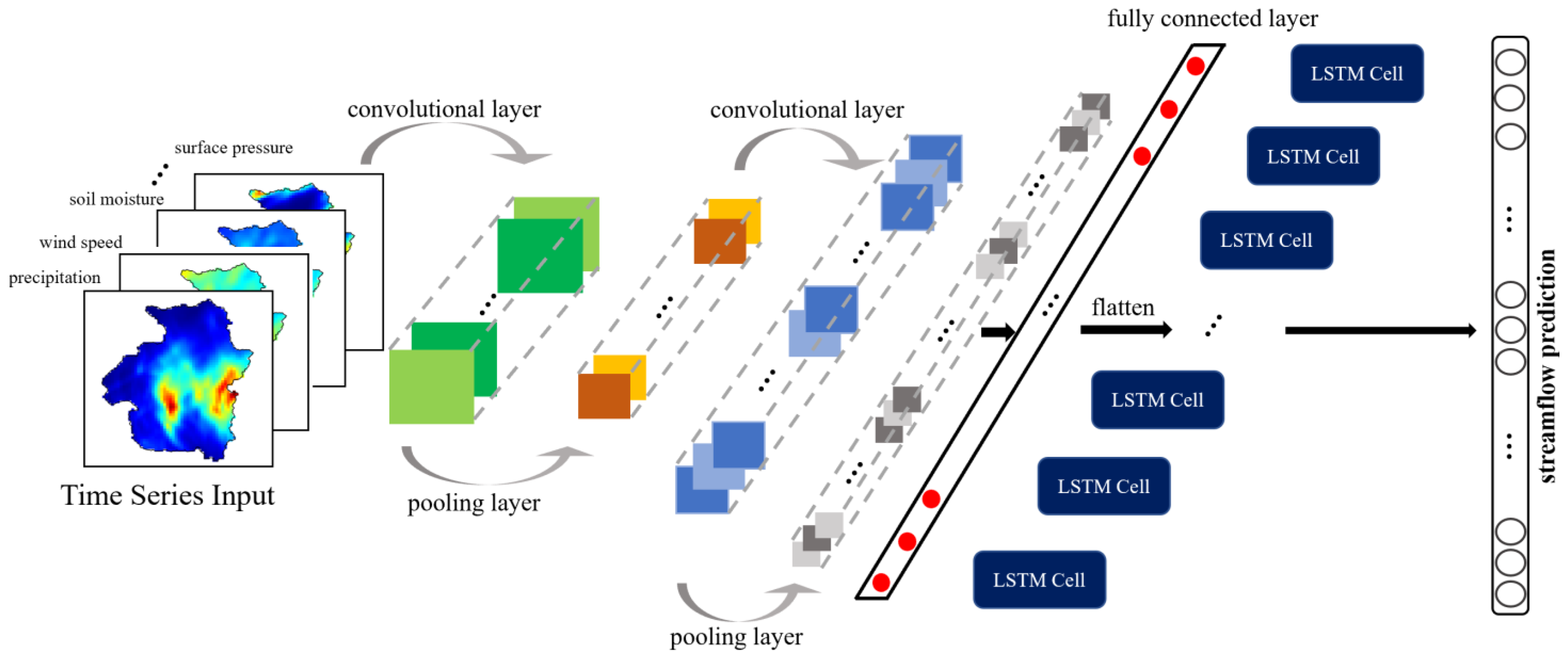
3.3. The CNN-LSTM Hybrid Model
3.4. Data Preparation and Model Training
3.5. Model Evaluation Criteria
4. Results and Discussion
4.1. Model Input Selection Based on Gamma Test
4.1.1. Variable Selection in the Spatial Dimension
4.1.2. Variable Selection in the Temporal Dimension
4.1.3. Variable Combination Schemes as the Model Input
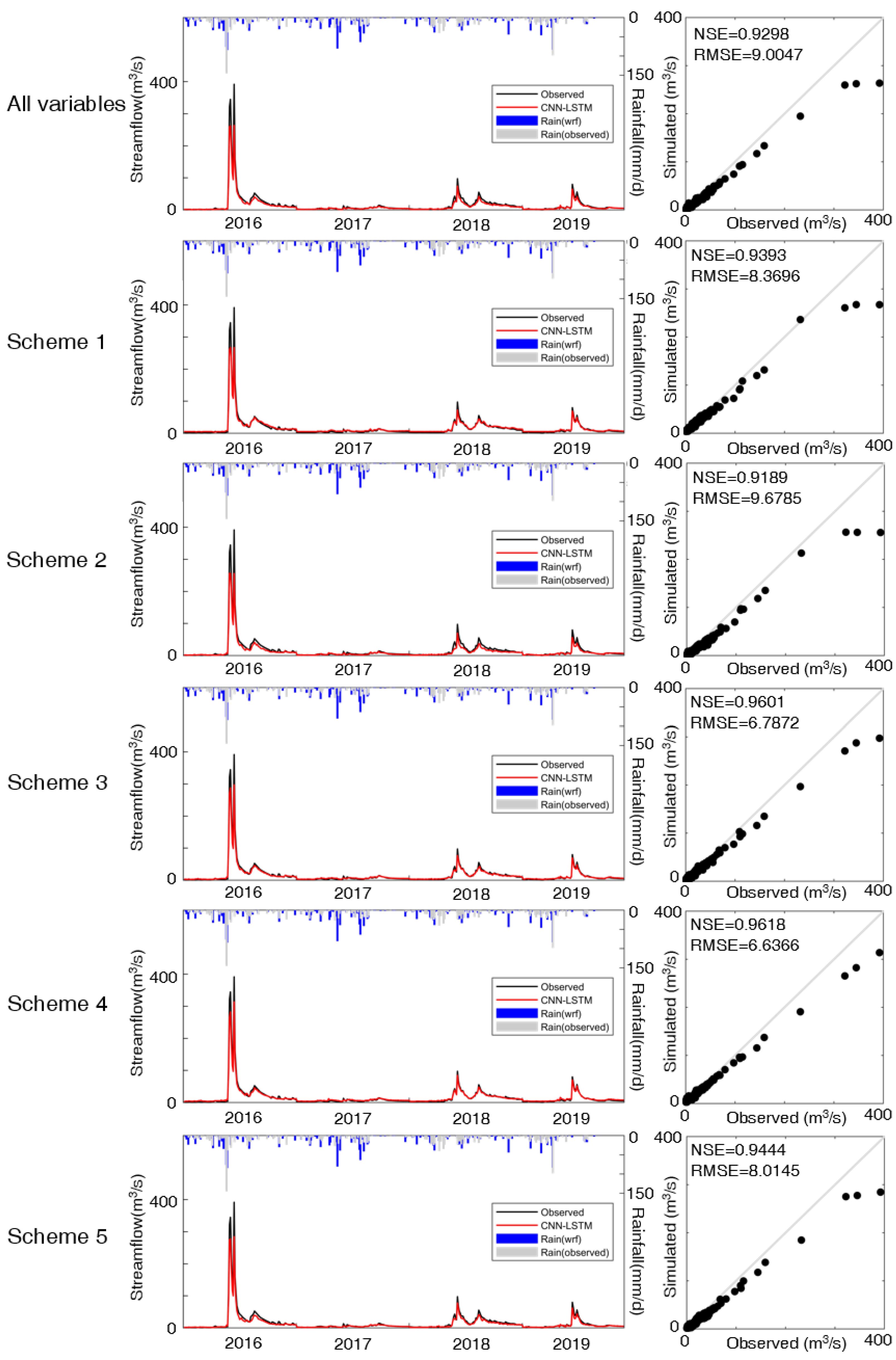
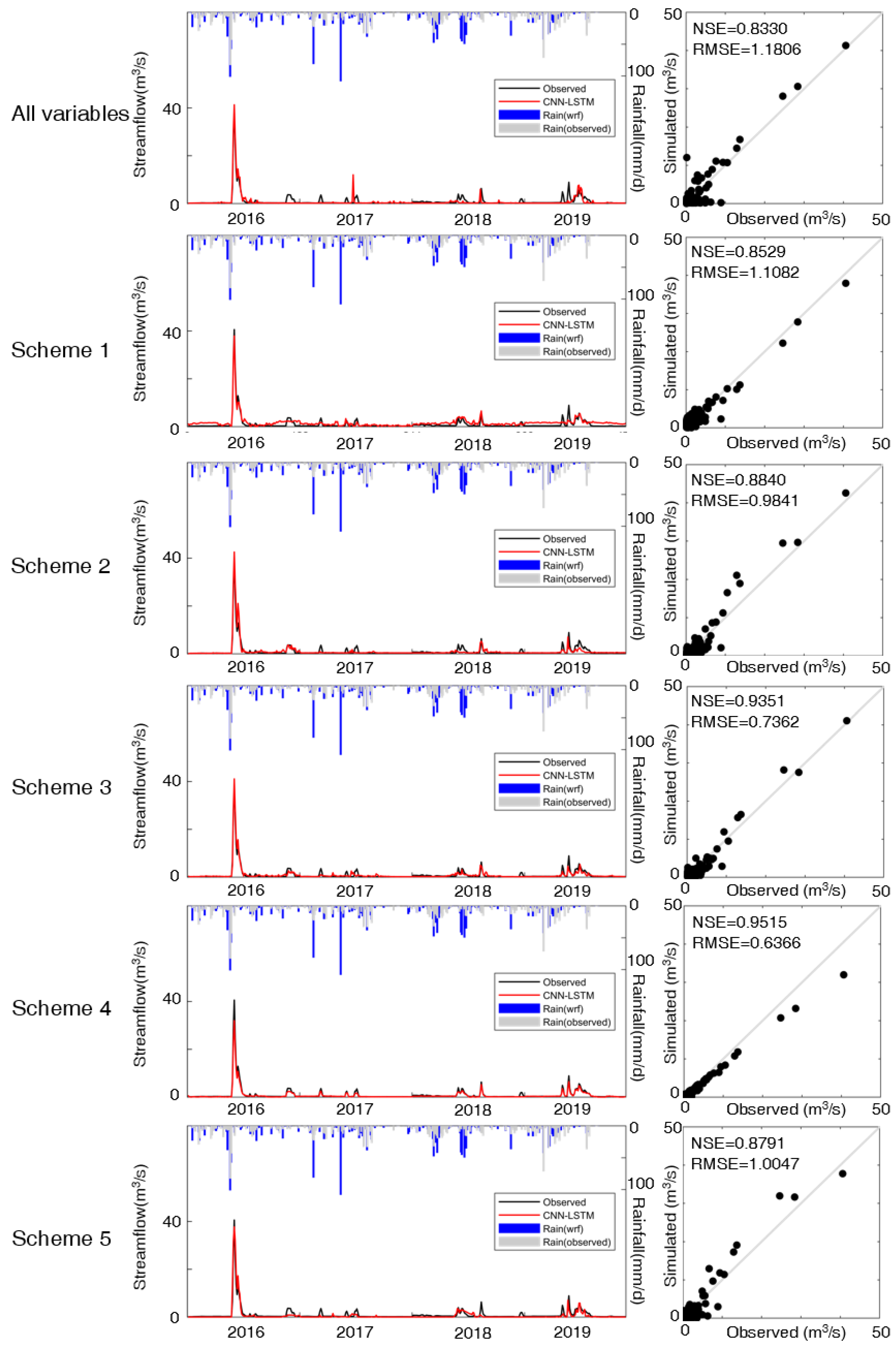
4.2. Performance of the CNN-LSTM Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Emerton, R.E.; Stephens, E.M.; Pappenberger, F.; Pagano, T.C.; Weerts, A.H.; Wood, A.W.; Salamon, P.; Brown, J.D.; Hjerdt, N.; Donnelly, C.; et al. Continental and global scale flood forecasting systems. Wiley Interdiscip. Rev. Water 2016, 3, 391–418. [Google Scholar] [CrossRef] [Green Version]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2018, 569, 387–408. [Google Scholar] [CrossRef]
- Wang, W.; Vrijling, J.K.; Van Gelder, P.H.; Ma, J. Testing for nonlinearity of streamflow processes at different timescales. J. Hydrol. 2006, 322, 247–268. [Google Scholar] [CrossRef]
- Skamarock, W. A Description of the Advanced Research WRF Version 3; NCAR Tech. Note; NCAR/TN-475+ STR; University Corporation for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Bass, B.; Rahimi, S.; Goldenson, N.; Hall, A.; Norris, J.; Lebow, Z.J. Achieving Realistic Runoff in the Western United States with a Land Surface Model Forced by Dynamically Downscaled Meteorology. J. Hydrometeorol. 2023, 24, 269–283. [Google Scholar] [CrossRef]
- Tyson, C.; Longyang, Q.; Neilson, B.T.; Zeng, R.; Xu, T. Effects of Meteorological Forcing Uncertainty on High-Resolution Snow Modeling and Streamflow Prediction in a Mountainous Karst Watershed. J. Hydrol. 2023, 619, 129304. [Google Scholar] [CrossRef]
- Naabil, E.; Lamptey, B.L.; Arnault, J.; Olufayo, A.; Kunstmann, H. Water resources management using the WRF-Hydro modelling system: Case-study of the Tono dam in West Africa. J. Hydrol. Reg. Stud. 2017, 12, 196–209. [Google Scholar] [CrossRef]
- Wang, J.; Bao, W.; Gao, Q.; Si, W.; Sun, Y. Coupling the Xinanjiang model and wavelet-based random forests method for improved daily streamflow simulation. J. Hydroinformatics 2021, 23, 589–604. [Google Scholar] [CrossRef]
- Gu, Y.; Peng, D.; Deng, C.; Zhao, K.; Pang, B.; Zuo, D. Atmospheric–hydrological modeling for Beijing’s sub-center based on WRF and SWMM. Urban Clim. 2022, 41, 101066. [Google Scholar] [CrossRef]
- Nourani, V. An emotional ANN (EANN) approach to modeling rainfall-runoff process. J. Hydrol. 2017, 544, 267–277. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Singh, V.P.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J. Streamflow and rainfall forecasting by two long short-term memory-based models. J. Hydrol. 2020, 583, 124296. [Google Scholar] [CrossRef]
- Choi, J.; Lee, J.; Kim, S. Utilization of the Long Short-Term Memory network for predicting streamflow in ungauged basins in Korea. Ecol. Eng. 2022, 182, 106699. [Google Scholar] [CrossRef]
- Wegayehu, E.B.; Muluneh, F.B. Short-Term Daily Univariate Streamflow Forecasting Using Deep Learning Models. Adv. Meteorol. 2022, 2022, 1860460. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Thapa, S.; Zhao, Z.; Li, B.; Lu, L.; Fu, D.; Shi, X.; Tang, B.; Qi, H. Snowmelt-driven streamflow prediction using machine learning techniques (LSTM, NARX, GPR, and SVR). Water 2020, 12, 1734. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet classification with deep convolutional neural networks. Commun. Acm 2017, 60, 84–90. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Lei, X.; Pan, H.; Huang, X. A dilated CNN model for image classification. IEEE Access 2019, 7, 124087–124095. [Google Scholar] [CrossRef]
- Poma, X.S.; Riba, E.; Sappa, A. Dense extreme inception network: Towards a robust CNN model for edge detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 2–5 March 2020. [Google Scholar]
- AlBdairi, A.J.A.; Xiao, Z.; Alkhayyat, A.; Humaidi, A.J.; Fadhel, M.A.; Taher, B.H.; Alzubaidi, L.; Santamaría, J.; Al-Shamma, O. Face Recognition Based on Deep Learning and FPGA for Ethnicity Identification. Appl. Sci. 2022, 12, 2605. [Google Scholar] [CrossRef]
- Van, S.P.; Le, H.M.; Thanh, D.V.; Dang, T.D.; Loc, H.H.; Anh, D.T. Deep learning convolutional neural network in rainfall–runoff modelling. J. Hydroinformatics 2020, 22, 541–561. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Fang, Z.; Hong, H.; Peng, L. Flood susceptibility mapping using convolutional neural network frameworks. J. Hydrol. 2020, 582, 124482. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Coupling a hybrid CNN-LSTM deep learning model with a boundary corrected maximal overlap discrete wavelet transform for multiscale lake water level forecasting. J. Hydrol. 2021, 598, 126196. [Google Scholar] [CrossRef]
- Li, P.; Zhang, J.; Krebs, P. Prediction of flow based on a CNN-LSTM combined deep learning approach. Water 2022, 14, 993. [Google Scholar] [CrossRef]
- Tran, H.; Leonarduzzi, E.; De la Fuente, L.; Hull, R.B.; Bansal, V.; Chennault, C.; Gentine, P.; Melchior, P.; Condon, L.E.; Maxwell, R.M. Development of a Deep Learning Emulator for a Distributed Groundwater–Surface Water Model: ParFlow-ML. Water 2021, 13, 3393. [Google Scholar] [CrossRef]
- Koncar, N. Optimisation Methodologies for Direct Inverse Neurocontrol. Ph.D. Thesis, University of London, London, UK, 1997. [Google Scholar]
- Malik, A.; Tikhamarine, Y.; Souag-Gamane, D.; Kisi, O.; Pham, Q.B. Support vector regression optimized by meta-heuristic algorithms for daily streamflow prediction. Stoch. Environ. Res. Risk Assess. 2020, 34, 1755–1773. [Google Scholar] [CrossRef]
- Hassan, M.; Hassan, I. Improving Artificial Neural Network Based Streamflow Forecasting Models through Data Preprocessing. KSCE J. Civ. Eng. 2021, 25, 3583–3595. [Google Scholar] [CrossRef]
- Panahi, F.; Ehteram, M.; Ahmed, A.N.; Huang, Y.F.; Mosavi, A.; El-Shafie, A. Streamflow prediction with large climate indices using several hybrid multilayer perceptrons and copula Bayesian model averaging. Ecol. Indic. 2021, 133, 108285. [Google Scholar] [CrossRef]
- Zhuo, L.; Han, D. Multi-source hydrological soil moisture state estimation using data fusion optimisation. Hydrol. Earth Syst. Sci. 2017, 21, 3267–3285. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Li, C.; Liu, J.; Yu, F.; Cheng, S.; Zhao, N.; Wan Jaafar, W.Z. Groundwater Depth Prediction Using Data-Driven Models with the Assistance of Gamma Test. Sustainability 2016, 8, 1076. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, R.M.; Soares PM, M.; Miranda PM, A.; Belo-Pereira, M. WRF high resolution simulation of Iberian mean and extreme precipitation climate. Int. J. Climatol. 2013, 33, 2591–2608. [Google Scholar] [CrossRef]
- Toride, K.; Iseri, Y.; Duren, A.M.; England, J.F.; Kavvas, M.L. Evaluation of physical parameterizations for atmospheric river induced precipitation and application to long-term reconstruction based on three reanalysis datasets in Western Oregon. Sci. Total Environ. 2018, 658, 570–581. [Google Scholar] [CrossRef]
- Lin, Y.L.; Farley, R.D.; Orville, H.D. Bulk parameterization of the snow field in a cloud model. J. Clim. Appl. Meteorol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a vali-dated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef] [Green Version]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Tian, J.; Liu, J.; Wang, J.; Li, C.; Yu, F.; Chu, Z. A spatio-temporal evaluation of the WRF physical parameterisations for numerical rainfall simulation in semi-humid and semi-arid catchments of northern China. Atmos. Res. 2017, 191, 141–155. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Li, C.; Yu, F.; Wang, W.; Qiu, Q. Parameter sensitivity analysis of the WRF-hydro modeling system for streamflow simulation: A case study in semi-humid and semi-arid Catchments of Northern China. Asia-Pac. J. Atmos. Sci. 2021, 57, 451–466. [Google Scholar] [CrossRef]
- Stefánsson, A.; Končar, N.; Jones, A.J. A note on the gamma test. Neural Comput. Appl. 1997, 5, 131–133. [Google Scholar] [CrossRef]
- Evans, D.; Jones, A.J. A proof of the Gamma test. Proc. R. Soc. Lond. Ser. A 2002, 458, 2759–2799. [Google Scholar] [CrossRef]
- Tsui, A.P.; Jones, A.J.; Guedes de Oliveira, A. The construction of smooth models using irregular embeddings determined by a gamma test analysis. Neural Comput. Appl. 2002, 10, 318–329. [Google Scholar] [CrossRef]
- Wan Jaafar, W.Z.; Han, D. Variable Selection Using the Gamma Test Forward and Backward Selections. J. Hydrol. Eng. 2012, 17, 182–190. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, S.; Giles, C.L.; Tsoi, A.C.; Back, A.D. Face Recognition: A Convolutional Neural-Network Approach. IEEE Trans. Neural Netw. 1997, 8, 98–113. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Continual prediction using LSTM with forget gates. In Neural Nets WIRN Vietri-99; Springer: London, UK, 1999; pp. 133–138. [Google Scholar]
- Wu, Q.; Lin, H. Daily urban air quality index forecasting based on variational mode decomposition, sample entropy and LSTM neural network. Sustain. Cities Soc. 2019, 50, 101657. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. Predicting flood susceptibility using LSTM neural networks. J. Hydrol. 2021, 594, 125734. [Google Scholar] [CrossRef]
- Li, X.; Xu, W.; Ren, M.; Jiang, Y.; Fu, G. Hybrid CNN-LSTM models for river flow prediction. Water Supply 2022, 22, 4902–4919. [Google Scholar] [CrossRef]
- Hingerl, L.; Kunstmann, H.; Wagner, S.; Mauder, M.; Bliefernicht, J.; Rigon, R. Spatio-temporal variability of water and energy fluxes–a case study for a mesoscale catchment in pre-alpine environment. Hydrol. Process. 2016, 30, 3804–3823. [Google Scholar] [CrossRef] [Green Version]
- Fairbairn, D.; Barbu, A.L.; Napoly, A.; Albergel, C.; Mahfouf, J.F.; Calvet, J.C. The effect of satellite-derived surface soil moisture and leaf area index land data assimilation on streamflow simulations over France. Hydrol. Earth Syst. Sci. 2017, 21, 2015–2033. [Google Scholar] [CrossRef] [Green Version]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
| Subject | Chosen Option | Subject | Chosen Option |
|---|---|---|---|
| Forcing data | 6-hourly FNL | Fuping domain center | 39.0856 N, 113.9899 E |
| Time step | 150 s | Zijingguan domain center | 39.4430 N, 114.8274 E |
| Horizontal resolution | Dom1: 27 km | Domain area | Dom1: 613,089 km2 |
| Dom2: 9 km | Dom2: 88,209 km2 | ||
| Dom3: 3 km | Dom3: 18,225 km2 | ||
| Dom4: 1 km | Dom4: 6561 km2 | ||
| Projection | Lambert | WRF output interval | 1 day |
| No. | Variables | No. | Variables |
|---|---|---|---|
| 1 | Surface skin temperature | 9 | Downward long wave flux |
| 2 | Surface pressure | 10 | Downward short wave flux |
| 3 | Specific humidity | 11 | Latent heat flux |
| 4 | Precipitation | 12 | Albedo |
| 5 | Soil moisture (0–10 cm) | 13 | Orographic variance |
| 6 | Soil moisture (10–40 cm) | 14 | Terrain height |
| 7 | Soil moisture (40–100 cm) | 15 | Surface runoff |
| 8 | Wind speed | 16 | Underground runoff |
| Rankings | Combination of Variables | Index Removed/Added | Gradient | Standard Error | ||
|---|---|---|---|---|---|---|
| 17 | 1,2,3,4,5,6,7,8,9,10,11,12,13,14 | None | −0.00185 | 0.09375 | 0.00139 | −0.00739 |
| 7 | 1,2,3,4,5,6,7,8,9,11,12,13,14 | 10 | 0.00046 | 0.09747 | 0.00079 | 0.00182 |
| 6 | 1,2,3,4,5,7,8,9,11,12,13,14 | 6 | −0.00030 | 0.11748 | 0.00106 | −0.00121 |
| 1 | 2,3,4,5,7,8,9,11,12,13,14 | 1 | 0.00004 | 0.11931 | 0.00068 | 0.00016 |
| 3 | 2,3,4,5,7,8,9,11,12,14 | 13 | 0.00009 | 0.14111 | 0.00067 | 0.00035 |
| 8 | 2,3,4,5,7,8,11,12,14 | 9 | 0.00054 | 0.14198 | 0.00099 | 0.00217 |
| 12 | 2,3,4,5,7,8,11,12 | 14 | 0.00126 | 0.14024 | 0.00087 | 0.00504 |
| 14 | 2,4,5,7,8,11,12 | 3 | 0.00137 | 0.16144 | 0.00107 | 0.00547 |
| 15 | 2,4,5,7,8,12 | 11 | 0.00164 | 0.18716 | 0.00102 | 0.00655 |
| 20 | 2,4,5,8,12 | 7 | 0.00290 | 0.27572 | 0.00092 | 0.01160 |
| 22 | 2,4,5,12 | 8 | 0.00367 | 0.41271 | 0.00045 | 0.01470 |
| 24 | 2,4,5 | 12 | 0.00862 | 0.53273 | 0.00101 | 0.03448 |
| 25 | 4,5 | 2 | 0.02305 | 0.88020 | 0.00132 | 0.09219 |
| 27 | 4 | 5 | 0.05331 | −13.29160 | 0.00150 | 0.21322 |
| 26 | 4,5 | 4 | 0.02305 | 0.88020 | 0.00132 | 0.09219 |
| 23 | 3,4,5 | 3 | 0.00690 | 0.58707 | 0.00083 | 0.02761 |
| 21 | 3,4,5,12 | 12 | 0.00315 | 0.41890 | 0.00074 | 0.01259 |
| 19 | 3,4,5,12,14 | 14 | 0.00248 | 0.35439 | 0.00102 | 0.00993 |
| 16 | 3,4,5,10,12,14 | 10 | 0.00176 | 0.27234 | 0.00050 | 0.00704 |
| 11 | 1,3,4,5,10,12,14 | 1 | 0.00116 | 0.25718 | 0.00067 | 0.00464 |
| 13 | 1,3,4,5,10,11,12,14 | 11 | 0.00133 | 0.21165 | 0.00138 | 0.00530 |
| 5 | 1,3,4,5,6,10,11,12,14 | 6 | 0.00014 | 0.16723 | 0.00133 | 0.00058 |
| 2 | 1,3,4,5,6,8,10,11,12,14 | 8 | 0.00008 | 0.13437 | 0.00092 | 0.00030 |
| 4 | 1,3,4,5,6,7,8,10,11,12,14 | 7 | −0.00013 | 0.10444 | 0.00085 | −0.00054 |
| 9 | 1,3,4,5,6,7,8,9,10,11,12,14 | 9 | −0.00071 | 0.10468 | 0.00086 | −0.00284 |
| 10 | 1,3,4,5,6,7,8,9,10,11,12,13,14 | 13 | −0.00091 | 0.09054 | 0.00146 | −0.00364 |
| 18 | 1,2,3,4,5,6,7,8,9,10,11,12,13,14 | 2 | −0.00185 | 0.09375 | 0.00139 | −0.00739 |
| Rankings | Combination of Variables | Index Removed/Added | Gradient | Standard Error | ||
|---|---|---|---|---|---|---|
| 23 | 1,2,3,4,5,6,7,8,9,10,11,12,15,16 | None | 0.0434 | 0.1134 | 0.0127 | 0.1737 |
| 17 | 1,2,3,4,5,6,7,8,9,11,12,15,16 | 10 | 0.0263 | 0.1425 | 0.0134 | 0.1052 |
| 12 | 1,2,3,4,5,6,7,8,11,12,15,16 | 9 | 0.0217 | 0.1593 | 0.0116 | 0.0867 |
| 5 | 1,2,3,4,5,6,7,8,12,15,16 | 11 | 0.0098 | 0.1926 | 0.0089 | 0.0392 |
| 2 | 1,2,3,4,6,7,8,12,15,16 | 5 | 0.0047 | 0.2261 | 0.0145 | 0.0187 |
| 1 | 1,2,3,4,6,7,8,15,16 | 12 | −0.0009 | 0.3560 | 0.0140 | −0.0035 |
| 8 | 1,3,4,6,7,8,15,16 | 2 | 0.0152 | 0.4026 | 0.0072 | 0.0606 |
| 13 | 1,3,6,7,8,15,16 | 4 | 0.0217 | 0.5087 | 0.0115 | 0.0867 |
| 15 | 1,3,6,7,15,16 | 8 | 0.0222 | 0.8977 | 0.0128 | 0.0887 |
| 20 | 3,6,7,15,16 | 1 | 0.0327 | 1.4236 | 0.0077 | 0.1309 |
| 25 | 6,7,15,16 | 3 | 0.0445 | 3.1299 | 0.0059 | 0.1779 |
| 22 | 7,15,16 | 6 | 0.0375 | 8.4031 | 0.0073 | 0.1499 |
| 26 | 7,15 | 16 | 0.0484 | 19.2761 | 0.0054 | 0.1935 |
| 27 | 15 | 7 | 0.0786 | 669.5949 | 0.0193 | 0.3142 |
| 18 | 12,15 | 12 | 0.0302 | 0.6141 | 0.0106 | 0.1206 |
| 10 | 12,15,16 | 16 | 0.0215 | 0.5812 | 0.0136 | 0.0859 |
| 7 | 7,12,15,16 | 7 | 0.0150 | 0.3520 | 0.0052 | 0.0599 |
| 16 | 4,7,12,15,16 | 4 | 0.0223 | 0.3043 | 0.0098 | 0.0891 |
| 19 | 1,4,7,12,15,16 | 1 | 0.0308 | 0.3104 | 0.0056 | 0.1231 |
| 21 | 1,4,6,7,12,15,16 | 6 | 0.0343 | 0.2357 | 0.0077 | 0.1371 |
| 14 | 1,3,4,6,7,12,15,16 | 3 | 0.0218 | 0.2727 | 0.0093 | 0.0870 |
| 9 | 1,3,4,5,6,7,12,15,16 | 5 | 0.0152 | 0.2696 | 0.0060 | 0.0608 |
| 3 | 1,3,4,5,6,7,8,12,15,16 | 8 | 0.0077 | 0.2371 | 0.0072 | 0.0309 |
| 6 | 1,2,3,4,5,6,7,8,12,15,16 | 2 | 0.0098 | 0.1926 | 0.0089 | 0.0392 |
| 4 | 1,2,3,4,5,6,7,8,10,12,15,16 | 10 | 0.0094 | 0.1801 | 0.0094 | 0.0374 |
| 11 | 1,2,3,4,5,6,7,8,10,11,12,15,16 | 11 | 0.0217 | 0.1593 | 0.0116 | 0.0867 |
| 24 | 1,2,3,4,5,6,7,8,9,10,11,12,15,16 | 9 | 0.0434 | 0.1134 | 0.0127 | 0.1737 |
| Scheme ID | Combination of Variables |
|---|---|
| 1 | 1,2,3,4,5,6,7,8,9,11,12,13,14,15,16 |
| 2 | 1,3,4,5,6,7,8,11,12,14,15,16 |
| 3 | 2,4,5,6,7,8,11,12,14,15,16 |
| 4 | 1,3,4,5,7,8,11,12,14,15,16 |
| 5 | 2,4,5,7,8,11,12,14,15,16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, J.; Xu, L.; Yu, F.; Zhang, S. Streamflow Simulation with High-Resolution WRF Input Variables Based on the CNN-LSTM Hybrid Model and Gamma Test. Water 2023, 15, 1422. https://doi.org/10.3390/w15071422
Wang Y, Liu J, Xu L, Yu F, Zhang S. Streamflow Simulation with High-Resolution WRF Input Variables Based on the CNN-LSTM Hybrid Model and Gamma Test. Water. 2023; 15(7):1422. https://doi.org/10.3390/w15071422
Chicago/Turabian StyleWang, Yizhi, Jia Liu, Lin Xu, Fuliang Yu, and Shanjun Zhang. 2023. "Streamflow Simulation with High-Resolution WRF Input Variables Based on the CNN-LSTM Hybrid Model and Gamma Test" Water 15, no. 7: 1422. https://doi.org/10.3390/w15071422
APA StyleWang, Y., Liu, J., Xu, L., Yu, F., & Zhang, S. (2023). Streamflow Simulation with High-Resolution WRF Input Variables Based on the CNN-LSTM Hybrid Model and Gamma Test. Water, 15(7), 1422. https://doi.org/10.3390/w15071422







