Estimation of Evapotranspiration Based on a Modified Penman–Monteith–Leuning Model Using Surface and Root Zone Soil Moisture
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Description
2.1.1. PML Model
2.1.2. PML-SM Algorithm
2.1.3. Evaluation
2.2. Data
2.2.1. Forcing Data
2.2.2. Soil Moisture Data
2.2.3. Validation Data
3. Results
3.1. The Performance Comparison of Incorporating SM into ET
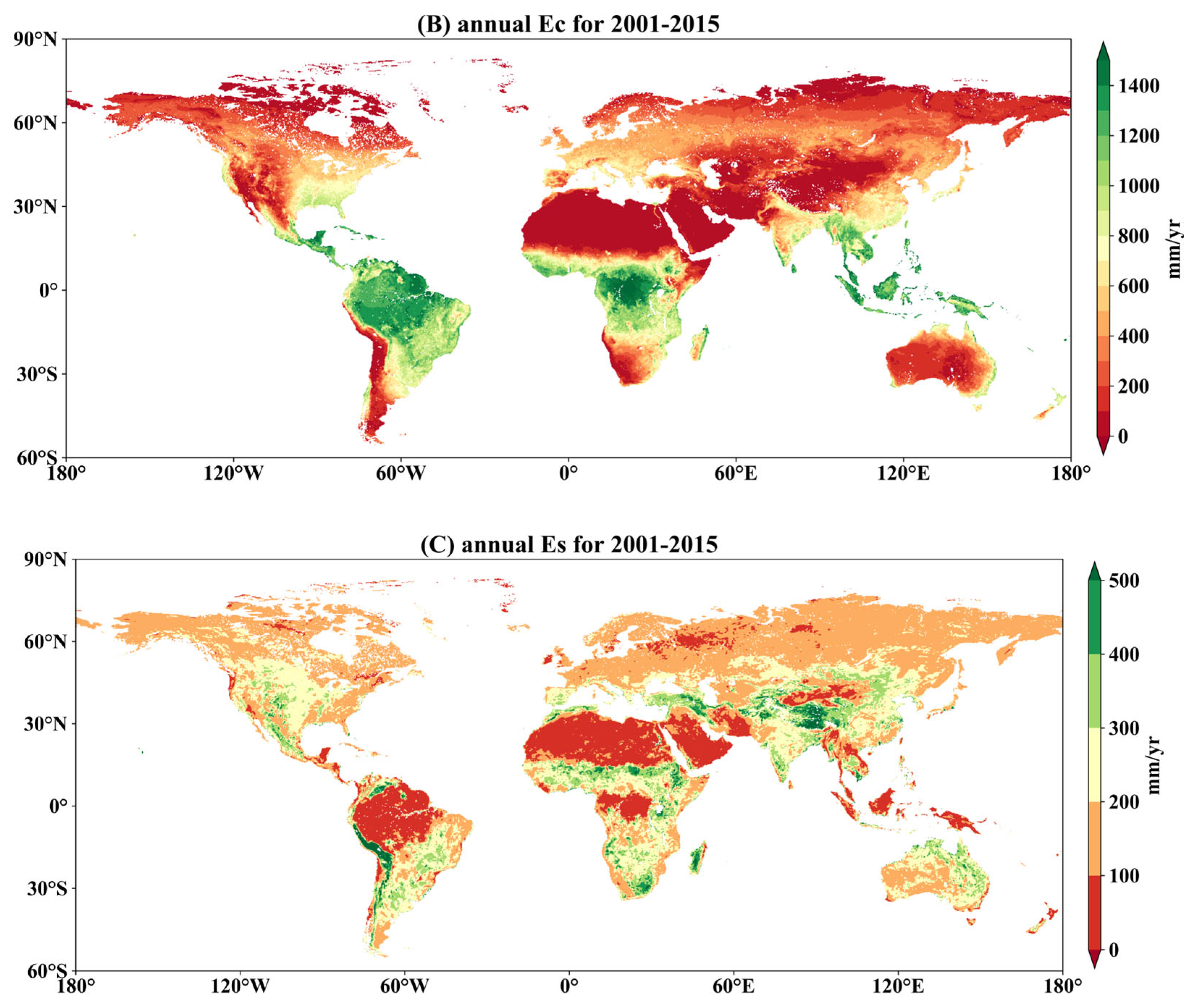
3.2. Spatial Distributions of Mean Annual ET
3.3. Latitudinal Evolution
4. Discussion
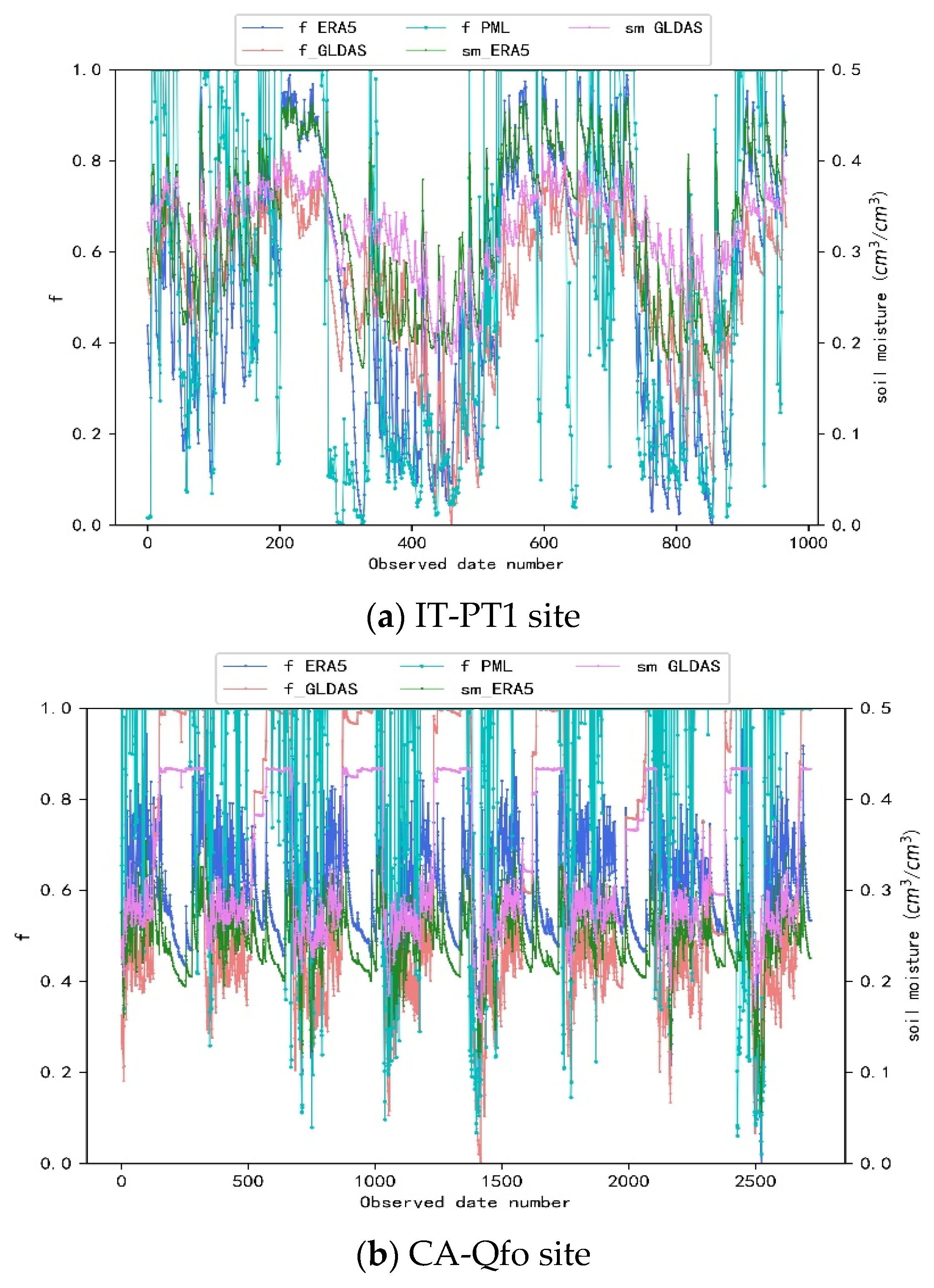
4.1. SM Constraint on and
4.2. Comparison with Other Global-Scale ET Simulation Studies
4.3. Limitations of This Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khoshravesh, M.; Sefidkouhi, M.A.G.; Valipour, M. Estimation of reference evapotranspiration using multivariate fractional polynomial, Bayesian regression, and robust regression models in three arid environments. Appl. Water Sci. 2015, 7, 1911–1922. [Google Scholar] [CrossRef] [Green Version]
- Chirouze, J.; Boulet, G.; Jarlan, L.; Fieuzal, R.; Rodriguez, J.C.; Ezzahar, J.; Er-Raki, S.; Bigeard, G.; Merlin, O.; Garatuza-Payan, J.; et al. Intercomparison of four remote-sensing-based energy balance methods to retrieve surface evapotranspiration and water stress of irrigated fields in semi-arid climate. Hydrol. Earth Syst. Sci. 2014, 18, 1165–1188. [Google Scholar] [CrossRef] [Green Version]
- Mishra, V.; Kumar, R.; Shah, H.L.; Samaniego, L.; Eisner, S.; Yang, T. Multimodel assessment of sensitivity and uncertainty of evapotranspiration and a proxy for available water resources under climate change. Clim. Chang. 2017, 141, 451–465. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Sun, S.; Fiifi Tawia Hagan, D.; Chen, T.; Dolman, H.; Liu, Y. Long-term changes in evapotranspiration over China and attribution to climatic drivers during 1980–2010. J. Hydrol. 2021, 595, 126037. [Google Scholar] [CrossRef]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar] [CrossRef]
- Liu, G.; Liu, Y.; Hafeez, M.; Xu, D.; Vote, C. Comparison of two methods to derive time series of actual evapotranspiration using eddy covariance measurements in the southeastern Australia. J. Hydrol. 2012, 454–455, 1–6. [Google Scholar] [CrossRef]
- Zou, M.; Zhong, L.; Ma, Y.; Hu, Y.; Huang, Z.; Xu, K.; Feng, L. Comparison of Two Satellite-Based Evapotranspiration Models of the Nagqu River Basin of the Tibetan Plateau. J. Geophys. Res.-Atmos. 2018, 123, 3961–3975. [Google Scholar] [CrossRef]
- Gao, G.; Zhang, X.; Yu, T.; Liu, B. Comparison of three evapotranspiration models with eddy covariance measurements for a Populus euphratica Oliv. forest in an arid region of northwestern China. J. Arid Land 2015, 8, 146–156. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.; Islam, S. A methodology for estimation of surface evapotranspiration over large areas using remote sensing observations. Geophys. Res. Lett. 1999, 26, 2773–2776. [Google Scholar] [CrossRef] [Green Version]
- Gan, R.; Zhang, Y.; Shi, H.; Yang, Y.; Eamus, D.; Cheng, L.; Chiew, F.H.S.; Yu, Q. Use of satellite leaf area index estimating evapotranspiration and gross assimilation for Australian ecosystems. Ecohydrology 2018, 11, e1974. [Google Scholar] [CrossRef]
- Ma, N.; Zhang, Y. Increasing Tibetan Plateau terrestrial evapotranspiration primarily driven by precipitation. Agric. For. Meteorol. 2022, 317, 108887. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.S.; Pena-Arancibia, J.; Sun, F.B.; Li, H.X.; Leuning, R. Global variation of transpiration and soil evaporation and the role of their major climate drivers. J. Geophys. Res.-Atmos. 2017, 122, 6868–6881. [Google Scholar] [CrossRef]
- Zhao, F.; Ma, S.; Wu, Y.; Qiu, L.; Wang, W.; Lian, Y.; Chen, J.; Sivakumar, B. The role of climate change and vegetation greening on evapotranspiration variation in the Yellow River Basin, China. Agric. For. Meteorol. 2022, 316, 108842. [Google Scholar] [CrossRef]
- Xing, W.; Wang, W.; Shao, Q.; Song, L.; Cao, M. Estimation of Evapotranspiration and Its Components across China Based on a Modified Priestley–Taylor Algorithm Using Monthly Multi-Layer Soil Moisture Data. Remote Sens. 2021, 13, 3118. [Google Scholar] [CrossRef]
- Qiu, J.; Crow, W.T.; Dong, J.; Nearing, G.S. Model representation of the coupling between evapotranspiration and soil water content at different depths. Hydrol. Earth Syst. Sci. 2020, 24, 581–594. [Google Scholar] [CrossRef] [Green Version]
- Morillas, L.; Leuning, R.; Villagarcía, L.; García, M.; Serrano-Ortiz, P.; Domingo, F. Improving evapotranspiration estimates in Mediterranean drylands: The role of soil evaporation. Water Resour. Res. 2013, 49, 6572–6586. [Google Scholar] [CrossRef]
- Teuling, A.J.; Seneviratne, S.I.; Williams, C.; Troch, P.A. Observed timescales of evapotranspiration response to soil moisture. Geophys. Res. Lett. 2006, 33, L23403. [Google Scholar] [CrossRef] [Green Version]
- Leuning, R.; Zhang, Y.Q.; Rajaud, A.; Cleugh, H.; Tu, K. A simple surface conductance model to estimate regional evaporation using MODIS leaf area index and the Penman-Monteith equation. Water Resour. Res. 2008, 44, W10419. [Google Scholar] [CrossRef]
- Duan, H.; He, X.; Zhao, H.; Jin, X.; Xu, H.; Wang, R. Analysis of the effect of seasonal changes on sensitive parameters of LAI-based Penman–Monteith evapotranspiration model based on particle swarm algorithm. Acta Geophys. 2022, 6, 1033–1043. [Google Scholar] [CrossRef]
- Li, F.; Cao, R.; Zhao, Y.; Mu, D.; Fu, C.; Ping, F. Remote sensing Penman–Monteith model to estimate catchment evapotranspiration considering the vegetation diversity. Theor. Appl. Climatol. 2015, 127, 111–121. [Google Scholar] [CrossRef]
- Wang, Q.M.; Jiang, S.; Zhai, J.Q.; He, G.H.; Zhao, Y.; Zhu, Y.N.; He, X.; Li, H.H.; Wang, L.Z.; He, F.; et al. Effects of vegetation restoration on evapotranspiration water consumption in mountainous areas and assessment of its remaining restoration space. J. Hydrol. 2022, 605, 127259. [Google Scholar]
- Zhang, Y.; Leuning, R.; Hutley, L.B.; Beringer, J.; McHugh, I.; Walker, J.P. Using long-term water balances to parameterize surface conductances and calculate evaporation at 0.05° spatial resolution. Water Resour. Res. 2010, 46, W05512. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Zhang, K.; Zhan, H.; Chao, L. Improved soil evaporation remote sensing retrieval algorithms and associated uncertainty analysis on the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2023, 27, 363–383. [Google Scholar] [CrossRef]
- Noilhan, J.; Planton, S. A simple parameterization of land surface processes for meteorological models. Mon. Weather Rev. 1989, 117, 536–549. [Google Scholar] [CrossRef]
- Ben Mehrez, M.; Taconet, O.; Vidal-Madjar, D.; Valencogne, C. Estimation of stomatal resistance and canopy evaporation during the HAPEX-MOBILHY experiment. Agric. For. Meteorol. 1992, 58, 285–313. [Google Scholar] [CrossRef]
- Xing, Z.; Fan, L.; Zhao, L.; De Lannoy, G.; Frappart, F.; Peng, J.; Li, X.; Zeng, J.; Al-Yaari, A.; Yang, K.; et al. A first assessment of satellite and reanalysis estimates of surface and root-zone soil moisture over the permafrost region of Qinghai-Tibet Plateau. Remote Sens. Environ. 2021, 265, 112666. [Google Scholar] [CrossRef]
- Liang, S.; Cheng, J.; Jia, K.; Jiang, B.; Liu, Q.; Xiao, Z.; Yao, Y.; Yuan, W.; Zhang, X.; Zhao, X.; et al. The Global Land Surface Satellite (GLASS) Product Suite. Bull. Am. Meteorol. Soc. 2021, 102, E323–E337. [Google Scholar] [CrossRef]
- Liang, S.; Zhang, X.; Xiao, Z.; Cheng, J.; Liu, Q.; Zhao, X. Global Land Surface Satellite (GLASS) Products: Algorithms, Validation and Analysis; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H.; et al. A long-term Global LAnd Surface Satellite (GLASS) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Zheng, J.; Zhao, T.; Lü, H.; Shi, J.; Cosh, M.H.; Ji, D.; Jiang, L.; Cui, Q.; Lu, H.; Yang, K.; et al. Assessment of 24 soil moisture datasets using a new in situ network in the Shandian River Basin of China. Remote Sens. Environ. 2002, 271, 112891. [Google Scholar] [CrossRef]
- Bi, H.; Ma, J.; Zheng, W.; Zeng, J. Comparison of soil moisture in GLDAS model simulations and in situ observations over the Tibetan Plateau. J. Geophys. Res.-Atmos. 2016, 121, 2658–2678. [Google Scholar] [CrossRef] [Green Version]
- Cai, J.; Zhang, Y.; Li, Y.; Liang, X.; Jiang, T. Analyzing the Characteristics of Soil Moisture Using GLDAS Data: A Case Study in Eastern China. Appl. Sci. 2017, 7, 566. [Google Scholar] [CrossRef] [Green Version]
- Kędzior, M.; Zawadzki, J. Comparative study of soil moisture estimations from SMOS satellite mission, GLDAS database, and cosmic-ray neutrons measurements at COSMOS station in Eastern Poland. Geoderma 2016, 283, 21–31. [Google Scholar] [CrossRef]
- Cui, Y.; Tan, J.; Jing, W.; Tan, G. Applicability evaluation of merged soil moisture in GLDAS and CLDAS products over Qinghai-Tibetan Plateau. Plateau Meteorol. 2018, 37, 123–136. [Google Scholar]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.; Christianson, D.; Cheah, Y.W.; Poindexter, C.; Chen, J.; Elbashandy, A.; Humphrey, M.; et al. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef]
- Rahmati, M.; Groh, J.; Graf, A.; Pütz, T.; Vanderborght, J.; Vereecken, H. On the impact of increasing drought on the relationship between soil water content and evapotranspiration of a grassland. Vadose Zone J. 2020, 19, e20029. [Google Scholar] [CrossRef]
- Yan, H.; Wang, S.Q.; Billesbach, D.; Oechel, W.; Zhang, J.H.; Meyers, T.; Martin, T.A.; Matamala, R.; Baldocchi, D.; Bohrer, G.; et al. Global estimation of evapotranspiration using a leaf area index-based surface energy and water balance model. Remote Sens. Environ. 2012, 124, 581–595. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Feng, H.; He, H.; Zhou, J.; Zhang, Y. Evaluation of soil moisture climatology and anomaly components derived from ERA5-Land and GLDAS-2.1 in China. Water Resour. Manag. 2021, 35, 629–643. [Google Scholar] [CrossRef]
- Williams, I.N.; Torn, M.S. Vegetation controls on surface heat flux partitioning, and land-atmosphere coupling. Geophys. Res. Lett. 2015, 42, 9416–9424. [Google Scholar] [CrossRef]
- Yang, S.; Zeng, J.; Fan, W.; Cui, Y. Evaluating root-zone soil moisture products from GLEAM, GLDAS, and ERA5 based on in situ observations and triple collection method over Tibetan Plateau. J. Hydrometeorol. 2022, 23, 1861–1878. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, Q.; Wang, Q.; Jin, Y.; Yue, Q.; Yu, J.; Zheng, Y.; Jiang, W.; Yao, X. The divergence between potential and actual evapotranspiration: An insight from climate, water, and vegetation change. Sci. Total Environ. 2022, 807 Pt 1, 150648. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Kong, D.; Gan, R.; Chiew, F.H.S.; McVicar, T.R.; Zhang, Q.; Yang, Y. Coupled estimation of 500 m and 8-day resolution global evapotranspiration and gross primary production in 2002–2017. Remote Sens. Environ. 2019, 222, 165–182. [Google Scholar] [CrossRef]
- Purdy, A.J.; Fisher, J.B.; Goulden, M.L.; Colliander, A.; Halverson, G.; Tu, K.; Famiglietti, J.S. SMAP soil moisture improves global evapotranspiration. Remote Sens. Environ. 2018, 219, 1–14. [Google Scholar] [CrossRef]
- Hssaine, B.A.; Merlin, O.; Rafi, Z.; Ezzahar, J.; Jarlan, L.; Khabba, S.; Er-Raki, S. Calibrating an evapotranspiration model using radiometric surface temperature, vegetation cover fraction and near-surface soil moisture data. Agric. For. Meteorol. 2018, 256–257, 104–115. [Google Scholar] [CrossRef] [Green Version]
- Ma, N.; Szilagyi, J.; Zhang, Y. Calibration-Free Complementary Relationship Estimates Terrestrial Evapotranspiration Globally. Water Resour. Res. 2021, 57, e2021WR029691. [Google Scholar] [CrossRef]
- Cui, Y.; Jia, L. Estimation of evapotranspiration of “soil-vegetation” system with a scheme combining a dual-source model and satellite data assimilation. J. Hydrol. 2021, 603, 127145. [Google Scholar] [CrossRef]



| Site ID | Climate | Years | Vegetation | Mean Annual Precipitation (mm) |
|---|---|---|---|---|
| AT-Neu | warm summer continental | 2002–2012 | grassland | 852 |
| AU-DaS | tropical savanna | 2008–2014 | savannas | 975.82 |
| CA-Qfo | subarctic | 2003–2010 | evergreen needleleaf forests | 962.32 |
| CA-SF1 | subarctic | 2003–2006 | evergreen needleleaf forests | 470 |
| CA-SF2 | subarctic | 2002–2005 | evergreen needleleaf forests | 470 |
| CH-Cha | warm summer continental | 2006–2012 | mixed forests | 663.59 |
| CN-HaM | tundra | 2002–2004 | grasslands | - |
| FI-Hyy | subarctic | 2004–2014 | evergreen needleleaf forests | 709 |
| FI-Lom | subarctic | 2007–2009 | permanent wetlands | 484 |
| FI-Sod | - | 2002–2010 | evergreen needleleaf forests | 500 |
| IT-PT1 | - | 2002–2004 | deciduous broadleaf forests | 984 |
| US-Me5 | Mediterranean | 2000–2002 | evergreen needleleaf forests | 590.81 |
| US-Syv | warm summer continental | 2001–2008 | mixed forests | 826 |
| EC Site | PML-SM (ERA5) Model | PML-SM (GLDAS) Model | PML Model | |||
|---|---|---|---|---|---|---|
| Pearson r | RMSE (mm/d) | Pearson r | RMSE (mm/d) | Pearson r | RMSE (mm/d) | |
| AT-Neu | 0.89 | 1.30 | 0.89 | 1.23 | 0.90 | 1.00 |
| AU-DaS | 0.89 | 1.78 | 0.87 | 1.75 | 0.72 | 0.87 |
| CA-Qfo | 0.86 | 1.80 | 0.86 | 1.71 | 0.72 | 1.59 |
| CA-SF1 | 0.87 | 1.77 | 0.60 | 1.48 | 0.77 | 1.44 |
| CA-SF2 | 0.85 | 1.69 | 0.83 | 1.54 | 0.67 | 1.22 |
| CH-Cha | 0.88 | 1.95 | 0.55 | 1.56 | 0.68 | 1.68 |
| CN-HaM | 0.80 | 1.56 | 0.65 | 1.21 | 0.74 | 0.99 |
| FI-Hyy | 0.92 | 1.59 | 0.89 | 1.51 | 0.88 | 1.29 |
| FI-Lom | 0.91 | 1.46 | 0.89 | 1.39 | 0.85 | 1.09 |
| FI-Sod | 0.89 | 1.43 | 0.86 | 1.38 | 0.82 | 0.98 |
| IT-PT1 | 0.73 | 1.87 | 0.70 | 1.22 | 0.60 | 1.32 |
| US-Me5 | 0.71 | 1.01 | 0.78 | 1.11 | 0.30 | 0.61 |
| US-Syv | 0.71 | 2.04 | 0.69 | 2.01 | 0.60 | 1.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, H.; Zhao, H.; Li, Q.; Xu, H.; Han, C. Estimation of Evapotranspiration Based on a Modified Penman–Monteith–Leuning Model Using Surface and Root Zone Soil Moisture. Water 2023, 15, 1418. https://doi.org/10.3390/w15071418
Duan H, Zhao H, Li Q, Xu H, Han C. Estimation of Evapotranspiration Based on a Modified Penman–Monteith–Leuning Model Using Surface and Root Zone Soil Moisture. Water. 2023; 15(7):1418. https://doi.org/10.3390/w15071418
Chicago/Turabian StyleDuan, Hao, Hongli Zhao, Qiuju Li, Haowei Xu, and Chengxin Han. 2023. "Estimation of Evapotranspiration Based on a Modified Penman–Monteith–Leuning Model Using Surface and Root Zone Soil Moisture" Water 15, no. 7: 1418. https://doi.org/10.3390/w15071418
APA StyleDuan, H., Zhao, H., Li, Q., Xu, H., & Han, C. (2023). Estimation of Evapotranspiration Based on a Modified Penman–Monteith–Leuning Model Using Surface and Root Zone Soil Moisture. Water, 15(7), 1418. https://doi.org/10.3390/w15071418






