Improvement of Hargreaves–Samani Reference Evapotranspiration Estimates in the Peruvian Altiplano
Abstract
:1. Introduction
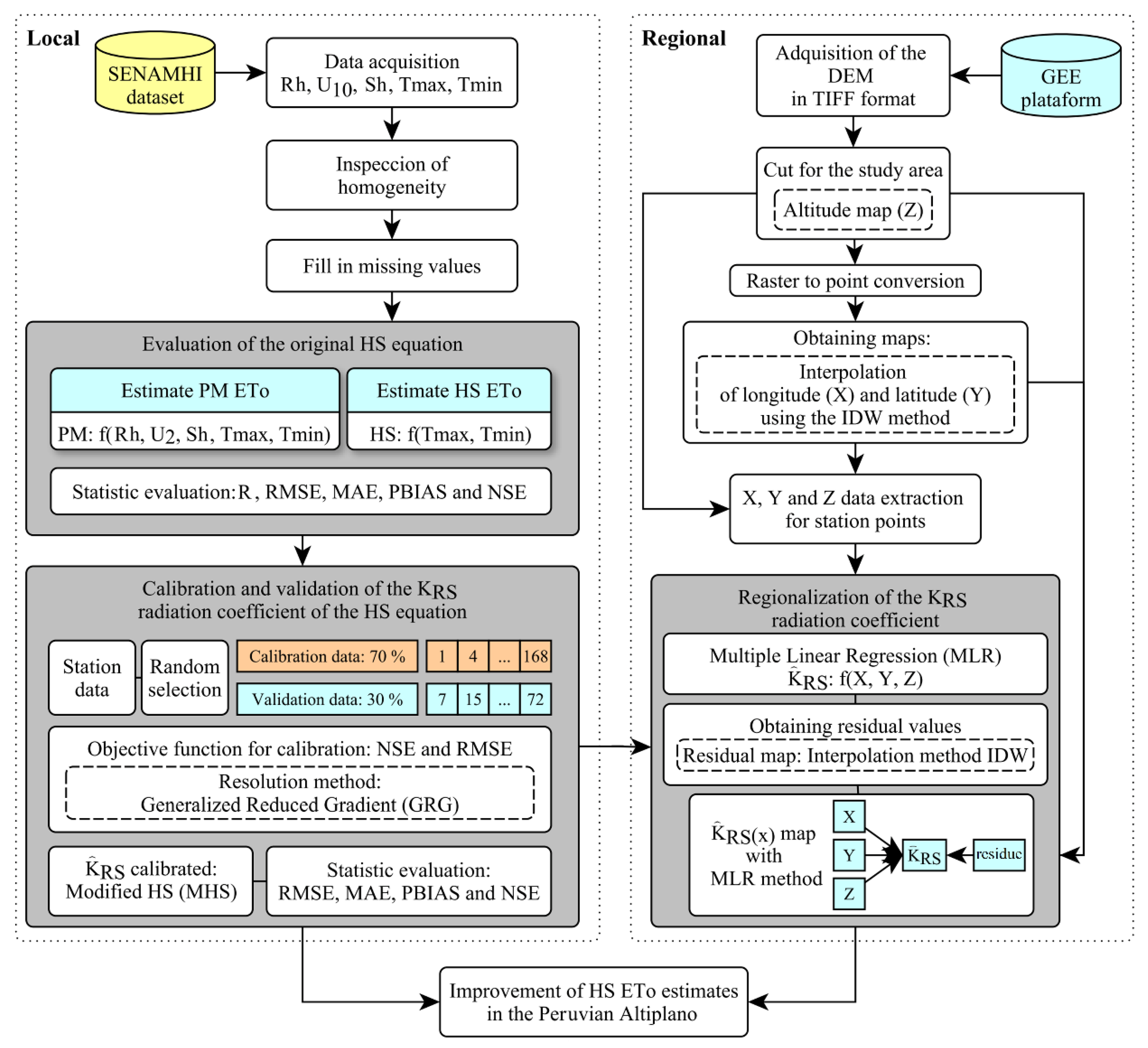
2. Materials and Method
2.1. Study Area
2.2. Climatic and Terrain Data
2.3. Evaluation of the Original Hargreaves-Samani Equation for Use in the Peruvian Altiplano
2.4. Statistical Performance Metrics
2.5. Calibration and Validation of the Radiation Coefficient KRS of the HS Equation
2.6. Regionalization of the Radiation Coefficient
3. Results and Discussion
3.1. Evaluation of the Original Hargreaves-Samani Equation
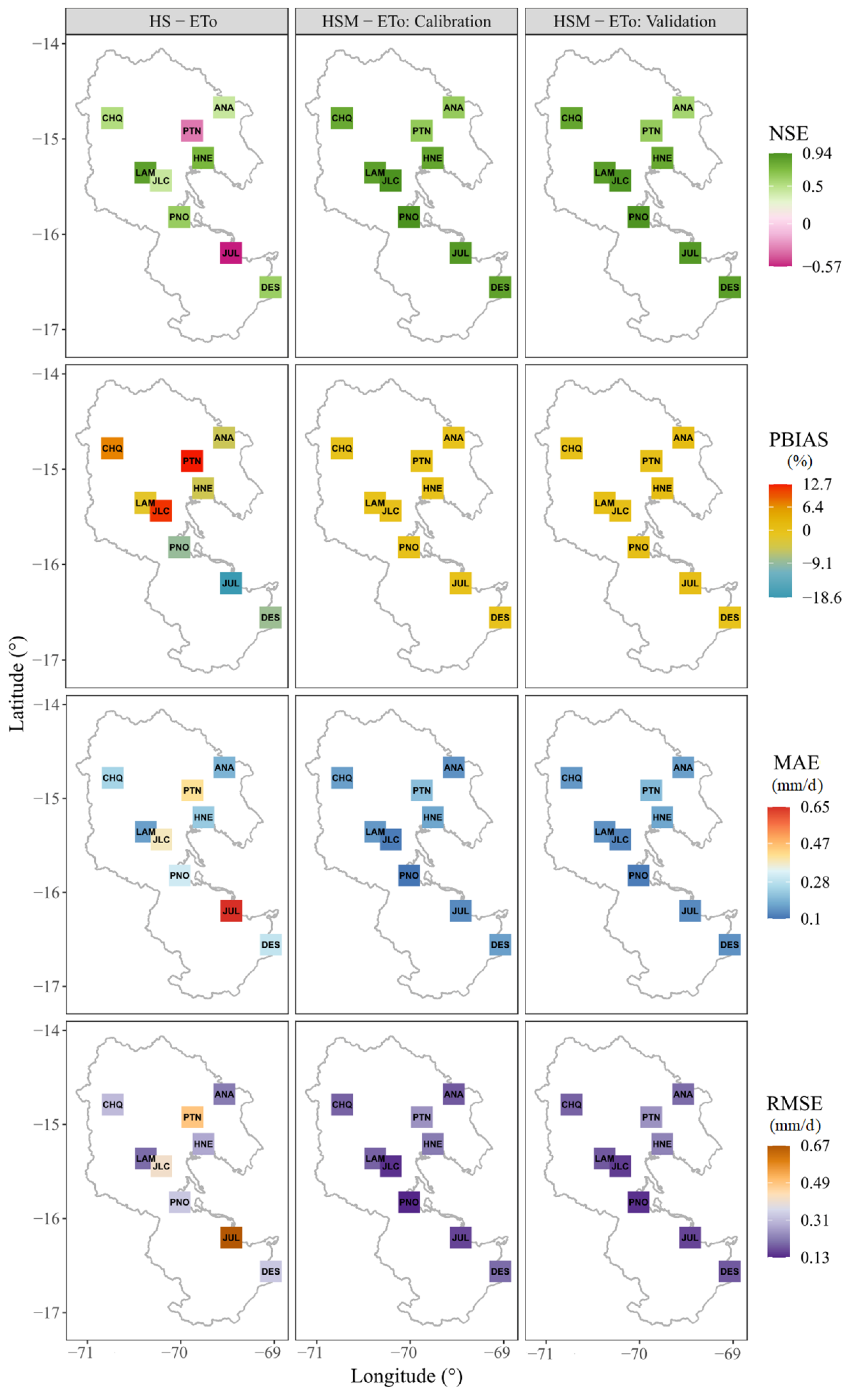
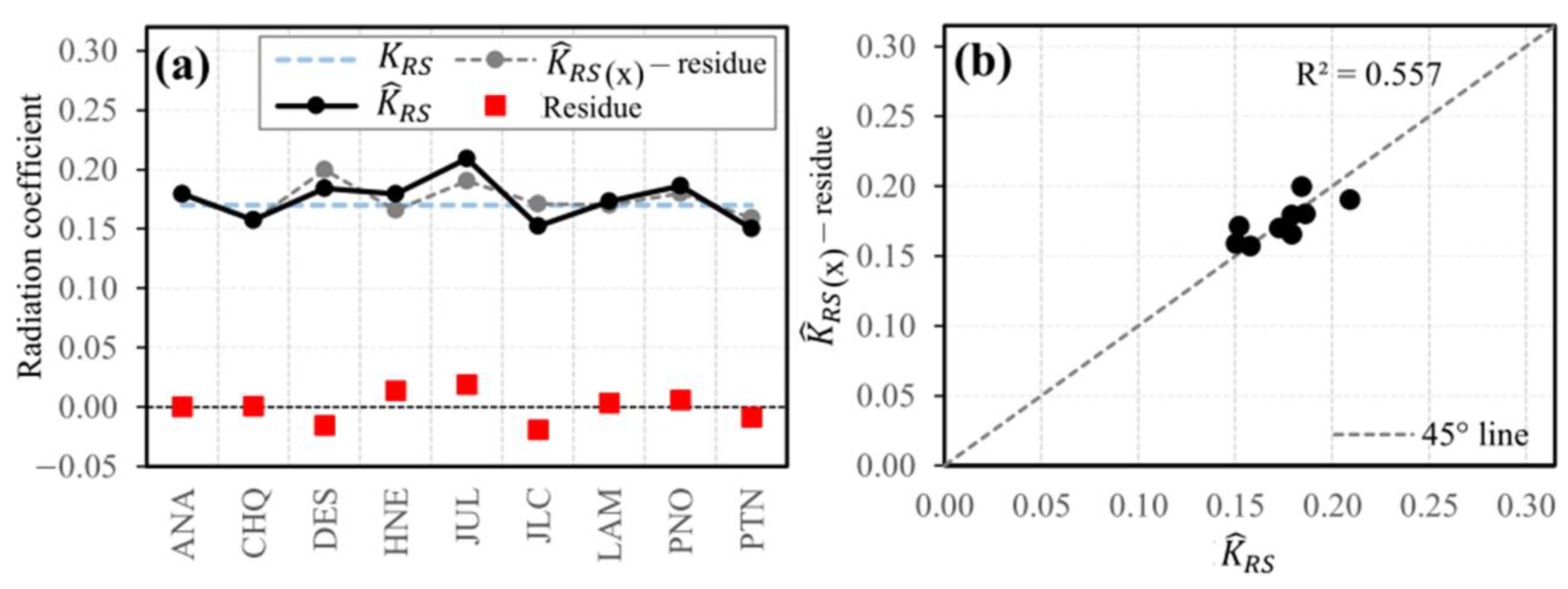
3.2. Calibration and Validation of the Radiation Coefficient KRS of the HS Equation
3.3. Regionalisation of the Radiation Coefficient
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Berti, A.; Tardivo, G.; Chiaudani, A.; Rech, F.; Borin, M. Assessing reference evapotranspiration by the Hargreaves method in north-eastern Italy. Agric. Water Manag. 2014, 140, 20–25. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Chipana, R.; Yujra, R.; Paredes, P.; Pereira, L.S. Determinación de la evapotranspiración de referencia con datos limitados en zonas de altura del Altiplano Boliviano aplicando la metodología de la FAO y la ecuación de Hargreaves-Samani. In I Congreso Boliviano de Riego y Drenaje; Facultad de Agronomía: La Paz, Argentina, 2010; pp. 12–14. [Google Scholar]
- Todorovic, M.; Karic, B.; Pereira, L.S. Reference Evapotranspiration estimate with limited weather data across a range of Mediterranean climates. J. Hydrol. 2013, 481, 166–176. [Google Scholar] [CrossRef] [Green Version]
- Raziei, T.; Pereira, L.S. Estimation of ETo with Hargreaves–Samani and FAO-PM temperature methods for a wide range of climates in Iran. Agric. Water Manag. 2013, 121, 1–18. [Google Scholar] [CrossRef]
- Trajkovic, S. Hargreaves versus Penman-Monteith under Humid Conditions. J. Irrig. Drain. Eng. 2007, 133, 38–42. [Google Scholar] [CrossRef]
- Muhammad, M.K.I.; Nashwan, M.S.; Shahid, S.; Ismail, T.B.; Song, Y.H.; Chung, E.S. Evaluation of empirical reference evapotranspiration models using compromise programming: A case study of Peninsular Malaysia. Sustainability 2019, 11, 4267. [Google Scholar] [CrossRef] [Green Version]
- Adamala, S.; Raghuwanshi, N.S.; Mishra, A.; Tiwari, M.K. Evapotranspiration modeling using second-order neural networks. J. Hydrol. Eng. 2014, 19, 1131–1140. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Singh, R. Evaluation of Variable-Infiltration Capacity Model and MODIS-Terra Satellite-Derived Grid-Scale Evapotranspiration Estimates in a River Basin with Tropical Monsoon-Type Climatology. J. Irrig. Drain. Eng. 2017, 143, 4017028. [Google Scholar] [CrossRef] [Green Version]
- Kumari, N.; Srivastava, A. An Approach for Estimation of Evapotranspiration by Standardizing Parsimonious Method. Agric. Res. 2020, 9, 301–309. [Google Scholar] [CrossRef]
- Hamed, M.M.; Khan, N.; Muhammad, M.K.I.; Shahid, S. Ranking of Empirical Evapotranspiration Models in Different Climate Zones of Pakistan. Land 2022, 11, 2168. [Google Scholar] [CrossRef]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop water requirements. FAO Irrigation and drainage paper 56. FAO Rome 1998, 300, D05109. [Google Scholar]
- Almorox, J.; Senatore, A.; Quej, V.H.; Mendicino, G. Worldwide assessment of the Penman–Monteith temperature approach for the estimation of monthly reference evapotranspiration. Theor. Appl. Climatol. 2018, 131, 693–703. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Almorox, J.; Grieser, J. Calibration of the Hargreaves–Samani method for the calculation of reference evapotranspiration in different Köppen climate classes. Hydrol. Res. 2016, 47, 521–531. [Google Scholar] [CrossRef] [Green Version]
- Bogawski, P.; Bednorz, E. Comparison and validation of selected evapotranspiration models for conditions in Poland (Central Europe). Water Resour. Manag. 2014, 28, 5021–5038. [Google Scholar] [CrossRef] [Green Version]
- Čadro, S.; Uzunović, M.; Žurovec, J.; Žurovec, O. Validation and calibration of various reference evapotranspiration alternative methods under the climate conditions of Bosnia and Herzegovina. Int. Soil Water Conserv. Res. 2017, 5, 309–324. [Google Scholar] [CrossRef]
- Awal, R.; Habibi, H.; Fares, A.; Deb, S. Estimating reference crop evapotranspiration under limited climate data in West Texas. J. Hydrol. Reg. Stud. 2020, 28, 100677. [Google Scholar] [CrossRef]
- Gavilán, P.; Lorite, I.J.; Tornero, S.; Berengena, J. Regional calibration of Hargreaves equation for estimating reference et in a semiarid environment. Agric. Water Manag. 2006, 81, 257–281. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H. Local calibration of the Hargreaves and Priestley-Taylor equations for estimating reference evapotranspiration in arid and cold climates of Iran based on the Penman-Monteith model. J. Hydrol. Eng. 2011, 16, 837. [Google Scholar] [CrossRef]
- Mohawesh, O.E.; Talozi, S.A. Comparison of Hargreaves and FAO56 equations for estimating monthly evapotranspiration for semi-arid and arid environments. Arch. Agron. Soil Sci. 2012, 58, 321–334. [Google Scholar] [CrossRef]
- Pandey, V.; Pandey, P.K.; Mahanta, A.P. Calibration and performance verification of Hargreaves Samani equation in a humid region. Irrig. Drain. 2014, 63, 659–667. [Google Scholar] [CrossRef]
- Dorji, U.; Olesen, J.E.; Seidenkrantz, M.S. Water balance in the complex mountainous terrain of Bhutan and linkages to land use. J. Hydrol. Reg. Stud. 2016, 7, 55–68. [Google Scholar] [CrossRef] [Green Version]
- Cobaner, M.; Citakoğlu, H.; Haktanir, T.; Kisi, O. Modifying Hargreaves–Samani equation with meteorological variables for estimation of reference evapotranspiration in Turkey. Hydrol. Res. 2017, 48, 480–497. [Google Scholar] [CrossRef]
- Ravazzani, G.; Corbari, C.; Morella, S.; Gianoli, P.; Mancini, M. Modified Hargreaves-Samani equation for the assessment of reference evapotranspiration in Alpine river basins. J. Irrig. Drain. Eng. 2012, 138, 592–599. [Google Scholar] [CrossRef]
- Lavado Casimiro, W.S.; Lhomme, J.P.; Labat, D.; Guyot, J.L.; Boulet, G. Estimación de la evapotranspiración de referencia (FAO-56 Penman-Monteith) con limitados datos climáticos en la cuenca andina amazónica peruana. Rev. Peru. Geo Atmosférica 2015, 4, 31–43. [Google Scholar]
- Morales-Salinas, L.; Ortega-Farías, S.; Riveros-Burgos, C.; Neira-Román, J.; Carrasco-Benavides, M.; López-Olivari, R. Monthly calibration of Hargreaves–Samani equation using remote sensing and topoclimatology in central-southern Chile. Int. J. Remote Sens. 2017, 38, 7497–7513. [Google Scholar] [CrossRef]
- Paredes, P.; Fontes, J.C.; Azevedo, E.B.; Pereira, L.S. Daily reference crop evapotranspiration in the humid environments of Azores islands using reduced data sets: Accuracy of FAO-PM temperature and Hargreaves-Samani methods. Theor. Appl. Climatol. 2018, 134, 595–611. [Google Scholar] [CrossRef]
- Rodrigues, G.C.; Braga, R.P. Estimation of Reference Evapotranspiration during the Irrigation Season Using Nine Temperature-Based Methods in a Hot-Summer Mediterranean Climate. Agriculture 2021, 11, 124. [Google Scholar] [CrossRef]
- Servicio Nacional de Meteorología e Hidrología del Perú (SENAMHI). Climas del Perú—Mapa de Clasificación Climática Nacional; Dirección de Meteorología y Evaluación Ambiental Atmosférica: Lima, Perú, 2020. [Google Scholar]
- Huerta, A.; Lavado, W. ATLAS Zonas Áridas Del Perú: Una Evaluación Presente Y Futura; SENAMHI: Lima, Perú, 2021. [Google Scholar]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M.; et al. Global land cover mapping at 30 m resolution: A POK-based operational approach. ISPRS J. Photogramm. Remote Sens. 2015, 103, 7–27. [Google Scholar] [CrossRef] [Green Version]
- Vera, L.; Villegas, E.; Oria, C.; Arboleda, F. Control de Calidad de Datos de Estaciones Meteorológicas E Hidrológicas Automáticas en El Centro de Procesamiento de Datos Del SENAMHI; Servicio Nacional de Meteorología e Hidrología del Perú (SENAMHI): Lima, Perú, 2021. [Google Scholar]
- Chiew, F.H.; Siriwardena, L. Trend/Change Detection Software. USER GUIDE; CRC for Catchment Hydrology: Clayton, Australia, 2005. [Google Scholar]
- Van Buuren, S.; Groothuis-Oudshoorn, K. Mice: Multivariate imputation by chained equations in R. J. Stat. Softw. 2011, 45, 1–67. [Google Scholar] [CrossRef] [Green Version]
- Tomas-Burguera, M.; Vicente-Serrano, S.M.; Beguería, S.; Reig, F.; Latorre, B. Reference 634 crop evapotranspiration database in Spain (1961–2014). Earth Syst. Sci. Data. 2019, 11, 1917–1930. [Google Scholar] [CrossRef] [Green Version]
- Woldesenbet, T.A.; Elagib, N.A.; Ribbe, L.; Heinrich, J. Gap filling and homogenization of climatological datasets in the headwater region of the Upper Blue Nile Basin, Ethiopia. Int. J. Climatol. 2017, 37, 2122–2140. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4. Available from the CGIAR-CSI SRTM 90m Database. 2008. Available online: http://srtm.csi.cgiar.org (accessed on 15 July 2022).
- Ye, J.; Guo, A.; Sun, G. Statistical analysis of reference evapotranspiration on the Tibetan Plateau. J. Irrig. Drain. Eng. 2009, 135, 134–140. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of ‘goodness-of-fifit’ measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.; Van Liew, M.; Bingner, R.; Harmel, R.; Veith, T. Model evaluation guidelines for systematic quantifification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Vu, T.T.; Li, L.; Jun, K.S. Evaluation of multi-satellite precipitation products for streamflow simulations: A case study for the Han River Basin in the Korean Peninsula, East Asia. Water 2018, 10, 642. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Shiri, J.; Sadraddini, A.A.; Nazemi, A.H.; Marti, P.; Fard, A.F.; Kisi, O.; Landeras, G. Independent testing for assessing the calibration of the Hargreaves–Samani equation: New heuristic alternatives for Iran. Comput. Electron. Agric. 2015, 117, 70–80. [Google Scholar] [CrossRef]
- Feng, Y.; Jia, Y.; Cui, N.; Zhao, L.; Li, C.; Gong, D. Calibration of Hargreaves model for reference evapotranspiration estimation in Sichuan basin of southwest China. Agric. Water Manag. 2017, 181, 1–9. [Google Scholar] [CrossRef]
- Samani, Z. Discussion of “History and Evaluation of Hargreaves Evapotranspiration Equation ”by George H. Hargreaves and Richard G. Allen. J. Irrig. Drain. Eng. 2003, 130, 447. [Google Scholar] [CrossRef]
- Paredes, P.; Fontes, J.C.; Azevedo, E.B.; Pereira, L.S. Daily reference crop evapotranspiration with reduced data sets in the humid environments of Azores islands using estimates of actual vapor pressure, solar radiation, and wind speed. Theor. Appl. Climatol. 2018, 134, 1115–1133. [Google Scholar] [CrossRef]

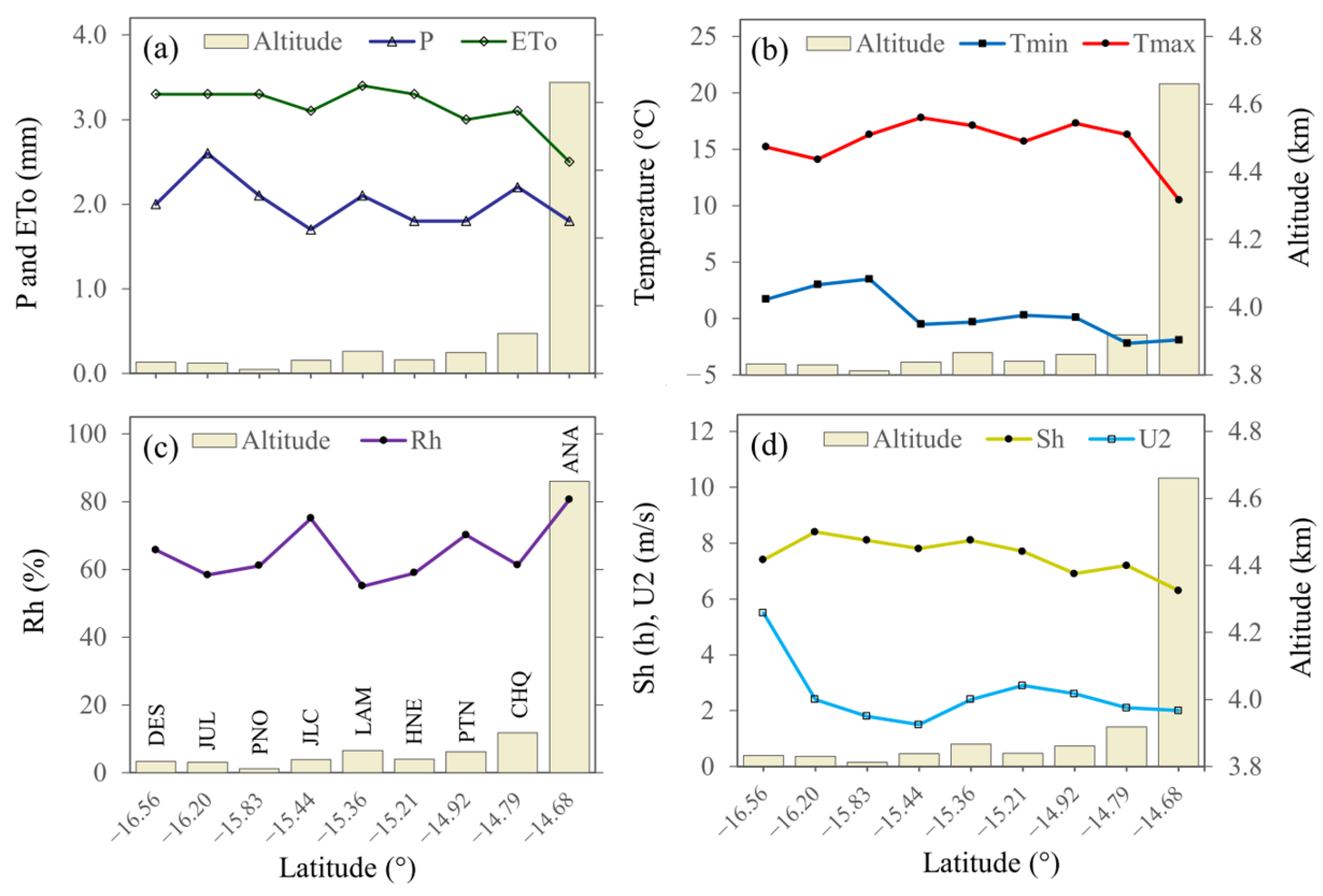
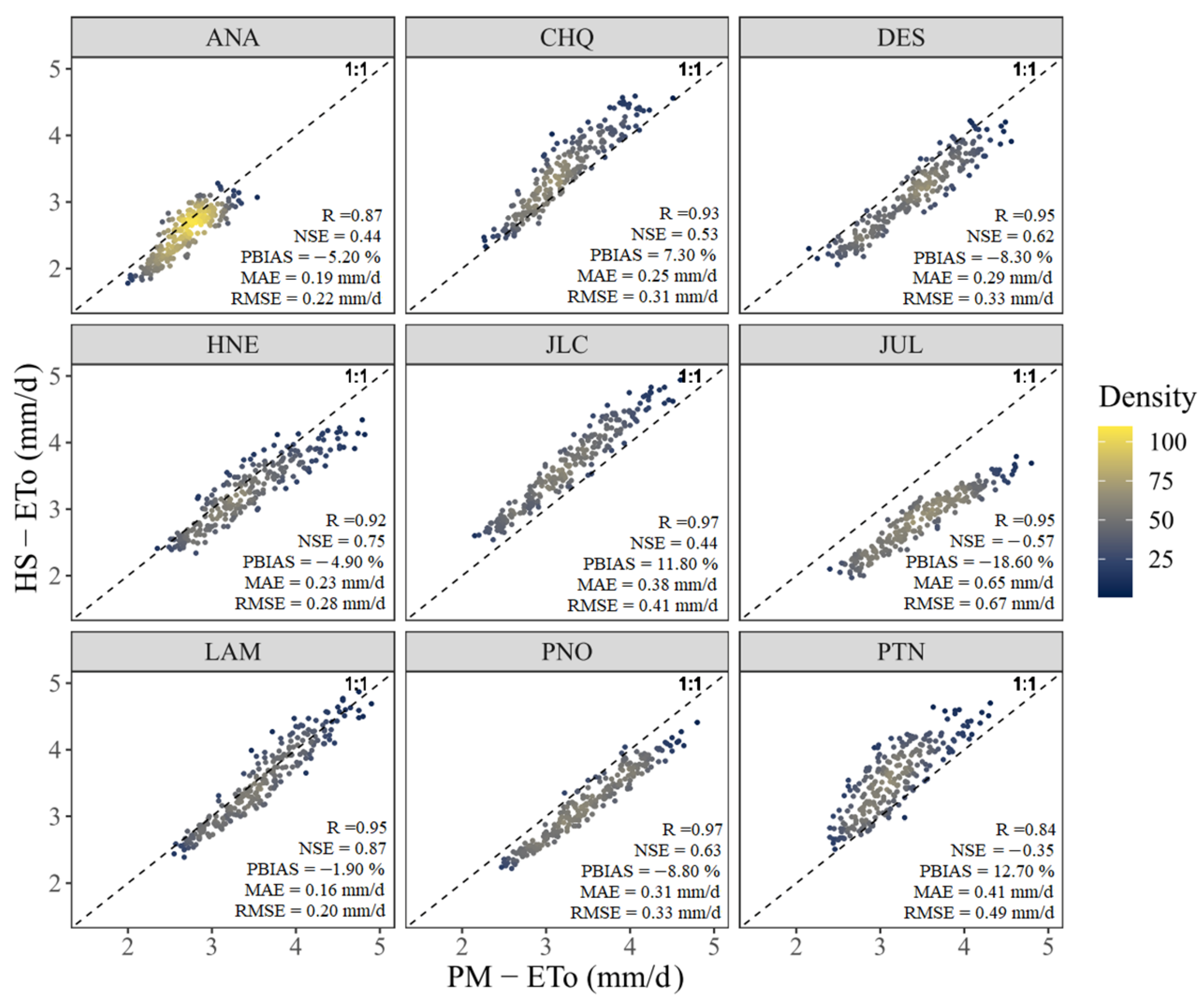
| Station | Lat. | Long. | Alt. | Tmax | Tmin | Rh | U2 | Sh | ETo | P | AI | CC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ananea (ANA) | −14.676 | −69.534 | 4660 | 10.5 | −1.9 | 80.6 | 2.0 | 6.3 | 2.7 | 658.4 | 0.67 | SH-h |
| Lampa (LAM) | −15.361 | −70.374 | 3866 | 17.1 | −0.3 | 55.0 | 2.4 | 8.1 | 3.6 | 757.1 | 0.60 | SH-d |
| Chuquibambilla (CHQ) | −14.788 | −70.728 | 3918 | 16.3 | −2.2 | 61.3 | 2.1 | 7.2 | 3.2 | 787.0 | 0.67 | SH-h |
| Putina (PTN) | −14.921 | −69.876 | 3861 | 17.3 | 0.1 | 70.1 | 2.6 | 6.9 | 3.1 | 643.9 | 0.56 | SH-d |
| Huancané (HNE) | −15.207 | −69.758 | 3840 | 15.7 | 0.3 | 58.9 | 2.9 | 7.7 | 3.4 | 650.5 | 0.52 | SH-d |
| Juliaca (JLC) | −15.444 | −70.208 | 3838 | 17.8 | −0.5 | 75.0 | 1.5 | 7.8 | 3.2 | 624.9 | 0.53 | SH-d |
| Puno (PNO) | −15.826 | −70.012 | 3812 | 16.3 | 3.5 | 61.1 | 1.8 | 8.1 | 3.5 | 750.6 | 0.59 | SH-d |
| Juli (JUL) | −16.204 | −69.460 | 3830 | 14.1 | 3.0 | 58.3 | 2.4 | 8.4 | 3.5 | 948.3 | 0.78 | SH-h |
| Desaguadero (DES) | −16.563 | −69.037 | 3833 | 15.2 | 1.7 | 65.7 | 5.5 | 7.4 | 3.4 | 736.9 | 0.60 | SH-d |
| Statistical Performance | Equation 1 | Unit | Optimal Value |
|---|---|---|---|
| Correlation coefficient (R) | - | ±1 | |
| Nash–Sutcliffe efficiency (NSE) | - | 1 | |
| Percent bias (PBIAS) | % | 0 | |
| Mean absolute error (MAE) | mm | 0 | |
| Root mean square error (RMSE) | mm | 0 |
| Station | Recommended Equations |
|---|---|
| Ananea (ANA) | |
| Lampa (LAM) | |
| Chuquibambilla (CHQ) | |
| Putina (PTN) | |
| Huancané (HNE) | |
| Juliaca (JLC) | |
| Puno (PNO) | |
| Juli (JUL) | |
| Desaguadero (DES) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lujano, A.; Sanchez-Delgado, M.; Lujano, E. Improvement of Hargreaves–Samani Reference Evapotranspiration Estimates in the Peruvian Altiplano. Water 2023, 15, 1410. https://doi.org/10.3390/w15071410
Lujano A, Sanchez-Delgado M, Lujano E. Improvement of Hargreaves–Samani Reference Evapotranspiration Estimates in the Peruvian Altiplano. Water. 2023; 15(7):1410. https://doi.org/10.3390/w15071410
Chicago/Turabian StyleLujano, Apolinario, Miguel Sanchez-Delgado, and Efrain Lujano. 2023. "Improvement of Hargreaves–Samani Reference Evapotranspiration Estimates in the Peruvian Altiplano" Water 15, no. 7: 1410. https://doi.org/10.3390/w15071410





