Evaluation of Different Methods on the Estimation of the Daily Crop Coefficient of Winter Wheat
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Area Profile
2.2. Experimental Facilities and Data Selection
2.3. Division of Growth Stages
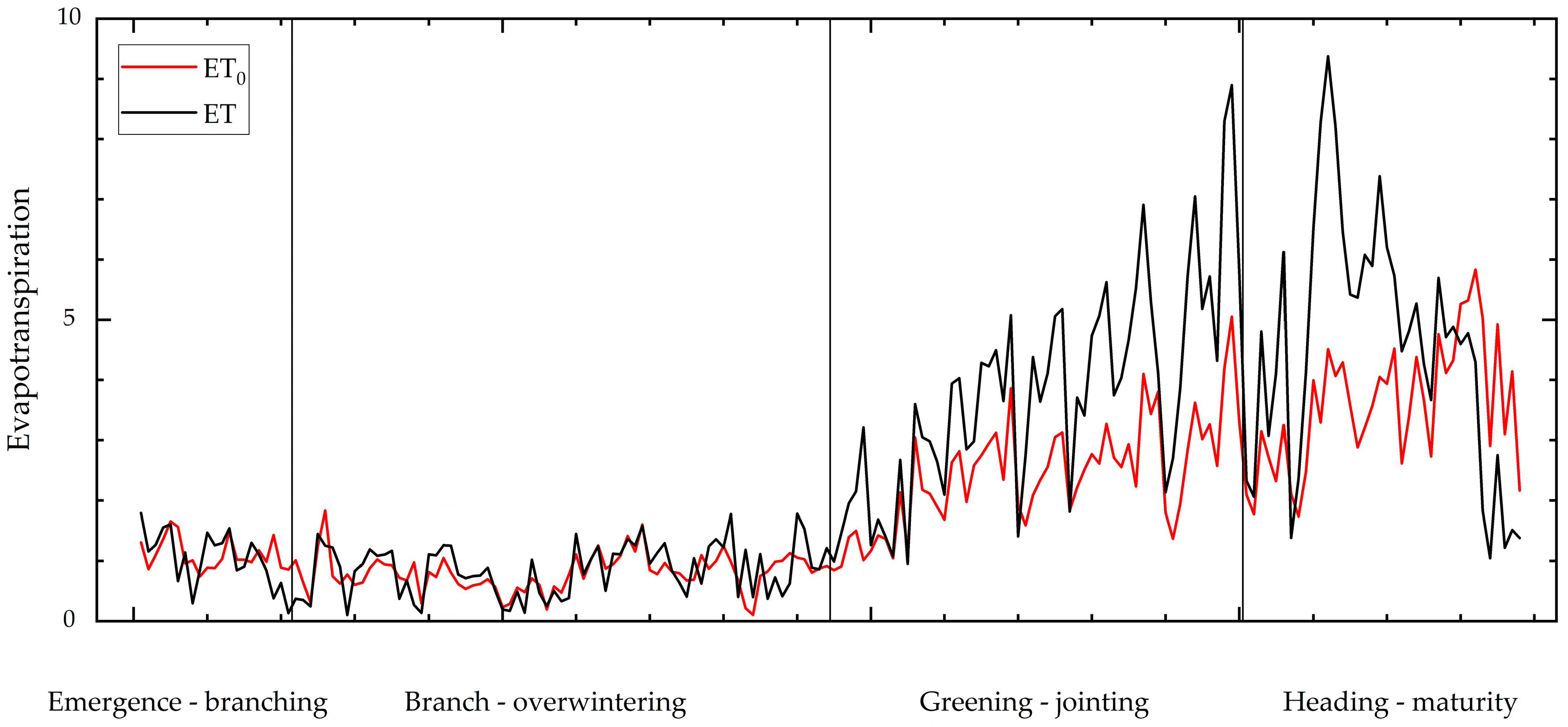
2.4. Crop Coefficient, Actual Evapotranspiration, and Reference Evapotranspiration
2.5. Crop Coefficient Estimation Method and Evaluation Indices
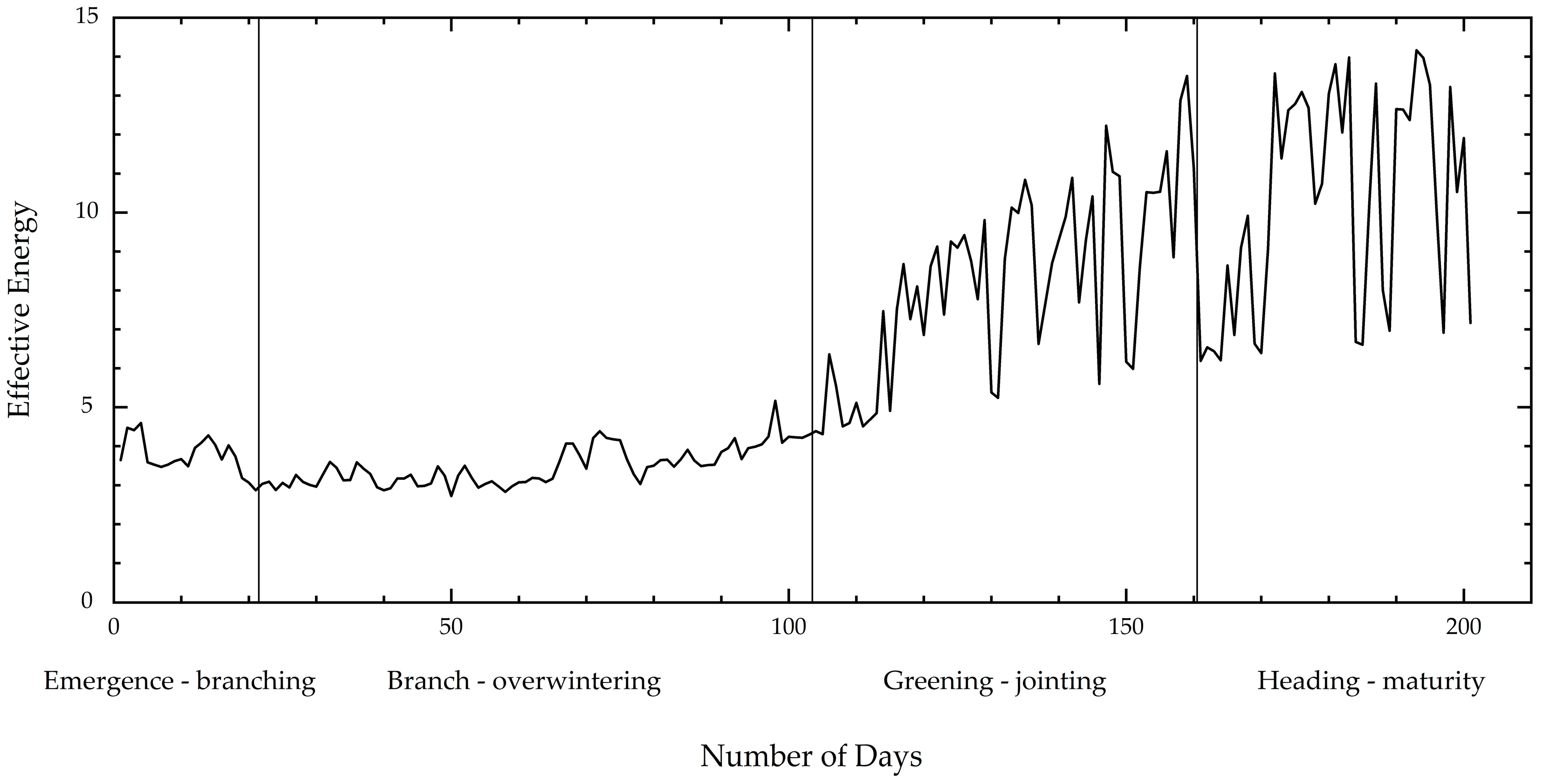
2.5.1. Temperature Effect Method
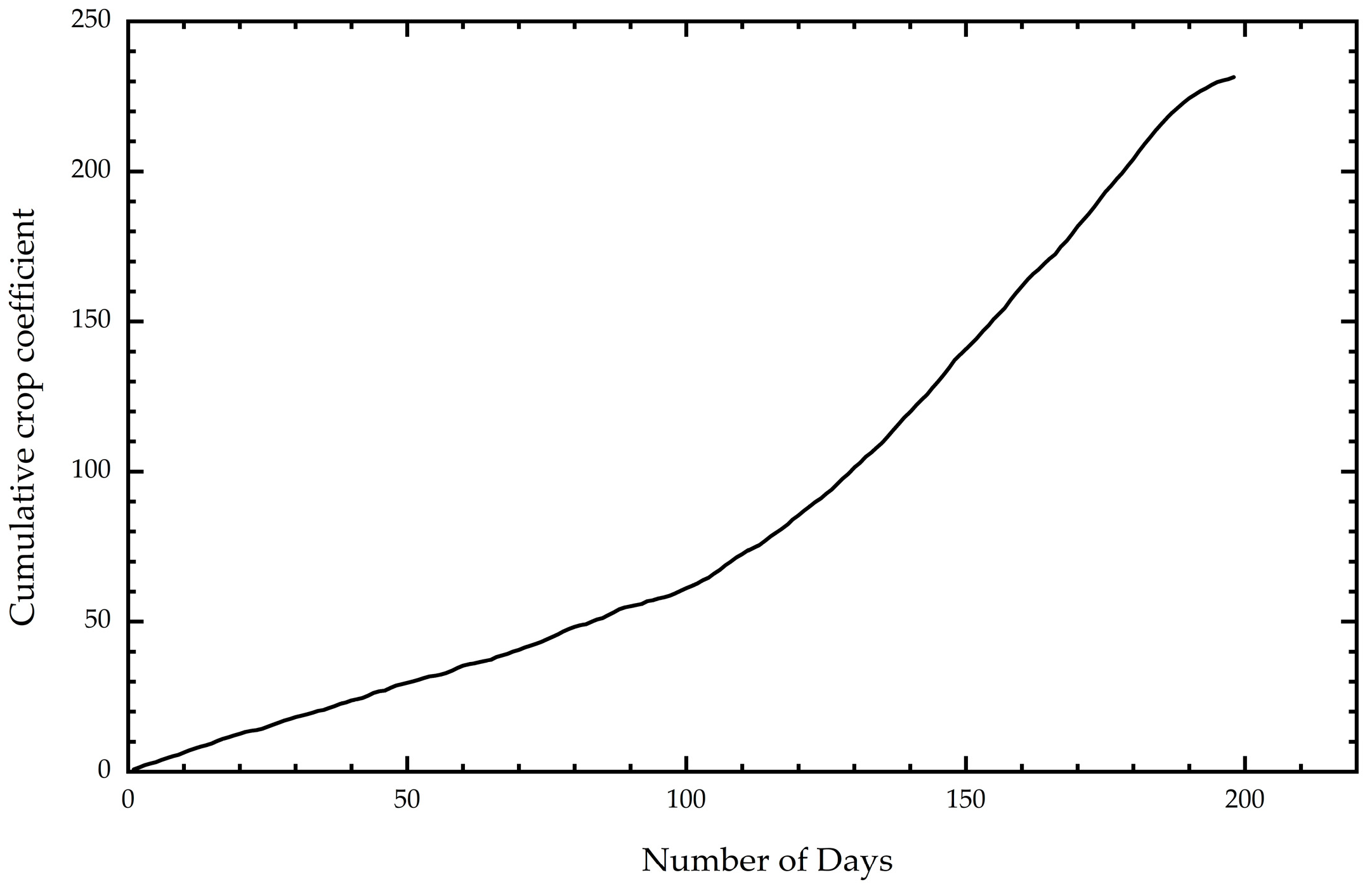
2.5.2. Cumulative Crop Coefficient Method
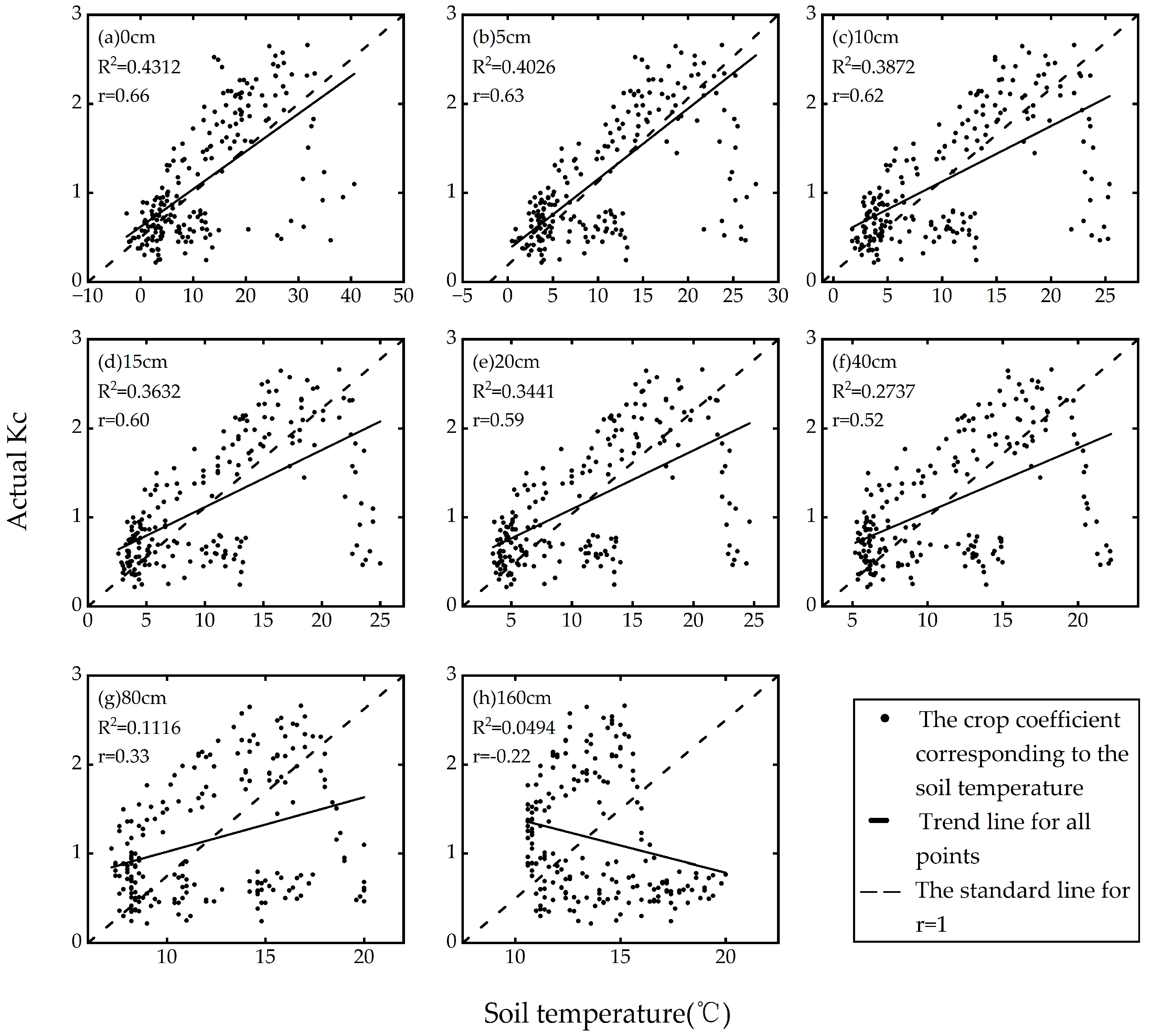
2.5.3. Radiative Soil Temperature Method
2.5.4. Indices of Evaluation
3. Results
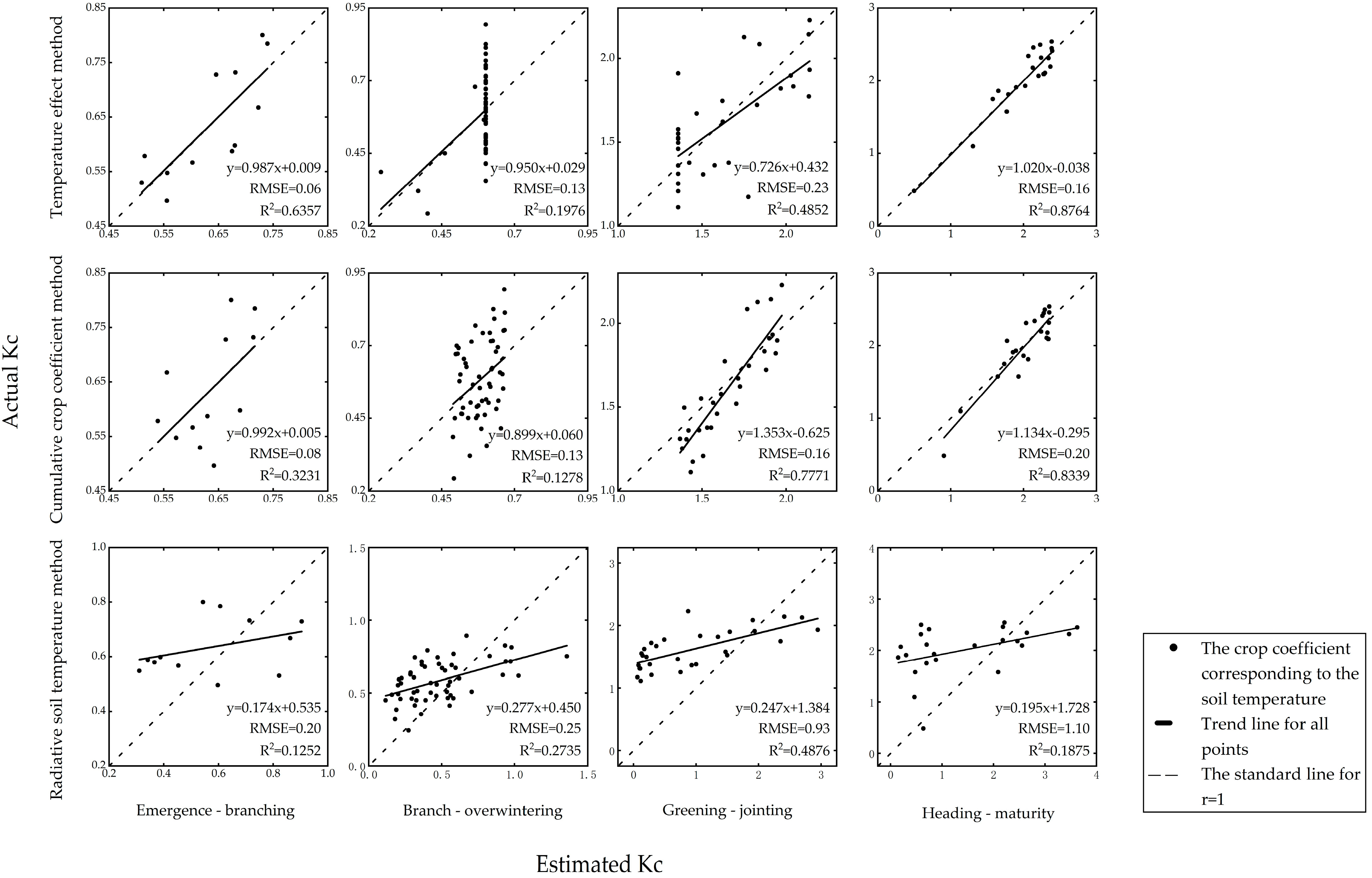
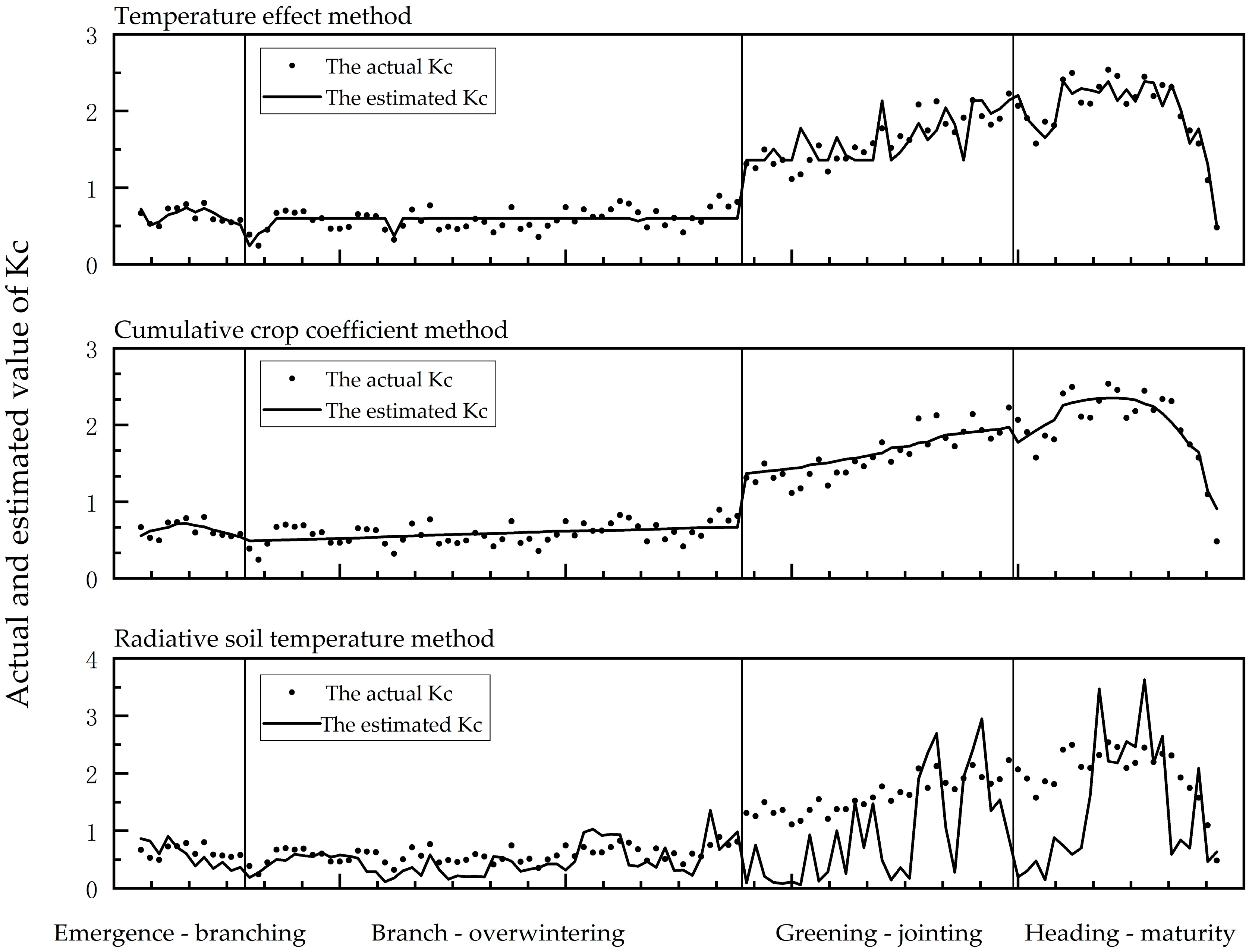
3.1. The Differences and Causes of Crop Coefficient Estimation by Different Methods
3.2. Determination of The Best Estimation Method for Each Growth Stage
4. Conclusions and Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FAO | Food and Agriculture Organization |
| FAO-56 | FAO Irrigation and Drainage Paper No. 56 |
| Kc | Crop coefficient |
| ET | Actual evapotranspiration |
| Ks | Water stress coefficient |
| TCARI | Transformed chlorophyll absorption in reflectance index |
| RDVI | Renormalized difference vegetation index |
| UAV | Unmanned aerial vehicle |
| TSEB | Two-source energy balance |
| ET0 | Reference evapotranspiration |
| SPSS | Statistical Product and Service Solutions |
| Rn-G | Effective energy |
| MATLAB | Matrix Laboratory |
| r | Correlation coefficient |
| dIA | Consistency index |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| TE | Temperature effect method |
| CCC | Cumulative crop coefficient method |
| RST | Radiative soil temperature method |
References
- Daszkiewicz, T. Food Production in the Context of Global Developmental Challenges. Agriculture 2022, 12, 832. [Google Scholar] [CrossRef]
- Wu, B.F.; Tian, F.Y.; Zhang, M.; Piao, S.L.; Zeng, H.W.; Zhu, W.W.; Liu, J.G.; Elnashar, A.; Lu, Y.M. Quantifying global agricultural water appropriation with data derived from earth observations. J. Clean. Prod. 2022, 358, 131891. [Google Scholar] [CrossRef]
- Kabbadj, A.; Makoudi, B.; Mouradi, M.; Pauly, N.; Frendo, P.; Ghoulam, C. Physiological and biochemical responses involved in water deficit tolerance of nitrogen-fixing vicia faba. PLoS ONE 2017, 12, e0190284. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paul, A.S.; Panwar, N.L.; Salvi, B.L.; Jain, S.; Sharma, D. Experimental investigation on the production of bio-oil from wheat straw. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 6, 1–16. [Google Scholar] [CrossRef]
- Langridge, P.; Alaux, M.; Almeida, N.F.; Ammar, K.; Baum, M.; Bekkaoui, F.; Bentley, A.R.; Beres, B.L.; Berger, B.; Braun, H.J.; et al. Meeting the Challenges Facing Wheat Production: The Strategic Research Agenda of the Global Wheat Initiative. Agronomy 2022, 12, 2767. [Google Scholar] [CrossRef]
- Xiang, C.; Huang, J.K. The role of exotic wheat germplasms in wheat breeding and their impact on wheat yield and production in china. China Econ. Rev. 2020, 62, 101239. [Google Scholar] [CrossRef]
- Dong, J.; Fu, Y.Y.; Wang, J.J.; Tian, H.F.; Fu, S.; Niu, Z.; Han, W.; Zheng, Y.; Huang, J.X.; Yuan, W.P. Early-season mapping of winter wheat in china based on landsat and sentinel images. Earth Syst. Sci. Data 2020, 12, 3081–3095. [Google Scholar] [CrossRef]
- Park, J.; Baik, J.; Choi, M. Satellite-based crop coefficient and evapotranspiration using surface soil moisture and vegetation indices in northeast asia. Catena 2017, 156, 305–314. [Google Scholar] [CrossRef]
- Shan, N.; Zhang, Y.G.; Cheng, J.M.; Ju, W.M.; Migliavacca, M.; Penuelas, J.; Yang, X.; Zhang, Z.Y.; Nelson, J.A.; Goulas, Y. A model for estimating transpiration from remotely sensed solar-induced chlorophyll fluorescence. Remote Sens. Environ. 2021, 252, 112–134. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 2008.
- Er-Raki, S.; Chehbouni, A.; Guemouria, N.; Duchemin, B.; Ezzahar, J.; Hadria, R. Combining fao-56 model and ground-based remote sensing to estimate water consumptions of wheat crops in a semi-arid region. Agric. Water Manag. 2007, 87, 41–54. [Google Scholar] [CrossRef] [Green Version]
- Vu, S.H.; Watanabe, H.; Takagi, K. Application of fao-56 for evaluating evapotranspiration in simulation of pollutant runoff from paddy rice field in japan. Agric. Water Manag. 2005, 76, 195–210. [Google Scholar] [CrossRef]
- Mokhtari, A.; Noory, H.; Vazifedoust, M.; Bahrami, M. Estimating net irrigation requirement of winter wheat using model- and satellite-based single and basal crop coefficients. Agric. Water Manag. 2018, 208, 95–106. [Google Scholar] [CrossRef]
- Spiliotopoulos, M.; Loukas, A. Hybrid Methodology for the Estimation of Crop Coefficients Based on Satellite Imagery and Ground-Based Measurements. Water 2019, 11, 1364. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Han, W.T.; Niu, X.T.; Li, G. Maize Crop Coefficient Estimated from UAV-Measured Multispectral Vegetation Indices. Sensors 2019, 19, 5250. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.L.; Gu, N.; Lu, H.S.; Hu, Y.S.; Zhu, Y.H.; Yang, M. Calculation method of crop coefficient and evapotranspiration basedon temperature effect. J. Hydraul. Eng. 2019, 50, 242–251. [Google Scholar]
- Tang, J.D. Estimation Method of Maize Water Use Efficiency and Biomass Based on UAV Remote Sensing. Master’s Thesis, Northwest A F University, Xianyang, China, 2021. [Google Scholar]
- Kool, D.; Kustas, W.P.; Ben-Gal, A.; Agam, N. Energy partitioning between plant canopy and soil, performance of the two-source energy balance model in a vineyard. Agric. For. Meteorol. 2021, 300, 108328. [Google Scholar] [CrossRef]
- Paulino, S.E.P.; Mourao, F.D.A.; Maia, A.D.N.; Aviles, T.E.C.; Neto, D.D. Agrometeorological models for ‘valencia’ and ‘hamlin’ sweet oranges to estimate the number of fruits per plant. Sci. Agric. 2007, 64, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Ju, Q.; Liu, X.N.; Liu, Z.T.; Gao, H.B.; Zhao, W.J.; Nimazhaxi; Hao, W.L. Response and prediction of groundwater depth change to climate change in Huaibei Plain. Trans. Chin. Soc. Agric. Eng. 2022, 38, 136–145. [Google Scholar]
- Zhu, Y.H.; Ren, L.L.; Horton, R.; Lu, H.S.; Wang, Z.L.; Yuan, F. Estimating the Contribution of Groundwater to the Root Zone of Winter Wheat Using Root Density Distribution Functions. Vadose Zone J. 2018, 17, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.Z.; Peng, S.Z.; Ding, J.L.; Wei, Q.; Yu, Y.M. Evaluation and calibration of simple methods for daily reference evapotranspiration estimation in humid East China. Arch. Agron. Soil Sci. 2013, 59, 845–858. [Google Scholar] [CrossRef]
- Huang, C.P.; Zhang, F.; Wang, A.H.; Hu, B.M.; Yang, J.H. Dynamic simulation of potato growth process. J. Appl. Ecol. 2004, 15, 1203–1206. [Google Scholar]
- Qureshi, Z.A.; Neibling, H. Response of two-row malting spring barley to water cutoff under sprinkler irrigation. Agric. Water Manag. 2009, 96, 141–148. [Google Scholar] [CrossRef]
- Rosa, H.T.; Walter, L.C.; Streck, N.A.; Alberto, C.M. Thermal time methods and sowing dates in phyllochron determination in wheat cultivars. Pesqui. Agropecuária Bras. 2009, 44, 1374–1382. [Google Scholar] [CrossRef]
- Wechsung, F.; Ritter, M.; Wall, G.W. The upper homeostatic range for the temperature–yield response of irrigated us wheat down revised from a theoretical and experimental perspective. Agric. For. Meteorol. 2021, 307, 108478. [Google Scholar] [CrossRef]
- Porter, J.R.; Gawith, M. Temperatures and the growth and development of wheat: A review. Eur. J. Agron. 1999, 10, 23–36. [Google Scholar] [CrossRef]
- Qi, S.H.; Wang, B.J.; Wu, Z.S. The relationship between agricultural production and temperature. J. Henan Inst. Sci. Technol. (Nat. Sci. Ed.) 2007, 35, 20–23. [Google Scholar]
- Su, L.J.; Wang, Q.J.; Bai, Y.G. An analysis of yearly trends in growing degree days and the relationship between growing degree day values and reference evapotranspiration in Turpan area, China. Theor. Appl. Climatol. 2013, 113, 711–724. [Google Scholar] [CrossRef]
- Lewis, C.S.; Allen, L.N. Potential crop evapotranspiration and surface evaporation estimates via a gridded weather forcing dataset. J. Hydrol. 2017, 546, 450–463. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Mao, X.M.; Shukla, M.K.; Tian, F.; Hou, M.J.; Zhang, T.; Li, S.E. How does film mulching modify available energy, evapotranspiration, and crop coefficient during the seed–maize growing season in northwest china? Agric. Water Manag. 2021, 245, 106666. [Google Scholar] [CrossRef]
- Weerasinghe, G.; Chi, H.M.; Cao, Y.Z. Particle Swarm Optimization Simulation via Optimal Halton Sequences. Procedia Comput. Sci. 2016, 80, 772–781. [Google Scholar] [CrossRef] [Green Version]
- Benuwa, B.B.; Ghansah, B.; Wornyo, D.K.; Adabunu, S.A. A Comprehensive Review of Particle Swarm Optimization. Int. J. Eng. Res. Afr. 2016, 23, 141–161. [Google Scholar] [CrossRef]
- Du, X.B.; Wang, Z.; Xi, M.; Wu, W.G.; Wei, Z.; Xu, Y.Z.; Zhou, Y.J.; Lei, W.X.; Kong, L.C. A novel planting pattern increases the grain yield of wheat after rice cultivation by improving radiation resource utilization. Agric. For. Meteorol. 2021, 310, 108625. [Google Scholar] [CrossRef]
- Li, Y.X.; Liu, H.J.; Ma, J.C.; Zhang, L.X. Estimation of leaf area index for winter wheat at early stages based on convolutional neural networks. Comput. Electron. Agric. 2021, 190, 106480. [Google Scholar] [CrossRef]
| Stage of Growth | Emergence-Branching | Branch-Overwintering | Greening-Jointing | Heading-Maturity |
|---|---|---|---|---|
| Date | 2018/11/11–2018/12/1 | 2018/12/2–2019/2/21 | 2019/2/22–2019/4/19 | 2019/4/20–2019/6/4 |
| Number of days | 21 | 82 | 57 | 46 |
| ET0 at this stage | 21.80 mm | 67.80 mm | 216.48 mm | 220.67 mm |
| Proportion of total ET0 | 4.14% | 12.87% | 41.10% | 41.89% |
| Average daily ET0 | 1.04 mm | 0.83 mm | 3.80 mm | 4.80 mm |
| Method | Temperature Effect | Cumulative Crop Coefficient | Radiative Soil Temperature | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | |||||||||
| Emergence-branching stage | 1.24 | 3.00 | 18.84 | 158.62 | −7.17 | 0.07 | 6.54 | 4.19 | 5.87 |
| Branch-overwintering stage | 1.96 | 3.00 | 12.42 | 216.22 | −79.90 | 0.01 | 60.00 | 0.26 | 3.21 |
| Greening-jointing stage | 2.14 | 20.95 | 6.61 | 180.23 | −382.33 | −0.01 | 26.25 | 0.41 | 5.62 |
| Heading-maturity stage | 2.39 | 20.37 | 5.16 | 227.91 | 0.02 | −0.05 | 43.52 | 6.16 | 8.81 |
| Stage | Emergence-Branching Stage | Branch-Overwintering Stage | Greening-Jointing Stage | Heading-Maturity Stage | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | RMSE | MAE | r | dIA | RMSE | MAE | r | dIA | RMSE | MAE | r | dIA | RMSE | MAE | r | dIA |
| TE | 0.06 | 0.06 | 0.80 | 0.88 | 0.13 | 0.11 | 0.44 | 0.55 | 0.23 | 0.18 | 0.70 | 0.83 | 0.16 | 0.13 | 0.94 | 0.97 |
| CCC | 0.08 | 0.07 | 0.57 | 0.69 | 0.13 | 0.12 | 0.36 | 0.51 | 0.16 | 0.13 | 0.88 | 0.89 | 0.20 | 0.16 | 0.91 | 0.94 |
| RST | 0.20 | 0.19 | 0.35 | 0.51 | 0.25 | 0.22 | 0.52 | 0.61 | 0.93 | 0.79 | 0.70 | 0.49 | 1.10 | 0.91 | 0.43 | 0.49 |
| Method | Root Mean Square Error | Mean Absolute Error | Correlation Coefficient | Consistency Index |
|---|---|---|---|---|
| TE | 0.34 | 0.25 | 0.87 | 0.93 |
| CCC | 0.25 | 0.20 | 0.93 | 0.96 |
| RST | 0.79 | 0.58 | 0.50 | 0.69 |
| The best | 0.13 | 0.09 | 0.98 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, J.; Wang, Y.; Jiang, P.; Ju, Q.; Zhou, C.; Lu, Y.; Gao, P.; Sun, B. Evaluation of Different Methods on the Estimation of the Daily Crop Coefficient of Winter Wheat. Water 2023, 15, 1395. https://doi.org/10.3390/w15071395
Fang J, Wang Y, Jiang P, Ju Q, Zhou C, Lu Y, Gao P, Sun B. Evaluation of Different Methods on the Estimation of the Daily Crop Coefficient of Winter Wheat. Water. 2023; 15(7):1395. https://doi.org/10.3390/w15071395
Chicago/Turabian StyleFang, Jingjing, Yining Wang, Peng Jiang, Qin Ju, Chao Zhou, Yiran Lu, Pei Gao, and Bo Sun. 2023. "Evaluation of Different Methods on the Estimation of the Daily Crop Coefficient of Winter Wheat" Water 15, no. 7: 1395. https://doi.org/10.3390/w15071395










