Understanding the Planform Complexity and Morphodynamic Properties of Brahmaputra River in Bangladesh: Protection and Exploitation of Riparian Areas
Abstract
:1. Introduction
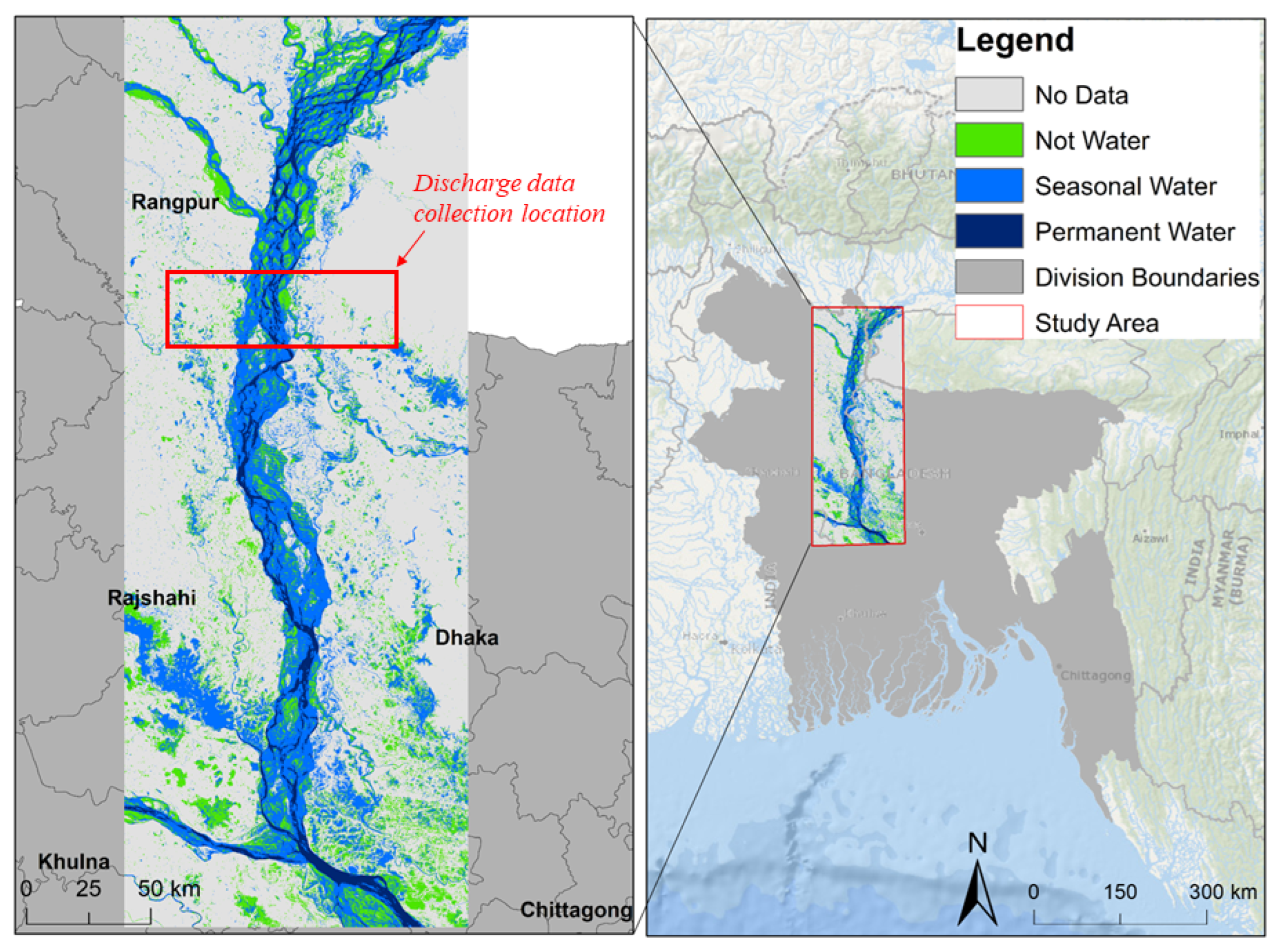
2. Study Area
3. Methods
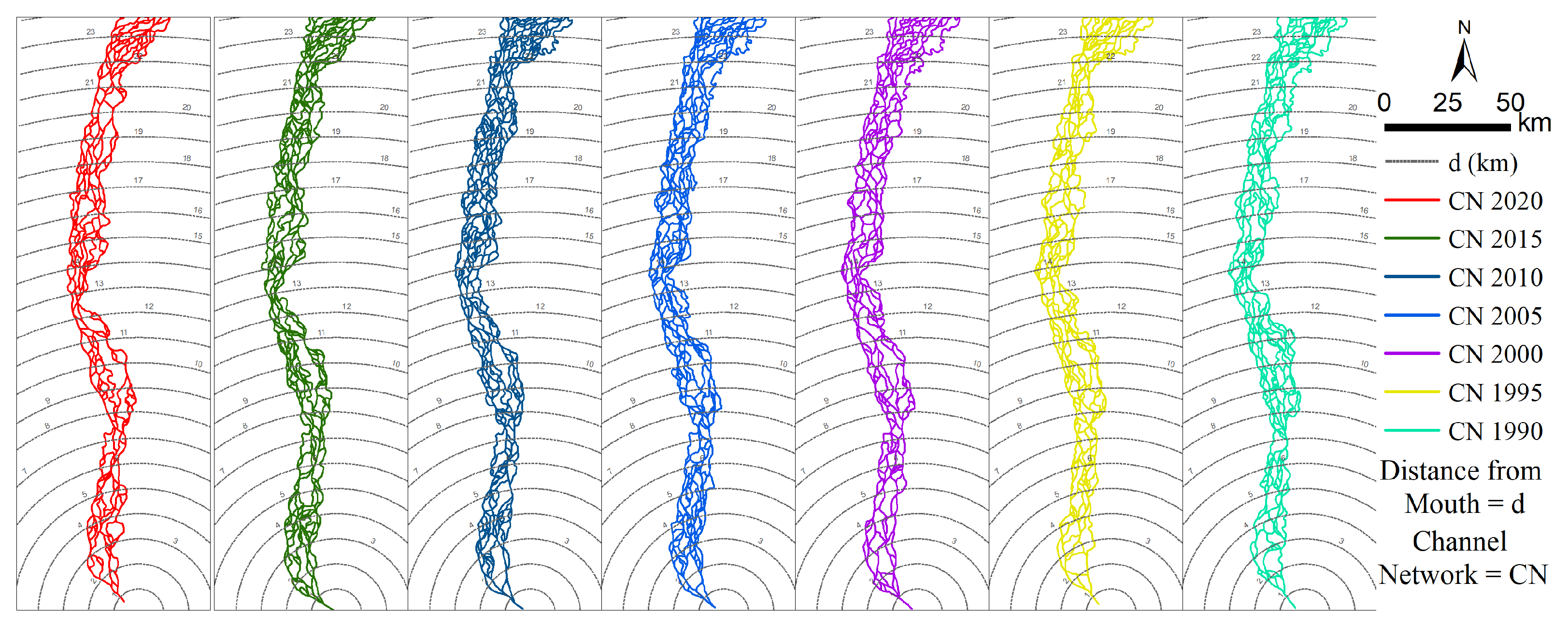
3.1. The Anastomosing River Principle
3.2. Channel Network Delineation
3.3. Anastomosing Function
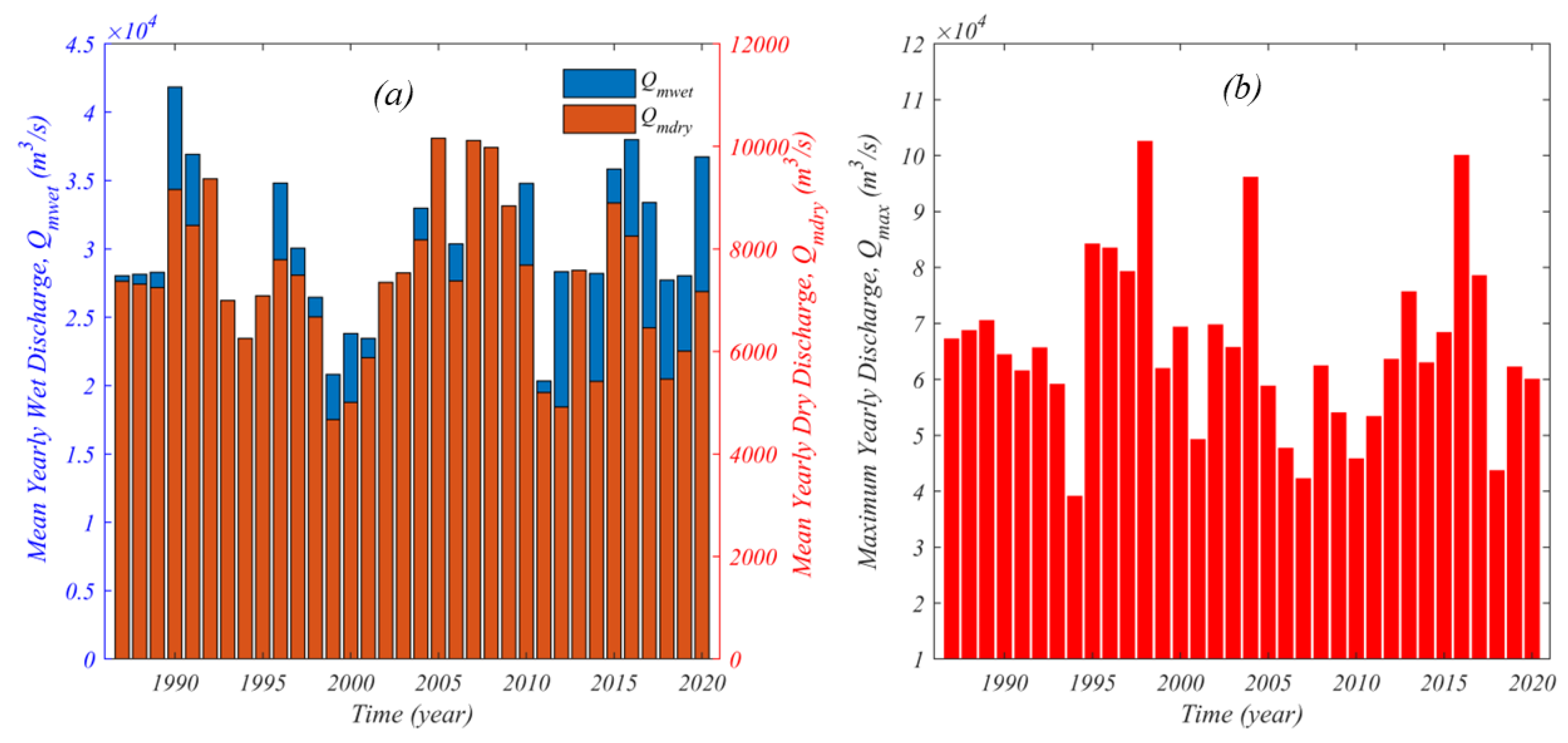
3.4. Discharge Data
3.5. Entropy
3.5.1. Approximate Entropy
3.5.2. Sample Entropy
3.6. Power Spectral Density
4. Results and Discussion
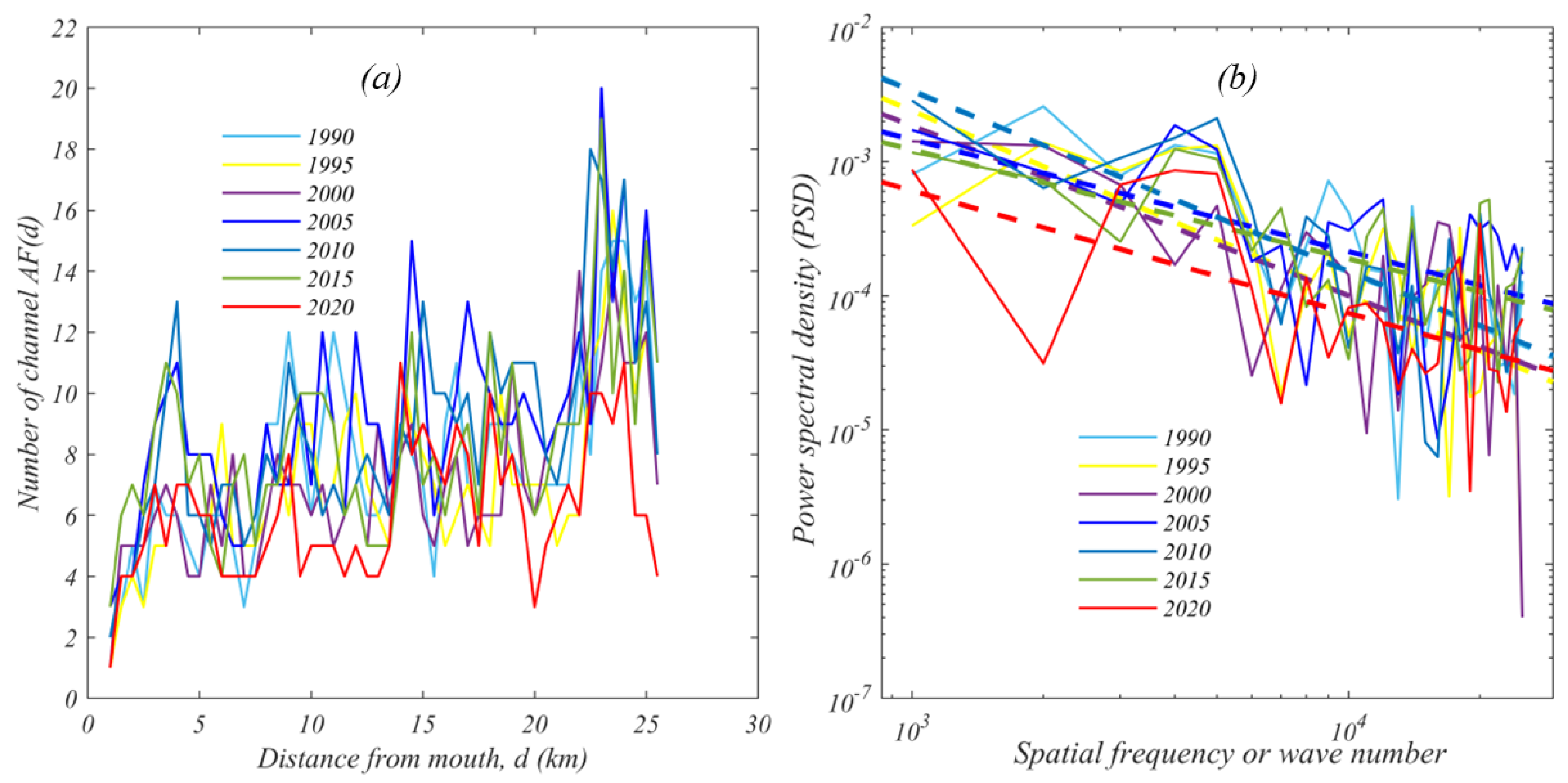
4.1. Extracted AF and Corresponding PSD of the Brahmaputra River’s Planform
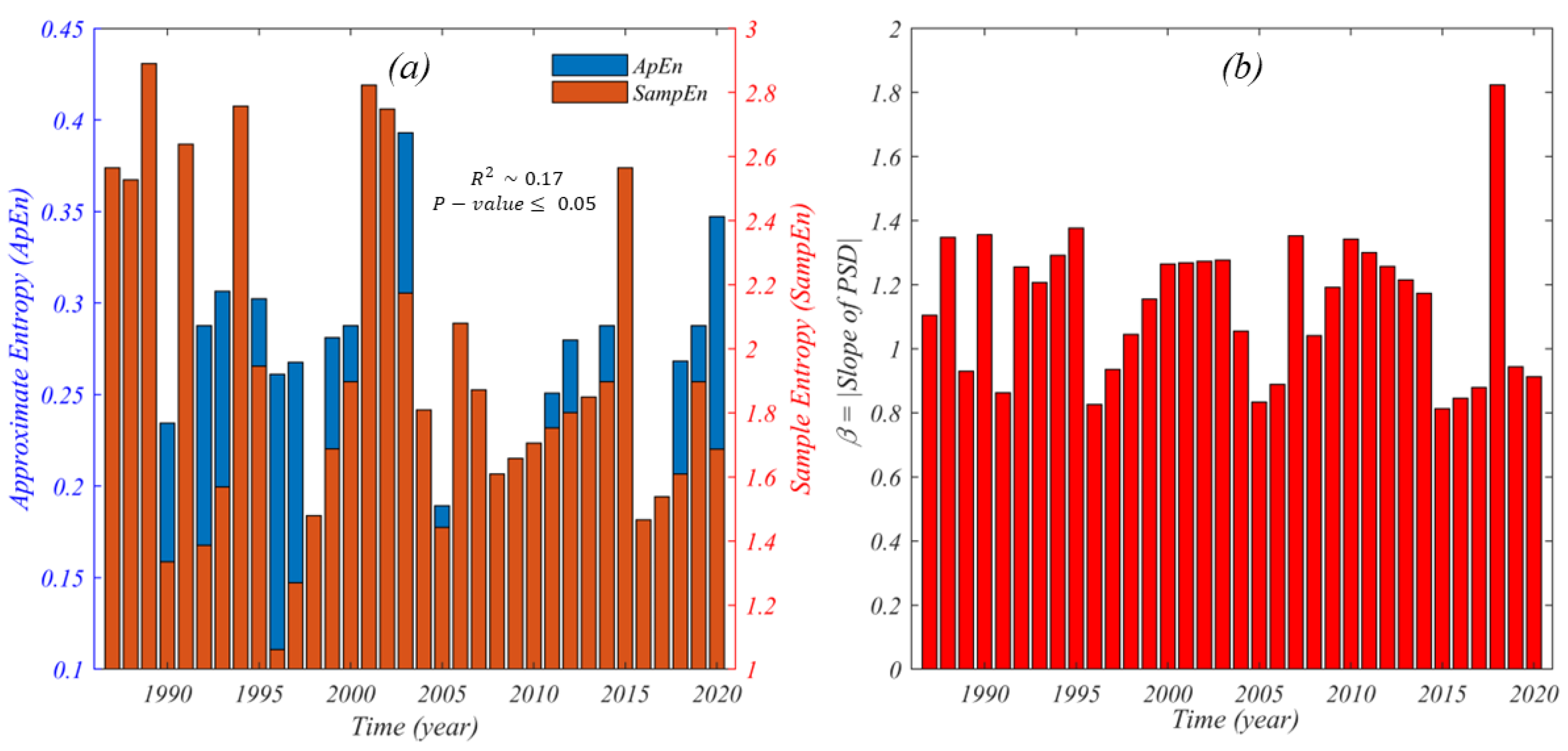
4.2. Disorder, Complexity and Fluctuation of the Brahmaputra River’s Planform
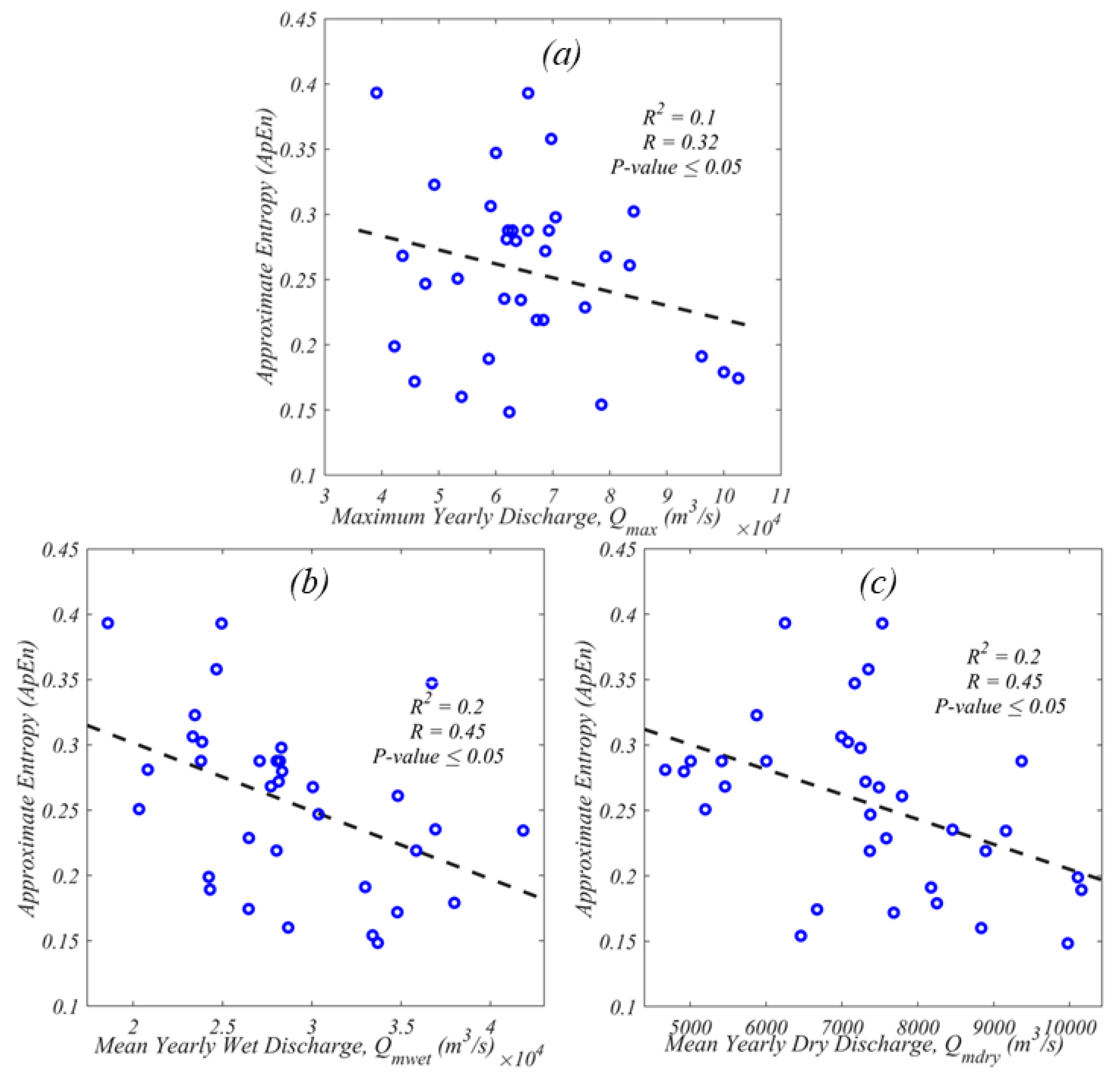
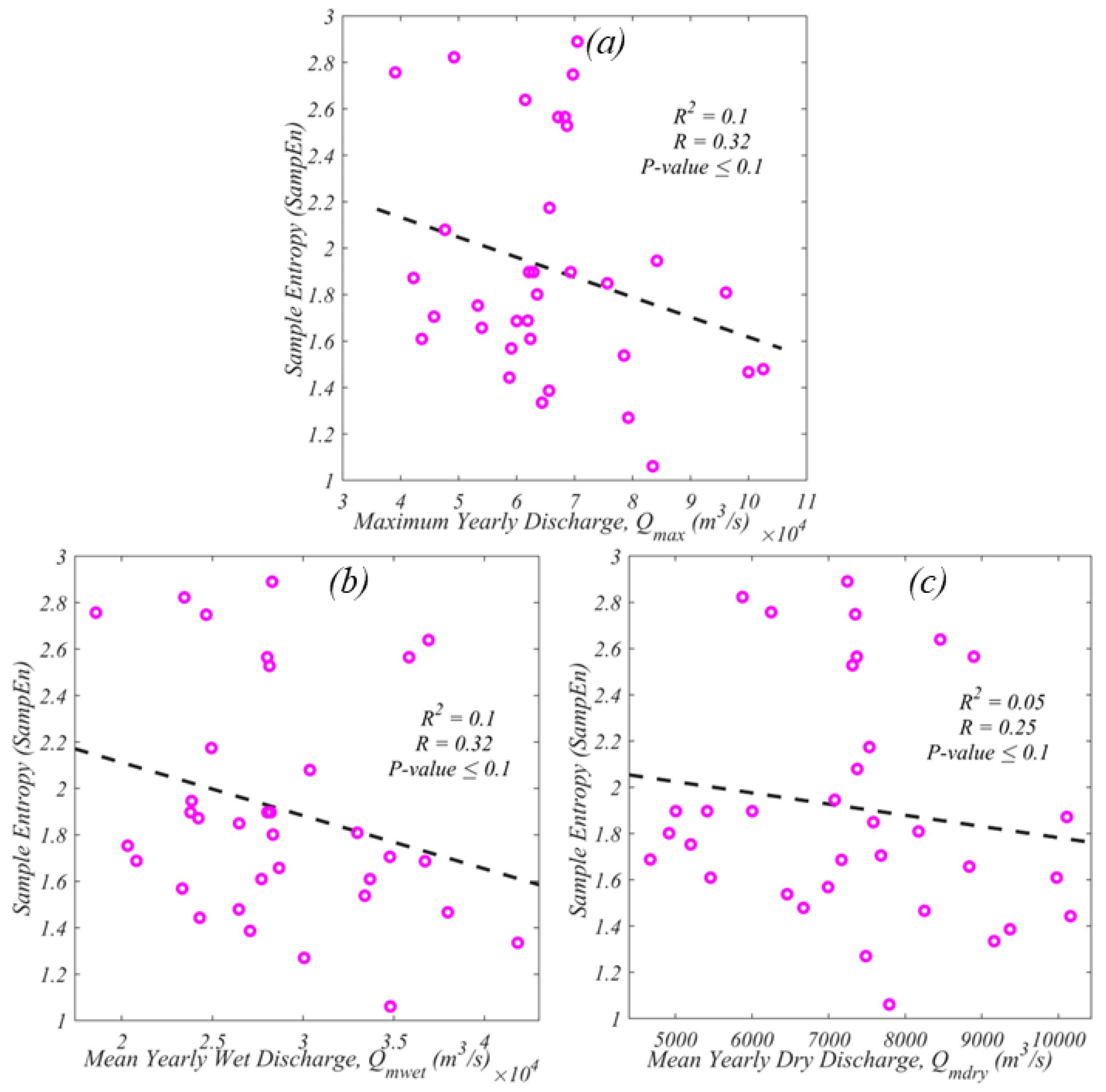
4.3. Association between River Discharge and Disorder, Complexity, and Fluctuation
5. Potential Implications towards Morphological Contexts
6. Conclusions
- The generated and investigated is capable of accurately transforming a two-dimensional complex network into a one-dimensional spatial signal.
- The Approximate Entropy () and Sample Entropy () can be used to quantify the disorder and complexity of river’s planforms, respectively, which confirms the reproducibility of the physical features of the river.
- Dynamic imprints, such as yearly maximum discharge (), have significant contributions to the river’s planform complexity.
- also showed a significant and consistent contribution to the Brahmaputra River’s planform fluctuation.
7. Limitations and Recommendations
Author Contributions
Funding
Conflicts of Interest
References
- Leopold, L.B.; Wolman, M.G. River Channel Patterns: Braided, Meandering, and Straight; US Government Printing Office: Washington, DC, USA, 1957.
- Charlton, R. Fundamentals of Fluvial Geomorphology; Routledge: London, UK; New York, NY, USA, 2007. [Google Scholar]
- Makaske, B. Anastomosing rivers: A review of their classification, origin and sedimentary products. Earth-Sci. Rev. 2001, 53, 149–196. [Google Scholar] [CrossRef]
- Sarker, S. Investigating Topologic and Geometric Properties of Synthetic and Natural River Networks under Changing Climate; University of Central Florida: Orlando, FL, USA, 2021. [Google Scholar]
- Sarker, S. Understanding the Complexity and Dynamics of Anastomosing River Planform: A Case Study of Brahmaputra River in Bangladesh. Earth Space Sci. Open Arch. 2021, 1. [Google Scholar] [CrossRef]
- Sarker, S.; Veremyev, A.; Boginski, V.; Singh, A. Critical nodes in river networks. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khan, I.; Ahammad, M.; Sarker, S. A study on River Bank Erosion of Jamuna River using GIS and Remote Sensing Technology. Int. J. Eng. Develop. Res. 2014, 2, 3365–3371. [Google Scholar]
- Gao, Y.; Sarker, S.; Sarker, T.; Leta, O.T. Analyzing the critical locations in response of constructed and planned dams on the Mekong River Basin for environmental integrity. Environ. Res. Commun. 2022, 4, 101001. [Google Scholar] [CrossRef]
- Bridge, J.S. The interaction between channel geometry, water flow, sediment transport and deposition in braided rivers. Geol. Soc. 1993, 75, 13–71. [Google Scholar] [CrossRef]
- Ferguson, R. Understanding braiding processes in gravel-bed rivers: Progress and unsolved problems. Geol. Soc. 1993, 75, 73–87. [Google Scholar] [CrossRef]
- Klaassen, G.J.; Mosselman, E.; Bruehl, H. On the Prediction of Planform Changes in Braided Sand-nd-Ed Rivers; Delft Hydraulics: Delft, The Netherlands, 1993. [Google Scholar]
- Pradhan, C.; Chembolu, V.; Bharti, R.; Dutta, S. Regulated rivers in India: Research progress and future directions. ISH J. Hydraul. Eng. 2021, 1–13. [Google Scholar] [CrossRef]
- Ashmore, P.E. Laboratory modelling of gravel braided stream morphology. Earth Surf. Process. Land. 1982, 7, 201–225. [Google Scholar] [CrossRef]
- Ashmore, P.E. How do gravel-bed rivers braid? Can. J. Earth Sci. 1991, 28, 326–341. [Google Scholar] [CrossRef] [Green Version]
- Ashmore, P. Anabranch confluence kinetics and sedimentation processes in gravel-braided streams. Geol. Soc. 1993, 75, 129–146. [Google Scholar] [CrossRef]
- Young, W.; Davies, T. Bedload transport processes in a braided gravel-bed river model. Earth Surf. Process. Land. 1991, 16, 499–511. [Google Scholar] [CrossRef]
- Murray, A.B.; Paola, C. A cellular model of braided rivers. Nature 1994, 371, 54–57. [Google Scholar] [CrossRef]
- Murray, A.B.; Paola, C. Properties of a cellular braided-stream model. Earth Surf. Process. Land. 1997, 22, 1001–1025. [Google Scholar] [CrossRef]
- Nykanen, D.K.; Foufoula-Georgiou, E.; Sapozhnikov, V.B. Study of spatial scaling in braided river patterns using synthetic aperture radar imagery. Water Resour. Res. 1998, 34, 1795–1807. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, C.; Bharti, R.; Dutta, S. Assessment of post-impoundment geomorphic variations along Brahmani River using remote sensing. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5598–5601. [Google Scholar]
- Pradhan, C.; Chembolu, V.; Dutta, S. Impact of river interventions on alluvial channel morphology. ISH J. Hydraul. Eng. 2019, 25, 87–93. [Google Scholar] [CrossRef]
- Sapozhnikov, V.B.; Foufoula-Georgiou, E. Do the current landscape evolution models show self-organized criticality? Water Resour. Res. 1996, 32, 1109–1112. [Google Scholar] [CrossRef]
- Sapozhnikov, V.B.; Foufoula-Georgiou, E. Experimental evidence of dynamic scaling and indications of self-organized criticality in braided rivers. Water Resour. Res. 1997, 33, 1983–1991. [Google Scholar] [CrossRef] [Green Version]
- Walsh, J.; Hicks, D.M. Braided channels: Self-similar or self-affine? Water Resour. Res. 2002, 38, 1–6. [Google Scholar] [CrossRef]
- Lane, S.N.; Westaway, R.M.; Murray Hicks, D. Estimation of erosion and deposition volumes in a large, gravel-bed, braided river using synoptic remote sensing. Earth Surf. Process. Land. 2003, 28, 249–271. [Google Scholar] [CrossRef]
- Westaway, R.; Lane, S.; Hicks, D. The development of an automated correction procedure for digital photogrammetry for the study of wide, shallow, gravel-bed rivers. Earth Surf. Process. Land. 2000, 25, 209–226. [Google Scholar] [CrossRef]
- Westaway, R.M.; Lane, S.N.; Hicks, D.M. Remote sensing of clear-water, shallow, gravel-bed rivers using digital photogrammetry. Photogramm. Eng. Remote Sens. 2001, 67, 1271–1282. [Google Scholar]
- Westaway, R.M.; Lane, S.; Hicks, D. Remote survey of large-scale braided, gravel-bed rivers using digital photogrammetry and image analysis. Int. J. Remote Sens. 2003, 24, 795–815. [Google Scholar] [CrossRef]
- Coleman, J.M. Brahmaputra River: Channel processes and sedimentation. Sediment. Geol. 1969, 3, 129–239. [Google Scholar] [CrossRef]
- Mosselman, E.; Huisink, M.; Koomen, E.; Seijmonsbergen, A. Morphological Changes in a Large Braided Sand-Bed River; John Wiley & Sons: Chichester, UK, 1995. [Google Scholar]
- Thorne, C.R.; Russell, A.P.; Alam, M.K. Planform pattern and channel evolution of the Brahmaputra River, Bangladesh. Geol. Soc. 1993, 75, 257–276. [Google Scholar] [CrossRef]
- Goswami, D.C. Brahmaputra River, Assam, India: Physiography, basin denudation, and channel aggradation. Water Resour. Res. 1985, 21, 959–978. [Google Scholar] [CrossRef]
- Sarker, S. Essence of MIKE 21C (FDM Numerical Scheme): Application on the River Morphology of Bangladesh. Open J. Modell. Simul. 2022, 10, 88–117. [Google Scholar] [CrossRef]
- Chembolu, V.; Dutta, S. An entropy based morphological variability assessment of a large braided river. Earth Surf. Process. Land. 2018, 43, 2889–2896. [Google Scholar] [CrossRef]
- Dubey, A.K.; Chembolu, V.; Dutta, S. Utilization of satellite altimetry retrieved river roughness properties in hydraulic flow modelling of braided river system. Int. J. River Basin Manag. 2020, 20, 1–14. [Google Scholar] [CrossRef]
- Karmaker, T.; Medhi, H.; Dutta, S. Study of channel instability in the braided Brahmaputra river using satellite imagery. Curr. Sci. 2017, 112, 1533–1543. [Google Scholar] [CrossRef]
- Sarker, M.H.; Thorne, C.R.; Aktar, M.N.; Ferdous, M.R. Morpho-dynamics of the Brahmaputra–Jamuna river, Bangladesh. Geomorphology 2014, 215, 45–59. [Google Scholar] [CrossRef]
- Valdiya, K. Why does river Brahmaputra remain untamed? Curr. Sci. 1999, 76, 1301–1305. [Google Scholar]
- Dutta, S.; Medhi, H.; Karmaker, T.; Singh, Y.; Prabu, I.; Dutta, U. Probabilistic flood hazard mapping for embankment breaching. ISH J. Hydraul. Eng. 2010, 16, 15–25. [Google Scholar] [CrossRef]
- Nayak, P.; Panda, B. Brahmaputra and the Socio-Economic Life of People of Assam. The Mahabahu Brahmaputra; Flood and River Management Agency of Assam: Guwahati, India, 2016; pp. 77–85.
- Singh, V.; Sharma, N.; Ojha, C.S.P. The Brahmaputra Basin Water Resources; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004; Volume 47. [Google Scholar]
- Government of Assam, Water Resources. Brahmaputra River System. Available online: https://waterresources.assam.gov.in/portlet-innerpage/brahmaputra-river-system (accessed on 1 October 2021).
- Marra, W.A.; Kleinhans, M.G.; Addink, E.A. Network concepts to describe channel importance and change in multichannel systems: Test results for the Jamuna River, Bangladesh. Earth Surf. Process. Land. 2014, 39, 766–778. [Google Scholar] [CrossRef]
- Fischer, S.; Pietroń, J.; Bring, A.; Thorslund, J.; Jarsjö, J. Present to future sediment transport of the Brahmaputra River: Reducing uncertainty in predictions and management. Region. Env. Change 2017, 17, 515–526. [Google Scholar] [CrossRef] [Green Version]
- Sarker, T. Role of Climatic and Non-Climatic Factors on Land Use and Land Cover Change in the Arctic: A Comparative Analysis of Vorkuta and Salekhard. Ph.D. Thesis, The George Washington University, Washington, DC, USA, 2020. [Google Scholar]
- Ranjbar, S.; Hooshyar, M.; Singh, A.; Wang, D. Quantifying climatic controls on river network branching structure across scales. Water Resour. Res. 2018, 54, 7347–7360. [Google Scholar] [CrossRef]
- Lashermes, B.; Foufoula-Georgiou, E. Area and width functions of river networks: New results on multifractal properties. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Delgado-Bonal, A.; Marshak, A. Approximate entropy and sample entropy: A comprehensive tutorial. Entropy 2019, 21, 541. [Google Scholar] [CrossRef] [Green Version]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [Green Version]
- Sarker, S.; Sarker, T. Spectral Properties of Water Hammer Wave. Appl. Mech. 2022, 3, 799–814. [Google Scholar] [CrossRef]
- Pincus, S.; Kalman, R.E. Irregularity, volatility, risk, and financial market time series. Proc. Natl. Acad. Sci. USA 2004, 101, 13709–13714. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Delgado-Bonal, A.; Marshak, A.; Yang, Y.; Holdaway, D. Analyzing changes in the complexity of climate in the last four decades using MERRA-2 radiation data. Sci. Rep. 2020, 10, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Ranjbar, S.; Singh, A. Entropy and intermittency of river bed elevation fluctuations. J. Geophys. Res. Earth Surf. 2020, 125, e2019JF005499. [Google Scholar] [CrossRef]
- Sarker, S. A Story on the Wave Spectral Properties of Water Hammer. engrXiv 2021. [Google Scholar] [CrossRef]
- Stoica, P.; Moses, R.L. Spectral Analysis of Signals; Pearson and Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 13. [Google Scholar]
- Gardner, W.A.; Robinson, E.A. Statistical Spectral Analysis—A Nonprobabilistic Theory; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Pilgram, B.; Kaplan, D.T. A comparison of estimators for 1f noise. Phys. D Nonlin. Phen. 1998, 114, 108–122. [Google Scholar] [CrossRef]
- Sarker, S. A Short Review on Computational Hydraulics in the context of Water Resources Engineering. Open J. Modell. Simul. 2022, 10, 1–31. [Google Scholar] [CrossRef]
- Smith, D.G.; Smith, N.D. Sedimentation in anastomosed river systems; examples from alluvial valleys near Banff, Alberta. J. Sediment. Res. 1980, 50, 157–164. [Google Scholar] [CrossRef]
- David Knighton, A.; Nanson, G.C. Anastomosis and the continuum of channel pattern. Earth Surf. Process. Land. 1993, 18, 613–625. [Google Scholar] [CrossRef]
- Sarker, S. Fundamentals of Climatology for Engineers: Lecture Note. Eng 2022, 3, 573–595. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarker, S.; Sarker, T.; Leta, O.T.; Raihan, S.U.; Khan, I.; Ahmed, N. Understanding the Planform Complexity and Morphodynamic Properties of Brahmaputra River in Bangladesh: Protection and Exploitation of Riparian Areas. Water 2023, 15, 1384. https://doi.org/10.3390/w15071384
Sarker S, Sarker T, Leta OT, Raihan SU, Khan I, Ahmed N. Understanding the Planform Complexity and Morphodynamic Properties of Brahmaputra River in Bangladesh: Protection and Exploitation of Riparian Areas. Water. 2023; 15(7):1384. https://doi.org/10.3390/w15071384
Chicago/Turabian StyleSarker, Shiblu, Tanni Sarker, Olkeba Tolessa Leta, Sarder Udoy Raihan, Imran Khan, and Nur Ahmed. 2023. "Understanding the Planform Complexity and Morphodynamic Properties of Brahmaputra River in Bangladesh: Protection and Exploitation of Riparian Areas" Water 15, no. 7: 1384. https://doi.org/10.3390/w15071384
APA StyleSarker, S., Sarker, T., Leta, O. T., Raihan, S. U., Khan, I., & Ahmed, N. (2023). Understanding the Planform Complexity and Morphodynamic Properties of Brahmaputra River in Bangladesh: Protection and Exploitation of Riparian Areas. Water, 15(7), 1384. https://doi.org/10.3390/w15071384







