Theoretical Analysis of an Integrated, CPVT Membrane Distillation System for Cooling, Heating, Power and Seawater Desalination
Abstract
:1. Introduction
2. Materials and Methods
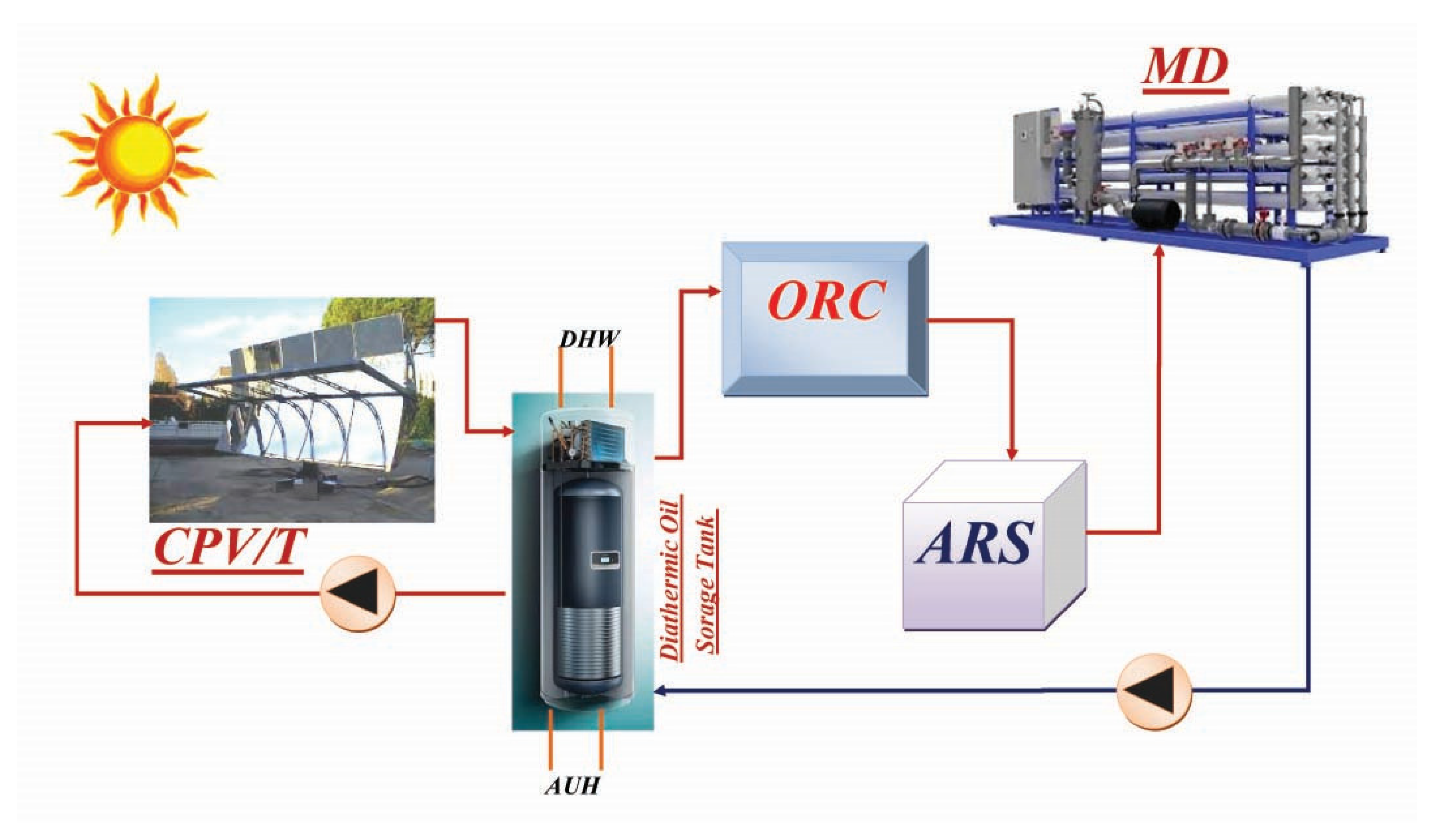
2.1. System Description
2.2. Governing Equations
2.2.1. Concentration Photovoltaic/Thermal
Energy Equations
Exergy Equations
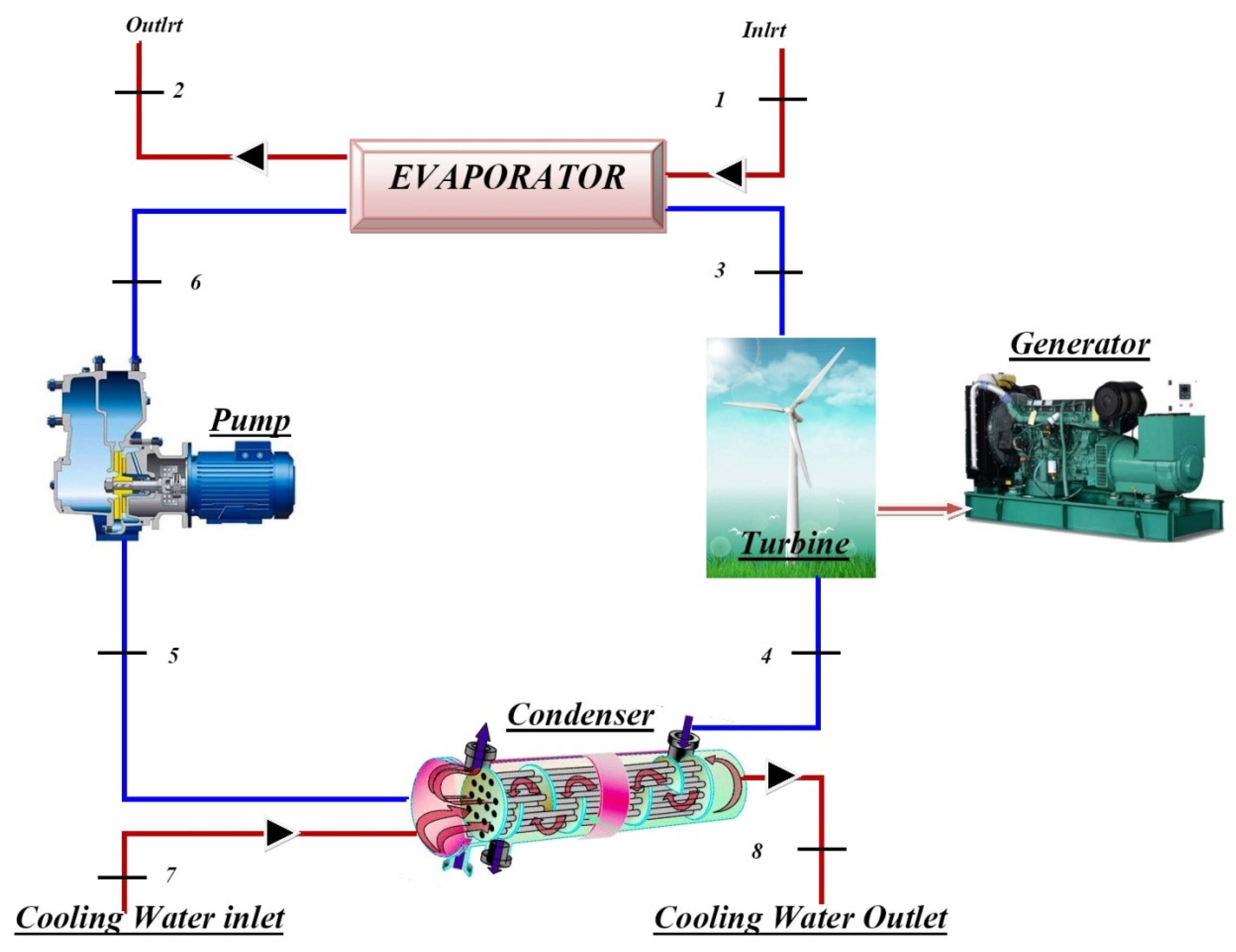
2.3. Rankine Cycle
Energy Equations
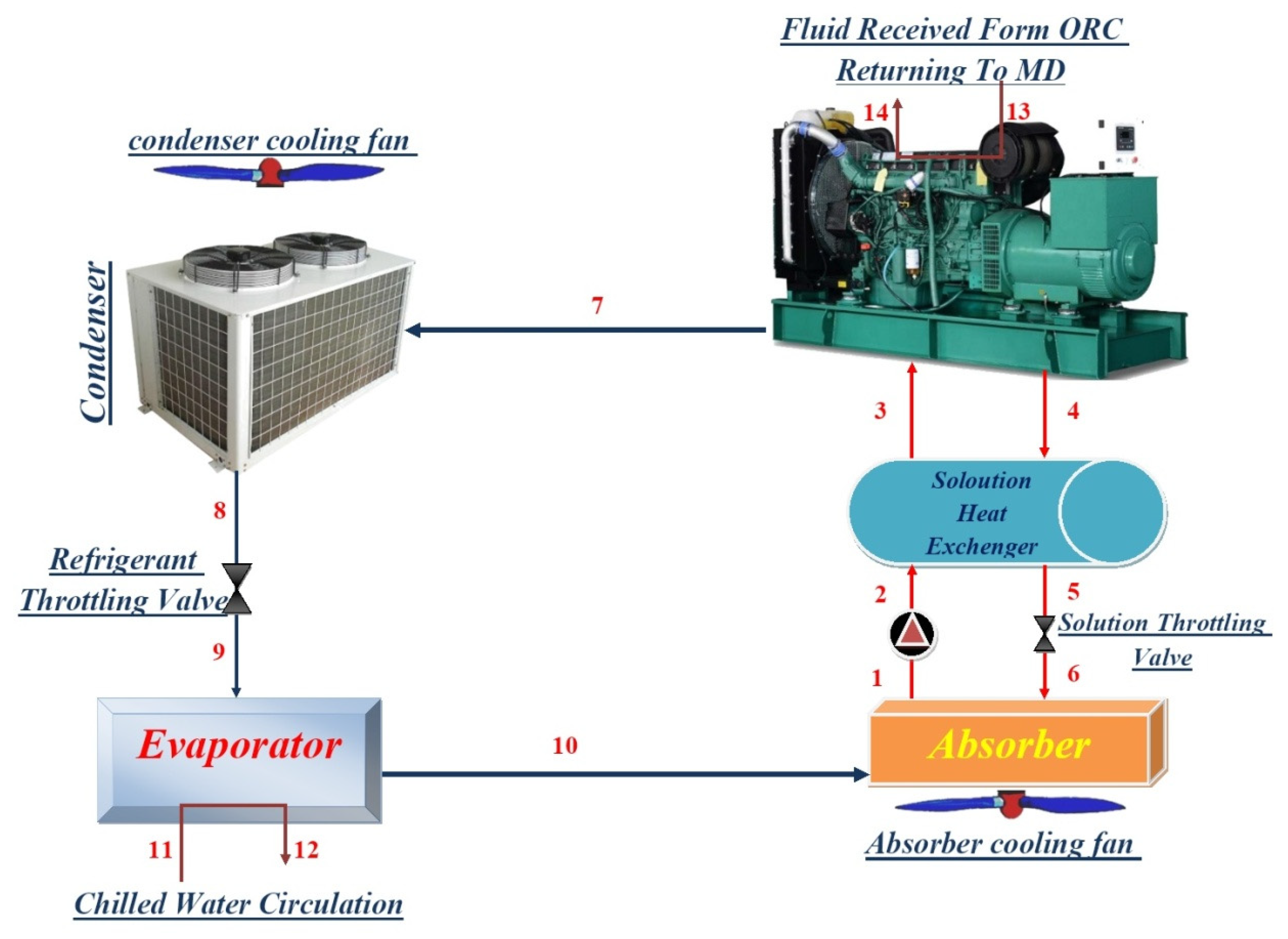
2.4. Absorption Cooling Cycle
2.4.1. Energy Equations
2.4.2. Exergy Equations
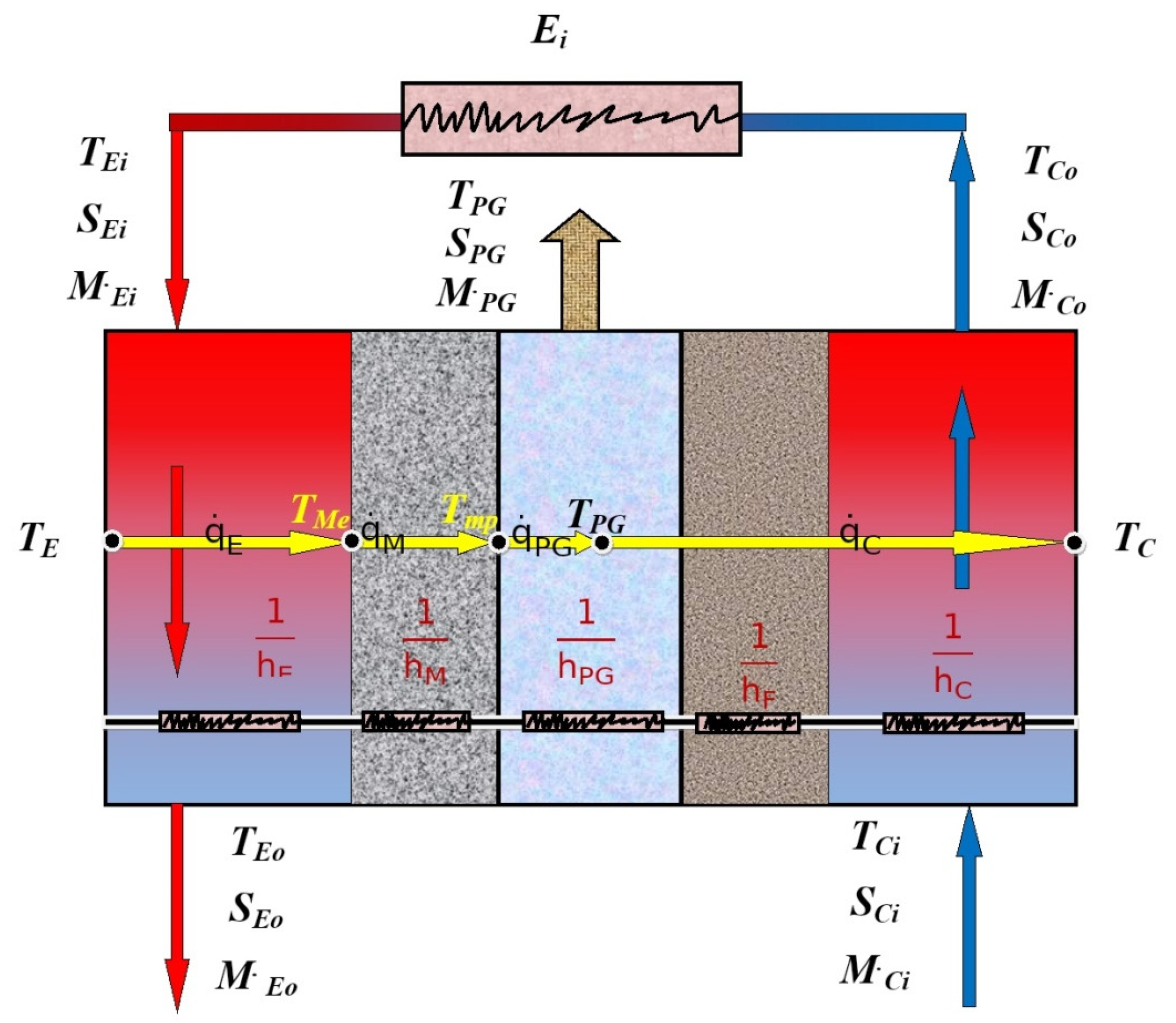
2.5. Distillation System
2.5.1. Energy Equations
2.5.2. Exergy Equations
3. Results
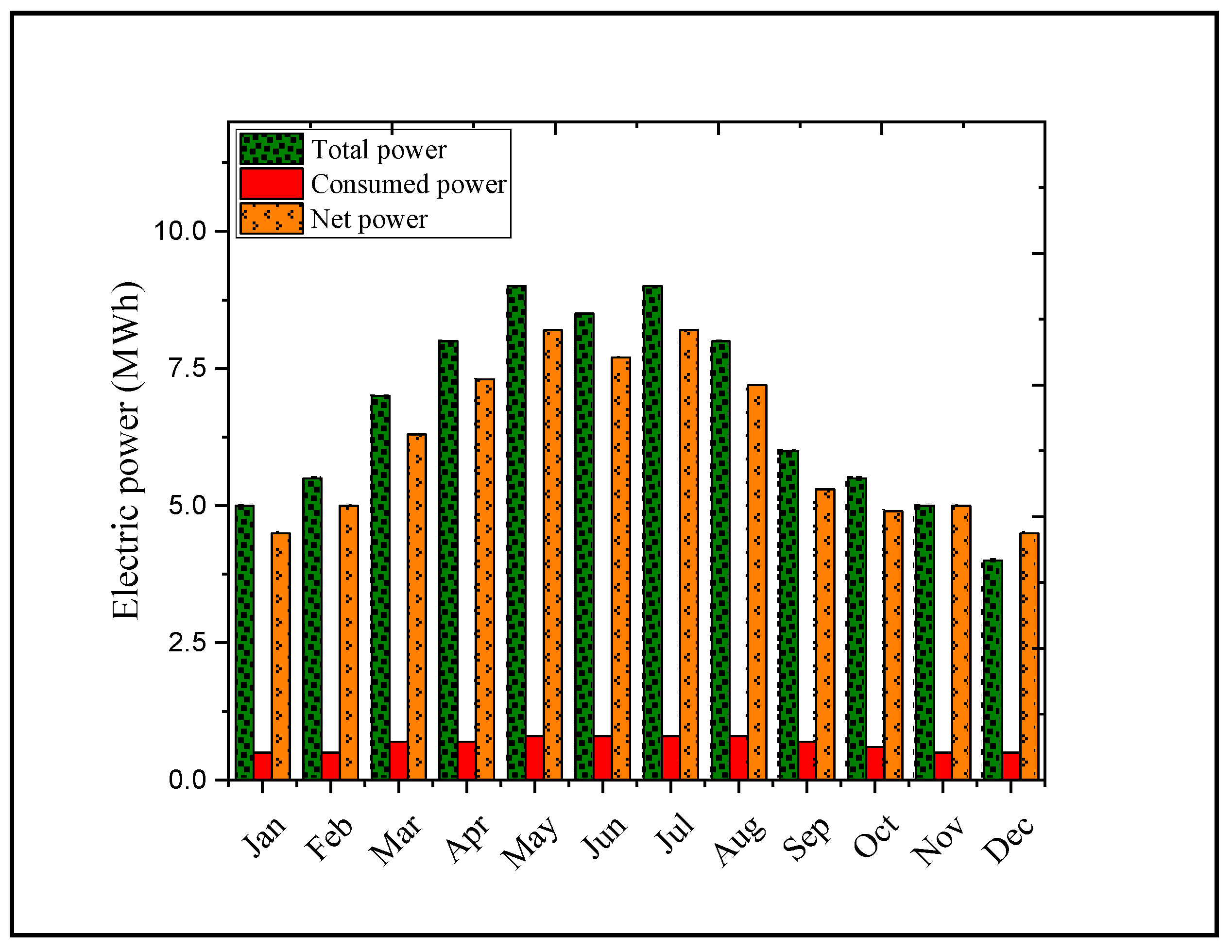
3.1. Concentration Photovoltaic/Thermal System
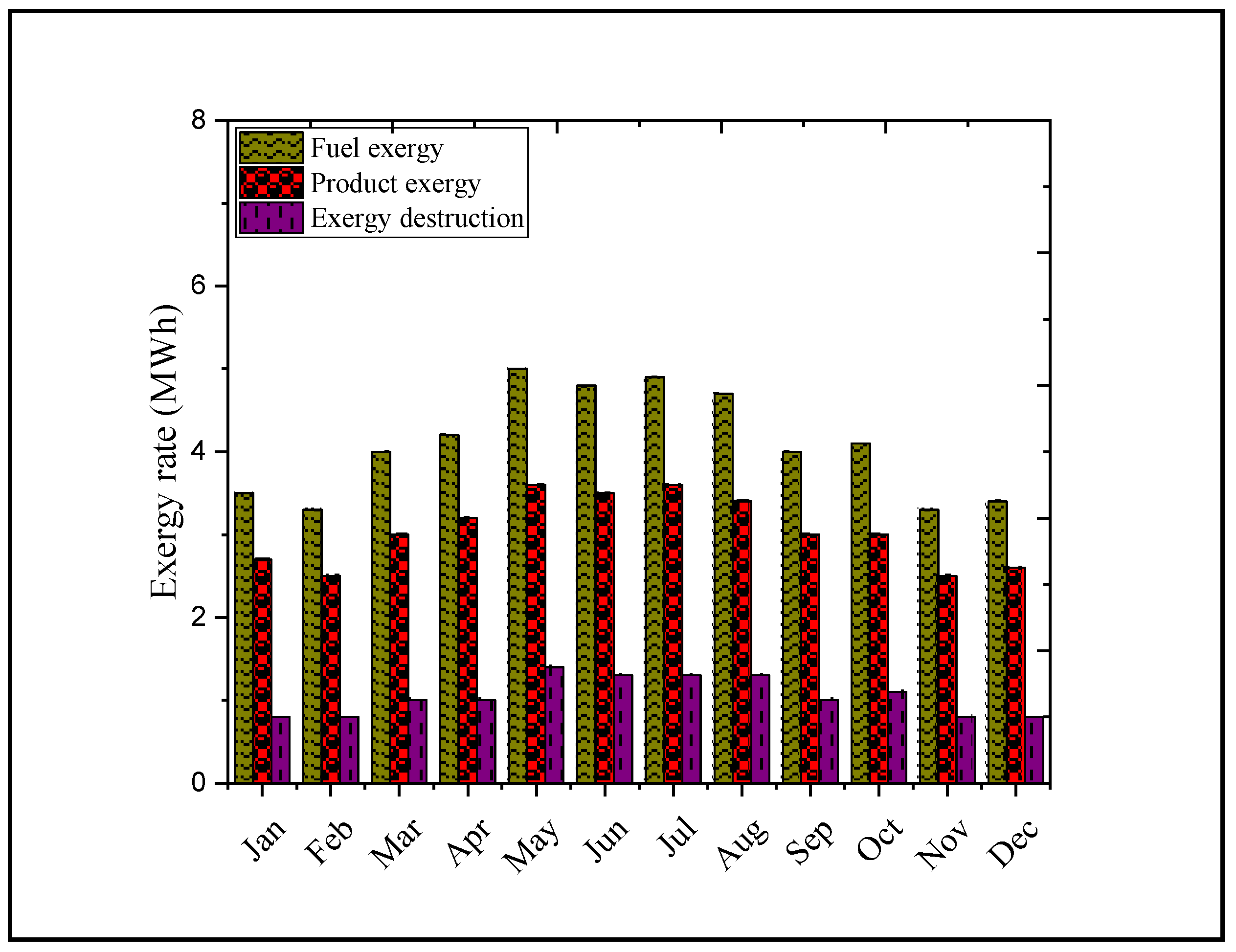
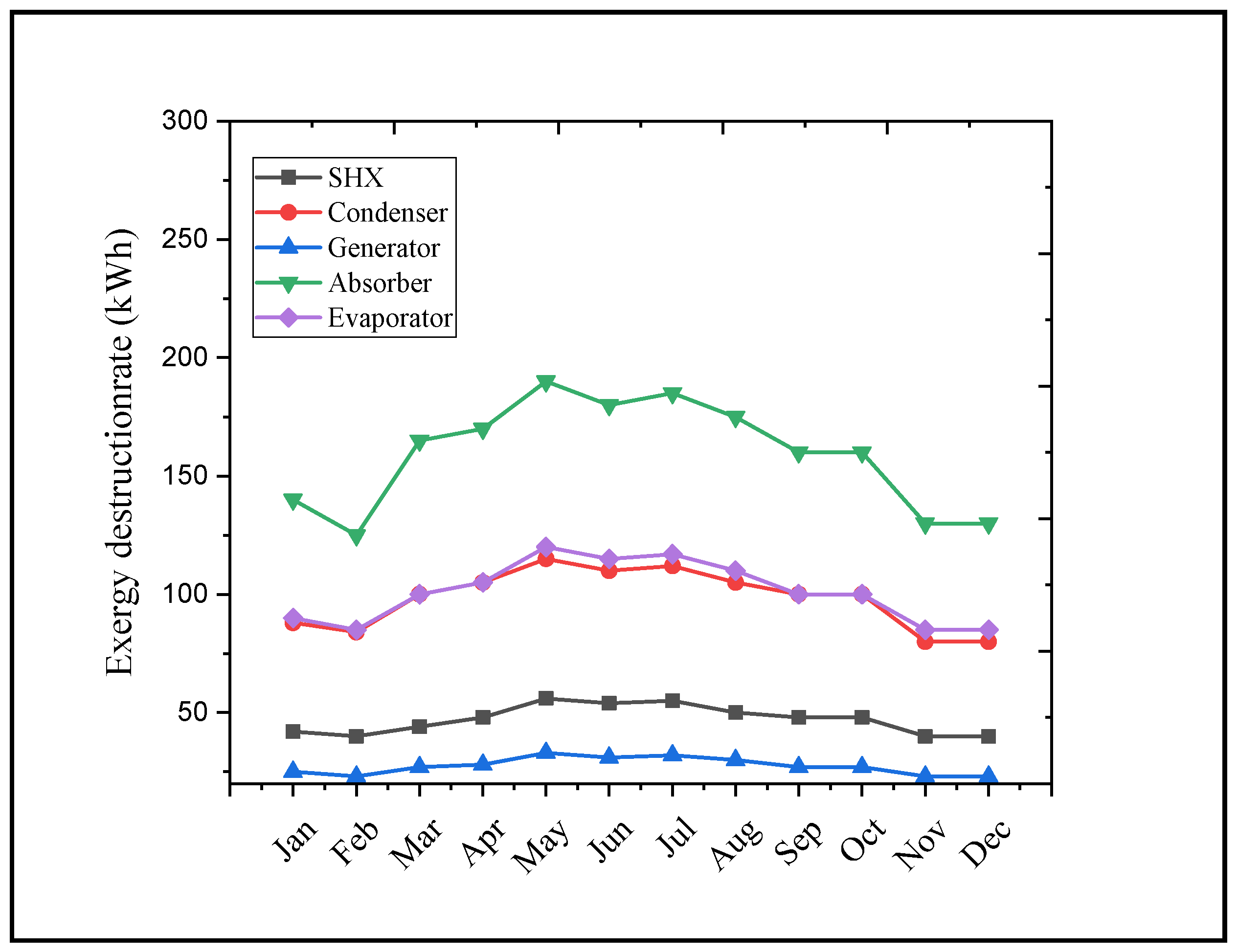
3.2. Organic Rankine Cycle
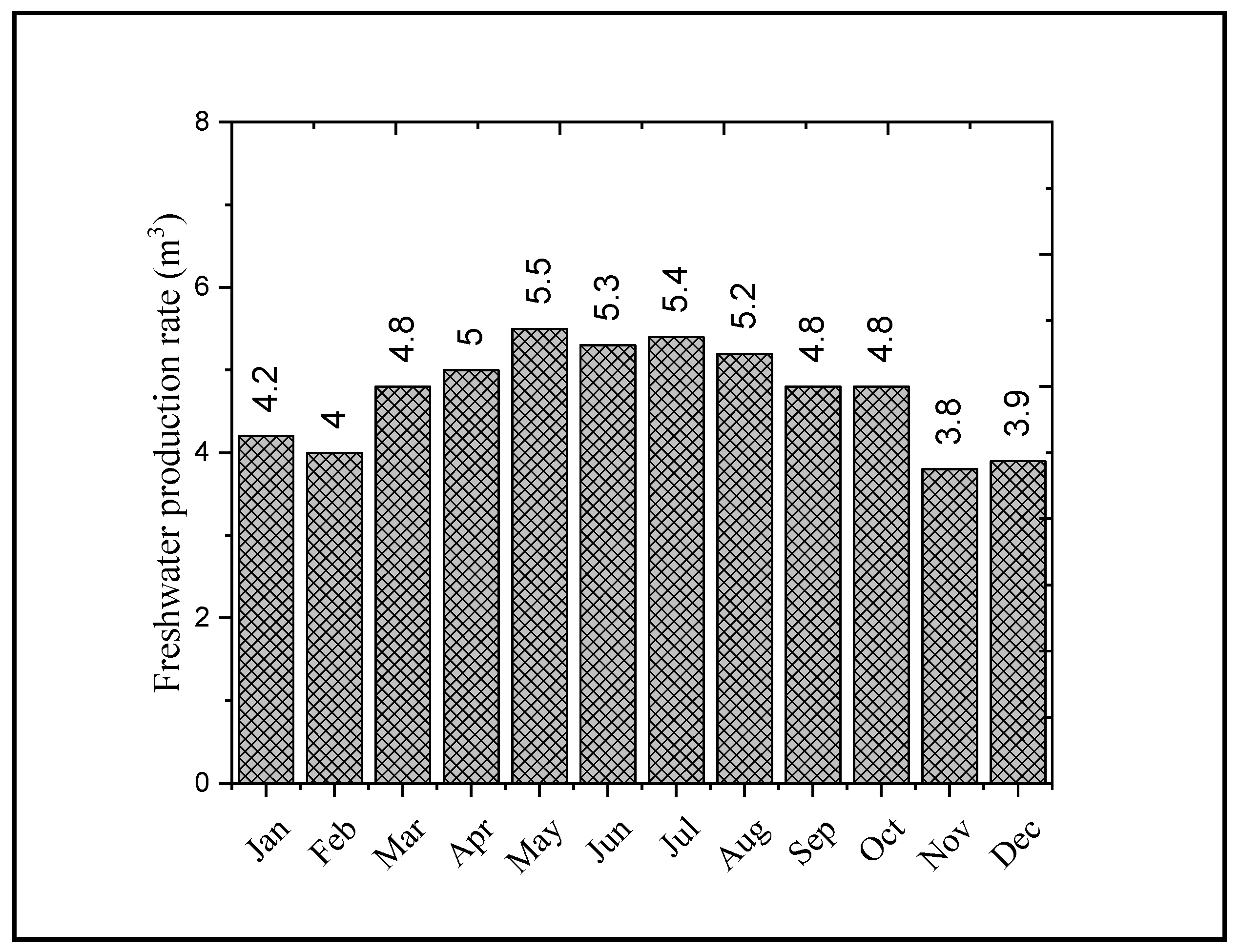
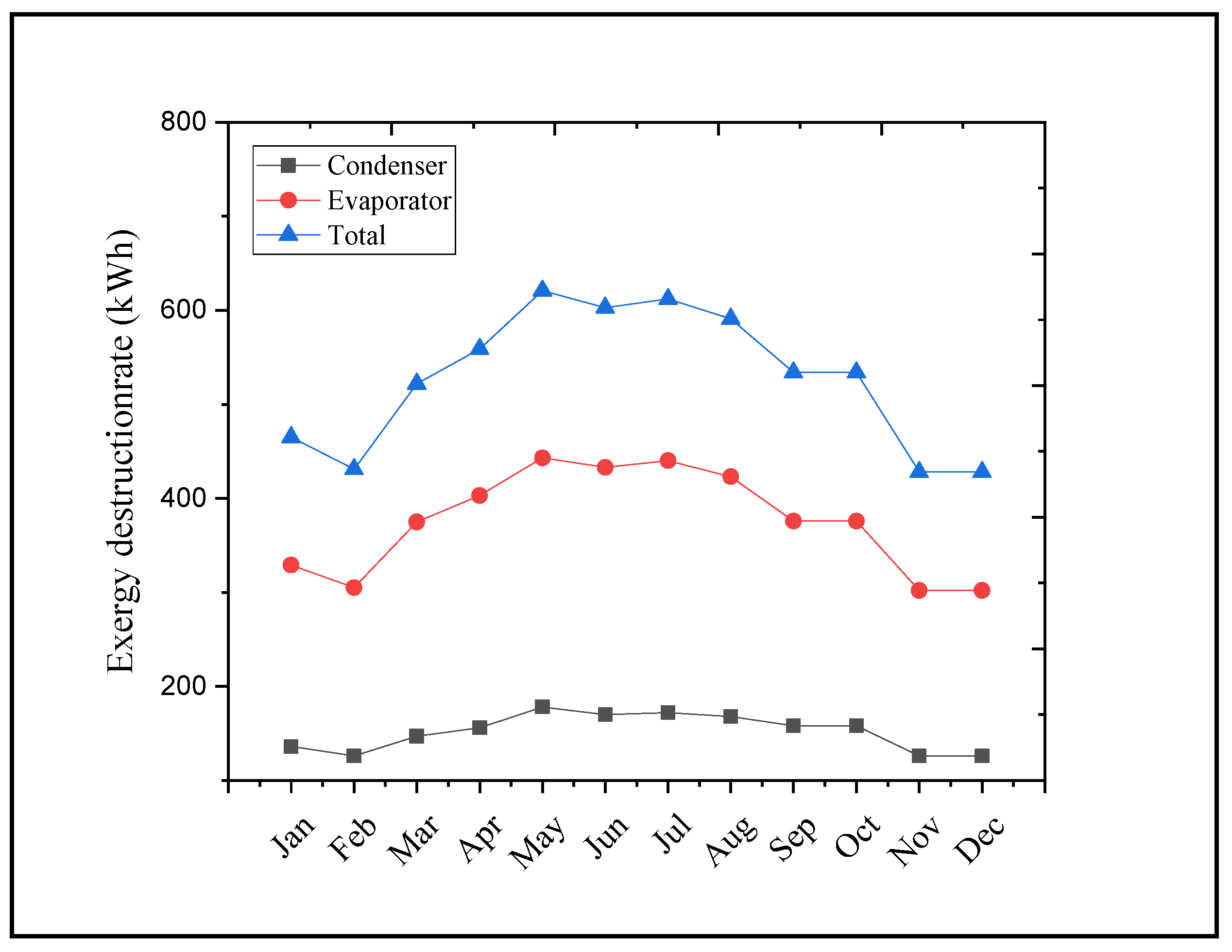
3.3. Desalination System
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Area (m2) |
| a | Temperature coefficient |
| C | Concentration ratio |
| EX | Exergy rate (kW) |
| e | Specific exergy |
| F | Fill factor |
| h | Specific enthalpy (kJ/kg) |
| IbT | Direct solar radiation (W/m2) |
| JP | Mass transfer rate |
| km | Conductivity coefficient |
| Mass flow rate (kg/s) | |
| n | Cells number |
| P | Power (kW) |
| Heat transfer rate (kW) | |
| s | Specific entropy (kJ/kg·K) |
| T | Temperature (°C) |
| Work (kW) | |
| X | Solution concentration ratio |
| Greek symbols | |
| δm | Membrane thickness |
| η | Thermal efficiency (%) |
| ψ | Exergy efficiency (%) |
| Subscripts | |
| a | ambient |
| abs | absorber |
| c | cell |
| coll | collector |
| con | condenser |
| ev | evaporator |
| gen | generator |
| id | ideal |
| in | inlet |
| opt | optical |
| out | outlet |
| par | parasitic loss |
| sol | solar |
| T | turbine |
| Abbreviations | |
| ARS | Absorption refrigeration system |
| COP | Coefficient of performance |
| CPV/T | Concentrator photovoltaic/thermal |
| EES | Engineering equation solver |
| MD | Membrane desalination |
| ORC | Organic Rankine cycle |
| PTC | Parabolic trough collector |
| SF | Solar fraction |
| TF | Thermal factor |
References
- Moltames, R.; Roshandel, R. Techno-economic analysis of a modified concentrating photovoltaic/organic Rankine cycle system. Int. J. Ambient. Energy 2022, 43, 2026–2038. [Google Scholar] [CrossRef]
- Rahbar, K.; Riasi, A.; Sangjoeei, H.K.B.; Razmjoo, N. Heat recovery of nano-fluid based concentrating Photovoltaic Thermal (CPV/T) Collector with Organic Rankine Cycle. Energy Convers. Manag. 2019, 179, 373–396. [Google Scholar] [CrossRef]
- Albaik, I.; Alamri, Y.A.; Elsheniti, M.B.; Al-Dadah, R.; Mahmoud, S.; Ismail, M.A. Assessment of a novel multi-generation solar CPV/T system combining adsorption and organic rankine cycle subsystems. Sol. Energy 2022, 236, 455–472. [Google Scholar] [CrossRef]
- Noorollahi, Y.; Yousefi, H.; Moltames, R.; Choubineh, K. Techno-economic Performance Analysis of a Hybrid Concentrated Photovoltaic/Thermal Combined with Organic Rankine Cycle (CPV/T-ORC) system for Simultaneous Generation of Power and Heat. J. Renew. New Energy 2022, 9, 113–120. [Google Scholar]
- Elminshawy, N.A.; Gadalla, M.A.; Bassyouni, M.; El-Nahhas, K.; Elminshawy, A.; Elhenawy, Y. A novel concentrated photovoltaic-driven membrane distillation hybrid system for the simultaneous production of electricity and potable water. Renew. Energy 2020, 162, 802–817. [Google Scholar] [CrossRef]
- Heng, Z.; Feipeng, C.; Yang, L.; Haiping, C.; Kai, L.; Boran, Y. The performance analysis of a LCPV/T assisted absorption refrigeration system. Renew. Energy 2019, 143, 1852–1864. [Google Scholar]
- Buonomano, A.; Calise, F.; Palombo, A. Solar heating and cooling systems by absorption and adsorption chillers driven by stationary and concentrating photovoltaic/thermal solar collectors: Modelling and simulation. Renew. Sustain. Energy Rev. 2018, 82, 1874–1908. [Google Scholar] [CrossRef]
- Rabiea, M.; Ali, A.Y.; Abo-Zahhad, E.M.; Elqady, H.I.; Elkady, M.F.; Ookawar, S.; El-Shazly, A.H.; Salem, M.S.; Radwan, A. Thermal analysis of a hybrid high concentrator photovoltaic/membrane distillation system for isolated coastal regions. Sol. Energy 2021, 215, 220–239. [Google Scholar] [CrossRef]
- Moaleman, A.; Kasaeianb, A.; Aramesh, M.; Ahian, O.; Sahota, L.; Tiwari, G.N. Simulation of the performance of a solar concentrating photovoltaic-thermal collector, applied in a combined cooling heating and power generation system. Energy Convers. Manag. 2018, 160, 191–208. [Google Scholar] [CrossRef]
- Flamant, G. Solar Power Plants: State of the Art. In Concentrating Solar Thermal Energy: Fundamentals and Applications; Wiley: Hoboken, NJ, USA, 2022; p. 1. [Google Scholar]
- Al-Nimr, M.A.; Dawahdeh, A.I.; Al-Omari, J.A. Dual power generation modes for thermally regenerative electrochemical cycle integrated with concentrated thermal photovoltaic and phase change material storage. J. Energy Storage 2023, 58, 106373. [Google Scholar] [CrossRef]
- Indira, S.S.; Vaithilingam, C.A.; Narasingamurthi, K.; Sivasubramanian, R.; Chong, K.K.; Saidur, R. Mathematical modelling, performance evaluation and exergy analysis of a hybrid photovoltaic/thermal-solar thermoelectric system integrated with compound parabolic concentrator and parabolic trough concentrator. Appl. Energy 2022, 320, 119294. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, B.; Xia, X.; Yang, H.; Zuo, Q.; Liu, Z. Energy loss of radial inflow turbine for organic Rankine cycle using mixture based on entropy production method. Energy 2022, 245, 123312. [Google Scholar] [CrossRef]
- Mohammadi, S.H. Theoretical investigation on performance improvement of a low-temperature transcritical carbon dioxide compression refrigeration system by means of an absorption chiller after-cooler. Appl. Therm. Eng. 2018, 138, 264–279. [Google Scholar] [CrossRef]
- Mahmoudi, G.; Goodarzi, M.; Dehghani, S.; Akbarzadeh, A. Experimental and theoretical study of a lab scale permeate gap membrane distillation setup for desalination. Desalination 2017, 419, 197–210. [Google Scholar] [CrossRef]
- Najib, A.; Orfi, J.; Ali, E.; Saleh, J. Thermodynamics analysis of a direct contact membrane distillation with/without heat recovery based on experimental data. Desalination 2019, 466, 52–67. [Google Scholar] [CrossRef]
- Ma, L.; Mao, J.; Marefati, M. Assessment of a new coal-fired power plant integrated with solid oxide fuel cell and parabolic trough solar collector. Process Saf. Environ. Prot. 2022, 163, 340–352. [Google Scholar] [CrossRef]


| Components | Equations |
|---|---|
| Generator | |
| Evaporator | |
| Condenser | |
| Absorber | |
| Heat exchanger | |
| Pump | |
| Cooling system expansion valve | |
| Pressure relief valve |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anazi, A.A.A.; Alghamdi, M.I.; Chammam, A.; Kadhm, M.S.; Al-Kharsan, I.H.; Alayi, R. Theoretical Analysis of an Integrated, CPVT Membrane Distillation System for Cooling, Heating, Power and Seawater Desalination. Water 2023, 15, 1345. https://doi.org/10.3390/w15071345
Anazi AAA, Alghamdi MI, Chammam A, Kadhm MS, Al-Kharsan IH, Alayi R. Theoretical Analysis of an Integrated, CPVT Membrane Distillation System for Cooling, Heating, Power and Seawater Desalination. Water. 2023; 15(7):1345. https://doi.org/10.3390/w15071345
Chicago/Turabian StyleAnazi, Abeer Abdullah Al, Mohammed I. Alghamdi, Abdeljelil Chammam, Mustafa Salam Kadhm, Ibrahim H. Al-Kharsan, and Reza Alayi. 2023. "Theoretical Analysis of an Integrated, CPVT Membrane Distillation System for Cooling, Heating, Power and Seawater Desalination" Water 15, no. 7: 1345. https://doi.org/10.3390/w15071345
APA StyleAnazi, A. A. A., Alghamdi, M. I., Chammam, A., Kadhm, M. S., Al-Kharsan, I. H., & Alayi, R. (2023). Theoretical Analysis of an Integrated, CPVT Membrane Distillation System for Cooling, Heating, Power and Seawater Desalination. Water, 15(7), 1345. https://doi.org/10.3390/w15071345









