Integrating Remote Sensing, Proximal Sensing, and Probabilistic Modeling to Support Agricultural Project Planning and Decision-Making for Waterlogged Fields
Abstract
1. Introduction
1.1. Remote Sensing of Waterlogging in Agroecosystems
1.2. Decision-Making and Management of Waterlogged Agricultural Fields
2. Materials and Methods
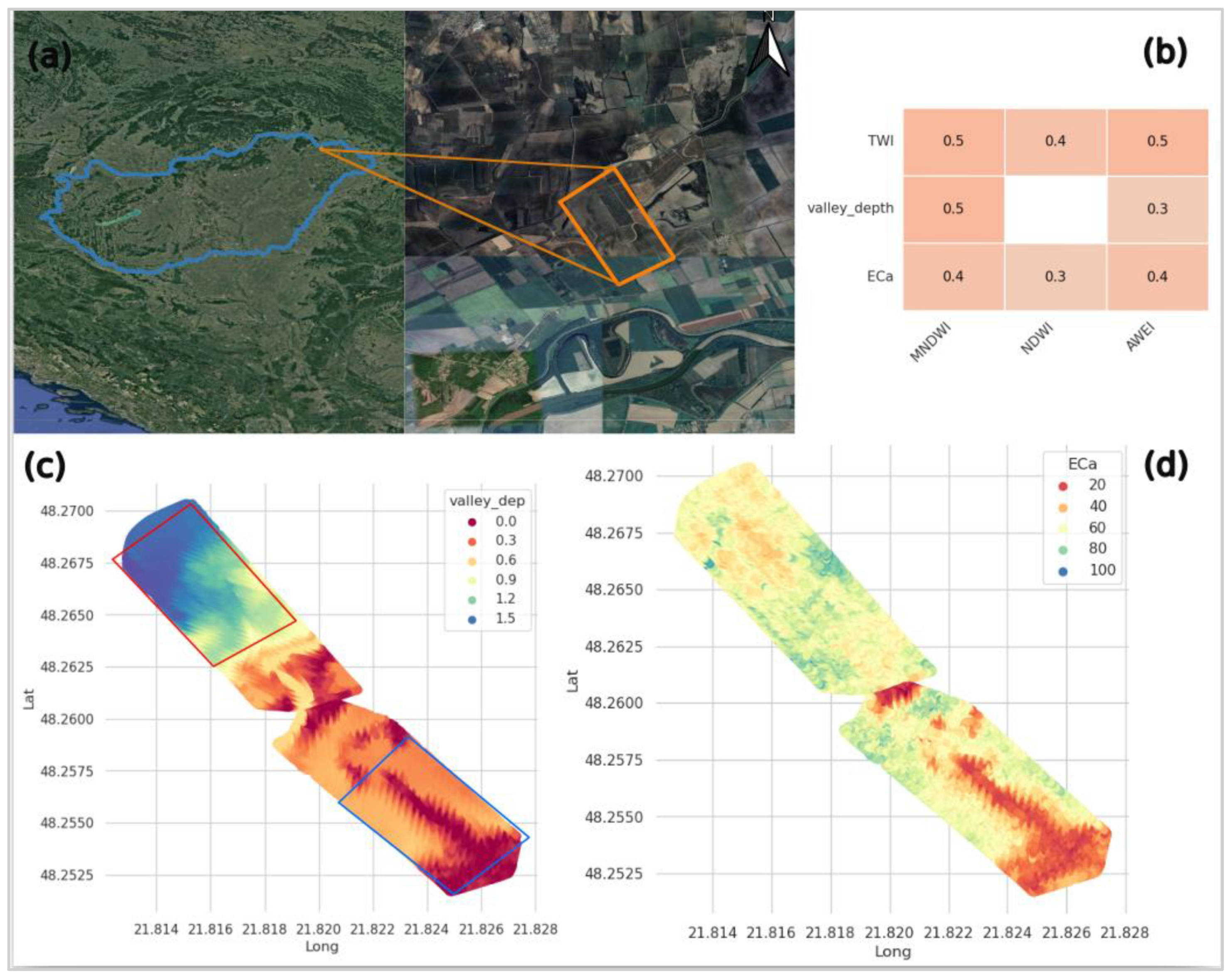
2.1. Study Area
2.2. Data Collection and Processing
Agricultural Production and Financial Data
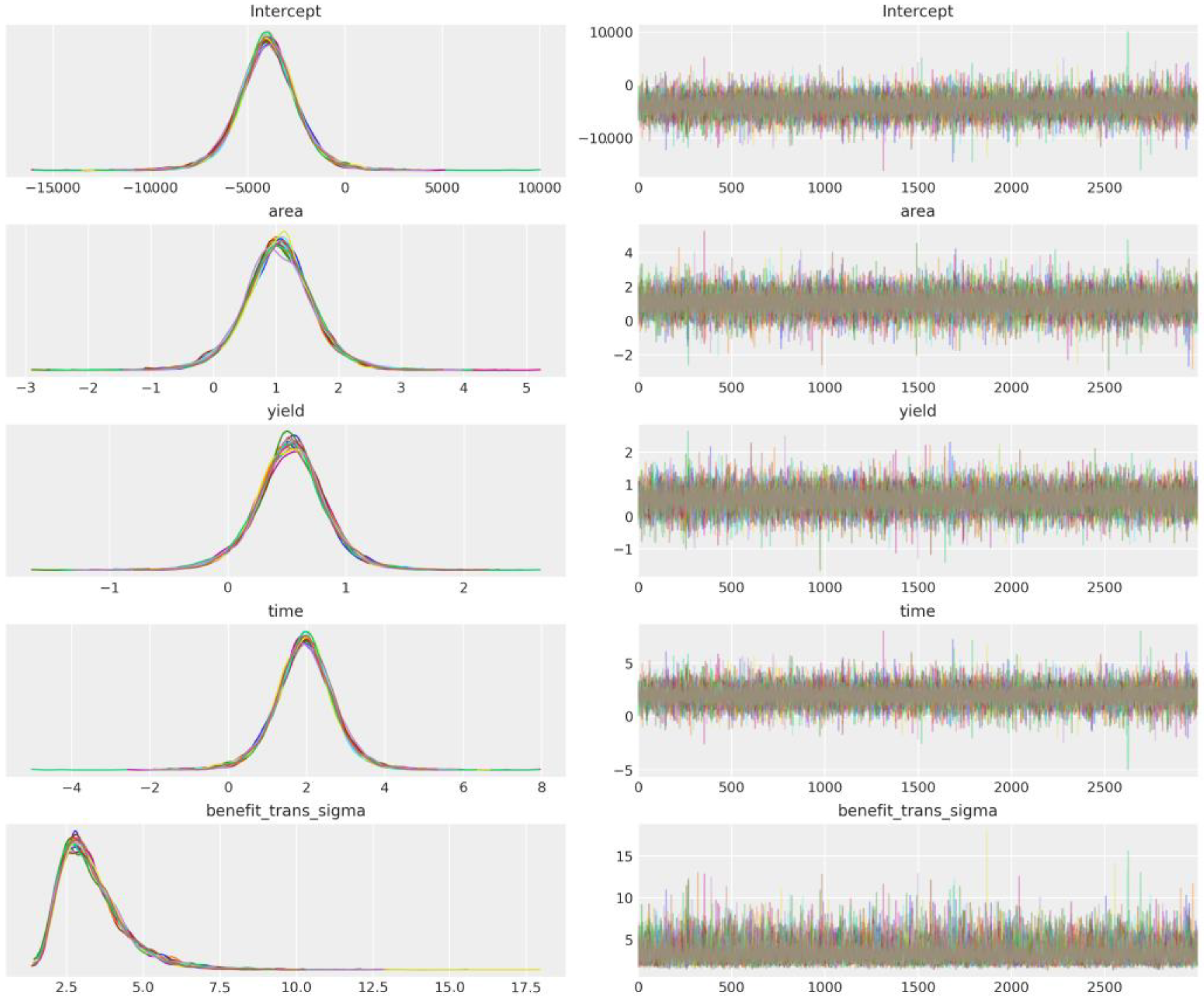
2.3. Statistical Analysis
3. Results and Discussion
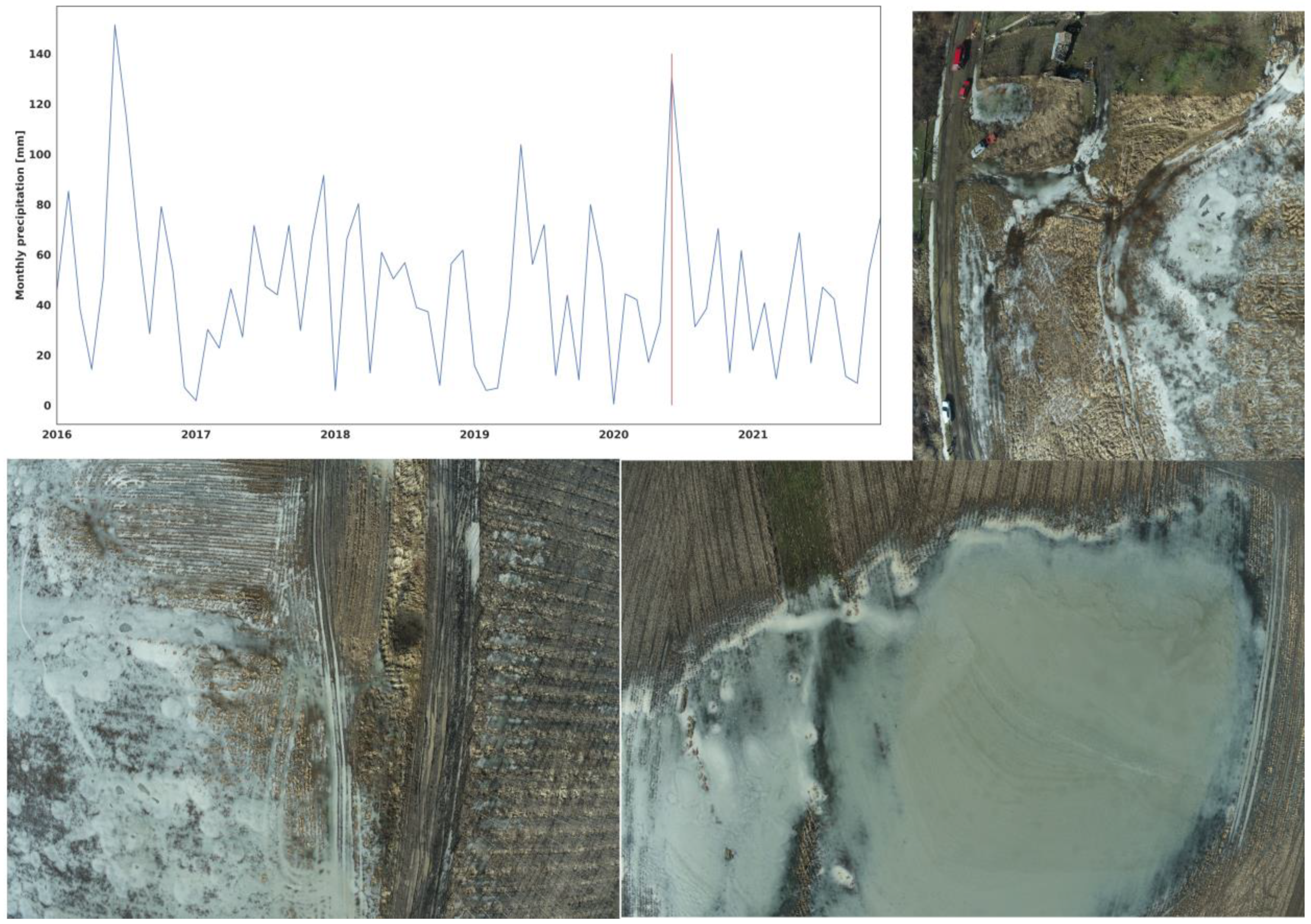
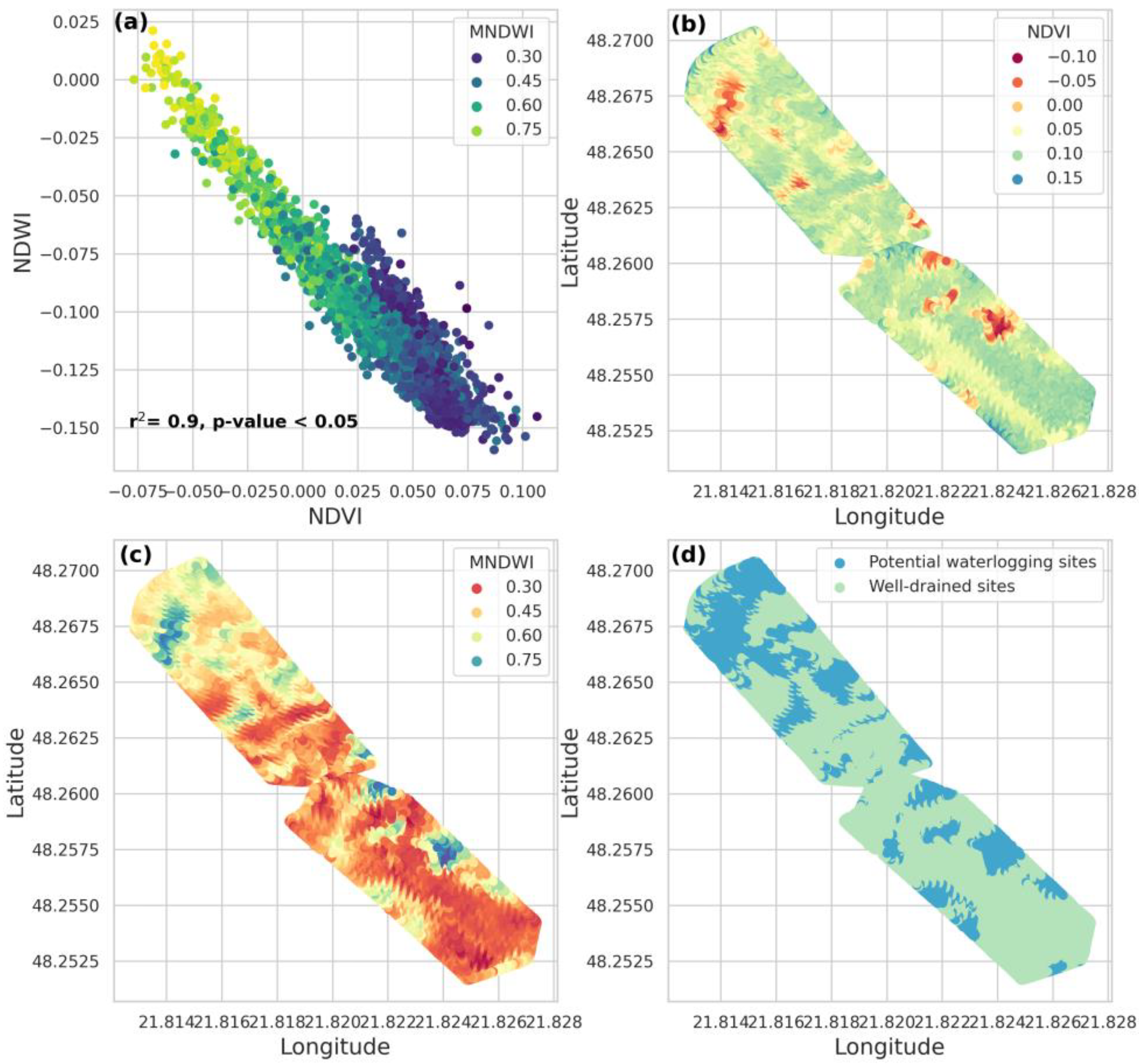
3.1. Field Hydrogeomorphic Features and Waterlogging in Agriculture
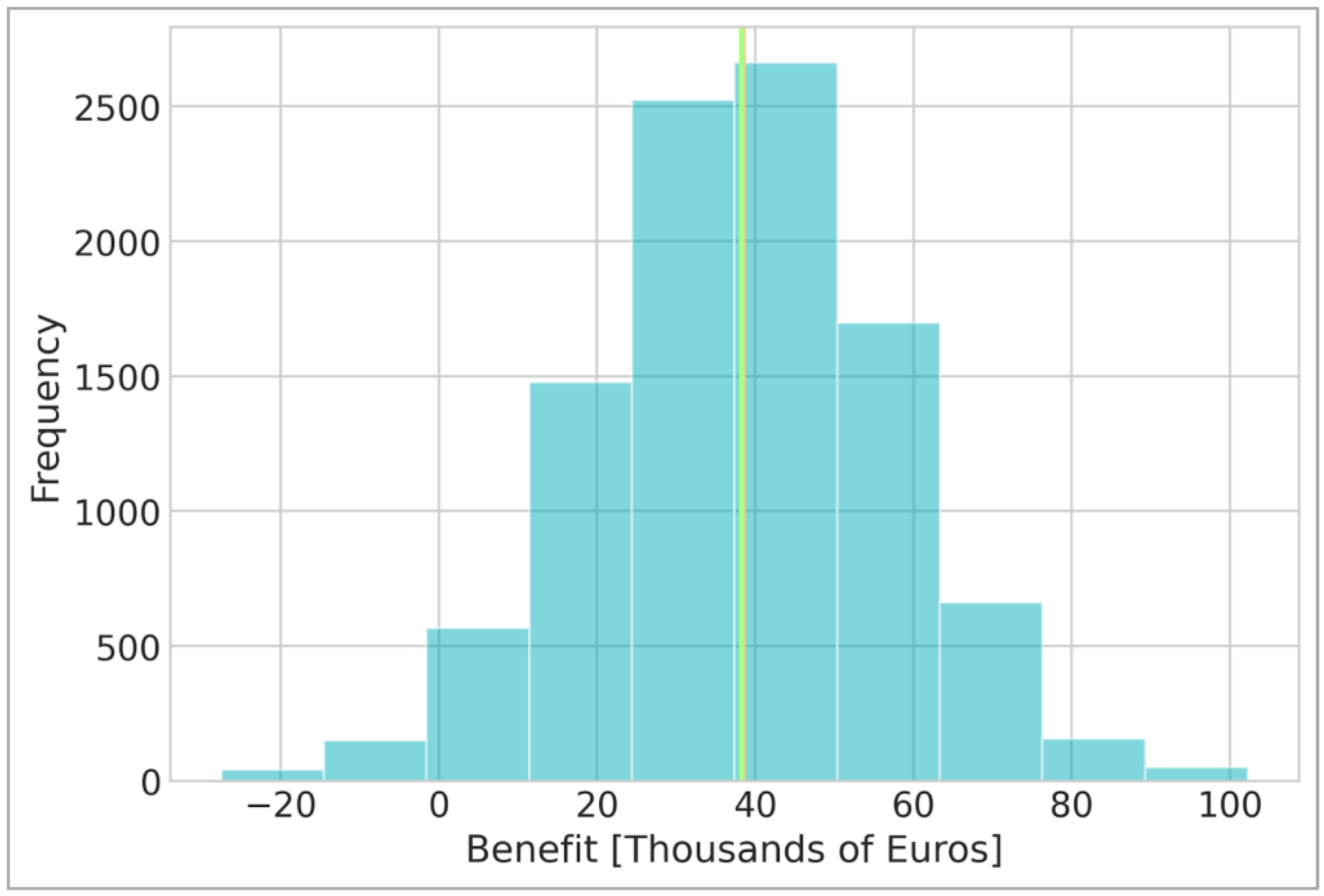
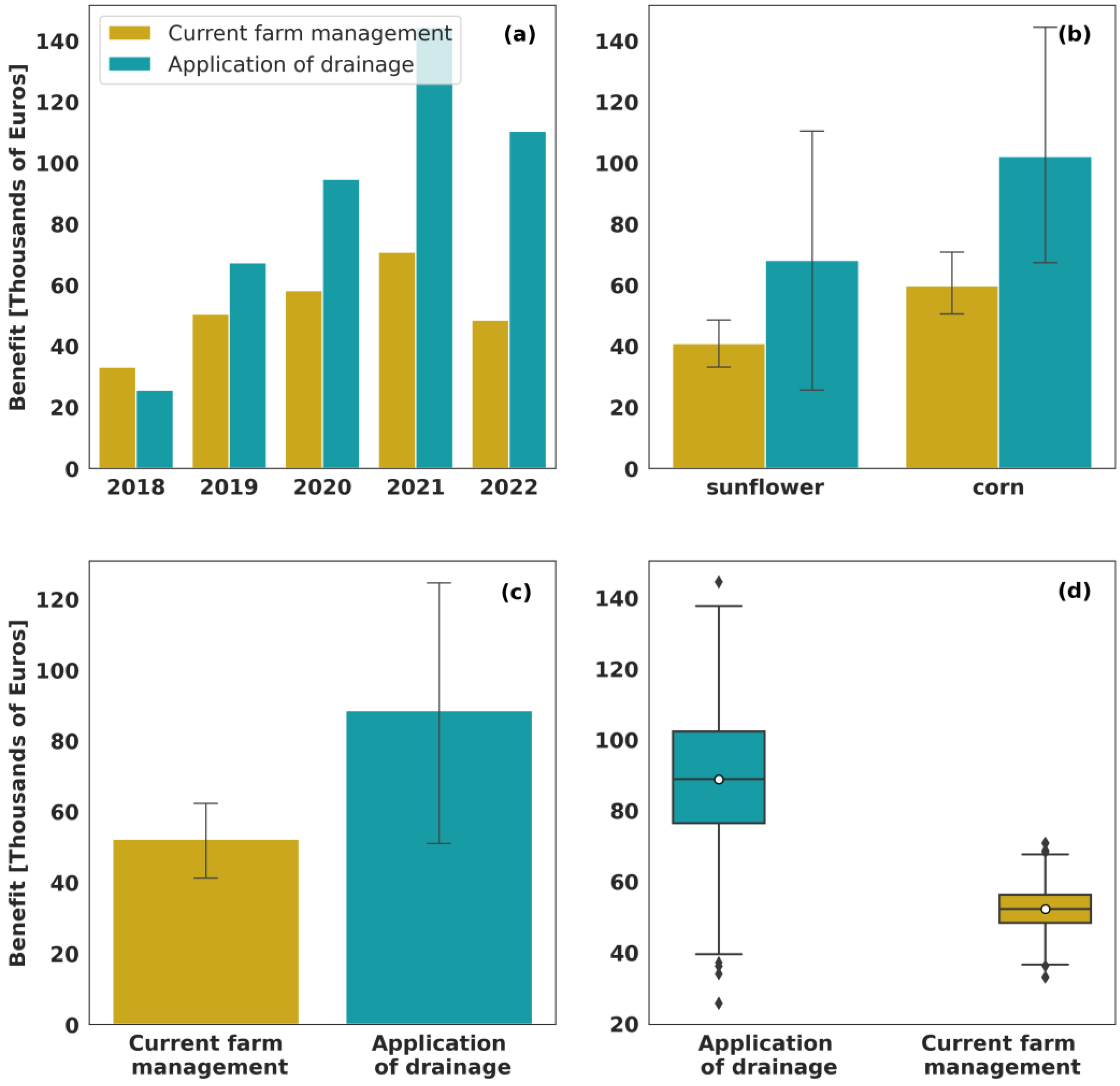
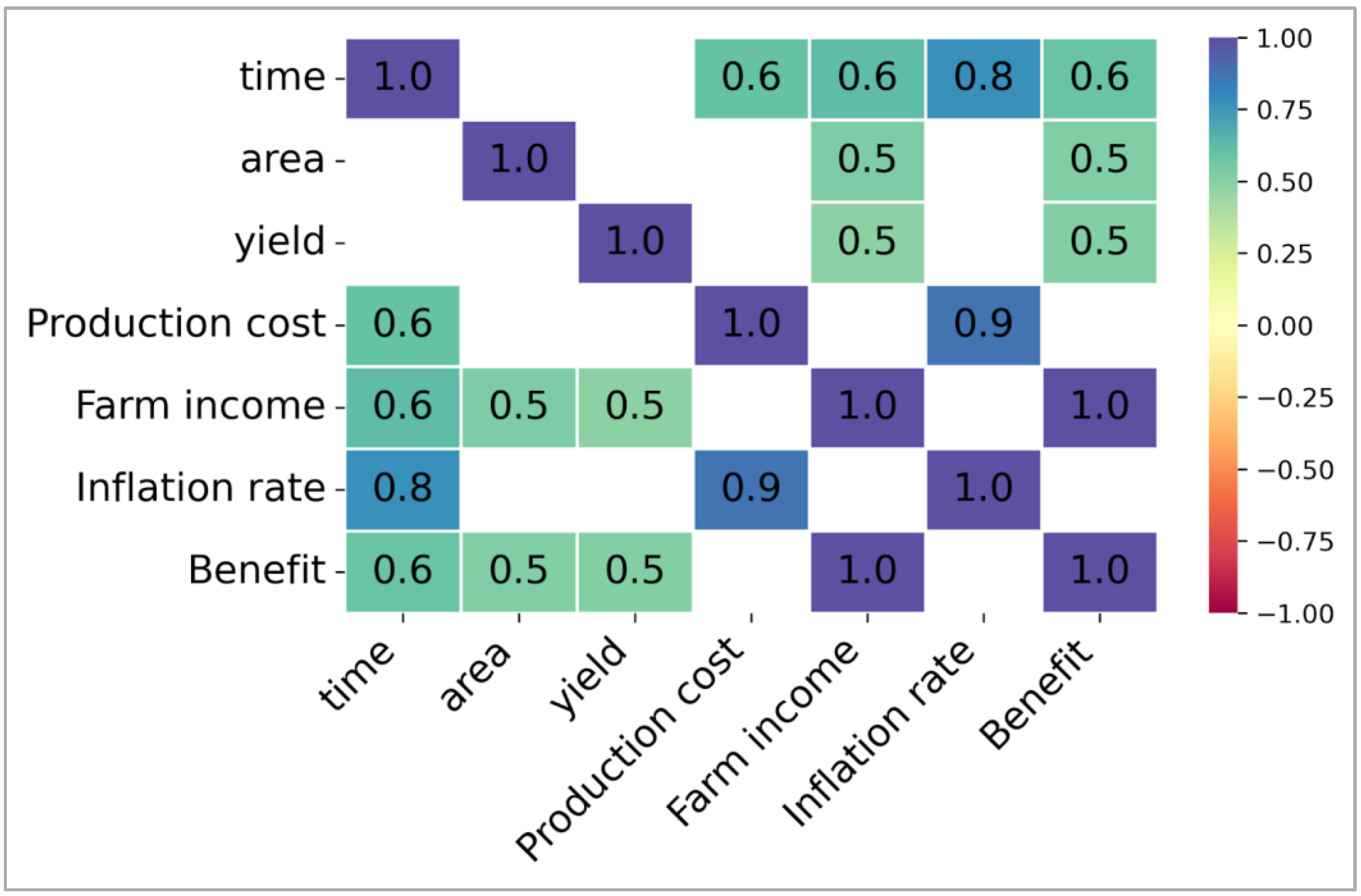
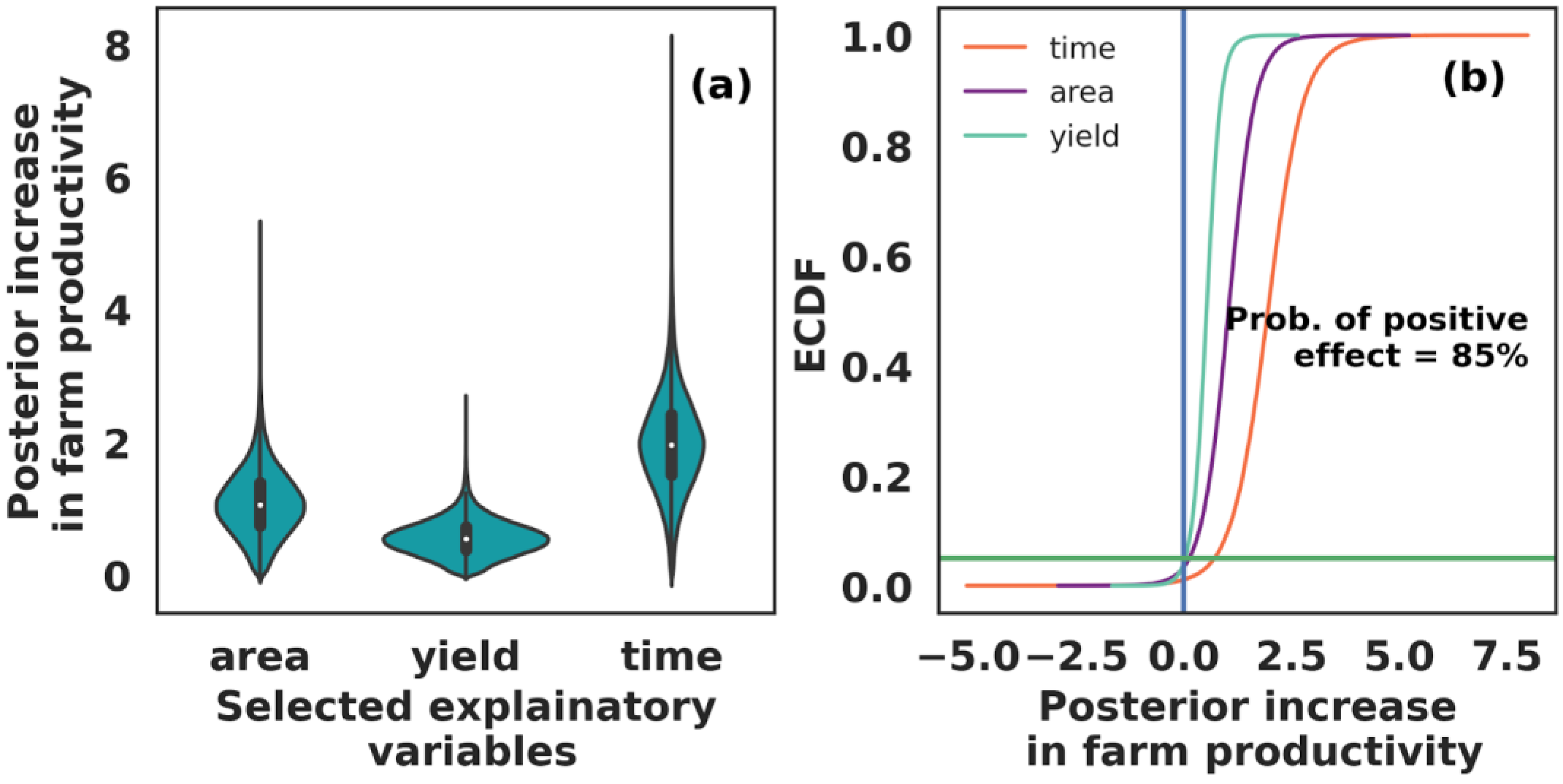
3.2. Data-Driven Decision-Making
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Lebay, M.; Abiye, W.; Taye, T.; Belay, S. Evaluation of Soil Drainage Methods for the Productivity of Waterlogged Vertisols in Jama District, Eastern Amhara Region, Ethiopia. Int. J. Agron. 2021, 2021, e5534866. [Google Scholar] [CrossRef]
- Pais, I.P.; Moreira, R.; Semedo, J.N.; Ramalho, J.C.; Lidon, F.C.; Coutinho, J.; Maçãs, B.; Scotti-Campos, P. Wheat Crop under Waterlogging: Potential Soil and Plant Effects. Plants 2023, 12, 149. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Shao, M. Effects of rainfall intensity on rainfall infiltration and redistribution in soil on Loess slope land. Ying Yong Sheng Tai Xue Bao 2006, 17, 2271–2276. [Google Scholar] [PubMed]
- Várallyay, G. Soils, as the most important natural resources in Hungary (potentialities and constraints)—A review. Agrokémia És Talajt. 2015, 64, 321–338. [Google Scholar] [CrossRef]
- Den Besten, N.; Steele-Dunne, S.; de Jeu, R.; van der Zaag, P. Towards Monitoring Waterlogging with Remote Sensing for Sustainable Irrigated Agriculture. Remote Sens. 2021, 13, 2929. [Google Scholar] [CrossRef]
- Kabała, C.; Charzyński, P.; Czigány, S.; Novák, T.J.; Saksa, M.; Świtoniak, M. Suitability of World Reference Base for Soil Resources (WRB) to Describe and Classify Chernozemic Soils in Central Europe. Soil Sci. Annu. 2019, 70, 244–257. [Google Scholar] [CrossRef]
- Tilahun, T.; Seyoum, W.M. High-Resolution Mapping of Tile Drainage in Agricultural Fields Using Unmanned Aerial System (UAS)-Based Radiometric Thermal and Optical Sensors. Hydrology 2021, 8, 2. [Google Scholar] [CrossRef]
- Rahman, M.M.; Chakraborty, T.K.; Al Mamun, A.; Kiaya, V. Land- and Water-Based Adaptive Farming Practices to Cope with Waterlogging in Variably Elevated Homesteads. Sustainability 2023, 15, 2087. [Google Scholar] [CrossRef]
- Singh, S.K.; Pandey, A.C. Geomorphology and the Controls of Geohydrology on Waterlogging in Gangetic Plains, North Bihar, India. Environ. Earth Sci. 2014, 71, 1561–1579. [Google Scholar] [CrossRef]
- Al-Maliki, S.; Ibrahim, T.I.M.; Jakab, G.; Masoudi, M.; Makki, J.S.; Vekerdy, Z. An Approach for Monitoring and Classifying Marshlands Using Multispectral Remote Sensing Imagery in Arid and Semi-Arid Regions. Water 2022, 14, 1523. [Google Scholar] [CrossRef]
- McFEETERS, S.K. The Use of the Normalized Difference Water Index (NDWI) in the Delineation of Open Water Features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of Normalised Difference Water Index (NDWI) to Enhance Open Water Features in Remotely Sensed Imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A New Technique for Surface Water Mapping Using Landsat Imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Fei, X.; Li, Y.-Z.; Du, Y.; Ling, F.; Yan, Y.; Feng, Q.; Ban, X. Monitoring Perennial Sub-Surface Waterlogged Croplands Based on MODIS in Jianghan Plain, Middle Reaches of the Yangtze River. J. Integr. Agric. 2014, 13, 1791–1801. [Google Scholar]
- Ibrahim, T.I.M.; Al-Maliki, S.; Salameh, O.; Waltner, I.; Vekerdy, Z. Improving LST Downscaling Quality on Regional and Field-Scale by Parameterizing the DisTrad Method. ISPRS Int. J. Geo-Inf. 2022, 11, 327. [Google Scholar] [CrossRef]
- Corwin, D.L.; Lesch, S.M. Application of Soil Electrical Conductivity to Precision Agriculture. Agron. J. 2003, 95, 455–471. [Google Scholar] [CrossRef]
- Kinoshita, R.; Tani, M.; Sherpa, S.; Ghahramani, A.; van Es, H.M. Soil Sensing and Machine Learning Reveal Factors Affecting Maize Yield in the Mid-Atlantic United States. Agron. J. 2023, 115, 181–196. [Google Scholar] [CrossRef]
- Lu, S.G.; Tang, C.; Rengel, Z. Combined Effects of Waterlogging and Salinity on Electrochemistry, Water-Soluble Cations and Water Dispersible Clay in Soils with Various Salinity Levels. Plant Soil 2004, 264, 231–245. [Google Scholar] [CrossRef]
- Valayamkunnath, P.; Barlage, M.; Chen, F.; Gochis, D.J.; Franz, K.J. Mapping of 30-Meter Resolution Tile-Drained Croplands Using a Geospatial Modeling Approach. Sci. Data 2020, 7, 257. [Google Scholar] [CrossRef]
- Yet, B.; Lamanna, C.; Shepherd, K.D.; Rosenstock, T.S. Evidence-Based Investment Selection: Prioritizing Agricultural Development Investments under Climatic and Socio-Political Risk Using Bayesian Networks. PLoS ONE 2020, 15, e0234213. [Google Scholar] [CrossRef]
- Pollino, C.A.; Woodberry, O.; Nicholson, A.; Korb, K.; Hart, B.T. Parameterisation and Evaluation of a Bayesian Network for Use in an Ecological Risk Assessment. Environ. Model. Softw. 2007, 22, 1140–1152. [Google Scholar] [CrossRef]
- Barton, D.N.; Saloranta, T.; Moe, S.J.; Eggestad, H.O.; Kuikka, S. Bayesian Belief Networks as a Meta-Modelling Tool in Integrated River Basin Management—Pros and Cons in Evaluating Nutrient Abatement Decisions under Uncertainty in a Norwegian River Basin. Ecol. Econ. 2008, 66, 91–104. [Google Scholar] [CrossRef]
- Freebairn, J.W. Assessing Some Effects of Inflation on the Agricultural Sector. Aust. J. Agric. Econ. 1981, 25, 107–122. [Google Scholar] [CrossRef]
- Yet, B.; Constantinou, A.; Fenton, N.; Neil, M.; Luedeling, E.; Shepherd, K. A Bayesian Network Framework for Project Cost, Benefit and Risk Analysis with an Agricultural Development Case Study. Expert Syst. Appl. 2016, 60, 141–155. [Google Scholar] [CrossRef]
- Puga, J.L.; Krzywinski, M.; Altman, N. Bayesian Statistics. Nat. Methods 2015, 12, 377–378. [Google Scholar] [CrossRef]
- Vogelgesang, J.; Scharkow, M. Bayesian Statistics. In The International Encyclopedia of Communication Research Methods; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2017; pp. 1–9. ISBN 978-1-118-90173-1. [Google Scholar]
- Van de Schoot, R.; Depaoli, S.; King, R.; Kramer, B.; Märtens, K.; Tadesse, M.G.; Vannucci, M.; Gelman, A.; Veen, D.; Willemsen, J.; et al. Bayesian Statistics and Modelling. Nat. Rev. Methods Prim. 2021, 1, 1. [Google Scholar] [CrossRef]
- Flaxman, S.; Mishra, S.; Gandy, A.; Unwin, H.J.T.; Mellan, T.A.; Coupland, H.; Whittaker, C.; Zhu, H.; Berah, T.; Eaton, J.W.; et al. Estimating the Effects of Non-Pharmaceutical Interventions on COVID-19 in Europe. Nature 2020, 584, 257–261. [Google Scholar] [CrossRef]
- Brauner, J.M.; Mindermann, S.; Sharma, M.; Johnston, D.; Salvatier, J.; Gavenčiak, T.; Stephenson, A.B.; Leech, G.; Altman, G.; Mikulik, V.; et al. Inferring the Effectiveness of Government Interventions against COVID-19. Science 2021, 371, eabd9338. [Google Scholar] [CrossRef]
- Govender, I.H.; Sahlin, U.; O’Brien, G.C. Bayesian Network Applications for Sustainable Holistic Water Resources Management: Modeling Opportunities for South Africa. Risk Anal. 2022, 42, 1346–1364. [Google Scholar] [CrossRef]
- Cornet, D.; Sierra, J.; Tournebize, R.; Gabrielle, B.; Lewis, F.I. Bayesian Network Modeling of Early Growth Stages Explains Yam Interplant Yield Variability and Allows for Agronomic Improvements in West Africa. Eur. J. Agron. 2016, 75, 80–88. [Google Scholar] [CrossRef]
- Rasmussen, S.; Madsen, A.L.; Lund, M. Bayesian Network as a Modelling Tool for Risk Management in Agriculture; IFRO Working Paper; University of Copenhagen, Department of Food and Resource Economics (IFRO): Copenhagen, Denmark, 2013. [Google Scholar]
- Constantinou, A.C.; Fenton, N.; Neil, M. Integrating Expert Knowledge with Data in Bayesian Networks: Preserving Data-Driven Expectations When the Expert Variables Remain Unobserved. Expert Syst. Appl. 2016, 56, 197–208. [Google Scholar] [CrossRef]
- Tari, F. A Bayesian Network for Predicting Yield Response of Winter Wheat to Fungicide Programmes. Comput. Electron. Agric. 1996, 15, 111–121. [Google Scholar] [CrossRef]
- IUSS Working Group WRB World Reference Base for Soil Resources 2014, Update 2015 International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; World Soil Resources Reports No. 106; FAO: Roma, Italy, 2015.
- FAO. Guidelines for Soil Description; FAO: Roma, Italy, 2006. [Google Scholar]
- Shepard, D. A Two-Dimensional Interpolation Function for Irregularly-Spaced Data. In Proceedings of the 1968 23rd ACM National Conference, New York, NY, USA, 27–29 August 1968; Association for Computing Machinery: New York, NY, USA, 1968; pp. 517–524. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Crippen, R.E. Calculating the Vegetation Index Faster. Remote Sens. Environ. 1990, 34, 71–73. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Pelleg, D.; Moore, A. Accelerating Exact K-Means Algorithms with Geometric Reasoning. In Proceedings of the Fifth ACM SIGKDD International Conference on KNOWLEDGE Discovery and Data Mining, San Diego, CA, USA, 15–18 August 1999; Association for Computing Machinery: New York, NY, USA, 1999; pp. 277–281. [Google Scholar]
- Goutte, C.; Hansen, L.K.; Liptrot, M.G.; Rostrup, E. Feature-Space Clustering for FMRI Meta-Analysis. Hum Brain Mapp 2001, 13, 165–183. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. Unsupervised Learning. In An Introduction to Statistical Learning: With Applications in R; Springer Texts in Statistics; James, G., Witten, D., Hastie, T., Tibshirani, R., Eds.; Springer: New York, NY, USA, 2013; pp. 373–418. ISBN 978-1-4614-7138-7. [Google Scholar]
- Thorndike, R.L. Who Belongs in the Family? Psychometrika 1953, 18, 267–276. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Kohavi, R.; Longbotham, R. Online Controlled Experiments and A/B Testing. In Encyclopedia of Machine Learning and Data Mining; Sammut, C., Webb, G.I., Eds.; Springer US: Boston, MA, USA, 2017; pp. 922–929. ISBN 978-1-4899-7687-1. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC: New York, NY, USA, 1994; ISBN 978-0-429-24659-3. [Google Scholar]
- Spiegelhalter, D.J.; Myles, J.P.; Jones, D.R.; Abrams, K.R. Bayesian Methods in Health Technology Assessment: A Review. Health Technol Assess 2000, 4, 1–130. [Google Scholar] [CrossRef]
- Kohavi, R.; Longbotham, R.; Sommerfield, D.; Henne, R.M. Controlled Experiments on the Web: Survey and Practical Guide. Data Min. Knowl. Disc. 2009, 18, 140–181. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-6848-6. [Google Scholar]
- Gleason, P.M.; Harris, J.E. The Bayesian Approach to Decision Making and Analysis in Nutrition Research and Practice. J. Acad. Nutr. Diet. 2019, 119, 1993–2003. [Google Scholar] [CrossRef] [PubMed]
- Harrell, F.E.; Shih, Y.C. Using Full Probability Models to Compute Probabilities of Actual Interest to Decision Makers. Int. J. Technol. Assess. Health Care 2001, 17, 17–26. [Google Scholar] [CrossRef] [PubMed]
- Salvatier, J.; Wiecki, T.V.; Fonnesbeck, C. Probabilistic Programming in Python Using PyMC3. PeerJ Comput. Sci. 2016, 2, e55. [Google Scholar] [CrossRef]
- Waskom, M.L. Seaborn: Statistical Data Visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, D.; Wang, S.; Xiang, H.; Zhang, W. Multisource Remote Sensing Data-Based Flood Monitoring and Crop Damage Assessment: A Case Study on the 20 July 2021 Extraordinary Rainfall Event in Henan, China. Remote Sens. 2022, 14, 5771. [Google Scholar] [CrossRef]
- Tran, K.H.; Menenti, M.; Jia, L. Surface Water Mapping and Flood Monitoring in the Mekong Delta Using Sentinel-1 SAR Time Series and Otsu Threshold. Remote Sens. 2022, 14, 5721. [Google Scholar] [CrossRef]
- Șerban, C.; Maftei, C.; Dobrică, G. Surface Water Change Detection via Water Indices and Predictive Modeling Using Remote Sensing Imagery: A Case Study of Nuntasi-Tuzla Lake, Romania. Water 2022, 14, 556. [Google Scholar] [CrossRef]
- Acharya, T.D.; Subedi, A.; Lee, D.H. Evaluation of Water Indices for Surface Water Extraction in a Landsat 8 Scene of Nepal. Sensors 2018, 18, 2580. [Google Scholar] [CrossRef]
- Pang, H.; Wang, X.; Hou, R.; You, W.; Bian, Z.; Sang, G. Multiwater Index Synergistic Monitoring of Typical Wetland Water Bodies in the Arid Regions of West-Central Ningxia over 30 Years. Water 2023, 15, 20. [Google Scholar] [CrossRef]
- Gulácsi, A.; Kovács, F. Sentinel-1-Imagery-Based High-Resolution Water Cover Detection on Wetlands, Aided by Google Earth Engine. Remote Sens. 2020, 12, 1614. [Google Scholar] [CrossRef]
- Buzási, A.; Pálvölgyi, T.; Esses, D. Drought-Related Vulnerability and Its Policy Implications in Hungary. Mitig Adapt Strat. Glob Change 2021, 26, 11. [Google Scholar] [CrossRef]
- Pinke, Z.; Lövei, G.L. Increasing Temperature Cuts Back Crop Yields in Hungary over the Last 90 Years. Glob. Change Biol. 2017, 23, 5426–5435. [Google Scholar] [CrossRef] [PubMed]
- Jäger, F.; Rudnick, J.; Lubell, M.; Kraus, M.; Müller, B. Using Bayesian Belief Networks to Investigate Farmer Behavior and Policy Interventions for Improved Nitrogen Management. Environ. Manag. 2022, 69, 1153–1166. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bukombe, B.; Csenki, S.; Szlatenyi, D.; Czako, I.; Láng, V. Integrating Remote Sensing, Proximal Sensing, and Probabilistic Modeling to Support Agricultural Project Planning and Decision-Making for Waterlogged Fields. Water 2023, 15, 1340. https://doi.org/10.3390/w15071340
Bukombe B, Csenki S, Szlatenyi D, Czako I, Láng V. Integrating Remote Sensing, Proximal Sensing, and Probabilistic Modeling to Support Agricultural Project Planning and Decision-Making for Waterlogged Fields. Water. 2023; 15(7):1340. https://doi.org/10.3390/w15071340
Chicago/Turabian StyleBukombe, Benjamin, Sándor Csenki, Dora Szlatenyi, Ivan Czako, and Vince Láng. 2023. "Integrating Remote Sensing, Proximal Sensing, and Probabilistic Modeling to Support Agricultural Project Planning and Decision-Making for Waterlogged Fields" Water 15, no. 7: 1340. https://doi.org/10.3390/w15071340
APA StyleBukombe, B., Csenki, S., Szlatenyi, D., Czako, I., & Láng, V. (2023). Integrating Remote Sensing, Proximal Sensing, and Probabilistic Modeling to Support Agricultural Project Planning and Decision-Making for Waterlogged Fields. Water, 15(7), 1340. https://doi.org/10.3390/w15071340






