A GPU-Accelerated Two-Dimensional Hydrodynamic Model for Unstructured Grids
Abstract
:1. Introduction
2. Governing Equations
3. Numerical Schemes
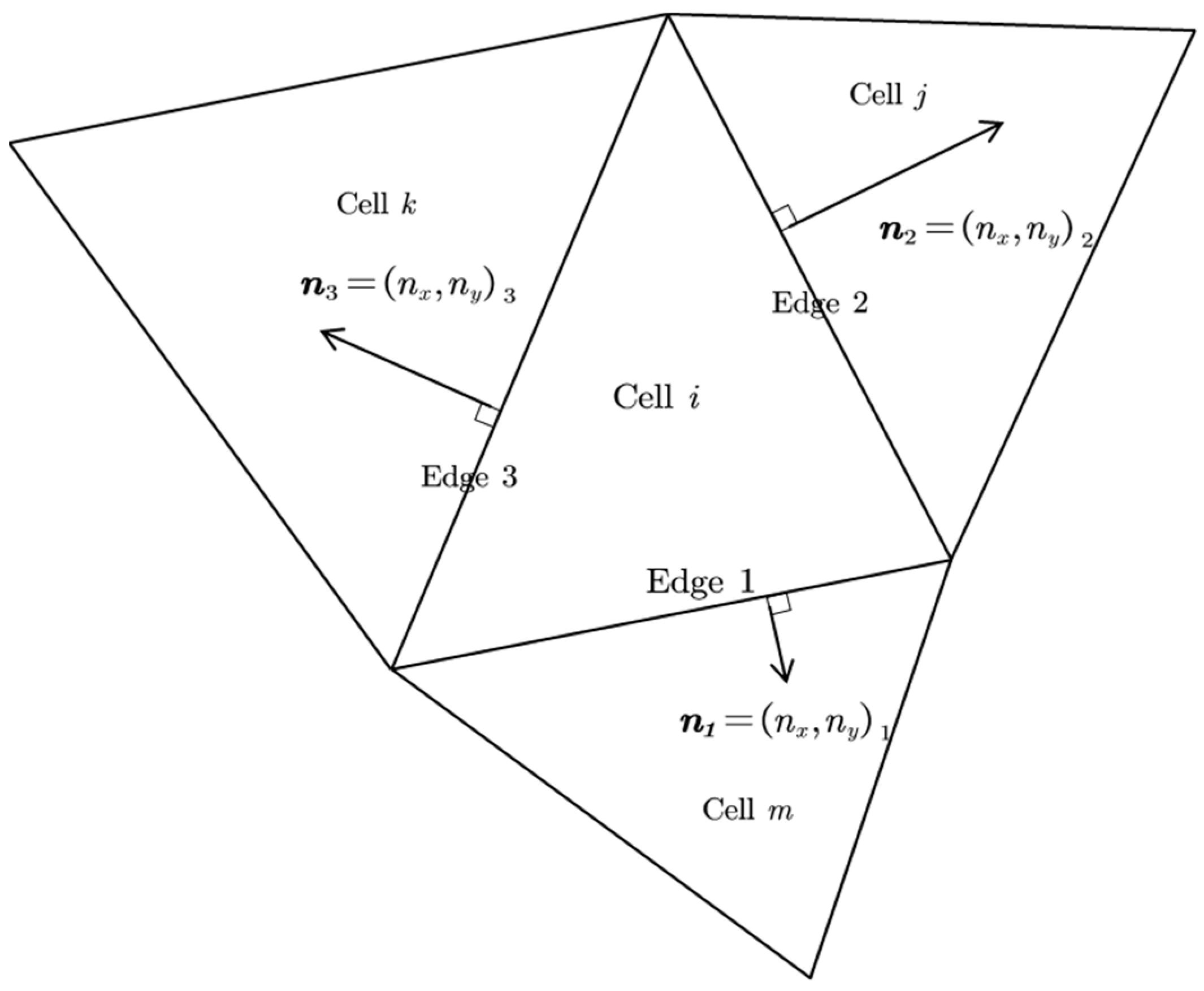
3.1. Finite Volume Method and Unstructured Grid Discretization
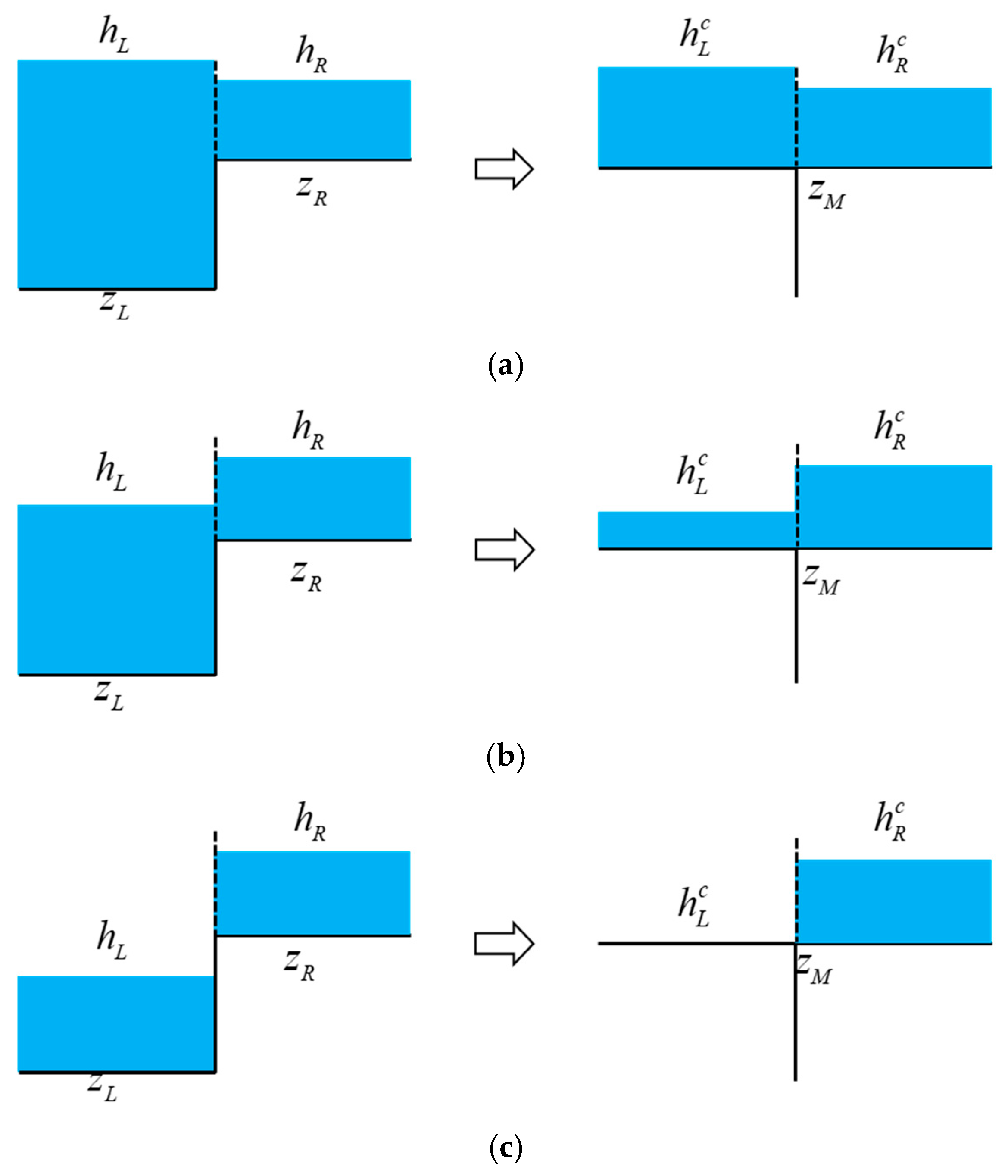
3.2. Water Depth Reconstruction
3.3. Interface Numerical Flux and Slope Source Term Discretization
3.4. Friction Source Term
3.5. Rainfall and Infiltration Source Term
3.6. Stability Criteria
3.7. GPU-Accelerated Procedure
4. Model Validation and Results
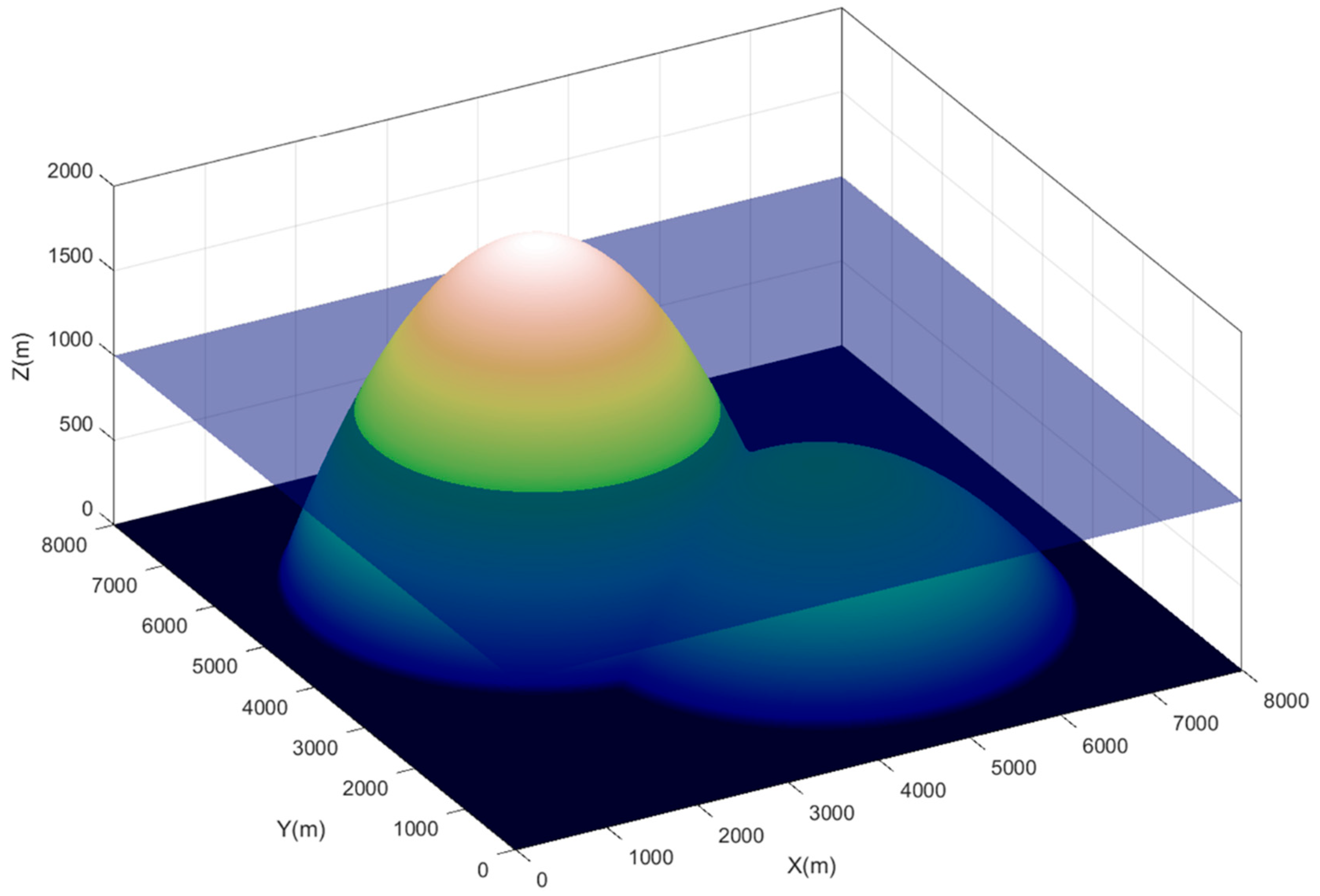
4.1. Still Water Test in an Uneven Bed
4.2. Dam-Break Flow in a 90° Curved Channel
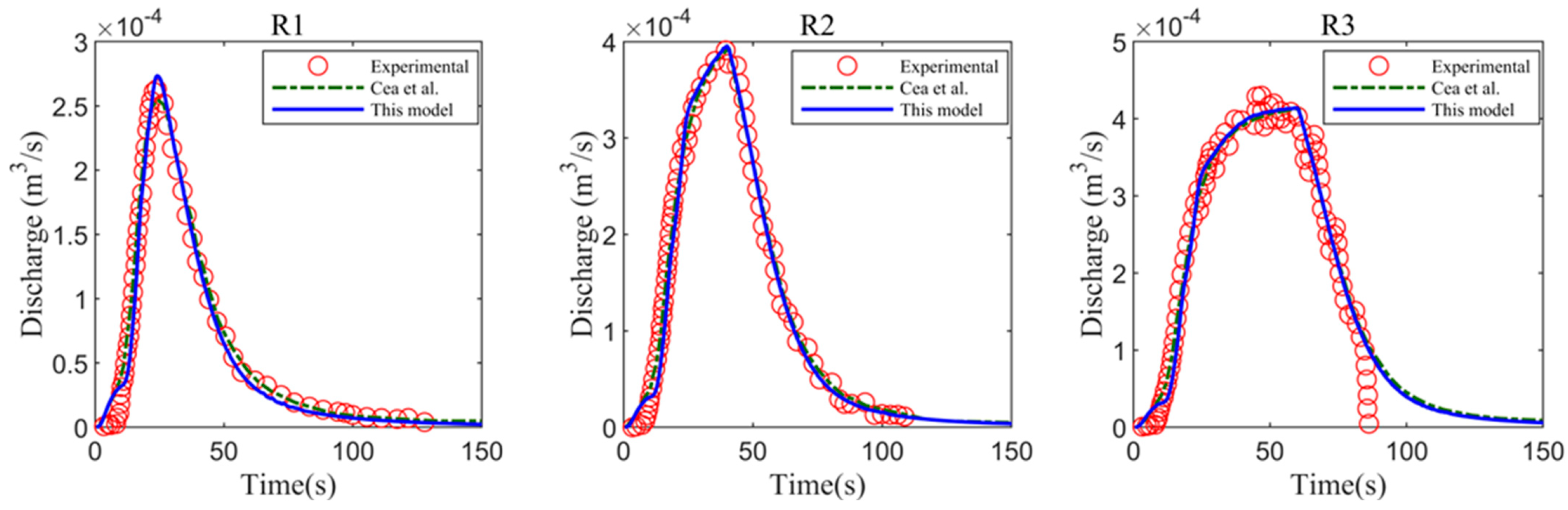
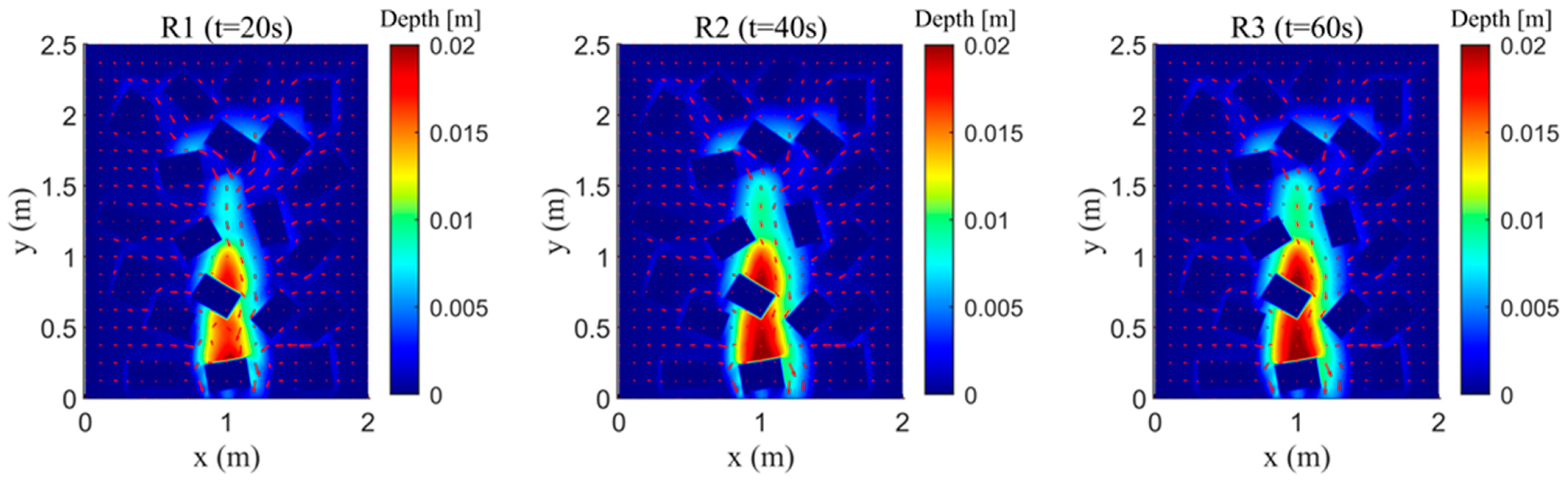
4.3. Urban Rainfall Runoff Experiment
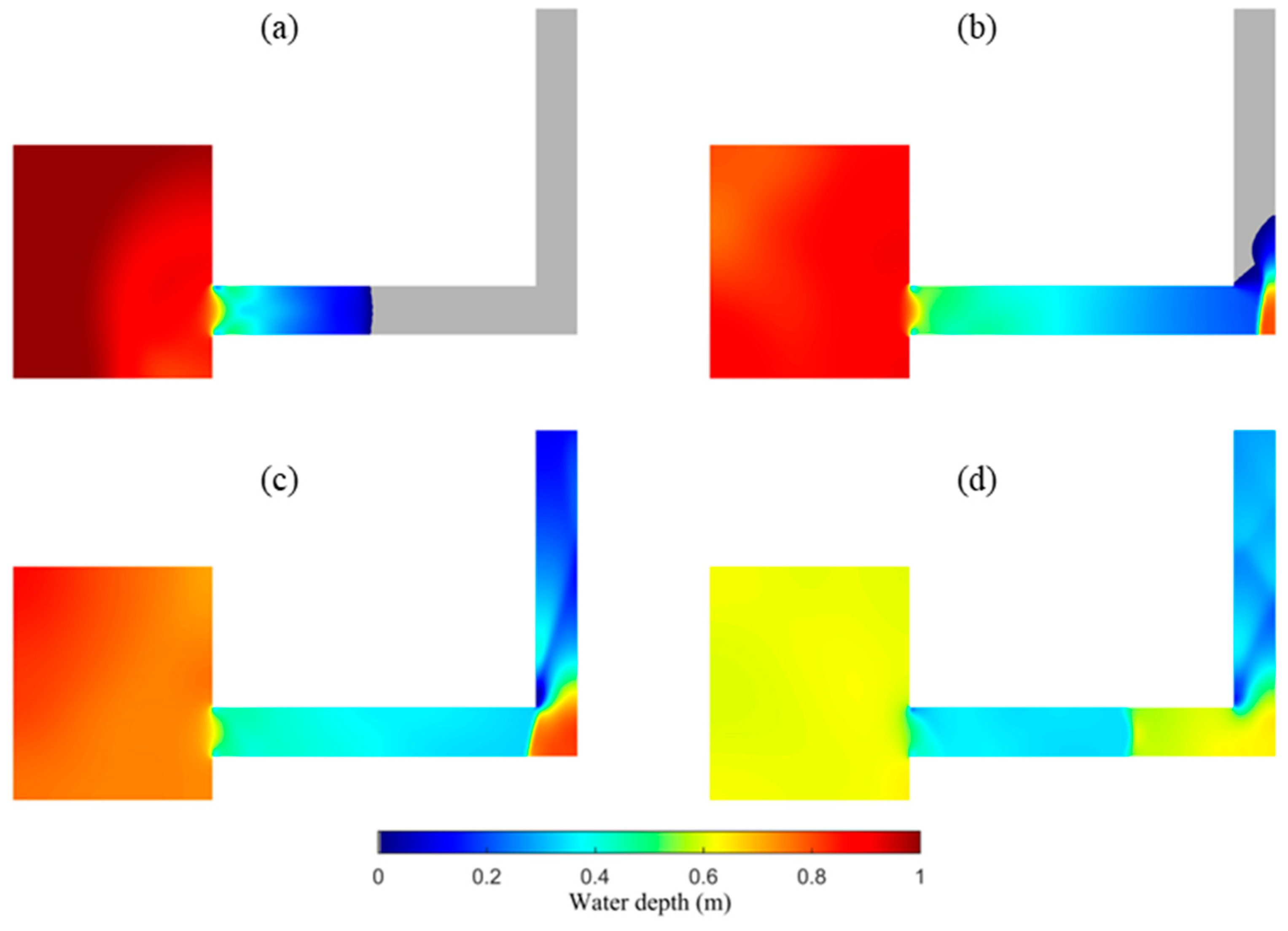
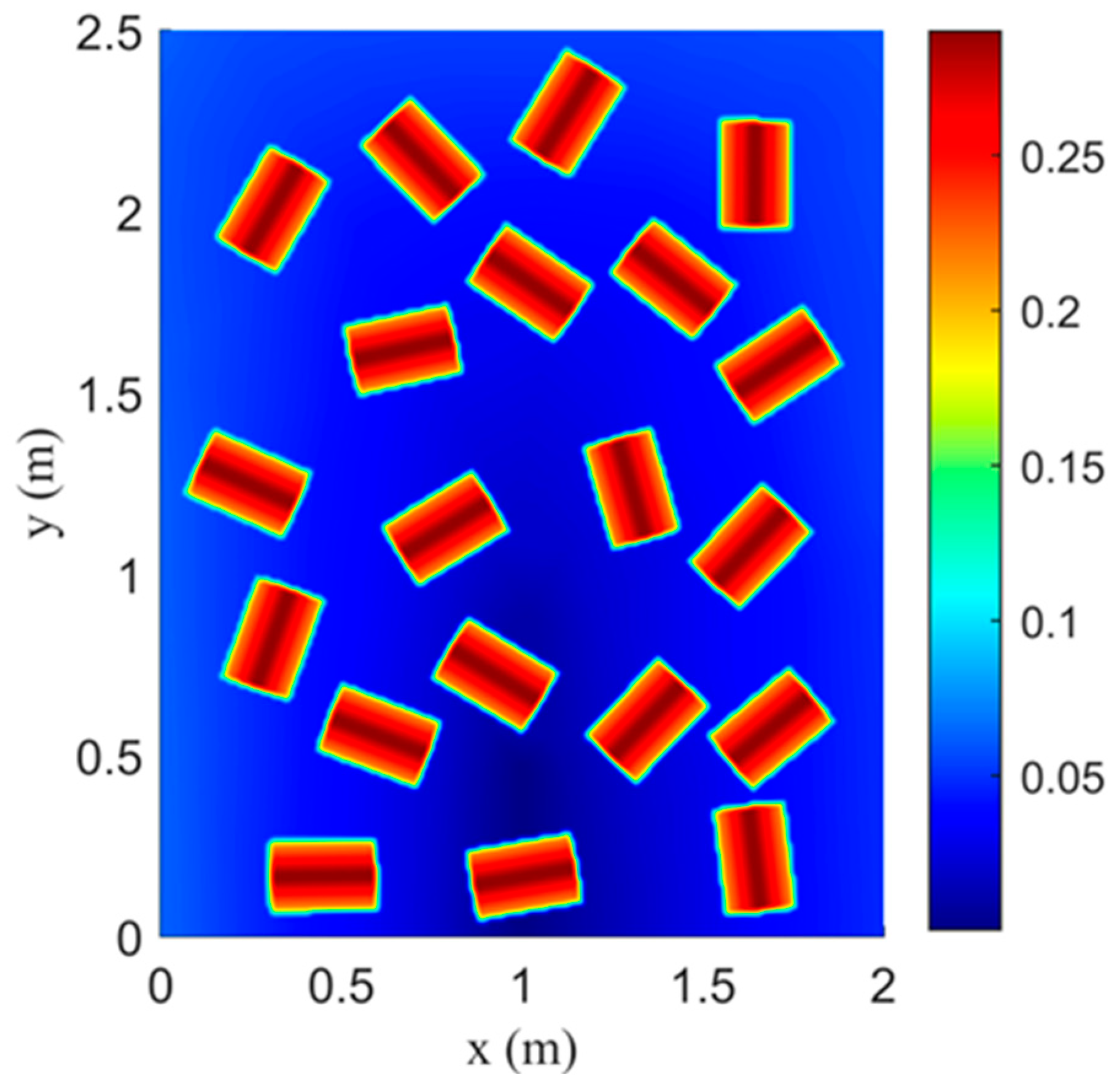
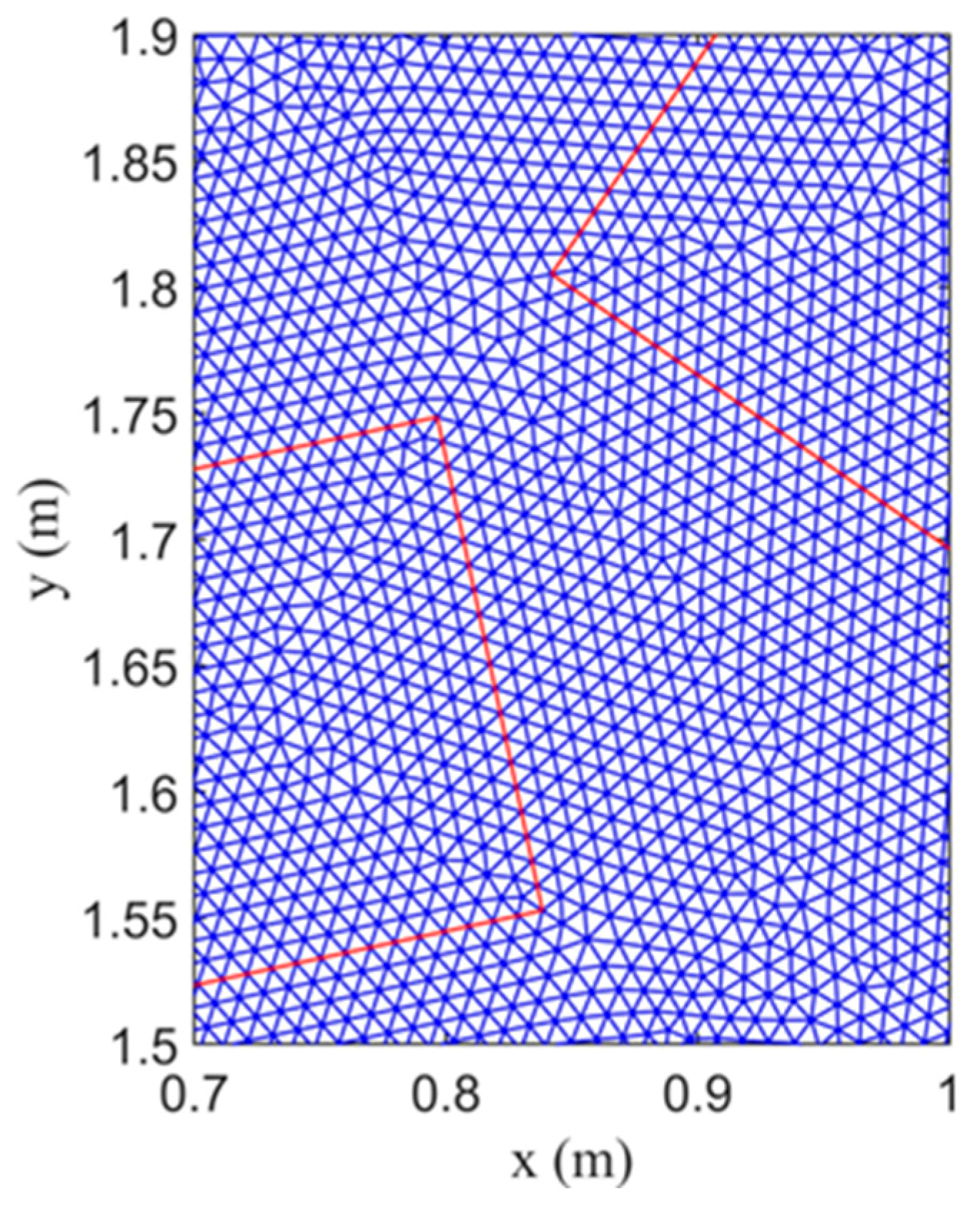
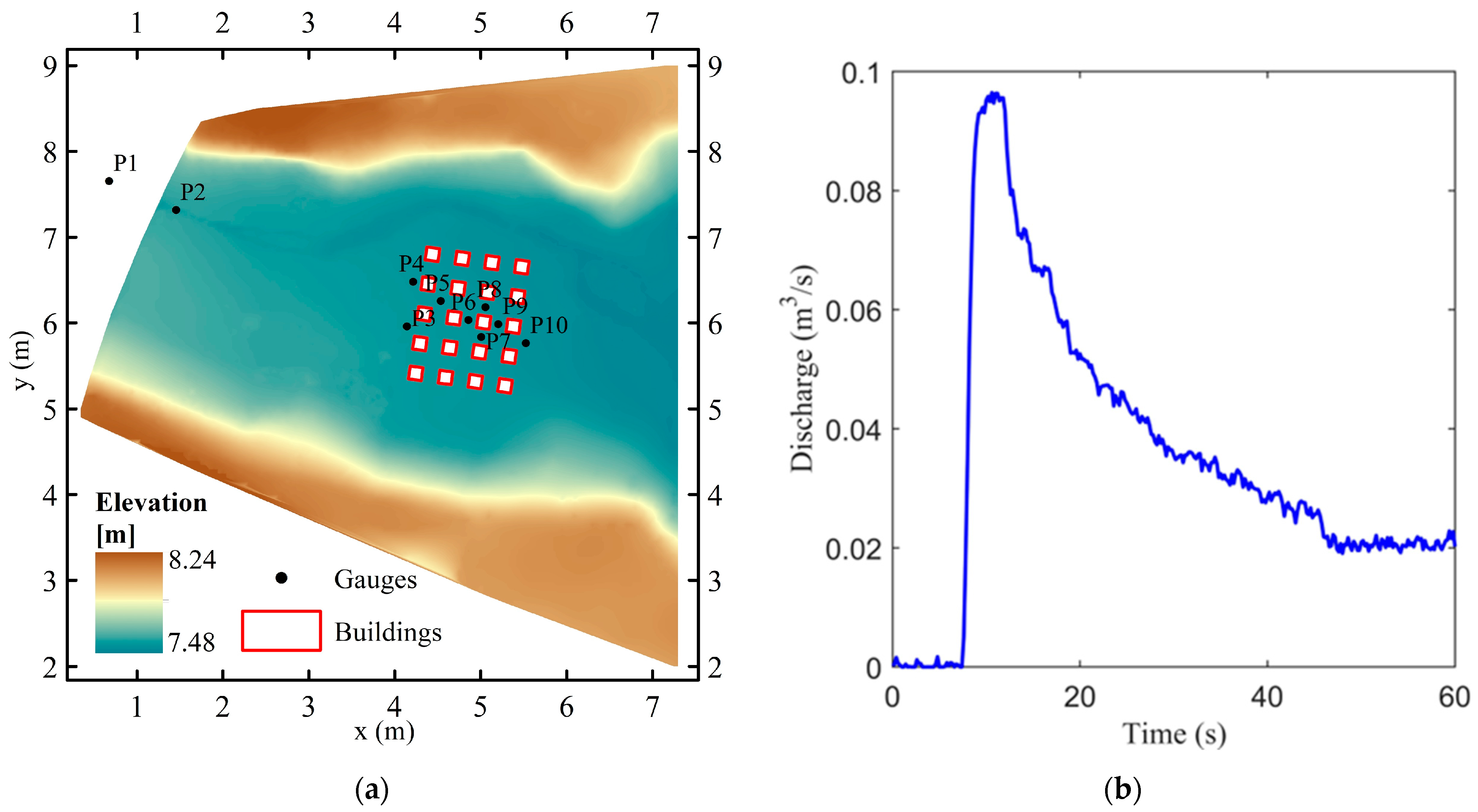
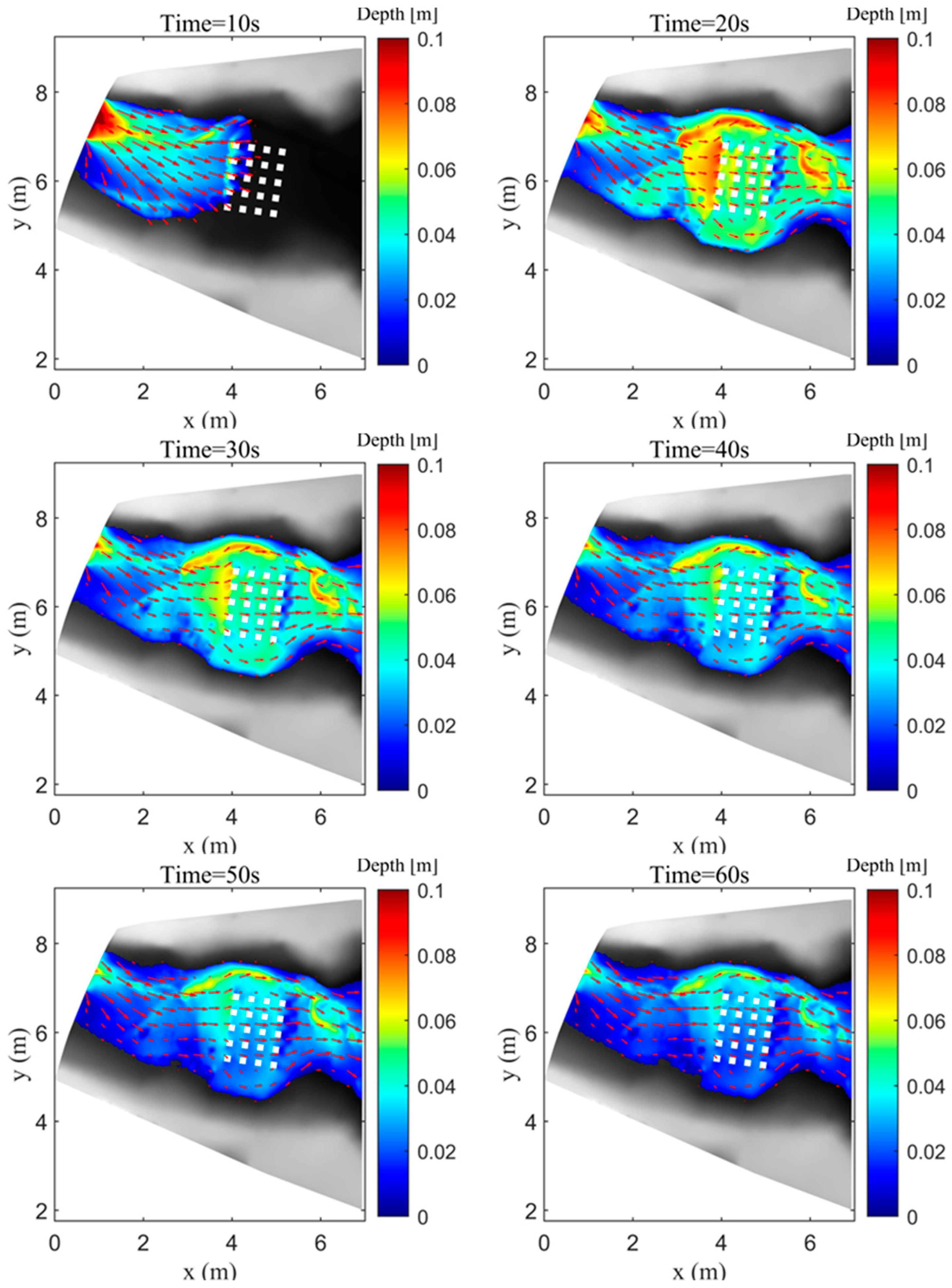
4.4. Experiment of a Flash Flood over Urban Topography
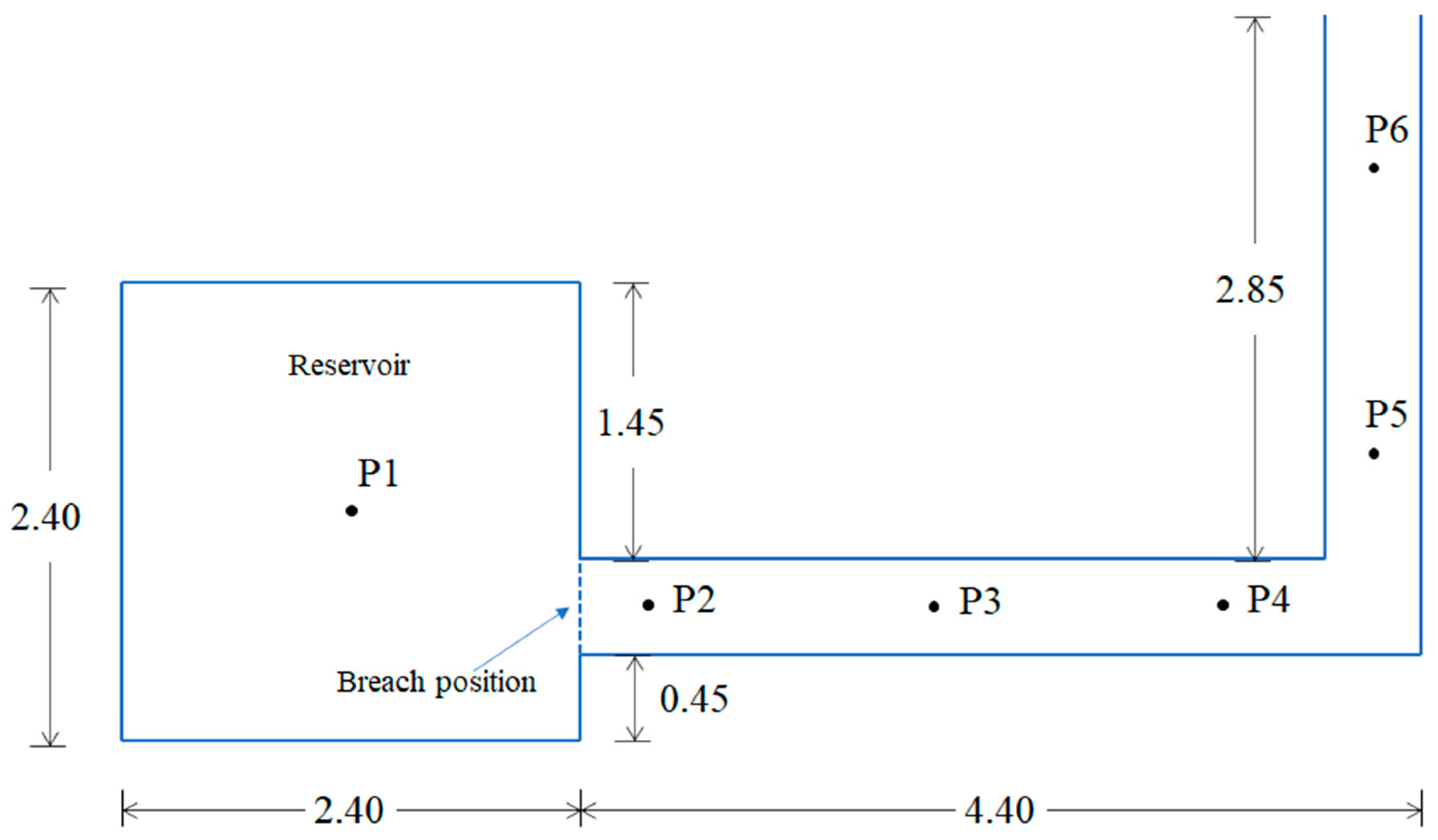
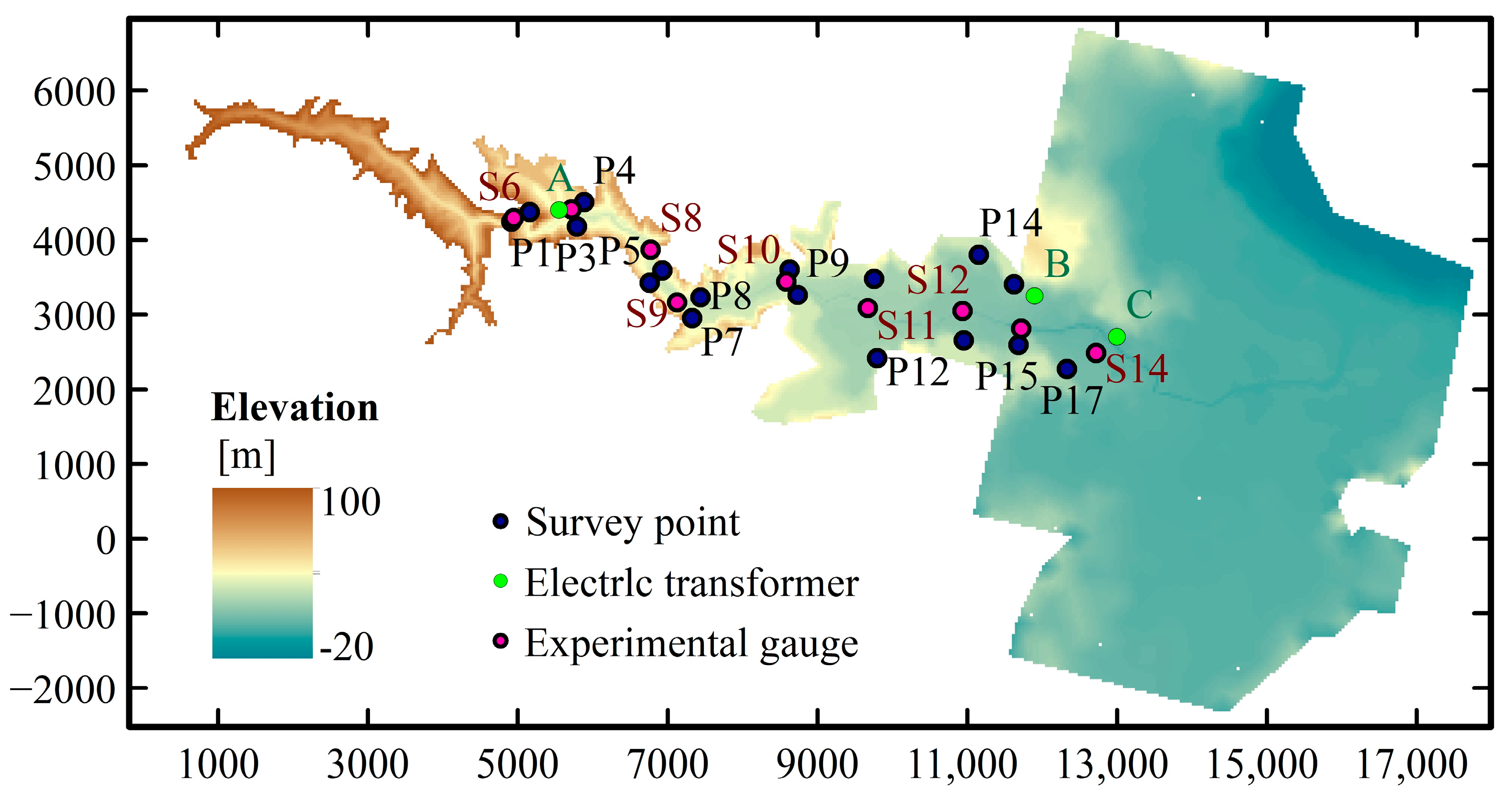
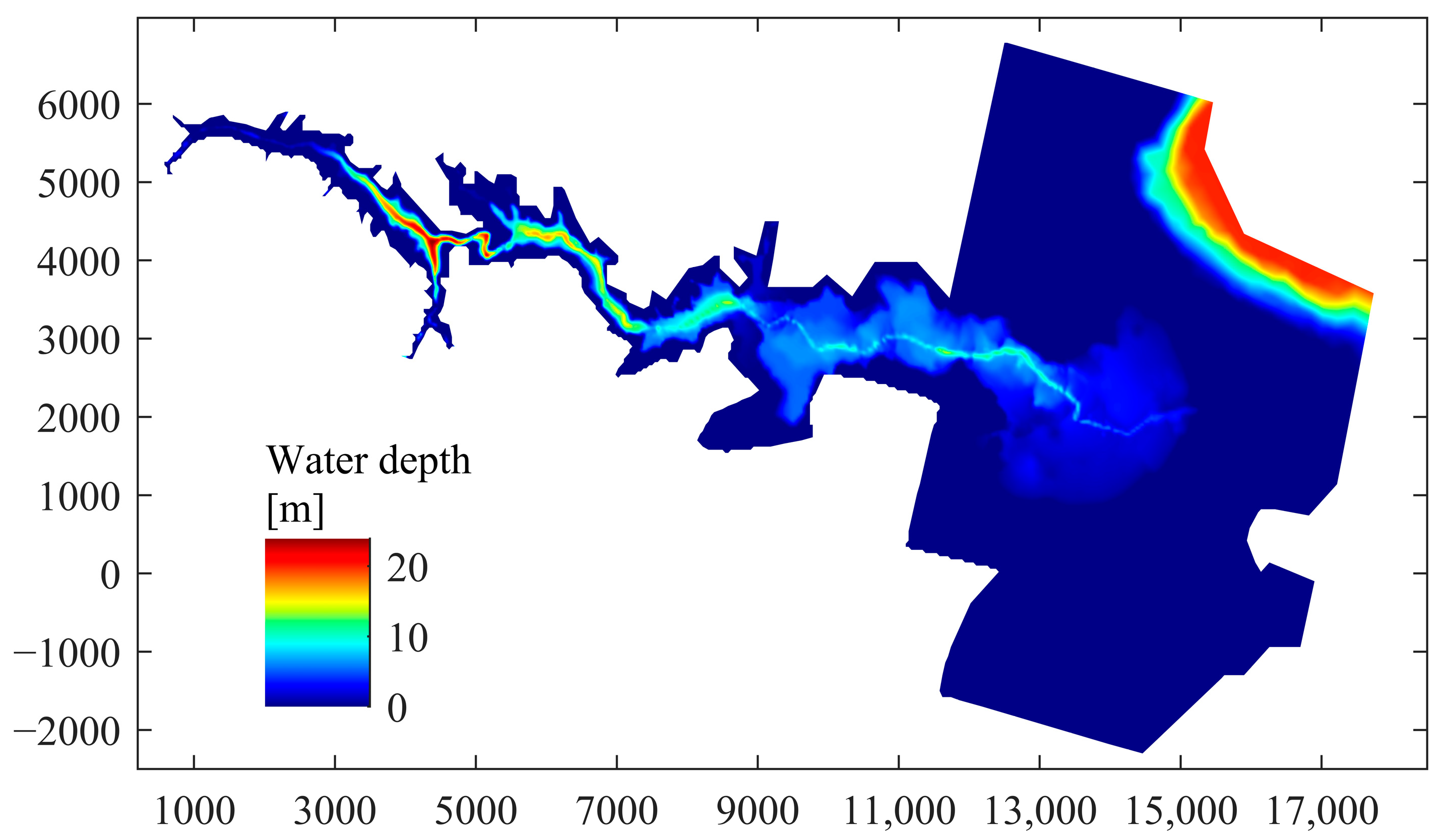
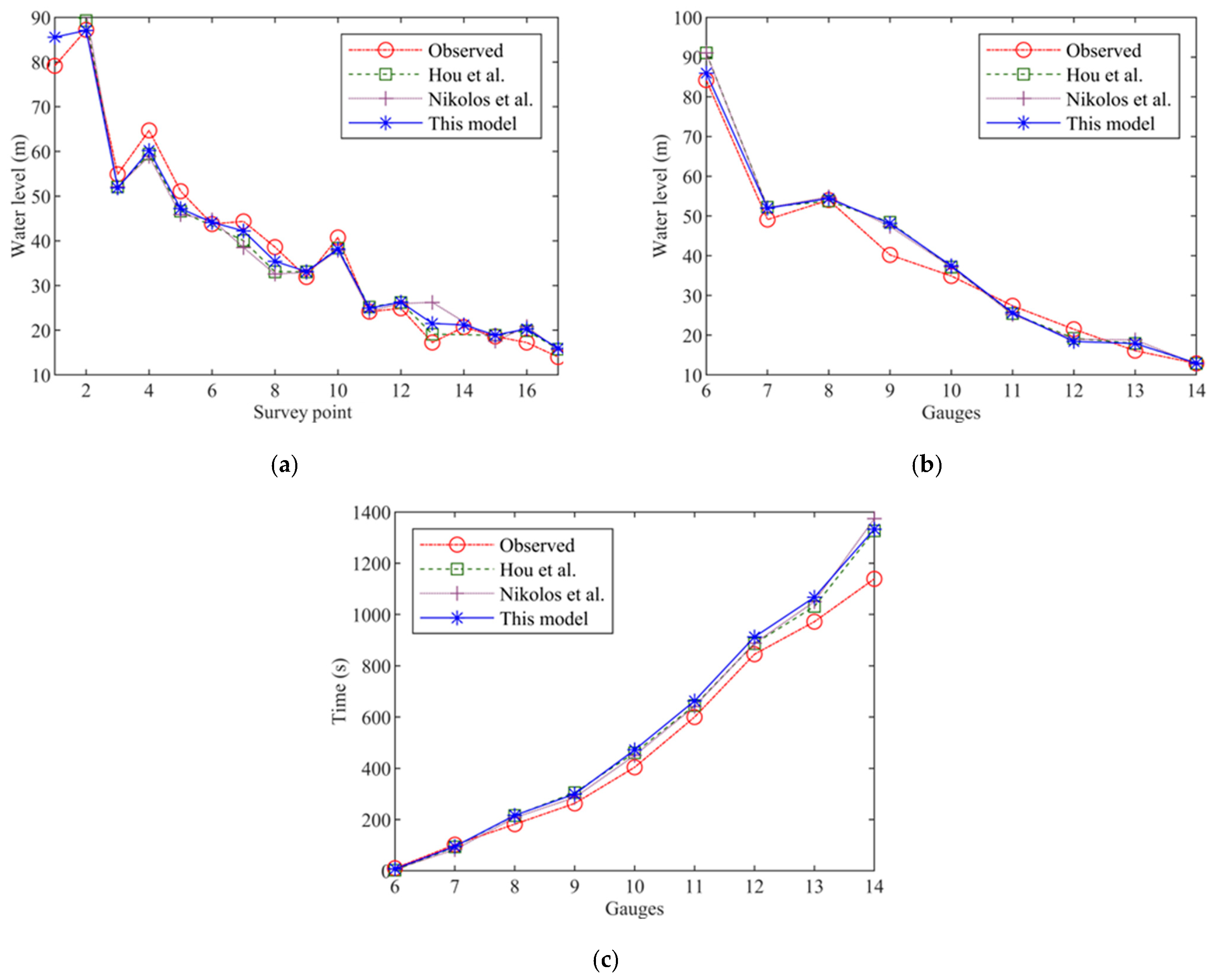
4.5. Malpasset Dam Break
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, S.; Duffy, C.J. Fully coupled approach to modeling shallow water flow, sediment transport, and bed evolution in rivers. Water Resour. Res. 2011, 47, W03508. [Google Scholar] [CrossRef]
- Aricò, C.; Sinagra, S.; Begnudelli, L.; Tucciarelli, T. MAST-2D diffusive model for flood prediction on domains with triangular Delaunay unstructured meshes. Adv. Water Resour. 2011, 34, 1427–1449. [Google Scholar] [CrossRef] [Green Version]
- Benkhaldoun, F.; Sahmim, S.; Sea, D.M. A two-dimensional finite volume morphodynamic model on unstructured triangular grids. Int. J. Numer. Methods Fluids 2010, 63, 1296–1327. [Google Scholar] [CrossRef]
- Canestrelli, A.; Fagherazzi, S.; Lanzoni, S. A mass-conservative centered finite volume model for solving two-dimensional two-layer shallow water equations for fluid mud propagation over varying topography and dry areas. Adv. Water Resour. 2012, 40, 54–70. [Google Scholar] [CrossRef]
- Fiedler, F.R.; Ramirez, J.A. A numerical method for simulating discontinuous shallow flow over an infiltrating surface. Int. J. Numer. Methods Fluids 2000, 32, 219–239. [Google Scholar] [CrossRef]
- Song, L.; Zhou, J.; Guo, J.; Zou, Q.; Liu, Y. A robust well-balanced finite volume model for shallow water flows with wetting and drying over irregular terrain. Adv. Water Resour. 2011, 34, 915–932. [Google Scholar] [CrossRef]
- Simons, F.; Busse, T.; Hou, J.; Özgen, I.; Hinkelmann, R. A model for overland flow and associated processes within the Hydroinformatics Modelling System. J. Hydroinformatics 2014, 16, 375–391. [Google Scholar] [CrossRef]
- Yu, C.; Duan, J. Two-dimensional hydrodynamic model for surface-flow routing. J. Hydraul. Eng. 2014, 140, 04014045. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, W.; Hu, C.; Hu, C.; Li, M.; Hao, X.; Liu, S. A distributed hydrodynamic model for urban storm flood risk assessment. J. Hydrol. 2021, 600, 126513. [Google Scholar] [CrossRef]
- Toro, E.F.; Garcia-Navarro, P. Godunov-type methods for free-surface shallow flows: A review. J. Hydraul. Res. 2007, 45, 736–751. [Google Scholar] [CrossRef]
- LeVeque, R.J. Balancing source terms and flux gradients in high-resolution Godunov methods: The quasi-steady wave-propagation algorithm. J. Comput. Phys. 1998, 146, 346–365. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Quan, J.; Wang, Z.; Zhang, H.; Ma, J. Numerical Simulation of Overland Flows Using Godunov Scheme Based on Finite Volume Method. EPiC Ser. Eng. 2018, 3, 2425–2432. [Google Scholar]
- LeFloch, P.G.; Thanh, M.D. A Godunov-type method for the shallow water equations with discontinuous topography in the resonant regime. J. Comput. Phys. 2011, 230, 7631–7660. [Google Scholar] [CrossRef] [Green Version]
- Brufau, P.; Garcia-Navarro, P. Two-dimensional dam break flow simulation. Int. J. Numer. Methods Fluids 2000, 33, 35–57. [Google Scholar] [CrossRef]
- George, D.L. Augmented Riemann solvers for the shallow water equations over variable topography with steady states and inundation. J. Comput. Phys. 2008, 227, 3089–3113. [Google Scholar] [CrossRef]
- Harten, A.; Lax, P.D.; Leer, B.V. On Upstream Differencing and Godunov-Type Schemes for Hyperbolic Conservation Laws. SIAM Rev. 1983, 25, 35–61. [Google Scholar] [CrossRef]
- Toro, E.F.; Spruce, M.; Speares, W. Restoration of the contact surface in the HLL-Riemann solver. Shock Waves 1994, 4, 25–34. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P. Weak solutions for partial differential equations with source terms: Application to the shallow water equations. J. Comput. Phys. 2010, 229, 4327–4368. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P. Augmented versions of the HLL and HLLC Riemann solvers including source terms in one and two dimensions for shallow flow applications. J. Comput. Phys. 2012, 231, 6861–6906. [Google Scholar] [CrossRef]
- Hou, J.; Liang, Q.; Simons, F.; Hinkelmann, R. A stable 2D unstructured shallow flow model for simulations of wetting and drying over rough terrains. Comput. Fluids 2013, 82, 132–147. [Google Scholar] [CrossRef]
- Marche, F.; Bonneton, P.; Fabrie, P.; Seguin, N. Evaluation of well-balanced bore-capturing schemes for 2D wetting and drying processes. Int. J. Numer. Methods Fluids 2007, 53, 867–894. [Google Scholar] [CrossRef]
- Song, L.; Zhou, J.; Li, Q.; Yang, X.; Zhang, Y. An unstructured finite volume model for dam-break floods with wet/dry fronts over complex topography. Int. J. Numer. Methods Fluids 2011, 67, 960–980. [Google Scholar] [CrossRef]
- Audusse, E.; Bouchut, F.; Bristeau, M.-O.; Klein, R.; Perthame, B.T. A Fast and Stable Well-Balanced Scheme with Hydrostatic Reconstruction for Shallow Water Flows. SIAM J. Sci. Comput. 2004, 25, 2050–2065. [Google Scholar] [CrossRef] [Green Version]
- Liang, Q.; Marche, F. Numerical resolution of well-balanced shallow water equations with complex source terms. Adv. Water Resour. 2009, 32, 873–884. [Google Scholar] [CrossRef]
- Xia, X.; Liang, Q.; Ming, X.; Hou, J. An efficient and stable hydrodynamic model with novel source term discretization schemes for overland flow and flood simulations. Water Resour. Res. 2017, 53, 3730–3759. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D. Effects of spatial resolution on a raster based model of flood flow. J. Hydrol. 2001, 253, 239–249. [Google Scholar] [CrossRef]
- Brown, J.D.; Spencer, T.; Moeller, I. Modeling storm surge flooding of an urban area with particular reference to modeling uncertainties: A case study of Canvey Island, United Kingdom. Water Resour. Res. 2007, 43, W06402. [Google Scholar] [CrossRef] [Green Version]
- Huxley, C. Rapid and Accurate Storm Water Drainage System Assessments Using GPU Technology; BMT: Brisbane, Australia, 2017. [Google Scholar]
- Fewtrell, T.; Bates, P.D.; Horritt, M.; Hunter, N. Evaluating the effect of scale in flood inundation modelling in urban environments. Hydrol. Process. Int. J. 2008, 22, 5107–5118. [Google Scholar] [CrossRef]
- Leandro, J.; Chen, A.S.; Schumann, A. A 2D parallel diffusive wave model for floodplain inundation with variable time step (P-DWave). J. Hydrol. 2014, 517, 250–259. [Google Scholar] [CrossRef]
- Wu, Y.; Tian, L.; Rubinato, M.; Gu, S.; Yu, T.; Xu, Z.; Cao, P.; Wang, X.; Zhao, Q. A New Parallel Framework of SPH-SWE for Dam Break Simulation Based on OpenMP. Water 2020, 12, 1395. [Google Scholar] [CrossRef]
- Xia, X.; Liang, Q.; Ming, X. A full-scale fluvial flood modelling framework based on a high-performance integrated hydrodynamic modelling system (HiPIMS). Adv. Water Resour. 2019, 132, 103392. [Google Scholar] [CrossRef]
- Hou, J.; Liang, Q.; Simons, F.; Hinkelmann, R. A 2D well-balanced shallow flow model for unstructured grids with novel slope source term treatment. Adv. Water Resour. 2013, 52, 107–131. [Google Scholar] [CrossRef]
- Gottardi, G.; Venutelli, M. Central scheme for two-dimensional dam-break flow simulation. Adv. Water Resour. 2004, 27, 259–268. [Google Scholar] [CrossRef]
- Frazão, S.S.; Zech, Y. Dam Break in Channels with 90° Bend. J. Hydraul. Eng. 2002, 128, 956–968. [Google Scholar] [CrossRef]
- Cea, L.; Garrido, M.; Puertas, J. Experimental validation of two-dimensional depth-averaged models for forecasting rainfall–runoff from precipitation data in urban areas. J. Hydrol. 2010, 382, 88–102. [Google Scholar] [CrossRef]
- Cea, L.; Garrido, M.; Puertas, J.; Jácome, A.; Del Río, H.; Suárez, J. Overland flow computations in urban and industrial catchments from direct precipitation data using a two-dimensional shallow water model. Water Sci. Technol. J. Int. Assoc. Water Pollut. Res. 2010, 62, 1998–2008. [Google Scholar] [CrossRef]
- Testa, G.; Zuccala, D.; Alcrudo, F.; Mulet, J.; Soares-Frazão, S. Flash flood flow experiment in a simplified urban district. J. Hydraul. Res. 2007, 45, 37–44. [Google Scholar] [CrossRef]
- Goutal, N. The Malpasset dam failure. An overview and test case definition. In Proceedings of the 4th CADAM Meeting, Zaragoza, Spain, 18–19 November 1999; pp. 18–19. [Google Scholar]
- Yoon, T.H.; Kang, S.-K. Finite volume model for two-dimensional shallow water flows on unstructured grids. J. Hydraul. Eng. 2004, 130, 678–688. [Google Scholar] [CrossRef]
- George, D. Adaptive finite volume methods with well-balanced Riemann solvers for modeling floods in rugged terrain: Application to the Malpasset dam-break flood (France, 1959). Int. J. Numer. Methods Fluids 2011, 66, 1000–1018. [Google Scholar] [CrossRef]
- Nikolos, I.; Delis, A. An unstructured node-centered finite volume scheme for shallow water flows with wet–dry fronts over complex topography. Comput. Methods Appl. Mech. Eng. 2009, 198, 3723–3750. [Google Scholar] [CrossRef]

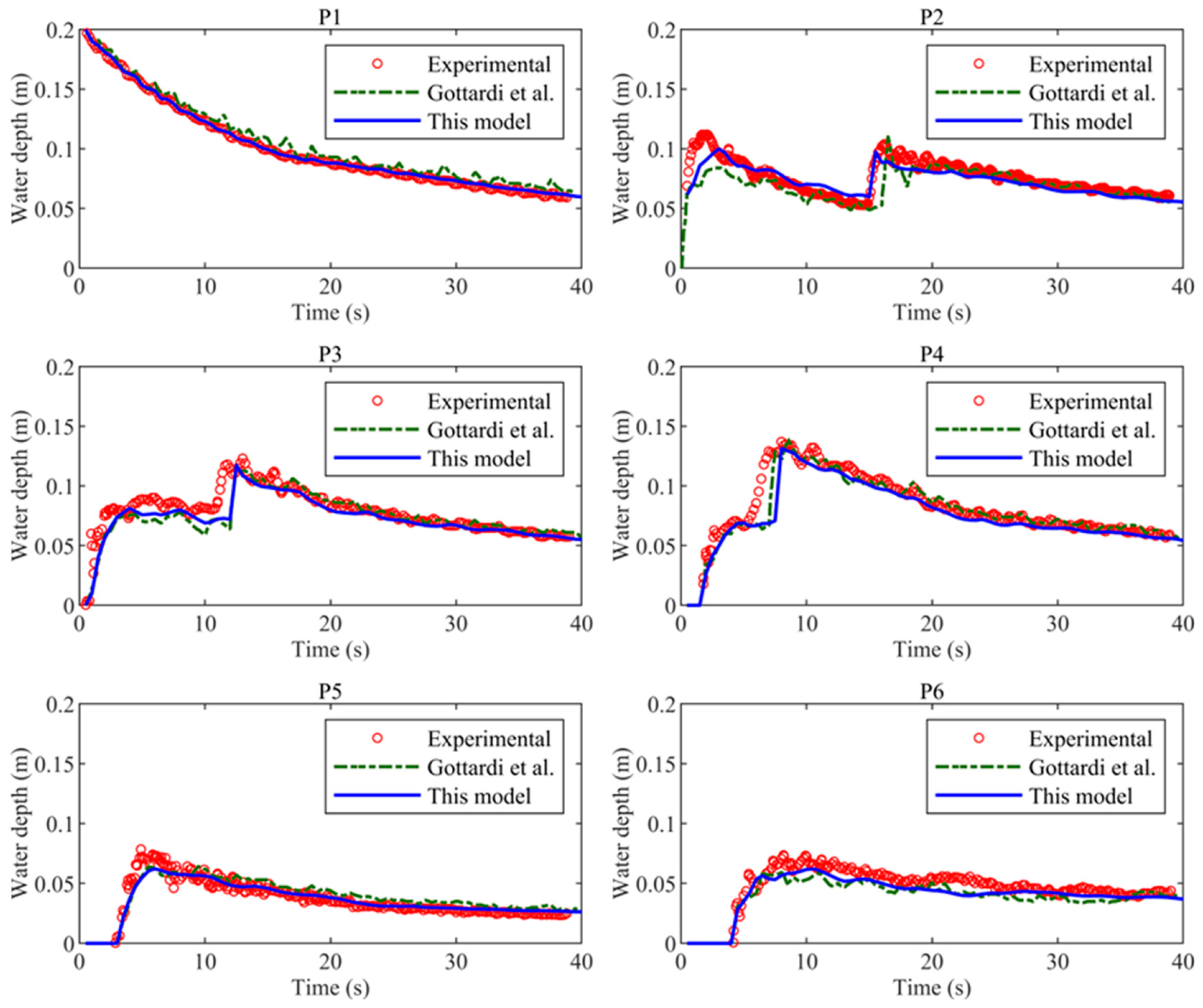

| Point | X (m) | Y (m) |
|---|---|---|
| P1 | 1.20 | 1.20 |
| P2 | 2.75 | 0.70 |
| P3 | 4.25 | 0.70 |
| P4 | 5.75 | 0.70 |
| P5 | 6.55 | 1.50 |
| P6 | 6.55 | 3.00 |
| Rainfall Events | Rainfall Intensity (mm/h) | Rainfall Duration (s) |
|---|---|---|
| R1 | 300 | 20 |
| R2 | 300 | 40 |
| R3 | 300 | 60 |
| Hardware | Hardware Setup | Hardware Cores | Computational Cost (s) | Speeding Up Ratio |
|---|---|---|---|---|
| CPU | INTER i9-10900 1 | 1 | 1034.235 | 1.00 |
| 2 | 699.198 | 1.48 | ||
| 4 | 448.042 | 2.31 | ||
| 6 | 315.580 | 3.28 | ||
| 8 | 297.681 | 3.47 | ||
| 10 | 275.372 | 3.76 | ||
| GPU | NVIDIA Geforce GTX 1660Ti 2 | 1536 | 77.210 | 13.40 |
| NVIDIA Geforce RTX 3070 Laptop 2 | 5120 | 50.283 | 20.57 | |
| NVIDIA RTX A4000 2 | 6144 | 47.012 | 22.00 | |
| NVIDIA Geforce RTX 3080Ti 2 | 10,240 | 39.612 | 26.11 | |
| NVIDIA Geforce RTX 3090 2 | 10,496 | 35.718 | 28.96 | |
| NVIDIA Geforce RTX 4090 2 | 16,384 | 13.888 | 74.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, F.; Hao, X.; Chai, F. A GPU-Accelerated Two-Dimensional Hydrodynamic Model for Unstructured Grids. Water 2023, 15, 1300. https://doi.org/10.3390/w15071300
Peng F, Hao X, Chai F. A GPU-Accelerated Two-Dimensional Hydrodynamic Model for Unstructured Grids. Water. 2023; 15(7):1300. https://doi.org/10.3390/w15071300
Chicago/Turabian StylePeng, Feng, Xiaoli Hao, and Fuxin Chai. 2023. "A GPU-Accelerated Two-Dimensional Hydrodynamic Model for Unstructured Grids" Water 15, no. 7: 1300. https://doi.org/10.3390/w15071300





