Downscaling and Merging of Daily Scale Satellite Precipitation Data in the Three River Headwaters Region Fused with Cloud Attributes and Rain Gauge Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. Satellite Precipitation Dataset
2.2.2. Rain Gauge Data
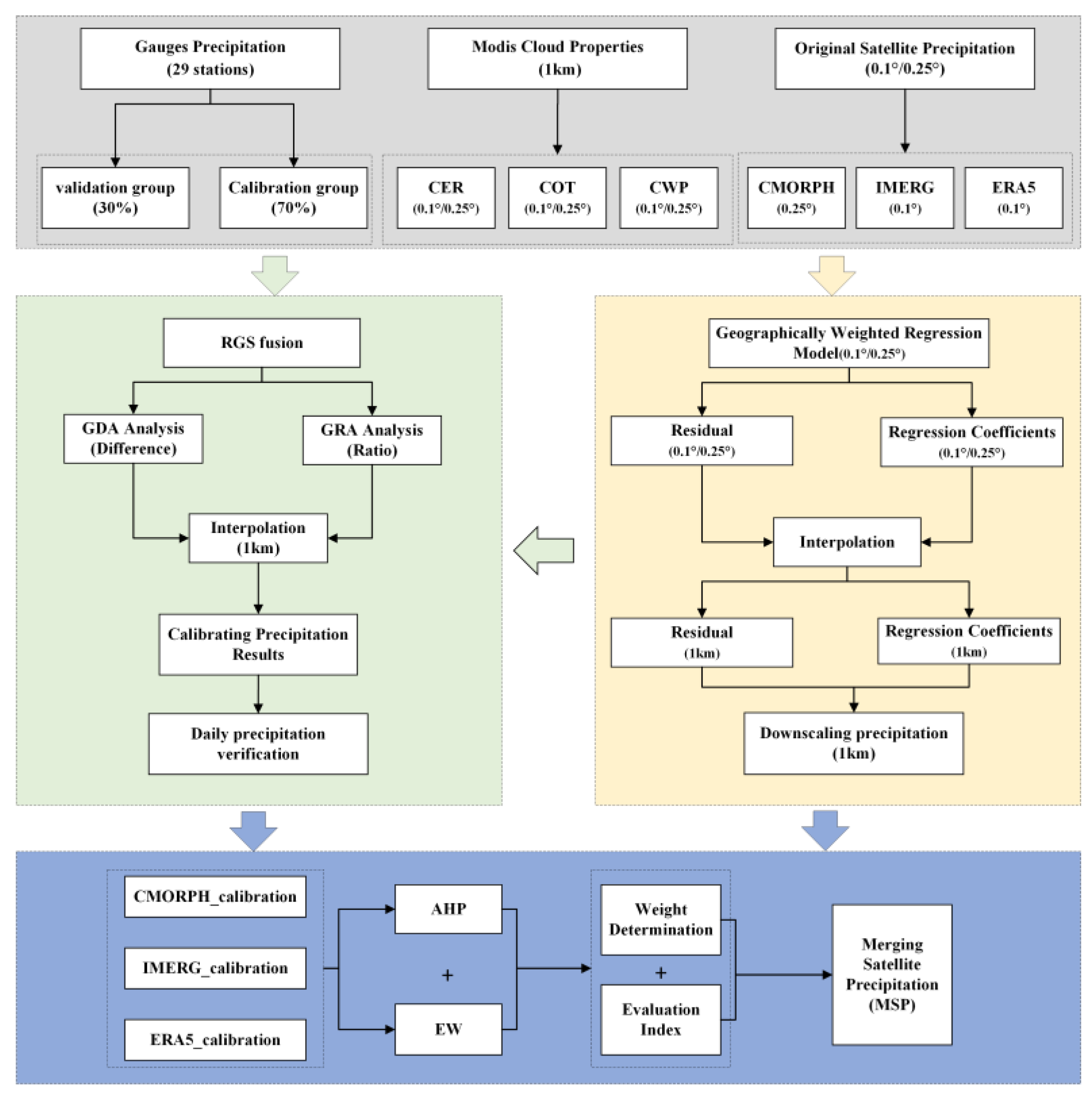
2.3. Methodology
2.3.1. Geographically Weighted Regression Models
- (1)
- Gaussian function
- (2)
- Bi-square function
2.3.2. Geographic Difference Analysis and Geographic Ratio Analysis
- (1)
- Calculate the difference/ratio between downscaled precipitation and RGS measurements:
- (2)
- Interpolate the difference/ratio to 1 km resolution using interpolation techniques (GDA: IDW, Kriging, RBF; GRA: IDW).
- (3)
- Calibrate downscaled precipitation to obtain the final downscaled results:
2.3.3. Satellite Precipitation Data Fusion
- (1)
- Construct a hierarchical structure, determine the judgment matrix according to the quality evaluation indicators and prior knowledge, and assign different values to represent the difference in the importance of the indicators.
- (2)
- Calculate the eigenvalues and eigenvectors of the judgment matrix:
- (3)
- Consistency verification:
- (1)
- Standardize evaluation indicators.
- (2)
- Calculate indicator proportion:
- (3)
- Calculate the entropy value and information entropy redundancy corresponding to each index as follows:
- (4)
- Calculate the weight of the indicator as follows:
2.3.4. Validation
3. Results
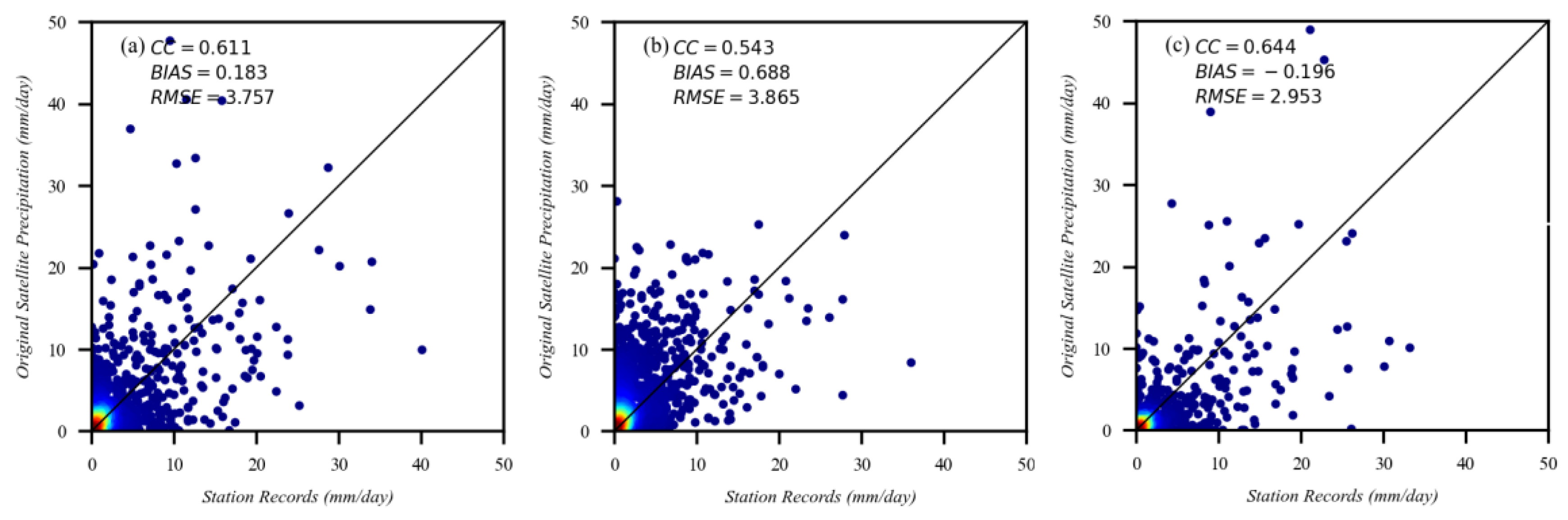
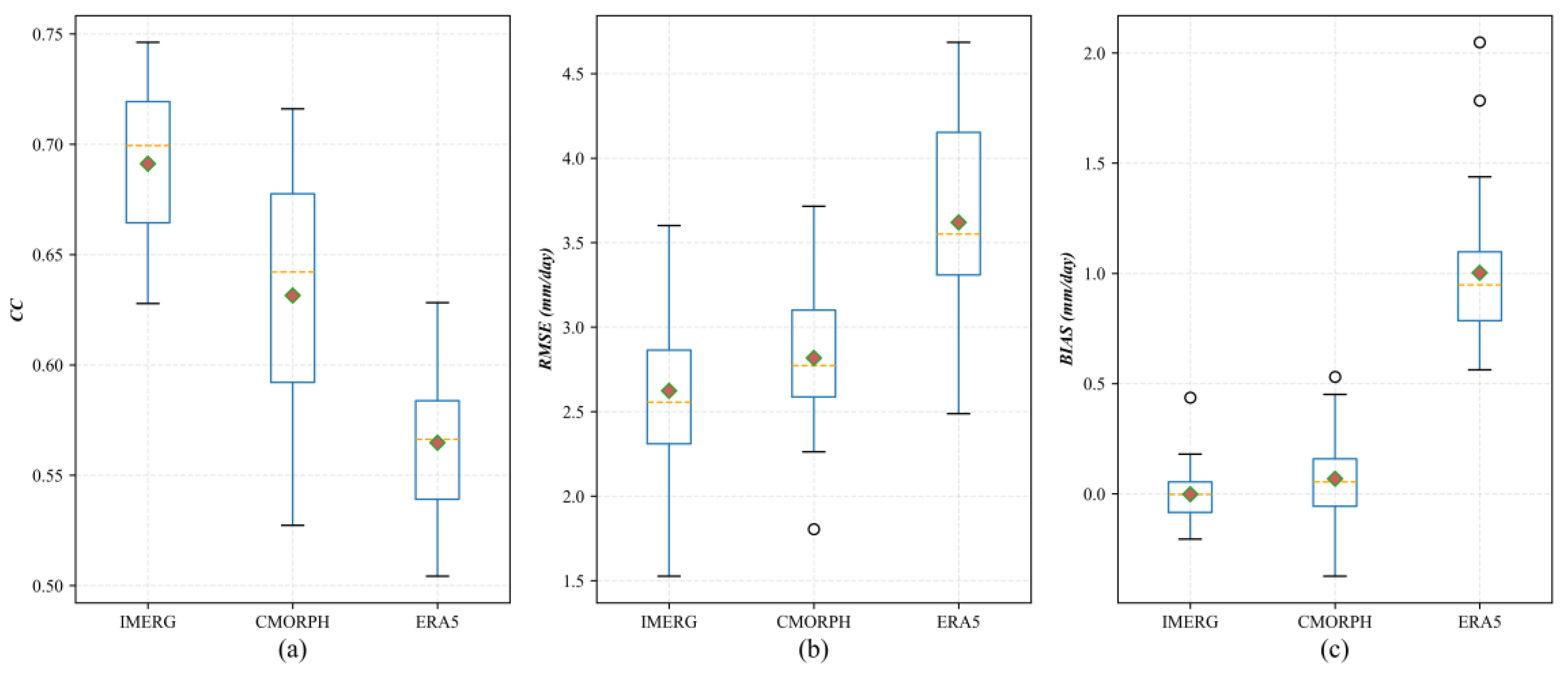
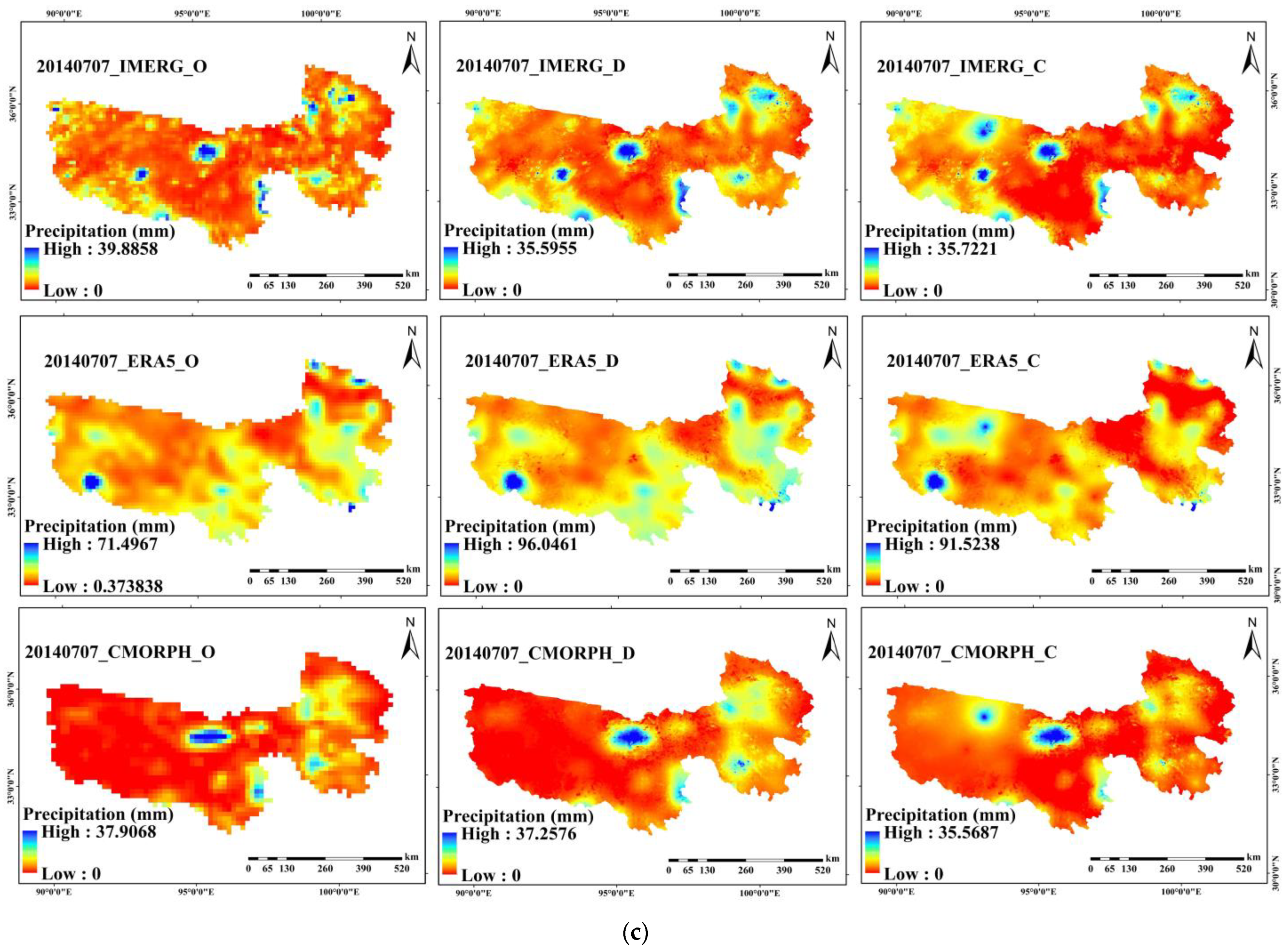
3.1. Accuracy of the Original Satellite Precipitation Dataset
3.2. The Relationship between Cloud Physical and Optical Properties and Precipitation
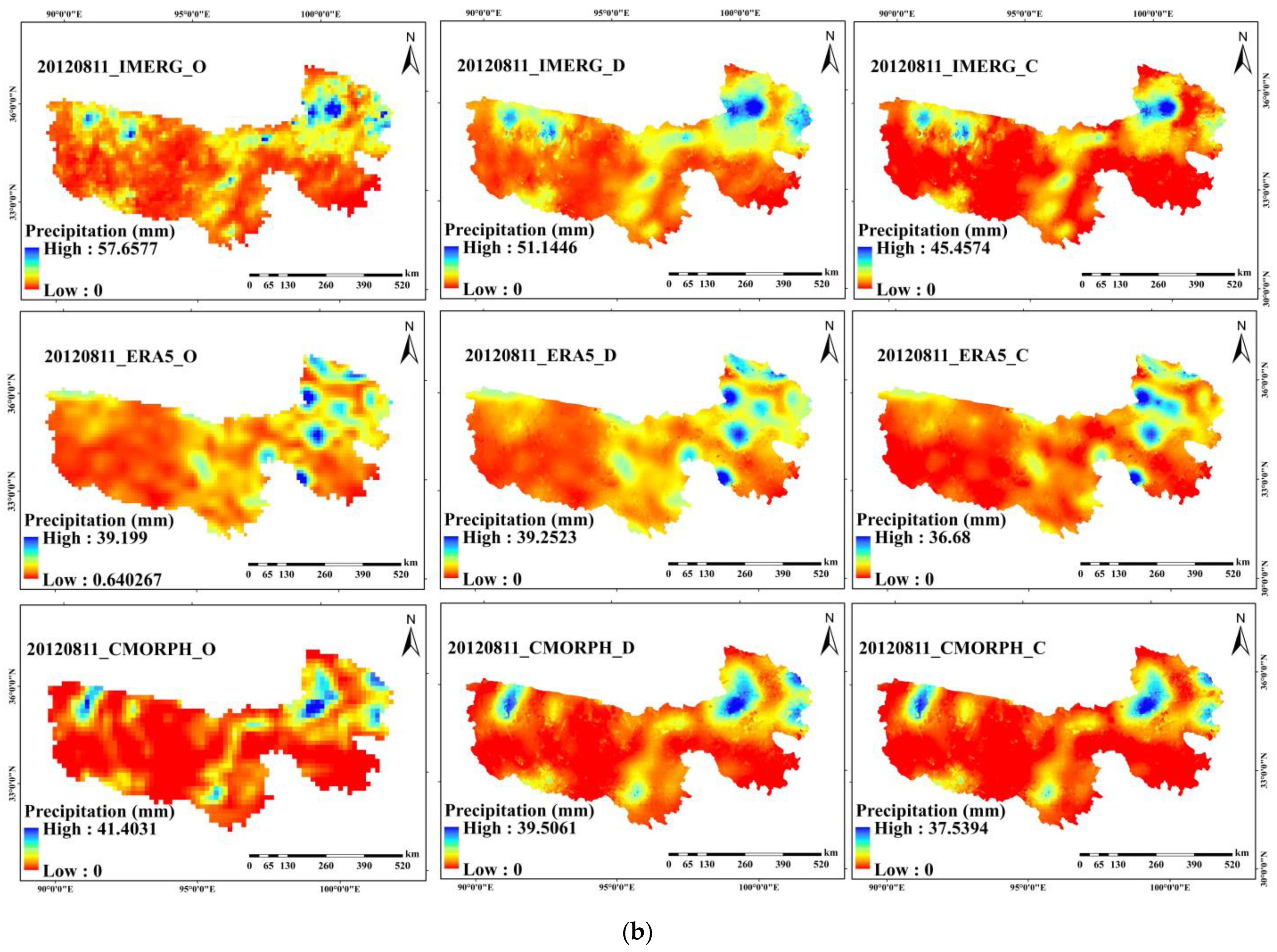
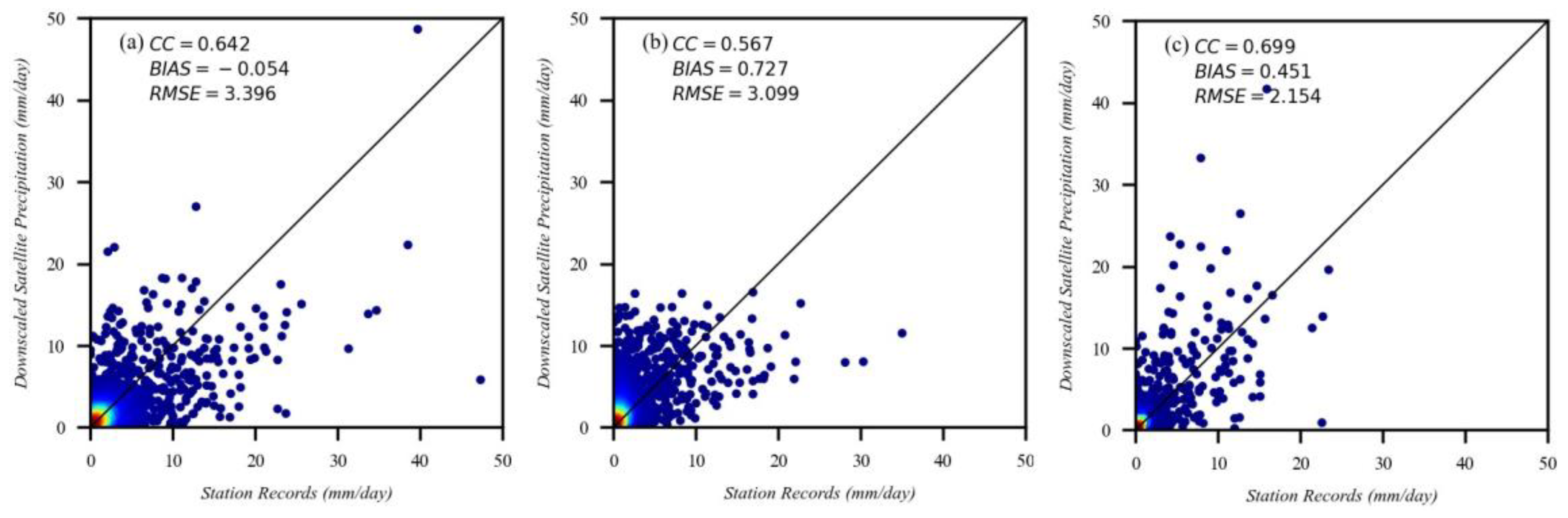
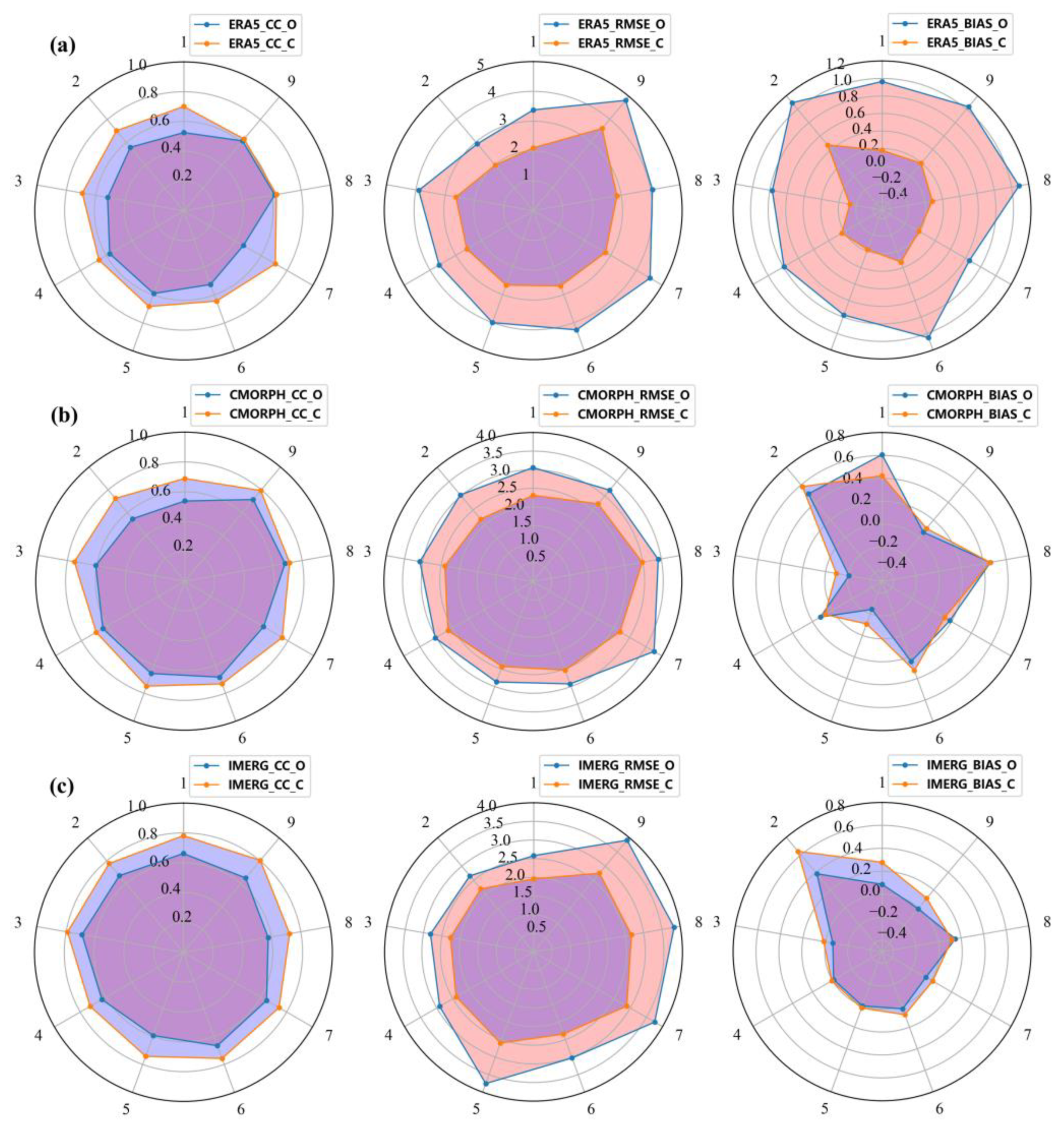
3.3. Evaluation of Downscaling Accuracy of Daily Scale Satellite Precipitation Datasets Based on GWR Model
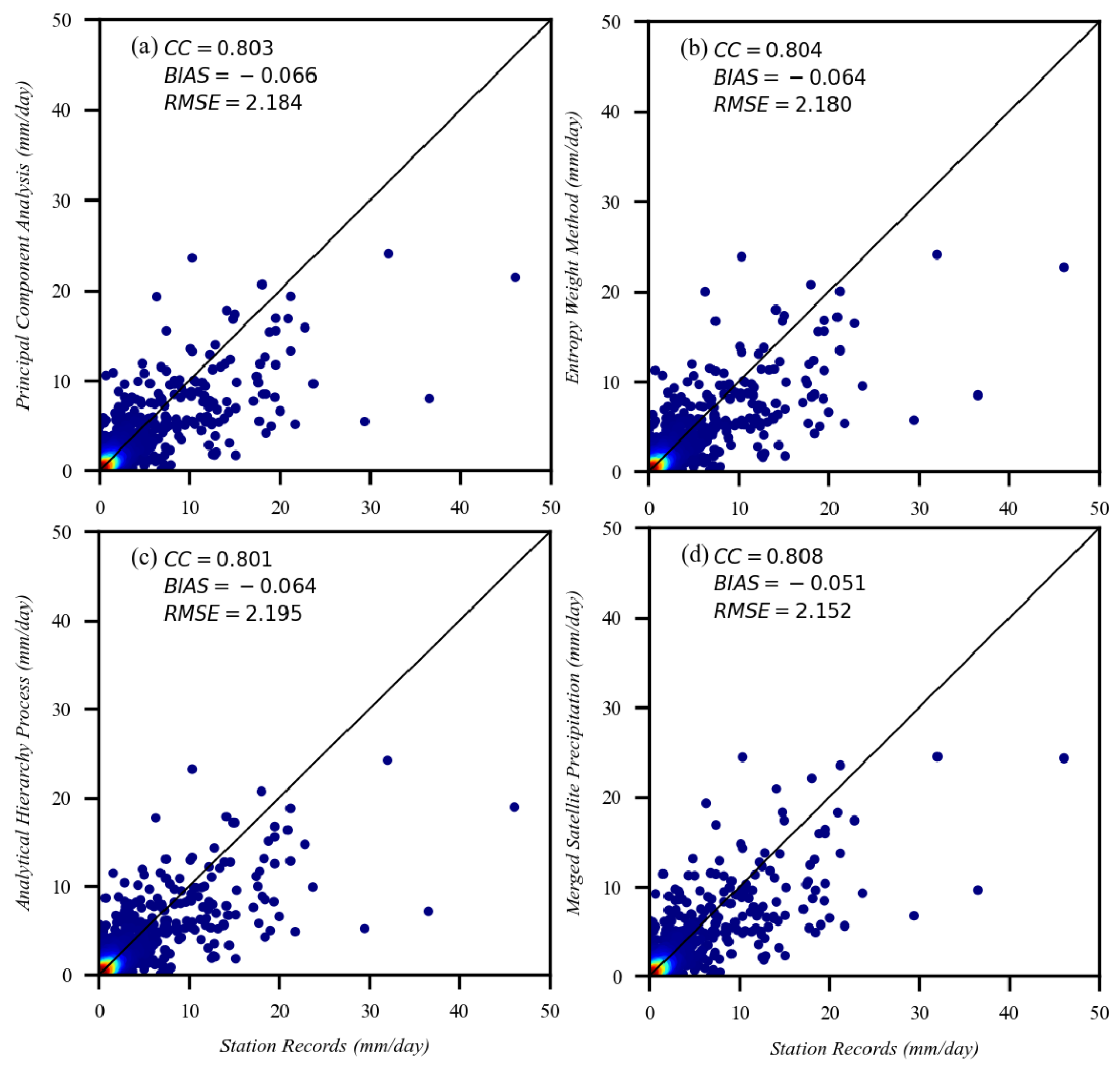
3.4. Data Fusion of Downscaled Precipitation with Rain Gauge Observations
3.5. Performance of the Merged Satellite Precipitation
3.6. Temporal and Spatial Characteristics of Precipitation Data
4. Discussion
4.1. Feasibility of a GWR Downscaling Model Based on the Correlation between Cloud Attributes and Daily Precipitation Data
4.2. Evaluation of Merged Satellite Precipitation
4.3. Sources of Error and Uncertainty in GWR Downscaling Models
4.4. Directions for Future Research Improvement
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, S.; Xiong, L.; Ma, Q.; Kim, J.-S.; Chen, J.; Xu, C.-Y. Improving Daily Spatial Precipitation Estimates by Merging Gauge Observation with Multiple Satellite-Based Precipitation Products Based on the Geographically Weighted Ridge Regression Method. J. Hydrol. 2020, 589, 125156. [Google Scholar] [CrossRef]
- Hussain, Y.; Satgé, F.; Hussain, M.B.; Martinez-Carvajal, H.; Bonnet, M.-P.; Cárdenas-Soto, M.; Roig, H.L.; Akhter, G. Performance of CMORPH, TMPA, and PERSIANN Rainfall Datasets over Plain, Mountainous, and Glacial Regions of Pakistan. Theor. Appl. Climatol. 2018, 131, 1119–1132. [Google Scholar] [CrossRef]
- Bohnenstengel, S.I.; Schlünzen, K.H.; Beyrich, F. Representativity of in Situ Precipitation Measurements—A Case Study for the LITFASS Area in North-Eastern Germany. J. Hydrol. 2011, 400, 387–395. [Google Scholar] [CrossRef]
- Arshad, A.; Zhang, W.; Zhang, Z.; Wang, S.; Zhang, B.; Cheema, M.J.M.; Shalamzari, M.J. Reconstructing High-Resolution Gridded Precipitation Data Using an Improved Downscaling Approach over the High Altitude Mountain Regions of Upper Indus Basin (UIB). Sci. Total Environ. 2021, 784, 147140. [Google Scholar] [CrossRef]
- Wang, S.; Xu, C.; Zhang, W.; Chen, H.; Zhang, B. Human-Induced Water Loss from Closed Inland Lakes: Hydrological Simulations in China’s Daihai Lake. J. Hydrol. 2022, 607, 127552. [Google Scholar] [CrossRef]
- Gao, Z.; Long, D.; Tang, G.; Zeng, C.; Huang, J.; Hong, Y. Assessing the Potential of Satellite-Based Precipitation Estimates for Flood Frequency Analysis in Ungauged or Poorly Gauged Tributaries of China’s Yangtze River Basin. J. Hydrol. 2017, 550, 478–496. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, L.; Hong, Y.; Yong, B.; Yang, X.; Yuan, F.; Ma, M. Comprehensive Evaluation of Multi-Satellite Precipitation Products with a Dense Rain Gauge Network and Optimally Merging Their Simulated Hydrological Flows Using the Bayesian Model Averaging Method. J. Hydrol. 2012, 452–453, 213–225. [Google Scholar] [CrossRef]
- Aslami, F.; Ghorbani, A.; Sobhani, B.; Esmali, A. Comprehensive Comparison of Daily IMERG and GSMaP Satellite Precipitation Products in Ardabil Province, Iran. Int. J. Remote Sens. 2019, 40, 3139–3153. [Google Scholar] [CrossRef]
- Skaugen, T.; Andersen, J. Simulated Precipitation Fields with Variance-Consistent Interpolation. Hydrol. Sci. J. 2010, 55, 676–686. [Google Scholar] [CrossRef]
- Darand, M.; Amanollahi, J.; Zandkarimi, S. Evaluation of the Performance of TRMM Multi-Satellite Precipitation Analysis (TMPA) Estimation over Iran. Atmospheric Res. 2017, 190, 121–127. [Google Scholar] [CrossRef]
- Zhang, T.; Li, B.; Yuan, Y.; Gao, X.; Sun, Q.; Xu, L.; Jiang, Y. Spatial Downscaling of TRMM Precipitation Data Considering the Impacts of Macro-Geographical Factors and Local Elevation in the Three-River Headwaters Region. Remote Sens. Environ. 2018, 215, 109–127. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method That Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Ushio, T.; Sasashige, K.; Kubota, T.; Shige, S.; Okamoto, K.; Aonashi, K.; Inoue, T.; Takahashi, N.; Iguchi, T.; Kachi, M.; et al. A Kalman Filter Approach to the Global Satellite Mapping of Precipitation (GSMaP) from Combined Passive Microwave and Infrared Radiometric Data. J. Meteorol. Soc. Jpn. Ser II 2009, 87A, 137–151. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G. Improving the Global Precipitation Record: GPCP Version 2.1. Geophys. Res. Lett. 2009, 36, L17808. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Arkin, P.; Chang, A.; Ferraro, R.; Gruber, A.; Janowiak, J.; McNab, A.; Rudolf, B.; Schneider, U. The Global Precipitation Climatology Project (GPCP) Combined Precipitation Dataset. Bull. Am. Meteorol. Soc. 1997, 78, 5–20. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, W.; Nie, N. Spatial Downscaling of TRMM Precipitation Data Using an Optimal Subset Regression Model with NDVI and Terrain Factors in the Yarlung Zangbo River Basin, China. Adv. Meteorol. 2018, 2018, 3491960. [Google Scholar] [CrossRef]
- Zhan, C.; Han, J.; Hu, S.; Liu, L.; Dong, Y. Spatial Downscaling of GPM Annual and Monthly Precipitation Using Regression-Based Algorithms in a Mountainous Area. Adv. Meteorol. 2018, 2018, 1506017. [Google Scholar] [CrossRef]
- Massari, C.; Crow, W.; Brocca, L. An Assessment of the Performance of Global Rainfall Estimates without Ground-Based Observations. Hydrol. Earth Syst. Sci. 2017, 21, 4347–4361. [Google Scholar] [CrossRef]
- Li, L.; Hong, Y.; Wang, J.; Adler, R.F.; Policelli, F.S.; Habib, S.; Irwn, D.; Korme, T.; Okello, L. Evaluation of the Real-Time TRMM-Based Multi-Satellite Precipitation Analysis for an Operational Flood Prediction System in Nzoia Basin, Lake Victoria, Africa. Nat. Hazards 2009, 50, 109–123. [Google Scholar] [CrossRef]
- Ringard, J.; Becker, M.; Seyler, F.; Linguet, L. Temporal and Spatial Assessment of Four Satellite Rainfall Estimates over French Guiana and North Brazil. Remote Sens. 2015, 7, 16441–16459. [Google Scholar] [CrossRef]
- Sohn, B.J.; Han, H.-J.; Seo, E.-K. Validation of Satellite-Based High-Resolution Rainfall Products over the Korean Peninsula Using Data from a Dense Rain Gauge Network. J. Appl. Meteorol. Climatol. 2010, 49, 701–714. [Google Scholar] [CrossRef]
- Tong, K.; Su, F.; Yang, D.; Hao, Z. Evaluation of Satellite Precipitation Retrievals and Their Potential Utilities in Hydrologic Modeling over the Tibetan Plateau. J. Hydrol. 2014, 519, 423–437. [Google Scholar] [CrossRef]
- Wang, W.; Lu, H.; Yang, D.; Sothea, K.; Jiao, Y.; Gao, B.; Peng, X.; Pang, Z. Modelling Hydrologic Processes in the Mekong River Basin Using a Distributed Model Driven by Satellite Precipitation and Rain Gauge Observations. PLoS ONE 2016, 11, e0152229. [Google Scholar] [CrossRef]
- Yaduvanshi, A.; Srivastava, P.K.; Pandey, A.C. Integrating TRMM and MODIS Satellite with Socio-Economic Vulnerability for Monitoring Drought Risk over a Tropical Region of India. Phys. Chem. Earth Parts ABC 2015, 83–84, 14–27. [Google Scholar] [CrossRef]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have Satellite Precipitation Products Improved over Last Two Decades? A Comprehensive Comparison of GPM IMERG with Nine Satellite and Reanalysis Datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Maggioni, V.; Meyers, P.C.; Robinson, M.D. A Review of Merged High-Resolution Satellite Precipitation Product Accuracy during the Tropical Rainfall Measuring Mission (TRMM) Era. J. Hydrometeorol. 2016, 17, 1101–1117. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. First Results from Version 7 TRMM 3B43 Precipitation Product in Combination with a New Downscaling–Calibration Procedure. Remote Sens. Environ. 2013, 131, 1–13. [Google Scholar] [CrossRef]
- Ma, Z.; Tan, X.; Yang, Y.; Chen, X.; Kan, G.; Ji, X.; Lu, H.; Long, J.; Cui, Y.; Hong, Y. The First Comparisons of IMERG and the Downscaled Results Based on IMERG in Hydrological Utility over the Ganjiang River Basin. Water 2018, 10, 1392. [Google Scholar] [CrossRef]
- Xu, S.; Wu, C.; Wang, L.; Gonsamo, A.; Shen, Y.; Niu, Z. A New Satellite-Based Monthly Precipitation Downscaling Algorithm with Non-Stationary Relationship between Precipitation and Land Surface Characteristics. Remote Sens. Environ. 2015, 162, 119–140. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.-L.; Sorooshian, S.; Gao, X. Precipitation Estimation from Remotely Sensed Imagery Using an Artificial Neural Network Cloud Classification System. J. Appl. Meteorol. 2004, 43, 1834–1853. [Google Scholar] [CrossRef]
- Tegos, A.; Ziogas, A.; Bellos, V.; Tzimas, A. Forensic Hydrology: A Complete Reconstruction of an Extreme Flood Event in Data-Scarce Area. Hydrology 2022, 9, 93. [Google Scholar] [CrossRef]
- Ma, Z.; Zhou, Y.; Hu, B.; Liang, Z.; Shi, Z. Downscaling Annual Precipitation with TMPA and Land Surface Characteristics in China. Int. J. Climatol. 2017, 37, 5107–5119. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, D.; Qin, Z.; Zheng, Y.; Guo, J. Assessment of the GPM and TRMM Precipitation Products Using the Rain Gauge Network over the Tibetan Plateau. J. Meteorol. Res. 2018, 32, 324–336. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, Y.; Dong, Z.; Gui, S. A Multiscale Assessment of Three Satellite Precipitation Products (TRMM, CMORPH, and PERSIANN) in the Three Gorges Reservoir Area in China. Adv. Meteorol. 2021, 2021, 9979216. [Google Scholar] [CrossRef]
- Tang, G.; Long, D.; Hong, Y. Systematic Anomalies Over Inland Water Bodies of High Mountain Asia in TRMM Precipitation Estimates: No Longer a Problem for the GPM Era? IEEE Geosci. Remote Sens. Lett. 2016, 13, 1762–1766. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.; Wang, Y.; Xie, P. Performance of High-Resolution Satellite Precipitation Products over China. J. Geophys. Res. 2010, 115, D02114. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S.; Dewan, A.; Ismail, T.; Alias, N. Performance of Five High Resolution Satellite-Based Precipitation Products in Arid Region of Egypt: An Evaluation. Atmos. Res. 2020, 236, 104809. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-Hourly 0.25° Global Gridded Precipitation (1979–2015) by Merging Gauge, Satellite, and Reanalysis Data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, J.; Sheng, S.; Mansaray, L.R.; Liu, Z.; Wu, H.; Wang, X. A New Downscaling-Integration Framework for High-Resolution Monthly Precipitation Estimates: Combining Rain Gauge Observations, Satellite-Derived Precipitation Data and Geographical Ancillary Data. Remote Sens. Environ. 2018, 214, 154–172. [Google Scholar] [CrossRef]
- Park, N.-W.; Kyriakidis, P.C.; Hong, S. Geostatistical Integration of Coarse Resolution Satellite Precipitation Products and Rain Gauge Data to Map Precipitation at Fine Spatial Resolutions. Remote Sens. 2017, 9, 255. [Google Scholar] [CrossRef]
- Zhang, J.; Qi, Y.; Langston, C.; Kaney, B.; Howard, K. A Real-Time Algorithm for Merging Radar QPEs with Rain Gauge Observations and Orographic Precipitation Climatology. J. Hydrometeorol. 2014, 15, 1794–1809. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, S.; Duan, Z.; Qin, Z. An Improved Spatial Downscaling Procedure for TRMM 3B43 Precipitation Product Using Geographically Weighted Regression. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4592–4604. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating Subpixel Surface Temperatures and Energy Fluxes from the Vegetation Index–Radiometric Temperature Relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Piles, M.; Sánchez, N.; Vall-llossera, M.; Camps, A.; Martínez-Fernández, J.; Martínez, J.; González-Gambau, V. A Downscaling Approach for SMOS Land Observations: Evaluation of High-Resolution Soil Moisture Maps Over the Iberian Peninsula. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3845–3857. [Google Scholar] [CrossRef]
- Xie, W.; Yi, S.; Leng, C. A Study to Compare Three Different Spatial Downscaling Algorithms of Annual TRMM 3B43 Precipitation. In Proceedings of the 2018 26th International Conference on Geoinformatics, Kunming, China, 28–30 June 2018; pp. 1–6. [Google Scholar]
- Immerzeel, W.W.; Rutten, M.M.; Droogers, P. Spatial Downscaling of TRMM Precipitation Using Vegetative Response on the Iberian Peninsula. Remote Sens. Environ. 2009, 113, 362–370. [Google Scholar] [CrossRef]
- Hunink, J.E.; Immerzeel, W.W.; Droogers, P. A High-Resolution Precipitation 2-Step Mapping Procedure (HiP2P): Development and Application to a Tropical Mountainous Area. Remote Sens. Environ. 2014, 140, 179–188. [Google Scholar] [CrossRef]
- Retalis, A.; Tymvios, F.; Katsanos, D.; Michaelides, S. Downscaling CHIRPS Precipitation Data: An Artificial Neural Network Modelling Approach. Int. J. Remote Sens. 2017, 38, 3943–3959. [Google Scholar] [CrossRef]
- Ma, Z.; Shi, Z.; Zhou, Y.; Xu, J.; Yu, W.; Yang, Y. A Spatial Data Mining Algorithm for Downscaling TMPA 3B43 V7 Data over the Qinghai–Tibet Plateau with the Effects of Systematic Anomalies Removed. Remote Sens. Environ. 2017, 200, 378–395. [Google Scholar] [CrossRef]
- He, X.; Chaney, N.W.; Schleiss, M.; Sheffield, J. Spatial Downscaling of Precipitation Using Adaptable Random Forests. Water Resour. Res. 2016, 52, 8217–8237. [Google Scholar] [CrossRef]
- Zheng, X.; Zhu, J. A Methodological Approach for Spatial Downscaling of TRMM Precipitation Data in North China. Int. J. Remote Sens. 2015, 36, 144–169. [Google Scholar] [CrossRef]
- Foody, G.M. Geographical Weighting as a Further Refinement to Regression Modelling: An Example Focused on the NDVI–Rainfall Relationship. Remote Sens. Environ. 2003, 88, 283–293. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Zhao, Z.; Gao, J.; Wang, Y.; Liu, J.; Li, S. Exploring Spatially Variable Relationships between NDVI and Climatic Factors in a Transition Zone Using Geographically Weighted Regression. Theor. Appl. Climatol. 2015, 120, 507–519. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 2010, 28, 281–298. [Google Scholar] [CrossRef]
- Chen, F.; Liu, Y.; Liu, Q.; Li, X. Spatial Downscaling of TRMM 3B43 Precipitation Considering Spatial Heterogeneity. Int. J. Remote Sens. 2014, 35, 3074–3093. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Ji, X.; Luo, X.; Li, X. Fine-Resolution Precipitation Mapping in a Mountainous Watershed: Geostatistical Downscaling of TRMM Products Based on Environmental Variables. Remote Sens. 2018, 10, 119. [Google Scholar] [CrossRef]
- Sun, X.; Wang, J.; Zhang, L.; Ji, C.; Zhang, W.; Li, W. Spatial Downscaling Model Combined with the Geographically Weighted Regression and Multifractal Models for Monthly GPM/IMERG Precipitation in Hubei Province, China. Atmosphere 2022, 13, 476. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Li, Z.; Zhu, Y.; Wang, J.; Yu, Z. Geographically Weighted Regression Based Methods for Merging Satellite and Gauge Precipitation. J. Hydrol. 2018, 558, 275–289. [Google Scholar] [CrossRef]
- Xie, P.; Xiong, A.-Y. A Conceptual Model for Constructing High-Resolution Gauge-Satellite Merged Precipitation Analyses. J. Geophys. Res. Atmos. 2011, 116, 21106. [Google Scholar] [CrossRef]
- Rozante, J.R.; Moreira, D.S.; de Goncalves, L.G.G.; Vila, D.A. Combining TRMM and Surface Observations of Precipitation: Technique and Validation over South America. Weather Forecast. 2010, 25, 885–894. [Google Scholar] [CrossRef]
- Shi, L.; Liang, S.; Cheng, J.; Zhang, Q. Integrating ASTER and GLASS Broadband Emissivity Products Using a Multi-Resolution Kalman Filter. Int. J. Digit. Earth 2016, 9, 1098–1116. [Google Scholar] [CrossRef]
- McKee, J.L.; Binns, A.D. A Review of Gauge–Radar Merging Methods for Quantitative Precipitation Estimation in Hydrology. Can. Water Resour. J. Rev. Can. Ressour. Hydr. 2016, 41, 186–203. [Google Scholar] [CrossRef]
- Shen, Y.; Zhao, P.; Pan, Y.; Yu, J. A High Spatiotemporal Gauge-Satellite Merged Precipitation Analysis over China. J. Geophys. Res. Atmos. 2014, 119, 3063–3075. [Google Scholar] [CrossRef]
- Cheema, M.J.M.; Bastiaanssen, W.G.M.; Rutten, M.M. Validation of Surface Soil Moisture from AMSR-E Using Auxiliary Spatial Data in the Transboundary Indus Basin. J. Hydrol. 2011, 405, 137–149. [Google Scholar] [CrossRef]
- Kobayashi, T.; Masuda, K. Changes in Cloud Optical Thickness and Cloud Drop Size Associated with Precipitation Measured with TRMM Satellite. J. Meteorol. Soc. Jpn. Ser II 2009, 87, 593–600. [Google Scholar] [CrossRef]
- VanZanten, M.C.; Stevens, B.; Vali, G.; Lenschow, D.H. Observations of Drizzle in Nocturnal Marine Stratocumulus. J. Atmospheric Sci. 2005, 62, 88–106. [Google Scholar] [CrossRef]
- Sharifi, E.; Saghafian, B.; Steinacker, R. Downscaling Satellite Precipitation Estimates with Multiple Linear Regression, Artificial Neural Networks, and Spline Interpolation Techniques. J. Geophys. Res. Atmos. 2019, 124, 789–805. [Google Scholar] [CrossRef]
- Ma, Z.; Xu, J.; He, K.; Han, X.; Ji, Q.; Wang, T.; Xiong, W.; Hong, Y. An Updated Moving Window Algorithm for Hourly-Scale Satellite Precipitation Downscaling: A Case Study in the Southeast Coast of China. J. Hydrol. 2020, 581, 124378. [Google Scholar] [CrossRef]
- Li, W.; Jiang, Q.; He, X.; Sun, H.; Sun, W.; Scaioni, M.; Chen, S.; Li, X.; Gao, J.; Hong, Y. Effective Multi-Satellite Precipitation Fusion Procedure Conditioned by Gauge Background Fields over the Chinese Mainland. J. Hydrol. 2022, 610, 127783. [Google Scholar] [CrossRef]
- Sapiano, M.R.P.; Smith, T.M.; Arkin, P.A. A New Merged Analysis of Precipitation Utilizing Satellite and Reanalysis Data. J. Geophys. Res. 2008, 113, D22103. [Google Scholar] [CrossRef]
- Chen, C.; He, M.; Chen, Q.; Zhang, J.; Li, Z.; Wang, Z.; Duan, Z. Triple Collocation-Based Error Estimation and Data Fusion of Global Gridded Precipitation Products over the Yangtze River Basin. J. Hydrol. 2022, 605, 127307. [Google Scholar] [CrossRef]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Beck, H.E.; McNamara, I.; Ribbe, L.; Nauditt, A.; Birkel, C.; Verbist, K.; Giraldo-Osorio, J.D.; Xuan Thinh, N. RF-MEP: A Novel Random Forest Method for Merging Gridded Precipitation Products and Ground-Based Measurements. Remote Sens. Environ. 2020, 239, 111606. [Google Scholar] [CrossRef]
- Pamučar, D.; Stević, Ž.; Sremac, S. A New Model for Determining Weight Coefficients of Criteria in MCDM Models: Full Consistency Method (FUCOM). Symmetry 2018, 10, 393. [Google Scholar] [CrossRef]
- Aykut, T. Determination of Groundwater Potential Zones Using Geographical Information Systems (GIS) and Analytic Hierarchy Process (AHP) between Edirne-Kalkansogut (Northwestern Turkey). Groundw. Sustain. Dev. 2021, 12, 100545. [Google Scholar] [CrossRef]
- Sivrikaya, F.; Küçük, Ö. Modeling Forest Fire Risk Based on GIS-Based Analytical Hierarchy Process and Statistical Analysis in Mediterranean Region. Ecol. Inform. 2022, 68, 101537. [Google Scholar] [CrossRef]
- Pradhan, R.K.; Markonis, Y.; Vargas Godoy, M.R.; Villalba-Pradas, A.; Andreadis, K.M.; Nikolopoulos, E.I.; Papalexiou, S.M.; Rahim, A.; Tapiador, F.J.; Hanel, M. Review of GPM IMERG Performance: A Global Perspective. Remote Sens. Environ. 2022, 268, 112754. [Google Scholar] [CrossRef]
- Lu, C.; Fang, G.; Ye, J.; Huang, X. Accuracy Assessment of IMERG and TRMM Remote Sensing Precipitation Data under the Influence of Monsoon over the Upper and Middle Lancang River Basin, China. Arab. J. Geosci. 2022, 15, 372. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, W.; Wen, J.; Qiu, C.; Sun, W.; Fang, Q.; Xu, M.; Tan, J. Accuracy Evaluation of Two High-Resolution Satellite-Based Rainfall Products: TRMM 3B42V7 and CMORPH in Shanghai. Water 2018, 10, 40. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, W.; Fan, Z.; He, X.; Sun, W.; Chen, S.; Wen, J.; Gao, J.; Wang, J. Evaluation of the ERA5 Reanalysis Precipitation Dataset over Chinese Mainland. J. Hydrol. 2021, 595, 125660. [Google Scholar] [CrossRef]
- Yi, X.; Li, G.; Yin, Y. Temperature Variation and Abrupt Change Analysis in the Three-River Headwaters Region during 1961–2010. J. Geogr. Sci. 2012, 22, 451–469. [Google Scholar] [CrossRef]
- Yi, X.; Li, G.; Yin, Y. Spatio-Temporal Variation of Precipitation in the Three-River Headwater Region from 1961 to 2010. J. Geogr. Sci. 2013, 23, 447–464. [Google Scholar] [CrossRef]
- Jiang, C.; Zhang, L. Ecosystem Change Assessment in the Three-River Headwater Region, China: Patterns, Causes, and Implications. Ecol. Eng. 2016, 93, 24–36. [Google Scholar] [CrossRef]
- Yi, X.; Li, G.; Yin, Y. Comparison of Three Methods to Develop Pedotransfer Functions for the Saturated Water Content and Field Water Capacity in Permafrost Region. Cold Reg. Sci. Technol. 2013, 88, 10–16. [Google Scholar] [CrossRef]
- Sims, E.M.; Liu, G. A Parameterization of the Probability of Snow–Rain Transition. J. Hydrometeorol. 2015, 16, 1466–1477. [Google Scholar] [CrossRef]
- Huffman, G.J.; Stocker, E.F.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. GPM IMERG Final Precipitation L3 Half Hourly 0.1 Degree x 0.1 Degree V06; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2019. [Google Scholar]
- Zhang, L.; Gao, L.; Chen, J.; Zhao, L.; Zhao, J.; Qiao, Y.; Shi, J. Comprehensive Evaluation of Mainstream Gridded Precipitation Datasets in the Cold Season across the Tibetan Plateau. J. Hydrol. Reg. Stud. 2022, 43, 101186. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.E.; Brunsdon, C. Geographically Weighted Regression: A Natural Evolution of the Expansion Method for Spatial Data Analysis. Environ. Plan. Econ. Space 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Lu, B.; Charlton, M.; Harris, P.; Fotheringham, A.S. Geographically Weighted Regression with a Non-Euclidean Distance Metric: A Case Study Using Hedonic House Price Data. Int. J. Geogr. Inf. Sci. 2014, 28, 660–681. [Google Scholar] [CrossRef]
- Gao, Y.; Huang, J.; Li, S.; Li, S. Spatial Pattern of Non-Stationarity and Scale-Dependent Relationships between NDVI and Climatic Factors—A Case Study in Qinghai-Tibet Plateau, China. Ecol. Indic. 2012, 20, 170–176. [Google Scholar] [CrossRef]
- Tu, J.; Xia, Z. Examining Spatially Varying Relationships between Land Use and Water Quality Using Geographically Weighted Regression I: Model Design and Evaluation. Sci. Total Environ. 2008, 407, 358–378. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Lal, R.; Liu, D. A Geographically Weighted Regression Kriging Approach for Mapping Soil Organic Carbon Stock. Geoderma 2012, 189–190, 627–634. [Google Scholar] [CrossRef]
- Ye, H.; Huang, W.; Huang, S.; Huang, Y.; Zhang, S.; Dong, Y.; Chen, P. Effects of Different Sampling Densities on Geographically Weighted Regression Kriging for Predicting Soil Organic Carbon. Spat. Stat. 2017, 20, 76–91. [Google Scholar] [CrossRef]
- Cheema, M.J.M.; Bastiaanssen, W.G.M. Local Calibration of Remotely Sensed Rainfall from the TRMM Satellite for Different Periods and Spatial Scales in the Indus Basin. Int. J. Remote Sens. 2012, 33, 2603–2627. [Google Scholar] [CrossRef]
- Saaty, T.L. Multicriteria Decision Making: The Analytic Hierarchy Process: Planning, Priority Setting Resource Allocation; RWS Pubns: Pittsburgh, PA, USA, 1990; ISBN 0-9620317-2-0. [Google Scholar]
- Wu, R.M.X.; Zhang, Z.; Yan, W.; Fan, J.; Gou, J.; Liu, B.; Gide, E.; Soar, J.; Shen, B.; Fazal-e-Hasan, S.; et al. A Comparative Analysis of the Principal Component Analysis and Entropy Weight Methods to Establish the Indexing Measurement. PLoS ONE 2022, 17, e0262261. [Google Scholar] [CrossRef] [PubMed]
- Heydarizad, M.; Minaei, M.; Ichiyanagi, K.; Sorí, R. The Effects of Local and Regional Parameters on the Δ18O and Δ2H Values of Precipitation and Surface Water Resources in the Middle East. J. Hydrol. 2021, 600, 126485. [Google Scholar] [CrossRef]
- Kumar, R.; Bilga, P.S.; Singh, S. Multi Objective Optimization Using Different Methods of Assigning Weights to Energy Consumption Responses, Surface Roughness and Material Removal Rate during Rough Turning Operation. J. Clean. Prod. 2017, 164, 45–57. [Google Scholar] [CrossRef]
- Teixeira, S.J.; Ferreira, J.J.; Wanke, P.; Moreira Antunes, J.J. Evaluation Model of Competitive and Innovative Tourism Practices Based on Information Entropy and Alternative Criteria Weight. Tour. Econ. 2021, 27, 23–44. [Google Scholar] [CrossRef]
- Mukhametzyanov, I. Specific Character of Objective Methods for Determining Weights of Criteria in MCDM Problems: Entropy, CRITIC and SD. Decis. Mak. Appl. Manag. Eng. 2021, 4, 76–105. [Google Scholar] [CrossRef]
- Sieck, L.C.; Burges, S.J.; Steiner, M. Challenges in Obtaining Reliable Measurements of Point Rainfall. Water Resour. Res. 2007, 43, WR004519. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Ren, L.; Zeng, Z. Spatial Distribution of Rainstorm Hazard Risk Based on EW-AHP in Mountainous Scenic Area of China. Hum. Ecol. Risk Assess. Int. J. 2017, 23, 925–943. [Google Scholar] [CrossRef]
- Hu, Y.; Li, W.; Wang, Q.; Liu, S.; Wang, Z. Evaluation of Water Inrush Risk from Coal Seam Floors with an AHP–EWM Algorithm and GIS. Environ. Earth Sci. 2019, 78, 290. [Google Scholar] [CrossRef]
- Ma, Y.; Shi, T.; Zhang, W.; Hao, Y.; Huang, J.; Lin, Y. Comprehensive Policy Evaluation of NEV Development in China, Japan, the United States, and Germany Based on the AHP-EW Model. J. Clean. Prod. 2019, 214, 389–402. [Google Scholar] [CrossRef]
- Asbahi, A.A.M.H.A.; Gang, F.Z.; Iqbal, W.; Abass, Q.; Mohsin, M.; Iram, R. Novel Approach of Principal Component Analysis Method to Assess the National Energy Performance via Energy Trilemma Index. Energy Rep. 2019, 5, 704–713. [Google Scholar] [CrossRef]
- Sun, B.; Yang, X.; Zhang, Y.; Chen, X. Evaluation of Water Use Efficiency of 31 Provinces and Municipalities in China Using Multi-Level Entropy Weight Method Synthesized Indexes and Data Envelopment Analysis. Sustainability 2019, 11, 4556. [Google Scholar] [CrossRef]
- Wang, P.; Bai, X.; Wu, X.; Yu, H.; Hao, Y.; Hu, B.X. GIS-Based Random Forest Weight for Rainfall-Induced Landslide Susceptibility Assessment at a Humid Region in Southern China. Water 2018, 10, 1019. [Google Scholar] [CrossRef]
- Wang, H.; Zang, F.; Zhao, C.; Liu, C. A GWR Downscaling Method to Reconstruct High-Resolution Precipitation Dataset Based on GSMaP-Gauge Data: A Case Study in the Qilian Mountains, Northwest China. Sci. Total Environ. 2022, 810, 152066. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian Model Averaging to Calibrate Forecast Ensembles. Mon. WEATHER Rev. 2005, 133, 20. [Google Scholar] [CrossRef]
- Ma, Y.; Hong, Y.; Chen, Y.; Yang, Y.; Tang, G.; Yao, Y.; Long, D.; Li, C.; Han, Z.; Liu, R. Performance of Optimally Merged Multisatellite Precipitation Products Using the Dynamic Bayesian Model Averaging Scheme Over the Tibetan Plateau. J. Geophys. Res. Atmos. 2018, 123, 814–834. [Google Scholar] [CrossRef]
- Wu, H.; Yang, Q.; Liu, J.; Wang, G. A Spatiotemporal Deep Fusion Model for Merging Satellite and Gauge Precipitation in China. J. Hydrol. 2020, 584, 124664. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Pai, D.S. Error Characterization of TRMM Multisatellite Precipitation Analysis (TMPA-3B42) Products over India for Different Seasons. J. Hydrol. 2015, 529, 1302–1312. [Google Scholar] [CrossRef]
- Shi, Y.; Song, L. Spatial Downscaling of Monthly TRMM Precipitation Based on EVI and Other Geospatial Variables Over the Tibetan Plateau From 2001 to 2012. Mt. Res. Dev. 2015, 35, 180–194. [Google Scholar] [CrossRef]
- Zhang, Q.; Shi, P.; Singh, V.P.; Fan, K.; Huang, J. Spatial Downscaling of TRMM-based Precipitation Data Using Vegetative Response in Xinjiang, China. Int. J. Clim. 2017, 37, 3895–3909. [Google Scholar] [CrossRef]
- Zhang, H.; Loáiciga, H.A.; Ha, D.; Du, Q. Spatial and Temporal Downscaling of TRMM Precipitation with Novel Algorithms. J. Hydrometeorol. 2020, 21, 1259–1278. [Google Scholar] [CrossRef]



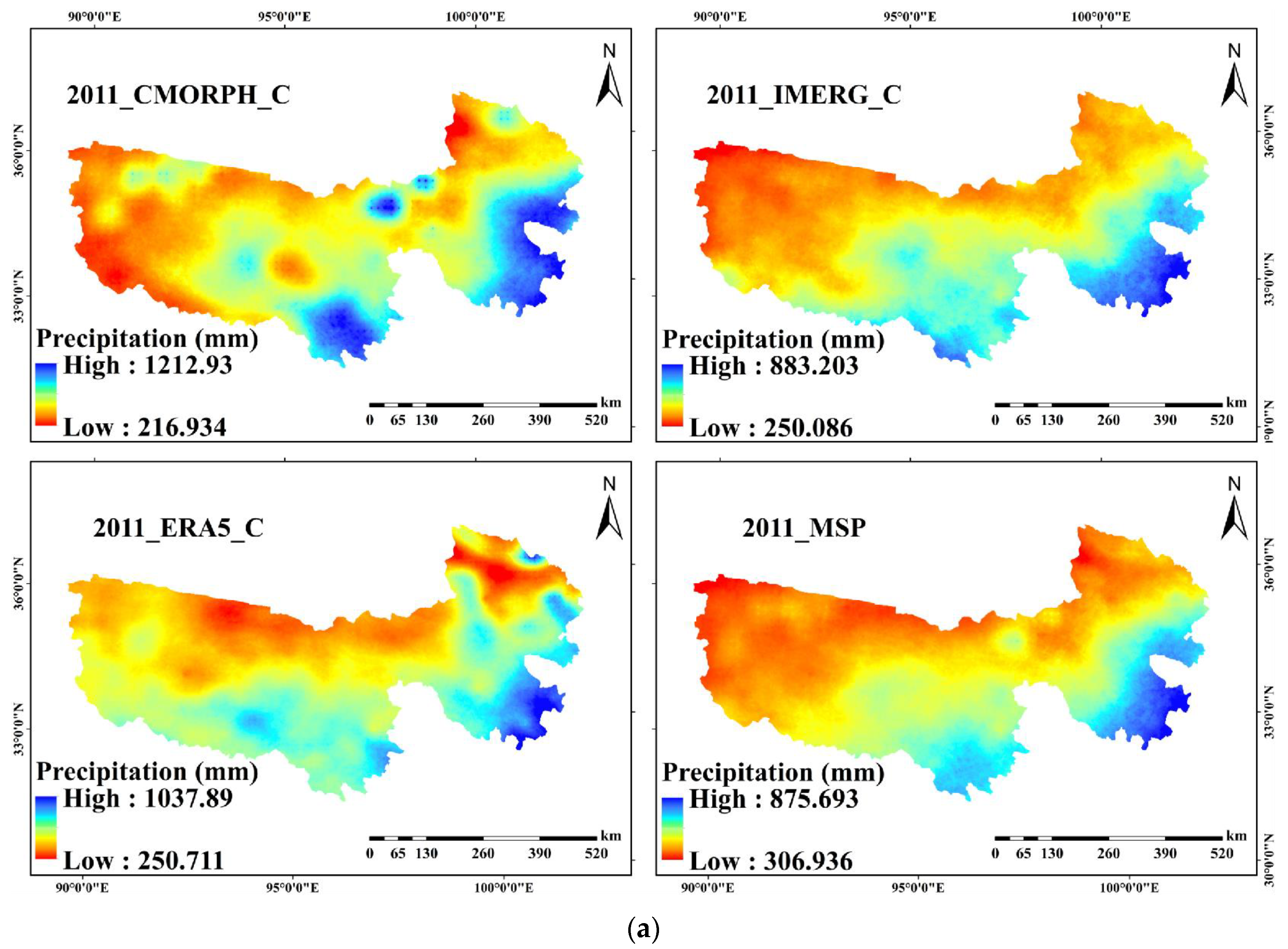

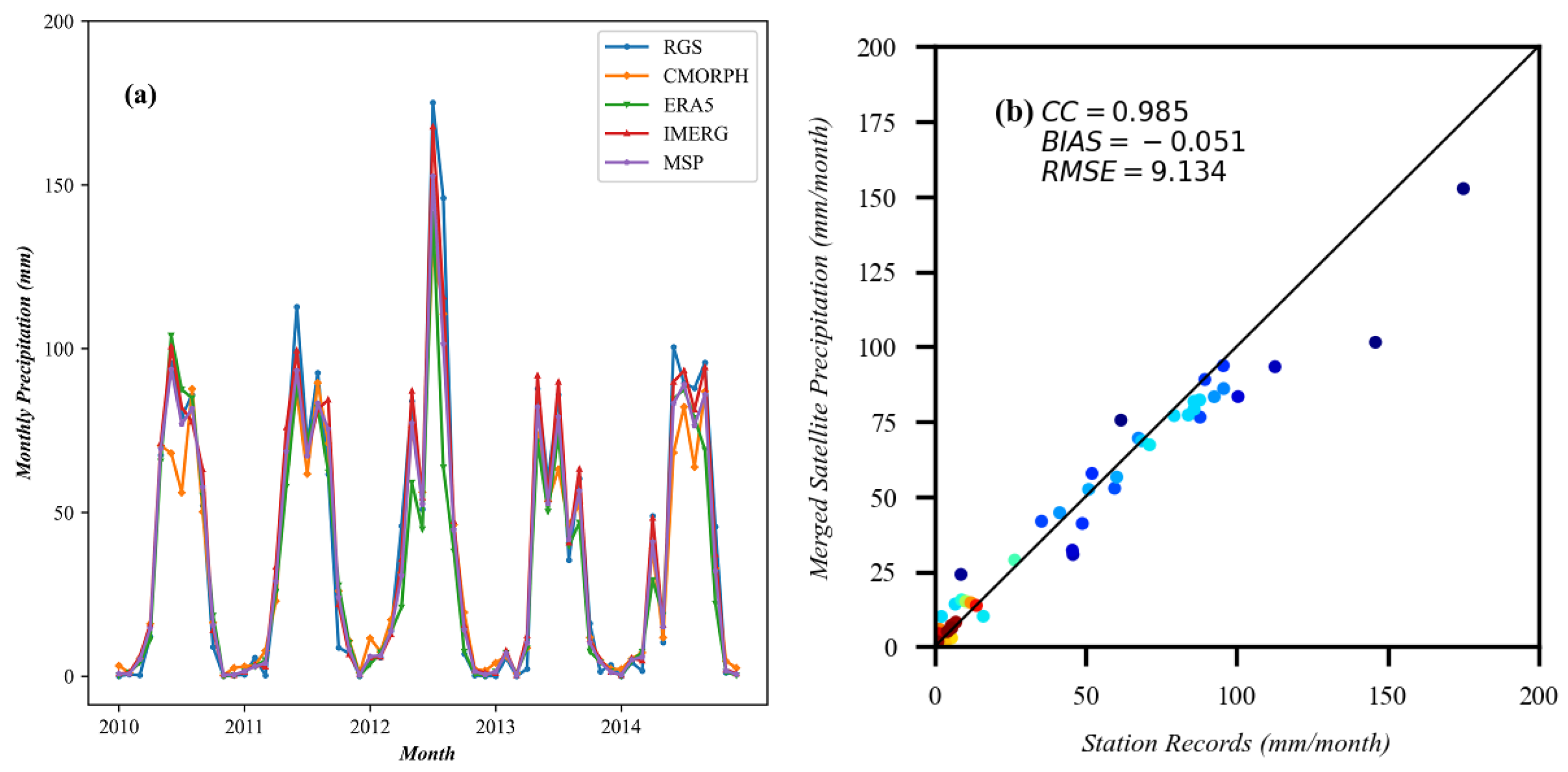
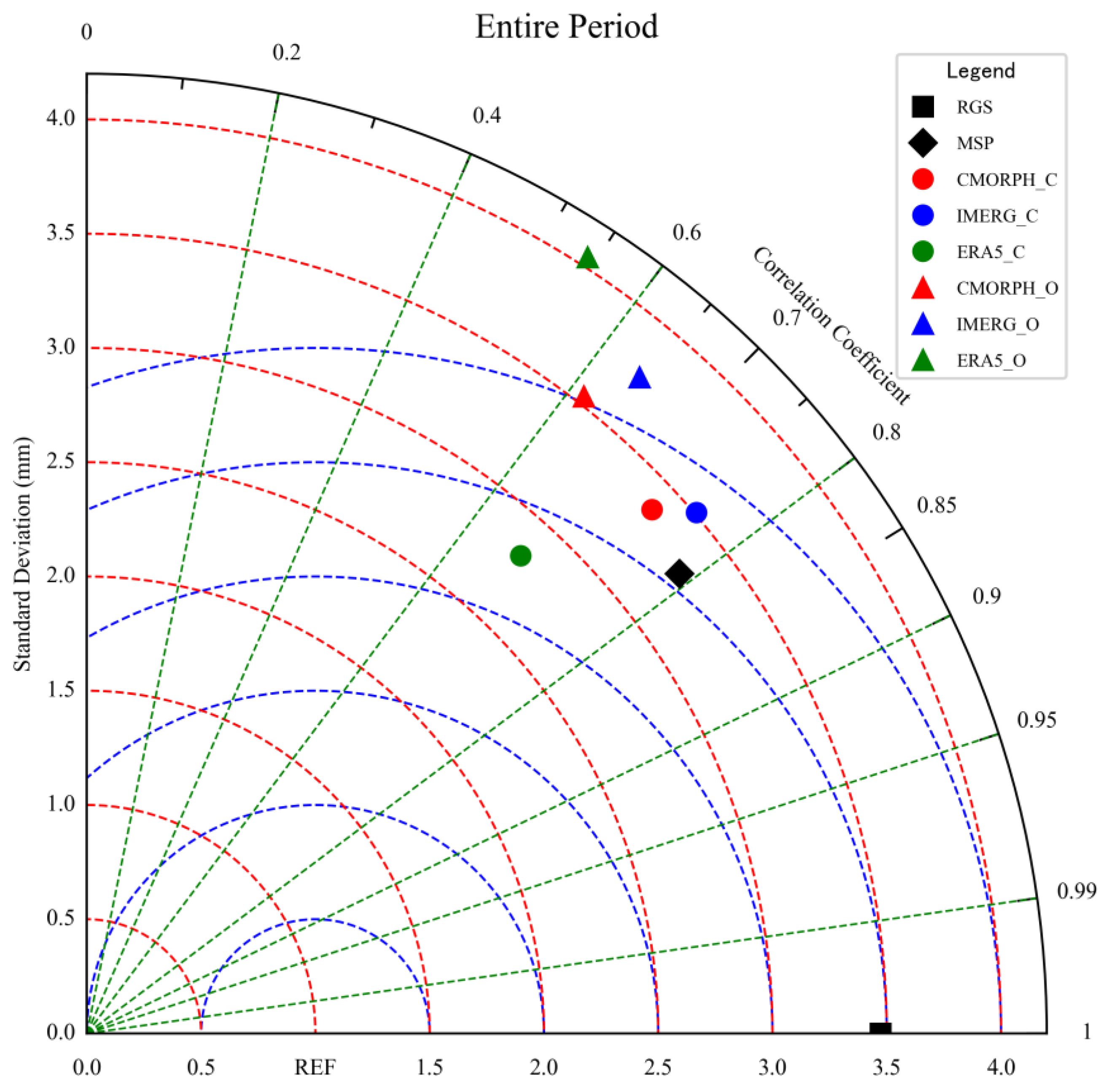
| Station ID | Longitude (°E) | Latitude (°N) | Elevation (m) | Average Annual Precipitation (mm/Year) |
|---|---|---|---|---|
| 52754 | 100.13 | 37.33 | 3301.5 | 427.8 |
| 52833 | 98.48 | 36.92 | 2950.0 | 199.6 |
| 52866 | 101.77 | 36.62 | 2261.2 | 420.3 |
| 52836 | 98.10 | 36.30 | 3191.1 | 240.6 |
| 52856 | 100.62 | 36.27 | 2835.0 | 320.6 |
| 52868 | 101.43 | 36.03 | 2237.1 | 264.9 |
| 52943 | 99.98 | 35.58 | 3323.2 | 378.6 |
| 52955 | 100.75 | 35.58 | 3200.6 | 455.2 |
| 52974 | 102.02 | 35.52 | 2491.4 | 421.6 |
| 52908 | 93.08 | 35.22 | 4612.2 | 369.2 |
| 56033 | 98.22 | 34.92 | 4272.3 | 362.1 |
| 56065 | 101.60 | 34.73 | 3500.0 | 582.1 |
| 56080 | 102.90 | 35.00 | 2910.0 | 589.2 |
| 56043 | 100.25 | 34.47 | 3719.0 | 520.2 |
| 56004 | 92.43 | 34.22 | 4533.1 | 355.7 |
| 56021 | 95.78 | 34.13 | 4175.0 | 497.5 |
| 56034 | 97.13 | 33.80 | 4415.4 | 602.1 |
| 56046 | 99.65 | 33.75 | 3967.5 | 599.1 |
| 56067 | 101.48 | 33.43 | 3628.5 | 758.5 |
| 56074 | 102.08 | 34.00 | 3471.6 | 612.4 |
| 56018 | 95.30 | 32.90 | 4067.5 | 567.7 |
| 56029 | 97.02 | 33.02 | 3681.2 | 528.8 |
| 56038 | 98.10 | 32.98 | 4200.0 | 631.2 |
| 56151 | 100.75 | 32.93 | 3750.0 | 708.4 |
| 56152 | 100.33 | 32.28 | 3893.9 | 694.0 |
| 56125 | 96.48 | 32.20 | 3643.7 | 570.4 |
| 56106 | 93.78 | 31.88 | 4022.8 | 668.0 |
| 56116 | 95.60 | 31.42 | 3873.1 | 684.1 |
| 56137 | 97.17 | 31.15 | 3306.0 | 491.7 |
| CC | RMSE (mm) | BIAS (mm) | |
|---|---|---|---|
| IMERG | 0.644 | 3.091 | −0.013 |
| CMORPH | 0.615 | 3.081 | 0.050 |
| ERA5 | 0.542 | 3.852 | 0.885 |
| CER | COT | CWP | Average | |
|---|---|---|---|---|
| CMORPH | 0.120 | 0.212 | 0.229 | 0.187 |
| ERA5 | 0.169 | 0.270 | 0.252 | 0.230 |
| IMERG | 0.144 | 0.240 | 0.259 | 0.214 |
| CC | RMSE (mm) | BIAS (mm) | |
|---|---|---|---|
| IMERG_O | 0.644 | 3.091 | −0.013 |
| IMERG_D | 0.691 | 2.623 | 0.002 |
| CMORPH_O | 0.615 | 3.081 | 0.050 |
| CMORPH_D | 0.631 | 2.817 | 0.076 |
| ERA5_O | 0.542 | 3.852 | 0.885 |
| ERA5_D | 0.565 | 3.620 | 1.008 |
| CC | RMSE (mm) | BIAS (mm) | |
|---|---|---|---|
| IMERG_D | 0.691 | 2.623 | 0.002 |
| IMERG_GDA | 0.760 | 2.453 | 0.147 |
| IMERG_GRA | 0.719 | 2.562 | 0.075 |
| CMORPH_D | 0.631 | 2.817 | 0.076 |
| CMORPH_GDA | 0.733 | 2.544 | 0.211 |
| CMORPH_GRA | 0.669 | 3.134 | 0.257 |
| ERA5_D | 0.565 | 3.620 | 1.008 |
| ERA5_GDA | 0.672 | 2.656 | 0.103 |
| ERA5_GRA | 0.663 | 2.657 | 0.065 |
| CC | RMSE (mm) | BIAS (mm) | |
|---|---|---|---|
| IMERG_IDW | 0.754 | 2.395 | 0.126 |
| IMERG_RBF | 0.758 | 2.482 | 0.144 |
| IMERG_OK | 0.750 | 2.458 | 0.133 |
| CMORPH_IDW | 0.729 | 2.559 | 0.222 |
| CMORPH_RBF | 0.729 | 2.575 | 0.204 |
| CMORPH_OK | 0.721 | 2.577 | 0.201 |
| ERA5_IDW | 0.660 | 2.700 | 0.143 |
| ERA5_RBF | 0.668 | 2.689 | 0.086 |
| ERA5_OK | 0.656 | 2.713 | 0.105 |
| CC | RMSE (mm) | BIAS (mm) | |
|---|---|---|---|
| IMERG_C | 0.760 | 2.453 | 0.147 |
| CMORPH_C | 0.733 | 2.544 | 0.211 |
| ERA5_C | 0.672 | 2.656 | 0.103 |
| EW | 0.786 | 2.203 | 0.155 |
| AHP | 0.780 | 2.197 | 0.148 |
| PCA | 0.785 | 2.202 | 0.150 |
| MSP | 0.790 | 2.189 | 0.142 |
| Station ID | Elevation (m) | CC | RMSE (mm) | BIAS (mm) |
|---|---|---|---|---|
| 52856 | 2835 | 0.800 | 1.763 | 0.252 |
| 52868 | 2237 | 0.789 | 1.864 | 0.560 |
| 52955 | 3200 | 0.808 | 2.152 | −0.051 |
| 56018 | 4067 | 0.755 | 2.230 | 0.028 |
| 56038 | 4200 | 0.790 | 2.220 | −0.040 |
| 56043 | 3719 | 0.785 | 2.154 | 0.163 |
| 56065 | 3500 | 0.801 | 2.386 | 0.034 |
| 56125 | 3643 | 0.761 | 2.429 | 0.219 |
| 56152 | 3893 | 0.824 | 2.506 | 0.115 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Liu, C.; Zhang, W.; Li, Z.; An, B. Downscaling and Merging of Daily Scale Satellite Precipitation Data in the Three River Headwaters Region Fused with Cloud Attributes and Rain Gauge Data. Water 2023, 15, 1233. https://doi.org/10.3390/w15061233
Xu C, Liu C, Zhang W, Li Z, An B. Downscaling and Merging of Daily Scale Satellite Precipitation Data in the Three River Headwaters Region Fused with Cloud Attributes and Rain Gauge Data. Water. 2023; 15(6):1233. https://doi.org/10.3390/w15061233
Chicago/Turabian StyleXu, Chi, Chuanqi Liu, Wanchang Zhang, Zhenghao Li, and Bangsheng An. 2023. "Downscaling and Merging of Daily Scale Satellite Precipitation Data in the Three River Headwaters Region Fused with Cloud Attributes and Rain Gauge Data" Water 15, no. 6: 1233. https://doi.org/10.3390/w15061233
APA StyleXu, C., Liu, C., Zhang, W., Li, Z., & An, B. (2023). Downscaling and Merging of Daily Scale Satellite Precipitation Data in the Three River Headwaters Region Fused with Cloud Attributes and Rain Gauge Data. Water, 15(6), 1233. https://doi.org/10.3390/w15061233






