Energy and Exergy Analysis of Solar Air Gap Membrane Distillation System for Seawater Desalination
Abstract
:1. Introduction
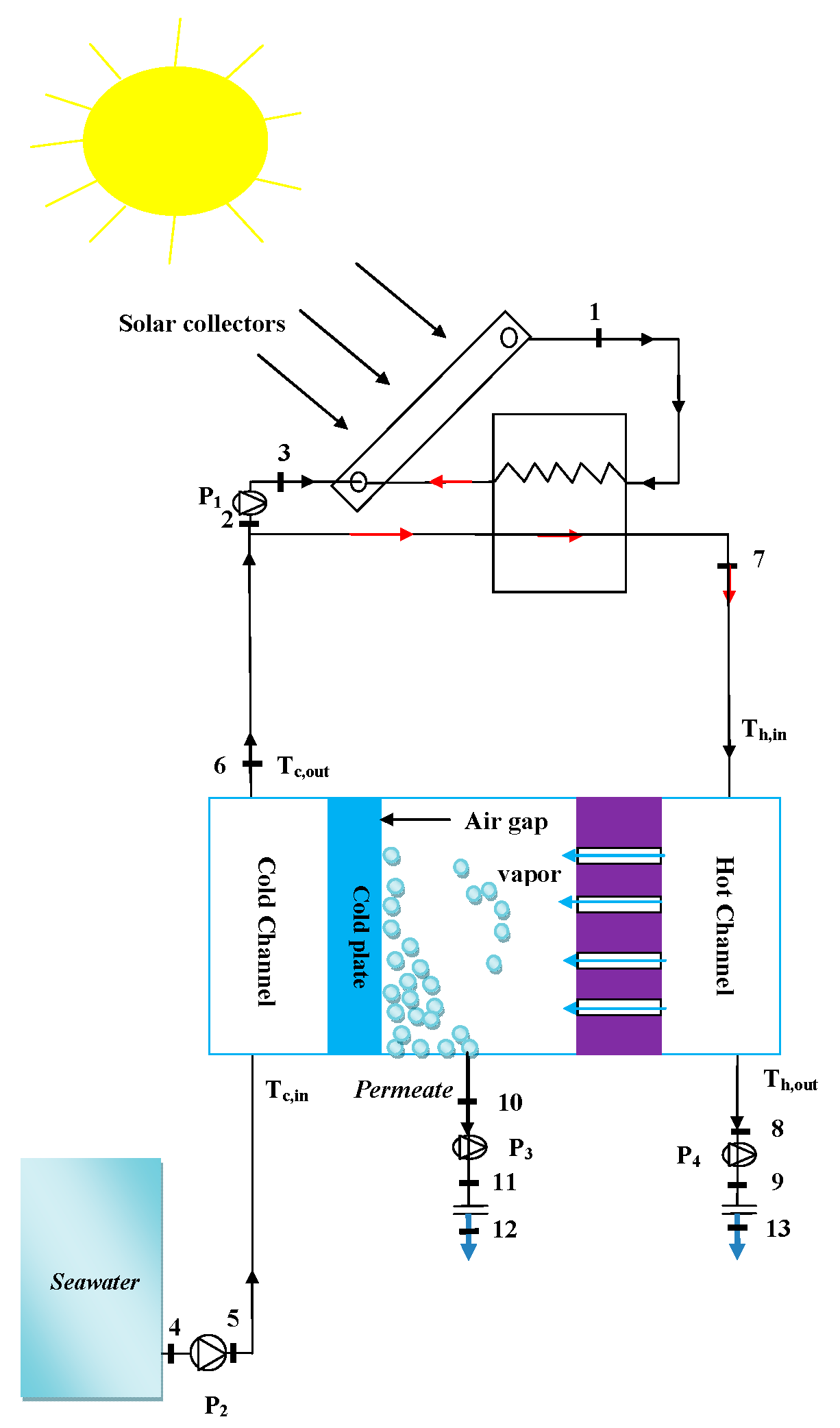
2. System Description
3. Numerical Modeling
3.1. Thermodynamic Analysis
- -
- The system runs at a dynamic state throughout;
- -
- Thermal losses have been studied;
- -
- Kinetic and potential exergies are ignored;
- -
- An average pump efficiency of 75% is estimated;
- -
- Dead state properties for fluids are evaluated at T0 = 25 °C and the dead state salinity X0 = 35 g.kg−1.
3.2. Exergy Analysis
4. Results and Discussion
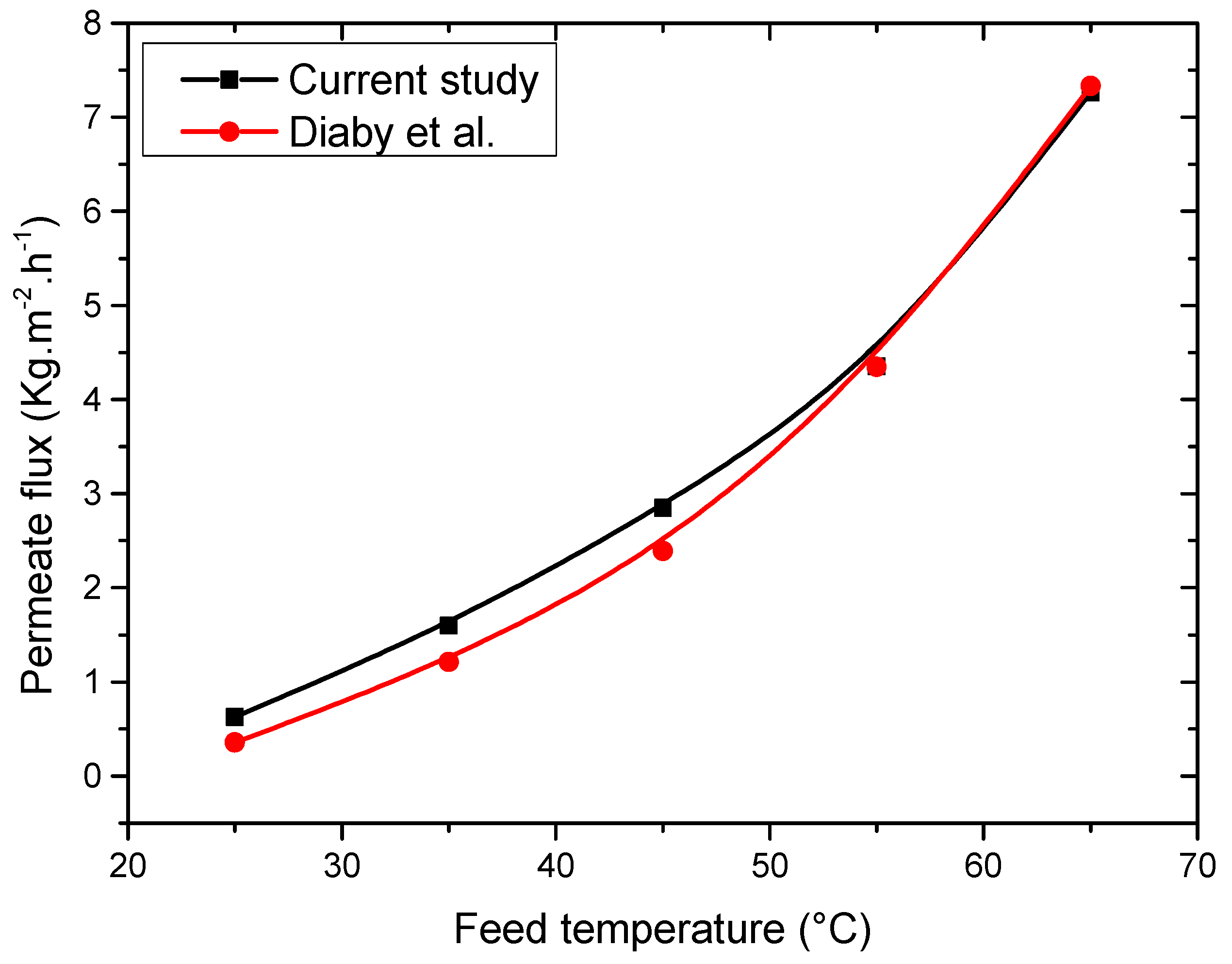
4.1. Model Validation
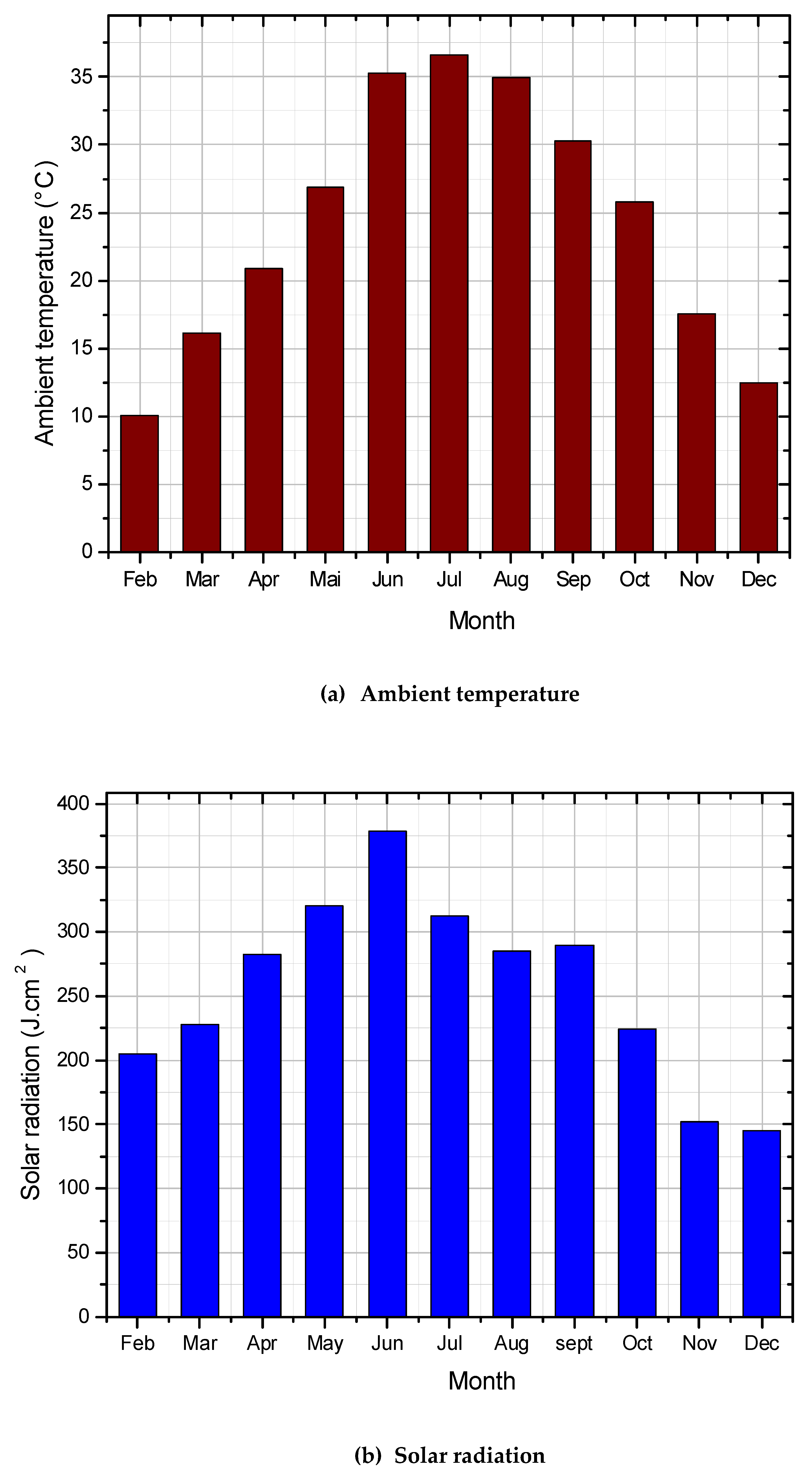
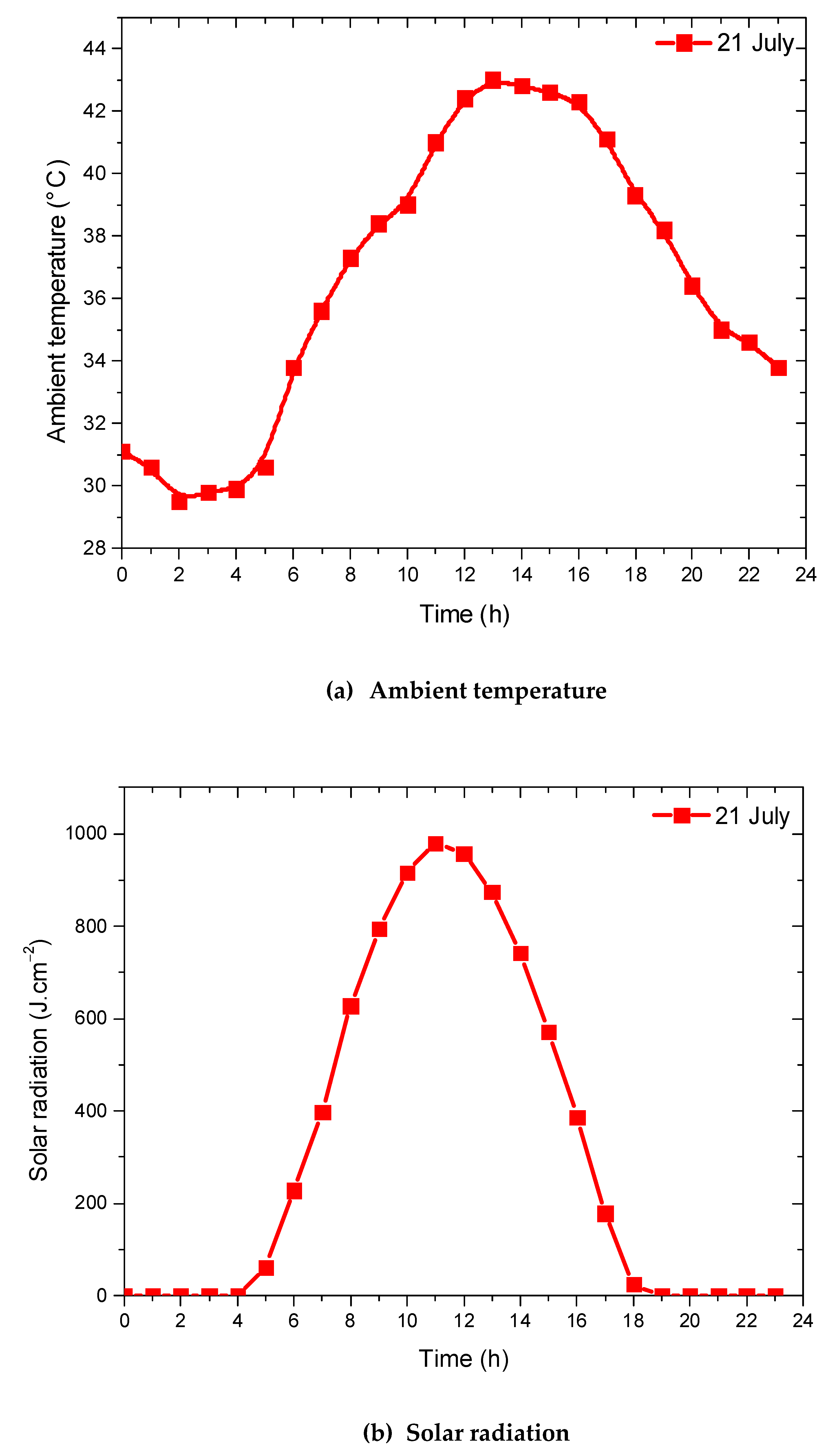
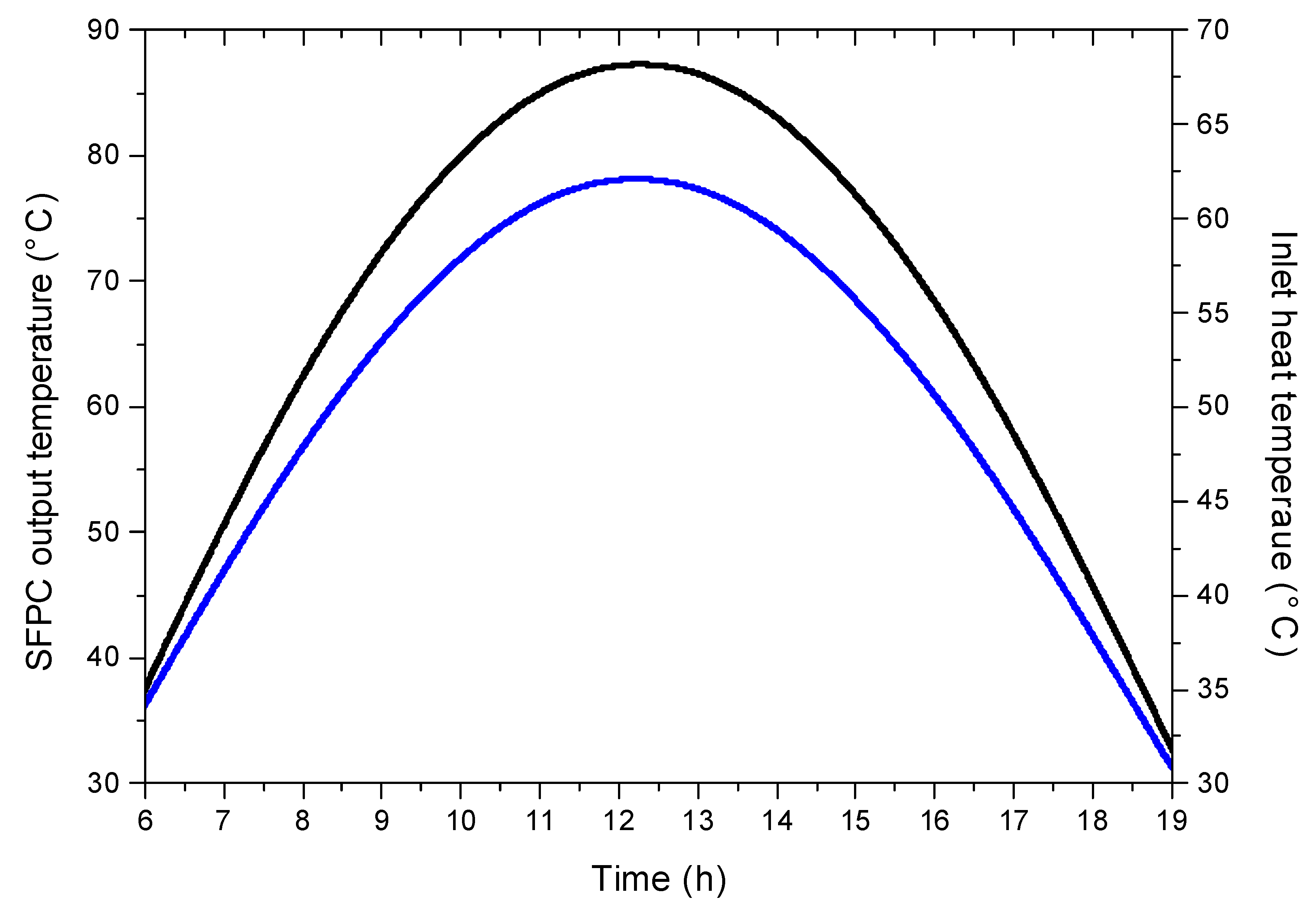
4.2. Evaluation of Solar Potential
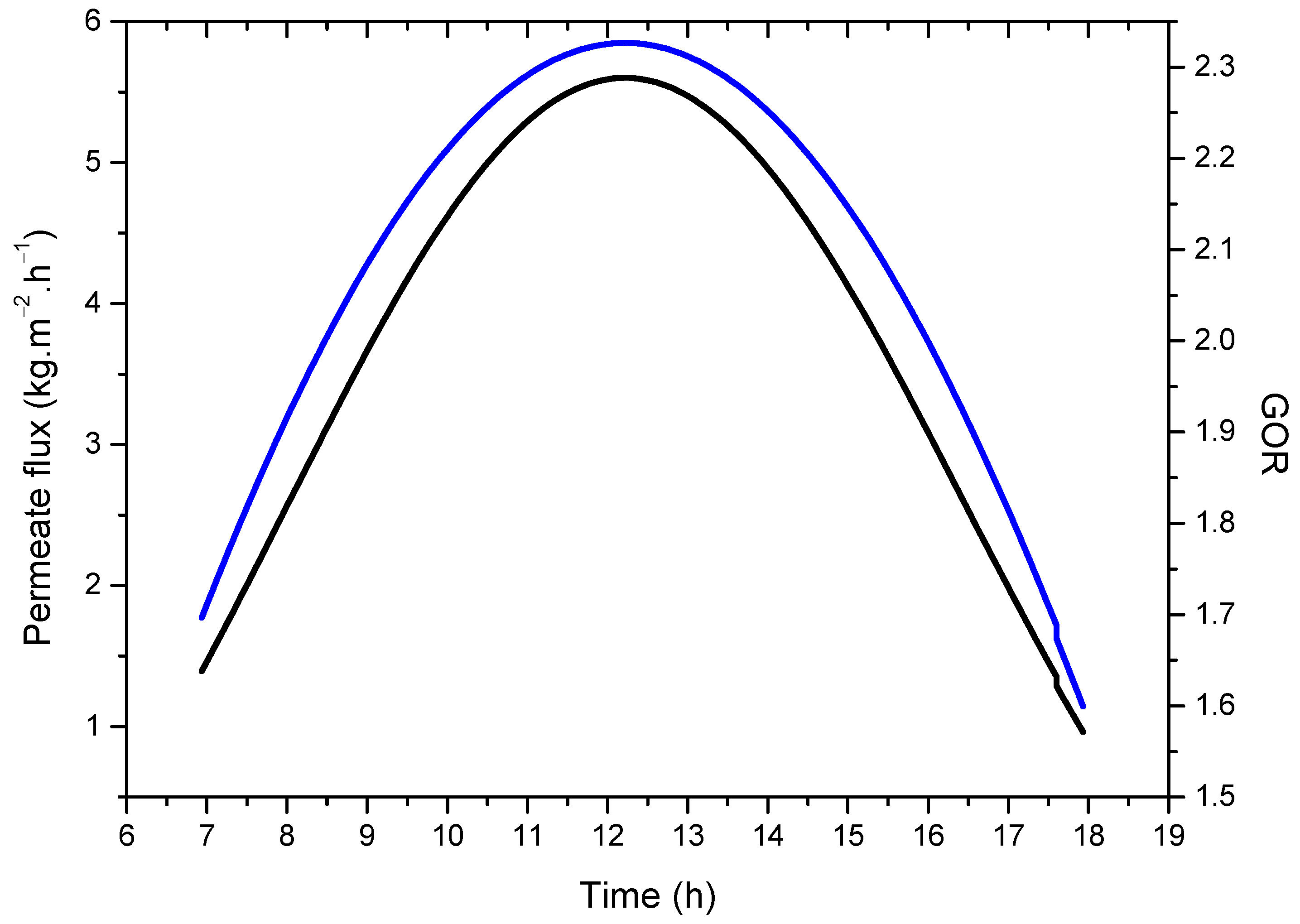
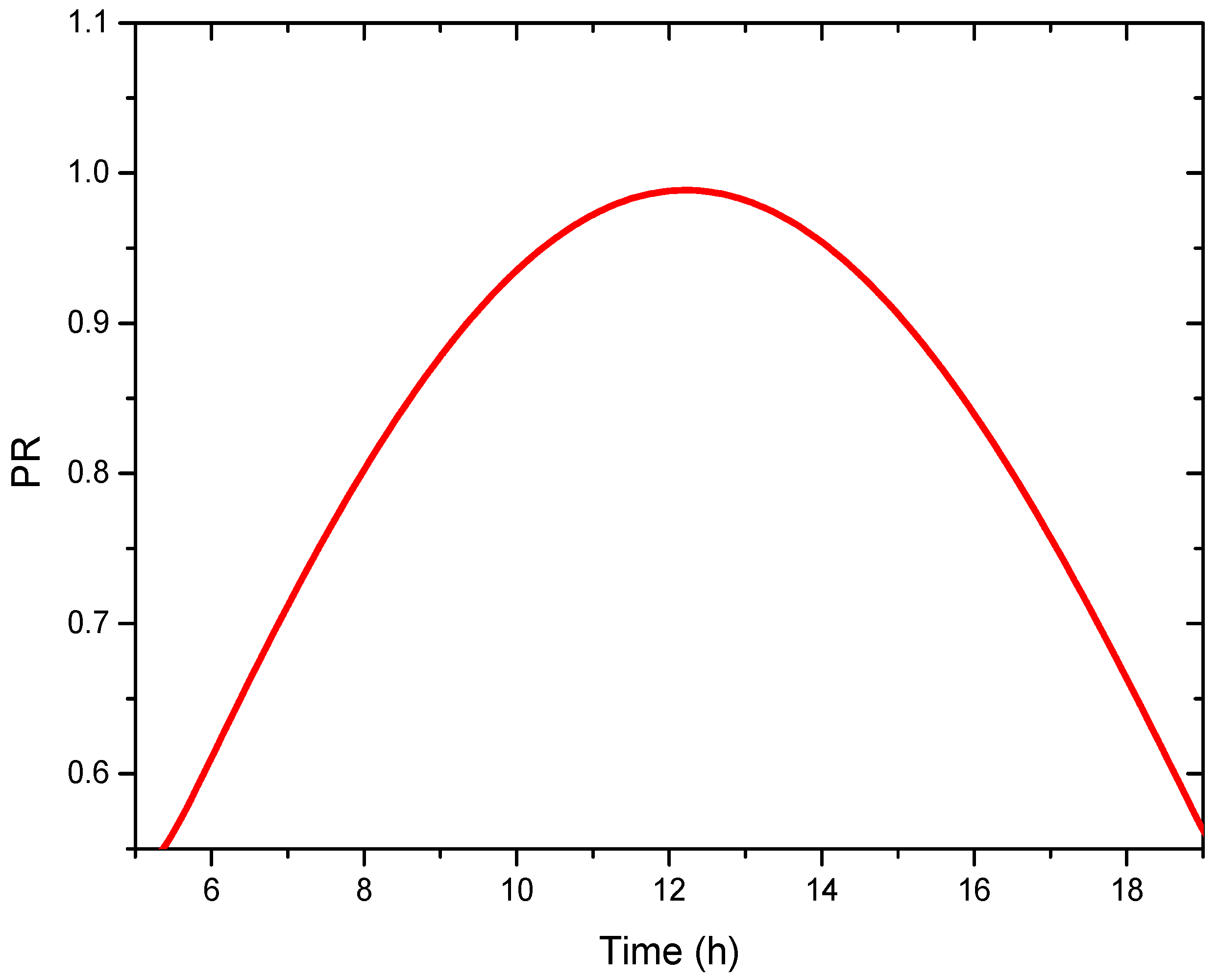
4.3. System Performance
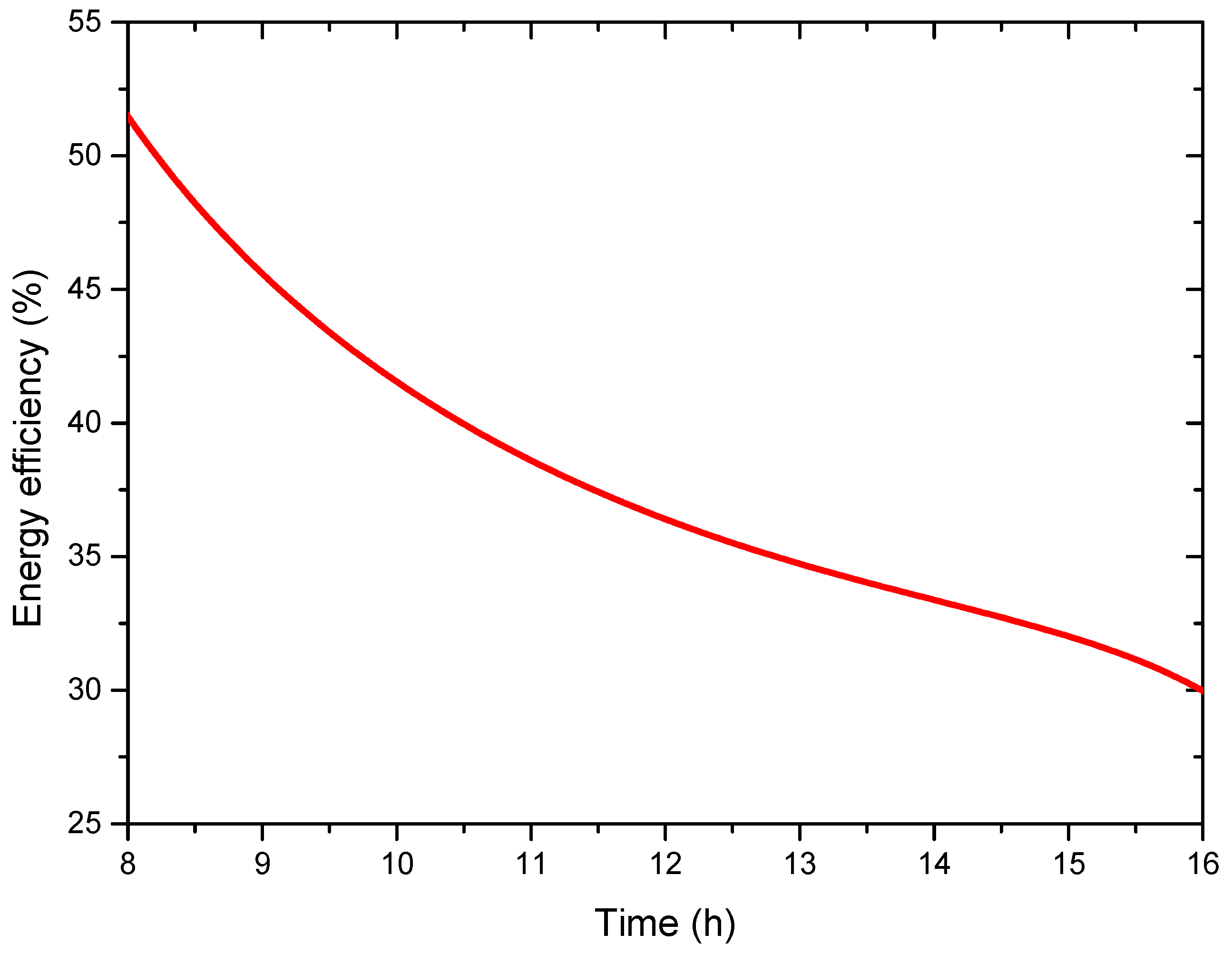
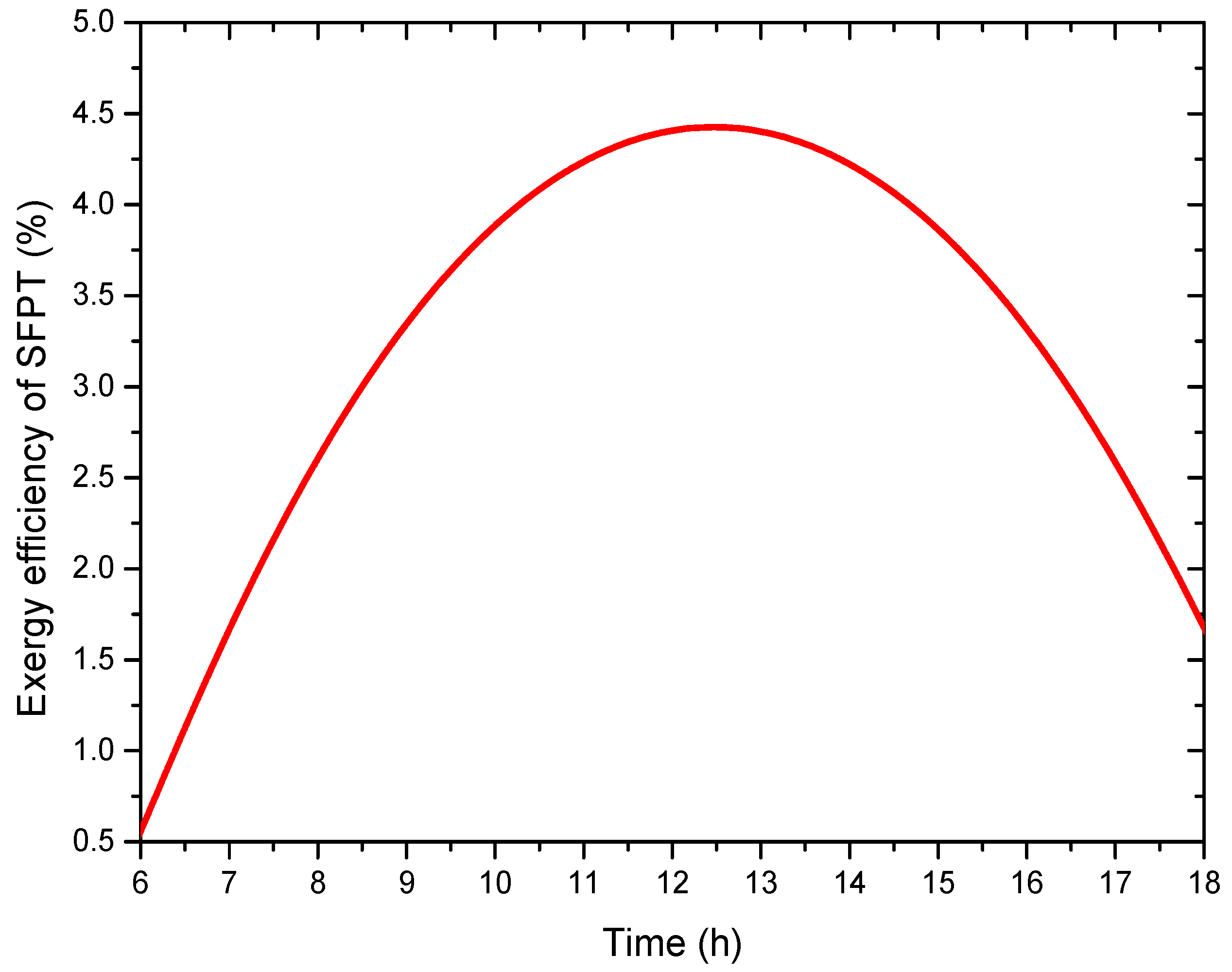
4.4. Energy and Exergy Analysis
4.5. Maximum Percentage of Component Destruction Exergy
- -
- Improving thermal insulation: A good thermal insulation system reduces thermal losses and helps to maintain the temperature of the collector. This can be achieved by using high-quality insulation materials and ensuring proper installation;
- -
- Reducing radiation losses: Solar collectors can lose energy through radiation to the environment. To reduce this, you can use selective coatings on the absorber plates, which absorb more solar radiation and reflect less thermal radiation. This can increase the efficiency of the collector;
- -
- Improving heat transfer: Heat transfer losses can occur due to poor fluid flow or inadequate heat transfer between the absorber plate and the fluid. You can reduce these losses by optimizing the fluid flow rate and using high-efficiency heat transfer fluids.
- -
- Optimizing collector design: The design of the solar collector can also impact its efficiency. A collector with a larger surface area and a smaller heat transfer distance can reduce exergy destruction by minimizing thermal losses;
- -
- Regular maintenance: Proper maintenance of the solar collector can help to ensure its efficiency over time. This includes cleaning the collector regularly to remove dust and debris and checking for leaks in the system.
5. Conclusions
- Based on the obtained numerical results, an average distillate water production of 5.5 kg.m−2.h−1 could be achieved at a feed temperature of 62 °C and feed flow rate of 2 L.min−1;
- Increasing the air gap thickness reduces the risk of direct contact between the membrane and the considered surface but will cause thermal and mass resistance, and thus a decrease in mass flux and thermal efficiency of the AGMD process. Therefore, it must be carefully considered based on the specific requirements and limitations of the system;
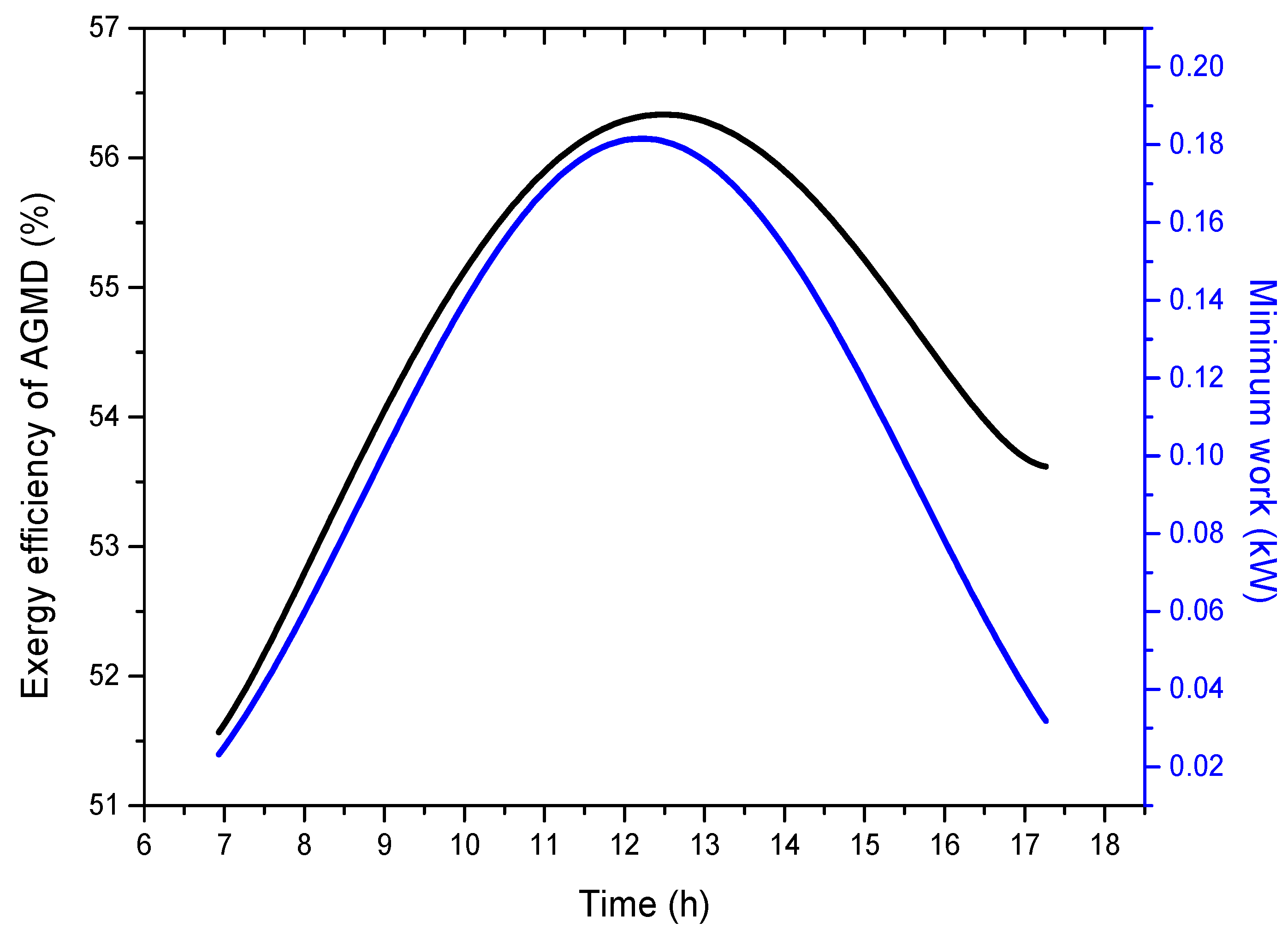
- The exergy efficiency for the AGMD system is found to be 56.3%, which indicates that the AGMD module of the current design is moderately efficient, and large amounts of energy can be saved. It is important to highlight that all desalination processes have very low energy efficiencies. However, what distinguishes AGMD is that it operates at a lower temperature compared to other thermal distillation processes. This facilitates its coupling with solar energy;
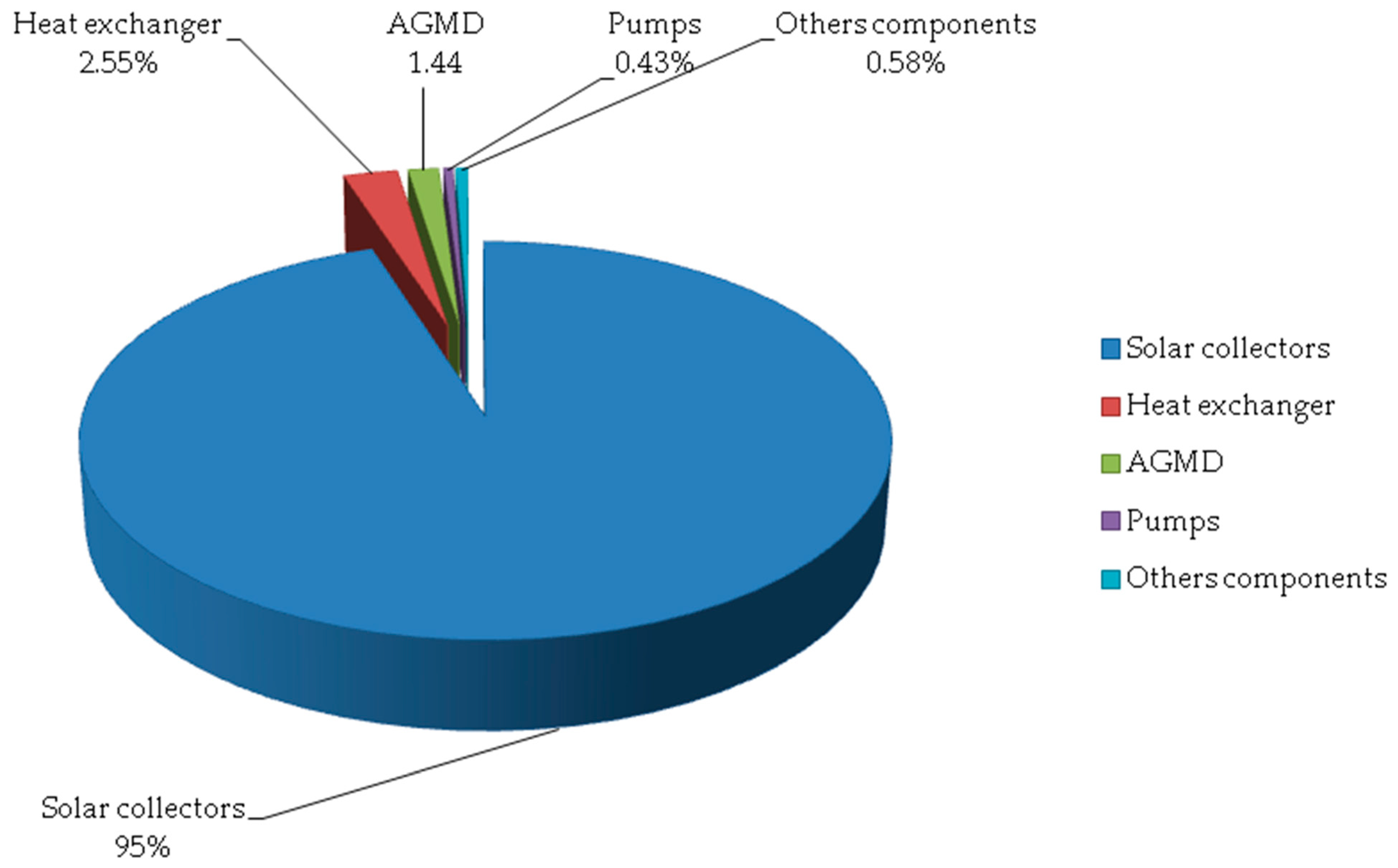
- The maximum exergy destruction occurs in the solar collector (95%) because of the large temperature difference between solar heat and the coolant fluid in the collector field, which results in high irreversibilities. Hence, effort should be made to reduce this exergy loss. Potential improvement of the solar collector field might be achieved by maximizing the collector’s optical efficiency as well as minimizing the overall heat losses of the collector area;
- The two main sources of exergy destruction are the solar thermal collector and the desalination unit 95% of the total exergy loss is destroyed in the collector, while 2.55% of the loss of total exergy is destroyed in the heat exchanger and only 1.44% of the total exergy loss is destroyed in the desalination system;
- Increasing the inlet temperature of the hot channel increases the system's overall energy and exergy efficiencies; while it reduces the total exergy destruction rate leading to the improvement in the performance of the system;
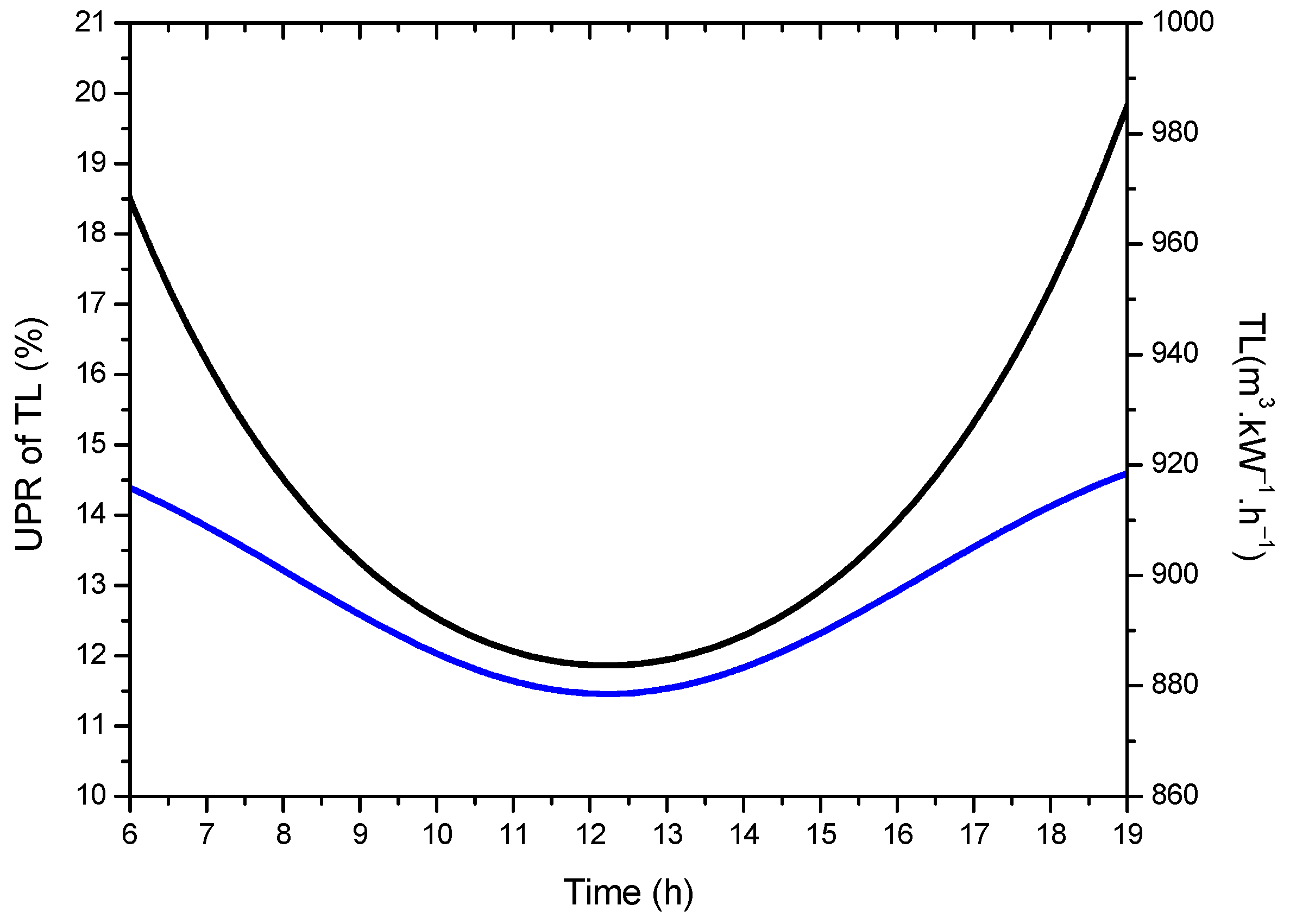
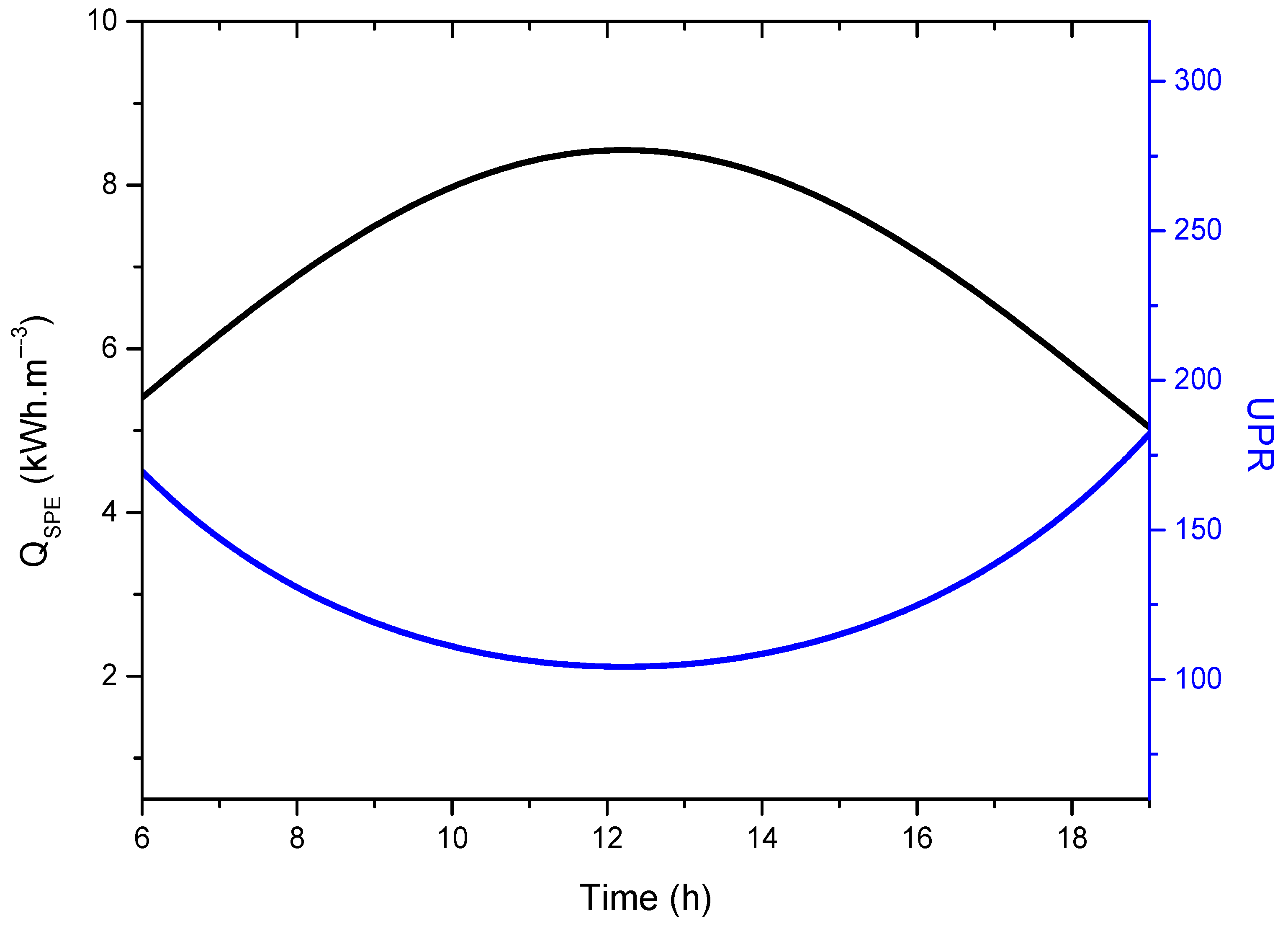
- The results also confirm that the solar AGMD process is operating at 20.43% of the thermodynamic limit of UPR, which is unsustainable for future desalinated water supplies; therefore, there are a lot of opportunities to improve desalination system performance to achieve UPR at greater rates by hybridizing existing processes and developing better materials.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | surface area [m2] |
| Bw | mass transfer coefficient [kg.m−2.h−1.Pa−1] |
| Cp | thermal capacity [J.kg−1·K−1] |
| Dva | thermal diffusivity of water vapor in the air [m2.s−1] |
| dh | hydraulic diameter [m] |
| L | module length [m] |
| mass flow rate [kg.s−1] | |
| P | pressure [Pa] |
| PR | Performance Ratio [–] |
| R | thermal resistance [m2·K.W−1] |
| S | salinity [g.kg−1] |
| T | temperature [°C] |
| T | time [s] |
| U | heat transfer coefficient [W.m−2·K−1] |
| Minimum work (kW) | |
| Greek letters | |
| α | activity coefficient [–] |
| β | water fraction [–] |
| δ | thickness [m] |
| ε | porosity [–] |
| ŋ | Efficiency |
| μ | dynamic viscosity [kg.m−1·s−1] |
| ρ | density [kg.m−3] |
| τ | tortuosity [–] |
| φ | thermal flux [W.m−2] |
| Subscripts | |
| 0 | reference state |
| a | Air |
| ag | air gap |
| c | Cold |
| ev | Evaporator |
| ex | Exergy |
| E | Feed |
| h | Hot |
| hm | hot fluid-membrane interface |
| In | Inlet |
| m | Membrane |
| ma | membrane-air gap interface |
| out | Outlet |
| P | Permeate |
| pc | cold fluid-plate interface |
| pp | temperature at the permeate-plate interface |
| So | Source |
| sw | Seawater |
| th | Thermal |
| v | Vapor |
References
- Kanoglu, M.; Dincer, I.; Rosen, M.A. Understanding Energy and Exergy Efficiencies for Improved Energy Management in Power Plants. Energy Policy 2007, 35, 3967–3978. [Google Scholar] [CrossRef]
- Tsatsaronis, G. Definitions and Nomenclature in Exergy Analysis and Exergoeconomics. Energy 2007, 32, 249–253. [Google Scholar] [CrossRef]
- Kerme, E.D.; Orfi, J.; Fung, A.S.; Salilih, E.M.; Khan, S.U.-D.; Alshehri, H.; Ali, E.; Alrasheed, M. Energetic and Exergetic Performance Analysis of a Solar Driven Power, Desalination and Cooling Poly-Generation System. Energy 2020, 196, 117150. [Google Scholar] [CrossRef]
- Guillén-Burrieza, E.; Blanco, J.; Zaragoza, G.; Alarcón, D.-C.; Palenzuela, P.; Ibarra, M.; Gernjak, W. Experimental Analysis of an Air Gap Membrane Distillation Solar Desalination Pilot System. J. Membr. Sci. 2011, 379, 386–396. [Google Scholar] [CrossRef]
- Moudjeber, D.-E.; Ruiz-Aguirre, A.; Ugarte-Judge, D.; Mahmoudi, H.; Zaragoza, G. Solar Desalination by Air-Gap Membrane Distillation: A Case Study from Algeria. Desalination Water Treat. 2016, 57, 22718–22725. [Google Scholar] [CrossRef]
- Sandid, A.; Nehari, D.; Elmeriah, A.; Remlaoui, A. Dynamic Simulation of an Air-Gap Membrane Distillation (AGMD) Process Using Photovoltaic Panels System and Flat Plate Collectors. J. Therm. Eng. 2021, 7, 117–133. [Google Scholar] [CrossRef]
- Sandida, A.M.; Neharia, T.; Neharia, D. Simulation Study of an Air-Gap Membrane Distillation System for Seawater Desalination Using Solar Energy. Desalination Water Treat. 2021, 229, 40–51. [Google Scholar] [CrossRef]
- Shahzad, M.W.; Burhan, M.; Ang, L.; Ng, K.C. Energy-Water-Environment Nexus Underpinning Future Desalination Sustainability. Desalination 2017, 413, 52–64. [Google Scholar] [CrossRef]
- Mericq, J.-P.; Laborie, S.; Cabassud, C. Evaluation of Systems Coupling Vacuum Membrane Distillation and Solar Energy for Seawater Desalination. Chem. Eng. J. 2011, 166, 596–606. [Google Scholar] [CrossRef]
- Frikha, N.; Matlaya, R.; Chaouachi, B.; Gabsi, S. Simulation of an Autonomous Solar Vacuum Membrane Distillation for Seawater Desalination. Desalination Water Treat. 2014, 52, 1725–1734. [Google Scholar] [CrossRef]
- Chen, T.-C.; Ho, C.-D. Immediate Assisted Solar Direct Contact Membrane Distillation in Saline Water Desalination. J. Membr. Sci. 2010, 358, 122–130. [Google Scholar] [CrossRef]
- Shim, W.G.; He, K.; Gray, S.; Moon, I.S. Solar Energy Assisted Direct Contact Membrane Distillation (DCMD) Process for Seawater Desalination. Sep. Purif. Technol. 2015, 143, 94–104. [Google Scholar] [CrossRef]
- Li, G.; Lu, L. Modeling and Performance Analysis of a Fully Solar-Powered Stand-Alone Sweeping Gas Membrane Distillation Desalination System for Island and Coastal Households. Energy Convers. Manag. 2020, 205, 112375. [Google Scholar] [CrossRef]
- Signorato, F.; Morciano, M.; Bergamasco, L.; Fasano, M.; Asinari, P. Exergy Analysis of Solar Desalination Systems Based on Passive Multi-Effect Membrane Distillation. Energy Rep. 2020, 6, 445–454. [Google Scholar] [CrossRef]
- Reddy, V.S.; Kaushik, S.C.; Tyagi, S.K. Exergetic Analysis and Performance Evaluation of Parabolic Trough Concentrating Solar Thermal Power Plant (PTCSTPP). Energy 2012, 39, 258–273. [Google Scholar] [CrossRef]
- He, Z.; Liang, C. Experimental Study on Energy and Exergy Analysis of a Counter Hollow Fiber Membrane-Based Humidifier. Int. J. Energy Power Eng. 2020, 9, 95–107. [Google Scholar] [CrossRef]
- Abdallah, S.B.; Frikha, N.; Gabsi, S. Simulation of Solar Vacuum Membrane Distillation Unit. Desalination 2013, 324, 87–92. [Google Scholar] [CrossRef]
- Zhai, H.; Dai, Y.J.; Wu, J.Y.; Wang, R.Z. Energy and Exergy Analyses on a Novel Hybrid Solar Heating, Cooling and Power Generation System for Remote Areas. Appl. Energy 2009, 86, 1395–1404. [Google Scholar] [CrossRef]
- Kalogirou, S.A.; Karellas, S.; Braimakis, K.; Stanciu, C.; Badescu, V. Exergy Analysis of Solar Thermal Collectors and Processes. Prog. Energy Combust. Sci. 2016, 56, 106–137. [Google Scholar] [CrossRef]
- KhoshgoftarManesh, M.H.; Onishi, V.C. Energy, Exergy, and Thermo-Economic Analysis of Renewable Energy-Driven Polygeneration Systems for Sustainable Desalination. Processes 2021, 9, 210. [Google Scholar] [CrossRef]
- Banat, F.; Jwaied, N. Exergy Analysis of Desalination by Solar-Powered Membrane Distillation Units. Desalination 2008, 230, 27–40. [Google Scholar] [CrossRef]
- Al-Obaidani, S.; Curcio, E.; Macedonio, F.; Di Profio, G.; Al-Hinai, H.; Drioli, E. Potential of Membrane Distillation in Seawater Desalination: Thermal Efficiency, Sensitivity Study and Cost Estimation. J. Membr. Sci. 2008, 323, 85–98. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, C.-Y. A Review of Solar Collectors and Thermal Energy Storage in Solar Thermal Applications. Appl. Energy 2013, 104, 538–553. [Google Scholar] [CrossRef] [Green Version]
- Shahzad, M.W.; Thu, K.; Kim, Y.; Ng, K.C. An Experimental Investigation on MEDAD Hybrid Desalination Cycle. Appl. Energy 2015, 148, 273–281. [Google Scholar] [CrossRef]
- Ng, K.C.; Thu, K.; Oh, S.J.; Ang, L.; Shahzad, M.W.; Ismail, A.B. Recent Developments in Thermally-Driven Seawater Desalination: Energy Efficiency Improvement by Hybridization of the MED and AD Cycles. Desalination 2015, 356, 255–270. [Google Scholar] [CrossRef]
- Shahzad, M.W.; Ng, K.C.; Thu, K.; Saha, B.B.; Chun, W.G. Multi Effect Desalination and Adsorption Desalination (MEDAD): A Hybrid Desalination Method. Appl. Therm. Eng. 2014, 72, 289–297. [Google Scholar] [CrossRef]
- Son, H.S.; Shahzad, M.W.; Ghaffour, N.; Ng, K.C. Pilot Studies on Synergetic Impacts of Energy Utilization in Hybrid Desalination System: Multi-Effect Distillation and Adsorption Cycle (MED-AD). Desalination 2020, 477, 114266. [Google Scholar] [CrossRef]
- Shahzad, M.W.; Burhan, M.; Ng, K.C. Pushing Desalination Recovery to the Maximum Limit: Membrane and Thermal Processes Integration. Desalination 2017, 416, 54–64. [Google Scholar] [CrossRef]
- Criscuoli, A.; Drioli, E. Energetic and Exergetic Analysis of an Integrated Membrane Desalination System. Desalination 1999, 124, 243–249. [Google Scholar] [CrossRef]
- Macedonio, F.; Drioli, E. An Exergetic Analysis of a Membrane Desalination System. Desalination 2010, 261, 293–299. [Google Scholar] [CrossRef]
- Macedonio, F.; Curcio, E.; Drioli, E. Integrated Membrane Systems for Seawater Desalination: Energetic and Exergetic Analysis, Economic Evaluation, Experimental Study. Desalination 2007, 203, 260–276. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, M.; Yang, H.; Cao, J.; Li, J.; Su, Y.; Pei, G. Energetic and Exergetic Analyses on Structural Optimized Parabolic Trough Solar Receivers in a Concentrated Solar–Thermal Collector System. Energy 2019, 171, 611–623. [Google Scholar] [CrossRef]
- Choi, J.; Choi, Y.; Lee, J.; Kim, Y.; Lee, S. Exergy Analysis of a Direct Contact Membrane Distillation (DCMD) System Based on Computational Fluid Dynamics (CFD). Membranes 2021, 11, 525. [Google Scholar] [CrossRef] [PubMed]
- Miladi, R.; Frikha, N.; Gabsi, S. Exergy Analysis of a Solar-Powered Vacuum Membrane Distillation Unit Using Two Models. Energy 2017, 120, 872–883. [Google Scholar] [CrossRef]
- Miladi, R.; Frikha, N.; Kheiri, A.; Gabsi, S. Energetic Performance Analysis of Seawater Desalination with a Solar Membrane Distillation. Energy Convers. Manag. 2019, 185, 143–154. [Google Scholar] [CrossRef]
- Miladi, R.; Frikha, N.; Gabsi, S. Modeling and Energy Analysis of a Solar Thermal Vacuum Membrane Distillation Coupled with a Liquid Ring Vacuum Pump. Renew. Energy 2021, 164, 1395–1407. [Google Scholar] [CrossRef]
- Elan, D.; Chung, W. (12) Patent Application Publication (10). U.S. Patent 2016/0074812 A1, 7 July.
- Woldemariam, D.; Martin, A.; Santarelli, M. Applied sciences Exergy Analysis of Air-Gap Membrane Distillation Systems for Water Purification Applications. Appl. Sci. 2017, 7, 301. [Google Scholar] [CrossRef] [Green Version]
- Ali, A.; Tufa, R.A.; Macedonio, F.; Curcio, E.; Drioli, E. Membrane technology in renewable-energy-driven desalination. Renew. Sustain. Energy Rev. 2018, 81, 1–21. [Google Scholar] [CrossRef]
- Ihm, S.; Al-Najdi, O.Y.; Hamed, O.A.; Jun, G.; Chung, H. Energy cost comparison between MSF, MED and SWRO: Case studies for dual purpose plants. Desalination 2016, 397, 116–125. [Google Scholar] [CrossRef]
- Khayet, M. Membranes and theoretical modeling of membrane distillation: A review. Adv. Colloid Interface Sci. 2011, 164, 56–88. [Google Scholar] [CrossRef]
- Guillén-Burrieza, E.; Alarcón-Padilla, D.-C.; Palenzuela, P.; Zaragoza, G. Technoeconomic assessment of a pilot-scale plant for solar desalination based on existing plate and frame MD technology. Desalination 2015, 374, 70–80. [Google Scholar] [CrossRef]
- Saffarini, R.B.; Summers, E.K.; Arafat, H.A.; Lienhard, J.H. Economic evaluation of stand-alone solar powered membrane distillation systems. Desalination 2012, 299, 55–62. [Google Scholar] [CrossRef]
- Banat, F.; Jwaied, N. Economic evaluation of desalination by small-scale autonomous solar-powered membrane distillation units. Desalination 2008, 220, 566–573. [Google Scholar] [CrossRef]
- Cerci, Y. Exergy analysis of a reverse osmosis desalination plant in California. Desalination 2002, 142, 257–266. [Google Scholar] [CrossRef]
- Drioli, E.; Curcio, E.; Di Profio, G.; Macedonio, F.; Criscuoli, A. Integrating Membrane Contactors Technology and Pressure-Driven Membrane Operations for Seawater Desalination. Chem. Eng. Res. Des. 2006, 84, 209–220. [Google Scholar] [CrossRef]
- Menasri, R.; Triki, Z.; Bouaziz, M.N.; Hamrouni, B. Energy and exergy analyses of a novel multi-effect distillation system with thermal vapor compression for seawater desalination. Desalination Water Treat. 2022, 246, 54–67. [Google Scholar] [CrossRef]
- Diaby, A.T.; Byrne, P.; Loulergue, P.; Balannec, B.; Szymczyk, A.; Maré, T.; Sow, O. Design Study of the Coupling of an Air Gap Membrane Distillation Unit to an Air Conditioner. Desalination 2017, 420, 308–317. [Google Scholar] [CrossRef]
- Shahzad, M.W.; Burhan, M.; Son, H.S.; Oh, S.J.; Ng, K.C. Desalination Processes Evaluation at Common Platform: A Universal Performance Ratio (UPR) Method. Appl. Therm. Eng. 2018, 134, 62–67. [Google Scholar] [CrossRef] [Green Version]
- Ng, K.C.; Shahzad, M.W.; Son, H.S.; Hamed, O.A. An Exergy Approach to Efficiency Evaluation of Desalination. Appl. Phys. Lett. 2017, 110, 184101. [Google Scholar] [CrossRef] [Green Version]
- Baaloudj, O.; Nasrallah, N.; Kebir, M.; Guedioura, B.; Amrane, A.; Nguyen-Tri, P.; Nanda, S.; Assadi, A.A. Artificial neural network modeling of cefixime photodegradation by synthesized CoBi2O4 nanoparticles. Environ. Sci. Pollut. Res. 2021, 28, 15436–15452. [Google Scholar] [CrossRef]
- Terzi, R. Application of Exergy Analysis to to Energy Systems. In Application of Exergy; InTech: London, UK, 2018; p. 109. [Google Scholar] [CrossRef] [Green Version]
- Sharqawy, M.H.; Lienhard, J.H.; Zubair, S.M. Thermophysical Properties of Seawater: A Review of Existing Correlations and Data. Desalination Water Treat. 2010, 16, 354–380. [Google Scholar] [CrossRef]
- Alsaadi, A.S.; Ghaffour, N.; Li, J.-D.; Gray, S.; Francis, L.; Maab, H.; Amy, G.L. Modeling of Air-Gap Membrane Distillation Process: A Theoretical and Experimental Study. J. Membr. Sci. 2013, 445, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Banat, F.A. Membrane Distillation for Desalination and Removal of Volatile Organic Compounds from Water. Ph.D. Dissertation, Department of Chemical Engineering, McGill University, Montreal, QC, Canada, 1994. [Google Scholar]
- Rahimi-Ahar, Z.; Hatamipour, M.S.; Ahar, L.R. Air Humidification-Dehumidification Process for Desalination: A Review. Prog. Energy Combust. Sci. 2020, 80, 100850. [Google Scholar] [CrossRef]
| Type | Capacity (m3/Day) | Exergy Efficiency (%) | Reference |
|---|---|---|---|
| RO | 7250 | 4.3 | [43] |
| MD on RO retentate | 22,344 | 19.1–21.9 | [44] |
| MED-TVC | 4,802,976 | 3.6 | [45] |
| MD | 0.31 | 0.3 | [46] |
| DCMD with HR | 24,000 | 28.3 | [22] |
| DCMD without HR | 24,000 | 25.6 | [22] |
| AGMD (Xzero) | 0.22–0.73 | 8.54–19.32 | [38] |
| AGMD (Elixir500) | 0.1–0.17 | 18.3–26.5 | [38] |
| AGMD Unit | ||
|---|---|---|
| Heat transfer | ||
| Parameter | Equation | No. |
| Energy conservation | (1) | |
| Heat flux in the hot channel | (2) | |
| Heat flux from the surface of the membrane to the condensate | (3) | |
| Heat flux through the air gap | (4) | |
| Heat flux in the boundary layer of the cold channel | (5) | |
| Mass transfer | ||
| Permeate flux | (6) | |
| Antoine equation | (7) | |
| Permeability of the membrane | (8) | |
| Heat exchangers | ||
| Heat exchanged | (9) | |
| (10) | ||
| (11) | ||
| Solar Flat Plate Collector | ||
| Energy gained by the absorber | (12) | |
| Quantity of solar radiation received by the collector | (13) | |
| Energy gained by the absorber | (14) | |
| Useful energy absorbed by the collector | (15) | |
| Collector heat removal factor | (16) | |
| Ratio of useable energy gain | (17) | |
| Properties | Value |
|---|---|
| Thickness | 0.28 |
| Pore size | 0.2 |
| Porosity | 80 |
| Tortuosity | 1.5 |
| N | Temperature (K) | Mass Fow Rate (kg/s) | Salinity (g/kg) | Enthalpy (kJ/kg.K) | Entropy (kJ/kg) | Exergy (kW) |
|---|---|---|---|---|---|---|
| 1 | 87.5 | 0.024 | 0 | 385.58 | 1.2619 | 0.556 |
| 2 | 62.66 | 0.024 | 0 | 262.08 | 0.8642 | 0.2344 |
| 3 | 62.69 | 0.024 | 0 | 262.47 | 0.8652 | 0.2352 |
| 4 | 62.95 | 0.033 | 0.35 | 117.76 | 0.4097 | 0 |
| 5 | 29.8 | 0.033 | 0.35 | 118.96 | 0.4137 | 0.2036 |
| 6 | 57.91 | 0.033 | 0.35 | 151.43 | 0.5195 | 0.0158 |
| 7 | 62.11 | 0.033 | 0.35 | 248.6 | 0.8202 | 0.2260 |
| 8 | 58.77 | 0.03 | 0.43 | 232.22 | 0.7760 | 0.1863 |
| 9 | 58.84 | 0.03 | 0.43 | 232.5 | 0.7668 | 0.1872 |
| 10 | 29.70 | 0.003 | 0 | 124.52 | 0.4317 | 0.030 |
| 11 | 29.88 | 0.003 | 0 | 125.28 | 0.4342 | 0.0310 |
| 12 | 29.8 | 0.003 | 0 | 125.17 | 0.4260 | 0.0303 |
| 13 | 29.8 | 0.03 | 0.43 | 118.04 | 0.4076 | 0.1510 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mibarki, N.; Triki, Z.; Belhadj, A.-E.; Tahraoui, H.; Amrane, A.; Cheikh, S.; Hadadi, A.; Bouchelkia, N.; Kebir, M.; Zhang, J.; et al. Energy and Exergy Analysis of Solar Air Gap Membrane Distillation System for Seawater Desalination. Water 2023, 15, 1201. https://doi.org/10.3390/w15061201
Mibarki N, Triki Z, Belhadj A-E, Tahraoui H, Amrane A, Cheikh S, Hadadi A, Bouchelkia N, Kebir M, Zhang J, et al. Energy and Exergy Analysis of Solar Air Gap Membrane Distillation System for Seawater Desalination. Water. 2023; 15(6):1201. https://doi.org/10.3390/w15061201
Chicago/Turabian StyleMibarki, Nawel, Zakaria Triki, Abd-Elmouneïm Belhadj, Hichem Tahraoui, Abdeltif Amrane, Sabrina Cheikh, Amina Hadadi, Nasma Bouchelkia, Mohamed Kebir, Jie Zhang, and et al. 2023. "Energy and Exergy Analysis of Solar Air Gap Membrane Distillation System for Seawater Desalination" Water 15, no. 6: 1201. https://doi.org/10.3390/w15061201








