Discharge Coefficients of a Specific Vertical Slot Fishway Geometry—New Fitting Parameters
Abstract
:1. Introduction
2. State-of-the-Art
3. Experimental Model Data
4. Results and Discussion
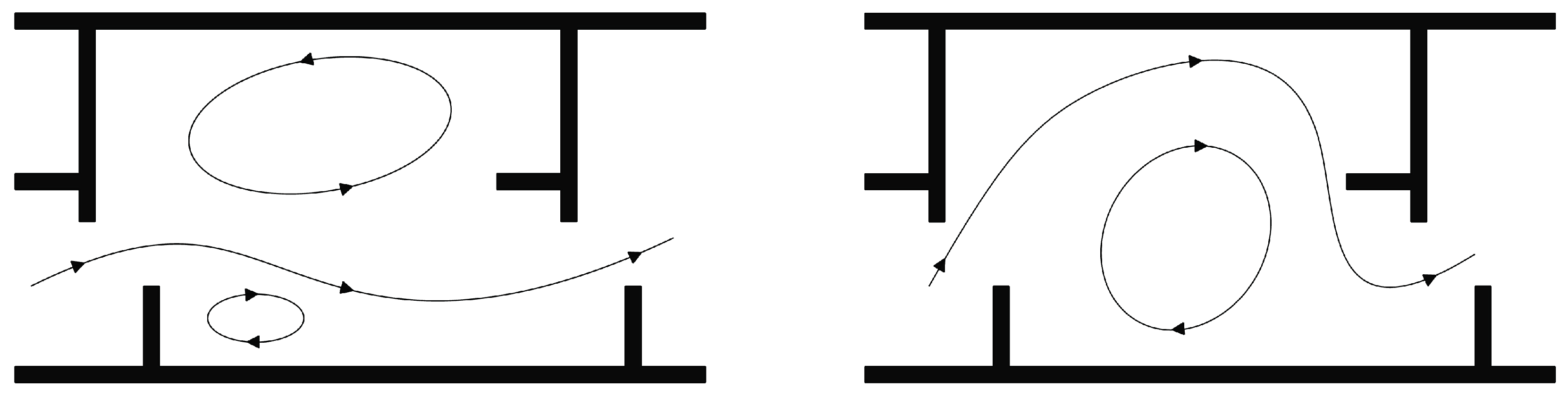
4.1. General
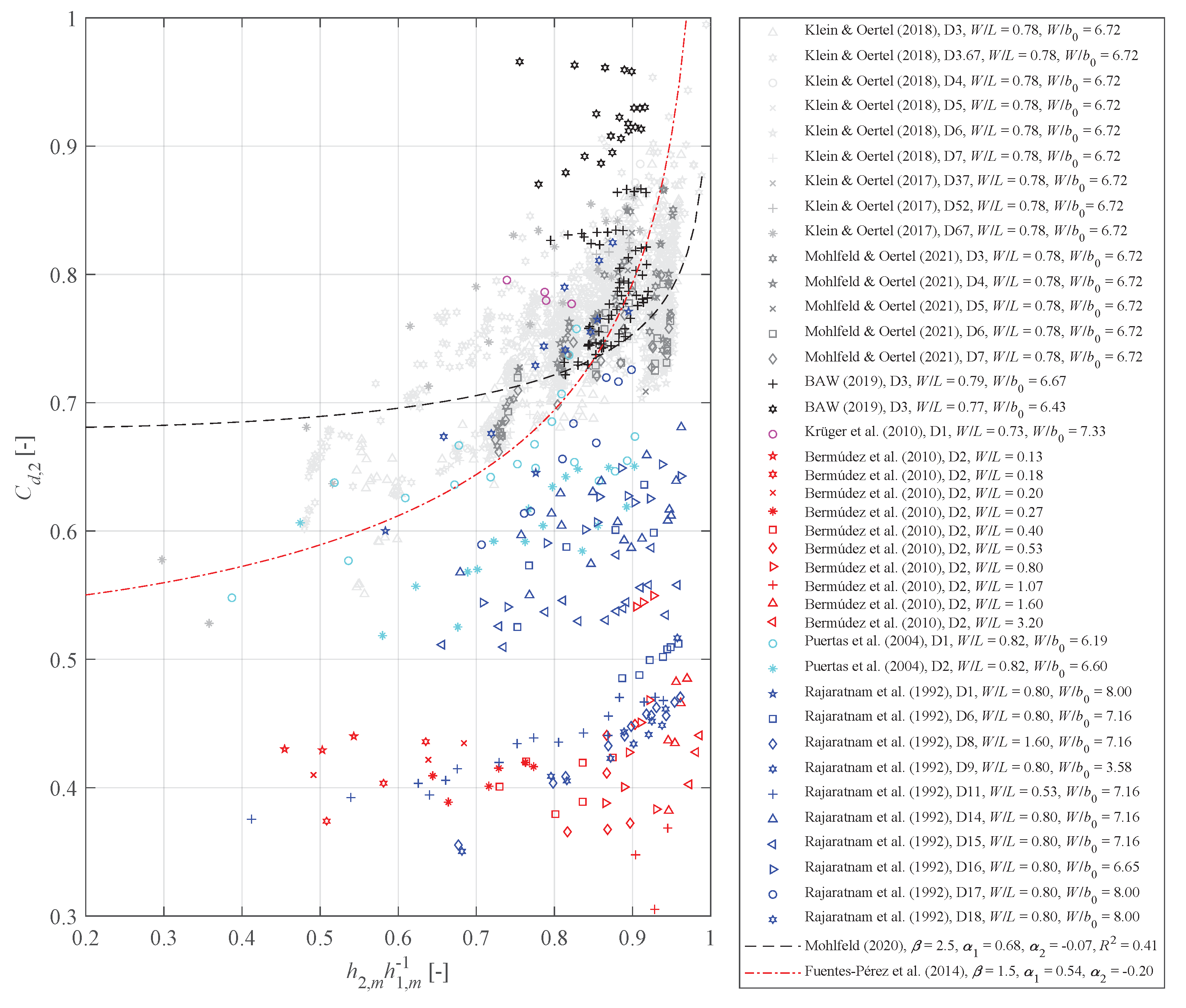
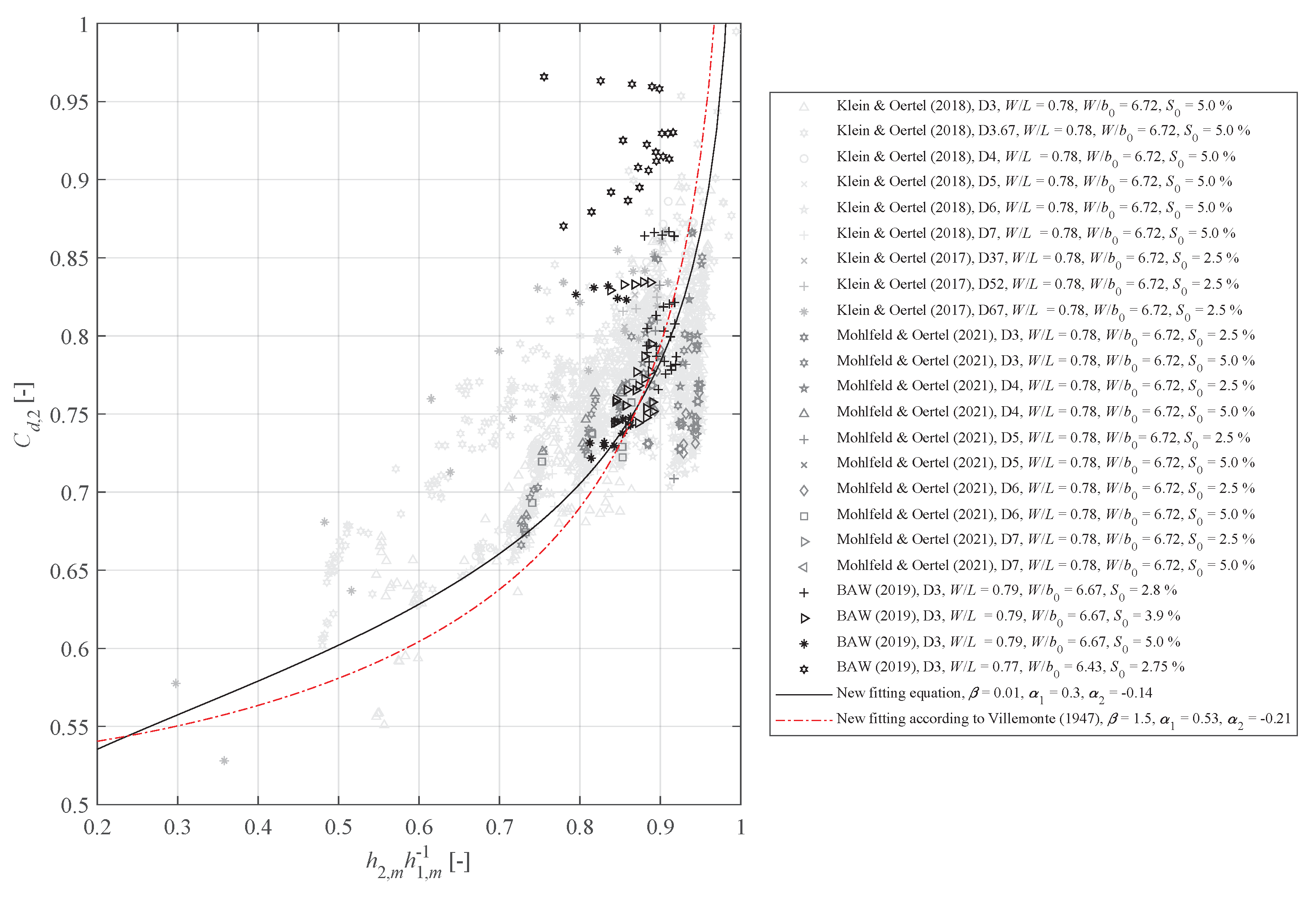
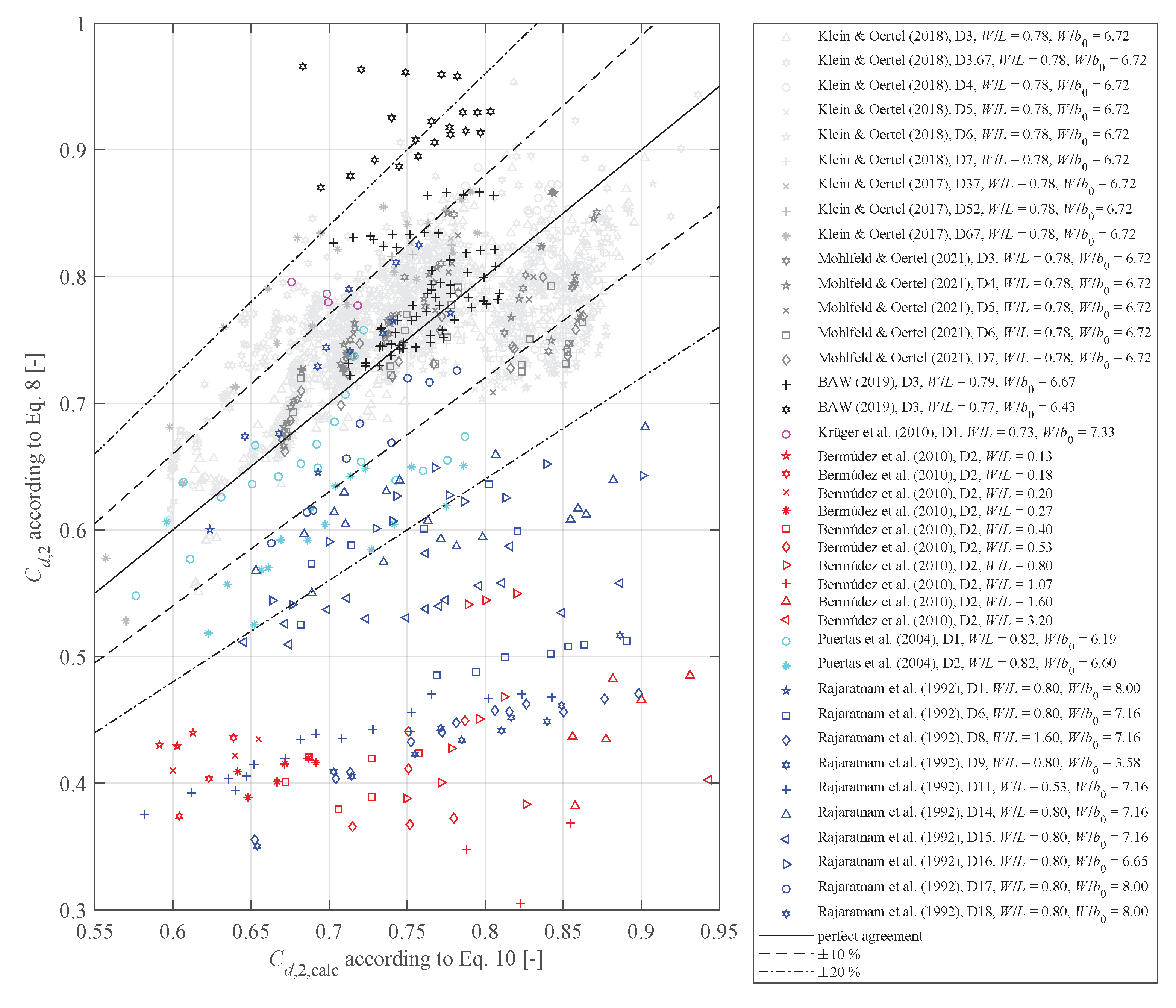
4.2. Discharge Coefficients in Accordance with Poleni
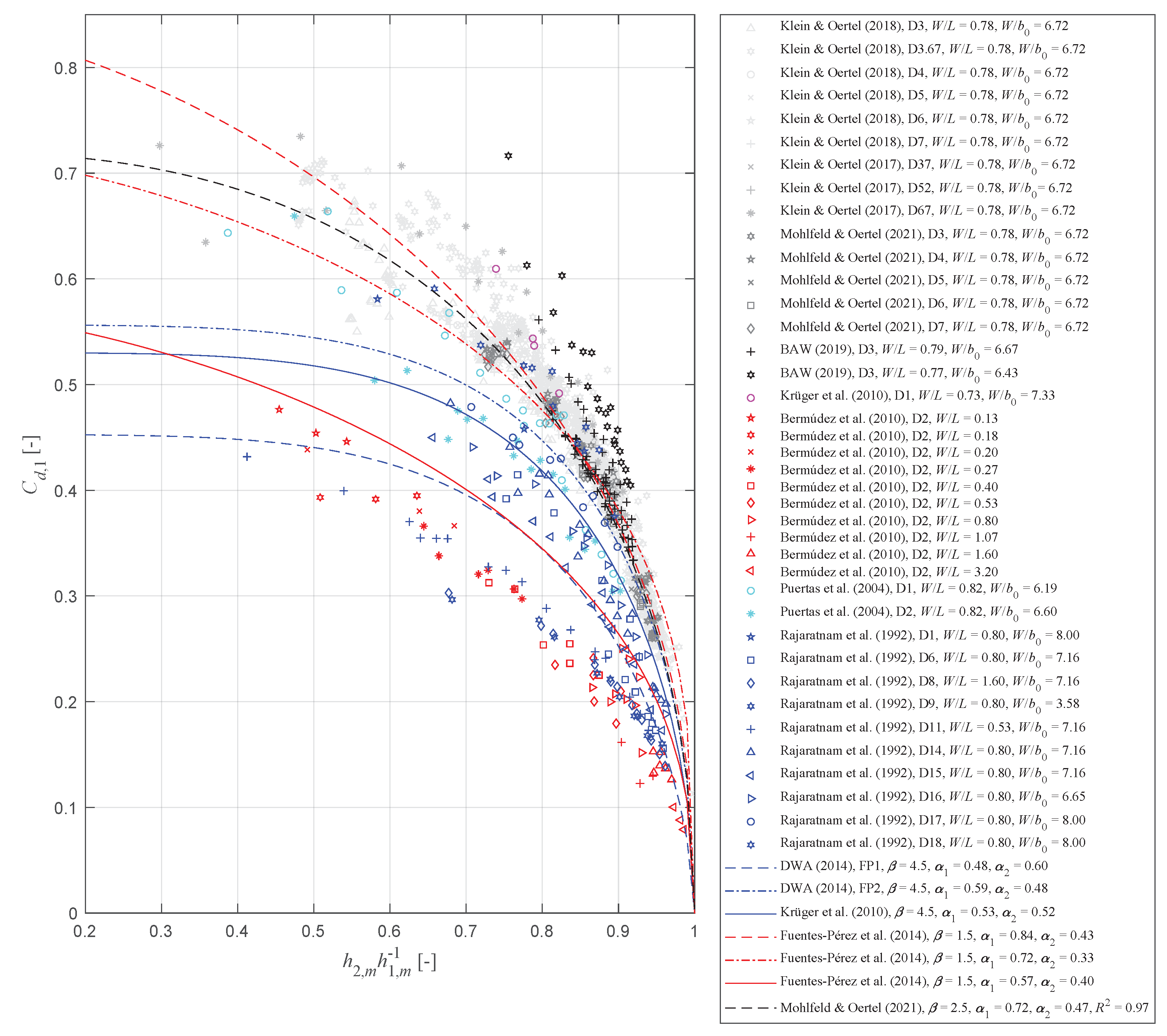
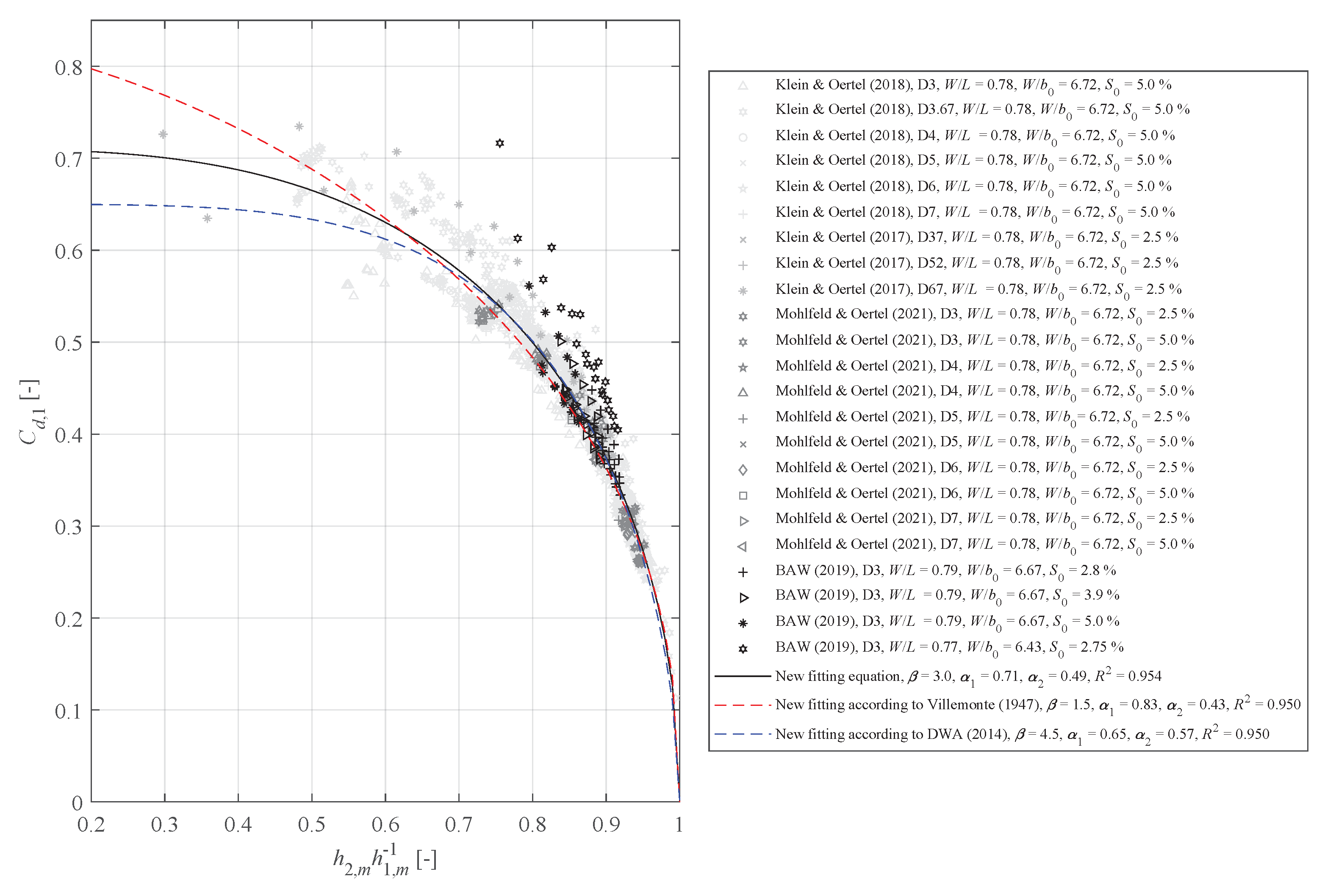
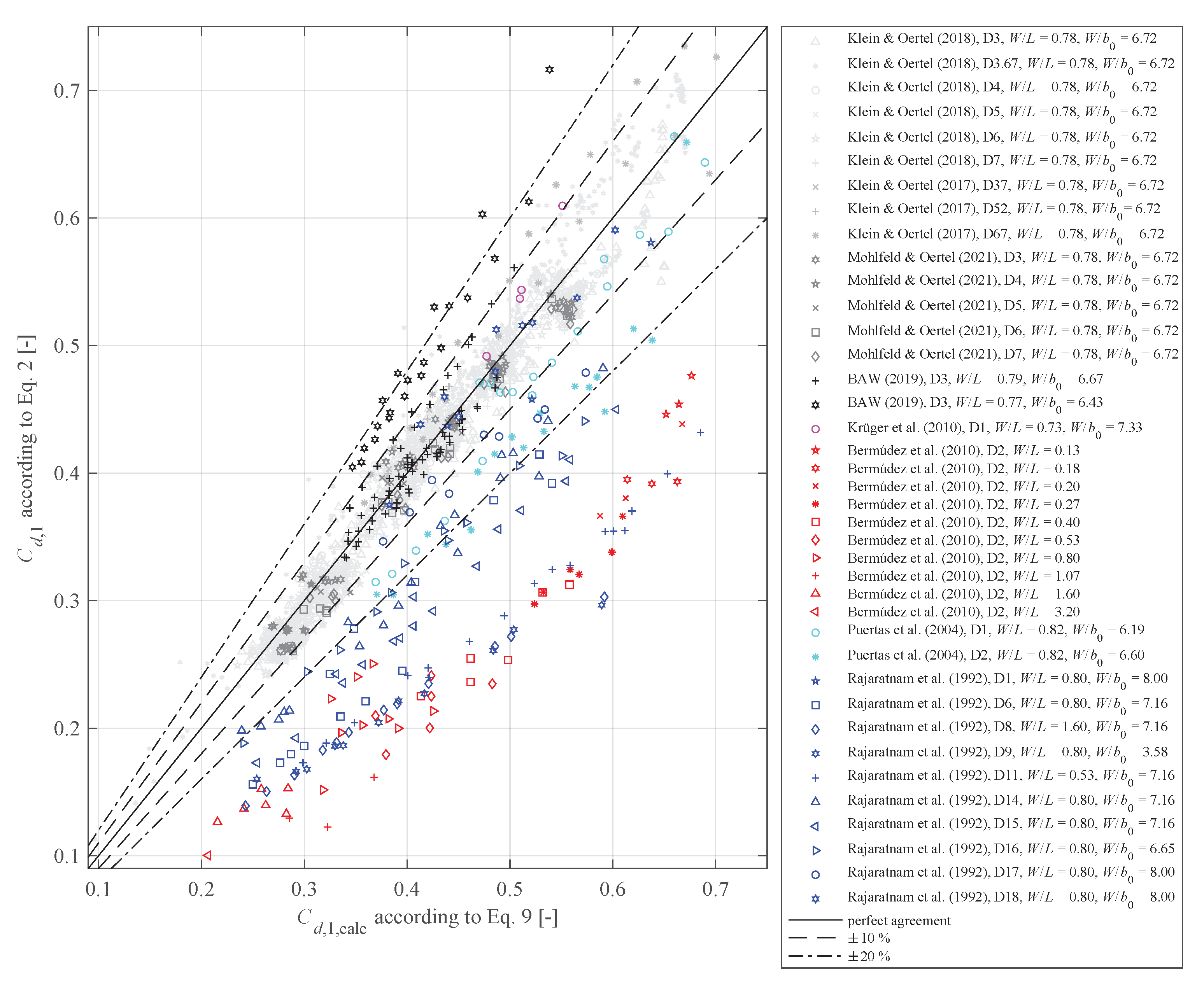
4.3. Discharge Coefficients in Accordance with Torricelli
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| coefficients depending on the fishway geometry (-) | |
| discharge area (m2) | |
| empirically determined coefficients (-) | |
| slot width (m) | |
| discharge coefficient (-) | |
| discharge coefficient according to Poleni (-) | |
| discharge coefficient according to Torricelli (-) | |
| calculated discharge coefficient (-) | |
| calculated discharge coefficient (-) | |
| water level difference (m) | |
| mean water level difference (m) | |
| geodetic height difference (m) | |
| g | acceleration due to gravity (ms−2) |
| h | water depth (m) |
| headwater depth (m) | |
| tailwater depth (m) | |
| calculated mean headwater depth (m) | |
| calculated mean tailwater depth (m) | |
| dimensionless calculated water depth (-) | |
| dimensionless calculated mean water depth (-) | |
| area-averaged mean water depth in the basin (m) | |
| guide element length (m) | |
| ratio of guide element length to slot width (-) | |
| L | basin length (m) |
| ratio of basin length to slot width (-) | |
| Q | discharge (m3s−1) |
| dimensionless discharge (-) | |
| coefficient of determination (-) | |
| S | slope (-) |
| maximum flow velocity (ms−1) | |
| W | basin width (m) |
| ratio of basin width to basin length (-) | |
| ratio of basin width to slot width (-) | |
| average flow depth (m) | |
| ratio of average flow depth to slot width (-) |
References
- Water Framework Directive (WFD). Directive 2000/60/EC of the European Parliament and of the Council establishing a framework for the Community action in the field of water policy. Off. J. 2000. Available online: https://www.semanticscholar.org/paper/Directive-2000-60-EC-of-the-European-Parliament-and-Other/a3115d92366398ea8b94c69d847b952041ac886d (accessed on 12 January 2023).
- Deutsche Vereinigung für Wasserwirtschaft, Abwasser und Abfall e. V. (DWA). Fischaufstiegsanlagen und fischpassierbare Bauwerke—Gestaltung, Bemessung, Qualitätssicherung. DWA-Regelw. 2014. Available online: https://www.baufachinformation.de/merkblatt-dwa-m-509-mai-2014/mb/241832 (accessed on 12 January 2023). (In German).
- Mohlfeld, J.; Oertel, M. Ermittlung von Abflussbeiwerten zur hydraulischen Bemessung von Fischaufstiegsanlagen in Schlitzpassbauweise. WasserWirtschaft 2021, 2–3, 27–32. (In German) [Google Scholar] [CrossRef]
- Mohlfeld, J. Einfluss unterschiedlicher Leitelemente auf die Hydraulik in flach geneigten Schlitzpässen; Shaker Verlag: Herzogenrath, Germany, 2020. (In German) [Google Scholar]
- Wu, S.; Rajaratnam, N.; Katopodis, C. Structure of flow in vertical slot fishway. J. Hydraul. Eng. 1999, 125, 351–360. [Google Scholar] [CrossRef]
- Klein, J.; Oertel, M. Untersuchung von Einflussparametern auf die Abflussbemessung von Fischaufstiegsanlagen in Schlitzbauweise. Dresdner Wasserbauliche Mitteilungen 2017, 58, 291–300. (In German) [Google Scholar]
- Bermúdez, M.; Puertas, J.; Cea, L.; Pena, L.; Balairón, L. Influence of pool geometry on the biological efficiency of vertical slot fishways. Ecol. Eng. 2010, 36, 1355–1364. [Google Scholar] [CrossRef]
- Tarrade, L.; Texier, A.; David, L.; Larinier, M. Topologies and measurements of turbulent flow in vertical slot fishways. Hydrobiologia 2008, 609, 177–188. [Google Scholar] [CrossRef] [Green Version]
- Tarrade, L.; Pineau, G.; Calluaud, D.; Texier, A.; David, L.; Larinier, M. Detailed experimental study of hydrodynamic turbulent flows generated in vertical slot fishways. Environ. Fluid Mech. 2011, 11, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.W.; David, L.; Larinier, M. Contribution of experimental fluid mechanics to the design of vertical slot fish passes. Knowl. Manag. Aquat. Ecosyst. 2010, 396, 2. [Google Scholar] [CrossRef]
- Stamou, A.I.; Mitsopoulos, G.; Rutschmann, P.; Biui, M.D. Verification of a 3D CFD model for vertical slot fish-passes. Environ. Fluid Mech. 2018, 18, 1435–1461. [Google Scholar] [CrossRef]
- Tuhtan, J.A.; Fuentes-Pérez, J.; Toming, G.; Schneider, M.; Schwarzenberger, R.; Schletterer, M.; Kruusmaa, M. Man-made flows from a fish’s perspective: Autonomous classification of turbulent fishway flows with field data collected using an artificial lateral line. Bioinspiration Biomim. 2018, 13, 046006. [Google Scholar] [CrossRef] [PubMed]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2000. [Google Scholar]
- Liu, M.; Rajaratnam, N.; Zhu, D.Z. Mean Flow and Turbulence Structure in Vertical Slot Fishways. J. Hydraul. Eng. 2006, 132, 765–777. [Google Scholar] [CrossRef]
- Rajaratnam, N.; van der Vinne, G.; Katopodis, C. Hydraulics of Vertical Slot Fishways. J. Hydraul. Eng. 1986, 112, 909–927. [Google Scholar] [CrossRef]
- Puertas, J.; Pena, L.; Teijeiro, T. Experimental Approach to the Hydraulics of Vertical Slot Fishways. J. Hydraul. Eng. 2004, 13, 10–23. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Katopodis, C.; Solanki, S. New design for vertical slot fishways. Can. J. Civ. Eng. 1992, 19, 402–414. [Google Scholar] [CrossRef]
- Fuentes-Pérez, J.; Sanz-Ronda, F.; Martínez de Azagra Paredes, A.; García-Vega, A. Modeling Water-Depth Distribution in Vertical-Slot Fishways under Uniform and Nonuniform Scenarios. J. Hydraul. Eng. 2014, 140, 06014016. [Google Scholar] [CrossRef] [Green Version]
- Fuentes-Pérez, J.; García-Vega, A.; Sanz-Ronda, F.; Martínez de Azagra Paredes, A. Villemonte’s approach: A general method for modeling uniform and non-uniform performance in stepped fishways. Knowl. Manag. Aquat. Ecosyst. 2017, 418, 23. [Google Scholar] [CrossRef] [Green Version]
- Krüger, F.; Heimerl, S.; Seidel, F.; Lehmann, B. Ein Diskussionsbeitrag zur hydraulischen Berechnung von Schlitzpässen. WasserWirtschaft 2010, 3, 30–36. (In German) [Google Scholar] [CrossRef]
- Villemonte, J.R. Submerged-Weir Discharge Studies. Eng. News Rec. 1947, 139, 866–869. [Google Scholar]
- Clay, C.H. Design of Fishways and Other Fish Facilities, 2nd ed.; Clay, C.H., Ed.; Department of Fisheries of Canada: Ottawa, ON, Canada, 1961.
- Federal Waterways Engineering and Research Institute (Bundesanstalt für Wasserbau—BAW). Dataset of Investigated Slot Passes. 2019. Available online: henry.baw.de (accessed on 12 January 2023).
- Höger, V.; Prinz, F.; Meltzer, J.V. Die Variabilität der Fließgeschwindigkeit in Schlitzpässen. HENRY-Hydraul. Eng. Respository 2020, 106, 23–32. (In German) [Google Scholar]
- Klein, J.; Oertel, M. Influence of Inflow and Outflow Boundary Conditions on Flow Situation in Vertical Slot Fishways. IAHR Int. Symp. Hydraul. Struct. 2018, 7. Available online: https://digitalcommons.usu.edu/cgi/viewcontent.cgi?article=1166&context=ishs (accessed on 12 January 2023).

| Design | W | L | S | Q | Typ of Guide Element | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mohlfeld and Oertel (2021) [3] | 3 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.025; 0.050 | 0.016; 0.024; 0.032 | 0.190 | 1.60 | linear |
| 4 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.178 | 1.50 | linear | |||
| 5 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.178 | 1.50 | bevelled | |||
| 6 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.178 | 1.50 | spline | |||
| 7 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.178 | 1.50 | quadrant | |||
| BAW (2019) [23] | 3 | 0.8 | 1.01 | 0.120 | 0.79 | 6.67 | 8.42 | 0.028; 0.039; | 0.010 to 0.035 | linear | ||
| 3 | 0.79 | 1.02 | 0.122 | 0.77 | 6.43 | 8.36 | 0.050; 0.028 | linear | ||||
| Klein and Oertel (2018) [25] | 3 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.190 | 1.60 | linear | ||
| 3.67 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.190 | 1.60 | linear | |||
| 4 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.025; 0.050 | 0.008 to 0.044 | 0.178 | 1.50 | linear | |
| 5 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.178 | 1.50 | bevelled | |||
| 6 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.178 | 1.50 | spline | |||
| 7 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.178 | 1.50 | quadrant | |||
| Klein and Oertel (2017) [6] | 37 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.005 to 0.056 | 0.190 | 1.60 | linear | |
| 52 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.050 | 0.190 | 1.60 | linear | ||
| 67 | 0.8 | 1.021 | 0.119 | 0.78 | 6.72 | 8.58 | 0.190 | 1.60 | linear | |||
| Krüger et al. (2010) [20] | 1 | 3.3 | 4.5 | 0.45 | 0.73 | 7.33 | 10.00 | 0.056 | 0.769; 0.933; 1.101 | none | ||
| Bermúdez et al. (2010) [7] | 2 | 0.3 | 0.38 | 0.168; 0.084; 0.043 | 0.80 | 1.79; 3.58; 7.16 | 2.24; 4.47; 8.94 | 0.050 | 0.0009 to 0.0270 | none | ||
| 2 | 0.3 | 0.75 | 0.168; 0.084 | 0.40 | 1.79; 3.58 | 4.47; 8.94 | none | |||||
| 2 | 0.3 | 1.50 | 0.168 | 0.20 | 1.79 | 8.94 | none | |||||
| 2 | 0.3 | 2.25 | 0.168 | 0.13 | 1.79 | 13.42 | none | |||||
| 2 | 0.3 | 0.28 | 0.126 | 1.07 | 2.39 | 2.24 | none | |||||
| 2 | 0.3 | 0.57 | 0.126; 0.043 | 0.53 | 2.39; 7.16 | 4.47; 13.42 | none | |||||
| 2 | 0.3 | 1.13 | 0.126; 0.084 | 0.27 | 2.39; 3.58 | 8.94; 13.42 | none | |||||
| 2 | 0.3 | 1.70 | 0.126 | 0.18 | 2.39 | 13.34 | none | |||||
| 2 | 0.3 | 0.19 | 0.084; 0.043 | 1.60 | 3.58; 7.16 | 2.24; 4.47 | none | |||||
| 2 | 0.3 | 0.095 | 0.043 | 3.20 | 7.16 | 2.24 | none | |||||
| Puertas et al. (2004) [16] | 1 | 0.99 | 1.21 | 0.16 | 0.82 | 6.19 | 7.58 | 0.0570; 0.1005 | 0.0159 to 0.1250 | 0.243 | 1.52 | linear |
| 2 | 0.99 | 1.21 | 0.15 | 0.82 | 6.60 | 8.09 | none | |||||
| Rajaratnam et al. (1992) [17] | 1 | 0.458 | 0.572 | 0.057 | 0.80 | 8.00 | 10.00 | 0.10 | 0.0009 to 0.026 | 0.086 | 1.50 | bevelled |
| 6 | 0.305 | 0.381 | 0.043 | 0.80 | 7.16 | 8.94 | 0.057; 0.10 | none | ||||
| 8 | 0.305 | 0.191 | 0.043 | 1.60 | 7.16 | 4.47 | 0.10; 0.149 | none | ||||
| 9 | 0.153 | 0.191 | 0.043 | 0.80 | 3.58 | 4.47 | 0.10; 0.149 | none | ||||
| 11 | 0.305 | 0.572 | 0.043 | 0.53 | 7.16 | 13.42 | 0.050; 0.10 | none | ||||
| 14 | 0.305 | 0.381 | 0.043 | 0.80 | 7.16 | 8.94 | 0.050; 0.10; 0.148 | 0.086 | 2.00 | linear | ||
| 15 | 0.305 | 0.381 | 0.043 | 0.80 | 7.16 | 8.94 | 0.050; 0.10; 0.148 | 0.086 | 2.00 | linear | ||
| 16 | 0.305 | 0.381 | 0.046 | 0.80 | 6.65 | 8.31 | 0.050; 0.10 | 0.092 | 2.00 | linear | ||
| 17 | 0.305 | 0.381 | 0.038 | 0.80 | 8.00 | 10.00 | 0.10; 0.150 | 0.057 | 1.50 | round | ||
| 18 | 0.305 | 0.381 | 0.038 | 0.80 | 8.00 | 10.00 | 0.10; 0.150 | 0.057 | 1.50 | spline |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kasischke, K.; Oertel, M. Discharge Coefficients of a Specific Vertical Slot Fishway Geometry—New Fitting Parameters. Water 2023, 15, 1193. https://doi.org/10.3390/w15061193
Kasischke K, Oertel M. Discharge Coefficients of a Specific Vertical Slot Fishway Geometry—New Fitting Parameters. Water. 2023; 15(6):1193. https://doi.org/10.3390/w15061193
Chicago/Turabian StyleKasischke, Kimberley, and Mario Oertel. 2023. "Discharge Coefficients of a Specific Vertical Slot Fishway Geometry—New Fitting Parameters" Water 15, no. 6: 1193. https://doi.org/10.3390/w15061193





