Forecasting Long-Series Daily Reference Evapotranspiration Based on Best Subset Regression and Machine Learning in Egypt
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets Description
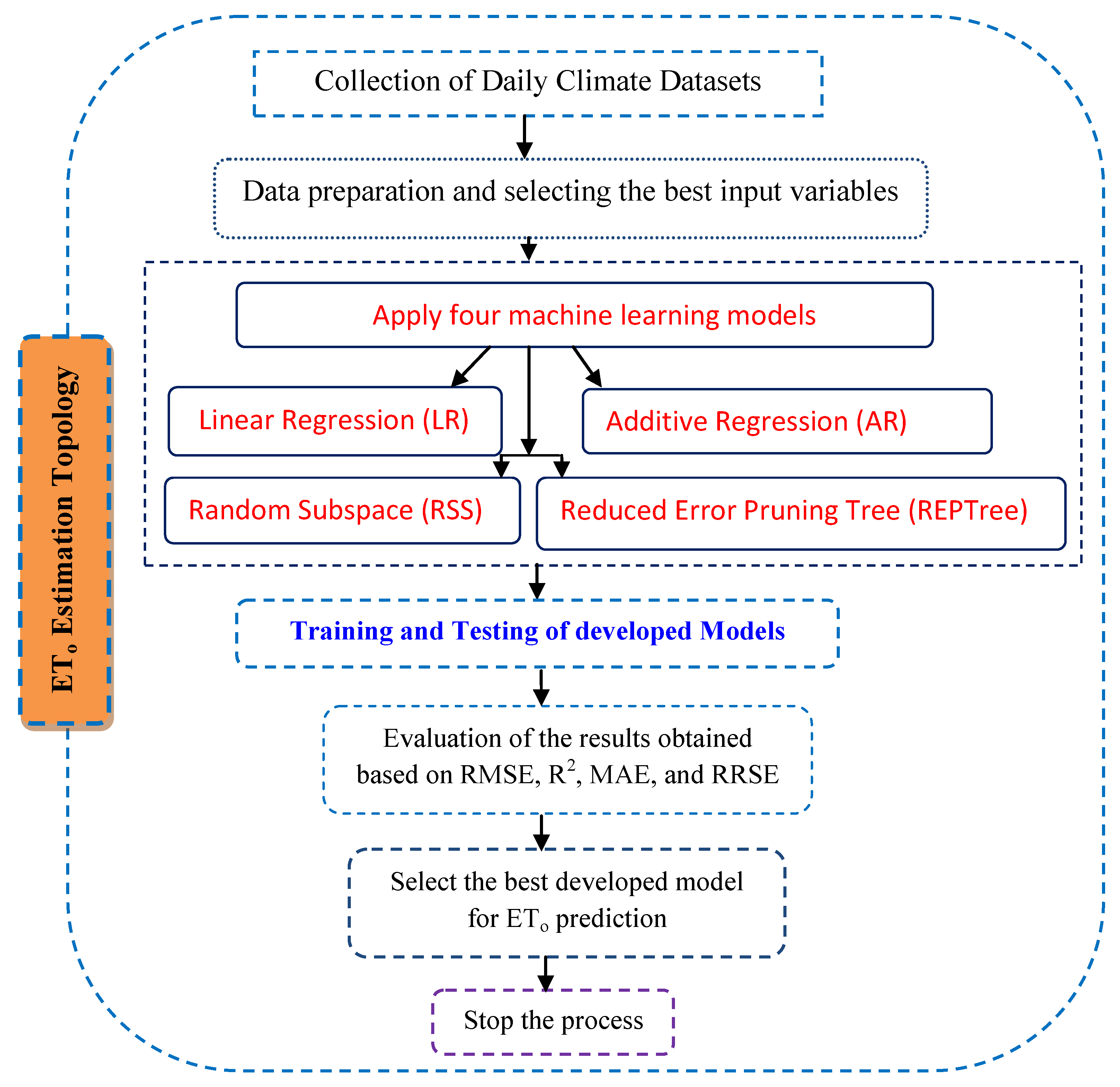
3. Methodology
3.1. Machine Learning (ML) Models
3.1.1. Random Subspace (RSS)
- Repeat for b = 1, 2, …, B;
- Choose an r-dimensional random subspace Xb˜;
- from the original p-dimensional feature space X;
- Build a classifier Cb(x) (with a decision boundary Cb(x) = 0) in Xb˜;
- Aggregate classifiers Cb(x), b = 1, 2, …, B, by utilizing majority voting for the final decision.
3.1.2. Additive Regression (AR)
3.1.3. Reduced Error Pruning Tree (REPTree)
3.1.4. Linear Regression (LR)
3.2. Performance Metrics
4. Results
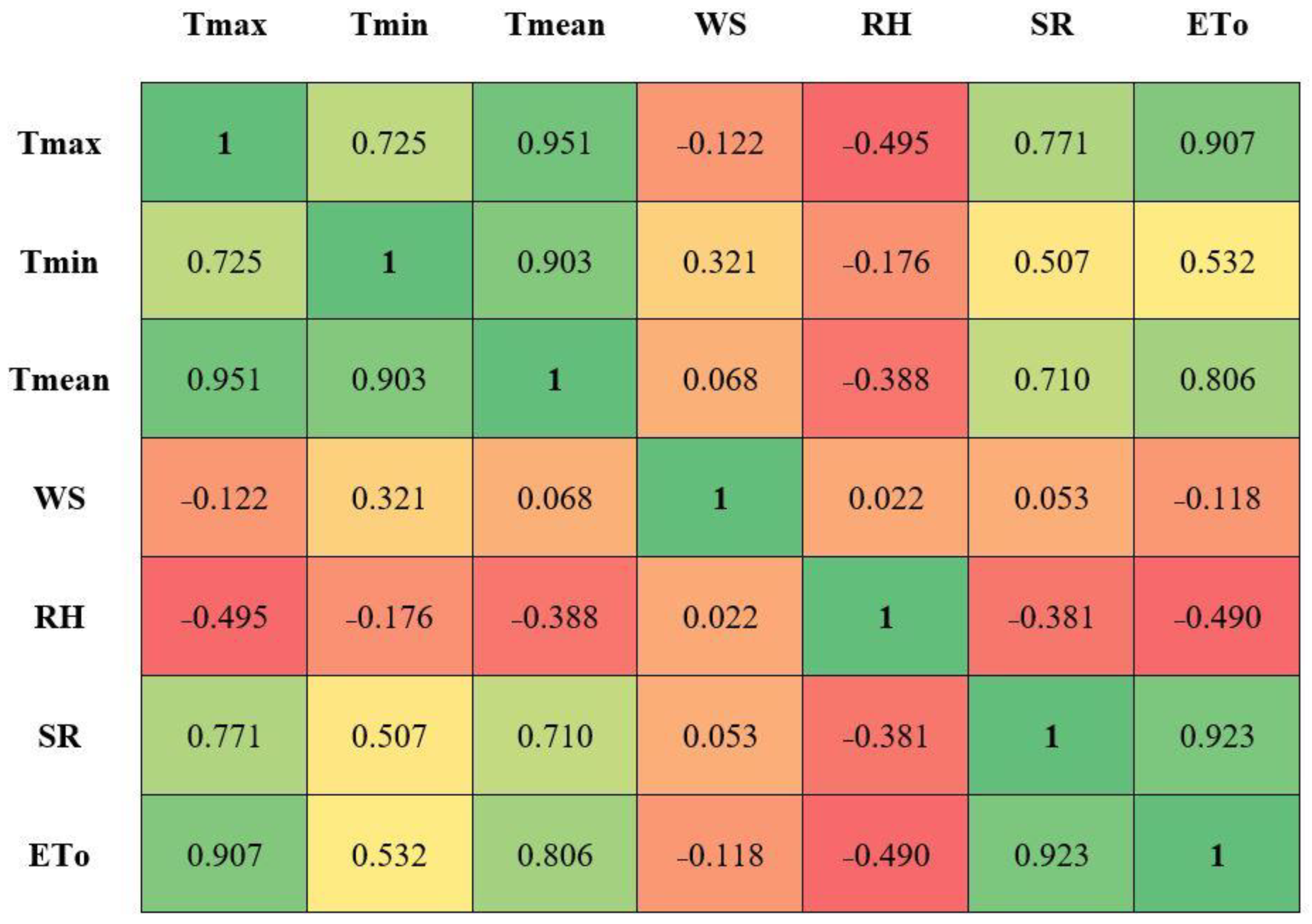
4.1. Analysis of Best Subset Regression for Determining Best Input Combinations
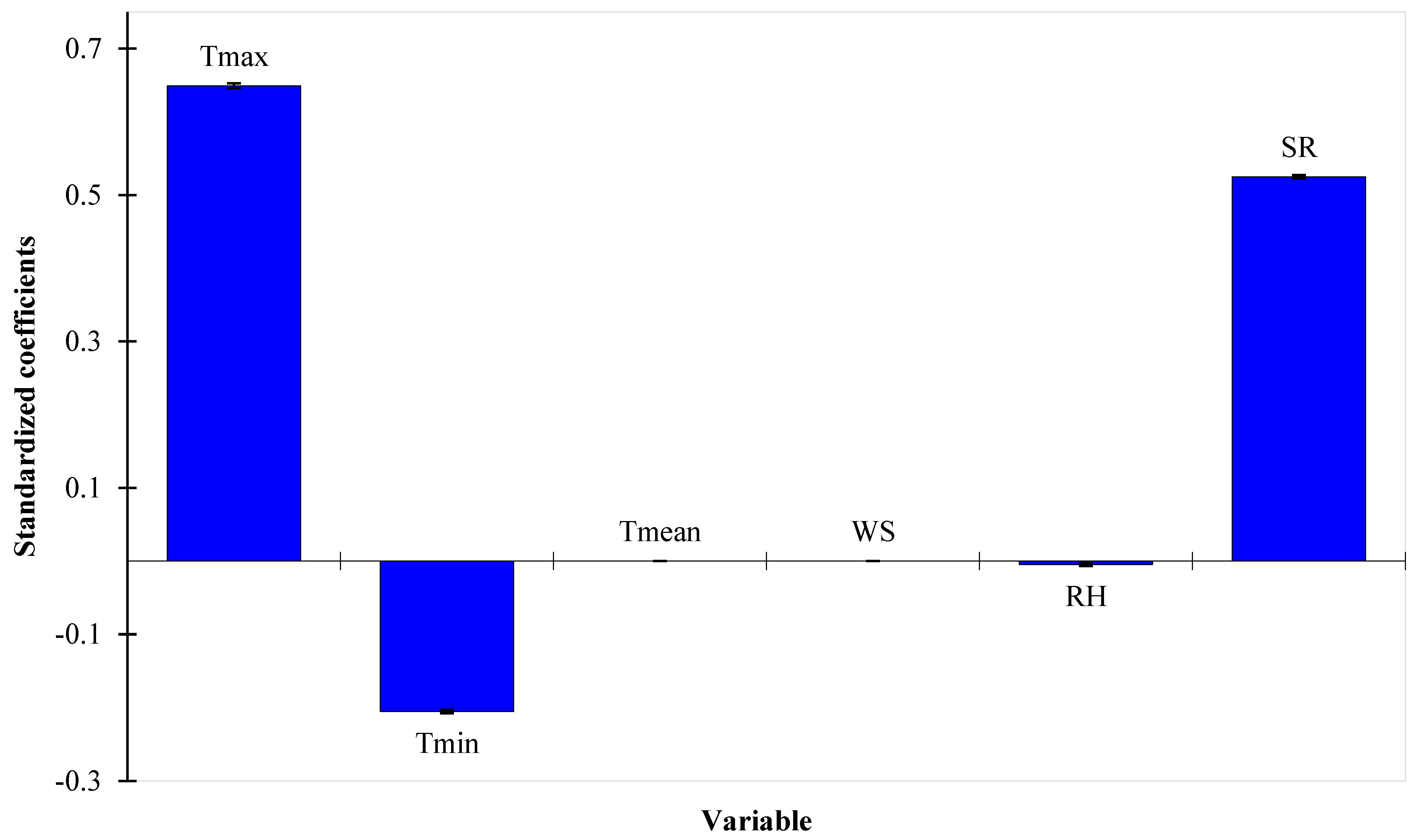
4.2. Sensitivity Analysis
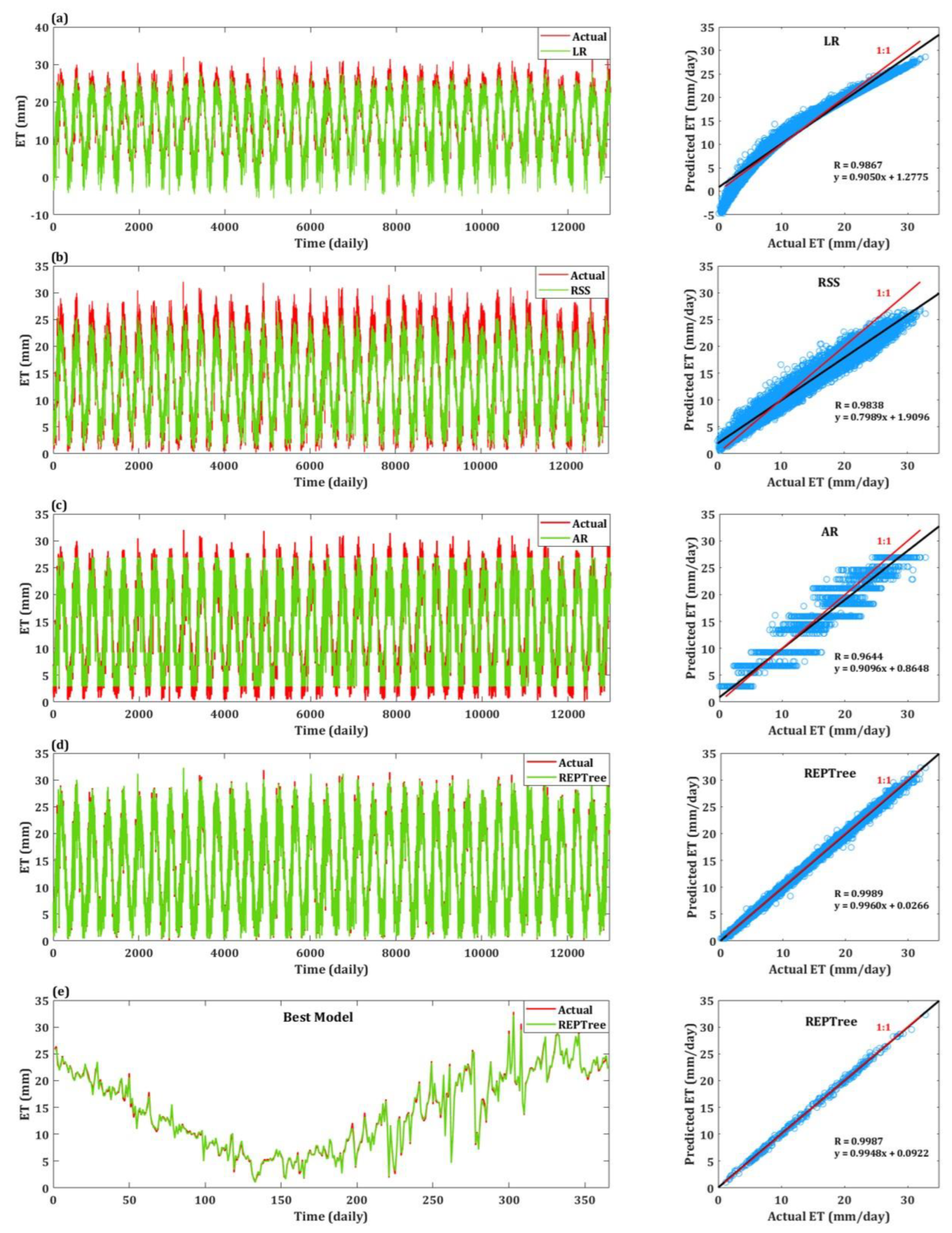
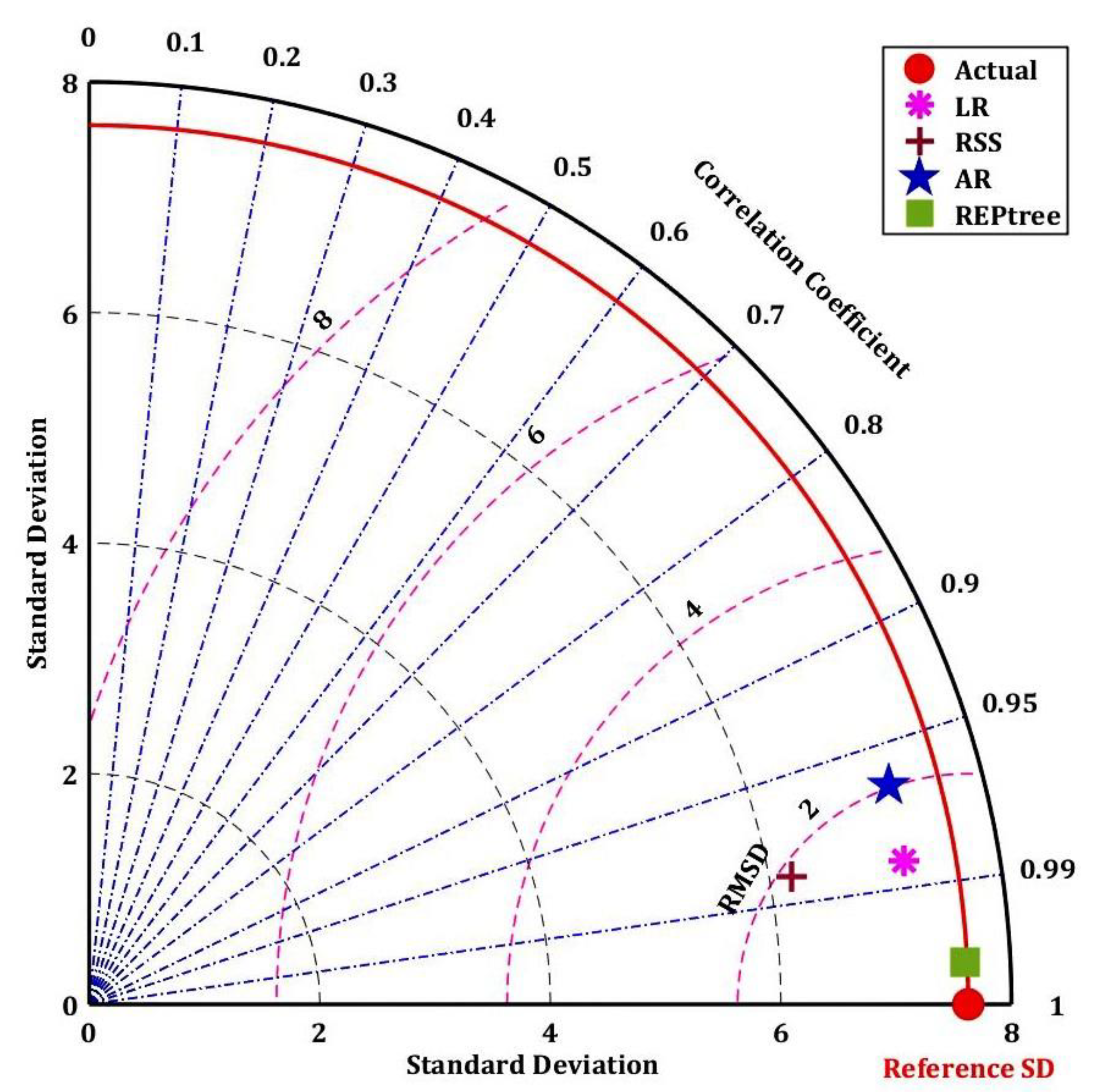
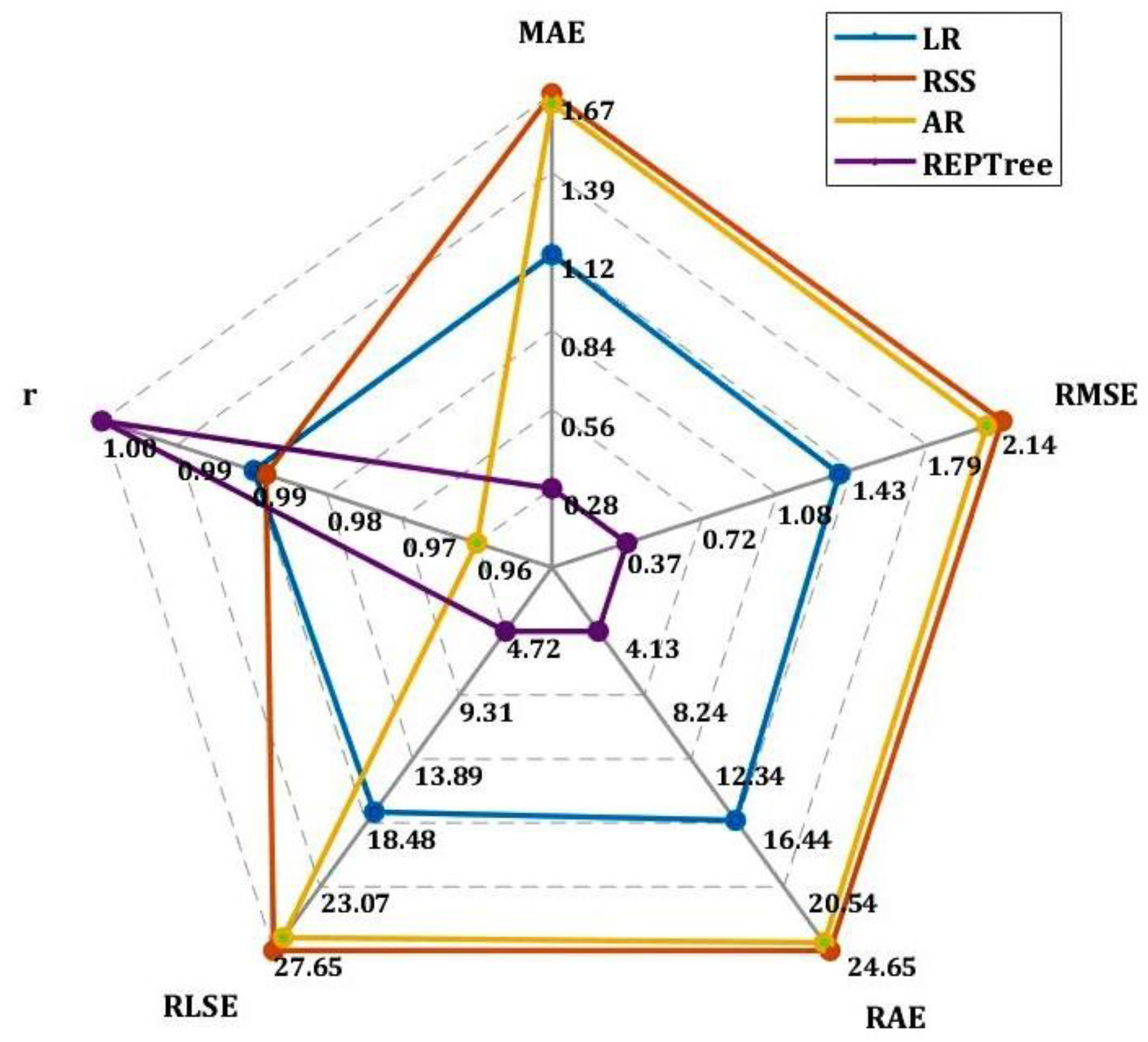
4.3. Comparison of ML Algorithms for ETo Estimation
5. Discussion
6. Conclusions
- -
- The results showed that the best input combination for the ETo model was determined as four input combinations (Tmax/Tmin/RH/SR) with high R2 (0.967) and high Adj-R2 (0.967) and MSE of 1.727;
- -
- The most sensitive input variables to predict the ETo with greater accuracy were Tmax, Tmin, and SR;
- -
- The REPTree model generated the best results with the highest value for r (0.99) and the lowest values for MAE (0.21), RMSE (0.28), RAE (3.45%), and RRSE (4.01%) during the training phase; it also generated the highest value for r (0.99) and the lowest values for MAE (0.28), RMSE (0.37), RAE (4.13%), and RRSE during the testing phase (4.72%);
- -
- The AR model generated the worst results with R = 0.9595, MAE = 1.5914, RMSE = 1.9876, RAE = 26.25%, and RRSE = 28.22% during the training phase.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-Fao Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. Available online: http://www.climasouth.eu/sites/default/files/FAO%2056.pdf (accessed on 1 October 2022).
- Dhillon, R.; Rojo, F.; Upadhyaya, S.K.; Roach, J.; Coates, R.; Delwiche, M. Prediction of plant water status in almond and walnut trees using a continuous leaf monitoring system. Precis. Agric. 2019, 20, 723–745. [Google Scholar] [CrossRef]
- Sharma, S.; Regulwar, D.G. Prediction of evapotranspiration by artificial neural network and conventional methods. Int. J. Eng. Res. 2016, 5, 184–187. [Google Scholar]
- Nouri, H.; Beecham, S.; Kazemi, F.; Hassanli, A.M.; Anderson, S. Remote sensing techniques for predicting evapotranspiration from mixed vegetated surfaces. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 3897–3925. [Google Scholar] [CrossRef]
- Lu, G.; Wu, Z.; He, H. Hydrological Cycle and Quantity Forecast; Science Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Jun-Fang, Z.H.A.O.; Jian-Ping, G.U.O.; Zhang, Y.H.; Jing-Wen, X.U. Advances in research of impacts of climate change on agriculture. Chin. J. Agrometeorol. 2010, 31, 200. [Google Scholar]
- Raza, A.; Hu, Y.; Shoaib, M.; Abd Elnabi, M.K.; Zubair, M.; Nauman, M.; Syed, N.R. A Systematic Review on Estimation of Reference Evapotranspiration under Prisma Guidelines. Pol. J. Environ. Stud. 2021, 30, 5413–5422. [Google Scholar] [CrossRef]
- Raza, A.; Shoaib, M.; Baig, M.A.I.; Ahmad, S.; Khan, M.M.; Ullah, M.K.; Hashim, S. Comparative study of powerful predictive modeling techniques for modeling monthly reference evapotranspiration in various climatic regions. Fresenius Environ. Bull. 2021, 30, 7490–7513. [Google Scholar]
- Mehdizadeh, S.; Behmanesh, J.; Khalili, K. Using MARS, SVM, GEP and empirical equations for estimation of monthly mean reference evapotranspiration. Comput. Electron. Agric. 2017, 139, 103–114. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F. New approach to estimate daily reference evapotranspiration based on hourly temperature and relative humidity using machine learning and deep learning. Agric. Water Manag. 2020, 234, 106113. [Google Scholar] [CrossRef]
- Guo, X.; Sun, X.; Ma, J. Prediction of daily crop reference evapotranspiration (ETo) values through a least-squares support vector machine model. Hydrol. Res. 2011, 42, 268–274. [Google Scholar] [CrossRef]
- Traore, S.; Luo, Y.; Fipps, G. Deployment of artificial neural network for short-term forecasting of evapotranspiration using public weather forecast restricted messages. Agric. Water Manag. 2016, 163, 363–379. [Google Scholar] [CrossRef]
- Valipour, M.; Gholami Sefidkouhi, M.A.; Raeini-Sarjaz, M.; Guzman, S.M. A hybrid data-driven machine learning technique for evapotranspiration modeling in various climates. Atmosphere 2019, 10, 311. [Google Scholar] [CrossRef] [Green Version]
- Mattar, M.A. Using gene expression programming in monthly reference evapotranspiration modeling: A case study in Egypt. Agric. Water Manag. 2018, 198, 28–38. [Google Scholar] [CrossRef]
- Gocic, M.; Petković, D.; Shamshirband, S.; Kamsin, A. Comparative analysis of reference evapotranspiration equations modelling by extreme learning machine. Comput. Electron. Agric. 2016, 127, 56–63. [Google Scholar] [CrossRef]
- Abdullah, S.S.; Malek, M.A.; Abdullah, N.S.; Kisi, O.; Yap, K.S. Extreme learning machines: A new approach for prediction of reference evapotranspiration. J. Hydrol. 2015, 527, 184–195. [Google Scholar] [CrossRef]
- Raza, A.; Shoaib, M.; Faiz, M.A.; Baig, F.; Khan, M.M.; Ullah, M.K.; Zubair, M. Comparative assessment of reference evapotranspiration estimation using conventional method and machine learning algorithms in four climatic regions. Pure Appl. Geophys. 2020, 177, 4479–4508. [Google Scholar] [CrossRef]
- Raza, A.; Shoaib, M.; Khan, A.; Baig, F.; Faiz, M.A.; Khan, M.M. Application of non-conventional soft computing approaches for estimation of reference evapotranspiration in various climatic regions. Theor. Appl. Climatol. 2020, 139, 1459–1477. [Google Scholar] [CrossRef]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration evaluation models based on machine learning algorithms—A comparative study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Raza, A.; Hu, Y.; Al-Ansari, N.; Kushwaha, N.L.; Srivastava, A.; Zubair, M. Data intelligence and hybrid metaheuristic algorithms-based estimation of reference evapotranspiration. Appl. Water Sci. 2022, 12, 152. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Gong, D.; Zhang, Q.; Zhao, L. Evaluation of random forests and generalized regression neural networks for daily reference evapotranspiration modelling. Agric. Water Manag. 2017, 193, 163–173. [Google Scholar] [CrossRef]
- Feng, Y.; Peng, Y.; Cui, N.; Gong, D.; Zhang, K. Modeling reference evapotranspiration using extreme learning machine and generalized regression neural network only with temperature data. Comput. Electron. Agric. 2017, 136, 71–78. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Huang, Q.; Huang, G.; Meng, E.; Luan, J. Reference evapotranspiration forecasting based on local meteorological and global climate information screened by partial mutual information. J. Hydrol. 2018, 561, 764–779. [Google Scholar] [CrossRef]
- Saggi, M.K.; Jain, S. Reference evapotranspiration estimation and modeling of the Punjab Northern India using deep learning. Comput. Electron. Agric. 2019, 156, 387–398. [Google Scholar] [CrossRef]
- Huang, G.; Wu, L.; Ma, X.; Zhang, W.; Fan, J.; Yu, X.; Zeng, W.; Zhou, H. Evaluation of CatBoost method for prediction of reference evapotranspiration in humid regions. J. Hydrol. 2019, 574, 1029–1041. [Google Scholar] [CrossRef]
- Torres, A.F.; Walker, W.R.; McKee, M. Forecasting daily potential evapotranspiration using machine learning and limited climatic data. Agric. Water Manag. 2011, 98, 553–562. [Google Scholar] [CrossRef]
- Tang, D.; Feng, Y.; Gong, D.; Hao, W.; Cui, N. Evaluation of artificial intelligence models for actual crop evapotranspiration modeling in mulched and non-mulched maize croplands. Comput. Electron. Agric. 2018, 152, 375–384. [Google Scholar] [CrossRef]
- Walls, S.; Binns, A.D.; Levison, J.; MacRitchie, S. Prediction of actual evapotranspiration by artificial neural network models using data from a Bowen ratio energy balance station. Neural Comput. Appl. 2020, 32, 14001–14018. [Google Scholar] [CrossRef]
- Nourani, V.; Elkiran, G.; Abdullahi, J. Multi-station artificial intelligence based ensemble modeling of reference evapotranspiration using pan evaporation measurements. J. Hydrol. 2019, 577, 123958. [Google Scholar] [CrossRef]
- Tabari, H.; Martinez, C.; Ezani, A.; Hosseinzadeh Talaee, P. Applicability of support vector machines and adaptive neurofuzzy inference system for modeling potato crop evapotranspiration. Irrig. Sci. 2013, 31, 575–588. [Google Scholar] [CrossRef]
- CAPMAS (Central Agency for Public Mobilization and Statistics). Egypt in Figures: Population. 2022. Available online: https://www.capmas.gov.eg/Pages/StaticPages.aspx?page_id=5035# (accessed on 15 October 2022).
- Ayaz, A.; Rajesh, M.; Singh, S.K.; Rehana, S. Estimation of reference evapotranspiration using machine learning models with limited data. AIMS Geosci. 2021, 7, 268–290. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Yaman, M.A.; Subasi, A.; Rattay, F. Comparison of random subspace and voting ensemble machine learning methods for face recognition. Symmetry 2018, 10, 651. [Google Scholar] [CrossRef] [Green Version]
- Skurichina, M.; Duin, R.P. Bagging, boosting and the random subspace method for linear classifiers. Pattern Anal. Appl. 2002, 5, 121–135. [Google Scholar] [CrossRef]
- Xia, C.; Pan, Z.; Polden, J.; Li, H.; Xu, Y.; Chen, S. Modelling and prediction of surface roughness in wire arc additive manufacturing using machine learning. J. Intell. Manuf. 2022, 33, 1467–1482. [Google Scholar] [CrossRef]
- Ravikumar, P.; Lafferty, J.; Liu, H.; Wasserman, L. Sparse additive models. J. R. Stat. Soc. Ser. B 2009, 71, 1009–1030. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized Additive Models. Stat. Sci. 1986, 6, 15–51. [Google Scholar] [CrossRef]
- Laanaya, F.; St-Hilaire, A.; Gloaguen, E. Water temperature modelling: Comparison between the generalized additive model, logistic, residuals regression and linear regression models. Hydrol. Sci. J. 2017, 62, 1078–1093. [Google Scholar] [CrossRef]
- Fu, J.C.; Huang, H.Y.; Jang, J.H.; Huang, P.H. River Stage Forecasting Using Multiple Additive Regression Trees. Water Resour. Manag. 2019, 33, 4491–4507. [Google Scholar] [CrossRef]
- Senthil Kumar, A.R.; Ojha, C.S.P.; Goyal, M.K.; Singh, R.D.; Swamee, P.K. Modeling of Suspended Sediment Concentration at Kasol in India Using ANN, Fuzzy Logic, and Decision Tree Algorithms. J. Hydrol. Eng. 2012, 17, 394–404. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E. Data mining: Practical machine learning tools and techniques with Java implementations. Acm Sigmod Record 2002, 31, 76–77. [Google Scholar] [CrossRef]
- Quinlan, J. Simplifying decision trees. Int. J. Man-Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef] [Green Version]
- Bharti, B.; Pandey, A.; Tripathi, S.K.; Kumar, D. Modelling of runoff and sediment yield using ANN, LS-SVR, REPTree and M5 models. Hydrol. Res. 2017, 48, 1489–1507. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Joseph, K.S.; Ravichandran, T. A comparative evaluation of software effort estimation using REPTree and K* in handling with missing values. Aust. J. Basic Appl. Sci. 2012, 6, 312–317. [Google Scholar]
- Pérez-Domínguez, L.; Garg, H.; Luviano-Cruz, D.; García Alcaraz, J.L. Estimation of Linear Regression with the Dimensional Analysis Method. Mathematics 2022, 10, 1645. [Google Scholar] [CrossRef]
- Hothorn, T.; Bretz, F.; Westfall, P. Simultaneous inference in general parametric models. Biom. J. J. Math. Methods Biosci. 2008, 50, 346–363. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, M.; Hu, S.; Ge, Y.; Heuvelink, G.B.; Ren, Z.; Huang, X. Using multiple linear regression and random forests to identify spatial poverty determinants in rural China. Spat. Stat. 2020, 42, 100461. [Google Scholar] [CrossRef]
- Park, J.Y.; Phillips, P.C. Statistical inference in regressions with integrated processes: Part 2. Econom. Theory 1989, 5, 95–131. [Google Scholar] [CrossRef] [Green Version]
- Sattari, M.T.; Apaydin, H.; Shamshirband, S. Performance evaluation of deep learning-based gated recurrent units (GRUs) and tree-based models for estimating ETo by using limited meteorological variables. Mathematics 2020, 8, 972. [Google Scholar] [CrossRef]
- Kushwaha, N.L.; Rajput, J.; Elbeltagi, A.; Elnaggar, A.Y.; Sena, D.R.; Vishwakarma, D.K.; Mani, I.; Hussein, E.E. Data intelligence model and meta-heuristic algorithms-based pan evaporation modelling in two different agro-climatic zones: A case study from northern India. Atmosphere 2021, 12, 1654. [Google Scholar] [CrossRef]
- Nhu, V.H.; Shahabi, H.; Nohani, E.; Shirzadi, A.; Al-Ansari, N.; Bahrami, S.; Miraki, S.; Geertsema, M.; Nguyen, H. Daily water level prediction of Zrebar Lake (Iran): A comparison between M5P, random forest, random tree and reduced error pruning trees algorithms. ISPRS Int. J. Geo-Inf. 2020, 9, 479. [Google Scholar] [CrossRef]
- Salam, R.; Islam, A.R.M.T. Potential of RT, Bagging and RS ensemble learning algorithms for reference evapotranspiration prediction using climatic data-limited humid region in Bangladesh. J. Hydrol. 2020, 590, 125241. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Malik, A.; Souag-Gamane, D.; Kisi, O. Artificial intelligence models versus empirical equations for modeling monthly reference evapotranspiration. Environ. Sci. Pollut. Res. 2020, 27, 30001–30019. [Google Scholar] [CrossRef] [PubMed]
- Kisi, O.; Keshtegar, B.; Zounemat-Kermani, M.; Heddam, S.; Trung, N.T. Modeling reference evapotranspiration using a novel regression-based method: Radial basis M5 model tree. Theor. Appl. Climatol. 2021, 145, 639–659. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, S.; Bhattarai, N.; Mallick, K.; Liu, Q.; Tang, L.; Im, J.; Guo, L.; Zhang, J. On the use of machine learning based ensemble approaches to improve evapotranspiration estimates from croplands across a wide environmental gradient. Agric. For. Meteorol. 2021, 298, 108308. [Google Scholar] [CrossRef]
- Bellido-Jiménez, J.A.; Estévez, J.; García-Marín, A.P. New machine learning approaches to improve reference evapotranspiration estimates using intra-daily temperature-based variables in a semi-arid region of Spain. Agric. Water Manag. 2021, 245, 106558. [Google Scholar] [CrossRef]
- Arnell, N.W.; Gosling, S.N. The impacts of climate change on river flood risk at the global scale. Clim. Change 2016, 134, 387–401. [Google Scholar] [CrossRef] [Green Version]
- Khadke, L.; Pattnaik, S. Impact of initial conditions and cloud parameterization on the heavy rainfall event of Kerala (2018). Model. Earth Syst. Environ. 2021, 7, 2809–2822. [Google Scholar] [CrossRef]
- Meza, I.; Siebert, S.; Döll, P.; Kusche, J.; Herbert, C.; Eyshi Rezaei, E.; Nouri, H.; Gerdener, H.; Popat, E.; Frischen, J.; et al. Global-scale drought risk assessment for agricultural systems. Nat. Hazards Earth Syst. Sci. 2020, 20, 695–712. [Google Scholar] [CrossRef] [Green Version]
- Sazib, N.; Mladenova, I.; Bolten, J. Leveraging the google earth engine for drought assessment using global soil moisture data. Remote Sens. 2018, 10, 1265. [Google Scholar] [CrossRef] [PubMed] [Green Version]

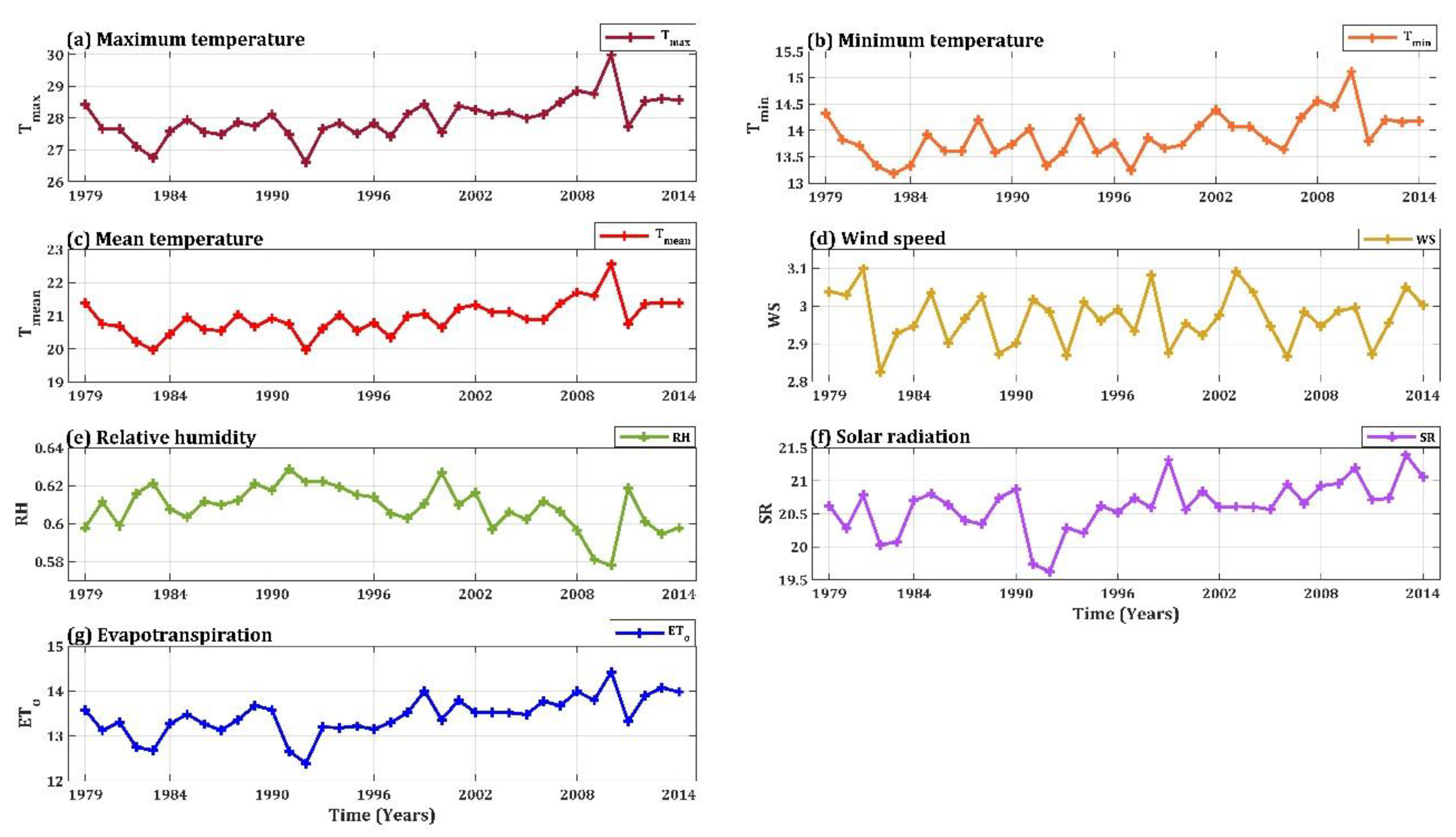
| Governorate | Metrics | Tmax (°C) | Tmin (°C) | Tmean (°C) | P (mm) | WS (Km/h) | RH (%) | SR (kWh/m2) | ETo (mm/day) |
|---|---|---|---|---|---|---|---|---|---|
| Al Buhayrah | Maximum | 47.59 | 26.38 | 35.09 | 40.50 | 9.14 | 0.98 | 30.68 | 34.01 |
| Minimum | 8.17 | −2.69 | 6.36 | 0.00 | 0.75 | 0.11 | 0.00 | 0.00 | |
| Average | 27.52 | 13.89 | 20.71 | 0.34 | 3.29 | 0.64 | 20.45 | 13.05 | |
| Std. deviation | 6.81 | 5.28 | 5.72 | 1.50 | 0.92 | 0.10 | 7.84 | 6.83 | |
| Variance | 46.40 | 27.84 | 32.70 | 2.24 | 0.84 | 0.01 | 61.53 | 46.70 | |
| Skewness | −0.21 | −0.20 | −0.15 | 8.84 | 0.96 | −0.98 | −0.51 | −0.06 | |
| Kurtosis | −0.93 | −0.97 | −1.20 | 118.55 | 2.43 | 2.41 | −0.89 | −1.13 | |
| Alexandria | Maximum | 43.43 | 29.82 | 35.15 | 32.97 | 12.88 | 0.94 | 30.49 | 29.83 |
| Minimum | 9.35 | 2.72 | 7.87 | 0.00 | 1.20 | 0.10 | 0.00 | 0.00 | |
| Average | 26.11 | 15.98 | 21.04 | 0.38 | 4.52 | 0.64 | 20.48 | 11.28 | |
| Std. deviation | 6.06 | 4.81 | 5.18 | 1.53 | 1.35 | 0.10 | 7.82 | 5.83 | |
| Variance | 36.72 | 23.17 | 26.82 | 2.33 | 1.83 | 0.01 | 61.13 | 33.98 | |
| Skewness | −0.19 | −0.08 | −0.12 | 7.69 | 1.01 | −1.43 | −0.53 | −0.06 | |
| Kurtosis | −0.93 | −1.09 | −1.21 | 83.65 | 2.33 | 3.14 | −0.84 | −1.03 | |
| Ismailiyah | Maximum | 47.76 | 27.64 | 35.59 | 33.74 | 4.98 | 0.96 | 30.74 | 32.82 |
| Minimum | 7.06 | −0.14 | 5.83 | 0.00 | 0.49 | 0.07 | 0.00 | 0.00 | |
| Average | 28.81 | 12.78 | 20.79 | 0.18 | 1.70 | 0.59 | 20.71 | 14.49 | |
| Std. deviation | 7.50 | 4.57 | 5.74 | 1.03 | 0.43 | 0.12 | 7.33 | 7.62 | |
| Variance | 56.18 | 20.87 | 32.95 | 1.06 | 0.18 | 0.01 | 53.75 | 58.14 | |
| Skewness | −0.24 | −0.11 | −0.15 | 13.61 | 1.44 | −0.72 | −0.42 | 0.02 | |
| Kurtosis | −1.03 | −0.96 | −1.18 | 281.36 | 5.21 | 0.97 | −0.98 | −1.24 | |
| Minufiyah | Maximum | 48.09 | 25.30 | 35.55 | 60.28 | 6.38 | 0.97 | 31.06 | 34.41 |
| Minimum | 6.77 | −2.23 | 5.29 | 0.00 | 0.62 | 0.09 | 0.00 | 0.00 | |
| Average | 29.42 | 12.84 | 21.13 | 0.16 | 2.36 | 0.57 | 20.92 | 15.00 | |
| Std. deviation | 7.74 | 5.34 | 6.28 | 1.01 | 0.63 | 0.13 | 7.43 | 7.82 | |
| Variance | 59.94 | 28.52 | 39.43 | 1.02 | 0.39 | 0.02 | 55.18 | 61.21 | |
| Skewness | −0.23 | −0.23 | −0.17 | 25.06 | 0.78 | −0.36 | −0.44 | −0.02 | |
| Kurtosis | −1.07 | −1.00 | −1.23 | 1134.97 | 1.95 | 0.37 | −0.97 | −1.28 |
| No. of Variables | Variables | MSE | R2 | Adjusted R2 | Mallows’ Cp | Akaike’s AIC | Schwarz’s SBC | Amemiya’s PC |
|---|---|---|---|---|---|---|---|---|
| 1 | SR | 7.670 | 0.853 | 0.853 | 178,771.227 | 105,837.493 | 105,855.209 | 0.147 |
| 2 | Tmax/SR | 2.773 | 0.947 | 0.947 | 31,471.556 | 52,988.983 | 53,015.557 | 0.053 |
| 3 | Tmax/Tmean/SR | 1.728 | 0.967 | 0.967 | 26.095 | 28,408.184 | 28,443.616 | 0.033 |
| 4 | Tmax/Tmean/RH/SR | 1.727 | 0.967 | 0.967 | 4.195 | 28,386.287 | 28,430.577 | 0.033 |
| 5 * | Tmax/Tmin/RH/SR | 1.727 | 0.967 | 0.967 | 4.195 | 28,386.287 | 28,430.577 | 0.033 |
| 6 | Tmax/Tmin/WS/RH/SR | 1.727 | 0.967 | 0.967 | 6.000 | 28,388.092 | 28,441.240 | 0.033 |
| Source | Value | Standard Error | t | Pr > |t| | Lower Bound (95%) | Upper Bound (95%) |
|---|---|---|---|---|---|---|
| Tmax | 0.649 | 0.002 | 366.370 | <0.0001 | 0.646 | 0.653 |
| Tmin | −0.205 | 0.001 | −167.137 | <0.0001 | −0.208 | −0.203 |
| Tmean | 0.000 | 0.000 | ||||
| WS | 0.000 | 0.000 | ||||
| RH | −0.005 | 0.001 | −4.889 | <0.0001 | −0.007 | −0.003 |
| SR | 0.525 | 0.001 | 414.793 | <0.0001 | 0.523 | 0.527 |
| ML Algorithms | Training Phase | Testing Phase | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | RAE (%) | RRSE (%) | r | MAE | RMSE | RAE (%) | RRSE (%) | r | |
| LR | 1.0099 | 1.3011 | 16.6612 | 18.4732 | 0.9828 | 1.1050 | 1.3717 | 16.2809 | 17.7032 | 0.9849 |
| RSS | 1.3673 | 1.7407 | 22.5558 | 24.7149 | 0.9757 | 1.6727 | 2.1425 | 24.6466 | 27.6511 | 0.9838 |
| AR | 1.5913 | 1.9876 | 26.2524 | 28.2209 | 0.9595 | 1.6378 | 2.0703 | 24.1312 | 26.7191 | 0.9644 |
| REPTree | 0.2095 | 0.2828 | 3.4565 | 4.0159 | 0.9992 | 0.2806 | 0.3659 | 4.1344 | 4.7224 | 0.9989 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elbeltagi, A.; Srivastava, A.; Al-Saeedi, A.H.; Raza, A.; Abd-Elaty, I.; El-Rawy, M. Forecasting Long-Series Daily Reference Evapotranspiration Based on Best Subset Regression and Machine Learning in Egypt. Water 2023, 15, 1149. https://doi.org/10.3390/w15061149
Elbeltagi A, Srivastava A, Al-Saeedi AH, Raza A, Abd-Elaty I, El-Rawy M. Forecasting Long-Series Daily Reference Evapotranspiration Based on Best Subset Regression and Machine Learning in Egypt. Water. 2023; 15(6):1149. https://doi.org/10.3390/w15061149
Chicago/Turabian StyleElbeltagi, Ahmed, Aman Srivastava, Abdullah Hassan Al-Saeedi, Ali Raza, Ismail Abd-Elaty, and Mustafa El-Rawy. 2023. "Forecasting Long-Series Daily Reference Evapotranspiration Based on Best Subset Regression and Machine Learning in Egypt" Water 15, no. 6: 1149. https://doi.org/10.3390/w15061149







