Can Remotely Sensed Snow Disappearance Explain Seasonal Water Supply?
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Description
2.2. Evaluation of the Relationship between DSD and Seasonal Water Supply
2.3. Analysis of Predictive Skill
2.4. Model Evaluation
3. Results
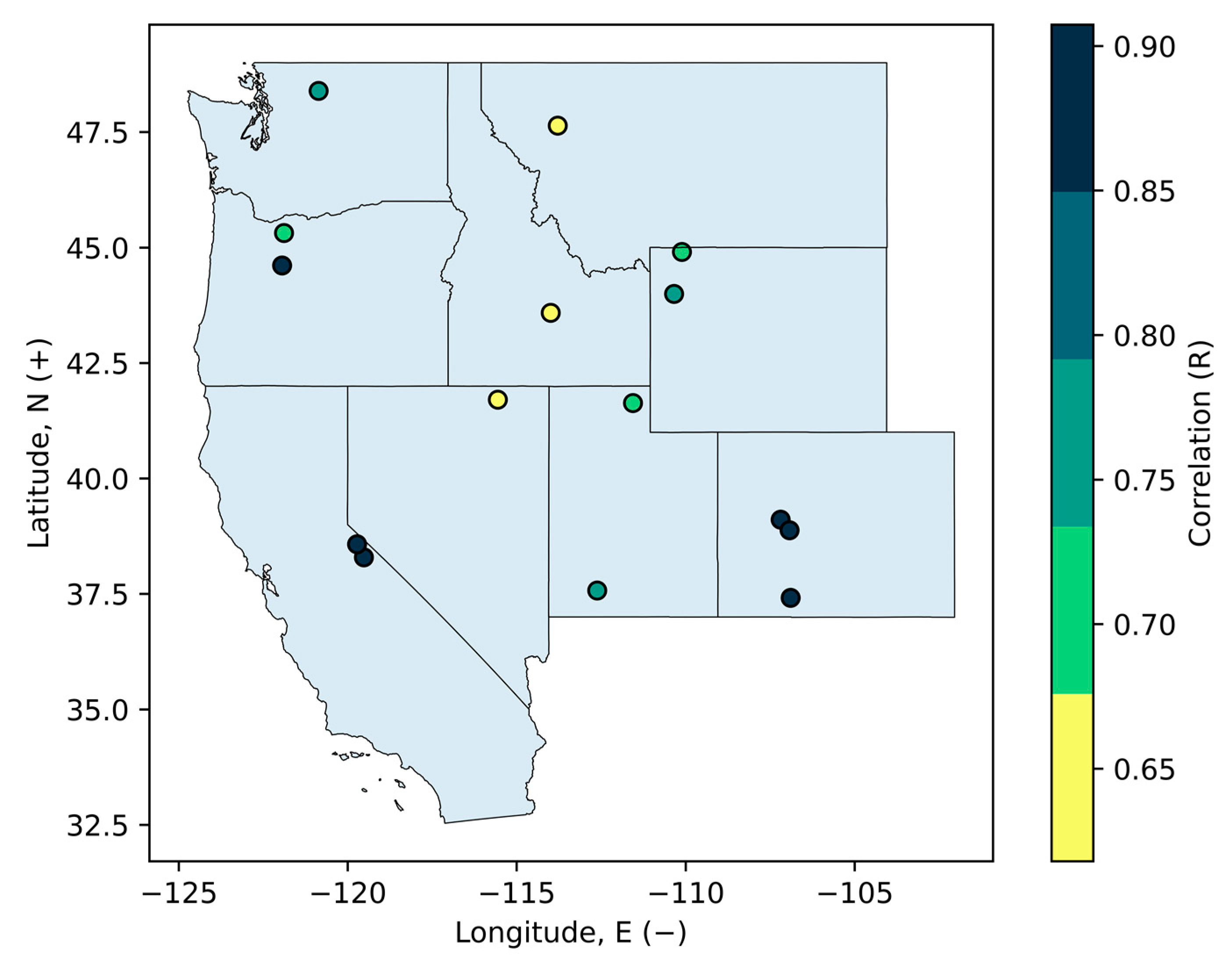
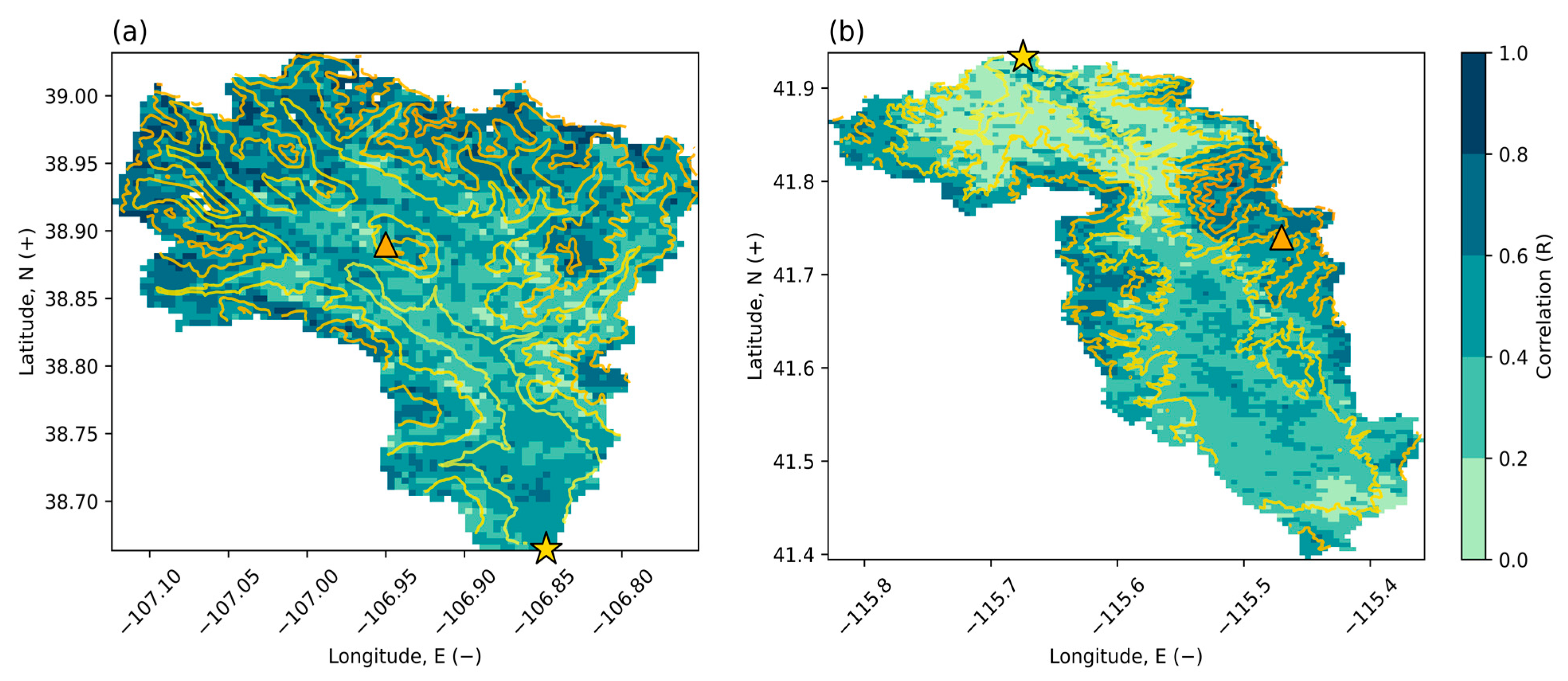
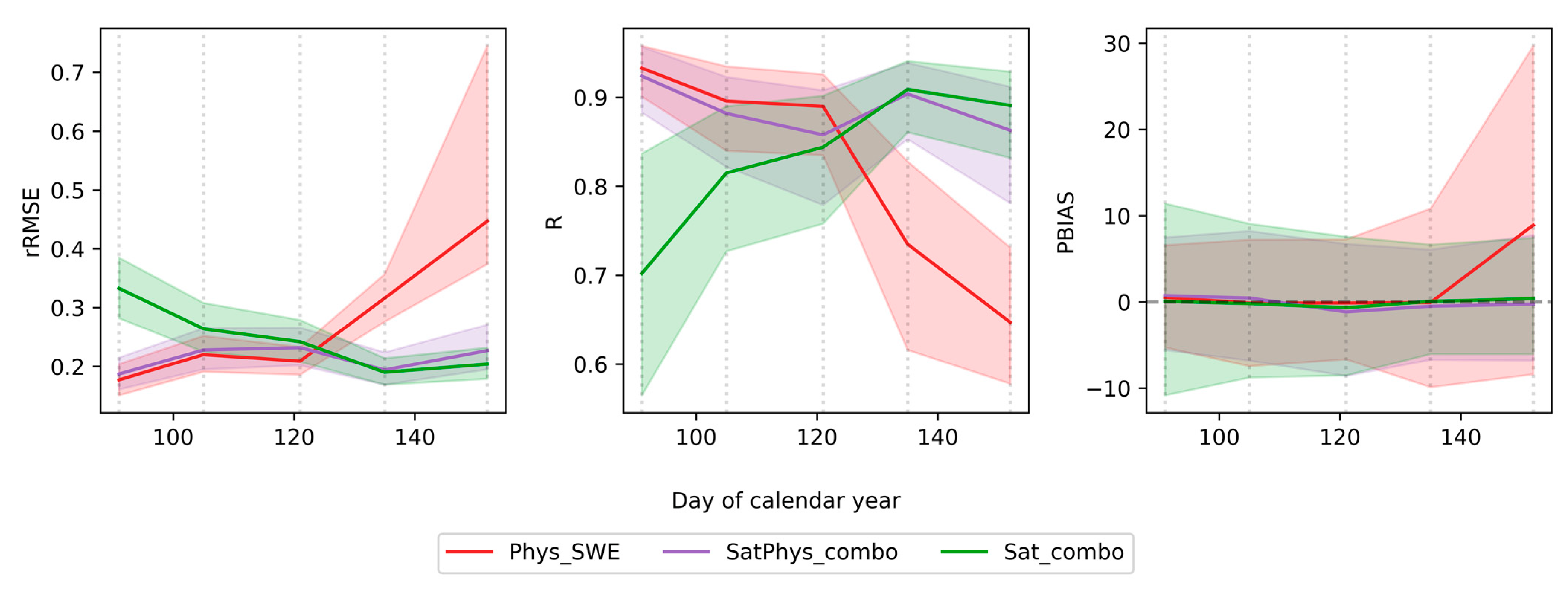
3.1. Evaluating the Relationship between Satellite Variables and Seasonal Water Supply
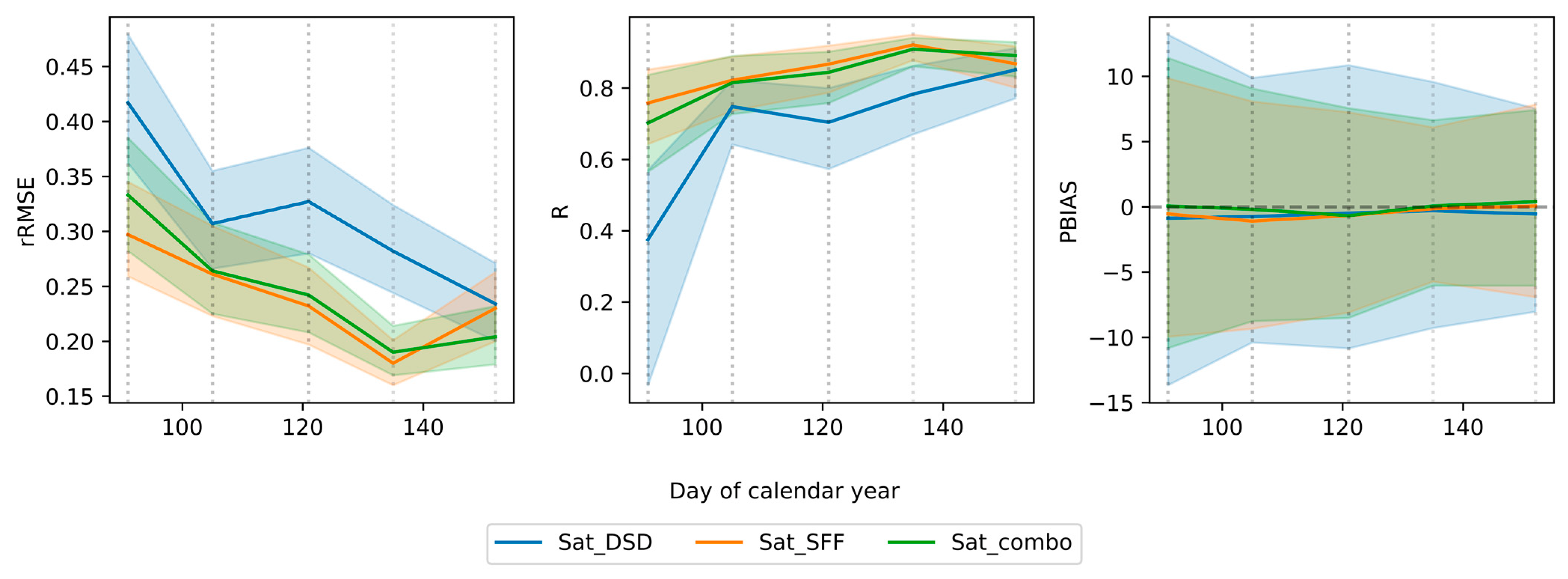
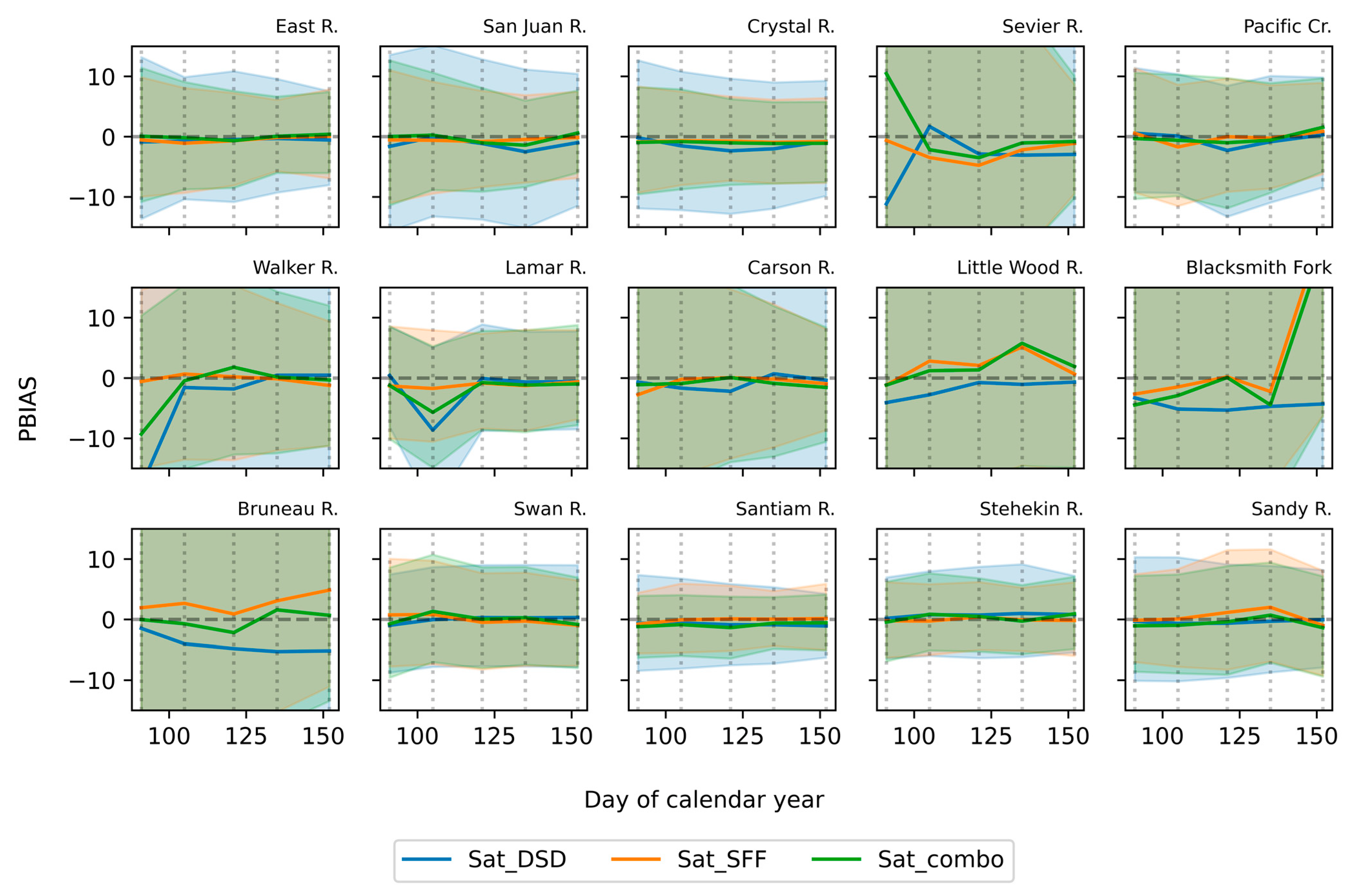
3.2. Evaluation of Forecast Skill of Linear Models Only Using Satellite Data
3.3. Evaluation of Skill of Linear Models Combining Satellite and In Situ Data
4. Discussion
4.1. Insights and Implications
4.2. Limitations
4.3. Future Research Directions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, D.; Wrzesien, M.L.; Durand, M.; Adam, J.; Lettenmaier, D.P. How Much Runoff Originates as Snow in the Western United States, and How Will That Change in the Future? Geophys. Res. Lett. 2017, 44, 6163–6172. [Google Scholar] [CrossRef] [Green Version]
- Schumacher, B.L.; Yost, M.A.; Burchfield, E.K.; Allen, N. Water in the West: Trends, Production Efficiency, and a Call for Open Data. J. Environ. Manag. 2022, 306, 114330. [Google Scholar] [CrossRef] [PubMed]
- Escriva-Bou, A.; McCann, H.; Hanak, E.; Lund, J.; Gray, B.; Blanco, E.; Jezdimirovic, J.; Magnuson-Skeels, B.; Tweet, A. Water Accounting in Western US, Australia, and Spain: Comparative Analysis. J. Water Resour. Plan. Manag. 2020, 146, 04020004. [Google Scholar] [CrossRef]
- Schwabe, K.; Nemati, M.; Landry, C.; Zimmerman, G. Water Markets in the Western United States: Trends and Opportunities. Water 2020, 12, 233. [Google Scholar] [CrossRef] [Green Version]
- Lundquist, J.; Hughes, M.; Gutmann, E.; Kapnick, S. Our Skill in Modeling Mountain Rain and Snow Is Bypassing the Skill of Our Observational Networks. Bull. Am. Meteorol. Soc. 2019, 100, 2473–2490. [Google Scholar] [CrossRef] [Green Version]
- Heldmyer, A.; Livneh, B.; Molotch, N.; Rajagopalan, B. Investigating the Relationship Between Peak Snow-Water Equivalent and Snow Timing Indices in the Western United States and Alaska. Water Resour. Res. 2021, 57, e2020WR029395. [Google Scholar] [CrossRef]
- Kuchment, L.S.; Romanov, P.; Gelfan, A.N.; Demidov, V.N. Use of Satellite-Derived Data for Characterization of Snow Cover and Simulation of Snowmelt Runoff through a Distributed Physically Based Model of Runoff Generation. Hydrol. Earth Syst. Sci. 2010, 14, 339–350. [Google Scholar] [CrossRef] [Green Version]
- Immerzeel, W.W.; Droogers, P.; de Jong, S.M.; Bierkens, M.F.P. Satellite Derived Snow and Runoff Dynamics in the Upper Indus River Basin. Grazer Schr. Geogr. Raumforsch. 2010, 45, 303–312. [Google Scholar]
- Rango, A.; Salomonson, V.V.; Foster, J.L. Seasonal Streamflow Estimation in the Himalayan Region Employing Meteorological Satellite Snow Cover Observations. Water Resour. Res. 1977, 13, 109–112. [Google Scholar] [CrossRef]
- Helms, D.; Phillips, S.E.; Reich, P.F. The History of Snow Survey and Water Supply Forecasting: Interviews with U.S. Department of Agriculture Pioneers; U.S. Department of Agriculture, Natural Resources Conservation Service: Washington, DC, USA, 2008. [Google Scholar]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity Is Dead: Whither Water Management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Dyer, J. Snow Depth and Streamflow Relationships in Large North American Watersheds. J. Geophys. Res. 2008, 113, D18113. [Google Scholar] [CrossRef]
- Godsey, S.E.; Kirchner, J.W.; Tague, C.L. Effects of Changes in Winter Snowpacks on Summer Low Flows: Case Studies in the Sierra Nevada, California, USA. Hydrol. Process. 2014, 28, 5048–5064. [Google Scholar] [CrossRef]
- Dudley, R.W.; Hodgkins, G.A.; McHale, M.R.; Kolian, M.J.; Renard, B. Trends in Snowmelt-Related Streamflow Timing in the Conterminous United States. J. Hydrol. 2017, 547, 208–221. [Google Scholar] [CrossRef] [Green Version]
- Miller, W.P.; Piechota, T.C. Trends in Western U.S. Snowpack and Related Upper Colorado River Basin Streamflow. J. Am. Water Resour. Assoc. 2011, 47, 1197–1210. [Google Scholar] [CrossRef]
- Selkowitz, D.J.; Painter, T.H.; Rittger, K.; Schmidt, G.; Forster, R. The USGS Landsat Snow Covered Area Products: Methods and Preliminary Validation. In Automated Approaches for Snow and Ice Cover Monitoring Using Optical Remote Sensing; University of Utah: Salt Lake City, UT, USA, 2017; pp. 76–119. [Google Scholar]
- National Operational Hydrologic Remote Sensing Center. Snow Data Assimilation System (SNODAS) Data Products at NSIDC, Version 1; National Snow and Ice Data Center: Boulder, CO, USA, 2004. [Google Scholar] [CrossRef]
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote Sensing of Snow—A Review of Available Methods. Int. J. Remote Sens. 2012, 33, 4094–4134. [Google Scholar] [CrossRef]
- Molotch, N.P. Reconstructing Snow Water Equivalent in the Rio Grande Headwaters Using Remotely Sensed Snow Cover Data and a Spatially Distributed Snowmelt Model. Hydrol. Process. 2009, 23, 1076–1089. [Google Scholar] [CrossRef]
- Molotch, N.P.; Margulis, S.A. Estimating the Distribution of Snow Water Equivalent Using Remotely Sensed Snow Cover Data and a Spatially Distributed Snowmelt Model: A Multi-Resolution, Multi-Sensor Comparison. Adv. Water Resour. 2008, 31, 1503–1514. [Google Scholar] [CrossRef]
- Bair, E.H.; Rittger, K.; Davis, R.E.; Painter, T.H.; Dozier, J. Validating Reconstruction of Snow Water Equivalent in California’s Sierra Nevada Using Measurements from the NASAAirborne Snow Observatory: SWE reconstruction compared to ASO. Water Resour. Res. 2016, 52, 8437–8460. [Google Scholar] [CrossRef]
- USDA. Statistical Techniques Used in the VIPER Water Supply Forecasting Software; United States Department of Agriculture: Washington, DC, USA, 2007. [Google Scholar]
- Werner, K.; Brandon, D.; Clark, M.; Gangopadhyay, S. Incorporating Medium-Range Numerical Weather Model Output into the Ensemble Streamflow Prediction System of the National Weather Service. J. Hydrometeorol. 2005, 6, 101–114. [Google Scholar] [CrossRef] [Green Version]
- Day, G.N. Extended Streamflow Forecasting Using NWSRFS. J. Water Resour. Plan. Manag. 1985, 111, 157–170. [Google Scholar] [CrossRef]
- Hamill, T. The national weather service river forecast system. In Proceedings of the 1999 Georgia Water Resources Conference, Athens, GA, USA, 30–31 March 1999. [Google Scholar]
- Guan, B.; Molotch, N.P.; Waliser, D.E.; Jepsen, S.M.; Painter, T.H.; Dozier, J. Snow Water Equivalent in the Sierra Nevada: Blending Snow Sensor Observations with Snowmelt Model Simulations: Snow water equivalent in the Sierra Nevada. Water Resour. Res. 2013, 49, 5029–5046. [Google Scholar] [CrossRef]
- Micheletty, P.; Perrot, D.; Day, G.; Rittger, K. Assimilation of Ground and Satellite Snow Observations in a Distributed Hydrologic Model for Water Supply Forecasting. J. Am. Water Resour. Assoc. 2021, 58, 1030–1048. [Google Scholar] [CrossRef]
- Yang, K.; Musselman, K.N.; Rittger, K.; Margulis, S.A.; Painter, T.H.; Molotch, N.P. Combining Ground-Based and Remotely Sensed Snow Data in a Linear Regression Model for Real-Time Estimation of Snow Water Equivalent. Adv. Water Resour. 2022, 160, 104075. [Google Scholar] [CrossRef]
- Page, R.; Dilling, L. The Critical Role of Communities of Practice and Peer Learning in Scaling Hydroclimatic Information Adoption. Weather Clim. Soc. 2019, 11, 851–862. [Google Scholar] [CrossRef]
- Livneh, B.; Badger, A.M. Drought Less Predictable under Declining Future Snowpack. Nat. Clim. Change 2020, 10, 452–458. [Google Scholar] [CrossRef]
- USDA Natural Resources Conservation Service. SNOwpack TELemetry Network (SNOTEL); Natural Resources Conservation Service—NRCS: Washington, DC, USA, 2022. [Google Scholar]
- US Geological Survey. USGS Water Data for the Nation; US Geological Survey: Washington, DC, USA, 1994. [Google Scholar] [CrossRef]
- Modi, P.A.; Small, E.E.; Kasprzyk, J.; Livneh, B. Investigating the Role of Snow Water Equivalent on Streamflow Predictability during Drought. J. Hydrometeorol. 2022, 23, 1607–1625. [Google Scholar] [CrossRef]
- US Geological Survey. GAGES-II: Geospatial Attributes of Gages for Evaluating Streamflow; US Geological Survey: Washington, DC, USA, 2011. [Google Scholar]
- Cayan, D.R. Interannual Climate Variability and Snowpack in the Western United States. J. Clim. 1996, 9, 928–948. [Google Scholar] [CrossRef]
- Loveridge, M.; Rahman, A.; Babister, M. Probabilistic Flood Hydrographs Using Monte Carlo Simulation: Potential Impact to Flood Inundation Mapping. In Proceedings of the MODSIM2013, 20th International Congress on Modelling and Simulation, Adelaide, Australia, 1–6 December 2013; Piantadosi, J., Anderssen, R.S., Boland, J., Eds.; Modelling and Simulation Society of Australia and New Zealand (MSSANZ), Inc.: Canberra, Australia, 2013. [Google Scholar]
- Charalambous, J.; Rahman, A.; Carroll, D. Application of Monte Carlo Simulation Technique to Design Flood Estimation: A Case Study for North Johnstone River in Queensland, Australia. Water Resour. Manag. 2013, 27, 4099–4111. [Google Scholar] [CrossRef]
- Joseph, V.R. Optimal Ratio for Data Splitting. Stat. Anal. Data Min. ASA Data Sci. J. 2022, 15, 531–538. [Google Scholar] [CrossRef]
- Kommineni, M.; Reddy, K.V.; Jagathi, K.; Reddy, B.D.; Roshini, A.; Bhavani, V. Groundwater Level Prediction Using Modified Linear Regression. In Proceedings of the 2020 6th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 6–7 March 2020; IEEE: Coimbatore, India, March, 2020; pp. 1164–1168. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and Statistical Modeling with Python. In Proceedings of the Proceedings of the 9th Python in Science Conference (SciPy 2010), Austin, TX, USA, 28 June–3 July 2010; pp. 92–96. [Google Scholar]
- Kroll, C.N.; Song, P. Impact of Multicollinearity on Small Sample Hydrologic Regression Models: Impact of Multicollinearity on Hydrologic Regression Models. Water Resour. Res. 2013, 49, 3756–3769. [Google Scholar] [CrossRef]
- Slater, A.G.; Barrett, A.P.; Clark, M.P.; Lundquist, J.D.; Raleigh, M.S. Uncertainty in Seasonal Snow Reconstruction: Relative Impacts of Model Forcing and Image Availability. Adv. Water Resour. 2013, 55, 165–177. [Google Scholar] [CrossRef]
- Heldmyer, A.; Livneh, B. Annual Snow Timing Index Rasters for the Western US and Alaska, WY2001–2019; Zenodo: Geneva, Switzerland, 2021. [Google Scholar]


| Basin Name | USGS Gage Name | USGS ID | Gage Location | Gage Elevation (m) | Basin Area (km2) | SNOTEL Station | SNOTEL Elevation (m) | SWE/P Ratio |
|---|---|---|---|---|---|---|---|---|
| Walker R. | W Walker River near Coleville, CA | 10,296,000 | 38.38, −119.45 | 2008 | 471 | 575 | 2191 | 0.84 |
| Carson R. | E F Carson River near Markleeville, CA | 10,308,200 | 38.71, −119.76 | 1646 | 718 | 697 | 2358 | 0.82 |
| East R. | East River at Almont, CO | 9,112,500 | 38.66, −106.85 | 2440 | 750 | 380 | 3109 | 0.92 |
| Crystal R. | Crystal River near Redstone, CO | 9,081,600 | 39.23, −107.23 | 2105 | 434 | 618 | 2674 | 0.82 |
| San Juan R. | San Juan River at Pagosa Springs, CO | 9,342,500 | 37.27, −107.01 | 2148 | 727 | 840 | 3091 | 0.80 |
| Little Wood R. | Little Wood River near Carey, ID | 13,147,900 | 43.49, −114.06 | 1621 | 655 | 805 | 2329 | 0.75 |
| Swan R. | Swan River near Bigfork, MT | 12,370,000 | 48.02, −113.98 | 933 | 1753 | 562 | 1448 | 0.76 |
| Bruneau R. | Bruneau River at Rowland, NV | 13,161,500 | 41.93, −115.67 | 1372 | 988 | 746 | 2240 | 0.68 |
| Sandy R. | Sandy River near Marmot, OR | 14,137,000 | 45.40, −112.14 | 0 | 711 | 655 | 1241 | 0.41 |
| Santiam R. | North Santiam River near Detroit, OR | 14,178,000 | 44.71, −122.10 | 485 | 553 | 614 | 789 | 0.24 |
| Blacksmith Fork | Blacksmith Fork near Hyrum, UT | 10,113,500 | 41.62, −111.74 | 1530 | 681 | 634 | 2722 | 0.98 |
| Sevier R. | Sevier River at Hatch, UT | 10,174,500 | 37.65, −113.43 | 2094 | 864 | 390 | 2928 | 0.74 |
| Lamar R. | Lamar River near Tower Falls Ranger Station, YNP | 6,188,000 | 44.93, −110.39 | 1829 | 1741 | 683 | 2865 | 0.96 |
| Pacific Cr. | Pacific Creek at Moran, WY | 13,011,500 | 43.85, −110.52 | 2048 | 407 | 314 | 2152 | 0.96 |
| Stehekin R. | Stehekin River at Stehekin, WA | 12,451,000 | 48.33, −120.69 | 335 | 839 | 681 | 1402 | 0.86 |
| Model Classifier | Input Variables | Units |
|---|---|---|
| Sat_DSD | Day of Snow Disappearance (DSD) | Day of year |
| Sat_SFF | Snow free fraction (SFF) | Percentage (%) |
| Sat_combo | DSD and SFF | Day of year; percentage (%) |
| Phys_SWE | SNOTEL snow water equivalent (SWE) | mm |
| SatPhys_combo | DSD, SFF, and SNOTEL SWE | Day of year; percentage (%); mm |
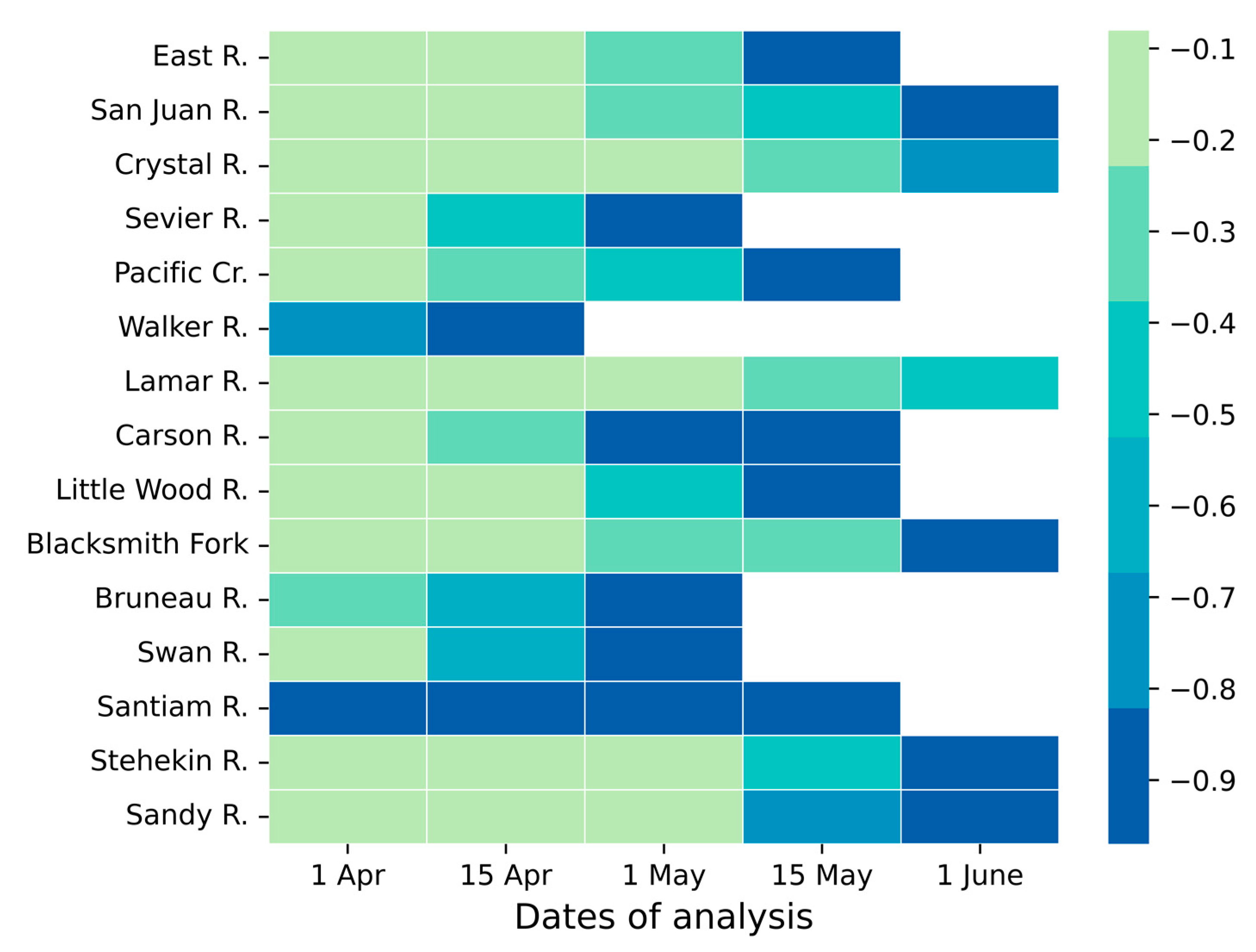
| Basin | Mean DSD | Center of Water Supply Volume | DSD-VAMJJ R2 | p-Value |
|---|---|---|---|---|
| East R. | 130 | 152 | 0.82 | 8.30 × 10−8 |
| San Juan R. | 114 | 143 | 0.80 | 2.20 × 10−7 |
| Crystal R. | 136 | 157 | 0.80 | 2.50 × 10−7 |
| Sevier R. | 95 | 143 | 0.57 | 1.80 × 10−4 |
| Pacific Cr. | 141 | 147 | 0.60 | 1.10 × 10−4 |
| Walker R. | 135 | 150 | 0.79 | 4.50 × 10−7 |
| Lamar R. | 140 | 152 | 0.46 | 1.50 × 10−3 |
| Carson R. | 119 | 141 | 0.74 | 2.10 × 10−6 |
| Little Wood R. | 107 | 142 | 0.41 | 3.00 × 10−3 |
| Blacksmith Fork | 105 | 139 | 0.48 | 1.00 × 10−3 |
| Bruneau R. | 83 | 130 | 0.38 | 4.80 × 10−3 |
| Swan R. | 111 | 153 | 0.39 | 4.00 × 10−3 |
| Santiam R. | 102 | 135 | 0.79 | 4.50 × 10−7 |
| Stehekin R. | 150 | 153 | 0.60 | 9.30 × 10−5 |
| Sandy R. | 75 | 132 | 0.52 | 4.90 × 10−4 |
| 1 April | 15 April | 1 May | 15 May | 1 June | Mean | Median | |
| Sat_DSD | −0.07 | −0.28 | −0.15 | −0.03 | 0.03 | −0.10 | −0.07 |
| Sat_SFF | −0.21 | −0.29 | −0.16 | −0.35 | 0.27 | −0.15 | −0.21 |
| Sat_combo | −0.11 | −0.20 | 0.22 | −0.26 | 0.33 | 0.00 | −0.11 |
| Phys_SWE | −0.17 | −0.26 | −0.57 * | −0.64 * | 0.11 | −0.31 | −0.26 |
| SatPhys_Combo | −0.28 | −0.23 | −0.09 | −0.19 | 0.24 | −0.11 | −0.19 |
| Mean | −0.17 | −0.25 | −0.15 | −0.29 | 0.20 | ||
| Median | −0.17 | −0.26 | −0.15 | −0.26 | 0.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bishay, K.; Bjarke, N.R.; Modi, P.; Pflug, J.M.; Livneh, B. Can Remotely Sensed Snow Disappearance Explain Seasonal Water Supply? Water 2023, 15, 1147. https://doi.org/10.3390/w15061147
Bishay K, Bjarke NR, Modi P, Pflug JM, Livneh B. Can Remotely Sensed Snow Disappearance Explain Seasonal Water Supply? Water. 2023; 15(6):1147. https://doi.org/10.3390/w15061147
Chicago/Turabian StyleBishay, Kaitlyn, Nels R. Bjarke, Parthkumar Modi, Justin M. Pflug, and Ben Livneh. 2023. "Can Remotely Sensed Snow Disappearance Explain Seasonal Water Supply?" Water 15, no. 6: 1147. https://doi.org/10.3390/w15061147





