Using Simple LSTM Models to Evaluate Effects of a River Restoration on Groundwater in Kushiro Wetland, Hokkaido, Japan
Highlights
- Groundwater level time series in the Kushiro Wetland were modelled using LSTM.
- A noticeable recovery in groundwater fluctuation characteristics was evaluated via the use of LSTM.
- Meandering river channel restoration partially restored the hydrological process in the wetland.
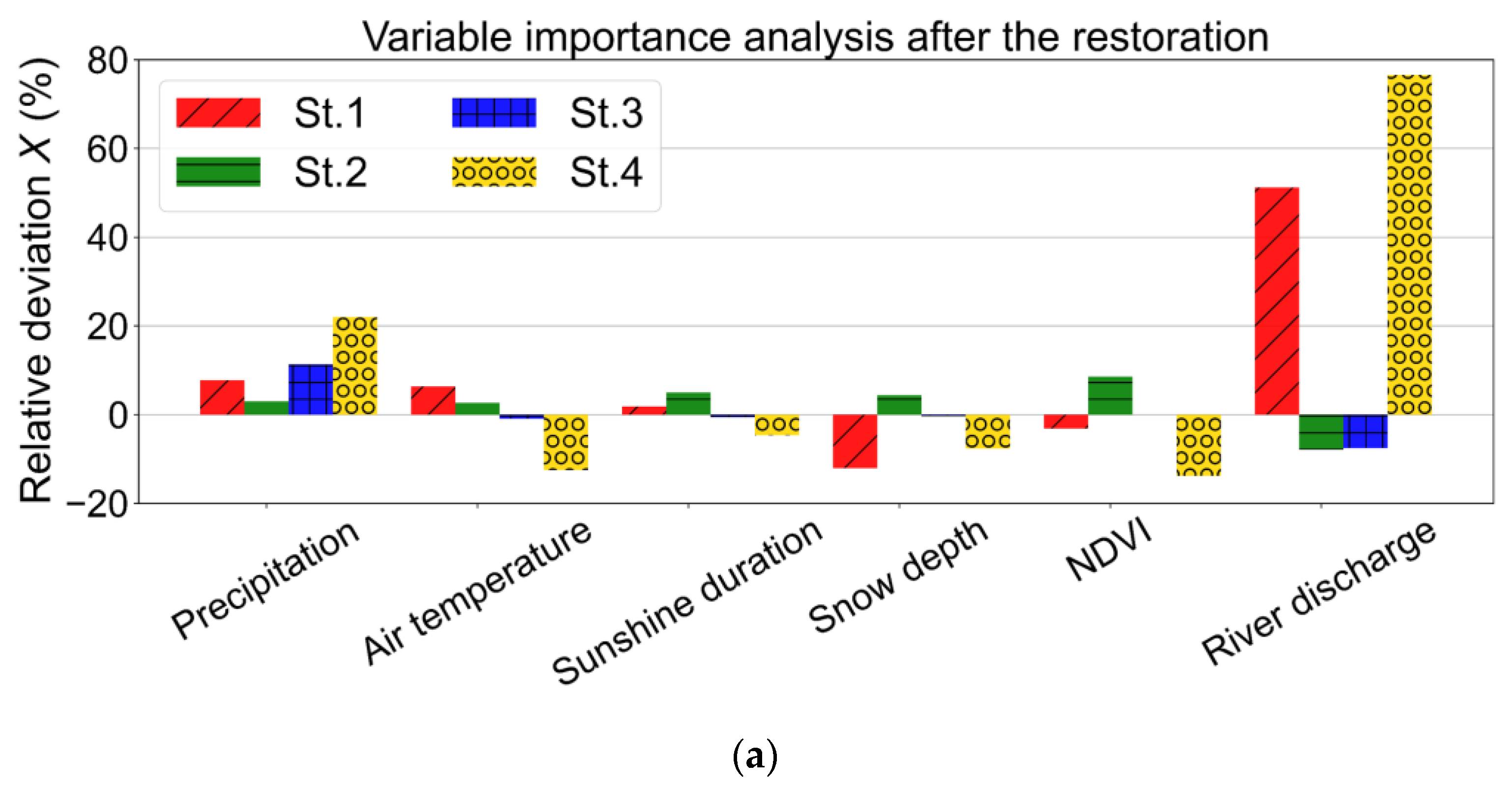
- The LSTM input analysis revealed the importance of river discharge and precipitation for the restoration of the meandering river channel.
Abstract
:1. Introduction
2. Materials and Methods
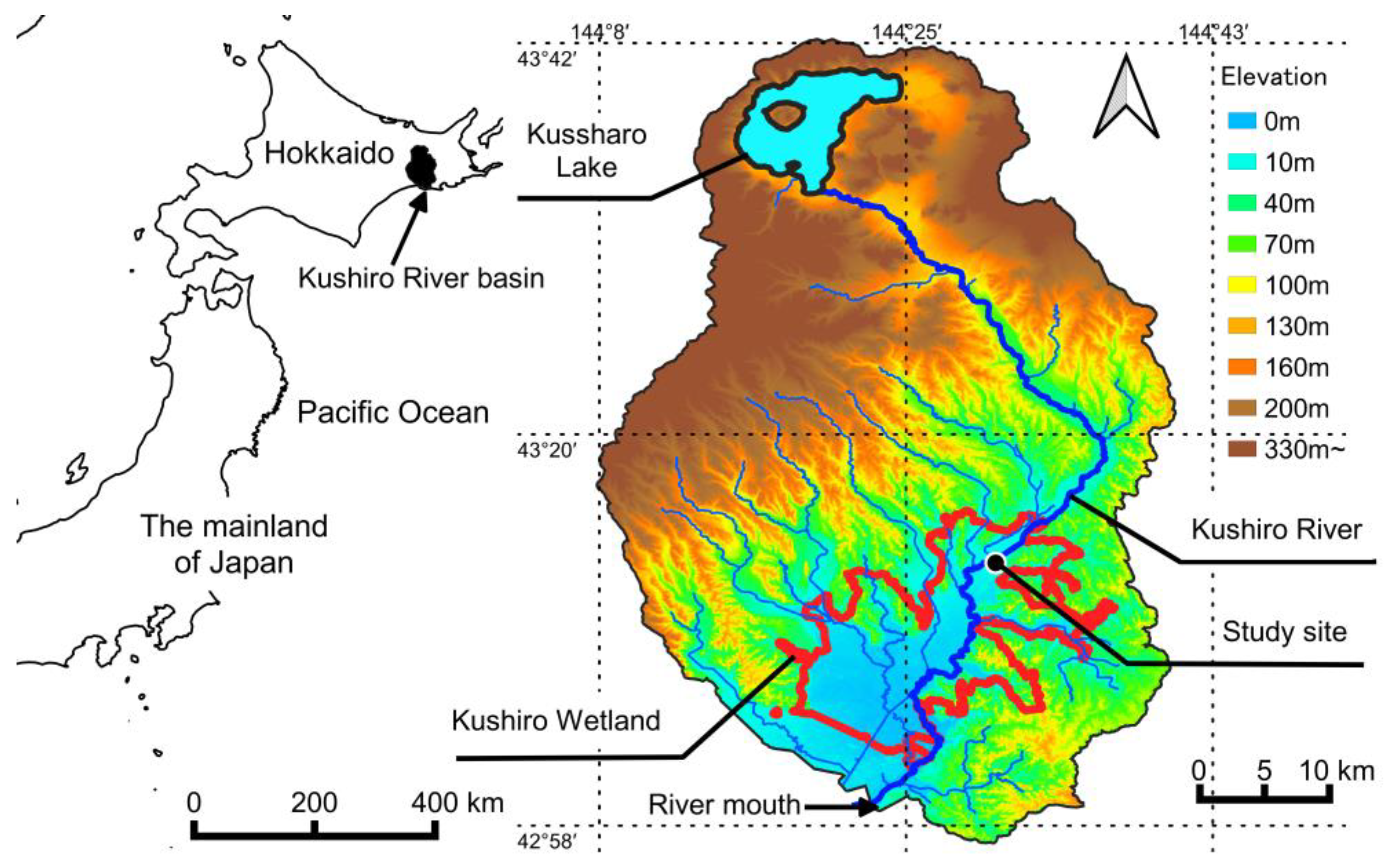
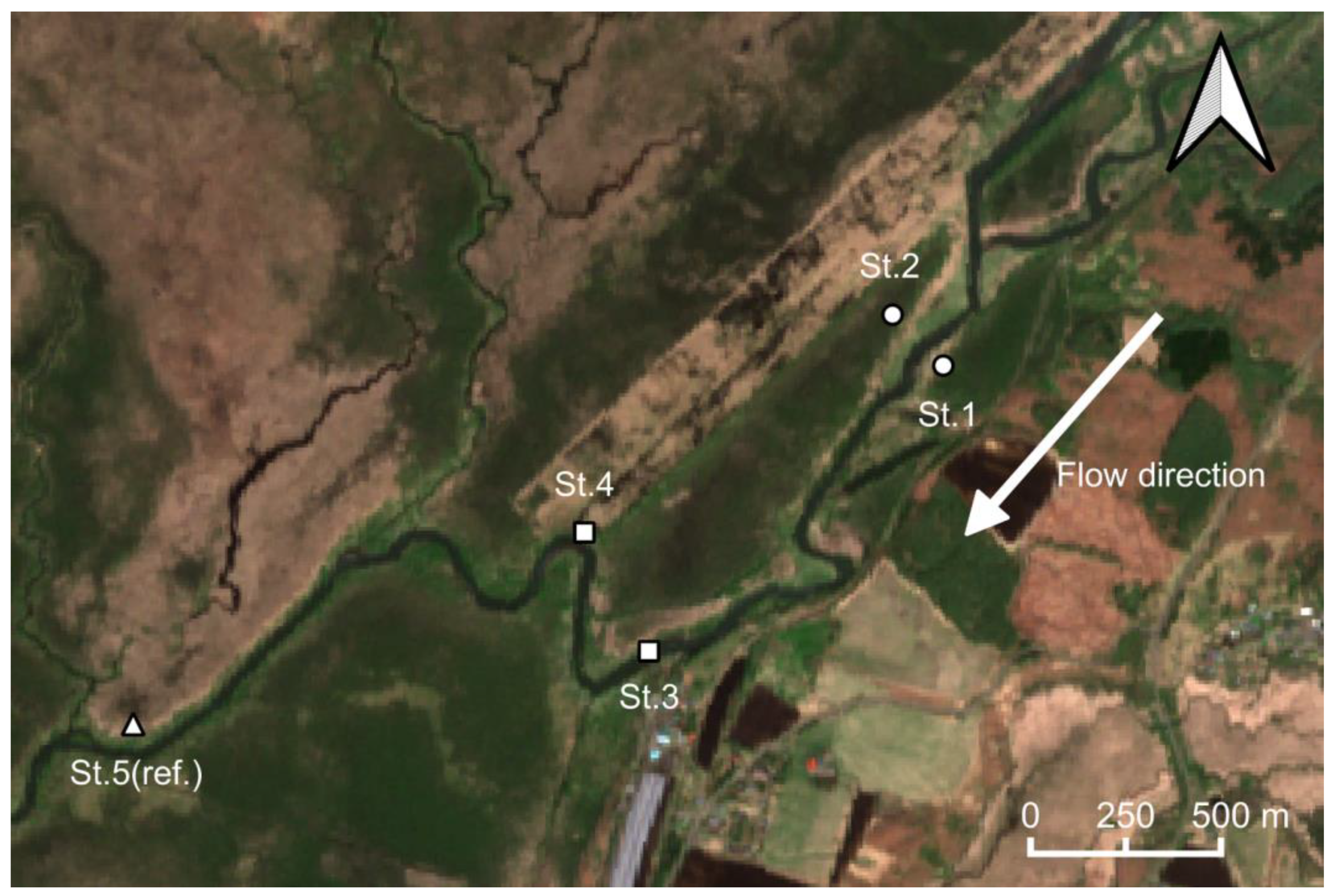
2.1. Target Site
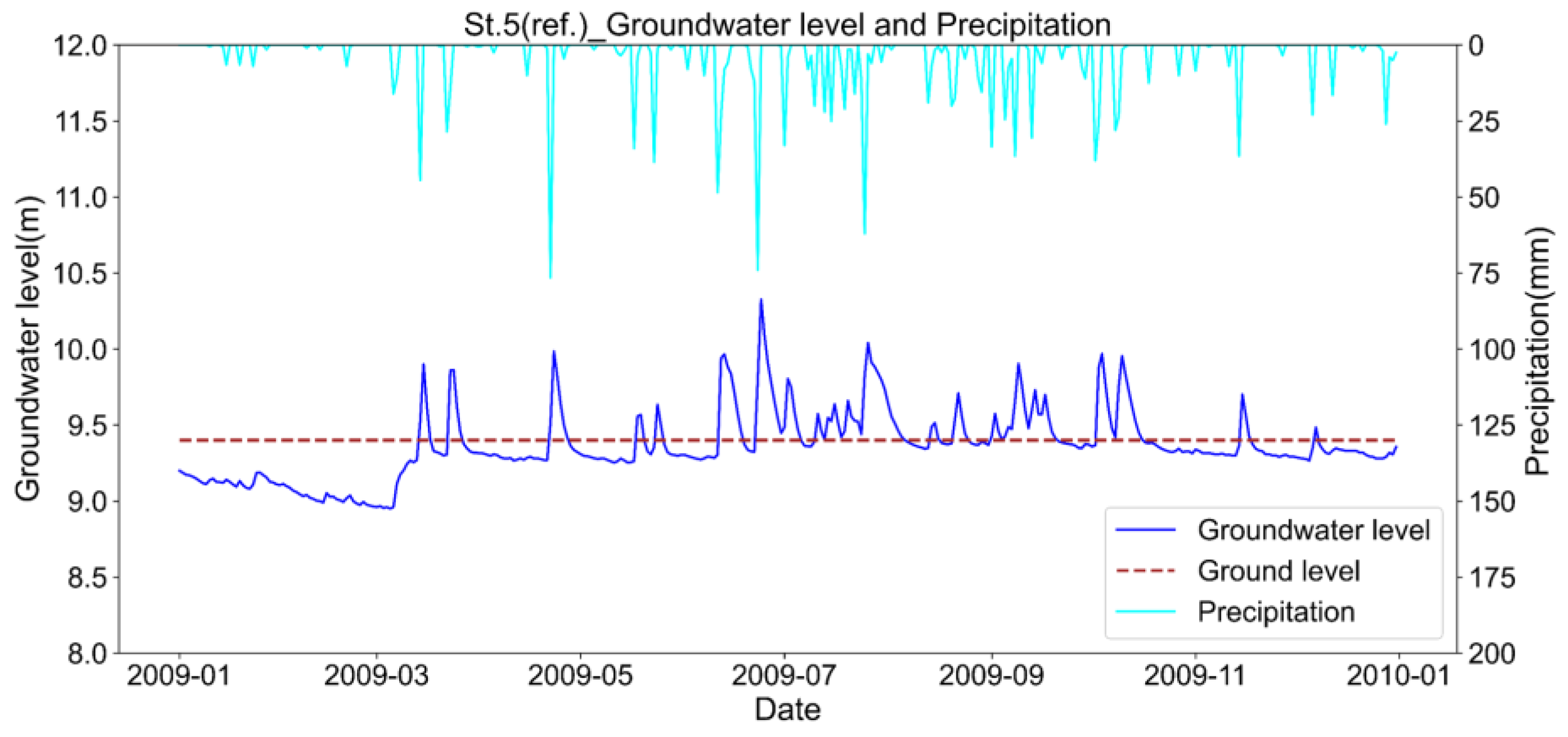
2.2. Data and Instrumentation
2.3. Deep Learning Model
2.4. Steps of the Assessment
2.4.1. Data Division for Pre- and Post-Restoration and the LSTM Evaluation Index
2.4.2. Evaluation of the Meandering Stream Channel Restoration
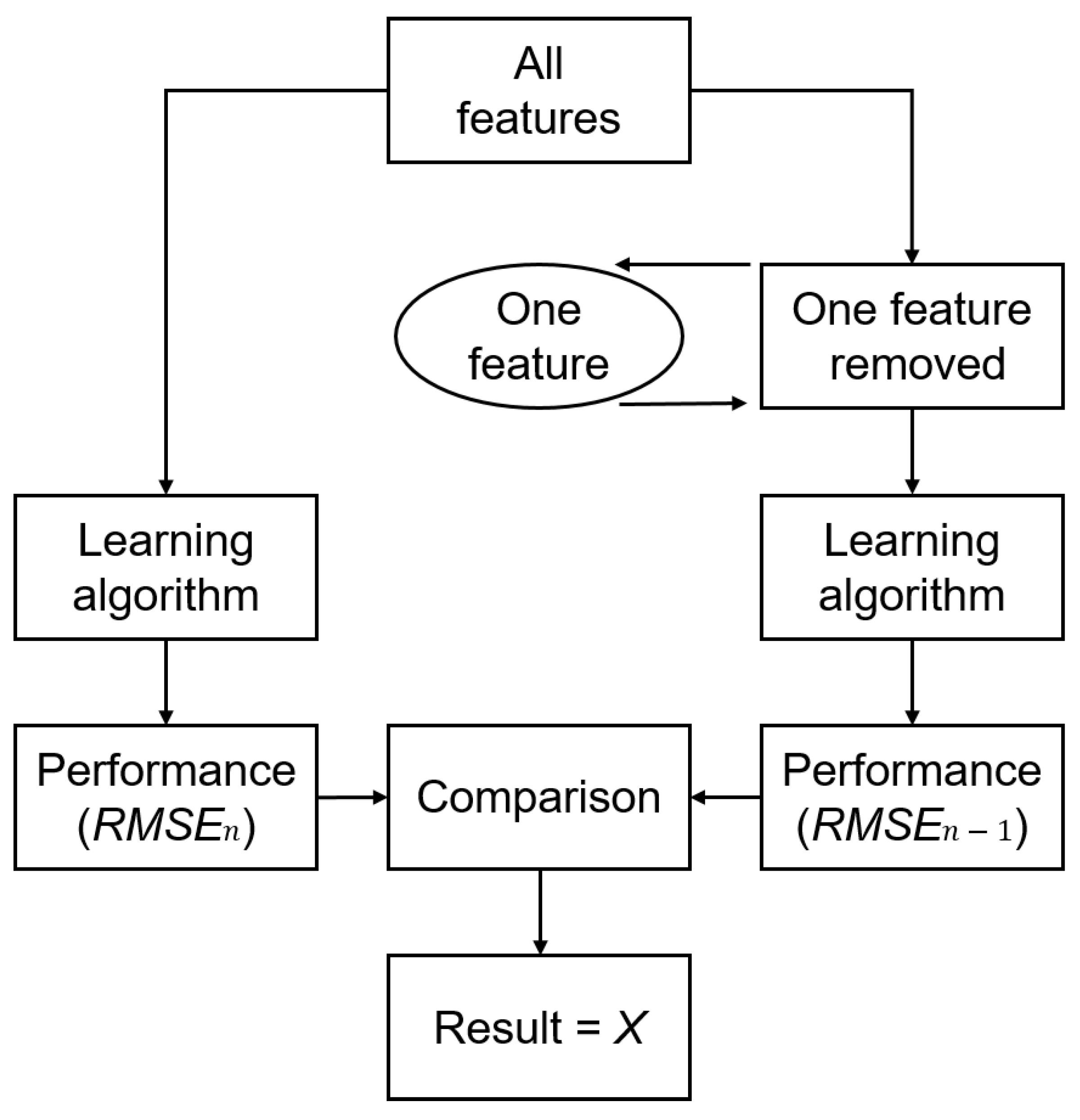
2.4.3. Importance Analysis of the LSTM Explanatory Variables
3. Results
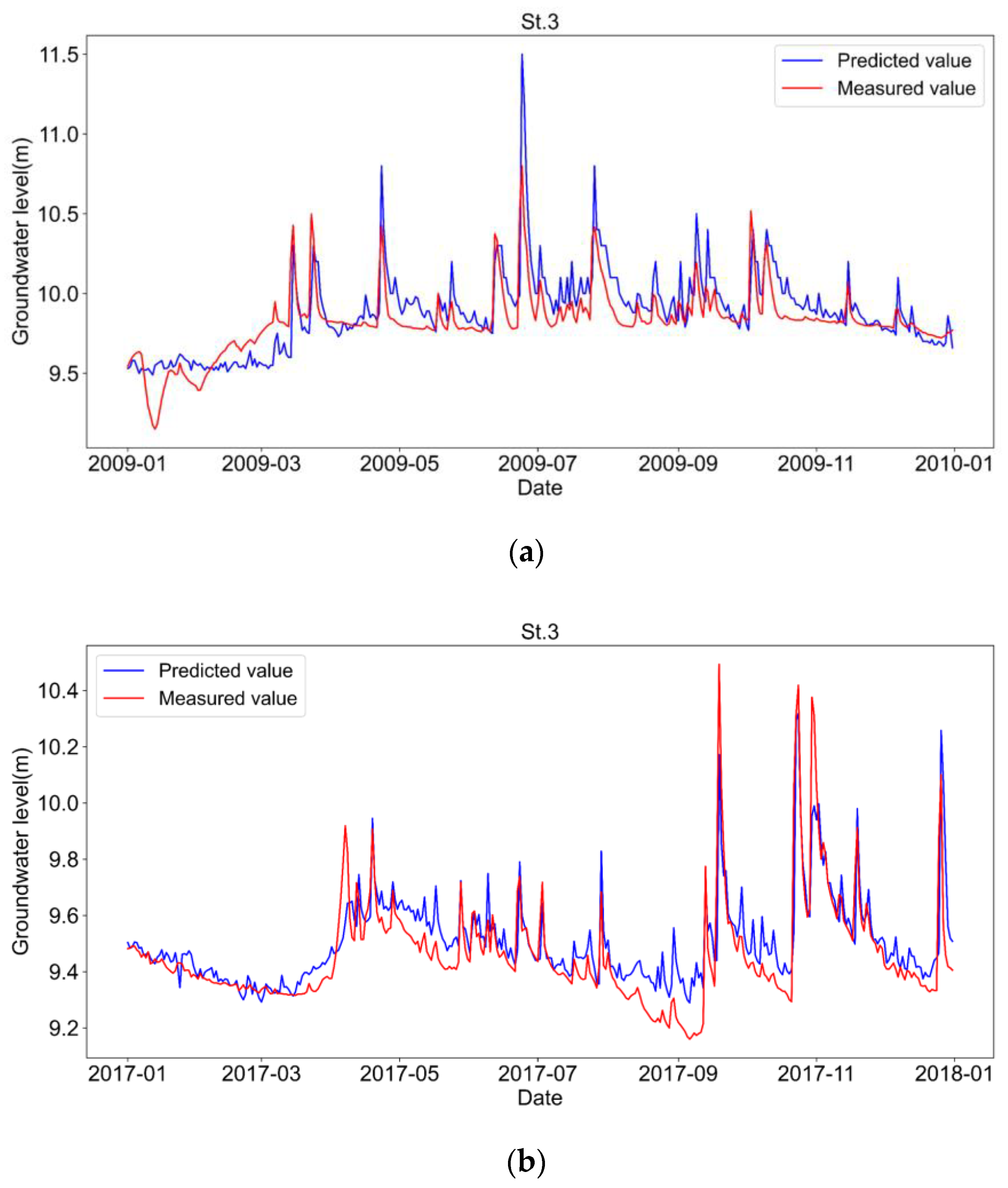
3.1. LSTM Model Accuracy for Groundwater Level Prediction
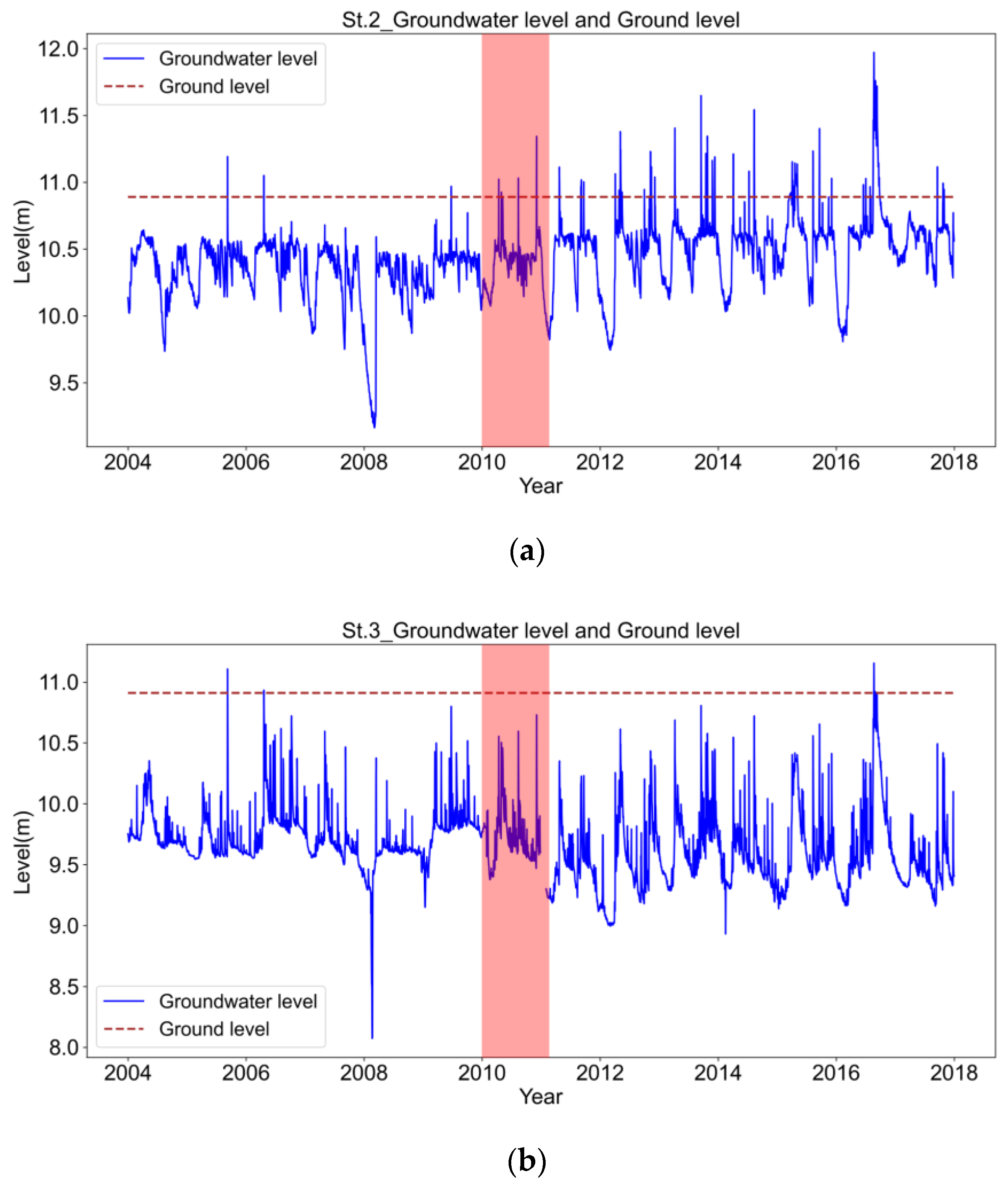
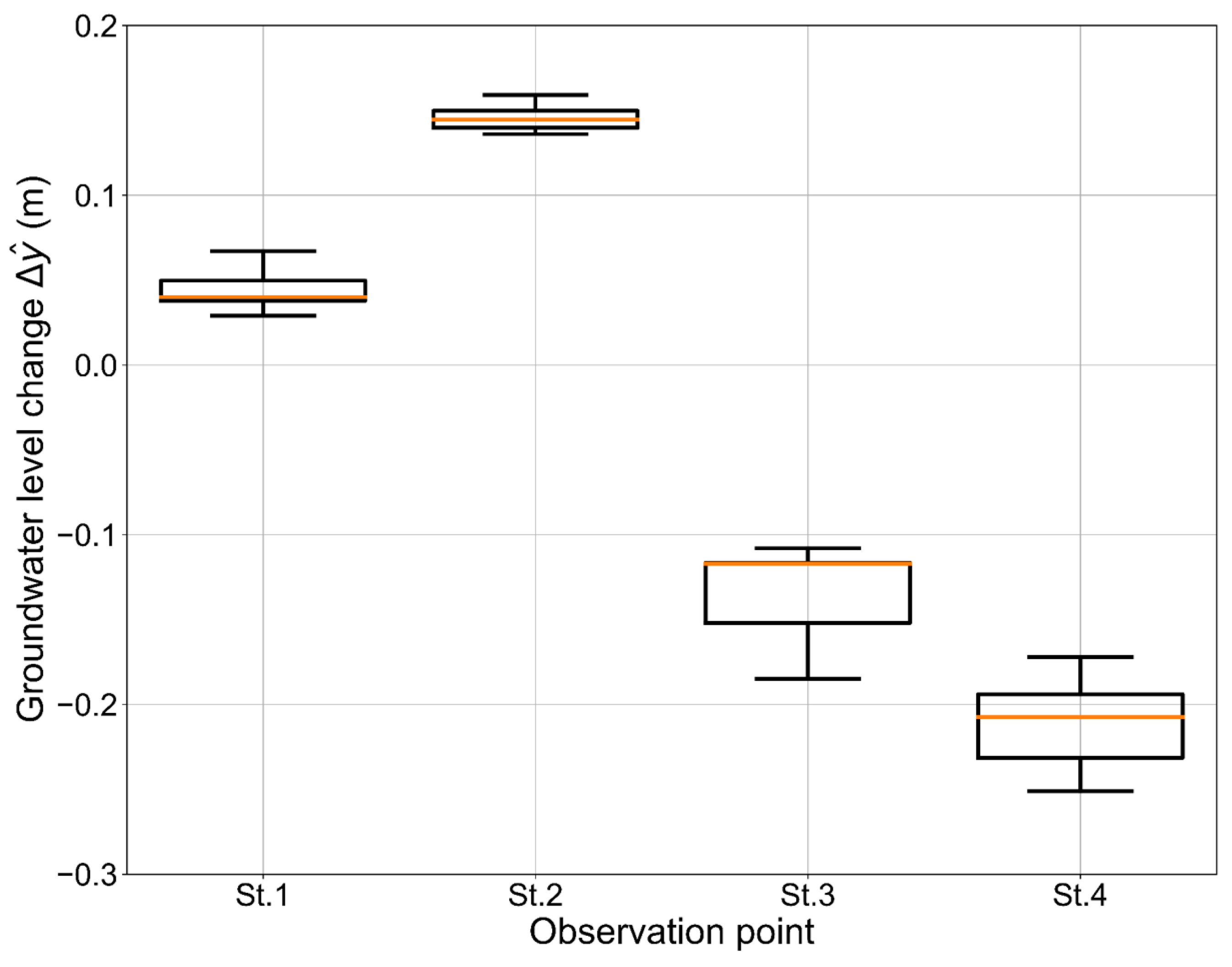
3.2. Evaluation of the Meandering Stream Channel Restoration
3.3. Importance Analysis for the LSTM Model Explanatory Variables
4. Discussion
4.1. Advantages and Limitations of the LSTM Model in This Study
4.2. Restoration of Hydrological Processes and Wetland Ecosystems in the Kushiro Wetland
4.3. Future Model Development
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Costanza, R.; d’Arge, R.; de Groot, R.; Farber, S.; Grasso, M.; Hannon, B.; Limburg, K.; Naeem, S.; O’Neill, R.V.; Paruelo, J.; et al. The value of the world’s ecosystem services and natural capital. Nature 1997, 387, 253–260. [Google Scholar] [CrossRef]
- Verhoeven, J.; Setter, T. Agricultural use of wetlands: Opportunities and limitations. Ann. Bot. 2009, 105, 155–163. [Google Scholar] [CrossRef] [Green Version]
- Hassan, R.; Scholes, R.; Ash, N. Ecosystems and Human Well-Being: Current State and Trends; Island Press: Washington, DC, USA, 2005. [Google Scholar]
- Mitsch, W.J.; Bernal, B.; Hernandez, M.E. Ecosystem services of wetlands. Int. J. Biodivers. Sci. Ecosyst. Serv. Manag. 2015, 11, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Gardner, R.C.; Finlayson, M. Global Wetland Outlook: State of the World’s Wetlands and Their Services to People 2018; Secretariat of the Ramsar Convention: Gland, Switzerland, 2018. [Google Scholar]
- Weise, K.; Höfer, R.; Franke, J.; Guelmami, A.; Simonson, W.; Muro, J.; O’Connor, B.; Strauch, A.; Flink, S.; Eberle, J.; et al. Wetland extent tools for SDG 6.6.1 reporting from the Satellite-based Wetland Observation Service (SWOS). Remote Sens. Environ. 2020, 247, 111892. [Google Scholar] [CrossRef]
- Zedler, J.B. Progress in wetland restoration ecology. Trends Ecol. Evol. 2000, 15, 402–407. [Google Scholar] [CrossRef]
- Harvey, M.C.; Hare, D.K.; Hackman, A.; Davenport, G.; Haynes, A.B.; Helton, A.; Lane, J.W.; Briggs, M.A. Evaluation of Stream and Wetland Restoration Using UAS-Based Thermal Infrared Mapping. Water 2019, 11, 1568. [Google Scholar] [CrossRef] [Green Version]
- Hunt, R.J.; Walker, J.F.; Krabbenhoft, D.P. Characterizing hydrology and the importance of ground-water discharge in natural and constructed wetlands. Wetlands 1999, 19, 458–472. [Google Scholar] [CrossRef]
- Acreman, M.C.; Fisher, J.; Stratford, C.J.; Mould, D.J.; Mountford, J.O. Hydrological science and wetland restoration: Some case studies from Europe. Hydrol. Earth Syst. Sci. 2007, 11, 158–169. [Google Scholar] [CrossRef] [Green Version]
- Banaszuk, P.; Kamocki, A. Effects of climatic fluctuations and land-use changes on the hydrology of temperate fluviogenous mire. Ecol. Eng. 2008, 32, 133–146. [Google Scholar] [CrossRef]
- Grodzka-Łukaszewska, M.; Sinicyn, G.; Grygoruk, M.; Mirosław-Świątek, D.; Kardel, I.; Okruszko, T. The role of the river in the functioning of marginal fen: A case study from the Biebrza Wetlands. PeerJ 2022, 10, e13418. [Google Scholar] [CrossRef]
- Dorau, K.; Gelhausen, H.; Esplör, D.; Mansfeldt, T. Wetland restoration management under the aspect of climate change at a mesotrophic fen in Northern Germany. Ecol. Eng. 2015, 84, 84–91. [Google Scholar] [CrossRef]
- Nakamura, K.; Tockner, K.; Amano, K. River and Wetland Restoration: Lessons from Japan. BioScience 2006, 56, 419–429. [Google Scholar] [CrossRef]
- Nakamura, F.; Ishiyama, N.; Sueyoshi, M.; Negishi, J.N.; Akasaka, T. The Significance of Meander Restoration for the Hydrogeomorphology and Recovery of Wetland Organisms in the Kushiro River, a Lowland River in Japan. Restor. Ecol. 2014, 22, 544–554. [Google Scholar] [CrossRef]
- Nakayama, T. Feedback and regime shift of mire ecosystem in northern Japan. Hydrol. Process. 2012, 26, 2455–2469. [Google Scholar] [CrossRef]
- Johansen, O.M.; Andersen, D.K.; Ejrnæs, R.; Pedersen, M.L. Relations between vegetation and water level in groundwater dependent terrestrial ecosystems (GWDTEs). Limnologica 2018, 68, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Toogood, S.E.; Joyce, C.B. Effects of raised water levels on wet grassland plant communities. Appl. Veg. Sci. 2009, 12, 283–294. [Google Scholar] [CrossRef]
- Hammersmark, C.T.; Rains, M.C.; Wickland, A.C.; Mount, J.F. Vegetation and water-table relationships in a hydrologically restored riparian meadow. Wetlands 2009, 29, 785–797. [Google Scholar] [CrossRef]
- Kopeć, D.; Michalska-Hejduk, D.; Krogulec, E. The relationship between vegetation and groundwater levels as an indicator of spontaneous wetland restoration. Ecol. Eng. 2013, 57, 242–251. [Google Scholar] [CrossRef]
- Orellana, F.; Verma, P.; Loheide II, S.P.; Daly, E. Monitoring and modeling water-vegetation interactions in groundwater-dependent ecosystems. Rev. Geophys. 2012, 50, RG3003. [Google Scholar] [CrossRef]
- Boswell, J.S.; Olyphant, G.A. Modeling the hydrologic response of groundwater dominated wetlands to transient boundary conditions: Implications for wetland restoration. J. Hydrol. 2007, 332, 467–476. [Google Scholar] [CrossRef]
- Hammersmark, C.T.; Rains, M.C.; Mount, J.F. Quantifying the hydrological effects of stream restoration in a montane meadow, northern California, USA. River Res. Appl. 2008, 24, 735–753. [Google Scholar] [CrossRef]
- Loheide, S.P.; Booth, E.G. Effects of changing channel morphology on vegetation, groundwater, and soil moisture regimes in groundwater-dependent ecosystems. Geomorphology 2011, 126, 364–376. [Google Scholar] [CrossRef]
- Montalto, F.A.; Parlange, J.-Y.; Steenhuis, T.S. A simple model for predicting water table fluctuations in a tidal marsh. Water Resour. Res. 2007, 43, W03439. [Google Scholar] [CrossRef] [Green Version]
- Gu, H.; Xu, Y.-P.; Ma, D.; Xie, J.; Liu, L.; Bai, Z. A surrogate model for the Variable Infiltration Capacity model using deep learning artificial neural network. J. Hydrol. 2020, 588, 125019. [Google Scholar] [CrossRef]
- Liu, W.; Yu, H.; Yang, L.; Yin, Z.; Zhu, M.; Wen, X. Deep Learning-Based Predictive Framework for Groundwater Level Forecast in Arid Irrigated Areas. Water 2021, 13, 2558. [Google Scholar] [CrossRef]
- Arel, I.; Rose, D.C.; Karnowski, T.P. Deep Machine Learning—A New Frontier in Artificial Intelligence Research [Research Frontier]. IEEE Comput. Intell. Mag. 2010, 5, 13–18. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Mohapatra, J.B.; Jha, P.; Jha, M.K.; Biswal, S. Efficacy of machine learning techniques in predicting groundwater fluctuations in agro-ecological zones of India. Sci. Total Environ. 2021, 785, 147319. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y. A review of artificial neural network techniques for environmental issues prediction. J Anal Calorim 2021, 145, 2191–2207. [Google Scholar] [CrossRef]
- Shen, C. A Transdisciplinary Review of Deep Learning Research and Its Relevance for Water Resources Scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Kamrava, S.; Bai, T.; Sahimi, M. Machine learning in geo- and environmental sciences: From small to large scale. Adv. Water Resour. 2020, 142, 103619. [Google Scholar] [CrossRef]
- Tao, H.; Hameed, M.M.; Marhoon, H.A.; Zounemat-Kermani, M.; Heddam, S.; Kim, S.; Sulaiman, S.O.; Tan, M.L.; Sa’adi, Z.; Mehr, A.D.; et al. Groundwater level prediction using machine learning models: A comprehensive review. Neurocomputing 2022, 489, 271–308. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Jeong, J.; Park, E. Comparative applications of data-driven models representing water table fluctuations. J. Hydrol. 2019, 572, 261–273. [Google Scholar] [CrossRef]
- Bowes, B.D.; Sadler, J.M.; Morsy, M.M.; Behl, M.; Goodall, J.L. Forecasting Groundwater Table in a Flood Prone Coastal City with Long Short-term Memory and Recurrent Neural Networks. Water 2019, 11, 1098. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.; Gao, L.; Crosbie, R.S.; Zhang, N.; Fu, G.; Doble, R. Groundwater Recharge Prediction Using Linear Regression, Multi-Layer Perception Network, and Deep Learning. Water 2019, 11, 1879. [Google Scholar] [CrossRef] [Green Version]
- Kim, G.-B.; Hwang, C.-I.; Choi, M.-R. PCA-based multivariate LSTM model for predicting natural groundwater level variations in a time-series record affected by anthropogenic factors. Environ. Earth Sci 2021, 80, 657. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, Y.; Hu, H.; Li, H.; Ma, Y.; Khan, M.Y.A. Combined Wavelet Transform with Long Short-Term Memory Neural Network for Water Table Depth Prediction in Baoding City, North China Plain. Front. Environ. Sci. 2021, 9, 780434. [Google Scholar] [CrossRef]
- He, L.; Hou, M.; Chen, S.; Zhang, J.; Chen, J.; Qi, H. Construction of a spatio-temporal coupling model for groundwater level prediction: A case study of Changwu area, Yangtze River Delta region of China. Water Supply 2021, 21, 3790–3809. [Google Scholar] [CrossRef]
- Guo, F.; Yang, J.; Li, H.; Li, G.; Zhang, Z. A ConvLSTM Conjunction Model for Groundwater Level Forecasting in a Karst Aquifer Considering Connectivity Characteristics. Water 2021, 13, 2759. [Google Scholar] [CrossRef]
- Dey, S.; Dey, A.K.; Mall, R.K. Long Short-Term Memory Neural Network (LSTM-NN) for Aquifer Level Time Series Forecasting Using in-Situ Piezo-metric Observations. Water Resour Manag. 2021, 35, 3395–3410. [Google Scholar] [CrossRef]
- Ghasemlounia, R.; Gharehbaghi, A.; Ahmadi, F.; Saadatnejadgharahassanlou, H. Developing a novel framework for forecasting groundwater level fluctuations using Bi-directional Long Short-Term Memory (BiLSTM) deep neural network. Comput. Electron. Agric. 2021, 191, 106568. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Groundwater level forecasting with artificial neural networks: A comparison of long short-term memory (LSTM), convolutional neural networks (CNNs), and non-linear autoregressive networks with exogenous input (NARX). Hydrol. Earth Syst. Sci. 2021, 25, 1671–1687. [Google Scholar] [CrossRef]
- Ma, Y.; Montzka, C.; Bayat, B.; Kollet, S. Using Long Short-Term Memory networks to connect water table depth anomalies to precipitation anomalies over Europe. Hydrol. Earth Syst. Sci. 2021, 25, 3555–3575. [Google Scholar] [CrossRef]
- Müller, J.; Park, J.; Sahu, R.; Varadharajan, C.; Arora, B.; Faybishenko, B.; Agarwal, D. Surrogate optimization of deep neural networks for groundwater predictions. J Glob Optim 2021, 81, 203–231. [Google Scholar] [CrossRef]
- Solgi, R.; Loáiciga, H.A.; Kram, M. Long short-term memory neural network (LSTM-NN) for aquifer level time series forecasting using in-situ piezometric observations. J. Hydrol. 2021, 601, 126800. [Google Scholar] [CrossRef]
- Hakim, W.L.; Nur, A.S.; Rezaie, F.; Panahi, M.; Lee, C.-W.; Lee, S. Convolutional neural network and long short-term memory algorithms for groundwater potential mapping in Anseong, South Korea. J. Hydrol. Reg. Stud. 2022, 39, 100990. [Google Scholar] [CrossRef]
- Japan Meteorological Agency Japan Meteorological Agency Web Site. Available online: https://www.data.jma.go.jp/obd/stats/etrn/ (accessed on 8 March 2023).
- Kushiro-shitsugen | Ramsar Sites Information Service. Available online: https://rsis.ramsar.org/ris/205 (accessed on 8 March 2023).
- Nakayama, T. Factors controlling vegetation succession in Kushiro Mire. Ecol. Model. 2008, 215, 225–236. [Google Scholar] [CrossRef]
- Nakamura, F.; Sudo, T.; Kameyama, S.; Jitsu, M. Influences of channelization on discharge of suspended sediment and wetland vegetation in Kushiro Marsh, northern Japan. Geomorphology 1997, 18, 279–289. [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure, Transport and Tourism, H.Q.D. Ministry of Land, Infrastructure, Transport and Tourism Hydrologic Quality Database. Available online: http://www1.river.go.jp/ (accessed on 8 March 2023).
- Geospatial Information Authority of Japan Geospatial Information Authority of Japan. Available online: https://www.gsi.go.jp/ENGLISH/index.html (accessed on 8 March 2023).
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Japan Meteorological Agency, W.S. Japan Meteorological Agency Web Site. Available online: https://www.data.jma.go.jp/gmd/risk/obsdl/ (accessed on 8 March 2023).
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Informatik, F.; Bengio, Y.; Frasconi, P.; Schmidhuber, J. Gradient Flow in Recurrent Nets: The Difficulty of Learning Long-Term Dependencies. In A Field Guide to Dynamical Recurrent Neural Networks; IEEE Press: Piscataway, NJ, USA, 2003. [Google Scholar]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Yao, L.; Guan, Y. An Improved LSTM Structure for Natural Language Processing. In Proceedings of the 2018 IEEE International Conference of Safety Produce Informatization (IICSPI), Chongqing, China, 10–12 December 2018; pp. 565–569. [Google Scholar]
- Python. Available online: https://www.python.org/ (accessed on 8 March 2023).
- TensorFlow. Available online: https://www.tensorflow.org/ (accessed on 8 March 2023).
- scikit-learn. Available online: https://scikit-learn.org/ (accessed on 8 March 2023).
- Pandas. Available online: https://pandas.pydata.org/ (accessed on 8 March 2023).
- NumPy. Available online: https://numpy.org/ (accessed on 8 March 2023).
- Keras. Available online: https://keras.io/ (accessed on 8 March 2023).
- Rodriguez-Galiano, V.F.; Luque-Espinar, J.A.; Chica-Olmo, M.; Mendes, M.P. Feature selection approaches for predictive modelling of groundwater nitrate pollution: An evaluation of filters, embedded and wrapper methods. Sci. Total Environ. 2018, 624, 661–672. [Google Scholar] [CrossRef]
- Yang, P.; Liu, W.; Zhou, B.B.; Chawla, S.; Zomaya, A.Y. Ensemble-Based Wrapper Methods for Feature Selection and Class Imbalance Learning. In Proceedings of the Advances in Knowledge Discovery and Data Mining; Pei, J., Tseng, V.S., Cao, L., Motoda, H., Xu, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 544–555. [Google Scholar]
- Gunning, D. Explainable Artificial Intelligence (XAI). Def. Adv. Res. Proj. Agency Web 2017, 2, 1. [Google Scholar]
- Adak, A.; Pradhan, B.; Shukla, N.; Alamri, A. Unboxing Deep Learning Model of Food Delivery Service Reviews Using Explainable Artificial Intelligence (XAI) Technique. Foods 2022, 11, 2019. [Google Scholar] [CrossRef]
- Ahmadi, A.; Olyaei, M.; Heydari, Z.; Emami, M.; Zeynolabedin, A.; Ghomlaghi, A.; Daccache, A.; Fogg, G.E.; Sadegh, M. Groundwater Level Modeling with Machine Learning: A Systematic Review and Meta-Analysis. Water 2022, 14, 949. [Google Scholar] [CrossRef]
- Vidon, P.; Jacinthe, P.-A.; Liu, X.; Fisher, K.; Baker, M. Hydrobiogeochemical Controls on Riparian Nutrient and Greenhouse Gas Dynamics: 10 Years Post-Restoration. JAWRA J. Am. Water Resour. Assoc. 2014, 50, 639–652. [Google Scholar] [CrossRef]
- Henry, C.P.; Amoros, C.; Giuliani, Y. Restoration ecology of riverine wetlands: II. An example in a former channel of the Rhône River. Environ. Manag. 1995, 19, 903–913. [Google Scholar] [CrossRef]
- Erwin, K.L. Wetlands and global climate change: The role of wetland restoration in a changing world. Wetl. Ecol Manag. 2008, 17, 71. [Google Scholar] [CrossRef]
- Klimkowska, A.; Van Diggelen, R.; Grootjans, A.P.; Kotowski, W. Prospects for fen meadow restoration on severely degraded fens. Perspect. Plant Ecol. Evol. Syst. 2010, 12, 245–255. [Google Scholar] [CrossRef]
- Hedberg, P.; Kotowski, W.; Saetre, P.; Mälson, K.; Rydin, H.; Sundberg, S. Vegetation recovery after multiple-site experimental fen restorations. Biol. Conserv. 2012, 147, 60–67. [Google Scholar] [CrossRef]
- Moosavi, V.; Vafakhah, M.; Shirmohammadi, B.; Behnia, N. A Wavelet-ANFIS Hybrid Model for Groundwater Level Forecasting for Different Prediction Periods. Water Resour Manag. 2013, 27, 1301–1321. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, X.; Wang, W.; Lu, C.; Zhang, Y.; Qin, W.; Tick, G.R.; Liu, B.; Shu, L. Groundwater level modeling framework by combining the wavelet transform with a long short-term memory data-driven model. Sci. Total Environ. 2021, 783, 146948. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Mostafa, R.R.; Chen, Z.; Parmar, K.S.; Kisi, O.; Zounemat-Kermani, M. Water Temperature Prediction Using Improved Deep Learning Methods through Reptile Search Algorithm and Weighted Mean of Vectors Optimizer. J. Mar. Sci. Eng. 2023, 11, 259. [Google Scholar] [CrossRef]
- Mostafa, R.R.; Kisi, O.; Adnan, R.M.; Sadeghifar, T.; Kuriqi, A. Modeling Potential Evapotranspiration by Improved Machine Learning Methods Using Limited Climatic Data. Water 2023, 15, 486. [Google Scholar] [CrossRef]





| Region/Country | Models | Purpose | Best Model | Reference |
|---|---|---|---|---|
| Hetao Irrigation District in China | LSTM, FFNN | Model development | R2: 0.789–0.952 | [35] |
| Pohang Gibuk in Republic of Korea | LSTM, NARX-DNNs, GRU, ARX | Model comparison | LSTM and NARX-DNNs | [36] |
| Virginia in United States | LSTM, RNN | Model comparison | LSTM | [37] |
| Otway and Murray Basins in Australia | LSTM, LR, MLP | Model comparison | LSTM | [38] |
| Republic of Korea | LSTM with PCA | Model development | Optimal input data, window size | [39] |
| Hebei Province in China | LSTM with WT | Model development | NSE: 0.819 | [40] |
| Jiangsu Province in China | LSTM with KNN and WT | Model comparison | KNN-LSTM | [41] |
| Shandong Province in China | Convolutional LSTM, etc. | Model comparison | Convolutional LSTM | [42] |
| Varuna River basin in India | Bidirectional LSTM | Model development | Comparison of 5 model settings | [43] |
| Miandoab Plain in Iran | Bidirectional LSTMs | Model development | Double-Bidirect-ional LSTM | [44] |
| Central Europe/Rhine River | LSTM, CNNs, NARX | Model comparison | LSTM, CNNs for larger datasets. | [45] |
| Europe | LSTM | Model development | water table depth < 3 m | [46] |
| California in United States | LSTM, MLP, RNN, CNN | Model comparison | MLP | [47] |
| Texas in United States | LSTM-NN, simple NN | Model comparison | LSTM-NN | [48] |
| Anseongsi area in Republic of Korea | LSTM with CNN | Model development | AUC > 0.8 for all locations | [49] |
| Observation Point | RMSE before Restoration in 2009 (m) | RMSE after Restoration in 2017 (m) |
|---|---|---|
| St.1 | 0.082 | 0.134 |
| St.2 | 0.094 | 0.139 |
| St.3 | 0.162 | 0.116 |
| St.4 | 0.161 | 0.136 |
| (a) | ||||
| Counts | St.1 | St.2 | St.3 | St.4 |
| Mean GWL +0.25 m | 13.4 | 12.2 | 20.0 | 29.3 |
| Mean GWL +0.50 m | 0.667 | 0.667 | 7.11 | 11.0 |
| Mean GWL +0.75 m | 0 | 0.333 | 2.00 | 4.44 |
| Mean GWL +1.00 m~ | 0 | 0 | 4.00 | 6.11 |
| Total counts | 14.1 | 13.2 | 33 | 50.9 |
| (b) | ||||
| Counts | St.1 | St.2 | St.3 | St.4 |
| Mean GWL +0.25 m | 20.1 | 22.4 | 29.2 | 34.0 |
| Mean GWL +0.50 m | 3.11 | 3.11 | 8.89 | 11.3 |
| Mean GWL +0.75 m | 1.78 | 1.22 | 5.22 | 3.89 |
| Mean GWL +1.00 m~ | 0.444 | 0.111 | 2.78 | 3.33 |
| Total counts | 25.4 | 26.9 | 46.1 | 52.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamaguchi, T.; Miyamoto, H.; Oishi, T. Using Simple LSTM Models to Evaluate Effects of a River Restoration on Groundwater in Kushiro Wetland, Hokkaido, Japan. Water 2023, 15, 1115. https://doi.org/10.3390/w15061115
Yamaguchi T, Miyamoto H, Oishi T. Using Simple LSTM Models to Evaluate Effects of a River Restoration on Groundwater in Kushiro Wetland, Hokkaido, Japan. Water. 2023; 15(6):1115. https://doi.org/10.3390/w15061115
Chicago/Turabian StyleYamaguchi, Takumi, Hitoshi Miyamoto, and Tetsuya Oishi. 2023. "Using Simple LSTM Models to Evaluate Effects of a River Restoration on Groundwater in Kushiro Wetland, Hokkaido, Japan" Water 15, no. 6: 1115. https://doi.org/10.3390/w15061115
APA StyleYamaguchi, T., Miyamoto, H., & Oishi, T. (2023). Using Simple LSTM Models to Evaluate Effects of a River Restoration on Groundwater in Kushiro Wetland, Hokkaido, Japan. Water, 15(6), 1115. https://doi.org/10.3390/w15061115








