Characteristics of Large-Scale Coherent Structures on Irregularly Arranged Rough-Bed Open-Channel Flows
Abstract
:1. Introduction
2. Methodology
2.1. Facilities and Experiments
2.2. Power Spectrum
3. Results and Discussion
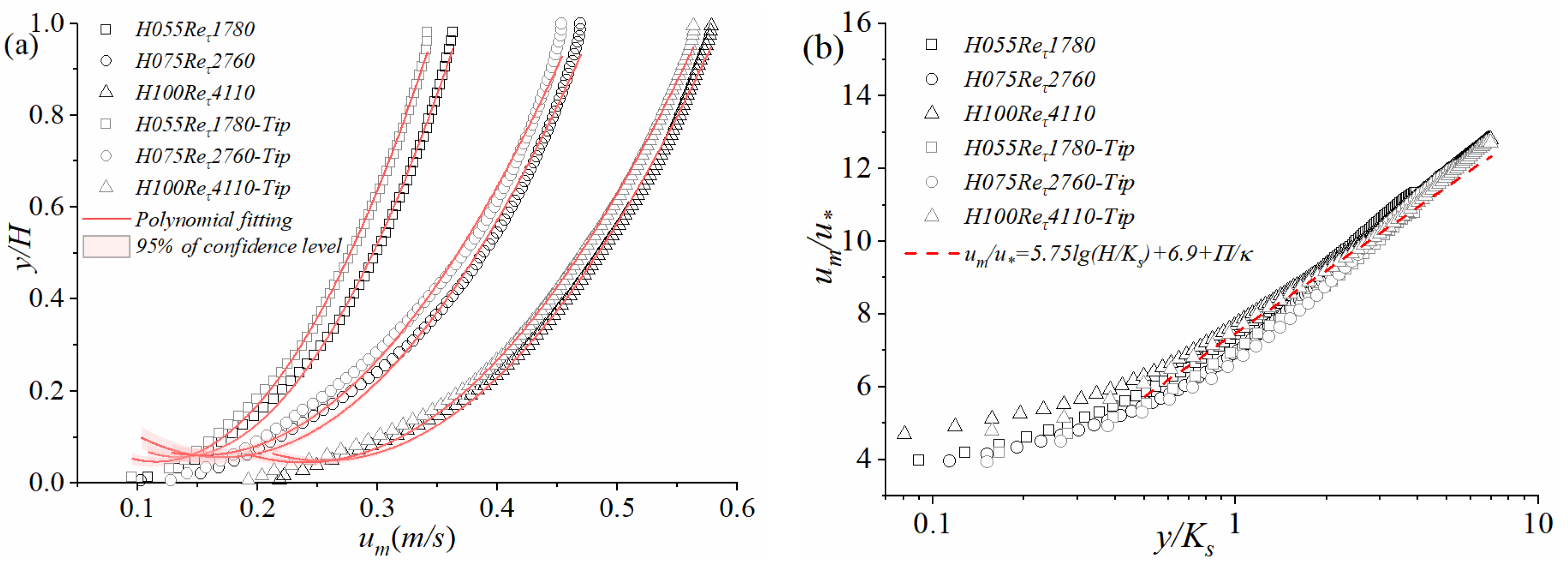
3.1. Determination of the Theoretical Zero Point of Irregularly Arranged Rough-Bed
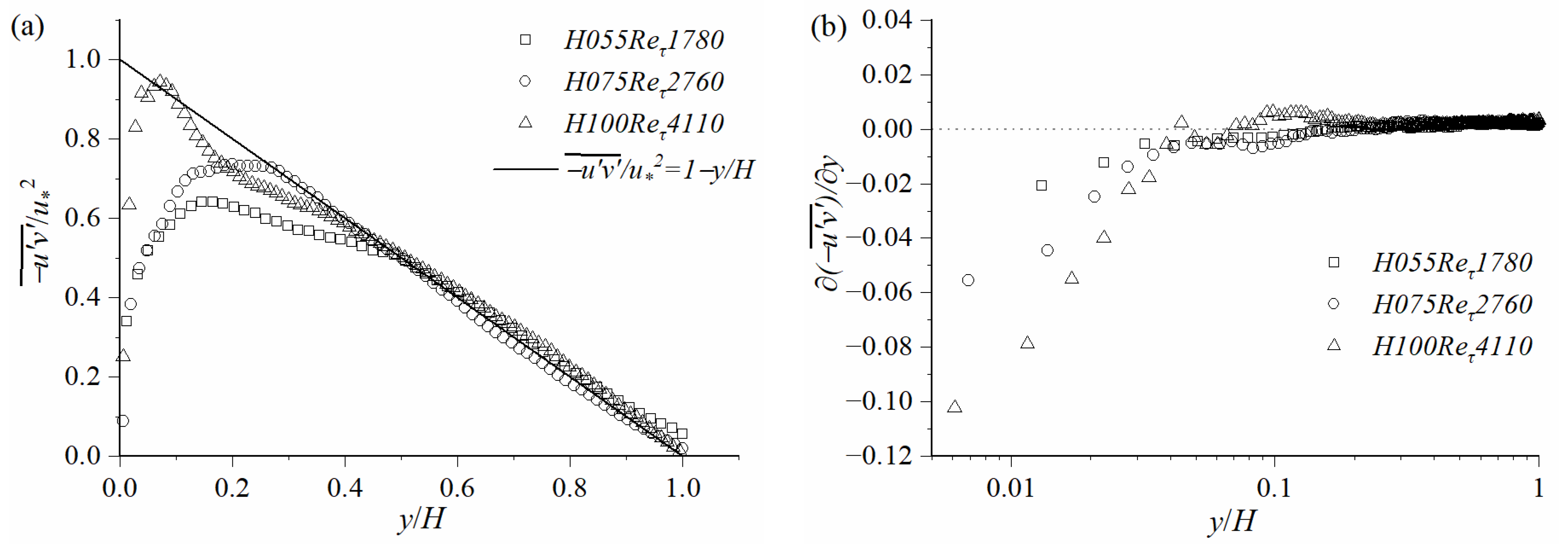
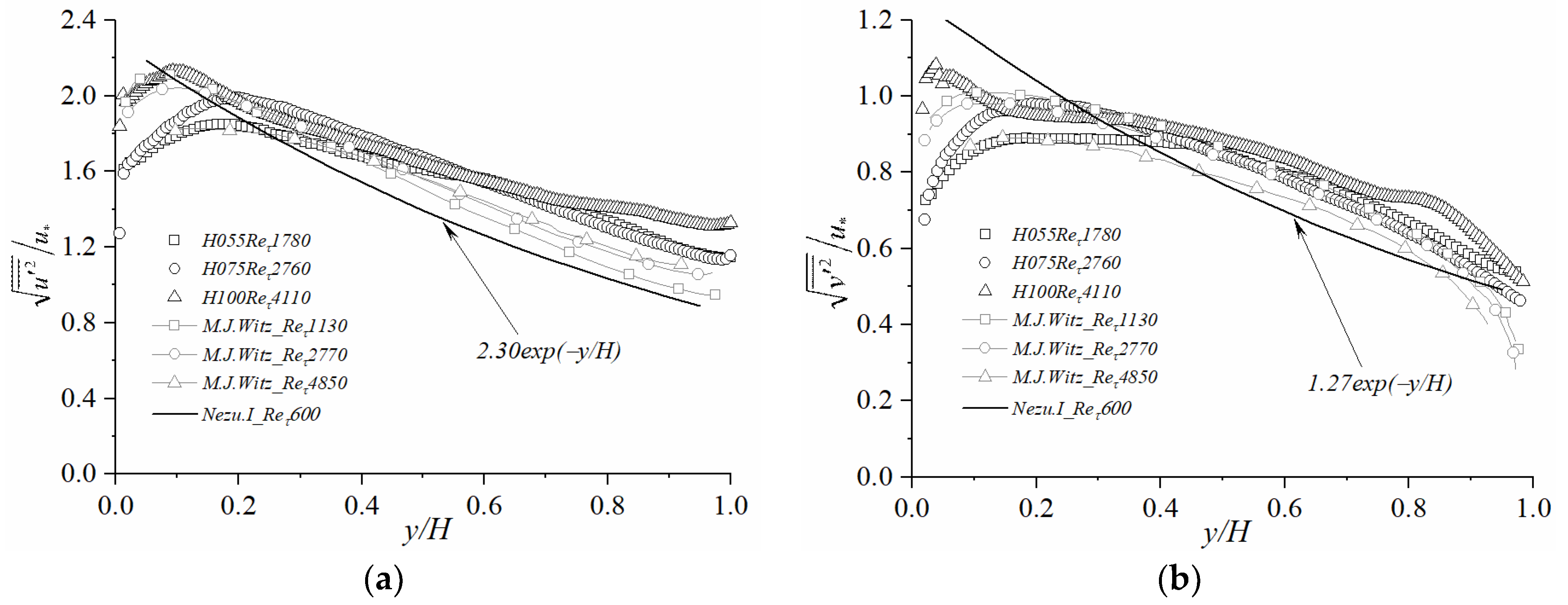
3.2. Profiles of Typical Statistics
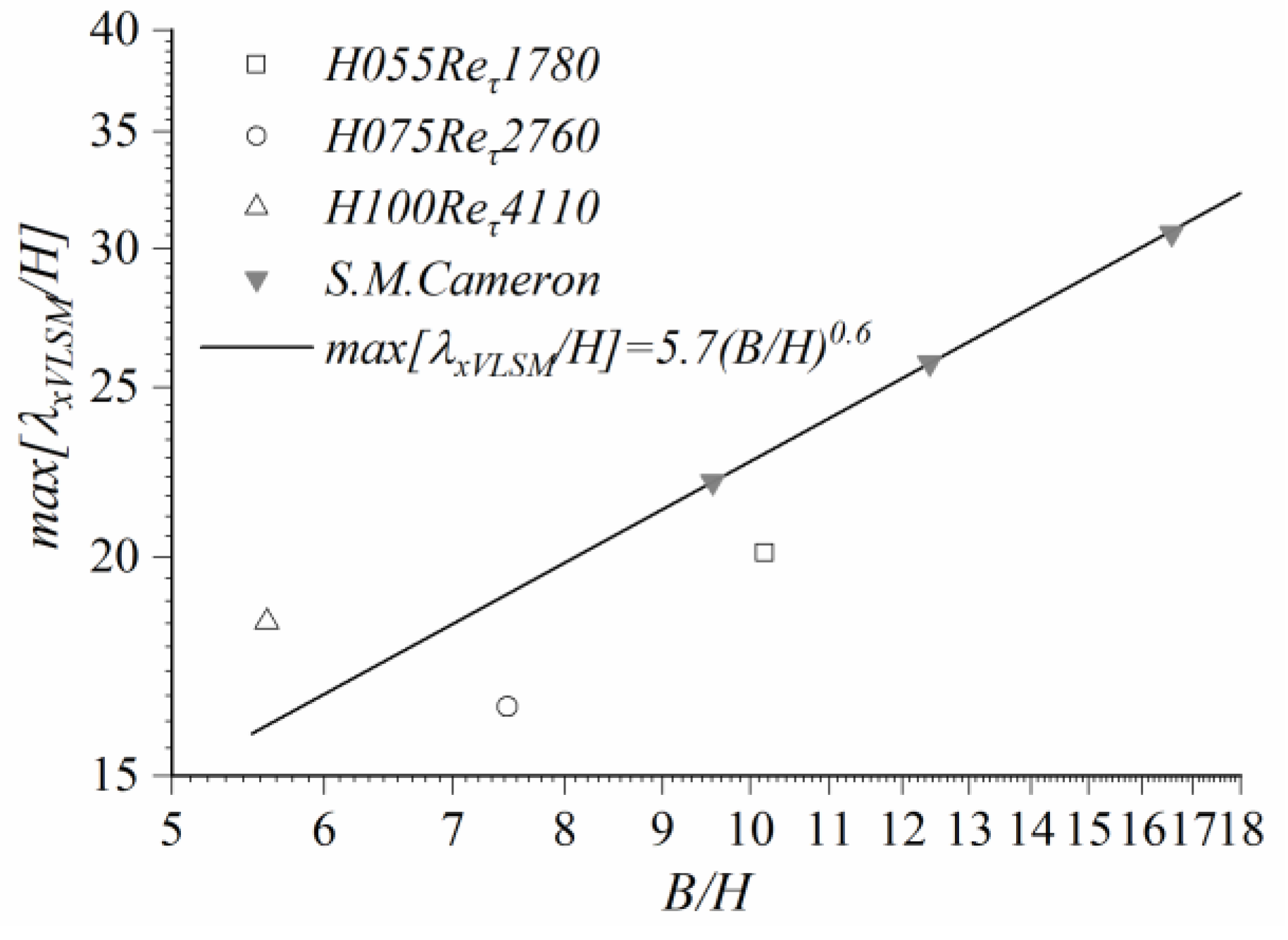
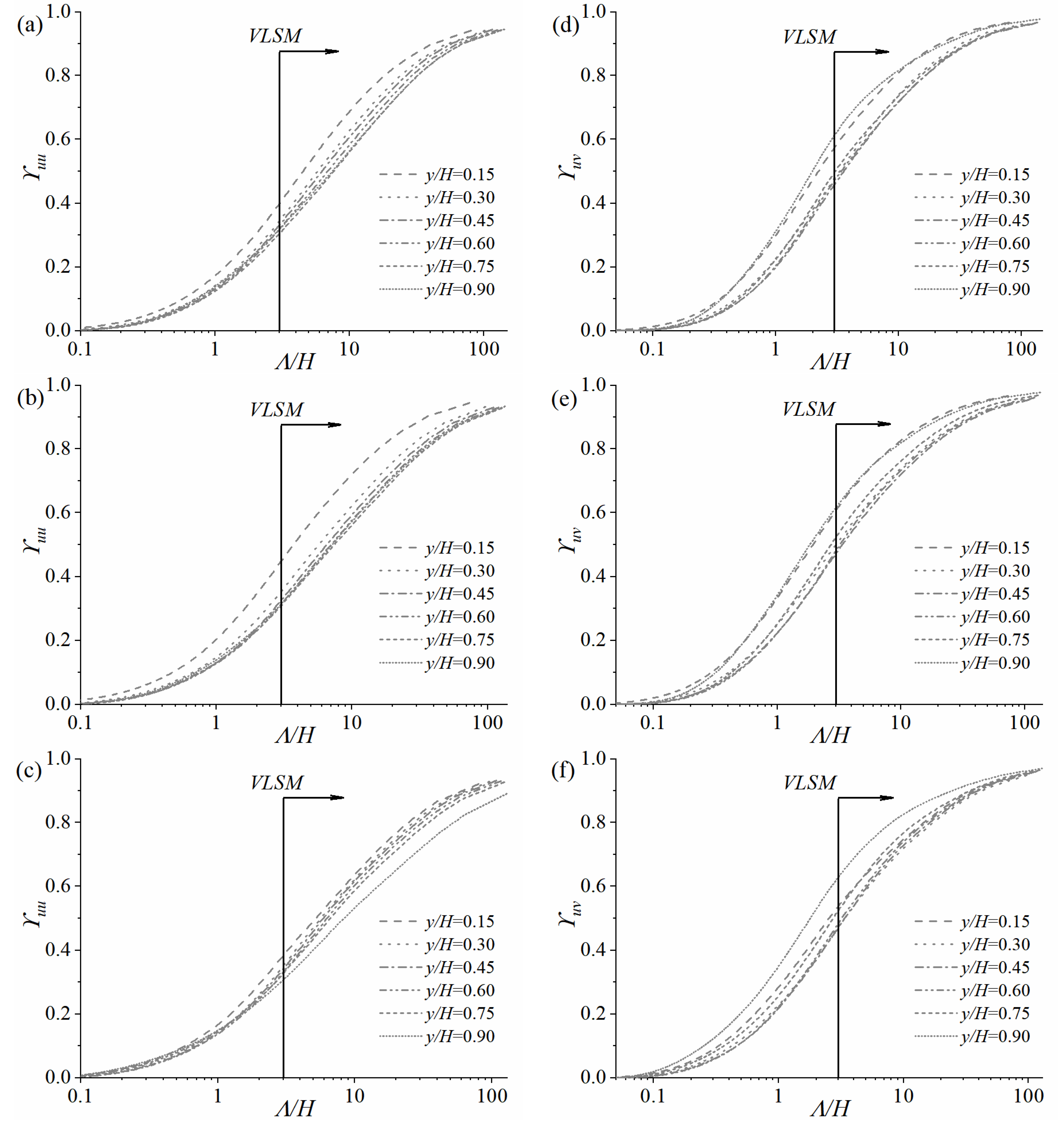
3.3. Presence of LSMs and VLSMs and Their Scales
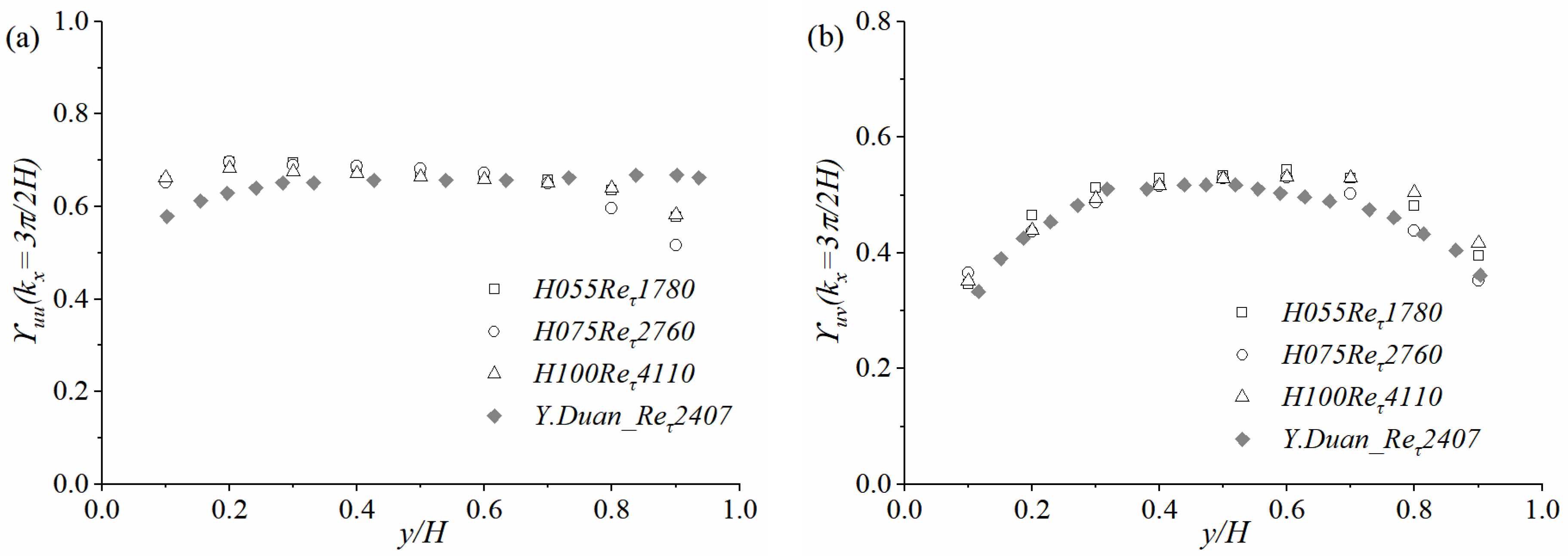
3.4. Strength of VLSMs
4. Conclusions
- (1)
- The difference in the measurement locations (pebble gap and top) had a considerably small influence on the standardized time average velocity distribution. The typical statistics of the irregularly arranged rough-bed OCF are consistent with previous classical research. The friction Reynolds number and roughness coefficient have a certain modulation effect on the radial and vertical velocity pulsations.
- (2)
- The double peak phenomenon of LSMs and VLSMs exists in the present irregularly arranged rough-bed OCF, which is similar to the results of the smooth-bed OCF and the regular rough-bed OCF. Under the same aspect ratio ranges, the wavelengths of VLSMs on the irregularly arranged rough-bed OCF appear minimal among different bed scenarios (i.e., smooth-bed OCF, regular rough-bed OCF, and irregularly arranged rough-bed OCF), and the result of the smooth-bed OCF is the opposite.
- (3)
- The contributions of VLSMs to the turbulent kinetic energy and the Reynolds shear stress in the irregularly arranged rough-bed OCF are greater than those in the smooth-bed OCF. More than 60% of the turbulent kinetic energy and 40% of the Reynolds shear stress originate from VLSMs in the present irregularly arranged rough-bed OCF. Similar to those in the smooth-bed OCF, VLSMs in the present, irregularly arranged rough-bed OCF also play major roles in contributing to the turbulent energy and Reynolds shear stress.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, K.C.; Adrian, R.J. Very large-scale motion in the outer layer. Phys. Fluids 1999, 11, 417–422. [Google Scholar] [CrossRef]
- Brandt, L.; Coletti, F. Particle-laden turbulence: Progress and perspectives. Annu. Rev. Fluid Mech. 2022, 54, 159–189. [Google Scholar] [CrossRef]
- Discetti, S.; Bellani, G.; Örlü, R.; Serpieri, J.; Sanmiguel Vila, C.; Raiola, M.; Zheng, X.; Mascotelli, L.; Talamelli, A.; Ianiro, A. Characterization of very-large-scale motions in high-Re pipe flows. Exp. Therm. Fluid Sci. 2019, 104, 1–8. [Google Scholar] [CrossRef]
- Avila, M.; Barkley, D.; Hof, B. Transition to turbulence in pipe flow. Annu. Rev. Fluid Mech. 2023, 55, 575–602. [Google Scholar] [CrossRef]
- Lee, J.H.; Sung, H.J.; Adrian, R.J. Space–time formation of very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 2019, 881, 1010–1047. [Google Scholar] [CrossRef]
- Bon, T.; Meyers, J. Stable channel flow with spanwise heterogeneous surface temperature. J. Fluid Mech. 2022, 933, A57. [Google Scholar] [CrossRef]
- Camporeale, C.; Cannamela, F.; Canuto, C.; Manes, C. Stability analysis of open-channel flows with secondary currents. J. Fluid Mech. 2021, 927, A32. [Google Scholar] [CrossRef]
- Hall, P. An instability mechanism for channel flows in the presence of wall roughness. J. Fluid Mech. 2020, 899, R2. [Google Scholar] [CrossRef]
- Wu, X.; Wallace, J.M.; Hickey, J.-P. Boundary layer turbulence and freestream turbulence interface, turbulent spot and freestream turbulence interface, laminar boundary layer and freestream turbulence interface. Phys. Fluids 2019, 31, 045104. [Google Scholar] [CrossRef]
- Li, D.; Luo, K.; Wang, Z.; Xiao, W.; Fan, J. Drag enhancement and turbulence attenuation by small solid particles in an unstably stratified turbulent boundary layer. Phys. Fluids 2019, 31, 063303. [Google Scholar]
- Barros, J.M.; Christensen, K.T. Characteristics of large-scale and superstructure motions in a turbulent boundary layer overlying complex roughness. J. Turbul. 2019, 20, 147–173. [Google Scholar] [CrossRef]
- Ren, H.; Laima, S.; Li, H. Numerical investigation of very-large-scale motions in a turbulent boundary layer for different roughness. Energies 2020, 13, 659. [Google Scholar] [CrossRef] [Green Version]
- Bailey, S.C.C.; Canter, C.A.; Sama, M.P.; Houston, A.L.; Smith, S.W. Unmanned aerial vehicles reveal the impact of a total solar eclipse on the atmospheric surface layer. Proc. R. Soc. A Math. Phys. Eng. Sci. 2019, 475, 20190212. [Google Scholar] [CrossRef] [Green Version]
- Efthimiou, G.C.; Kumar, P.; Giannissi, S.G.; Feiz, A.A.; Andronopoulos, S. Prediction of the wind speed probabilities in the atmospheric surface layer. Renew. Energy 2019, 132, 921–930. [Google Scholar] [CrossRef]
- Gemmell, F. Investigating neutral and stable atmospheric surface layers using computational fluid dynamics. Atmosphere 2022, 13, 221. [Google Scholar] [CrossRef]
- Alcántara-Ávila, F.; Hoyas, S. Direct numerical simulation of thermal channel flow for medium–high Prandtl numbers up to Reτ = 2000. Int. J. Heat Mass Transf. 2021, 176, 121412. [Google Scholar] [CrossRef]
- Fytanidis, D.K.; García, M.H.; Fischer, P.F. Mean flow structure and velocity–bed shear stress maxima phase difference in smooth wall, transitionally turbulent oscillatory boundary layers: Direct numerical simulations. J. Fluid Mech. 2021, 928, A33. [Google Scholar] [CrossRef]
- Zampiron, A.; Cameron, S.; Nikora, V. Momentum and energy transfer in open-channel flow over streamwise ridges. J. Fluid Mech. 2021, 915, A42. [Google Scholar] [CrossRef]
- Deng, B.-Q.; Yang, Z.; Xuan, A.; Shen, L. Localizing effect of Langmuir circulations on small-scale turbulence in shallow water. J. Fluid Mech. 2020, 893, A6. [Google Scholar] [CrossRef]
- Candelier, F.; Mehlig, B.; Magnaudet, J. Time-dependent lift and drag on a rigid body in a viscous steady linear flow. J. Fluid Mech. 2019, 864, 554–595. [Google Scholar] [CrossRef] [Green Version]
- Cameron, S.M.; Nikora, V.I.; Stewart, M.T. Very-large-scale motions in rough-bed open-channel flow. J. Fluid Mech. 2017, 814, 416–429. [Google Scholar] [CrossRef] [Green Version]
- Yao, J.; Chen, X.; Hussain, F. Direct numerical simulation of turbulent open channel flows at moderately high Reynolds numbers. J. Fluid Mech. 2022, 953, A19. [Google Scholar] [CrossRef]
- Duan, Y.; Chen, Q.; Li, D.; Zhong, Q. Contributions of very large-scale motions to turbulence statistics in open channel flows. J. Fluid Mech. 2020, 892, A3. [Google Scholar] [CrossRef]
- Duan, Y.; Zhong, Q.; Wang, G.; Zhang, P.; Li, D. Contributions of different scales of turbulent motions to the mean wall-shear stress in open channel flows at low-to-moderate Reynolds numbers. J. Fluid Mech. 2021, 918, A40. [Google Scholar] [CrossRef]
- Zhang, P.; Duan, Y.; Li, D.; Hu, J.; Li, W.; Yang, S. Turbulence statistics and very-large-scale motions in decelerating open-channel flow. Phys. Fluids 2019, 31, 125106. [Google Scholar]
- Peruzzi, C.; Poggi, D.; Ridolfi, L.; Manes, C. On the scaling of large-scale structures in smooth-bed turbulent open-channel flows. J. Fluid Mech. 2020, 889, A1. [Google Scholar] [CrossRef]
- Wang, G.; Richter, D.H. Two mechanisms of modulation of very-large-scale motions by inertial particles in open channel flow. J. Fluid Mech. 2019, 868, 538–559. [Google Scholar] [CrossRef] [Green Version]
- Ferraro, D.; Coscarella, F.; Gaudio, R. Scales of turbulence in open-channel flows with low relative submergence. Phys. Fluids 2019, 31, 125114. [Google Scholar] [CrossRef]
- Cameron, S.M.; Nikora, V.I.; Witz, M.J. Entrainment of sediment particles by very large-scale motions. J. Fluid Mech. 2020, 888, A7. [Google Scholar] [CrossRef]
- Diplas, P.; Dancey, C.L.; Celik, A.O.; Valyrakis, M.; Greer, K.; Akar, T. The Role of Impulse on the Initiation of Particle Movement Under Turbulent Flow Conditions. Science 2008, 322, 717–720. [Google Scholar] [CrossRef] [Green Version]
- Valyrakis, M.; Diplas, P.; Dancey, C.L. Entrainment of coarse particles in turbulent flows: An energy approach. J. Geophys. Res. Earth Surf. 2013, 118, 42–53. [Google Scholar] [CrossRef] [Green Version]
- Proust, S.; Berni, C.; Nikora, V.I. Shallow mixing layers over hydraulically smooth bottom in a tilted open channel. J. Fluid Mech. 2022, 951, A17. [Google Scholar] [CrossRef]
- Richard, G.L.; Couderc, F.; Vila, J.P. Reconstruction of the 3-D fields with a depth-averaged model for open-channel flows in the smooth turbulent case. J. Fluid Mech. 2023, 954, A24. [Google Scholar] [CrossRef]
- Ganju, S.; Bailey, S.C.C.; Brehm, C. Amplitude and wavelength scaling of sinusoidal roughness effects in turbulent channel flow at fixed Reτ = 720. J. Fluid Mech. 2022, 937, A22. [Google Scholar] [CrossRef]
- Jelly, T.O.; Ramani, A.; Nugroho, B.; Hutchins, N.; Busse, A. Impact of spanwise effective slope upon rough-wall turbulent channel flow. J. Fluid Mech. 2022, 951, A1. [Google Scholar] [CrossRef]
- Kovalenko, O.; Golyanik, V.; Malik, J.; Elhayek, A.; Stricker, D. Structure from articulated motion: Accurate and stable monocular 3D reconstruction without training data. Sensors 2019, 19, 4603. [Google Scholar] [CrossRef] [Green Version]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Nikora, V.I.; Goring, D.G.; Biggs, B.J.F. On gravel-bed roughness characterization. Water Resour. Res. 1998, 34, 517–527. [Google Scholar] [CrossRef]
- Wu, Z.; Singh, A.; Foufoula-Georgiou, E.; Guala, M.; Fu, X.; Wang, G. A velocity-variation-based formulation for bedload particle hops in rivers. J. Fluid Mech. 2021, 912, A33. [Google Scholar] [CrossRef]
- Nezu, I.; Rodi, W. Open-channel flow measurements with a laser Doppler anemometer. J. Hydraul. Eng. 1986, 112, 335–355. [Google Scholar] [CrossRef]
- Witz, M.J.; Cameron, S.; Nikora, V. Bed particle dynamics at entrainment. J. Hydraul. Res. 2019, 57, 464–474. [Google Scholar] [CrossRef]
- Monty, J.P.; Hutchins, N.; Ng, H.C.H.; Marusic, I.; Chong, M.S. A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 2009, 632, 431–442. [Google Scholar] [CrossRef]




| Case | H (m) | B/H | u (m2/s) | Um (m/s) | u* (m/s) | Fr | Re | Ret | ks+ |
|---|---|---|---|---|---|---|---|---|---|
| H055Ret1780 | 0.055 | 10.2 | 1.03 × 10−6 | 0.428 | 0.034 | 0.583 | 22,757 | 1785 | 442 |
| H075Ret2760 | 0.075 | 7.5 | 1.03 × 10−6 | 0.506 | 0.038 | 0.590 | 36,714 | 2762 | 494 |
| H100Ret4110 | 0.100 | 5.6 | 1.03 × 10−6 | 0.586 | 0.042 | 0.592 | 56,671 | 4110 | 546 |
| Case | Image Size (Pixels) | Resolution (Pixel/mm) | Fs | T (s) | Number of Images | Δx+ | TUm/h | ΔTUm/h | ΔT+ | y* (mm) |
|---|---|---|---|---|---|---|---|---|---|---|
| H055Ret1780 | 1024 × 128 | 0.062 | 800 | 1879.25 | 1503,400 | 4.22 | 14,616 | 0.0097 | 1.24 | 0.0323 |
| H075Ret2760 | 1496 × 128 | 0.062 | 800 | 1544.51 | 1235,610 | 7.52 | 10,422 | 0.0084 | 1.81 | 0.0267 |
| H100Ret4110 | 1600 × 128 | 0.062 | 800 | 1684.99 | 1347,990 | 11.99 | 9872 | 0.0073 | 2.46 | 0.0229 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, P.; Yang, S.; Hu, C.; Jin, J.; Zhang, R. Characteristics of Large-Scale Coherent Structures on Irregularly Arranged Rough-Bed Open-Channel Flows. Water 2023, 15, 1105. https://doi.org/10.3390/w15061105
Wang Y, Zhang P, Yang S, Hu C, Jin J, Zhang R. Characteristics of Large-Scale Coherent Structures on Irregularly Arranged Rough-Bed Open-Channel Flows. Water. 2023; 15(6):1105. https://doi.org/10.3390/w15061105
Chicago/Turabian StyleWang, Yongqiang, Peng Zhang, Shengfa Yang, Chunhong Hu, Jianling Jin, and Rangang Zhang. 2023. "Characteristics of Large-Scale Coherent Structures on Irregularly Arranged Rough-Bed Open-Channel Flows" Water 15, no. 6: 1105. https://doi.org/10.3390/w15061105
APA StyleWang, Y., Zhang, P., Yang, S., Hu, C., Jin, J., & Zhang, R. (2023). Characteristics of Large-Scale Coherent Structures on Irregularly Arranged Rough-Bed Open-Channel Flows. Water, 15(6), 1105. https://doi.org/10.3390/w15061105







