Quantification of Groundwater Vertical Flow from Temperature Profiles: Application to Agua Amarga Coastal Aquifer (SE Spain) Submitted to Artificial Recharge
Abstract
:1. Introduction
2. Study Area
3. Methodology
3.1. Experimental Data Introduction and Processing
3.2. The Inverse Problem Protocol
4. Numerical Model
5. Inverse Problem Applied to Vertical Flow Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| capacitor | |
| volumetric heat capacity of the rock–fluid matrix (J m−3 k−1) | |
| volumetric heat capacity of water (J m−3 k−1) | |
| electrical conductivity (mS/cm) | |
| gravity (m s−2) | |
| current generator relative to the heating circuit, placed in the lower half of the cell, parallel to the lower resistance | |
| current generator relative to the heating circuit, placed in the upper half of the cell, parallel to the upper resistance | |
| vertical depth of the aquifer (m) | |
| JC | current intensity flowing through a capacitor (A) |
| permeability (m2) | |
| heat conductivity of the rock–fluid matrix (J/(s m °C)) | |
| hydraulic conductivity (m s−1) | |
| Mancomunidad de los Canales del Taibilla | |
| resistor placed in the lower half of the cell, relative to heat flow | |
| resistor placed in the upper half of the cell, relative to heat flow | |
| temperature (°C) | |
| temperature at depth z (°C) | |
| temperature simulated at depth z (°C) | |
| temperature at the bottom of the domain (°C) | |
| temperature–depth profile time series | |
| TI | thermal inertia |
| initial temperature (°C) | |
| mean surface soil temperature (°C) | |
| time (s) | |
| voltage (V) | |
| advective component of velocity (m s−1) | |
| velocity caused by buoyancy effects (m s−1) | |
| vertical water flow velocity (m s−1) | |
| vertical upward water flow velocity component (m s−1) | |
| vertical downward water flow velocity component (m s−1) | |
| inverse problem protocol velocity “i” | |
| inverse problem protocol initial velocity | |
| vertical spatial coordinate (m) | |
| thermal diffusivity (m2 s−1) | |
| thermal expansion coefficient of water (°C−1) | |
| gradient operator | |
| T | amplitude due to sinusoidal boundary condition at the surface (°C) |
| temperature gradient for each depth interval (°C) | |
| amplitude of the temperature variation at (°C) | |
| groundwater velocity increase (ms−1) | |
| water viscosity (kg m−1 s−1) | |
| wet bulk density of the rock–fluid matrix (kg m−3) | |
| water density (kg m−3) | |
| period of the sinusoidal thermal wave (s) | |
| mathematical function |
References
- Lapham, W.W. Use of Temperature Profiles Beneath Streams to Determine Rates of Vertical Ground-Water Flow and Vertical Hydraulic Conductivity; Paper 2337; U.S. Geological Survey Water-Supply: Reston, VA, USA, 1989.
- Reiter, M. Using precision temperature logs to estimate horizontal and vertical groundwater flow components. Water Resour. Res. 2001, 37, 663–674. [Google Scholar] [CrossRef]
- Ferguson, G.; Woodbury, A.D. The effects of climatic variability on estimates of recharge from temperature profiles. Groundwater 2008, 43, 837–842. [Google Scholar] [CrossRef]
- Duque, C.; Calvache, M.L.; Engesgaard, P. Investigating river–aquifer relations using water temperature in an anthropized environment (Motril-Salobreña aquifer). J. Hydrol. 2010, 381, 121–133. [Google Scholar] [CrossRef]
- Tirado-Conde, J.; Engesgaard, P.; Karan, S.; Müller, S.; Duque, C. Evaluation of temperature profiling and seepage meter methods for quantifying submarine groundwater discharge to coastal lagoons: Impacts of saltwater intrusion and the associated thermal regime. Water 2019, 11, 1648. [Google Scholar] [CrossRef] [Green Version]
- Blanco-Coronas, A.M.; Calvache, M.L.; López-Chicano, M.; Martín-Montañés, C.; Jiménez-Sánchez, J.; Duque, C. Salinity and Temperature Variations near the Freshwater-Saltwater Interface in Coastal Aquifers Induced by Ocean Tides and Changes in Recharge. Water 2022, 14, 2807. [Google Scholar] [CrossRef]
- Fahs, M.; Graf, T.; Tran, T.V.; Ataie-Ashtiani, B.; Simmons, C.T.; Younes, A. Study of the effect of thermal dispersion on internal natural convection in porous media using Fourier series. Transp. Porous Media 2020, 131, 537–568. [Google Scholar] [CrossRef]
- Bejan, A. Convection Heat Transfer, 4th ed.; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Suzuki, S. Percolation measurements based on heat flow through soil with special reference to paddy fields. J. Geophys. Res. 1960, 65, 2883–2885. [Google Scholar] [CrossRef]
- Bredehoeft, J.D.; Papadopulos, I.S. Rates of vertical groundwater movement estimated from the Earth’s thermal profile. Water Resour. Res. 1965, 1, 325–328. [Google Scholar] [CrossRef]
- Cartwright, K. Tracing shallow groundwater systems by soil temperatures. Water Resour. Res. 1974, 10, 847–855. [Google Scholar] [CrossRef]
- Taniguchi, M.; Sharma, M.L. Determination of groundwater recharge using the change in soil temperature. J. Hydrol. 1993, 148, 219–229. [Google Scholar] [CrossRef]
- Tabbagh, A.; Bendjoudi, H.; Benderitter, Y. Determination of recharge in unsaturated soils using temperature monitoring. Water Resour. Res. 1999, 35, 2439–2446. [Google Scholar] [CrossRef]
- Kulongoski, J.T.; Izbicki, J.A. Simulation of fluid, heat transport to estimate desert stream infiltration. Groundwater 2008, 46, 462–474. [Google Scholar] [CrossRef] [PubMed]
- Silliman, S.E.; Booth, D.F. Analysis of time-series measurements of sediment temperature for identification of gaining vs. losing portions of Juday Creek, Indiana. J. Hydrol. 1993, 146, 131–148. [Google Scholar] [CrossRef]
- Malcolm, I.A.; Soulsby, C.; Youngson, A.F.; Hannah, D.; McLaren, I.S.; Thorne, A. Influence of flow extremes on the hyporheic zone of salmon spawning streams, Water Extremes and Water Stress: Science, Policy and Practice. In Proceedings of the British Hydrological Society 8th National Symposium, Birmingham, UK, 8–11 September 2002. [Google Scholar]
- Calvache, M.L.; Duque, C.; Fontalva, J.M.; Crespo, F. Processes affecting groundwater temperature patterns in a coastal aquifer. Int. J. Environ. Sci. Technol. 2011, 8, 223–236. [Google Scholar] [CrossRef] [Green Version]
- Cartwright, K. Redistribution of geothermal heat by a shallow aquifer. Geol. Soc. Am. Bull. 1971, 82, 3197–3200. [Google Scholar] [CrossRef]
- Birman, J.H. Geothermal exploration for ground water. Geol. Soc. Am. Bull. 1969, 80, 617–630. [Google Scholar] [CrossRef]
- Constantz, J. Heat as a tracer to determine streambed water exchanges. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Duque, C.; Müller, S.; Sebok, E.; Haider, K.; Engesgaard, P. Estimating groundwater discharge to surface waters using heat as a tracer in low flux environments: The role of thermal conductivity. Hydrol. Process. 2016, 30, 383–395. [Google Scholar] [CrossRef]
- Woodbury, A.D.; Smith, L. On the thermal effects of three-dimensional groundwater flow. J. Geophys. Res. Solid Earth 1985, 90, 759–767. [Google Scholar] [CrossRef]
- Lautz, L.K. Observing temporal patterns of vertical flux through streambed sediments using time-series analysis of temperature records. J. Hydrol. 2012, 464, 199–215. [Google Scholar] [CrossRef]
- Alhama Manteca, I.; Alhama, F.; Rodríguez-Estrella, T. Chemical and physical parameters as trace markers of anthropogenic-induced salinity in the Agua Amarga coastal aquifer (southern Spain). Hydrogeol. J. 2012, 20, 1315–1329. [Google Scholar] [CrossRef]
- Alhama, I.; García-Ros, G.; González-Alcaraz, M.N.; Álvarez-Rogel, J. Long-term artificial seawater irrigation as a sustainable environmental management strategy for abandoned solar salt works: The case study of Agua Amarga salt marsh (SE Spain). CATENA 2022, 217, 106429. [Google Scholar] [CrossRef]
- Box Amorós, M. Las Zonas Húmedas de la Provincia de Alicante y los Procesos de Intervención Antrópica. Ph.D. Thesis, Universitat d’Alacant-Universidad de Alicante, Alicante, Spain, 1985. [Google Scholar]
- González-Alcaraz, M.N.; Aránega, B.; Tercero, M.C.; Conesa, H.M.; Álvarez-Rogel, J. Irrigation with seawater as a strategy for the environmental management of abandoned solar saltworks: A case-study in SE Spain based on soil–vegetation relationships. Ecol. Eng. 2014, 71, 677–689. [Google Scholar] [CrossRef]
- Rodríguez-Estrella, T.; Pulido-Bosch, A. Methodologies for abstraction from coastal aquifers for supplying desalination plants in the south-east of Spain. Desalination 2009, 249, 1088–1098. [Google Scholar] [CrossRef]
- Alhama, I. Environmental and hydrogeological relations between the Mediterranean Sea and the Agua Amarga salt marsh and aquifer (Alicante province): Effect of desalination plants and corrective measures. In Effect of Desalination Plants and Corrective Measures; UPCT: Cartagena, Spain, 2011. [Google Scholar]
- Navarro, R.; Sanchez Lizaso, J.L. Mitigation cost of desalination intake impact on coastal wetlands. Desalin. Water Treat 2021, 224, 136–143. [Google Scholar] [CrossRef]
- Manteca, I.A.; Estrella, T.R.; Alhama, F. Hydric restoration of the Agua Amarga Salt Marsh (SE Spain) affected by abstraction from the underlying coastal aquifer. Water Resour. Manag. 2012, 26, 1763–1777. [Google Scholar] [CrossRef]
- Alhama Manteca, I. Simulation and consequences of successive anthropogenic activity in the Agua Amarga coastal aquifer (southeast Spain). Hydrol. Sci. J. 2013, 58, 1072–1087. [Google Scholar] [CrossRef] [Green Version]
- Tutiempo.net. Available online: https://www.tutiempo.net/clima/2013/ws-83600.html (accessed on 26 December 2022).
- Stallman, R.W. Computation of ground-water velocity from temperature data. USGS Water Supply Pap. 1963, 1544, 36–46. [Google Scholar]
- Bedekar, V.; Morway, E.D.; Langevin, C.D.; Tonkin, M.J. MT3D-USGS Version 1: A US Geological Survey Release of MT3DMS Updated with New and Expanded Transport Capabilities for Use With MODFLOW (No. 6-A53); US Geological Survey: Reston, VA, USA, 2016.
- Beegum, S.; Vanderborght, J.; Šimůnek, J.; Herbst, M.; Sudheer, K.P.; Nambi, I.M. Investigating atrazine concentrations in the Zwischenscholle aquifer using MODFLOW with the HYDRUS-1D package and MT3DMS. Water 2020, 12, 1019. [Google Scholar] [CrossRef] [Green Version]
- Healy, R.W.; Ronan, A.D. Documentation of computer program VS2DH for simulation of energy transport in variably saturated porous media—Modification of the US Geological Survey’s computer program VS2DT. Water-Resour. Investig. Rep. 1996, 96, 4230. [Google Scholar]
- Owen, S.J.; Jones, N.L.; Holland, J.P. A comprehensive modeling environment for the simulation of groundwater flow and transport. Eng. Comput. 1996, 12, 235–242. [Google Scholar] [CrossRef]
- Aghlmand, R.; Abbasi, A. Application of MODFLOW with boundary conditions analyses based on limited available observations: A case study of Birjand plain in East Iran. Water 2019, 11, 1904. [Google Scholar] [CrossRef] [Green Version]
- Horno, J. Network Simulation Method; Research Signpost: Trivandrum, India, 2002. [Google Scholar]
- Jiménez-Valera, J.A.; Alhama, F. Dimensionless Characterization to Estimate Horizontal Groundwater Velocity from Temperature–Depth Profiles in Aquifers. Mathematics 2022, 10, 2717. [Google Scholar] [CrossRef]
- Cánovas, M.; Alhama, I.; García, G.; Trigueros, E.; Alhama, F. Numerical simulation of density-driven flow and heat transport processes in porous media using the network method. Energies 2017, 10, 1359. [Google Scholar] [CrossRef] [Green Version]
- Cánovas, M.; Alhama, I.; Trigueros, E.; Alhama, F. A review of classical dimensionless numbers for the Yusa problem based on discriminated non-dimensionalization of the governing equations. Hydrol. Process. 2016, 30, 4101–4112. [Google Scholar] [CrossRef]
- Manteca, I.A.; Alcaraz, M.; Trigueros, E.; Alhama, F. Dimensionless characterization of salt intrusion benchmark scenarios in anisotropic media. Appl. Math. Comput. 2014, 247, 1173–1182. [Google Scholar] [CrossRef]
- Ngspice. Open Source Mixed Mode, Mixed Level Circuit Simulator (Based on Berkeley’s Spice3f5). 2016. Available online: http://ngspice.sourceforge.net/ (accessed on 1 December 2022).
- PSPICE. Version 6.0: Microsim Corporation. 20 Fairbanks, Irvine, California 92718. 1994. Available online: https://www.pspice.com (accessed on 1 December 2022).

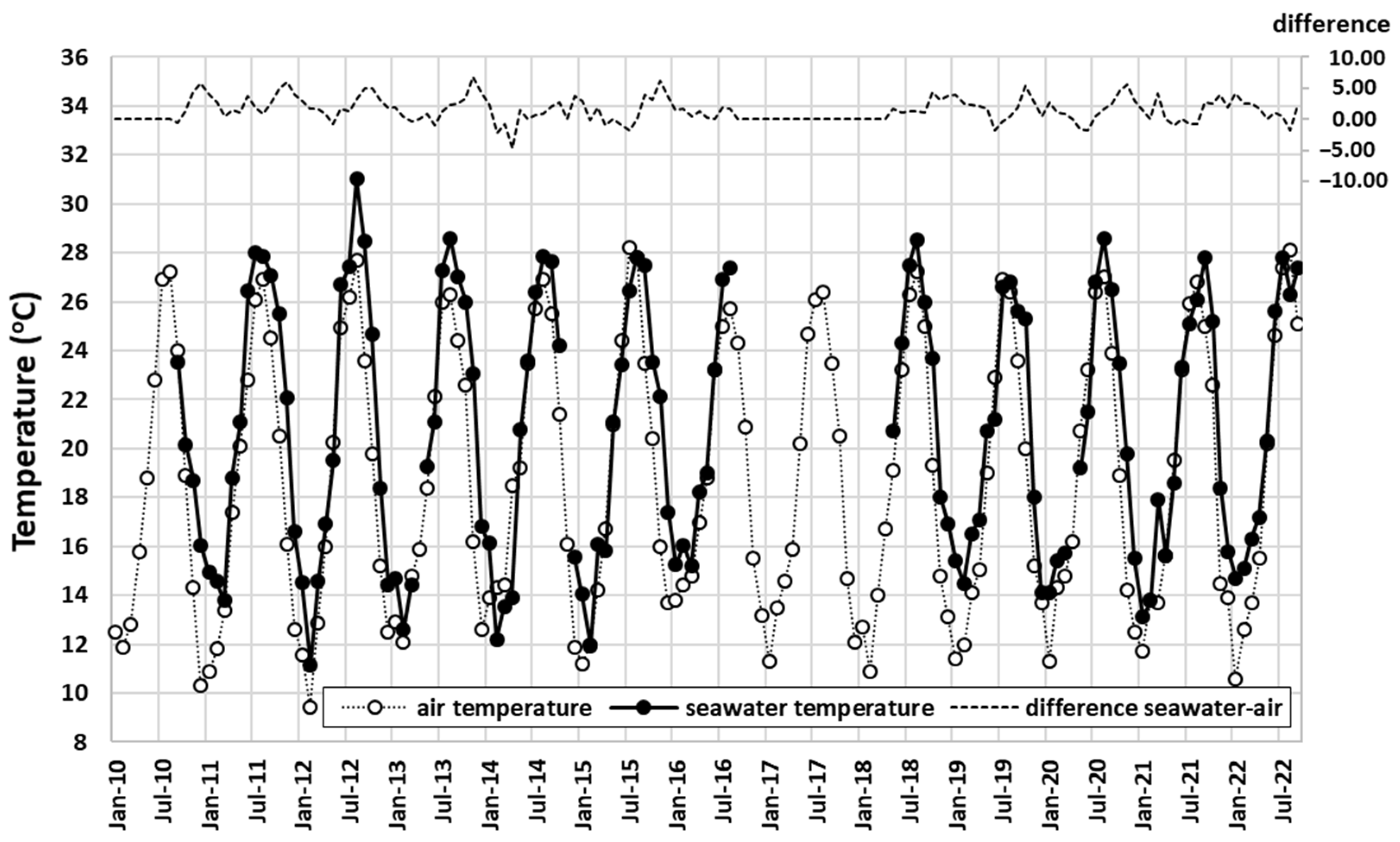
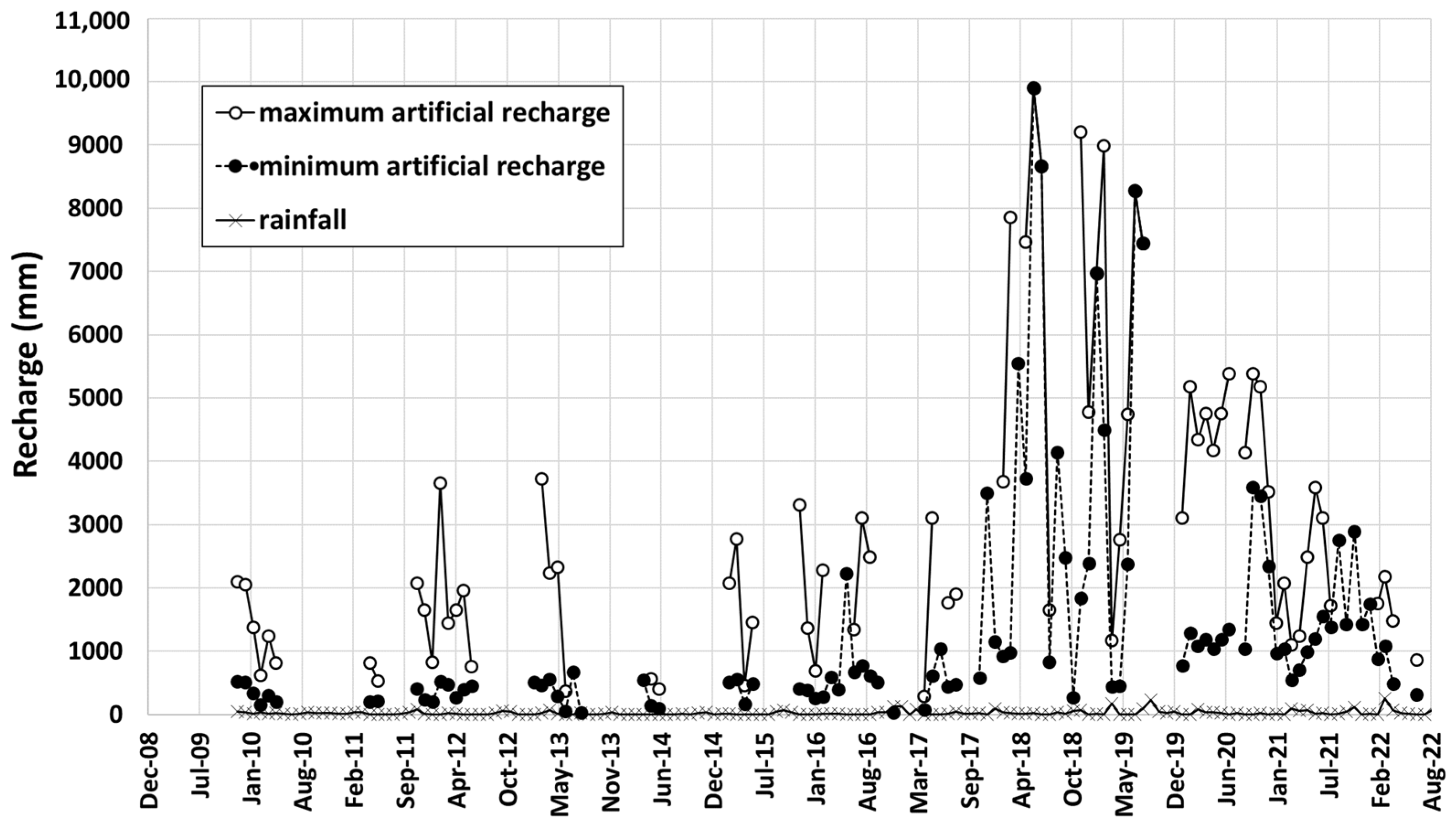
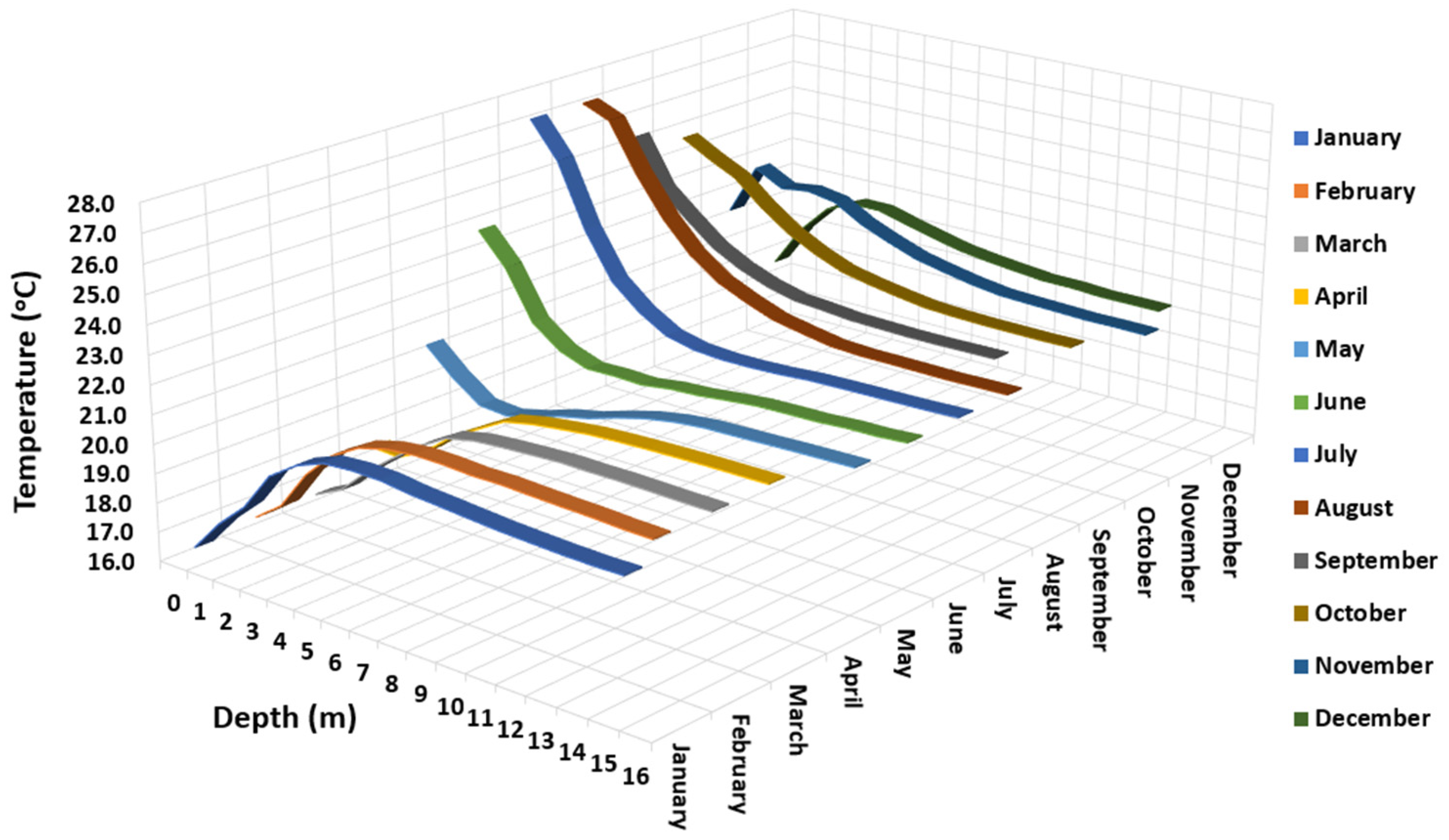
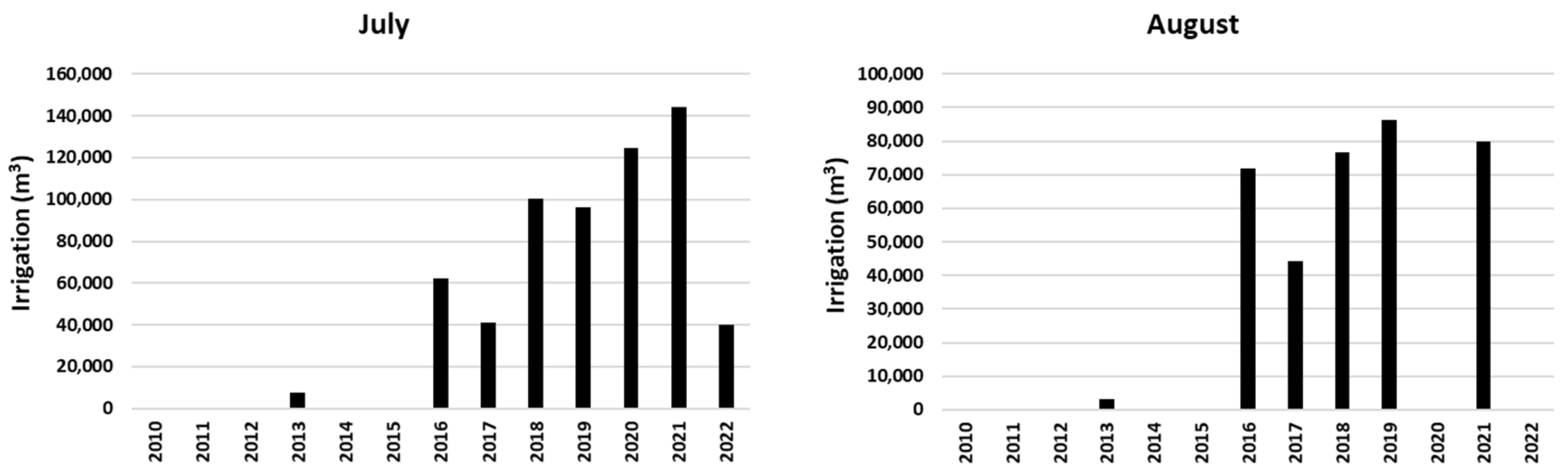
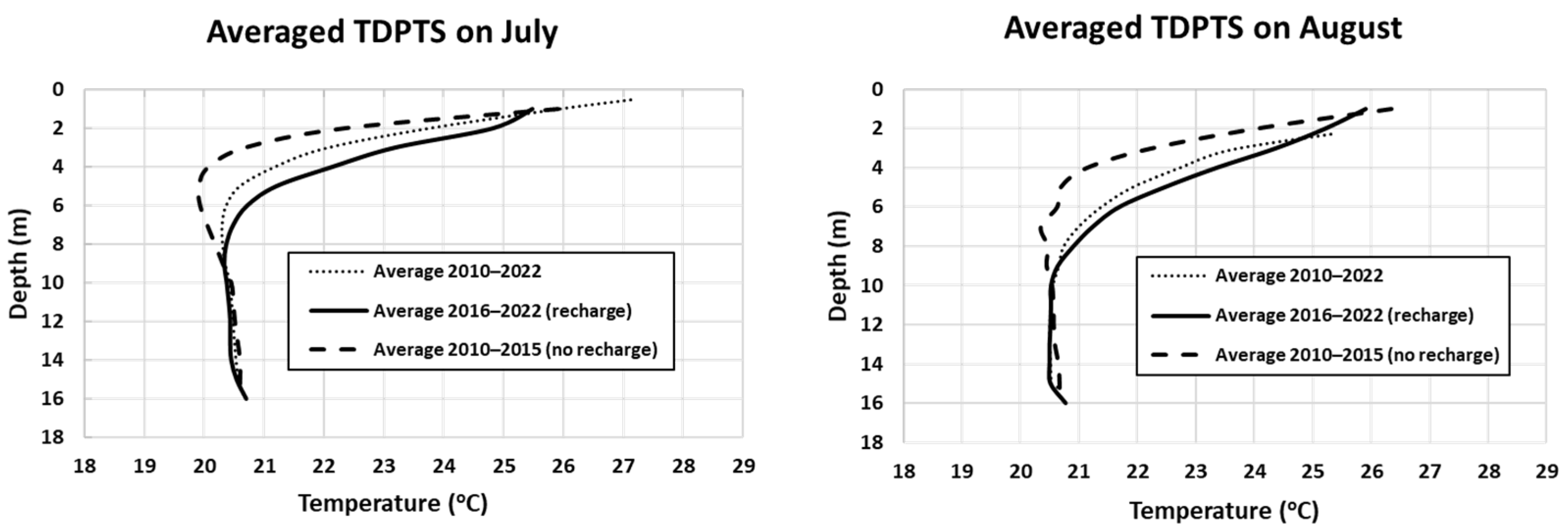
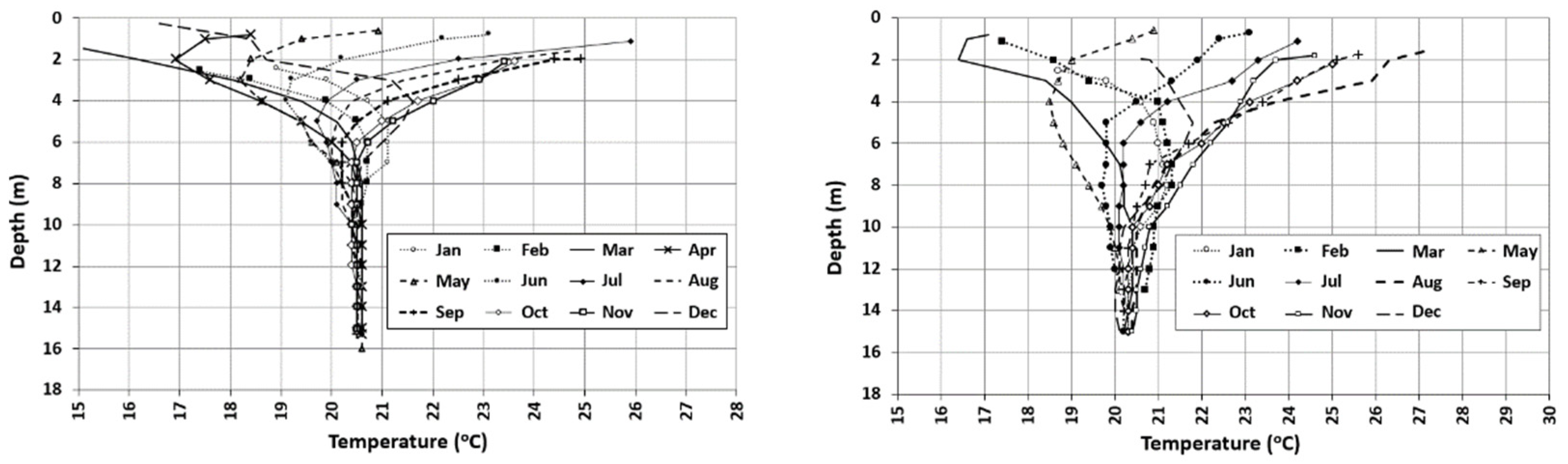

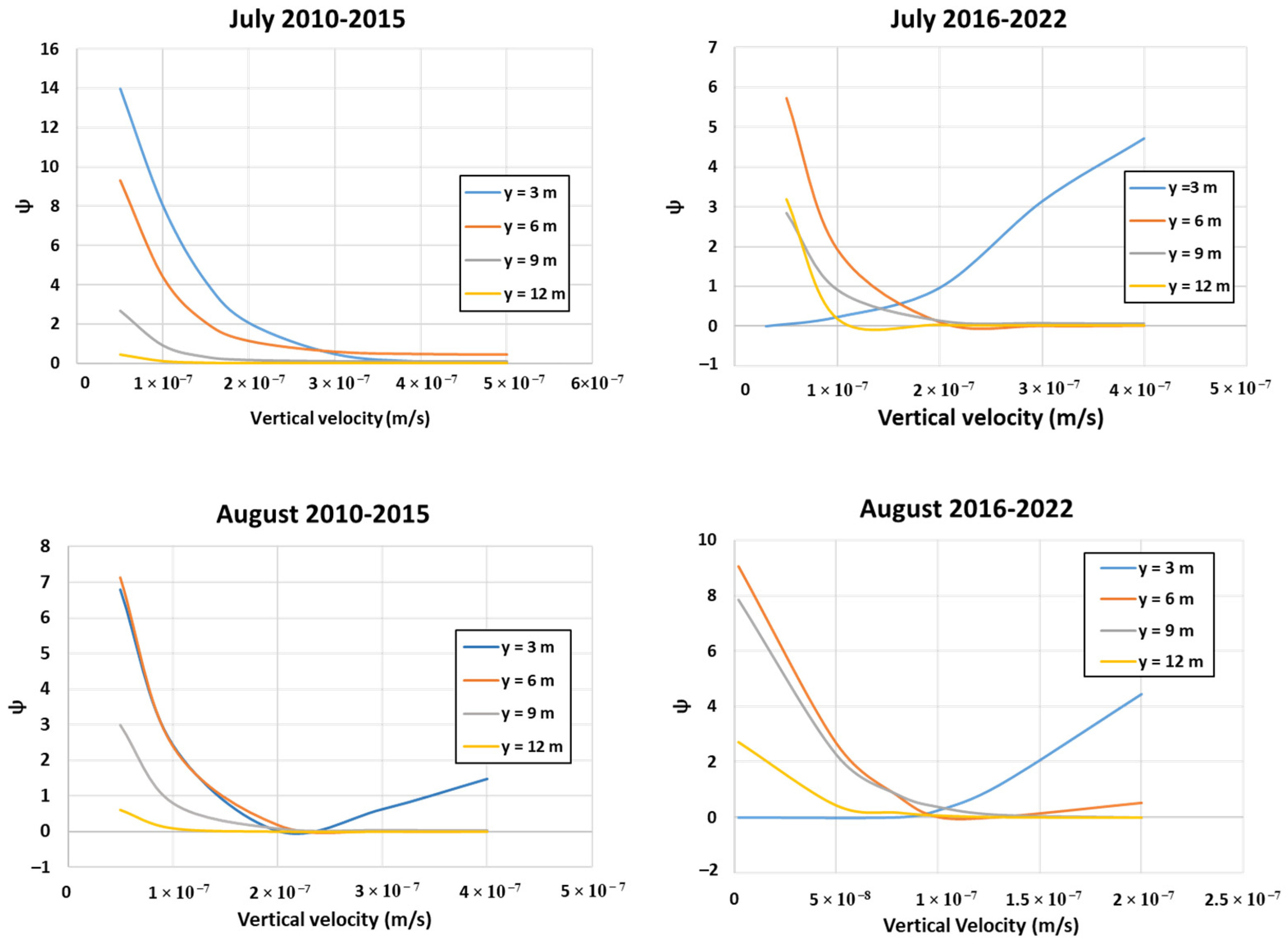
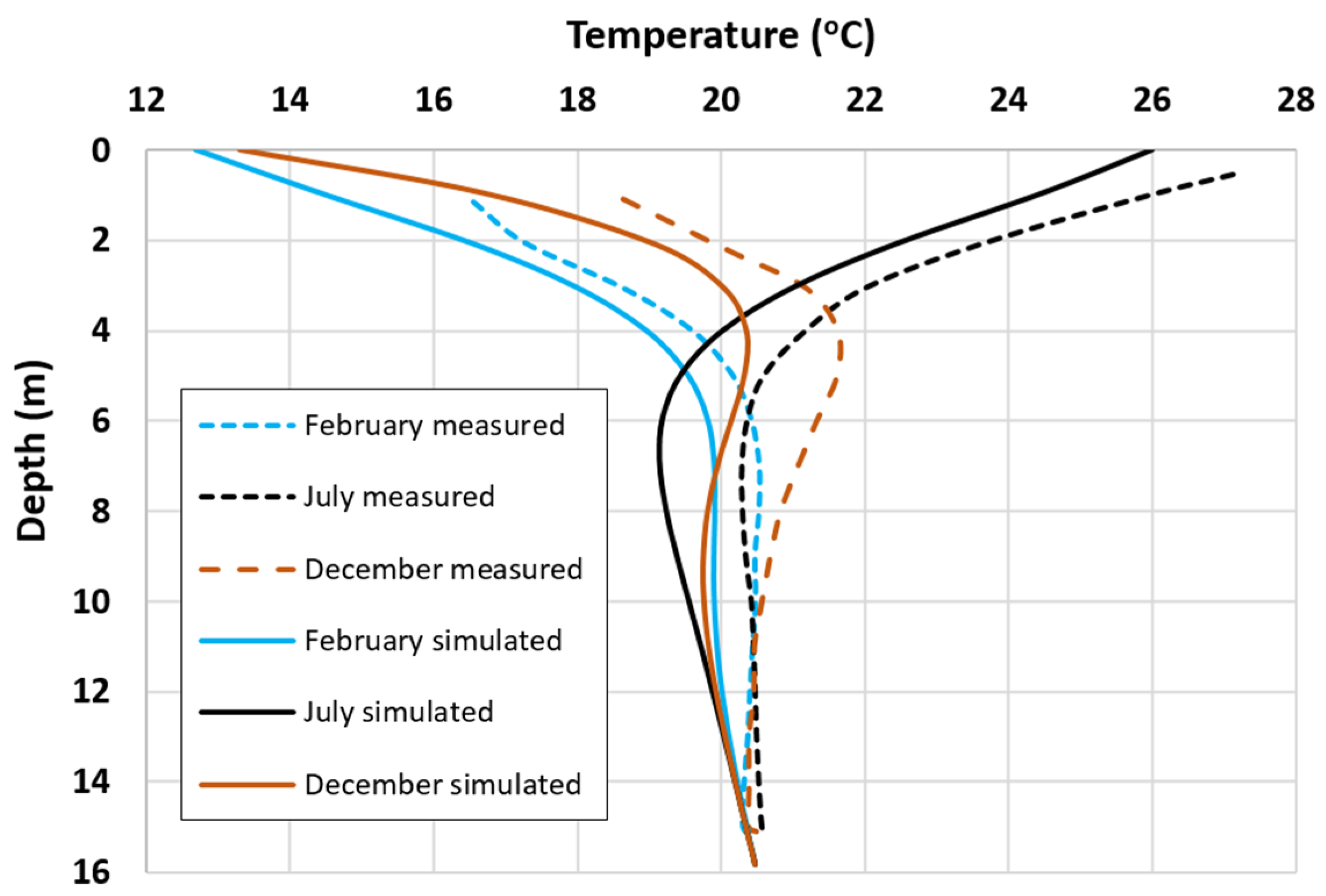
| Scenario | Time Interval | (cal °C−1 s−1 m−1) | (cal °C−1 m−3) | (°C) | (°C) |
|---|---|---|---|---|---|
| 1 | July 2010–2015 | 0.45 | 0.75 × 10−6 | Average air temperature 2010–2015: 26.5 | Average temperature at 16 m depth in the piezometer 2010–2015: 20.5 |
| 2 | July 2016–2022 | 0.45 | 0.75 × 10−6 | Average seawater temperature 2016–2022: 26.8 | Average temperature at 16 m depth in the piezometer 2016–2022: 20.5 |
| 3 | August 2010–2015 | 0.45 | 0.75 × 10−6 | Average air temperature 2010–2015: 27.1 | Average temperature at 16 m depth in the piezometer 2010–2015: 20.6 |
| 4 | August 2016–2022 | 0.45 | 0.75 × 10−6 | Average seawater temperature 2016–2022: 27.3 | Average temperature at 16 m depth in the piezometer 2016–2022: 20.5 |
| Scenario | Time Interval | (cal °C−1 s−1 m−1) | (cal °C−1 m−3) | (°C) | (°C) |
|---|---|---|---|---|---|
| 5 | 2011 | 0.45 | 0.75 × 10−6 | Sinusoidal function based on monthly air temperature 2011 | Constant value calculated from mean temperature at 16 m depth 2011: 20.6 |
| 6 | 2020 | 0.45 | 0.75 × 10−6 | Sinusoidal function based on monthly air temperature 2020 | Constant value calculated from mean temperature at 16 m depth 2020: 20.3 |
| Scenario | Velocity at 3 m Depth (m/s) | Velocity at 6 m Depth (m/s) | Velocity at 9 m Depth (m/s) | Velocity at 12 m Depth (m/s) |
|---|---|---|---|---|
| 1 | 7 × 10−7 | 7 × 10−7 | 7 × 10−7 | 7 × 10−7 |
| 2 | 3 × 10−8 * | 4 × 10−7 | 4 × 10−7 | 4 × 10−7 |
| 3 | 2 × 10−7 | 4 × 10−7 | 4 × 10−7 | 4 × 10−7 |
| 4 | 2 × 10−9 * | 1 × 10−7 | 2 × 10−7 | 2 × 10−7 |
| Month (Year) | Velocity at 3 m Depth (m/s) | Velocity at 6 m Depth (m/s) | Velocity at 9 m Depth (m/s) | Velocity at 12 m Depth (m/s) |
|---|---|---|---|---|
| January (2011) | 4.0 × 10−7 | 6.0 × 10−7 | 6.0 × 10−7 | 6.0 × 10−7 |
| February (2011) | 1.5 × 10−7 | 7.5 × 10−7 | 7.5 × 10−7 | 7.5 × 10−7 |
| March (2011) | 1.0 × 10−7 | 2.5 × 10−7 | 5.0 × 10−7 | 5.0 × 10−7 |
| August (2011) | 2.5 × 10−7 | 7.5 × 10−7 | 7.5 × 10−7 | 7.5 × 10−7 |
| September (2011) | 0.0 * | 7.0 × 10−7 | 7.0 × 10−7 | 7.0 × 10−7 |
| October (2011) | 0.0 * | 7.0 × 10−7 | 7.0 × 10−7 | 7.0 × 10−7 |
| November (2011) | 1.0 × 10−8 * | 2.0 × 10−7 | 5.0 × 10−7 | 5.0 × 10−7 |
| January (2020) | 4.0 × 10−7 | 5.0 × 10−7 | 5.0 × 10−7 | 5.0 × 10−7 |
| February (2020) | 1.5 × 10−7 | 7.0 × 10−7 | 7.0 × 10−7 | 7.0 × 10−7 |
| March (2020) | 1.5 × 10−7 | 1.5 × 10−7 | 1.5 × 10−7 | 3.5 × 10−7 |
| June (2020) | 5.0 × 10−8 * | 6.0 × 10−7 | 6.0 × 10−7 | 6.0 × 10−7 |
| July (2020) | −3.0 × 10−8 * | 7.0 × 10−7 | 7.0 × 10−7 | 7.0 × 10−7 |
| August (2020) | −2.0 × 10−7 | 8.0 × 10−8 | 2.0 × 10−7 | 2.0 × 10−7 |
| September (2020) | 4.0 × 10−9 * | 8.0 × 10−8 | 1.5 × 10−7 | 4.0 × 10−7 |
| October (2020) | 4.5 × 10−8 * | 8.0 × 10−8 | 1.0 × 10−7 | 4.0 × 10−7 |
| November (2020) | 3.5 × 10−8 * | 3.5 × 10−8 | 6.0 × 10−8 | 1.0 × 10−7 |
| Vz,1 (m/s) | Vz,2 (m/s) | Transient Time (days) |
|---|---|---|
| 0.0 × 10−7 | 7.00 × 10−7 | 111 |
| 1.00 × 10−7 | 7.00 × 10−7 | 104 |
| 2.00 × 10−7 | 7.00 × 10−7 | 82 |
| 4.00 × 10−7 | 7.00 × 10−7 | 65 |
| Depth Interval (m) | ΔTinterval (°C) | vadvection P1 (m/s) | vadvection P2 (m/s) | vbouyancy (m/s) |
|---|---|---|---|---|
| 0–4.5 | 5.75 | [2 × 10−9–7 × 10−7] | [0–4 × 10−7] | 9.79 × 10−9 |
| 4.5–7.5 | 2.25 | [1 × 10−7–7 × 10−7] | [3.5 × 10−8–7.5 × 10−7] | 3.83 × 10−9 |
| 7.5–10.5 | 1.05 | [2 × 10−7–7 × 10−7] | [6 × 10−8–7.5 × 10−7] | 1.79 × 10−9 |
| 10.5–16 | 0.35 | [2 × 10−7–7 × 10−7] | [1 × 10−7–7.5 × 10−7] | 5.96 × 10−10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez-Valera, J.A.; Alhama, I.; Trigueros, E. Quantification of Groundwater Vertical Flow from Temperature Profiles: Application to Agua Amarga Coastal Aquifer (SE Spain) Submitted to Artificial Recharge. Water 2023, 15, 1093. https://doi.org/10.3390/w15061093
Jiménez-Valera JA, Alhama I, Trigueros E. Quantification of Groundwater Vertical Flow from Temperature Profiles: Application to Agua Amarga Coastal Aquifer (SE Spain) Submitted to Artificial Recharge. Water. 2023; 15(6):1093. https://doi.org/10.3390/w15061093
Chicago/Turabian StyleJiménez-Valera, José Antonio, Iván Alhama, and Emilio Trigueros. 2023. "Quantification of Groundwater Vertical Flow from Temperature Profiles: Application to Agua Amarga Coastal Aquifer (SE Spain) Submitted to Artificial Recharge" Water 15, no. 6: 1093. https://doi.org/10.3390/w15061093





