The Significance of Groundwater Table Inclination for Nature-Based Replenishment of Groundwater-Dependent Ecosystems by Managed Aquifer Recharge
Abstract
:1. Introduction
- i.
- to evaluate the effects of groundwater table inclination and further influencing parameters (topography, model length, groundwater depth, material properties, heterogeneity, and infiltration basin parameters) on downgradient water level increase and to estimate infiltration-based MAR efficiency from the perspective of water level and GDE restoration for a simple half-basin; and
- ii.
- to demonstrate the applicability of this method through a close-to-real situation, answering the hypothetical question: “Can this be a possible measure to rehabilitate the former Lake Kondor, Danube-Tisza Interfluve, Hungary?”
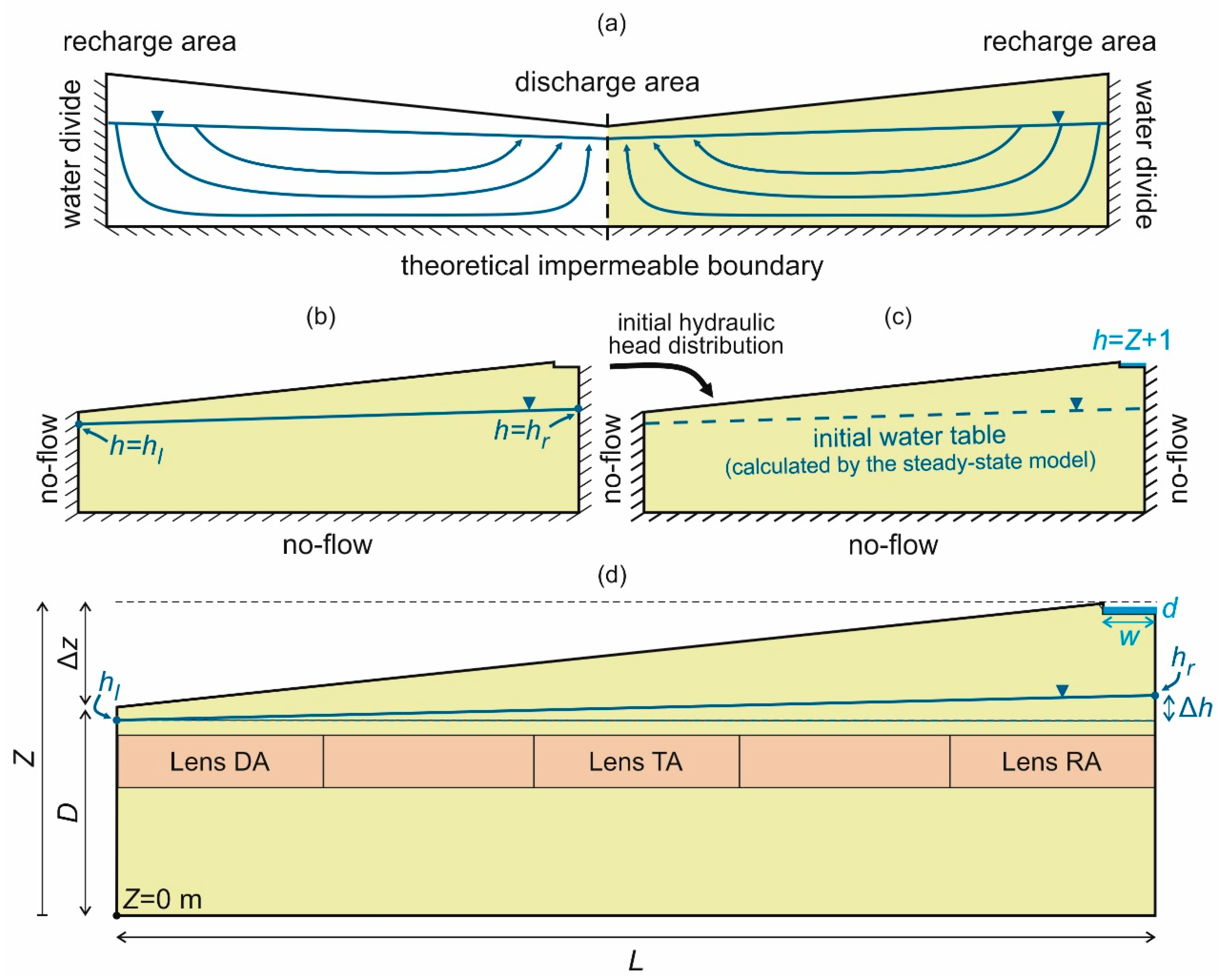
2. Theoretical Models
2.1. Methods
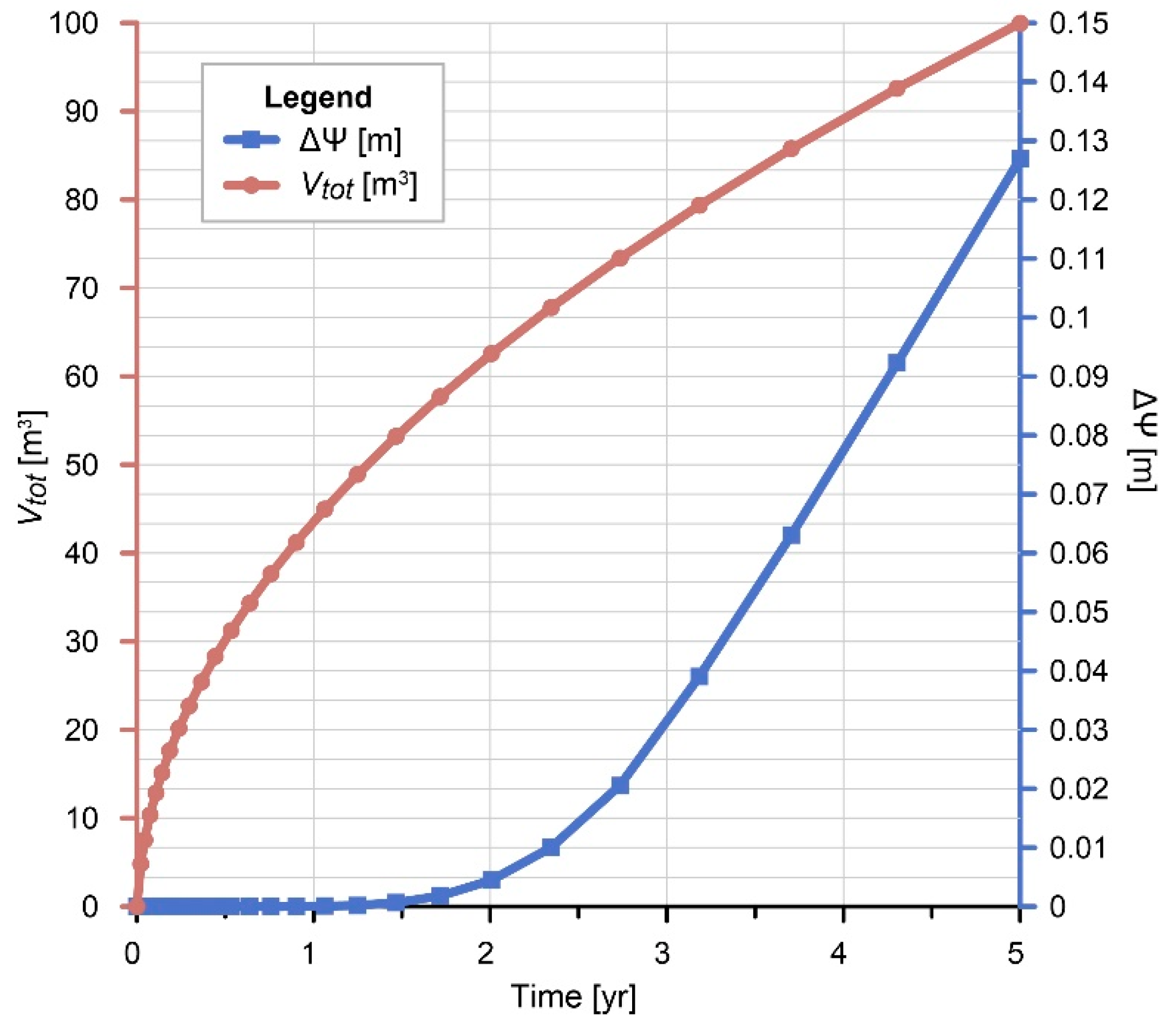
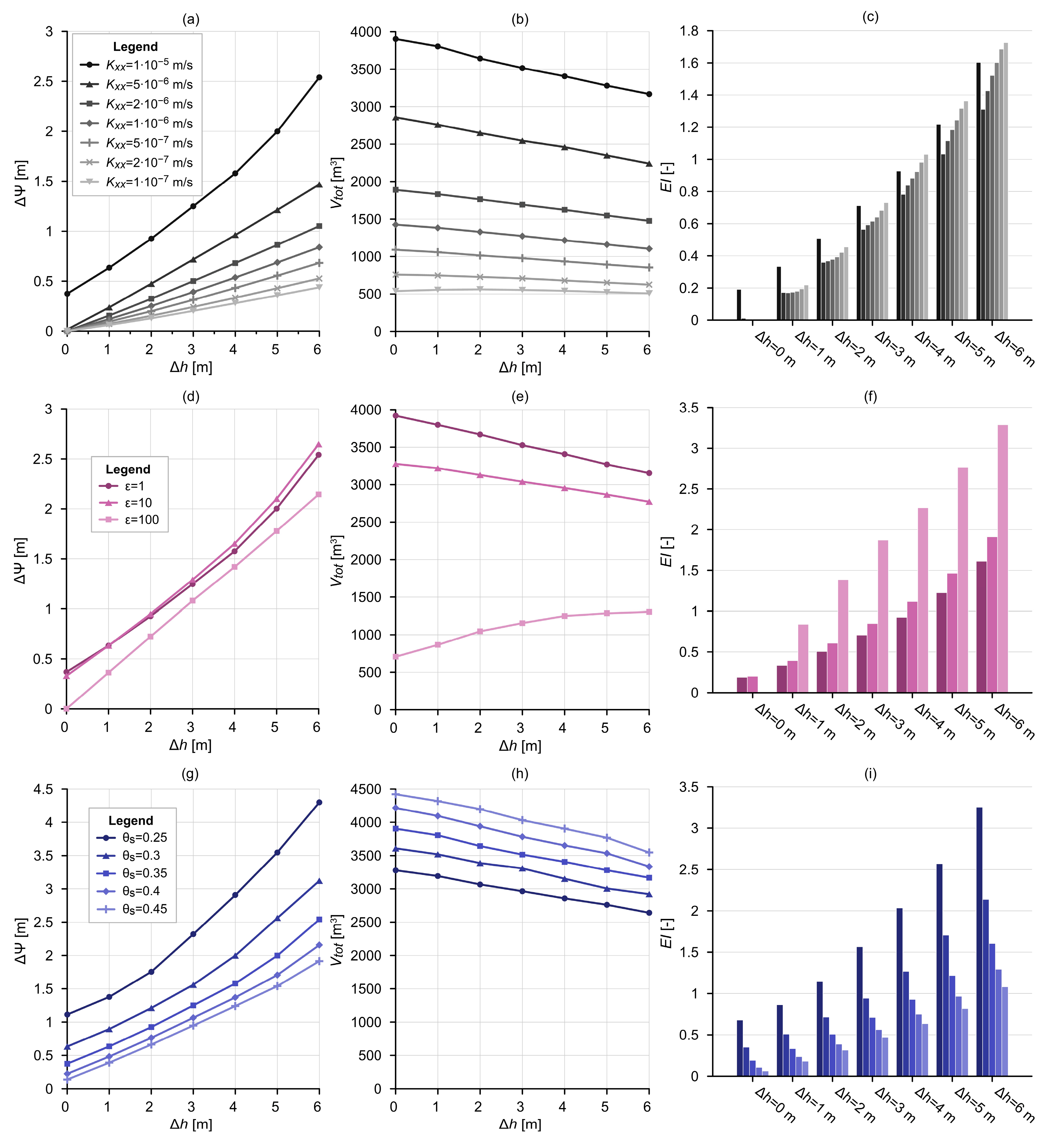
2.2. Results
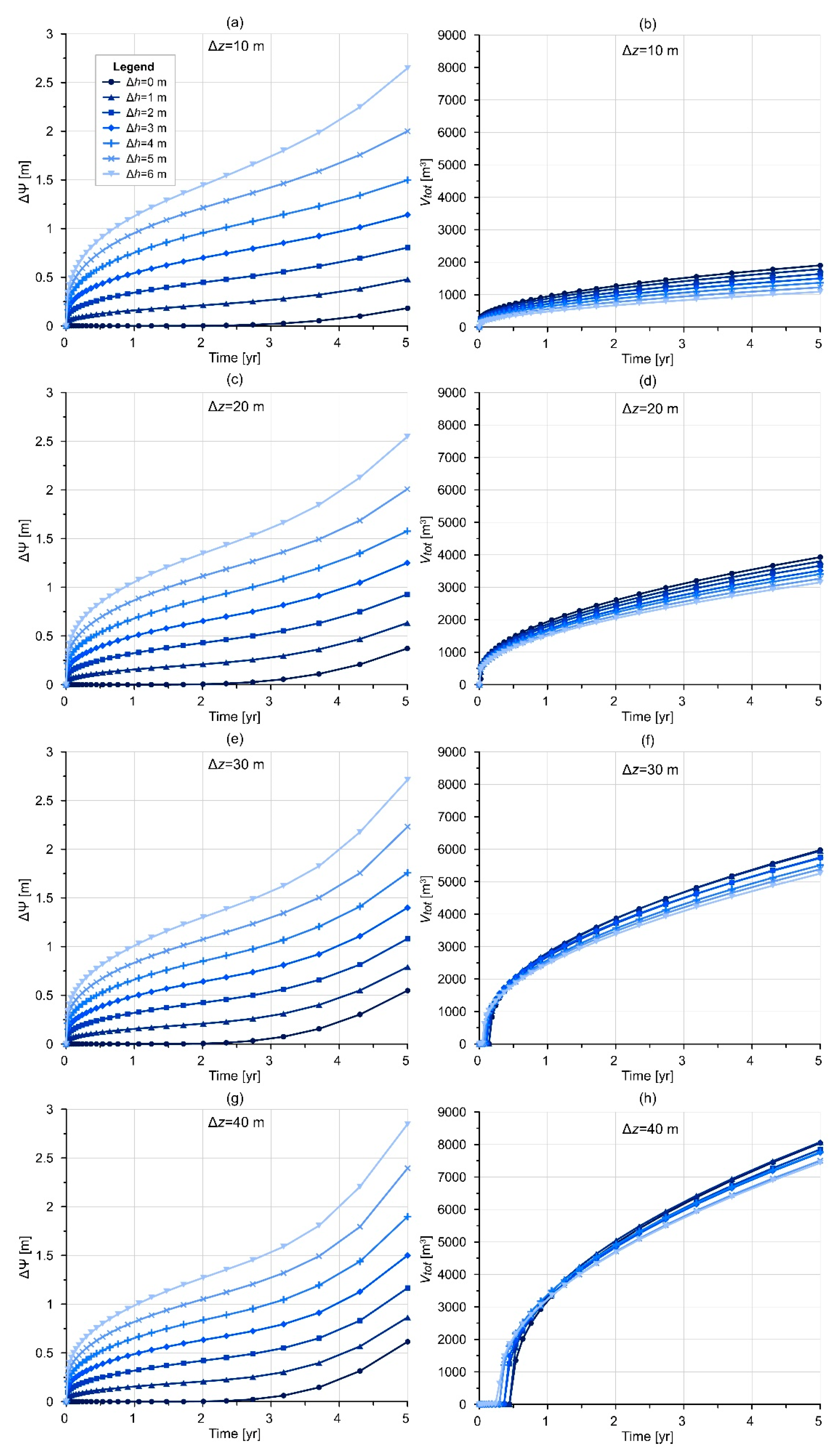
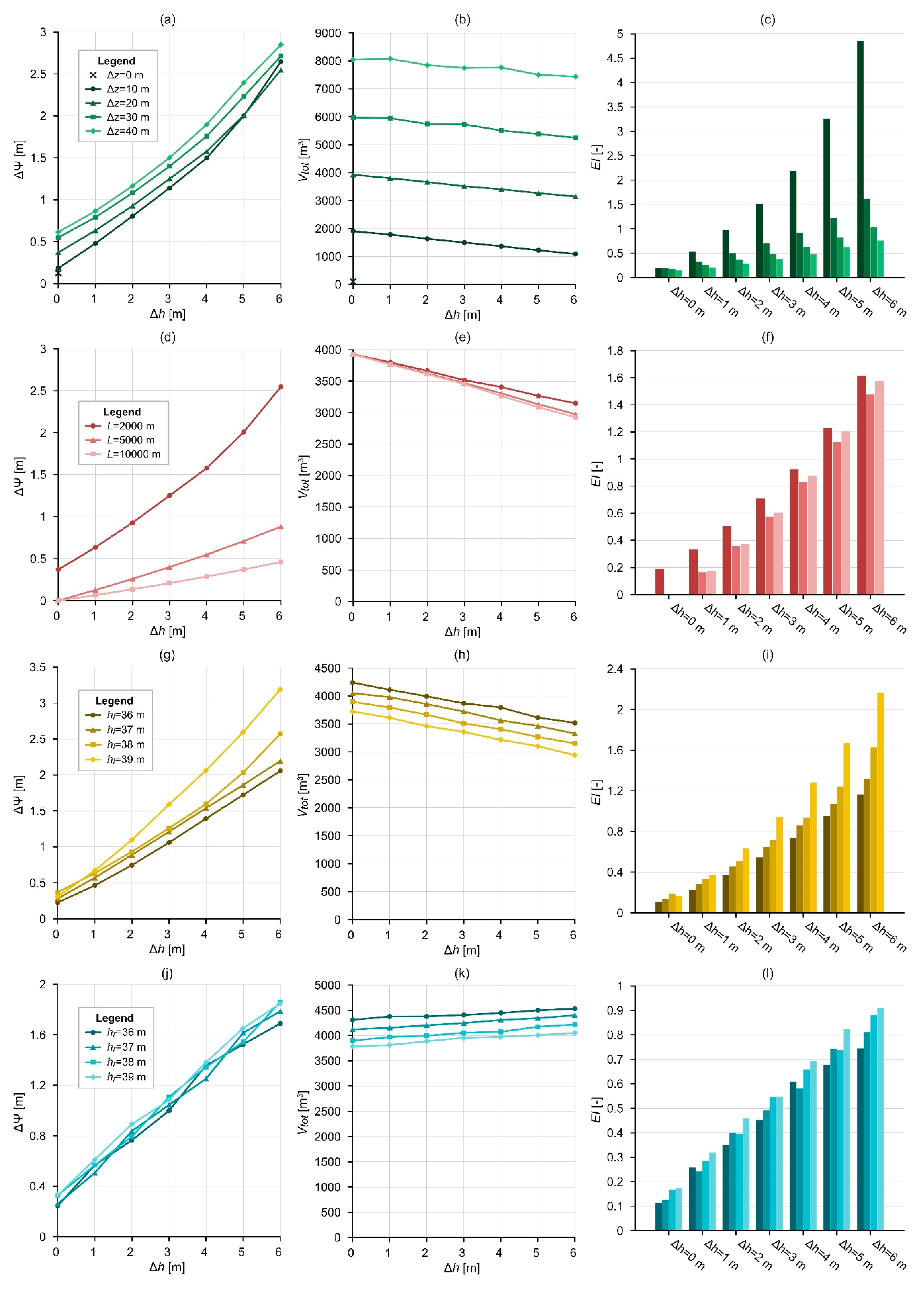
2.2.1. Topography and Hydraulic Head Difference (SG-1)
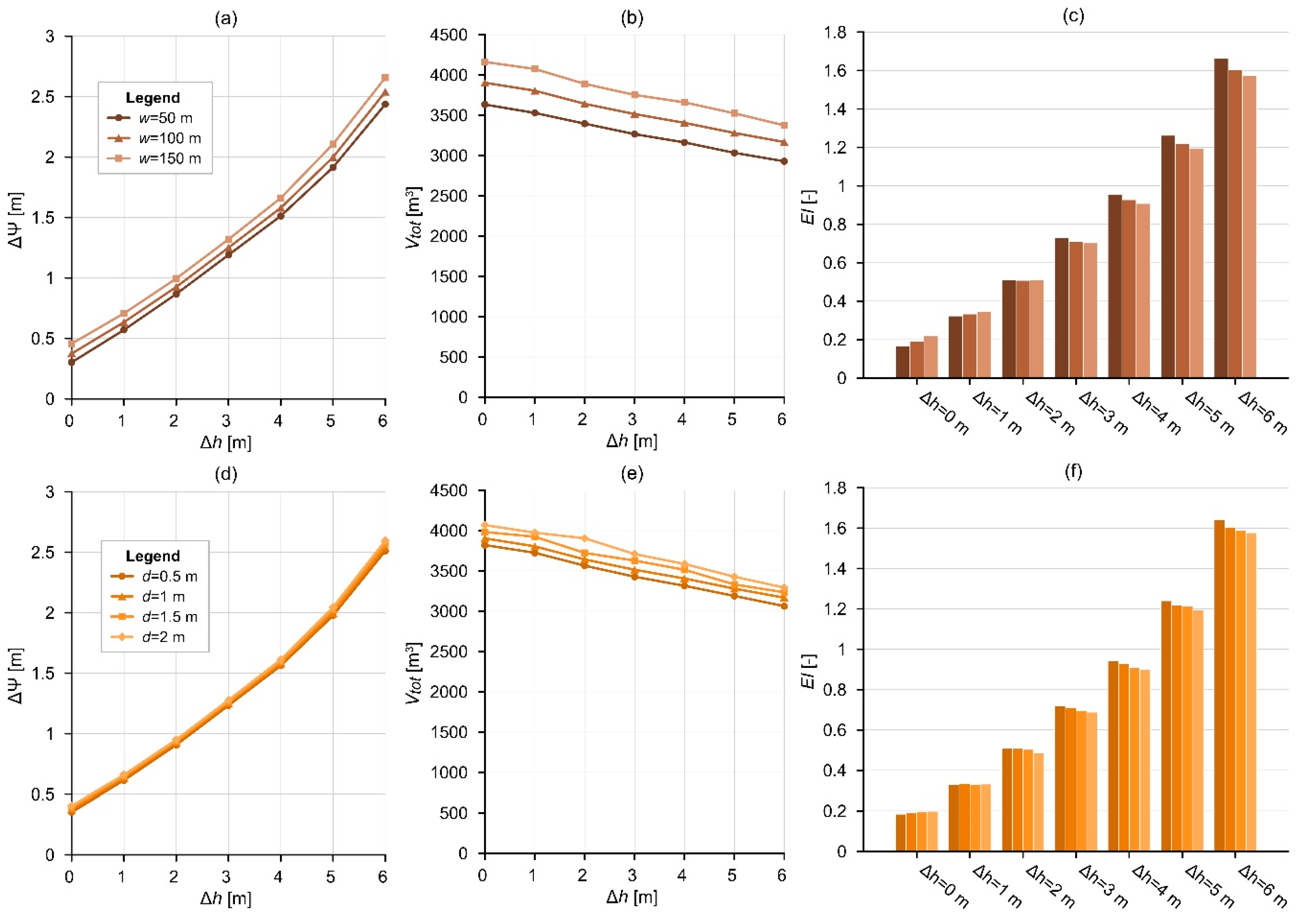
2.2.2. Model Length (SG-2)
2.2.3. Elevation of Water Table (SG-3)
2.2.4. Material Properties (SG-4)
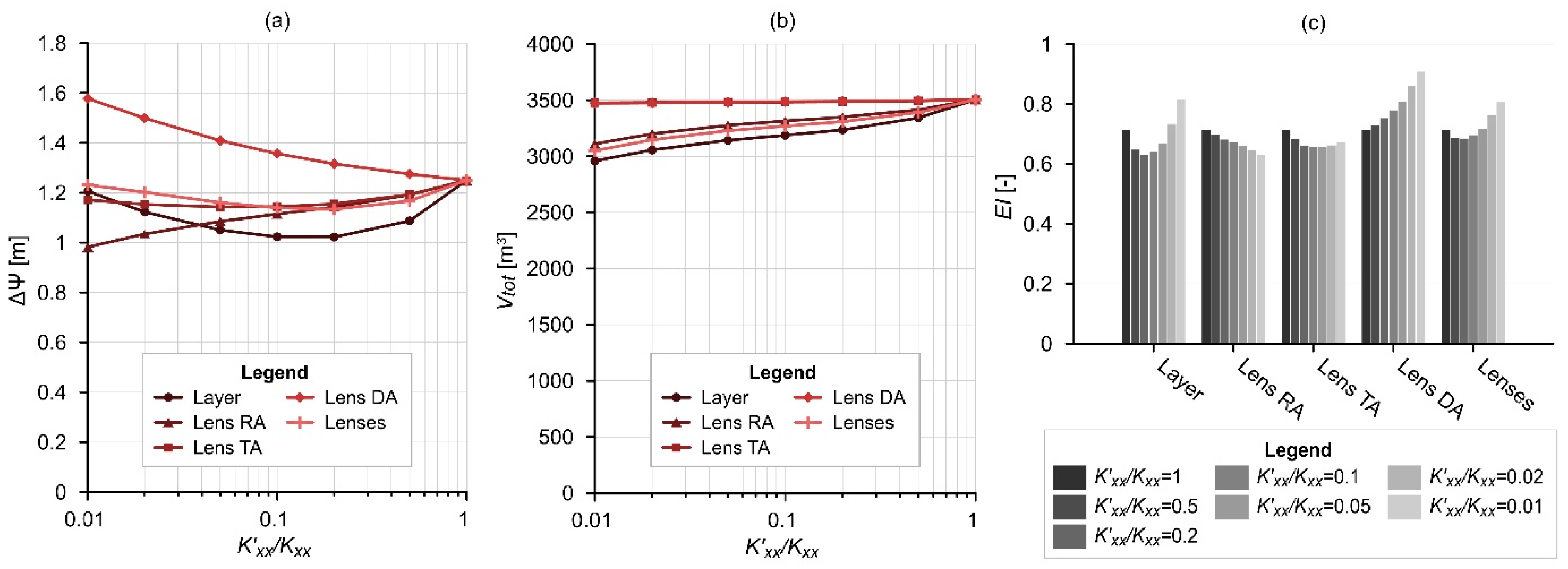
2.2.5. Heterogeneity (SG-5)
- with a continuous layer (“Layer”);
- with a lens below the recharge area (“Lens RA”);
- with a lens below the throughflow area (“Lens TA”);
- with a lens below the discharge area (“Lens DA”);
- with all three of these lenses (“Lenses”).
2.2.6. Parameters of the Infiltration Basin (SG-6)
2.3. Interpretation
3. Case Study
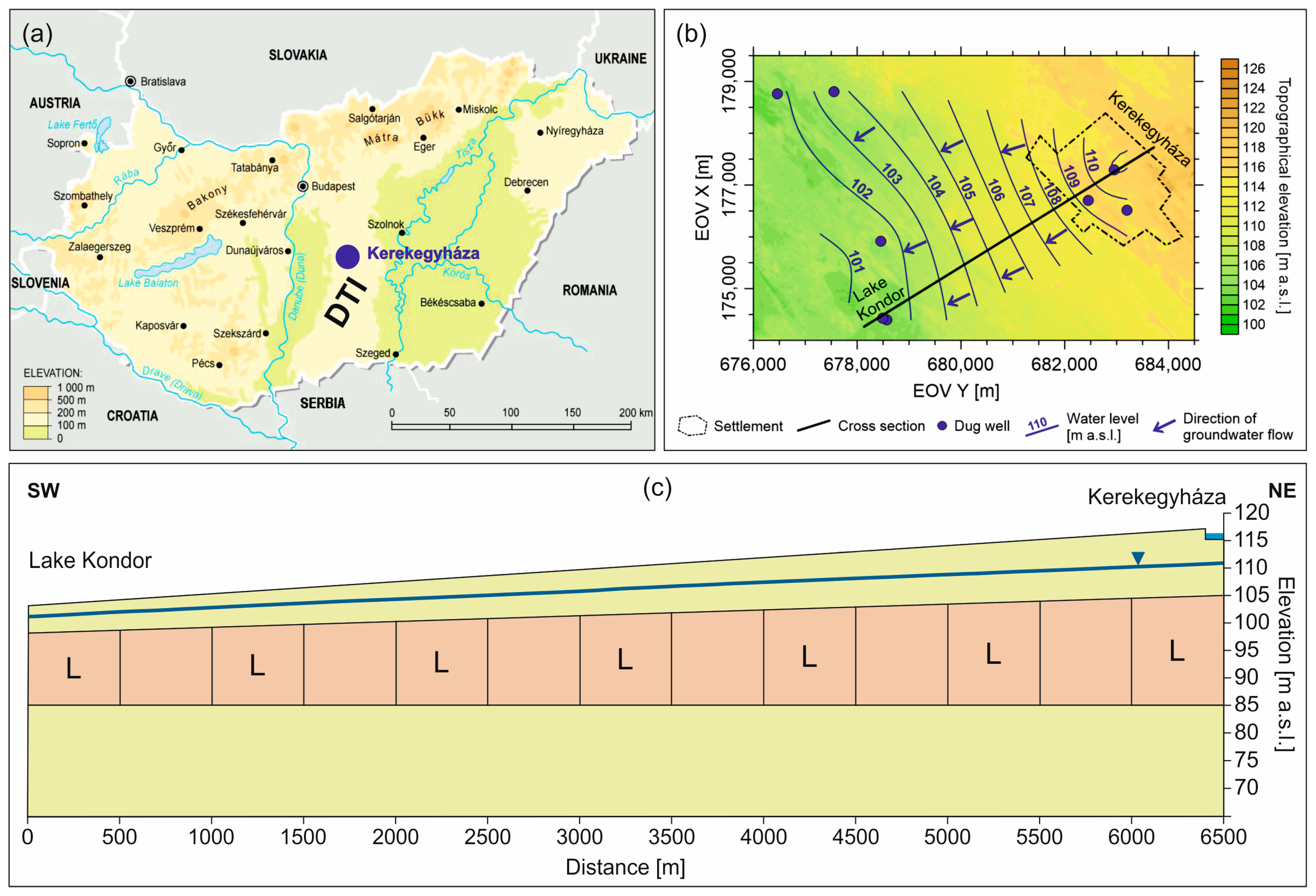
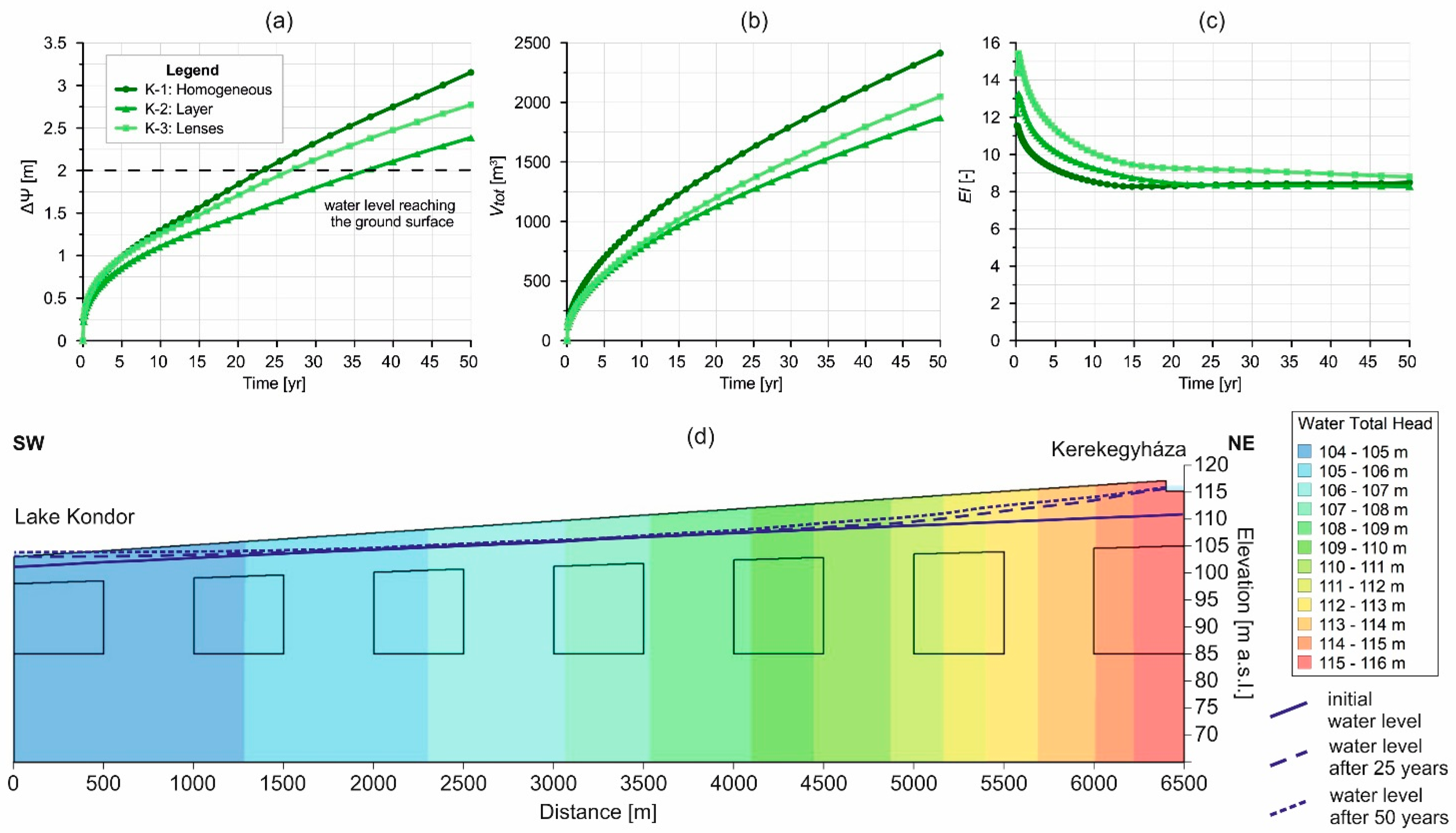
3.1. Study Area
3.2. Numerical Settings
- “K-1”: A homogeneous model with horizontal hydraulic conductivity (Kxx) of 5∙10−6 m/s.
- “K-2”: A model with three layers, where the upper and lower layers were described by Kxx = 5∙10−6 m/s and the middle layer by Kxx = 5∙10−7 m/s. The upper layer was 5 m thick on the left side and 10 m thick on the right side; the bottom of the middle layer was at 85 m a.s.l.
- “K-3”: A model with lenses, where the model domain and the lenses were characterised by Kxx = 5∙10−6 m/s and Kxx = 5∙10−7 m/s, respectively.
3.3. Results
3.4. Interpretation
4. Discussion
4.1. Relevance and Limitations of the Theoretical Models
4.2. The Relevance and Limitations of the Case Study
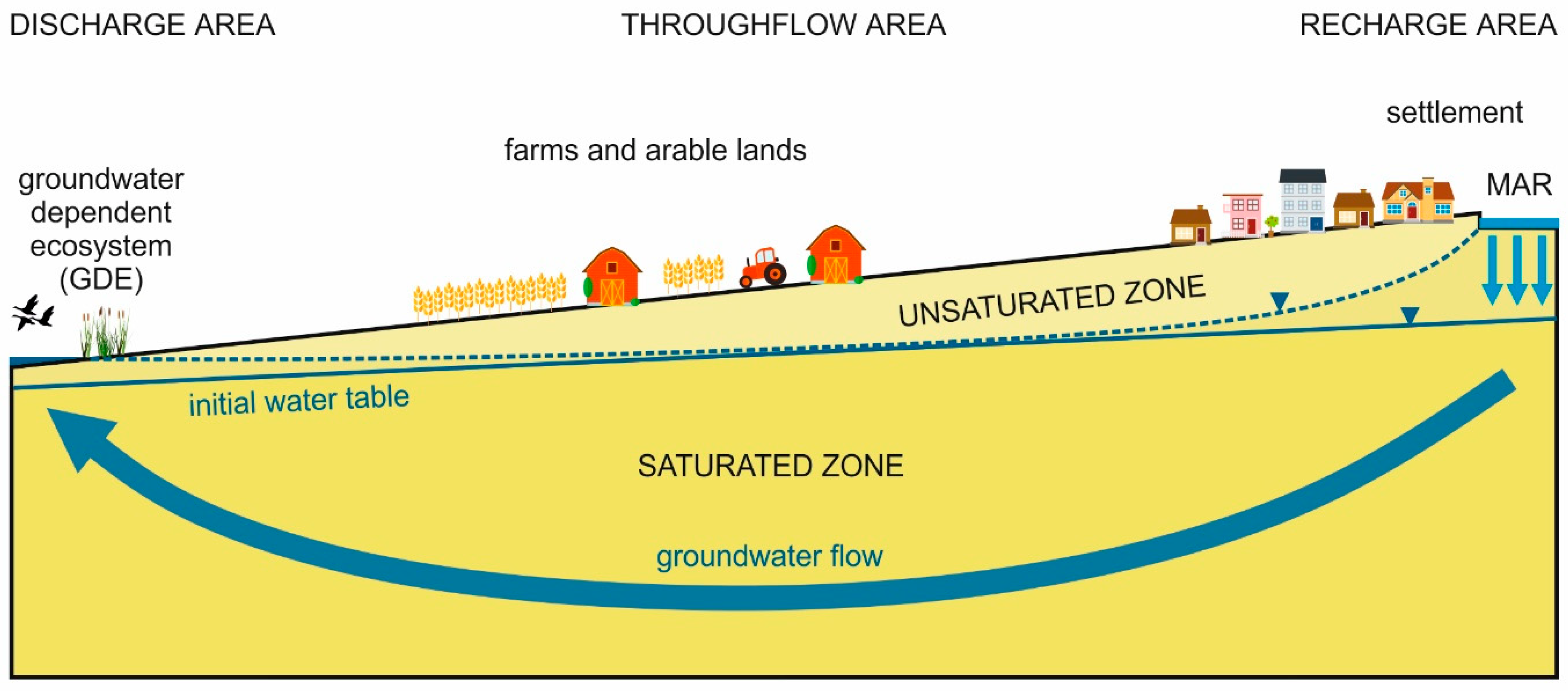
4.3. Nature-Based Solutions and GDE Replenishment
5. Conclusions
- The theoretical models for a simple basin revealed the significance of groundwater table inclination for infiltration-based MAR planning and operation.
- The achieved water level increase (ΔΨ) was approx. one order of magnitude higher in the case of higher initial hydraulic head difference (Δh = 6 m) than in the case of Δh = 0 m. In addition, the distance between the recharge and discharge areas and the hydraulic conductivity has the most significant effect on the water level increase at the discharge area.
- The results showed that the amount of water infiltrated from the infiltration basin (Vtot) is principally governed by topographic difference and the depth of water table, thus by the thickness of the unsaturated zone. There was a sevenfold difference between the cumulative water volumes related to the scenarios with Δz = 10 m and Δz = 40 m, in the case of Δh = 6 m. Furthermore, the material properties of the aquifer, such as hydraulic conductivity, anisotropy, saturated water content, and heterogeneity, have an effect on the infiltrated volumes.
- From the perspective of groundwater-dependent ecosystem preservation and restoration, the most efficient scenarios are when the hydraulic gradient and the horizontal hydraulic conductivity are high, and the aquifer has a lower storage capacity. This means that exactly the opposite conditions are required, as in the case of long-term water storage in an aquifer.
- The established efficiency index, involving the achieved water level increase and the infiltrated water volumes, can be used to differentiate between realistic scenarios and to optimise the MAR design in the future.
- The investigated case study proved the applicability and efficiency of the initial concept and offered a possible water management measure for increasing the water reserves and restoring the GDE of the area. The applied approach offers a smart, diverse, and nature-based solution, and it can be advantageous compared to the previously proposed water replenishment plans for the area.
- Based on the results of the theoretical and simplified case study models, a conceptual model was built: if water is infiltrated at the local recharge area (elevated area), the water table will increase at the local discharge area (local topographical depression), as well, due to hydraulic continuity, which can have a positive effect on GDEs, using natural settings and processes. Furthermore, the water level beneficially increases around the recharge and discharge area, as well.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- NRMMC; EPHC; NHMRC. Australian Guidelines for Water Recycling, Managing Health and Environmental Risks, Vol 2C: Managed Aquifer Recharge; Biotext: Canberra, Australia, 2009; 237p. [Google Scholar]
- Bouwer, H. Artificial Recharge of Groundwater: Hydrogeology and Engineering. Hydrogeol. J. 2002, 10, 121–142. [Google Scholar] [CrossRef] [Green Version]
- Gale, I. Strategies for Managed Aquifer Recharge in Semi-Arid Areas; UNESCO: Paris, France, 2005; 30p. [Google Scholar]
- Dillon, P.; Toze, S.; Page, D.; Vanderzalm, J.; Bekele, E.; Sidhu, J.; Rinck-Pfeiffer, S. Managed Aquifer Recharge: Rediscovering Nature as a Leading Edge Technology. Water Sci. Technol. 2010, 62, 2338–2345. [Google Scholar] [CrossRef] [PubMed]
- Casanova, J.; Devau, N.; Pettenati, M. Managed Aquifer Recharge: An Overview of Issues and Options. In Integrated Groundwater Management; Springer International Publishing: Cham, Switzerland, 2016; pp. 413–434. [Google Scholar]
- Dillon, P. Future Management of Aquifer Recharge. Hydrogeol. J. 2005, 13, 313–316. [Google Scholar] [CrossRef]
- Gale, I.N.; Macdonald, D.M.J.; Calow, R.C.; Neumann, I.; Moench, M.; Kulkarni, H.; Mudrakartha, S.; Palanisami, K. Managed Aquifer Recharge: An Assessment of Its Role and Effectiveness in Watershed Management; British Geological Survey: Nottingham, UK, 2006. [Google Scholar]
- Scherberg, J.; Baker, T.; Selker, J.S.; Henry, R. Design of Managed Aquifer Recharge for Agricultural and Ecological Water Supply Assessed Through Numerical Modeling. Water Resour. Manag. 2014, 28, 4971–4984. [Google Scholar] [CrossRef]
- Van Houtte, E.; Verbauwhede, J. Environmental Benefits from Water Reuse Combined with Managed Aquifer Recharge in the Flemish Dunes (Belgium). Int. J. Water Resour. Dev. 2021, 37, 1027–1034. [Google Scholar] [CrossRef]
- O’Hogain, S.; McCarton, L. A Technology Portfolio of Nature Based Solutions; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-73280-0. [Google Scholar]
- UN WATER. The United Nations World Water Development Report 2018: Nature-Based Solutions for Water; UN WATER: Paris, France, 2018. [Google Scholar]
- Sprenger, C.; Hartog, N.; Hernández, M.; Vilanova, E.; Grützmacher, G.; Scheibler, F.; Hannappel, S. Inventory of Managed Aquifer Recharge Sites in Europe: Historical Development, Current Situation and Perspectives. Hydrogeol. J. 2017, 25, 1909–1922. [Google Scholar] [CrossRef] [Green Version]
- Dillon, P.; Stuyfzand, P.; Grischek, T.; Lluria, M.; Pyne, R.D.G.; Jain, R.C.; Bear, J.; Schwarz, J.; Wang, W.; Fernandez, E.; et al. Sixty Years of Global Progress in Managed Aquifer Recharge. Hydrogeol. J. 2019, 27, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Stefan, C.; Ansems, N. Web-Based Global Inventory of Managed Aquifer Recharge Applications. Sustain. Water Resour. Manag. 2018, 4, 153–162. [Google Scholar] [CrossRef] [Green Version]
- Fernández Escalante, E.; Henao Casas, J.D.; San Sebastián Sauto, J.; Calero Gil, R. Monitored and Intentional Recharge (MIR): A Model for Managed Aquifer Recharge (MAR) Guideline and Regulation Formulation. Water 2022, 14, 3405. [Google Scholar] [CrossRef]
- Fernandez Escalante, E.; Henao Casas, J.D.; Vidal Medeiros, A.M.; San Sebastián Sauto, J.S.S.S. Regulations and Guidelines on Water Quality Requirements for Managed Aquifer Recharge. International Comparison. Acque Sotter.-Ital. J. Groundw. 2020, 9, 7–22. [Google Scholar] [CrossRef]
- Imig, A.; Szabó, Z.; Halytsia, O.; Vrachioli, M.; Kleinert, V.; Rein, A. A Review on Risk Assessment in Managed Aquifer Recharge. Integr. Environ. Assess. Manag. 2022, 18, 1513–1529. [Google Scholar] [CrossRef]
- Tóth, J. Groundwater as a Geologic Agent: An Overview of the Causes, Processes, and Manifestations. Hydrogeol. J. 1999, 7, 1–14. [Google Scholar] [CrossRef]
- Tóth, J. A Conceptual Model of the Groundwater Regime and the Hydrogeologic Environment. J. Hydrol. 1970, 10, 164–176. [Google Scholar] [CrossRef]
- IGRAC. Artificial Recharge of Groundwater in the World; IGRAC: Delft, The Netherlands, 2007. [Google Scholar]
- Pyne, R.D.G. Aquifer Storage Recovery: A Guide to Groundwater Recharge through Wells, 2nd ed.; ASR Press: Gainesville, FL, USA, 2005. [Google Scholar]
- Ward, J.D.; Simmons, C.T.; Dillon, P.J.; Pavelic, P. Integrated Assessment of Lateral Flow, Density Effects and Dispersion in Aquifer Storage and Recovery. J. Hydrol. 2009, 370, 83–99. [Google Scholar] [CrossRef]
- Gale, I.; Neumann, I.; Calow, R.; Moench, D.M. The Effectiveness of Artificial Recharge of Groundwater: A Review; British Geological Survey: Nottingham, UK, 2002. [Google Scholar]
- Dillon, P.; Pavelic, P.; Page, D.; Beringen, H.; Ward, J. Managed Aquifer Recharge: An Introduction. Waterlines Report Series No. 13; National Water Commission: Canberra, Australia, 2009. [Google Scholar]
- Dillon, P.J. General Design Considerations. In Water Reclamation Technologies for Safe Managed Aquifer Recharge; Kazner, C., Wintgens, T., Dillon, P., Eds.; IWA Publishing: London, UK, 2012; pp. 299–310. [Google Scholar]
- Ward, J.; Dillon, P. Principles to Coordinate Managed Aquifer Recharge with Natural Resource Management Policies in Australia. Hydrogeol. J. 2012, 20, 943–956. [Google Scholar] [CrossRef]
- Missimer, T.; Guo, W.; Woolschlager, J.; Maliva, R. Long-Term Managed Aquifer Recharge in a Saline-Water Aquifer as a Critical Component of an Integrated Water Scheme in Southwestern Florida, USA. Water 2017, 9, 774. [Google Scholar] [CrossRef] [Green Version]
- Hantush, M.S. Growth and Decay of Groundwater-Mounds in Response to Uniform Percolation. Water Resour. Res. 1967, 3, 227–234. [Google Scholar] [CrossRef] [Green Version]
- Marino, M.A. Growth and Decay of Groundwater Mounds Induced by Percolation. J. Hydrol. 1974, 22, 295–301. [Google Scholar] [CrossRef]
- Marino, M.A. Rise and Decline of the Water Table Induced by Vertical Recharge. J. Hydrol. 1974, 23, 289–298. [Google Scholar] [CrossRef]
- Marino, M.A. Hele-Shaw Model Study of the Growth and Decay of Groundwater Ridges. J. Geophys. Res. 1967, 72, 1195–1205. [Google Scholar] [CrossRef]
- Singh, R. Prediction of Mound Geometry under Recharge Basins. Water Resour. Res. 1976, 12, 775–780. [Google Scholar] [CrossRef]
- Ganot, Y.; Holtzman, R.; Weisbrod, N.; Nitzan, I.; Katz, Y.; Kurtzman, D. Monitoring and Modeling Infiltration–Recharge Dynamics of Managed Aquifer Recharge with Desalinated Seawater. Hydrol. Earth Syst. Sci. 2017, 21, 4479–4493. [Google Scholar] [CrossRef] [Green Version]
- Alkhatib, J.; Engelhardt, I.; Sauter, M. Identification of Suitable Sites for Managed Aquifer Recharge under Semi-Arid Conditions Employing a Combination of Numerical and Analytical Techniques. Environ. Earth Sci. 2021, 80, 554. [Google Scholar] [CrossRef]
- Masetti, M.; Pedretti, D.; Sorichetta, A.; Stevenazzi, S.; Bacci, F. Impact of a Storm-Water Infiltration Basin on the Recharge Dynamics in a Highly Permeable Aquifer. Water Resour. Manag. 2016, 30, 149–165. [Google Scholar] [CrossRef]
- Rahman, M.A.; Rusteberg, B.; Uddin, M.S.; Lutz, A.; Saada, M.A.; Sauter, M. An Integrated Study of Spatial Multicriteria Analysis and Mathematical Modelling for Managed Aquifer Recharge Site Suitability Mapping and Site Ranking at Northern Gaza Coastal Aquifer. J. Environ. Manag. 2013, 124, 25–39. [Google Scholar] [CrossRef]
- Massuel, S.; Perrin, J.; Mascre, C.; Mohamed, W.; Boisson, A.; Ahmed, S. Managed Aquifer Recharge in South India: What to Expect from Small Percolation Tanks in Hard Rock? J. Hydrol. 2014, 512, 157–167. [Google Scholar] [CrossRef]
- Bahar, T.; Oxarango, L.; Castebrunet, H.; Rossier, Y.; Mermillod-Blondin, F. 3D Modelling of Solute Transport and Mixing during Managed Aquifer Recharge with an Infiltration Basin. J. Contam. Hydrol. 2021, 237, 103758. [Google Scholar] [CrossRef]
- Caligaris, E.; Agostini, M.; Rossetto, R. Using Heat as a Tracer to Detect the Development of the Recharge Bulb in Managed Aquifer Recharge Schemes. Hydrology 2022, 9, 14. [Google Scholar] [CrossRef]
- Smith, A.J.; Pollock, D.W. Assessment of Managed Aquifer Recharge Potential Using Ensembles of Local Models. Ground Water 2012, 50, 133–143. [Google Scholar] [CrossRef]
- Zlotnik, V.A.; Kacimov, A.; Al-Maktoumi, A. Estimating Groundwater Mounding in Sloping Aquifers for Managed Aquifer Recharge. Groundwater 2017, 55, 797–810. [Google Scholar] [CrossRef]
- Pavelic, P.; Hoanh, C.T.; Viossanges, M.; Vinh, B.N.; Chung, D.T.; D’haeze, D.; Dat, L.Q.; Ross, A. Managed Aquifer Recharge for Sustaining Groundwater Supplies for Smallholder Coffee Production in the Central Highlands of Vietnam: Report on Pilot Trial Design and Results from Two Hydrological Years (May 2017 to April 2019); International Water Management Institute (IWMI): Colombo, Sri Lanka, 2020. [Google Scholar]
- Da Costa, L.R.D.; Monteiro, J.P.P.G.; Hugman, R.T. Assessing the Use of Harvested Greenhouse Runoff for Managed Aquifer Recharge to Improve Groundwater Status in South Portugal. Environ. Earth Sci. 2020, 79, 253. [Google Scholar] [CrossRef]
- Amanambu, A.C.; Obarein, O.A.; Mossa, J.; Li, L.; Ayeni, S.S.; Balogun, O.; Oyebamiji, A.; Ochege, F.U. Groundwater System and Climate Change: Present Status and Future Considerations. J. Hydrol. 2020, 589, 125163. [Google Scholar] [CrossRef]
- Atawneh, D.; Cartwright, N.; Bertone, E. Climate Change and Its Impact on the Projected Values of Groundwater Recharge: A Review. J. Hydrol. 2021, 601, 126602. [Google Scholar] [CrossRef]
- Harrison, P.A.; Dunford, R.; Savin, C.; Rounsevell, M.D.A.; Holman, I.P.; Kebede, A.S.; Stuch, B. Cross-Sectoral Impacts of Climate Change and Socio-Economic Change for Multiple, European Land- and Water-Based Sectors. Clim. Chang. 2015, 128, 279–292. [Google Scholar] [CrossRef]
- Arnell, N.W.; Brown, S.; Gosling, S.N.; Gottschalk, P.; Hinkel, J.; Huntingford, C.; Lloyd-Hughes, B.; Lowe, J.A.; Nicholls, R.J.; Osborn, T.J.; et al. The Impacts of Climate Change across the Globe: A Multi-Sectoral Assessment. Clim. Chang. 2016, 134, 457–474. [Google Scholar] [CrossRef] [Green Version]
- Scanlon, B.R.; Reedy, R.C.; Faunt, C.C.; Pool, D.; Uhlman, K. Enhancing Drought Resilience with Conjunctive Use and Managed Aquifer Recharge in California and Arizona. Environ. Res. Lett. 2016, 11, 035013. [Google Scholar] [CrossRef] [Green Version]
- Dahlke, H.E.; LaHue, G.T.; Mautner, M.R.L.; Murphy, N.P.; Patterson, N.K.; Waterhouse, H.; Yang, F.; Foglia, L. Managed Aquifer Recharge as a Tool to Enhance Sustainable Groundwater Management in California. In Advances in Chemical Pollution, Environmental Management and Protection Vol. 3; Elsevier: Amsterdam, Netherlands, 2018; pp. 215–275. [Google Scholar] [CrossRef]
- Alam, S.; Borthakur, A.; Ravi, S.; Gebremichael, M.; Mohanty, S.K. Managed Aquifer Recharge Implementation Criteria to Achieve Water Sustainability. Sci. Total Environ. 2021, 768, 144992. [Google Scholar] [CrossRef]
- Van Engelenburg, J.; Hueting, R.; Rijpkema, S.; Teuling, A.J.; Uijlenhoet, R.; Ludwig, F. Impact of Changes in Groundwater Extractions and Climate Change on Groundwater-Dependent Ecosystems in a Complex Hydrogeological Setting. Water Resour. Manag. 2018, 32, 259–272. [Google Scholar] [CrossRef] [Green Version]
- Havril, T.; Tóth, Á.; Molson, J.W.; Galsa, A.; Mádl-Szőnyi, J. Impacts of Predicted Climate Change on Groundwater Flow Systems: Can Wetlands Disappear Due to Recharge Reduction? J. Hydrol. 2018, 563, 1169–1180. [Google Scholar] [CrossRef] [Green Version]
- Trásy-Havril, T.; Szkolnikovics-Simon, S.; Mádl-Szőnyi, J. How Complex Groundwater Flow Systems Respond to Climate Change Induced Recharge Reduction? Water 2022, 14, 3026. [Google Scholar] [CrossRef]
- Aldous, A.R.; Gannett, M.W. Groundwater, Biodiversity, and the Role of Flow System Scale. Ecohydrology 2021, 14, 1–14. [Google Scholar] [CrossRef]
- Engelen, G.B.; Kloosterman, F.H. Hydrological Systems Analysis: Methods and Applications. Water Science and Technology Library; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996; Volume 20. [Google Scholar]
- Fernández Escalante, E.; San Sebastián Sauto, J.; Calero Gil, R. Sites and Indicators of MAR as a Successful Tool to Mitigate Climate Change Effects in Spain. Water 2019, 11, 1943. [Google Scholar] [CrossRef] [Green Version]
- Henao Casas, J.D.; Fernández Escalante, E.; Calero Gil, R.; Ayuga, F. Managed Aquifer Recharge as a Low-Regret Measure for Climate Change Adaptation: Insights from Los Arenales, Spain. Water 2022, 14, 3703. [Google Scholar] [CrossRef]
- Ghasemi, A.; Saghafian, B.; Golian, S. Optimal Location of Artificial Recharge of Treated Wastewater Using Fuzzy Logic Approach. J. Water Supply Res. Technol.-Aqua 2017, 66, 141–156. [Google Scholar] [CrossRef]
- Tóth, J. A Theory of Groundwater Motion in Small Drainage Basins in Central Alberta, Canada. J. Geophys. Res. 1962, 67, 4375–4388. [Google Scholar] [CrossRef]
- Jiang, X.-W.; Wan, L.; Wang, X.-S.; Ge, S.; Liu, J. Effect of Exponential Decay in Hydraulic Conductivity with Depth on Regional Groundwater Flow. Geophys. Res. Lett. 2009, 36, L24402. [Google Scholar] [CrossRef]
- Freeze, R.A.; Witherspoon, P.A. Theoretical Analysis of Regional Groundwater Flow: 1. Analytical and Numerical Solutions to the Mathematical Model. Water Resour. Res. 1966, 2, 641–656. [Google Scholar] [CrossRef] [Green Version]
- Domenico, P.A.; Palciauskas, V.V. Theoretical Analysis of Forced Convective Heat Transfer in Regional Ground-Water Flow. Geol. Soc. Am. Bull. 1973, 84, 3803. [Google Scholar] [CrossRef]
- An, R.; Jiang, X.-W.; Wang, J.-Z.; Wan, L.; Wang, X.-S.; Li, H. A Theoretical Analysis of Basin-Scale Groundwater Temperature Distribution. Hydrogeol. J. 2015, 23, 397–404. [Google Scholar] [CrossRef]
- Szijártó, M.; Galsa, A.; Tóth, Á.; Mádl-Szőnyi, J. Numerical Investigation of the Combined Effect of Forced and Free Thermal Convection in Synthetic Groundwater Basins. J. Hydrol. 2019, 572, 364–379. [Google Scholar] [CrossRef]
- GEO-SLOPE. Seepage Modeling with SEEP/W—An Engineering Methodology. Users Guide; GEO-SLOPE International Ltd.: Calgary, AB, Canada, 2015. [Google Scholar]
- Van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Woessner, W.W.; Poeter, E.P. Hydrogeologic Properties of Earth Materials and Principles of Groundwater Flow; The Groundwater Project: Guelph, ON, Canada, 2020. [Google Scholar]
- Kiss, T.; Hernesz, P.; Sümeghy, B.; Györgyövics, K.; Sipos, G. The Evolution of the Great Hungarian Plain Fluvial System—Fluvial Processes in a Subsiding Area from the Beginning of the Weichselian. Quat. Int. 2015, 388, 142–155. [Google Scholar] [CrossRef] [Green Version]
- Gábris, G. Pleistocene Evolution of the Danube in the Carpathian Basin. Terra Nova 1994, 6, 495–501. [Google Scholar] [CrossRef]
- Gábris, G.Y.; Horváth, E.; Novothny, Á.; Ruszkiczay-Rüdiger, Z.S. Fluvial and Aeolian Landscape Evolution in Hungary—Results of the Last 20 Years Research. Neth. J. Geosci.-Geol. Mijnb. 2012, 91, 111–128. [Google Scholar] [CrossRef] [Green Version]
- Major, P.; Neppel, F. A Duna-Tisza Közi Talajvízszint-Süllyedések (Water Level Decline in the Danube-Tisza Interfluve). Vízügyi Közlemények 1988, 70, 605–623. [Google Scholar]
- Kovács, A.D.; Hoyk, E.; Farkas, J.Z. Homokhátság—A Special Rural Area Affected by Aridification in the Carpathian Basin, Hungary. Eur. Countrys. 2017, 9, 29–50. [Google Scholar] [CrossRef] [Green Version]
- Pálfai, I. A Duna-Tisza Közi Hátság Vízháztartási Sajátosságai (Water Management in the Region between Danube and Tisza). Hidrológiai Közlöny 2010, 90, 40–44. [Google Scholar]
- Pálfai, I. Talajvízszint-Süllyedés a Duna-Tisza Közén (Water Level Decline in the Danube-Tisza Interfluve). Vízügyi Közlemények 1993, 75, 431–434. [Google Scholar]
- Szilágyi, J.; Vorosmarty, C.J. Modelling Unconfined Aquifer Level Reductions in the Area between the Danube and Tisza Rivers in Hungary. J. Hydrol. Hydromech. 1997, 45, 328–347. [Google Scholar]
- Orlóci, I. A Tiszát a Dunával Összekötő Csatorna: A Duna-Tisza Csatorna (A Conception over the Canal between Danube and Tisza in Our Days). Hidrol. Közlöny 2003, 83, 243–250. [Google Scholar]
- Alföldi, L.; Kapolyi, L. Szükséges-e a Tisza Térség Vízhiányának a Pótlására És/Vagy a Hajózó Út Vonal Lerövidítésére Duna-Tisza Csatornát Építeni? Ha Igen, Miért Nem, És Ha Nem, Miért Igen? (Conception over the Canal between the Danube and Tisza in Hungary). Hidrol. Közlöny 2011, 91, 1–28. [Google Scholar]
- Nagy, I.; Tombácz, E.; László, T.; Magyar, E.; Mészáros, S.; Puskás, E.; Scheer, M. Vízvisszatartási Mintaprojektek a Homokhátságon: „Nyugati És Keleti” Mintaterületek (Surface Water Detention Pilot Projects in the Danube-Tisza Sand Plateau Region of Hungary: „Western and Eastern” Sample Areas). Hidrol. Közlöny 2016, 96, 42–60. [Google Scholar]
- Nemere, P. Javaslat a Duna-Tisza Közi Hátság Mélységi Vízkészletének Pótlására (Supplementing the Deep Groundwater Resource of the Area between the Rivers Danube and Tisza). Vízügyi Közlemények 1994, 76, 339–342. [Google Scholar]
- Gyirán, I. A Duna-Tisza Közi Homokhátság Vízgazdálkodásának Fenntartható Fejlesztése (Sustainable Development of the Water Management of the Danube-Tisza Interfluve Area). In Proceedings of the A Magyar Hidrológiai Társaság XXVII. Országos Vándorgyűlése, 2. Szekció, Baja, Hungary, 1–3 July 2009. [Google Scholar]
- Ujházy, N.; Biró, M. A Vizes Élőhelyek Változásai Szabadszállás Határában (Changes of Wetland Habitats in the Territory of Szabadszállás, Hungary). Tájökológiai Lapok 2013, 11, 291–310. [Google Scholar] [CrossRef]
- Mádl-Szőnyi, J.; Tóth, J. A Hydrogeological Type Section for the Duna-Tisza Interfluve, Hungary. Hydrogeol. J. 2009, 17, 961–980. [Google Scholar] [CrossRef]
- Kuti, L.; Kőrössy, L. Az Alföld Földtani Atlasza—Magyarázó. Dunaújváros–Izsák (The Geological Atlas of the Great Hungarian Plain—Map Explainer. Dunaújváros–Izsák); Magyar Állami Földtani Intézet: Budapest, Hungary, 1989. [Google Scholar]
- Oláh, S. Felszínközeli Víztartók Vízgazdálkodási Célú Térképezés Geofizikai Módszerekkel Kerekegyháza Területén (Mapping of near-Surface Aquifers for Water Management Purposes with Geophysical Methods in the Kerekegyháza Area). Bachelor’s Thesis, Eötvös Loránd University, Budapest, Hungary, 2022. [Google Scholar]
- Yousif, N. Potential of Rooftop-Rainwater Harvesting through Shallow Wells for Kerekegyháza -Hungary. Master’s Thesis, Eötvös Loránd University, Budapest, Hungary, 2022. [Google Scholar]
- Szabó, Z.; Pedretti, D.; Masetti, M.; Ridavits, T.; Csiszár, E.; Falus, G.; Palcsu, L.; Mádl-Szőnyi, J. Rooftop Rainwater Harvesting by a Shallow Well—Impacts and Potential from a Field Experiment in the Danube-Tisza Interfluve, Hungary. Groundw. Sustain. Dev. 2023, 20, 100884. [Google Scholar] [CrossRef]
- Wu, P.; Shu, L.; Comte, J.-C.; Zuo, Q.; Wang, M.; Li, F.; Chen, H. The Effect of Typical Geological Heterogeneities on the Performance of Managed Aquifer Recharge: Physical Experiments and Numerical Simulations. Hydrogeol. J. 2021, 29, 2107–2125. [Google Scholar] [CrossRef]
- Clark, R.; Gonzalez, D.; Dillon, P.; Charles, S.; Cresswell, D.; Naumann, B. Reliability of Water Supply from Stormwater Harvesting and Managed Aquifer Recharge with a Brackish Aquifer in an Urbanising Catchment and Changing Climate. Environ. Model. Softw. 2015, 72, 117–125. [Google Scholar] [CrossRef]
- Racz, A.J.; Fisher, A.T.; Schmidt, C.M.; Lockwood, B.S.; Huertos, M.L. Spatial and Temporal Infiltration Dynamics During Managed Aquifer Recharge. Groundwater 2012, 50, 562–570. [Google Scholar] [CrossRef]
- Qi, T.; Shu, L.; Li, H.; Wang, X.; Men, Y.; Opoku, P.A. Water Distribution from Artificial Recharge via Infiltration Basin under Constant Head Conditions. Water 2021, 13, 1052. [Google Scholar] [CrossRef]
- Zou, Z.; Shu, L.; Min, X.; Chifuniro Mabedi, E. Clogging of Infiltration Basin and Its Impact on Suspended Particles Transport in Unconfined Sand Aquifer: Insights from a Laboratory Study. Water 2019, 11, 1083. [Google Scholar] [CrossRef] [Green Version]
- Cannavo, P.; Coulon, A.; Charpentier, S.; Béchet, B.; Vidal-Beaudet, L. Water Balance Prediction in Stormwater Infiltration Basins Using 2-D Modeling: An Application to Evaluate the Clogging Process. Int. J. Sediment Res. 2018, 33, 371–384. [Google Scholar] [CrossRef]
- Alam, M.F.; Pavelic, P. Underground Transfer of Floods for Irrigation (UTFI): Exploring Potential at the Global Scale; International Water Management Institute (IWMI): Colombo, Sri Lanka, 2020. [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005, the US Geological Survey Modular Ground-Water Model: The Ground-Water Flow Process; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2005; Volume 6. [Google Scholar]
- Diersch, H.J.G. FEFLOW: Finite Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zimmerman, W.B. Multiphysics Modeling with Finite Element Methods; World Scientific Publishing Company: Singapore, 2006; Volume 18. [Google Scholar]
- Tzoraki, O.; Dokou, Z.; Christodoulou, G.; Gaganis, P.; Karatzas, G. Assessing the Efficiency of a Coastal Managed Aquifer Recharge (MAR) System in Cyprus. Sci. Total Environ. 2018, 626, 875–886. [Google Scholar] [CrossRef]
- Abbo, H.; Gev, I. Numerical Model as a Predictive Analysis Tool for Rehabilitation and Conservation of the Israeli Coastal Aquifer: Example of the SHAFDAN Sewage Reclamation Project. Desalination 2008, 226, 47–55. [Google Scholar] [CrossRef]
- Ringleb, J.; Sallwey, J.; Stefan, C. Assessment of Managed Aquifer Recharge through Modeling—A Review. Water 2016, 8, 579. [Google Scholar] [CrossRef] [Green Version]
- Simon, S.; Mádl-Szőnyi, J.; Müller, I.; Pogácsás, G. Conceptual Model for Surface Salinization in an Overpressured and a Superimposed Gravity-Flow Field, Lake Kelemenszék Area, Hungary. Hydrogeol. J. 2011, 19, 701–717. [Google Scholar] [CrossRef]
- Kacimov, A.R.; Zlotnik, V.; Al-Maktoumi, A.; Al-Abri, R. Modeling of Transient Water Table Response to Managed Aquifer Recharge: A Lagoon in Muscat, Oman. Environ. Earth Sci. 2016, 75, 318. [Google Scholar] [CrossRef]
- Yaraghi, N.; Ronkanen, A.; Darabi, H.; Kløve, B.; Torabi Haghighi, A. Impact of Managed Aquifer Recharge Structure on River Flow Regimes in Arid and Semi-Arid Climates. Sci. Total Environ. 2019, 675, 429–438. [Google Scholar] [CrossRef]
- Kourakos, G.; Dahlke, H.E.; Harter, T. Increasing Groundwater Availability and Seasonal Base Flow Through Agricultural Managed Aquifer Recharge in an Irrigated Basin. Water Resour. Res. 2019, 55, 7464–7492. [Google Scholar] [CrossRef] [Green Version]
- Tóth, J. Hydraulic Continuity in Large Sedimentary Basins. Hydrogeol. J. 1995, 3, 4–16. [Google Scholar] [CrossRef]
| Parameters | Units | 1. Topography (SG-1) | 2. Model Length (SG-2) | 3. Elevation of Water Table (SG-3) | 4. Material Properties (SG-4) | 5. Heterogeneity (SG-5) | 6. Basin Parameters (SG-6) | 7. Case Study (K1–3) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A. Discharge Area | B. Recharge Area | A. Kxx | B. ε | C. θs | A. w | B. d | ||||||
| Length (L) | m | 2000 | 2000–10,000 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 6500 |
| Topography (Δz) | m | 0–40 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 14 |
| Hydraulic head difference (Δh) | m | 0–6 | 0–6 | 0–6 | 0–6 | 0–6 | 0–6 | 0–6 | 3 | 0–6 | 0–6 | 10 |
| Water level at the left side (hl) | m | 38 | 38 | 36–39 | changing based on Δh and hr | 38 | 38 | 38 | 38 | 38 | 38 | 101 |
| Water level at the right side (hr) | m | changing based on Δh | changing based on Δh | changing based on Δh and hl | 36–39 | changing based on Δh | changing based on Δh | changing based on Δh | 41 | changing based on Δh | changing based on Δh | 111 |
| Horizontal hydraulic conductivity (Kxx) | m/s | 1∙10−5 | 1∙10−5 | 1∙10−5 | 1∙10−5 | 1∙10−7–1∙10−5 | 1∙10−5 | 1∙10−5 | 1∙10−5, layer/lenses with different K’xx changing between 1∙10−7 and 1∙10−5 | 1∙10−5 | 1∙10−5 | 5∙10−6, layer/lenses with K’xx = 5∙10−7 |
| Anisotropy coefficient (ε) | - | 1 | 1 | 1 | 1 | 1 | 1, 10, 100 | 1 | 1 | 1 | 1 | 1 |
| Saturated water content (θs) | - | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 | 0.25–0.45 | 0.35 | 0.35 | 0.35 | 0.35 |
| Infiltration basin width (w) | m | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 50–150 | 100 | 100 |
| Water depth in the infiltration basin (d) | m | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.5–2 | 1 |
| Number of scenarios | 29 | 21 | 28 | 28 | 49 | 21 | 35 | 35 | 21 | 28 | 3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szabó, Z.; Szijártó, M.; Tóth, Á.; Mádl-Szőnyi, J. The Significance of Groundwater Table Inclination for Nature-Based Replenishment of Groundwater-Dependent Ecosystems by Managed Aquifer Recharge. Water 2023, 15, 1077. https://doi.org/10.3390/w15061077
Szabó Z, Szijártó M, Tóth Á, Mádl-Szőnyi J. The Significance of Groundwater Table Inclination for Nature-Based Replenishment of Groundwater-Dependent Ecosystems by Managed Aquifer Recharge. Water. 2023; 15(6):1077. https://doi.org/10.3390/w15061077
Chicago/Turabian StyleSzabó, Zsóka, Márk Szijártó, Ádám Tóth, and Judit Mádl-Szőnyi. 2023. "The Significance of Groundwater Table Inclination for Nature-Based Replenishment of Groundwater-Dependent Ecosystems by Managed Aquifer Recharge" Water 15, no. 6: 1077. https://doi.org/10.3390/w15061077








