Estimation of the Evapotranspiration of Irrigated Açaí (Euterpe oleracea M.), through the Surface Energy Balance Algorithm for Land—SEBAL, in Eastern Amazonia
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data from Landsat 8 Satellite Sensors
2.3. Surface Energy Balance Algorithm for Land (SEBAL) Method
2.4. Algorithm Performance
3. Results
3.1. Weather Conditions
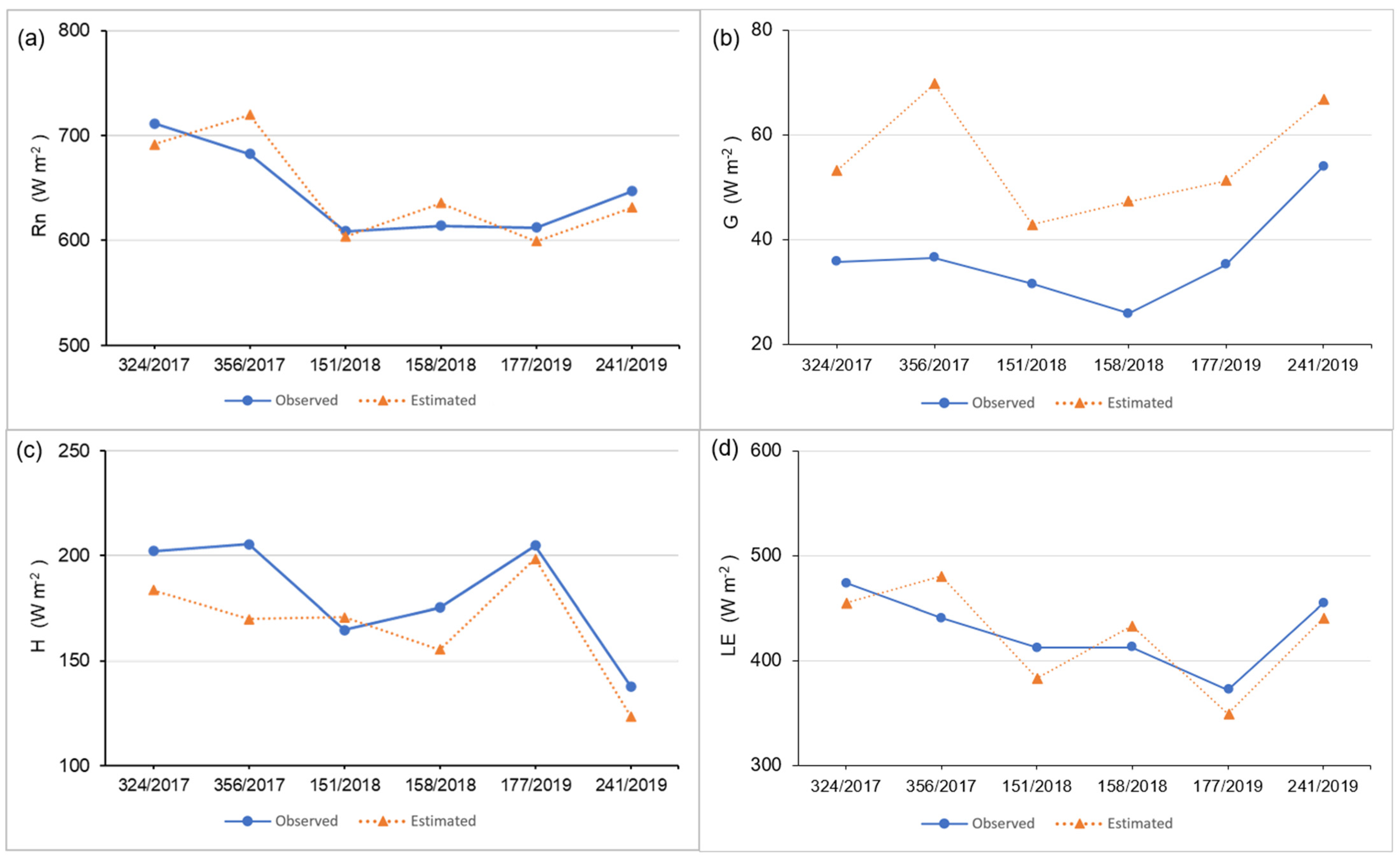
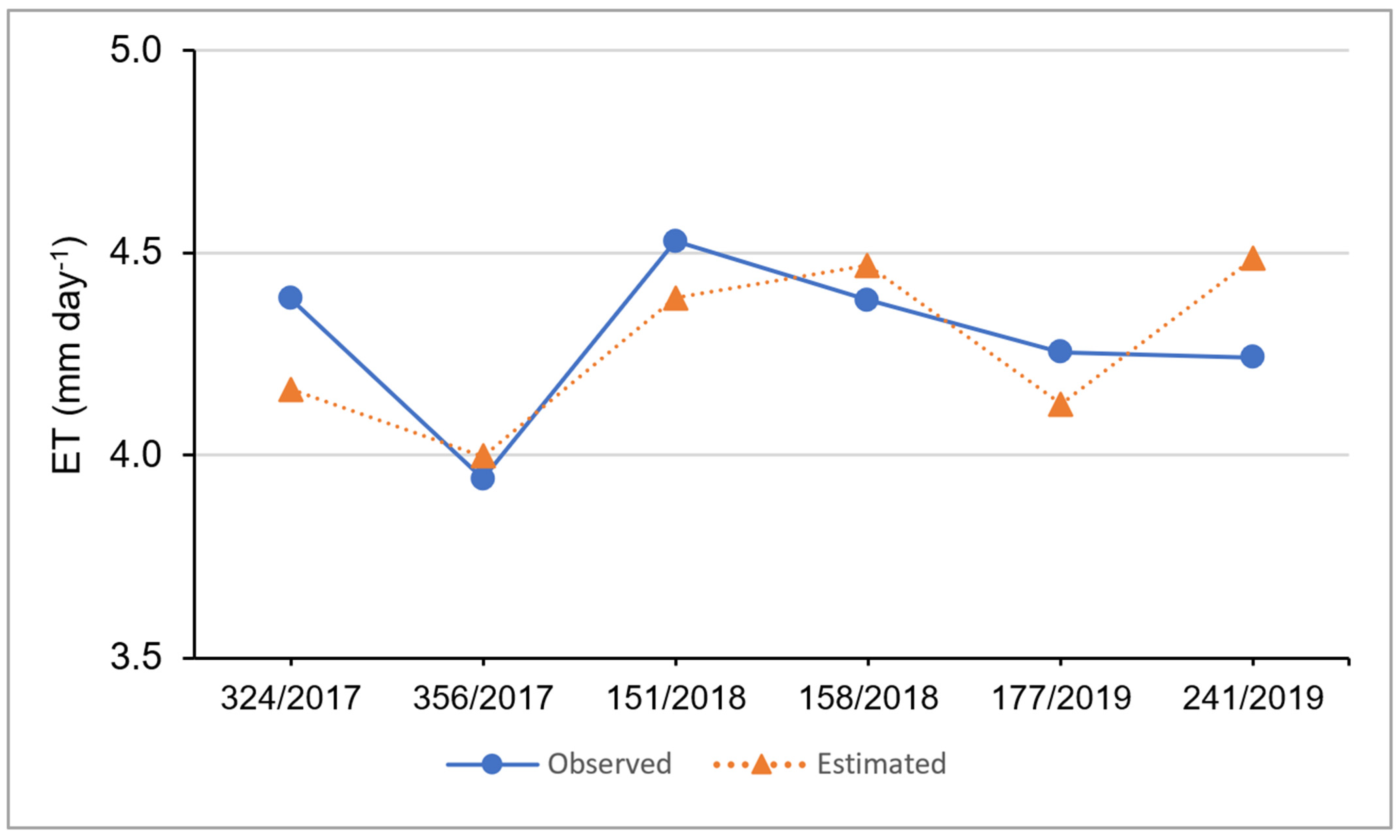
3.2. Comparison with Field Data
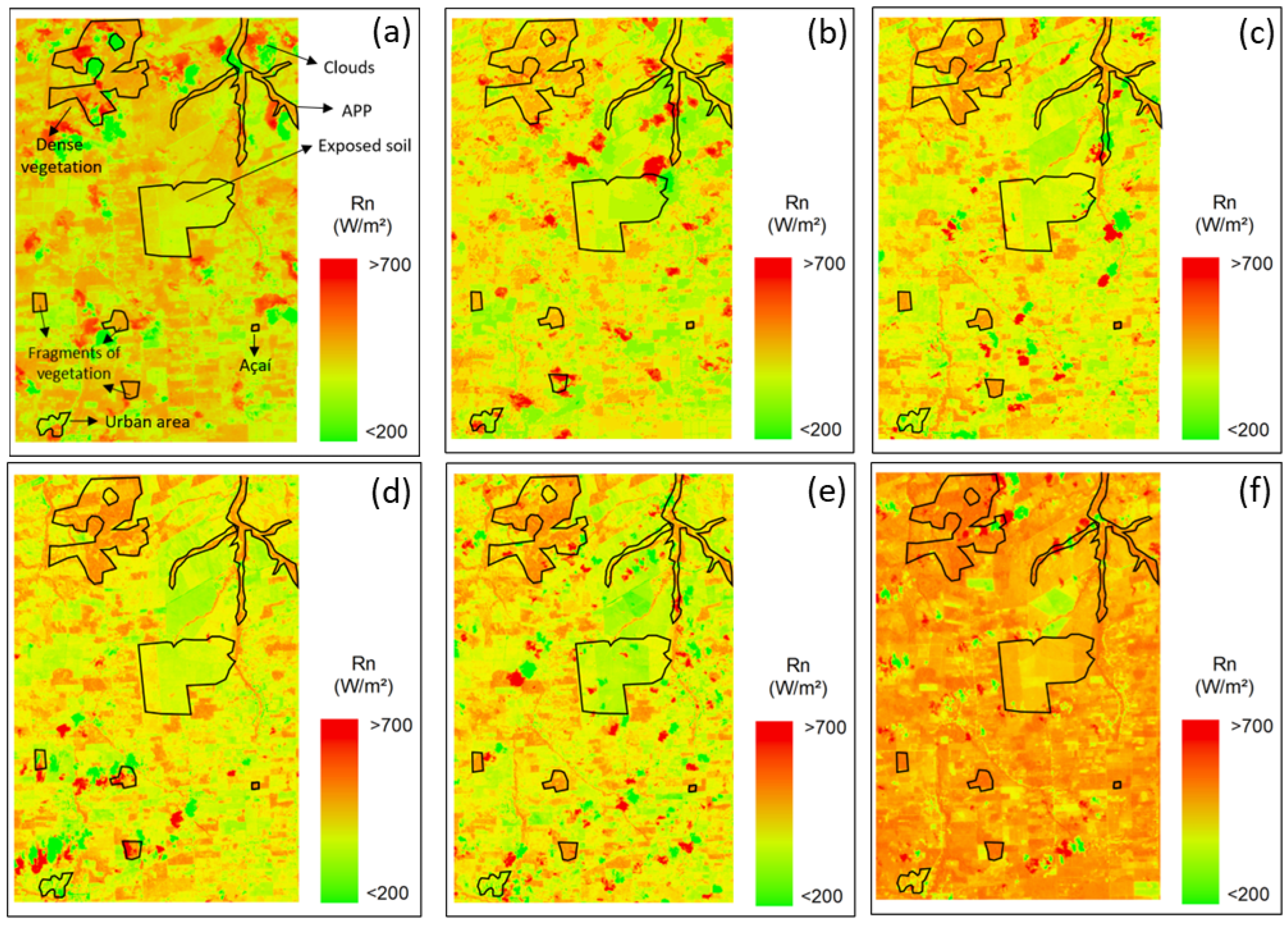
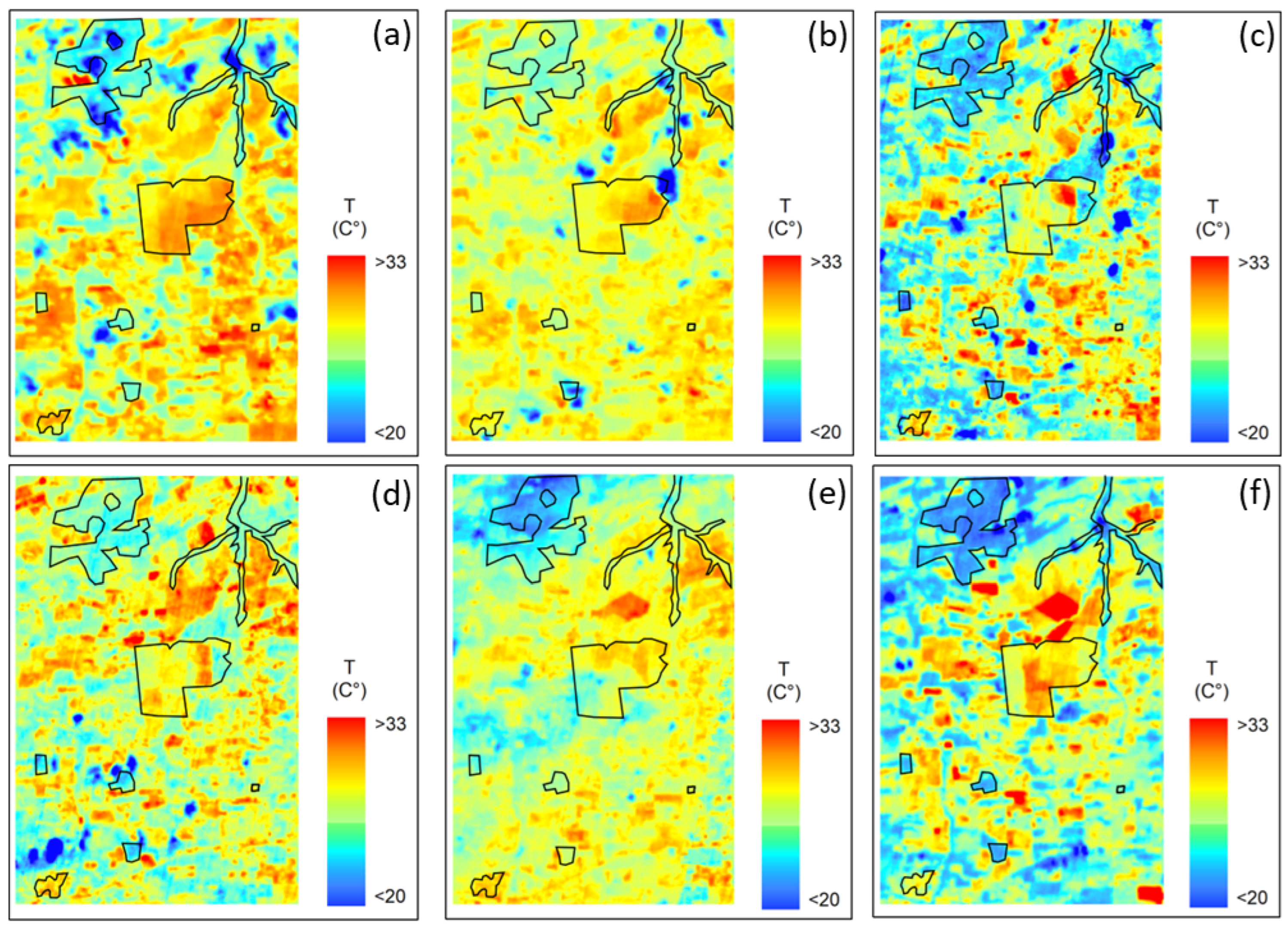
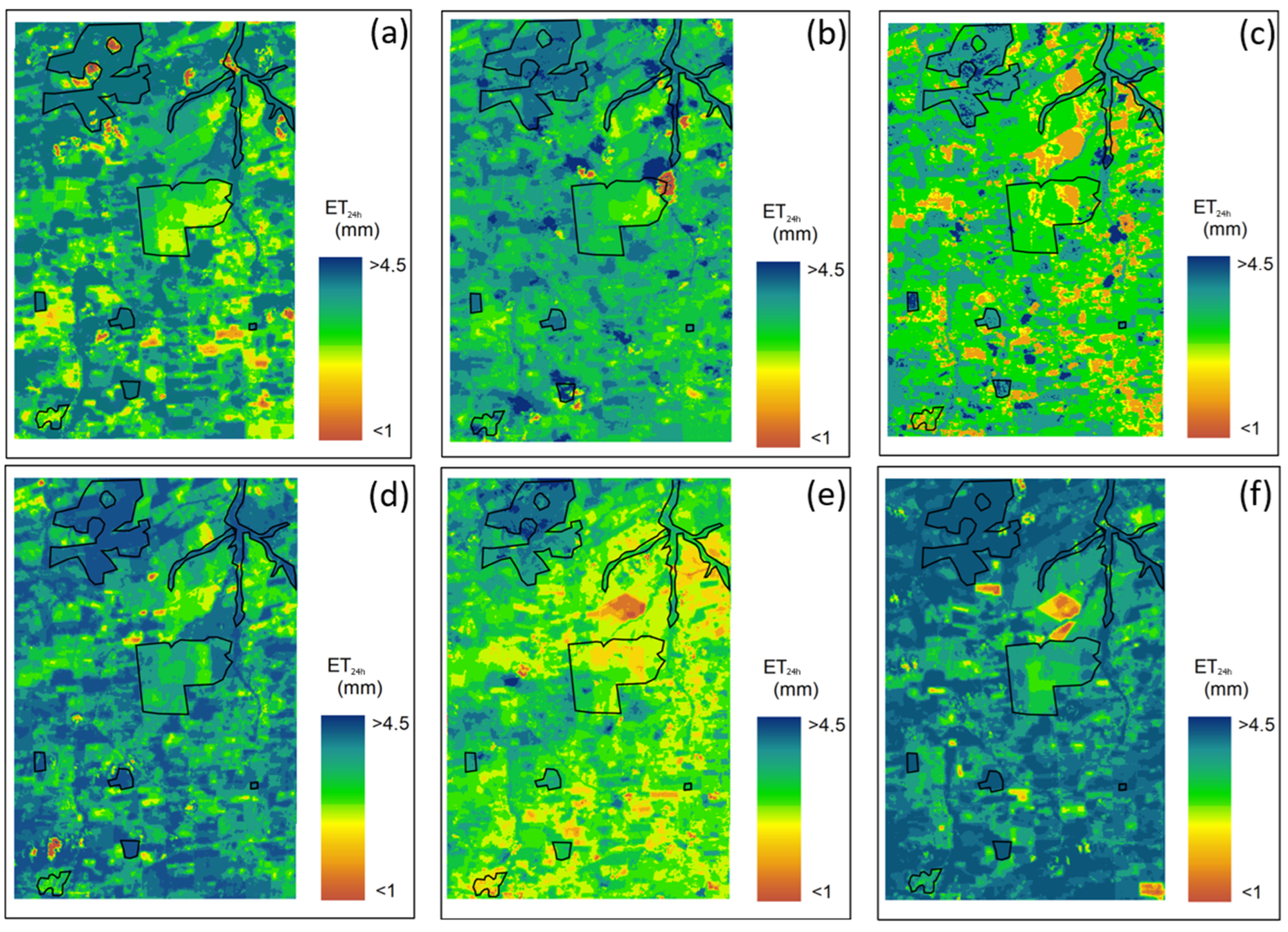
3.3. Spatialization of Energy Balance and Evapotranspiration Components
4. Discussion
4.1. Comparison with Field Data
4.2. Spatialization of Energy Balance and Evapotranspiration Components
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Elliott, J.; Deryng, D.; Müller, C.; Frieler, K.; Konzmann, M.; Gerten, D.; Glotter, M.; Flörke, M.; Wada, Y.; Best, N.; et al. Constraints and Potentials of Future Irrigation Water Availability on Agricultural Production under Climate Change. Proc. Natl. Acad. Sci. USA 2014, 111, 3239–3244. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, S.; Bhatta, B.; Shrestha, M.; Shrestha, P.K. Integrated Assessment of the Climate and Landuse Change Impact on Hydrology and Water Quality in the Songkhram River Basin, Thailand. Sci. Total Environ. 2018, 643, 1610–1622. [Google Scholar] [CrossRef] [PubMed]
- Rosa, L.; Chiarelli, D.D.; Rulli, M.C.; Dell’Angelo, J. Global agricultual economic water scarcity. Sci. Adv. 2020, 6, eaaz6031. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Xu, Y.; Fu, Q.; Singh, V.P.; Liu, D.; Li, T. Efficient irrigation water allocation and its impact on agricultural sustainability and water scarcity under uncertainty. J. Hidrol. 2020, 586, 124888. [Google Scholar] [CrossRef]
- Sousa, F.F.; Vieira-Da-Silva, C.; Barros, F.B. The (in)Visible Market of Miriti (Mauritia flexuosa L.f.) Fruits, the ‘Winter Acai’ in Amazonian Riverine Communities of Abaetetuba, Northern Brazil. Glob. Ecol. Conserv. 2018, 14, e00393. [Google Scholar] [CrossRef]
- Sousa, D.D.P.; Fernandes, T.F.S.; Tavares, L.B.; Farias, V.D.D.S.; De Lima, M.J.A.; Nunes, H.G.G.C.; Costa, D.L.P.; Ortega-Farias, S.; Souza, P.J.D.O.P. Estimation of Evapotranspiration and Single and Dual Crop Coefficients of Acai Palm in the Eastern Amazon (Brazil) Using the Bowen Ratio System. Irrig. Sci. 2021, 39, 5–22. [Google Scholar] [CrossRef]
- Canalis-Ide, F.; Zubelzu, S.; Rodríguez-Sinobas, L. Irrigation systems in smart cities coping with water scarcity: The case of Valdebebas, Madrid (Spain). J. Environ. Manag. 2019, 247, 187–195. [Google Scholar] [CrossRef]
- Xu, G.; Xue, X.; Wang, P.; Yang, Z.; Yuan, W.; Liu, X.; Lou, C. A lysimeter study for the effects of different canopy sizes on evapotranspiration and crop coefficient of summer maize. Agric. Water Manag. 2018, 208, 1–6. [Google Scholar] [CrossRef]
- Paço, T.A.; Paredes, P.; Pereira, L.S.; Silvestre, J.; Santos, F.L. Crop Coefficients and Transpiration of a Super Intensive Arbequina Olive Orchard using the Dual Kc Approach and the Kcb Computation with the Fraction of Ground Cover and Height. Water 2019, 11, 383. [Google Scholar] [CrossRef]
- Domínguez-Niño, J.M.; Oliver-Manera, J.; Girona, J.; Casadesús, J. Differential irrigation scheduling by an automated algorithm of water balance tuned by capacitance-type soil moisture sensors. Agric. Water Manag. 2020, 228, 105880. [Google Scholar] [CrossRef]
- Xiong, Y.; Chen, X.; Tang, L.; Wang, H. Comparison of surface renewal and Bowen ratio derived evapotranspiration measurements in an arid vineyard. J. Hidrol. 2022, 613, 128474. [Google Scholar] [CrossRef]
- Martins, S.L.F.; Santos, M.A.; Lyra, G.B.; Souza, J.L.; Lyra, G.B.; Teodoro, I.; Ferreira, F.F.; Ferreira, R.A., Jr.; Almeida, A.C.S.; Souza, R.C. Actual Evapotranspiration for Sugarcane Based on Bowen Ratio-Energy Balance and Soil Water Balance Models with Optimized Crop Coefficients. Water Resour. Manag. 2022, 36, 4557–4574. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL Model with Remotely Sensed Data to Improve Water-Resources Management under Actual Field Conditions. J. Irrig. Drain. Eng. 2005, 6, 85–93. [Google Scholar] [CrossRef]
- Sarwar, A.; Bill, R. Mapping Evapotranspiration in the Indus Basin Using ASTER Data. Int. J. Remote Sens. 2007, 28, 5037–5046. [Google Scholar] [CrossRef]
- Ferreira, T.R.; Silva, B.B.; Moura, M.S.B.; Verhof, A.; Nobrega, R.L.B. The use of remote sensing for reliable estimation of net radiation and its components: A case study for contrasting land covers in an agricultural hotspot of the Brazilian semiarid region. Agric. For. Meteorol. 2020, 291, 188052. [Google Scholar] [CrossRef]
- Kool, D.; Kustas, W.P.; Ben-Gal, A.; Agam, N. Energy partitioning between plant canopy and soil, performance of the two-source energy balance model in a vineyard. Agric. For. Meteorol. 2021, 300, 108328. [Google Scholar] [CrossRef]
- Fuentes-Peñailillo, F.; Ortega-Farías, S.; Acevedo-Opazo, C.; Fonseca-Luengo, D. Implementation of a two-source model for estimating the spatial variability of olive evapotranspiration using satellite images and ground-based climate data. Water 2018, 10, 339. [Google Scholar] [CrossRef]
- Bwambale, E.; Abagale, F.K.; Anornu, G.K. Smart irrigation monitoring and control strategies for improving water use efficiency in precision agriculture: A review. Agric. Water Manag. 2022, 260, 107324. [Google Scholar] [CrossRef]
- Qiu, L.; Wu, Y.; Shi, Z.; Chen, Y.; Zhao, F. Quantifying the Responses of Evapotranspiration and Its Components to Vegetation Restoration and Climate Change on the Loess Plateau of China. Remote Sens. 2021, 13, 2358. [Google Scholar] [CrossRef]
- Jardim, A.M.R.F.; Araújo Junior, G.N.; Silva, M.V.; Santos, A.; Silva, J.L.B.; Pandorfi, H.; Oliveira-Junior, J.F.; Teixeira, A.H.C.; Teodoro, P.E.; Lima, J.L.M.P.; et al. Using Remote Sensing to Quantify the Joint Effects of Climate and Land Use/Land Cover Changes on the Caatinga Biome of Northeast Brazilian. Remote Sens. 2022, 14, 1911. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL) 1. Forlmutaion. J. Hydrol. 1998, 213, 198–212. [Google Scholar] [CrossRef]
- Mendonça, J.C.; De Sousa, E.F.; André, R.G.B.; Da Silva, B.B.; Ferreira, N.D.J. Estimativa Do Fluxo Do Calor Sensível Utilizando o Algoritmo SEBAL e Imagens MODIS Para a Região Norte Fluminense, RJ. Rev. Bras. Meteorol. 2012, 27, 85–94. [Google Scholar] [CrossRef]
- Silva, B.B.; Braga, A.C.; Braga, C.C.; De Oliveira, L.M.M.; Galvíncio, J.D.; Montenegro, S.M.G.L. Evapotranspiration and Assessment of Water Consumed in Irrigated Area of the Brazilian Semiarid Region by Remote Sensing|Evapotranspiração e Estimativa Da Água Consumida Em Perímetro Irrigado Do Semiárido Brasileiro Por Sensoriamento Remoto. Pesqui. Agropecu. Bras. 2012, 47, 1218–1226. [Google Scholar] [CrossRef]
- Oliveira, L.M.M.; Montenegro, S.M.G.L.; Da Silva, B.B.; Antonino, A.C.D.; De Moura, A.E.S.S. Evapotranspiração real em bacia hidrográfica do Nordeste brasileiro por meio do SEBAL e produtos MODIS. Rev. Bras. Eng. Agríc. Ambient. 2014, 18, 1039–1046. [Google Scholar] [CrossRef]
- Bezerra, B.G.; da Silva, B.B.; dos Santos, C.A.C.; Bezerra, J.R.C. Actual Evapotranspiration Estimation Using Remote Sensing: Comparison of SEBAL and SSEB Approaches. Adv. Remote Sens. 2015, 4, 234–247. [Google Scholar] [CrossRef]
- Silva, B.B.; Mercante, E.; Boas, M.A.V.; Wrublack, S.C.; Oldoni, L.V.; Melo, F.B.; Cardoso, M.J.; Júnior, A.S.A.; Ribeiro, V.Q. Satellite-Based ET Estimation Using Landsat 8 Images and SEBAL Model. Rev. Cienc. Agron. 2018, 49, 221–227. [Google Scholar] [CrossRef]
- Santos, C.A.C.; Mariano, D.A.; Nascimento, F.D.C.A.D.; Dantas, F.R.D.C.; de Oliveira, G.; Silva, M.T.; da Silva, L.L.; da Silva, B.B.; Bezerra, B.G.; Safa, B.; et al. Spatio-Temporal Patterns of Energy Exchange and Evapotranspiration during an Intense Drought for Drylands in Brazil. Int. J. Appl. Earth Obs. Geoinf. 2019, 85, 101982. [Google Scholar] [CrossRef]
- Moraes, B.C.; Da Costa, J.M.N.; Da Costa, A.C.L.; Costa, M.H. Variação Espacial e Temporal Da Precipitação No Estado Do Pará. Acta Amaz. 2005, 35, 207–214. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N. Measurement and Estimation of Actual Evapotranspiration in the Field under Mediterranean Climate: A Review. Eur. J. Agron. 2000, 13, 125–153. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M. SEBAL-Based Sensible and Latent Heat Fluxes in the Irrigated Gediz Basin, Turkey. J. Hydrol. 2000, 229, 87–100. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Bezerra, B.G.; Da Silva, B.B.; Ferreira, N.J. Estimativa Da Evapotranspiração Real Diária Utilizando-Se Imagens Digitais TM—Landsat 5. Rev. Bras. Meteorol. 2008, 23, 305–317. [Google Scholar] [CrossRef]
- Perez, P.; Castellvi, F.; Ibáñez, M.; Rosell, J. Assessment of Reliability of Bowen Ratio Method for Partitioning Fluxes. Agric. For. Meteorol. 1999, 97, 141–150. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’donnell, J.; Rowe, C.M. Statistics for the Evaluation and Comparison of Models. J. Geophys. Res. Ocean. 1985, 90, 8995–9005. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Paper 56; FAO Irrigation and Drainage: Rome, Italy, 1998; 300p. [Google Scholar]
- Farias, V.D.S.; Costa, D.L.P.; Pinto, J.V.N.; Souza, P.J.O.P.; Souza, E.B.; Ortega-Farias, S. Calibration of reference evapotranspiration models in Pará. Acta Sci. 2020, 42, e42475. [Google Scholar] [CrossRef]
- Souza, P.J.D.O.P.D.; Da Rocha, E.J.P.; Ribeiro, A. Impacts of Soybean Expansion on Radiation Balance in Eastern Amazon. Acta Amaz. 2013, 43, 169–178. [Google Scholar] [CrossRef]
- Oliveira, G.; Brunsell, N.A.; Moraes, E.C.; Bertani, G.; Dos Santos, T.V.; Shimabukuro, Y.E.; Aragão, L.E.O.C. Use of MODIS Sensor Images Combined with Reanalysis Products to Retrieve Net Radiation in Amazonia. Sensors 2016, 16, 956. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, G.; Moraes, E.C. Validação Do Balanço de Radiação Obtido a Partir de Dados MODIS/TERRA Na Amazônia Com Medidas de Superfície Do LBA. Acta Amaz. 2013, 43, 353–363. [Google Scholar] [CrossRef]
- Ruhoff, A.L.; Paz, A.R.; Collischonn, W.; Aragao, L.E.; Rocha, H.R.; Malhi, Y.S. A MODIS-Based Energy Balance to Estimate Evapotranspiration for Clear-Sky Days in Brazilian Tropical Savannas. Remote Sens. 2012, 4, 703–725. [Google Scholar] [CrossRef]
- Santos, C.C.D.; Nascimento, R.L.; Rao, T.V.R.; Manzi, A.O. Net Radiation Estimation under Pasture and Forest in Rondônia, Brazil, with TM Landsat 5 Images. Atmosfera 2011, 24, 435–446. [Google Scholar]
- Timmermans, W.J.; Kustas, W.P.; Anderson, M.C.; French, A.N. An Intercomparison of the Surface Energy Balance Algorithm for Land (SEBAL) and the Two-Source Energy Balance (TSEB) Modeling Schemes. Remote Sens. Environ. 2007, 108, 369–384. [Google Scholar] [CrossRef]
- Monteiro, P.F.C.; Fontana, D.C.; Santos, T.V.D.; Roberti, D.R. Estimativa dos componentes do balanço de energia e da evapotranspiração para áreas de cultivo de soja no sul do Brasil utilizando imagens do sensor TM Landsat 5. Bragantia 2014, 73, 72–80. [Google Scholar] [CrossRef]
- French, A.N.; Jacob, F.; Schmugger, T.J.; Kustas, W.P. TSEB vs. SEBAL: Comparison of two Surface Energy Flux Models. In Proceedings of the AGU Spring Meeting Abstracts, Washington, DC, USA, 28–31 May 2002; p. H51D-07. [Google Scholar]
- Passos, E.E.M.; Prado, C.H.B.A.; Aragão, W.M. The Influence of Vapour Pressure Deficit on Leaf Water Relations of Cocos Nucifera in Northeast Brazil. Exp. Agric. 2009, 45, 93–106. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Mallick, K.; Patel, N.; Parihar, J. Regional Clear Sky Evapotranspiration over Agricultural Land Using Remote Sensing Data from Indian Geostationary Meteorological Satellite. J. Hydrol. 2010, 387, 65–80. [Google Scholar] [CrossRef]
- French, A.N.; Hunsaker, D.J.; Sanchez, C.A.; Saber, M.; Gonzalez, J.R.; Anderson, R. Satellite-based NDVI crop coefficients and evapotranspiration with eddy covariance validation for multiple durum wheat fields in the US Southwest. Agric. Water Manag. 2020, 239, 106266. [Google Scholar] [CrossRef]
- Carrasco-Benavides, M.; Ortega-Farías, S.; Lagos, L.O.; Kleissl, J.; Morales-Salinas, L.; Kilic, A. Parameterization of the Satellite-Based Model (METRIC) for the Estimation of Instantaneous Surface Energy Balance Components over a Drip-Irrigated Vineyard. Remote Sens. 2014, 6, 11342–11371. [Google Scholar] [CrossRef]
- Moreira, A.A.; Adamatti, D.S.; Ruhoff, A.L. Avaliação dos produtos de evapotranspiração baseados em sensoriamento remoto MOD16 e GLEAM em sítios de fluxos turbulentos do programa LBA. Ciência Nat. 2018, 40, 112. [Google Scholar] [CrossRef]
- Odi-Lara, M.; Campos, I.; Neale, C.M.U.; Ortega-Farías, S.; Poblete-Echeverría, C.; Balbontín, C.; Calera, A. Estimating Evapotranspiration of an Apple Orchard Using a Remote Sensing-Based Soil Water Balance. Remote Sens. 2016, 8, 253. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, Z.; Zhao, C.; Qu, Y.; Liu, Q.; Zhang, H.; Tong, Y.; Wang, C.; Li, S.; Guo, J.; et al. Statistics for the Evaluation and Comparison of Models. Remote Sens. 2022, 14, 1382. [Google Scholar] [CrossRef]
- Biudes, M.S.; Vourlitis, G.L.; Machado, N.G.; de Arruda, P.H.Z.; Neves, G.A.R.; Lobo, F.D.A.; Neale, C.M.U.; Nogueira, J.D.S. Patterns of Energy Exchange for Tropical Ecosystems across a Climate Gradient in Mato Grosso, Brazil. Agric. For. Meteorol. 2015, 202, 112–124. [Google Scholar] [CrossRef]
- Freire, A.S.; Vitorino, M.I.; Souza, A.M.L.; Germano, M.F. Analysis of the energy balance and CO2 fow under the infuence of the seasonality of climatic elements in a mangrove ecosystem in Eastern Amazon. Int. J. Biometeorol. 2021, 66, 647–659. [Google Scholar] [CrossRef] [PubMed]
- Pereira, P.L.; Rodrigues, H.J.B. Análise e Estimativa Dos Componentes Do Balanço de Energia Em Ecossistema de Manguezal Amazônico. Rev. Bras. Meteorol. 2013, 28, 75–84. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. SEBAL Surface Energy Balance Algorithms for Land: Advanced Training and Users Manual, Idaho Implementation, 1st ed.; Department of Water Resources, University of Idaho: Moscow, ID, USA, 2002.
- Fayech, D.; Tarhouni, J. Climate variability and its efect on normalized diference vegetation index (NDVI) using remote sensing in semiarid area. Model. Earth Syst. Environ. 2021, 7, 1667–1682. [Google Scholar] [CrossRef]




| Weather Variables | Instrument and Model | Sensor Level (m) |
|---|---|---|
| Air temperature | Vaisala thermohygrometer (HMP35A) | 2 and 8 above the ground |
| Relative humidity | Vaisala thermohygrometer (HMP35A) | 2 and 8 above the ground |
| Air temperature | Hobo (STHB-M002) | 0.5 and 2 above the canopy |
| Relative humidity | Hobo (STHB-M002) | 0.5 and 2 above the canopy |
| Soil moisture | Time Domain Reflectometer (CS615) | −0.3 soil surface |
| Rain | Rain gauge (TB4-L) | 0.5 above the canopy |
| Global incident radiation | Pyranometer (CMP6-L) | 2 above the canopy |
| Balance of radiation | Net Radiometer (NR-LITE2-L) | 2 above the canopy |
| Ground heat flow | Soil Heat Flux Plate (HFP01SC-L) | −0.08 soil surface |
| Wind speed and direction | Wind Monitor (05106-L) | 2 above the canopy |
| DOY | cosZ | ||||||
|---|---|---|---|---|---|---|---|
| 324/2017 | 22.6 | 13.6 | 32.5 | 66.5 | 924.06 | 0.722 | 0.871 |
| 356/2017 | 20.3 | 12.7 | 31.3 | 72.5 | 844.67 | 0.721 | 0.829 |
| 151/2018 | 22.0 | 15.2 | 29.6 | 79.6 | 776.36 | 0.706 | 0.817 |
| 158/2018 | 21.2 | 14.7 | 29.4 | 76.7 | 766.94 | 0.709 | 0.810 |
| 177/2019 | 21.9 | 15.3 | 29.3 | 82.6 | 774.03 | 0.703 | 0.801 |
| 241/2019 | 22.2 | 15.5 | 30.2 | 74.6 | 645.98 | 0.717 | 0.872 |
| Rn | G | H | LE | ET24h | |
|---|---|---|---|---|---|
| MAE (W m−2) | 18.65 | 20.81 | 17.97 | 24.03 | 0.45 (mm day−1) |
| MRE (%) | 2.84 | 64.42 | 9.89 | 5.75 | 4.23 |
| RMSE (W m−2) | 25.80 | 22.28 | 24.62 | 31.14 | 0.52 (mm dia−1) |
| d | 0.79 | 0.47 | 0.73 | 0.83 | 0.80 |
| DOY | ETc_O | Kc_E | |||
|---|---|---|---|---|---|
| 324/2017 | 5.36 | 4.16 | 4.44 | 0.78 | 0.83 |
| 356/2017 | 4.22 | 4.00 | 3.99 | 0.94 | 0.95 |
| 151/2018 | 3.88 | 4.39 | 4.53 | 1.13 | 1.17 |
| 158/2018 | 4.08 | 4.47 | 4.38 | 1.09 | 1.07 |
| 177/2019 | 5.13 | 4.13 | 4.52 | 0.80 | 0.88 |
| 241/2019 | 5.61 | 4.49 | 4.59 | 0.80 | 0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souza, P.J.d.O.P.d.; Silva, E.R.R.; Silva, B.B.d.; Ferreira, T.R.; Sousa, D.d.P.; Luz, D.B.d.; Adami, M.; Sousa, A.M.L.d.; Nunes, H.G.G.C.; Fernandes, G.S.T.; et al. Estimation of the Evapotranspiration of Irrigated Açaí (Euterpe oleracea M.), through the Surface Energy Balance Algorithm for Land—SEBAL, in Eastern Amazonia. Water 2023, 15, 1073. https://doi.org/10.3390/w15061073
Souza PJdOPd, Silva ERR, Silva BBd, Ferreira TR, Sousa DdP, Luz DBd, Adami M, Sousa AMLd, Nunes HGGC, Fernandes GST, et al. Estimation of the Evapotranspiration of Irrigated Açaí (Euterpe oleracea M.), through the Surface Energy Balance Algorithm for Land—SEBAL, in Eastern Amazonia. Water. 2023; 15(6):1073. https://doi.org/10.3390/w15061073
Chicago/Turabian StyleSouza, Paulo Jorge de Oliveira Ponte de, Ewelyn Regina Rocha Silva, Bernardo Barbosa da Silva, Thomás Rocha Ferreira, Denis de Pinho Sousa, Denilson Barreto da Luz, Marcos Adami, Adriano Marlison Leão de Sousa, Hildo Giuseppe Garcia Caldas Nunes, Gabriel Siqueira Tavares Fernandes, and et al. 2023. "Estimation of the Evapotranspiration of Irrigated Açaí (Euterpe oleracea M.), through the Surface Energy Balance Algorithm for Land—SEBAL, in Eastern Amazonia" Water 15, no. 6: 1073. https://doi.org/10.3390/w15061073
APA StyleSouza, P. J. d. O. P. d., Silva, E. R. R., Silva, B. B. d., Ferreira, T. R., Sousa, D. d. P., Luz, D. B. d., Adami, M., Sousa, A. M. L. d., Nunes, H. G. G. C., Fernandes, G. S. T., Pinto, J. V. d. N., Farias, V. D. d. S., Oliveira, I. A. d., Silva, S. A. S. d., Costa, J. F., Rua, M. L., Costa, D. L. P., Moura, V. B., Lima, M. J. A. d., ... Ortega-Farias, S. (2023). Estimation of the Evapotranspiration of Irrigated Açaí (Euterpe oleracea M.), through the Surface Energy Balance Algorithm for Land—SEBAL, in Eastern Amazonia. Water, 15(6), 1073. https://doi.org/10.3390/w15061073








