Cross-Correlation Analysis of the Stability of Heterogeneous Slopes
Abstract
:1. Introduction
2. Methodology
2.1. Random Field Modeling of Heterogeneity
2.2. Slope Stability Analysis
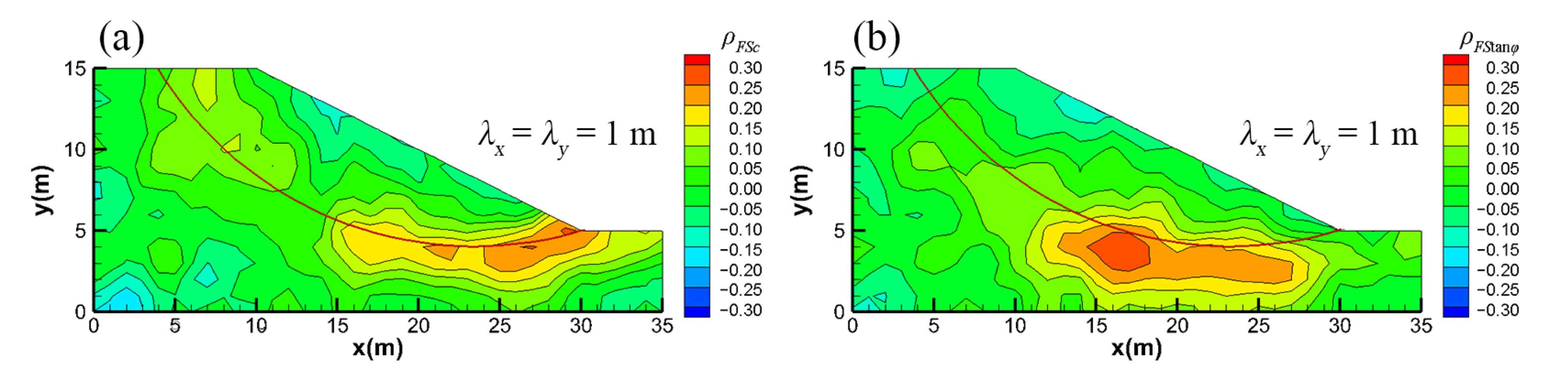
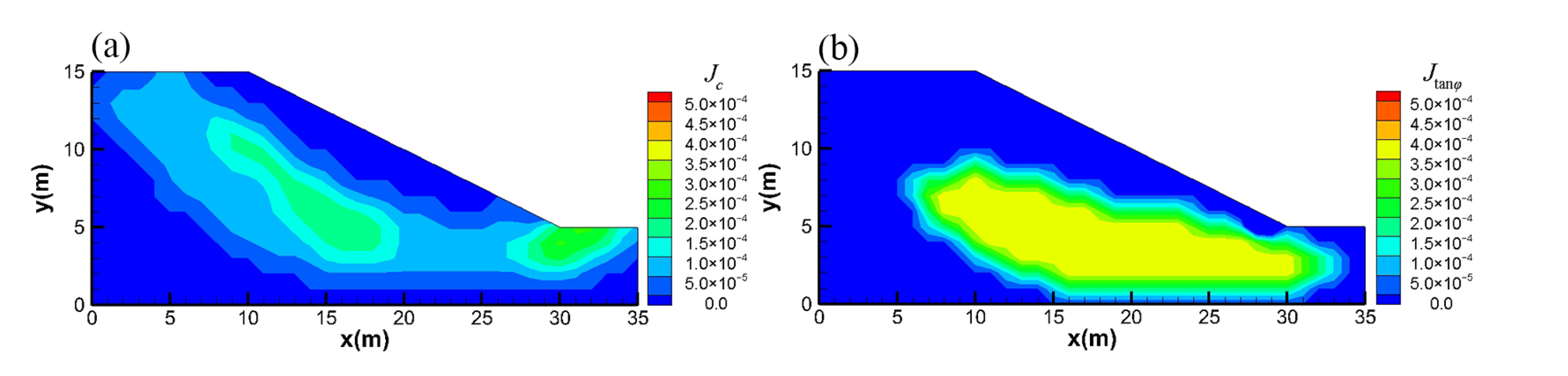
2.3. Cross-Correlation Analysis
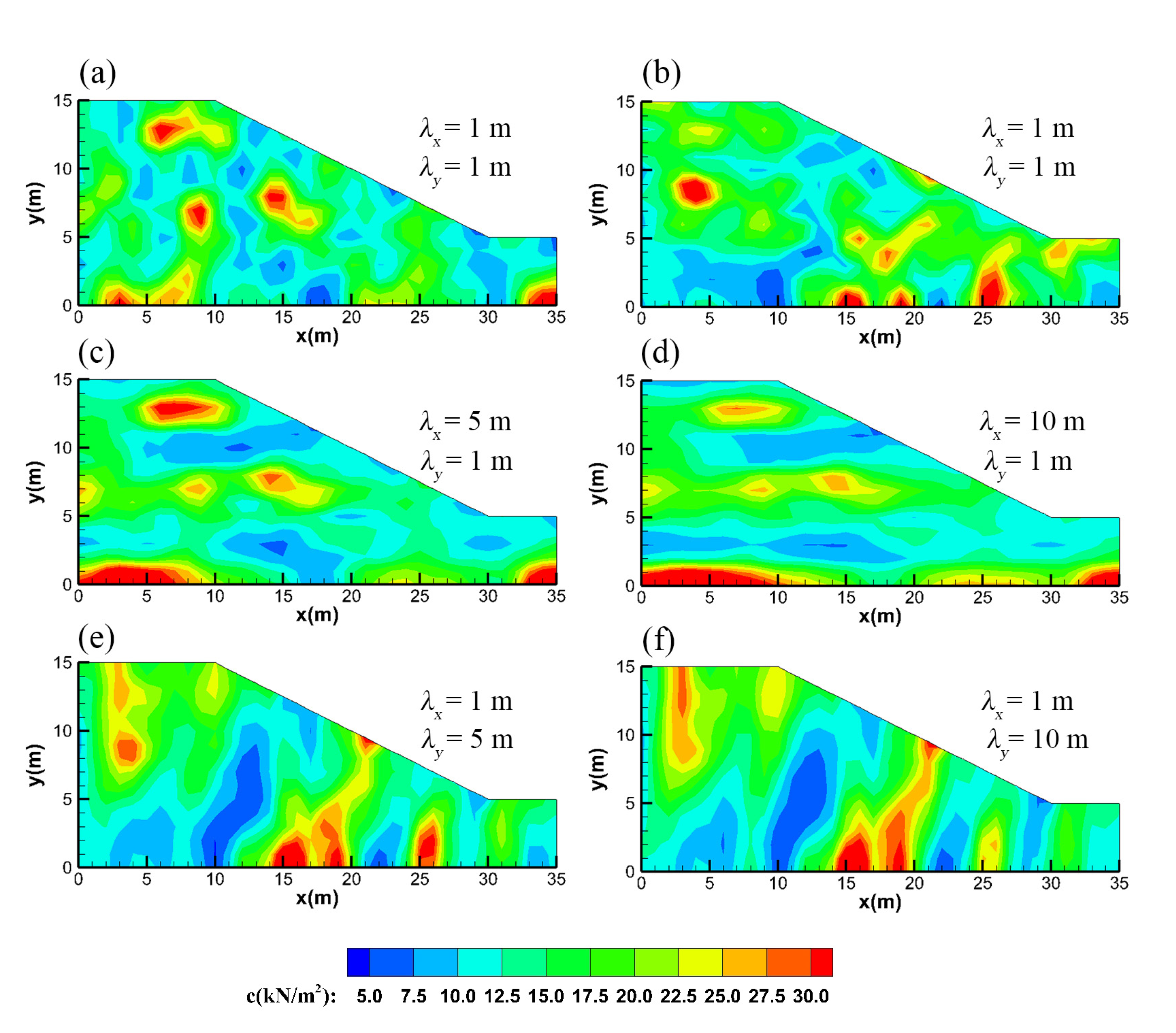
3. Results of Cross-Correlation Analysis for Statistical Isotropy
4. Results of Cross-Correlation Analysis for Statistical Anisotropy
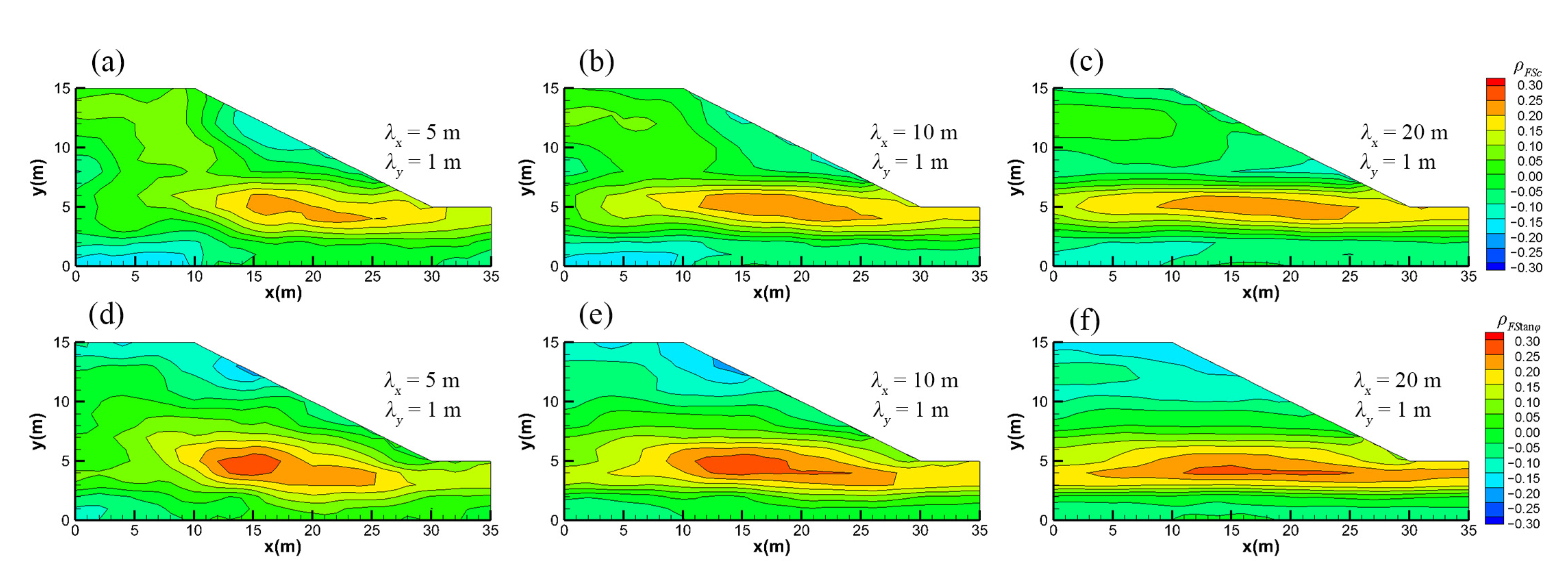
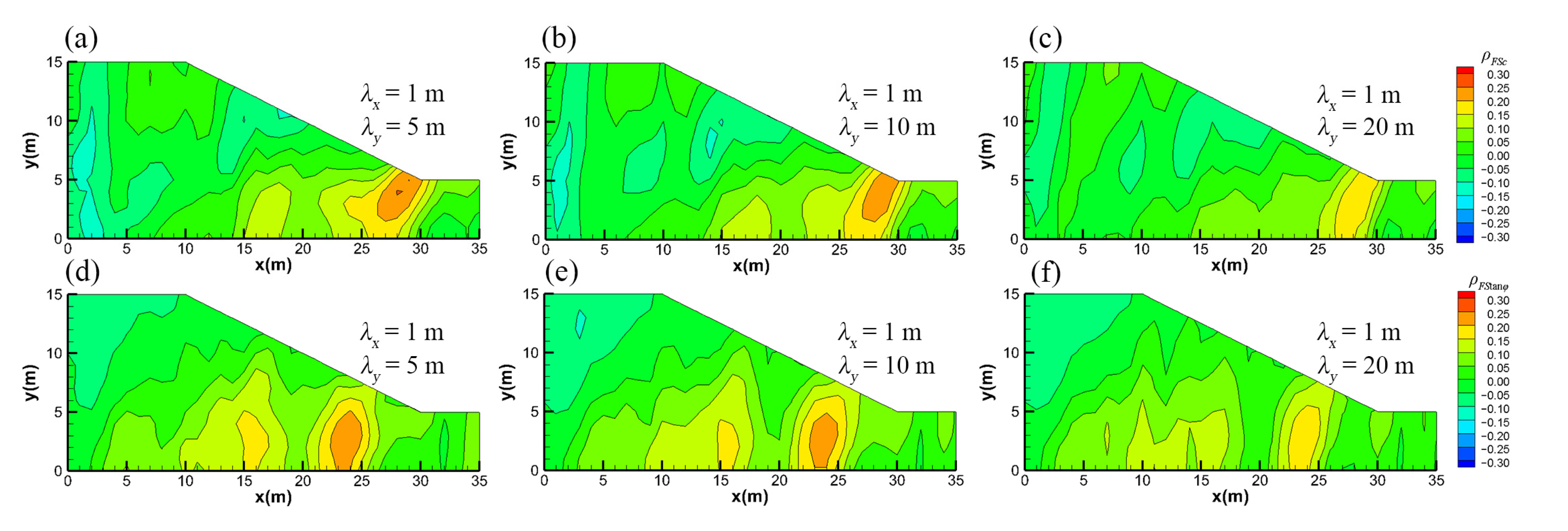
4.1. Statistical Horizontal Anisotropy (Horizontal Correlation Scale > Vertical Correlation Scale)
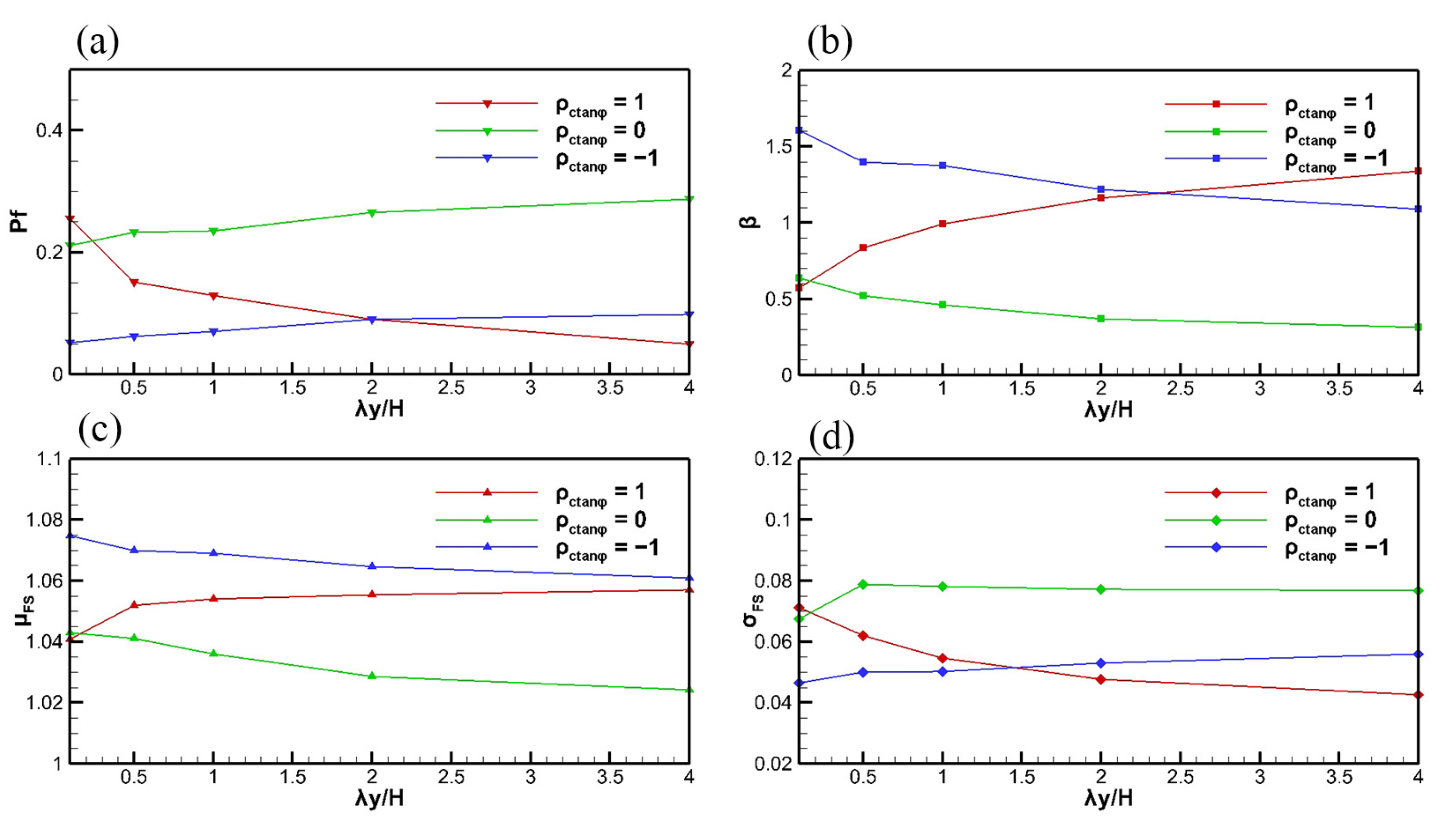
4.2. Statistical Vertical Anisotropy (Horizontal Correlation Scale < Vertical Correlation Scale)
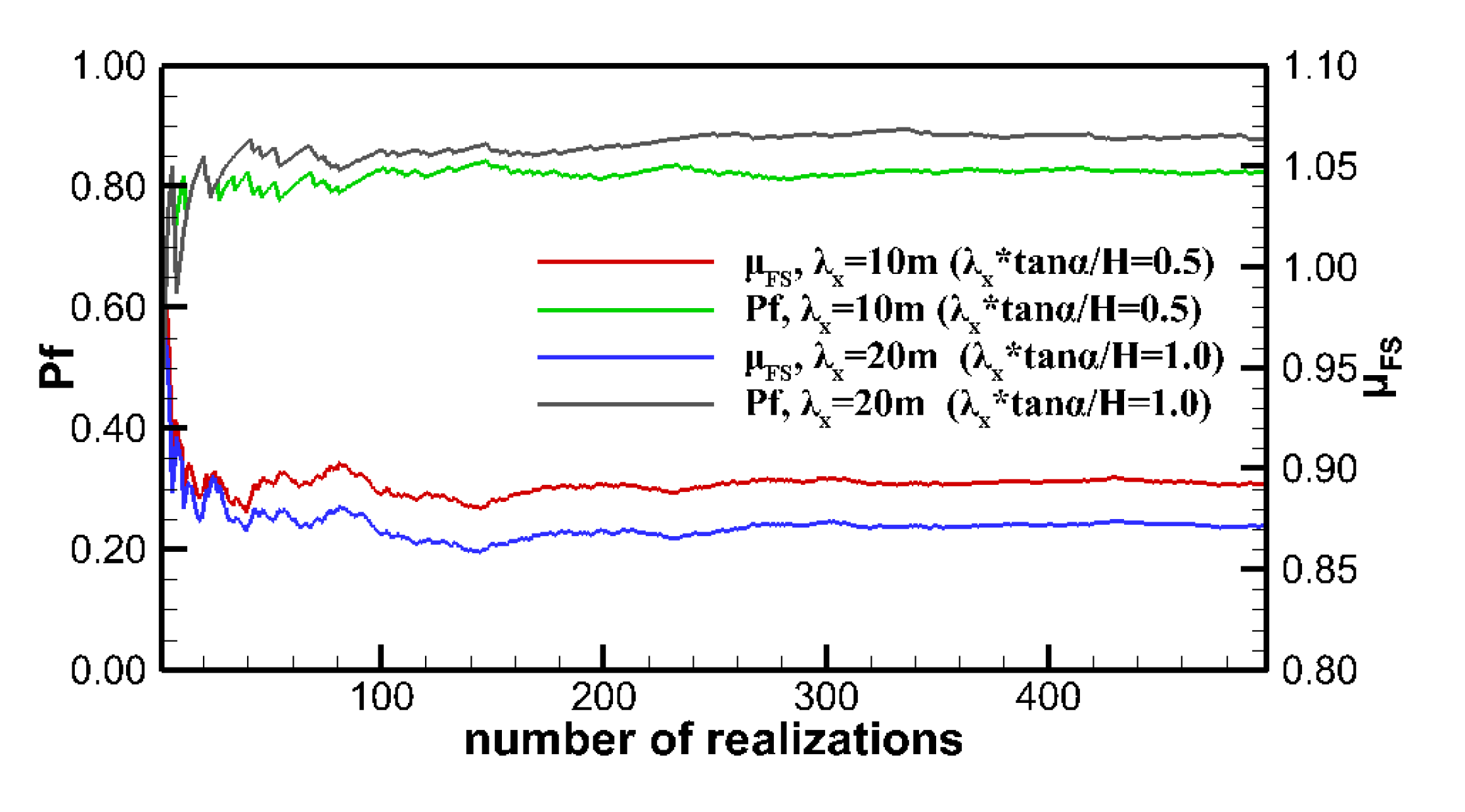
4.3. Effects of the Number of Realizations in MCS
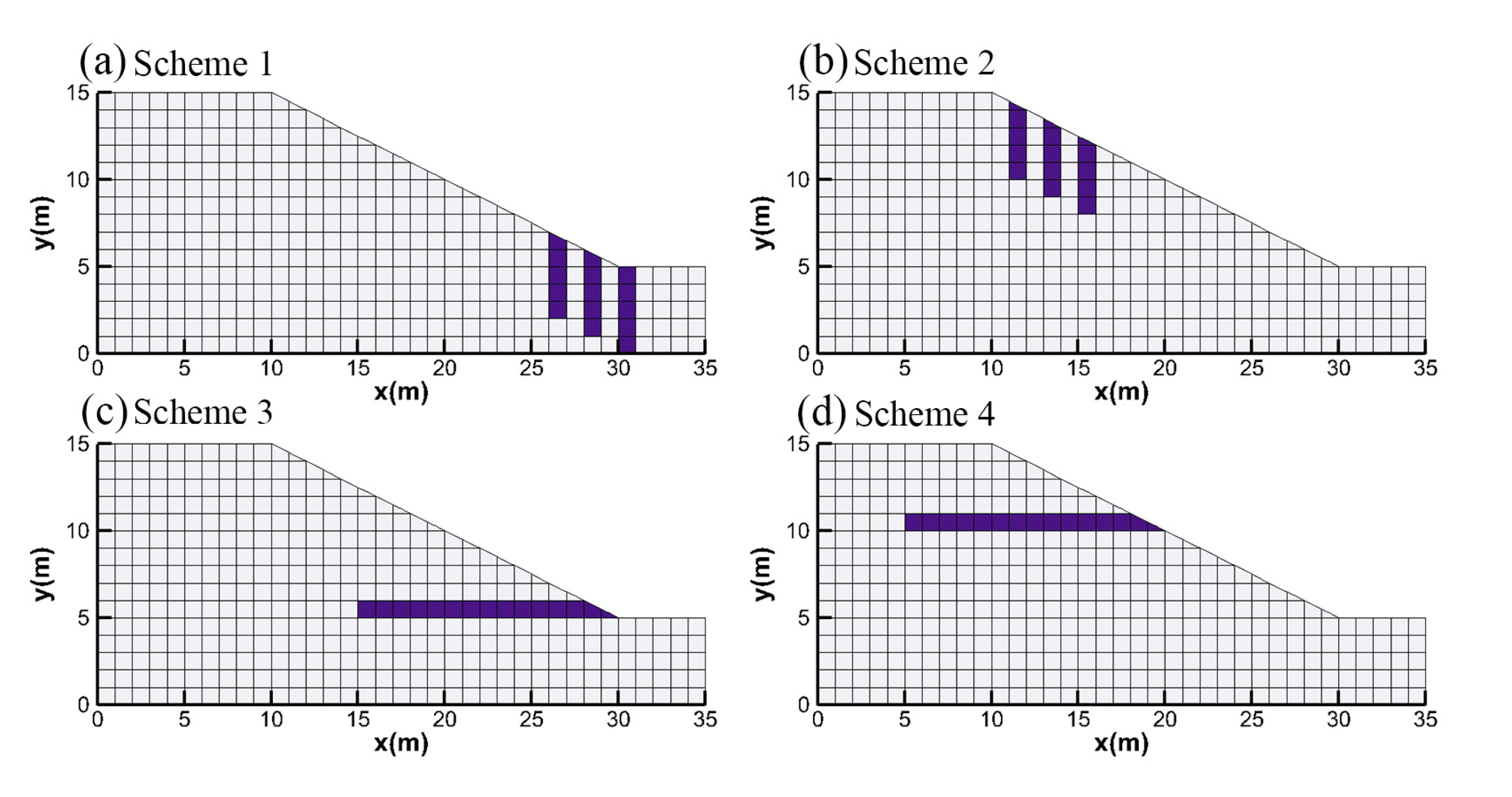
5. Effects of Conditional Random Fields
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rackwitz, R. Reviewing probabilistic soils modelling. Comput. Geotech. 2000, 26, 199–223. [Google Scholar] [CrossRef]
- Nielsen, D.R.; Biggar, J.W.; Erh, K.T. Spatial Variability of Field-measured Soil-water Characteristics. Hilgardia 1985, 42, 215–260. [Google Scholar] [CrossRef] [Green Version]
- Phoon, K.K.; Kulhawy, F.H. Characterization of geotechnical variability. Can. Geotech. J. 1999, 36, 612–624. [Google Scholar] [CrossRef]
- Xiao, T.; Li, D.Q.; Cao, Z.J.; Au, S.K.; Phoon, K.K. Three-dimensional slope reliability and risk assessment using auxiliary random finite element method. Comput. Geotech. 2016, 79, 146–158. [Google Scholar] [CrossRef] [Green Version]
- Jiang, S.H.; Huang, J.; Griffiths, D.V.; Deng, Z.P. Advances in reliability and risk analyses of slopes in spatially variable soils: A state-of-the-art review. Comput. Geotech. 2022, 141, 104498. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A. Probabilistic Slope Stability Analysis by Finite Elements. J. Geotech. Geoenviron. Eng. 2004, 23, 1390–1392. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.H.; Li, D.Q. Effect of spatial variability of shear strength parameters on critical slip surfaces of slopes. Eng. Geol. 2018, 239, 41–49. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Huang, J.; Fenton, G.A. Influence of spatial variability on slope reliability using 2-D random fields. J. Geotech. Geoenviron. Eng. 2009, 135, 1367–1378. [Google Scholar] [CrossRef] [Green Version]
- Jiang, S.H.; Li, D.Q.; Zhang, L.M.; Zhou, C.B. Slope reliability analysis considering spatially variable shear strength parameters using a non-intrusive stochastic finite element method. Eng. Geol. 2014, 168, 120–128. [Google Scholar] [CrossRef]
- Cho, S.E. Effects of spatial variability of soil properties on slope stability. Eng. Geol. 2007, 92, 97–109. [Google Scholar] [CrossRef]
- Ciurleo, M.; Cascini, L.; Calvello, M. A Comparison of Statistical and Deterministic Methods for Shallow Landslide Susceptibility Zoning in Clayey Soils. Eng. Geol. 2017, 223, 71–81. [Google Scholar] [CrossRef]
- Tropeano, G.; Silvestri, F.; Ausilio, E. An Uncoupled Procedure for Performance Assessment of Slopes in Seismic Conditions. Bull. Earthq. Eng. 2017, 15, 3611–3637. [Google Scholar] [CrossRef] [Green Version]
- Miao, F.; Wu, Y.; Xie, Y.; Li, Y. Prediction of Landslide Displacement with Step-like Behavior Based on Multialgorithm Optimization and a Support Vector Regression Model. Landslides 2018, 15, 475–488. [Google Scholar] [CrossRef]
- Miao, F.; Zhao, F.; Wu, Y.; Li, L.; Török, Á. Landslide Susceptibility Mapping in Three Gorges Reservoir Area Based on GIS and Boosting Decision Tree Model. Stoch. Environ. Res. Risk Assess. 2023, 4, 1–21. [Google Scholar] [CrossRef]
- Yeh, T.C.J.; Ye, M.; Khaleel, R. Estimation of effective unsaturated hydraulic conductivity tensor using spatial moments of observed moisture plume. Water Resour. Res. 2005, 41, 1–12. [Google Scholar] [CrossRef]
- Cai, J.S.; Yeh, T.C.J.; Yan, E.C.; Tang, R.X.; Hao, Y.H. Design of borehole deployments for slope stability analysis based on a probabilistic approach. Comput. Geotech. 2021, 133, 103909. [Google Scholar] [CrossRef]
- Gao, X.; Yan, E.C.; Yeh, T.C.J.; Wang, Y.L.; Cai, J.S.; Hao, Y.H. Sequential back analysis of spatial distribution of geomechanical properties around an unlined rock cavern. Comput. Geotech. 2018, 99, 177–190. [Google Scholar] [CrossRef]
- Mao, D.; Yeh, T.C.J.; Wan, L.; Lee, C.H.; Hsu, K.C.; Wen, J.C.; Lu, W. Cross-correlation analysis and information content of observed heads during pumping in unconfined aquifers. Water Resour. Res. 2013, 49, 713–731. [Google Scholar] [CrossRef]
- Sun, R.; Yeh, T.C.J.; Mao, D.; Jin, M.; Lu, W.; Hao, Y. A temporal sampling strategy for hydraulic tomography analysis. Water Resour. Res. 2013, 49, 3881–3896. [Google Scholar] [CrossRef]
- Zhao, C.; Gong, W.; Li, T.; Juang, C.H.; Tang, H.; Wang, H. Probabilistic characterization of subsurface stratigraphic configuration with modified random field approach. Eng. Geol. 2021, 288, 106138. [Google Scholar] [CrossRef]
- Wang, M.; Tang, X.; Li, D.; Qi, X. Subset simulation for efficient slope reliability analysis involving copula- based cross-correlated random fields. Comput. Geotech. 2020, 118, 103326. [Google Scholar] [CrossRef]
- Gong, W.; Zhao, C.; Juang, C.H.; Zhang, Y.; Tang, H.; Lu, Y. Coupled characterization of stratigraphic and geo-properties uncertainties—A conditional random field approach. Eng. Geol. 2021, 294, 106348. [Google Scholar] [CrossRef]
- Ye, M.; Khaleel, R.; Yeh, T.C.J. Stochastic analysis of moisture plume dynamics of a field injection experiment. Water Resour. Res. 2005, 41, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Cruden, D.M.; Varnes, D.J. Landslide Types and Processes. In Landslides: Investigation and Mitigation; National Academy Press: Washington, WA, USA, 1996; Volume 247, pp. 36–75. [Google Scholar]
- Terzaghi, K. Mechanism of Landslides. In Application of Geology to Engineering Practice; Geological Society of America: New York, NY, USA, 1950; pp. 83–123. [Google Scholar]
- Leroueil, S. Natural Slopes and Cuts: Movement and Failure Mechanisms. Géotechnique 2001, 51, 197–243. [Google Scholar] [CrossRef]
- Cai, J.S.; Yan, E.C.; Yeh, T.C.J.; Zha, Y.Y.; Liang, Y.; Huang, S.Y.; Wang, W.K.; Wen, J.C. Effect of spatial variability of shear strength on reliability of infinite slopes using analytical approach. Comput. Geotech. 2017, 81, 77–86. [Google Scholar] [CrossRef] [Green Version]
- Johari, A.; Fooladi, H. Simulation of the conditional models of borehole’s characteristics for slope reliability assessment. Transp. Geotech. 2022, 35, 100778. [Google Scholar] [CrossRef]
- Liu, L.L.; Cheng, Y.M.; Zhang, S.H. Conditional random field reliability analysis of a cohesion-frictional slope. Comput. Geotech. 2017, 82, 173–186. [Google Scholar] [CrossRef]
- Yang, R.; Huang, J.; Griffiths, D.V.; Sheng, D. Probabilistic Stability Analysis of Slopes by Conditional Random Fields. In Proceedings of the Geo-Risk, Denver, CO, USA, 4–7 June 2017; American Society of Civil Engineers: Reston, VA, USA, 2017; pp. 450–459. [Google Scholar] [CrossRef]
- Johari, A.; Fooladi, H. Comparative study of stochastic slope stability analysis based on conditional and unconditional random field. Comput. Geotech. 2020, 125, 103707. [Google Scholar] [CrossRef]
- Yeh, T.C.J.; Khaleel, R.; Carroll, K.C. Flow through Heterogeneous Geologic Media; Cambridge University Press: New York, NY, USA, 2015; ISBN 9781139879323. [Google Scholar]
- Gutjahr, A.L. Fast fourier transforms for random field generation. In New Mexico Tech Project Report 4-R58-2690R; New Mexico Institute of Mining and Technology: Socorro, NM, USA, 1989; Volume 29, pp. 2385–2397. [Google Scholar]
- Robin, M.J.L.; Gutjahr, A.L.; Sudicky, E.A.; Wilson, J.L. Cross-correlated random field generation with the direct Fourier Transform Method. Water Resour. Res. 1993, 29, 2385–2397. [Google Scholar] [CrossRef]
- Elia, G.; Falcone, G.; Cotecchia, F.; Rouainia, M. Analysis of the Effects of Seasonal Pore Pressure Variations on the Slope Stability Through Advanced Numerical Modelling. In Lecture Notes in Civil Engineering; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; Volume 40, pp. 184–194. ISBN 9783030213596. [Google Scholar]
- Pedone, G.; Tsiampousi, A.; Cotecchia, F.; Zdravkovic, L. Coupled Hydro-Mechanical Modelling of Soil–Vegetation–Atmosphere Interaction in Natural Clay Slopes. Can. Geotech. J. 2022, 59, 272–290. [Google Scholar] [CrossRef]
- Gao, X.; Yan, E.-C.; Yeh, T.-C.J.; Wang, Y.; Liang, Y.; Hao, Y. Reliability Analysis of Hydrologic Containment of Underground Storage of Liquefied Petroleum Gas. Tunn. Undergr. Sp. Technol. 2018, 79, 12–26. [Google Scholar] [CrossRef]
- Zhang, X.; Bi, J.; Guo, D.; Li, Z. Numerical Simulation of Stability Analysis of Soil Slope Using General Particle Dynamics with Elastic-plastic Constitutive Model. Mater. Des. Process. Commun. 2019, 1, e51. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, D.V.; Lane, P.A. Slope stability analysis by finite elements. Geotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Smith, I.M.; Griffiths, D.V.; Margetts, L. Programming the Finite Element Method; John Wiley & Sons: Chichester, UK, 2014; ISBN 9781119973348. [Google Scholar]
- Morgenstern, N.R.; Price, V.E. The analysis of the stability of general slip surfaces. Geotechnique 1965, 15, 79–93. [Google Scholar] [CrossRef]
- Gao, X.; Chuan Yan, E.; Yeh, T.C.J.; Cai, J.S.; Liang, Y.; Wang, M. A geostatistical inverse approach to characterize the spatial distribution of deformability and shear strength of rock mass around an unlined rock cavern. Eng. Geol. 2018, 245, 106–119. [Google Scholar] [CrossRef]
- Gao, X.; Yeh, T.C.J.; Yan, E.C.; Wang, Y.L.; Hao, Y. Conditional mean, effective, and realizations of hydraulic conductivity fields. J. Hydrol. 2021, 592, 125606. [Google Scholar] [CrossRef]
- Yeh, T.C.J. Stochastic modelling of groundwater flow and solute transport in aquifers. Hydrol. Process. 1992, 6, 369–395. [Google Scholar] [CrossRef] [Green Version]


| Parameters | Values |
|---|---|
| Mean of cohesion, μc | 15 kN/m2 |
| Coefficient of variation of cohesion, COVc | 0.5 |
| Mean of friction angle, μφ | 10° |
| Coefficient of variation of friction angle, COVφ | 0.5 |
| Dilation angle, ψ | 0° |
| Young’s modulus, E | 1 × 105 kPa |
| Poisson’s ratio, υ | 0.3 |
| Unit weight, γ | 20 kN/m3 |
| Scheme 1 | Scheme 2 | Scheme 3 | Scheme 4 | |
|---|---|---|---|---|
| μFS of Case 1 | 1.033 | 1.041 | 1.031 | 1.040 |
| σFS of Case 1 | 0.066 | 0.072 | 0.058 | 0.072 |
| μFS of Case 2 | 0.935 | 0.939 | 0.924 | 0.935 |
| σFS of Case 2 | 0.094 | 0.105 | 0.082 | 0.112 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhang, F.; Yeh, T.-C.J.; Hou, X.; Dong, M. Cross-Correlation Analysis of the Stability of Heterogeneous Slopes. Water 2023, 15, 1050. https://doi.org/10.3390/w15061050
Li Y, Zhang F, Yeh T-CJ, Hou X, Dong M. Cross-Correlation Analysis of the Stability of Heterogeneous Slopes. Water. 2023; 15(6):1050. https://doi.org/10.3390/w15061050
Chicago/Turabian StyleLi, Yukun, Faming Zhang, Tian-Chyi Jim Yeh, Xiaolan Hou, and Menglong Dong. 2023. "Cross-Correlation Analysis of the Stability of Heterogeneous Slopes" Water 15, no. 6: 1050. https://doi.org/10.3390/w15061050





