Multimethodological Revisit of the Surface Water and Groundwater Interaction in the Balaton Highland Region—Implications for the Overlooked Groundwater Component of Lake Balaton, Hungary
Abstract
:1. Introduction
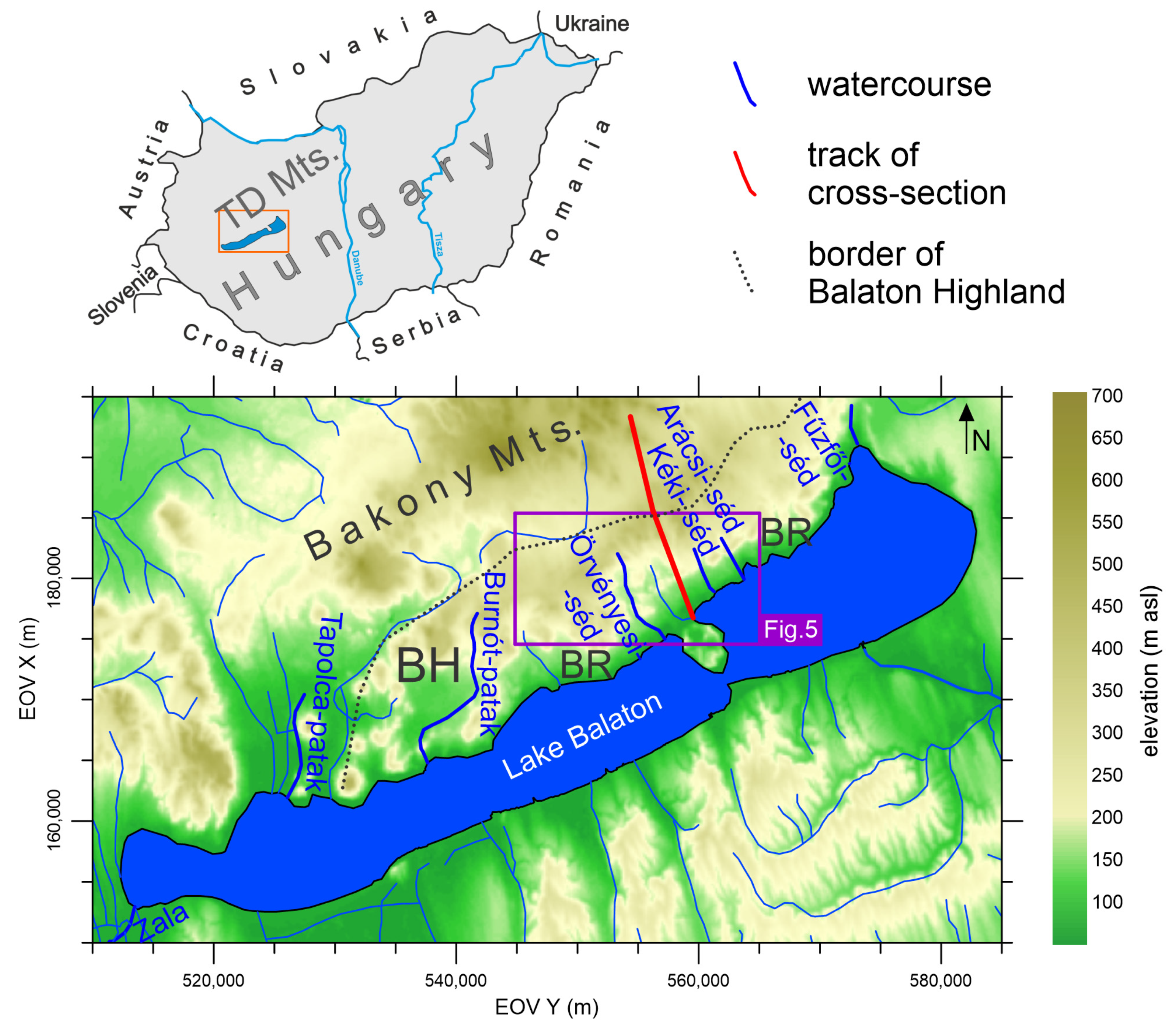
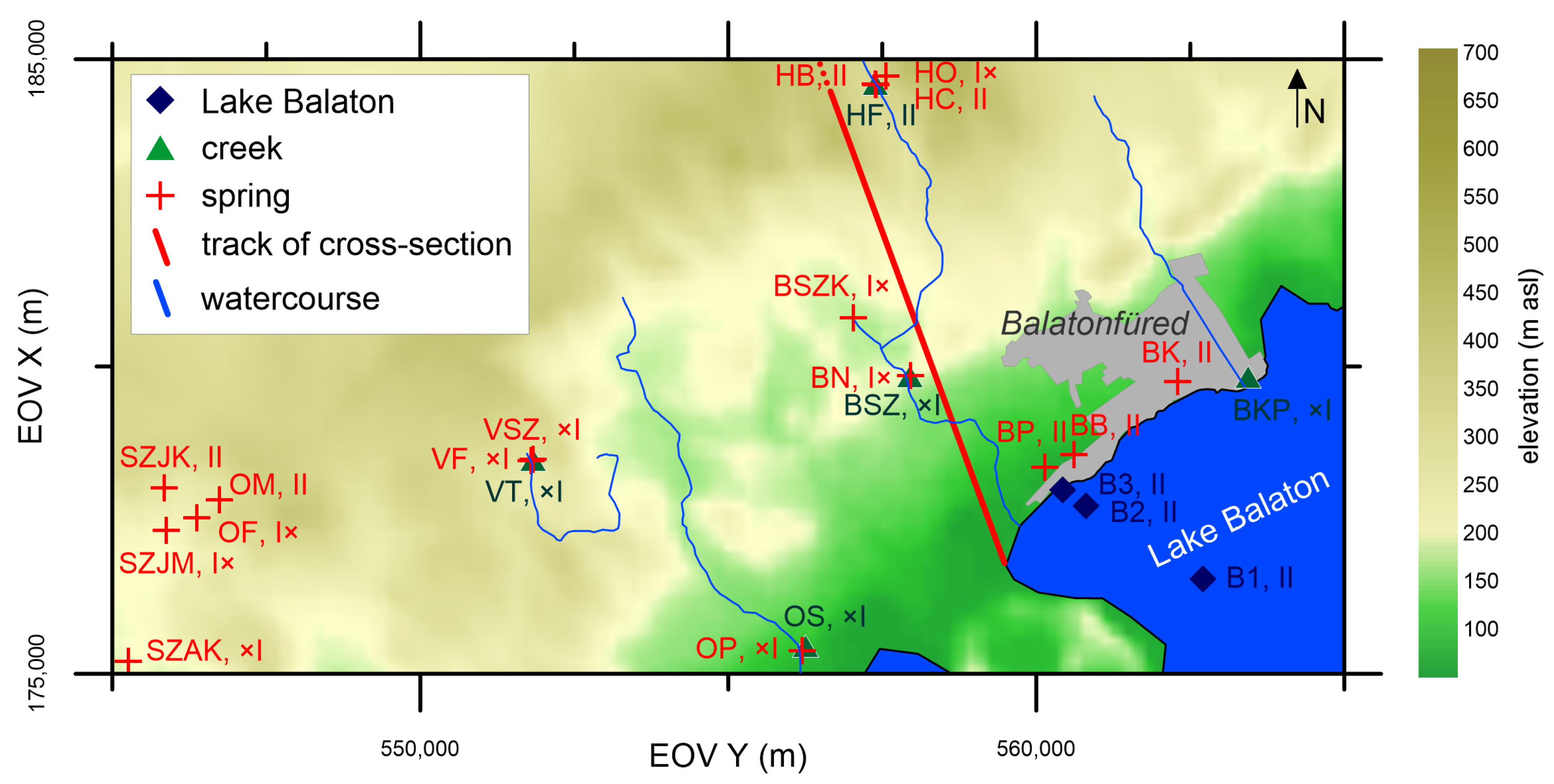
2. Study Area
3. Hydrostratigraphic Classification
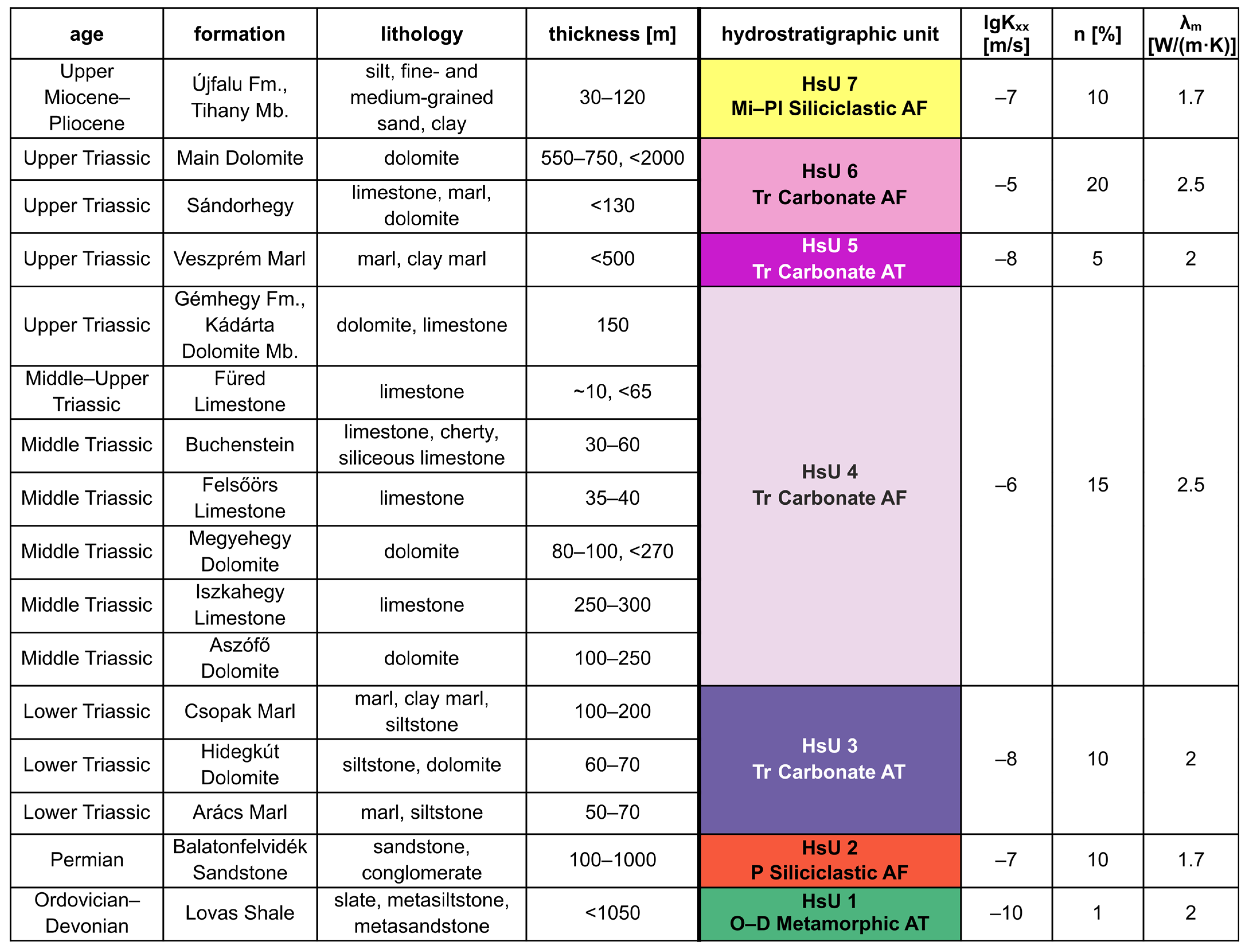
3.1. Methods and Materials
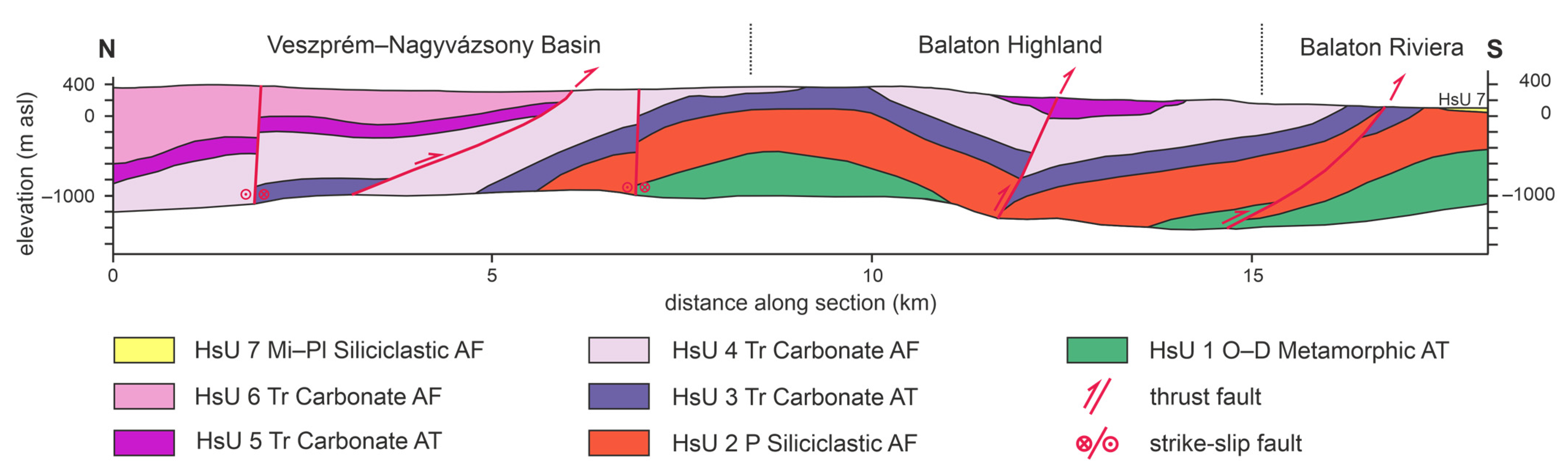
3.2. Results
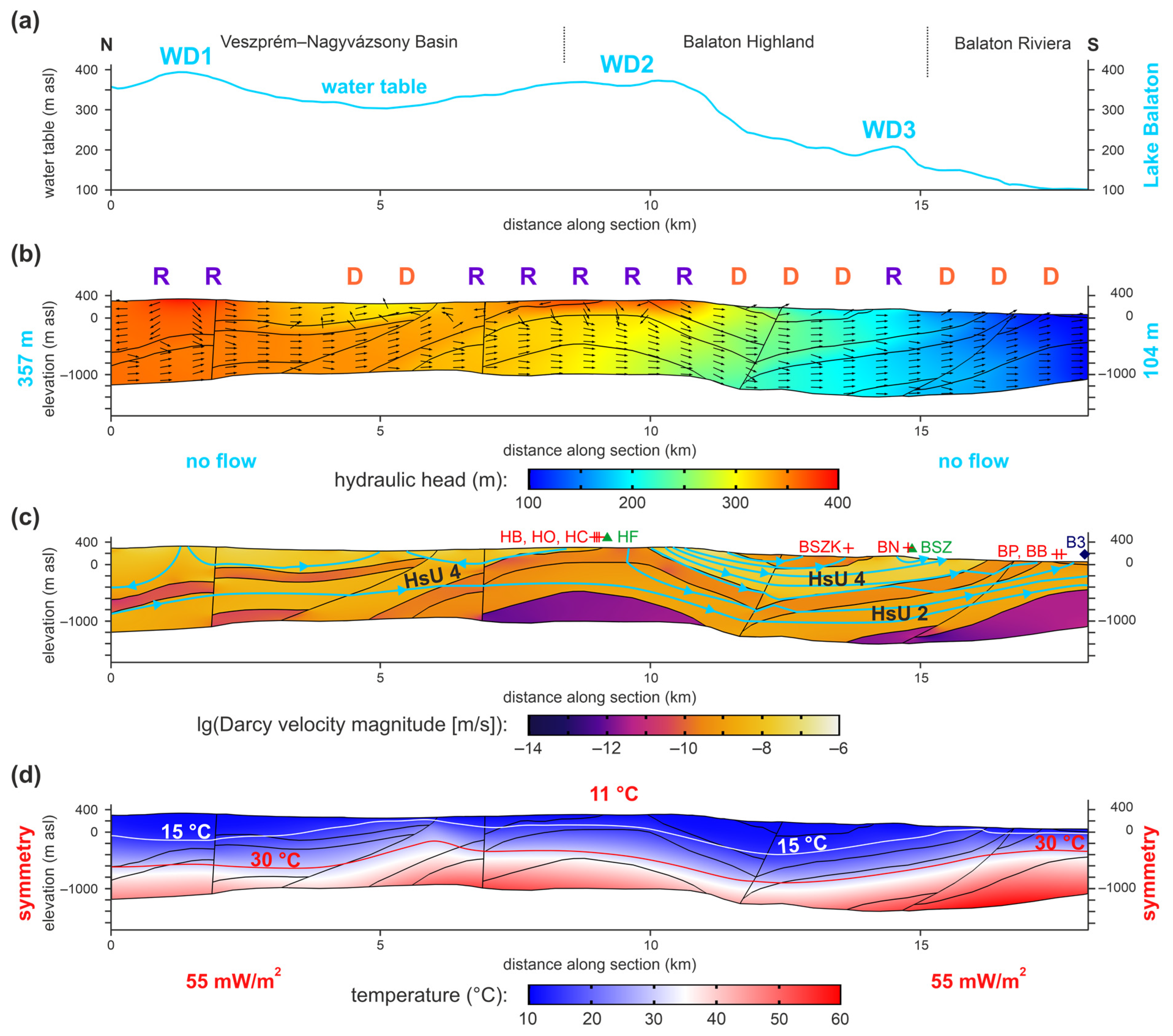
4. Fluid Potential Distribution
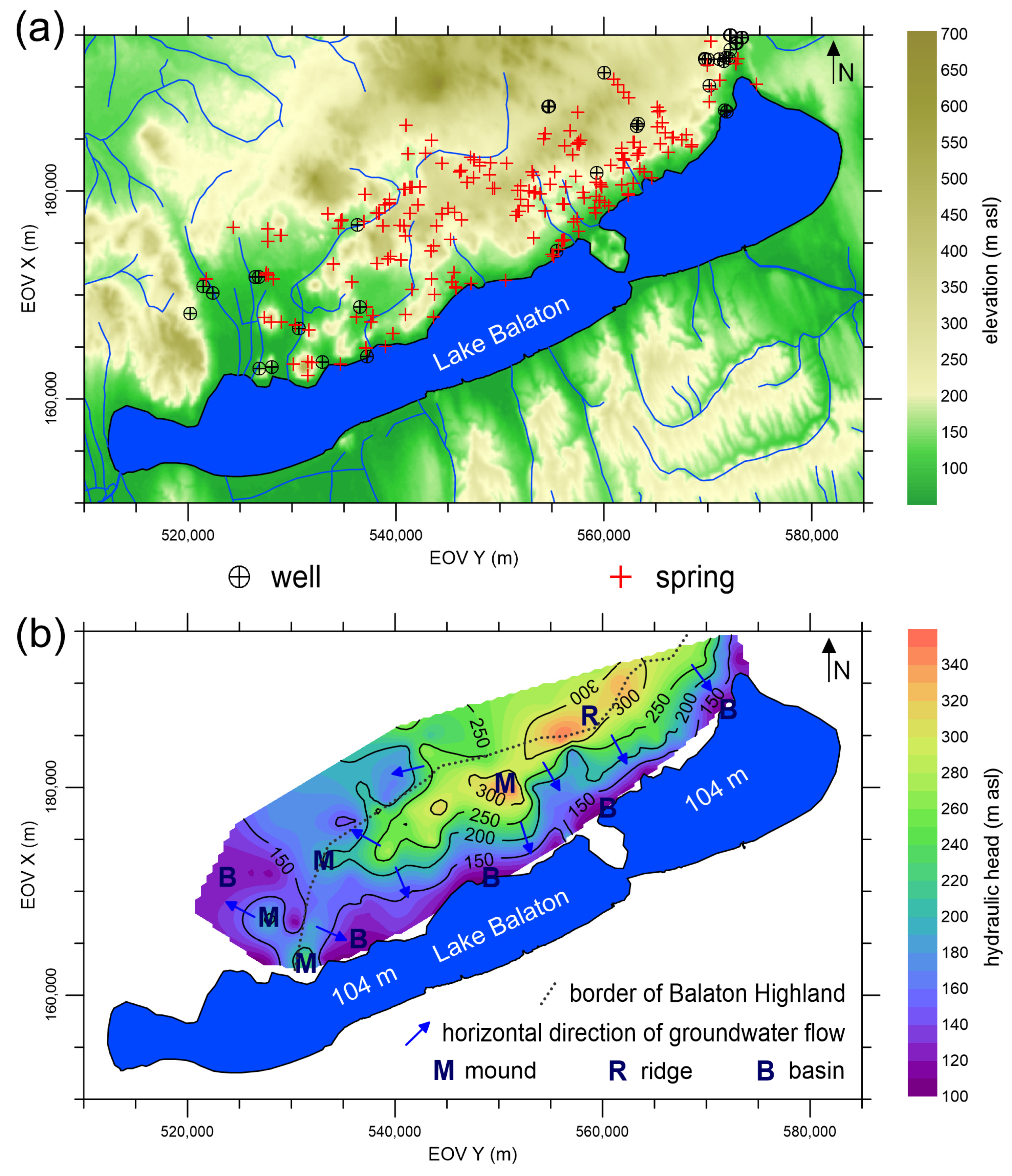
4.1. Methods and Materials
4.2. Results, Interpretation and Comparison
5. Baseflow Index Calculation
5.1. Methods and Materials
5.2. Results, Interpretation and Comparison
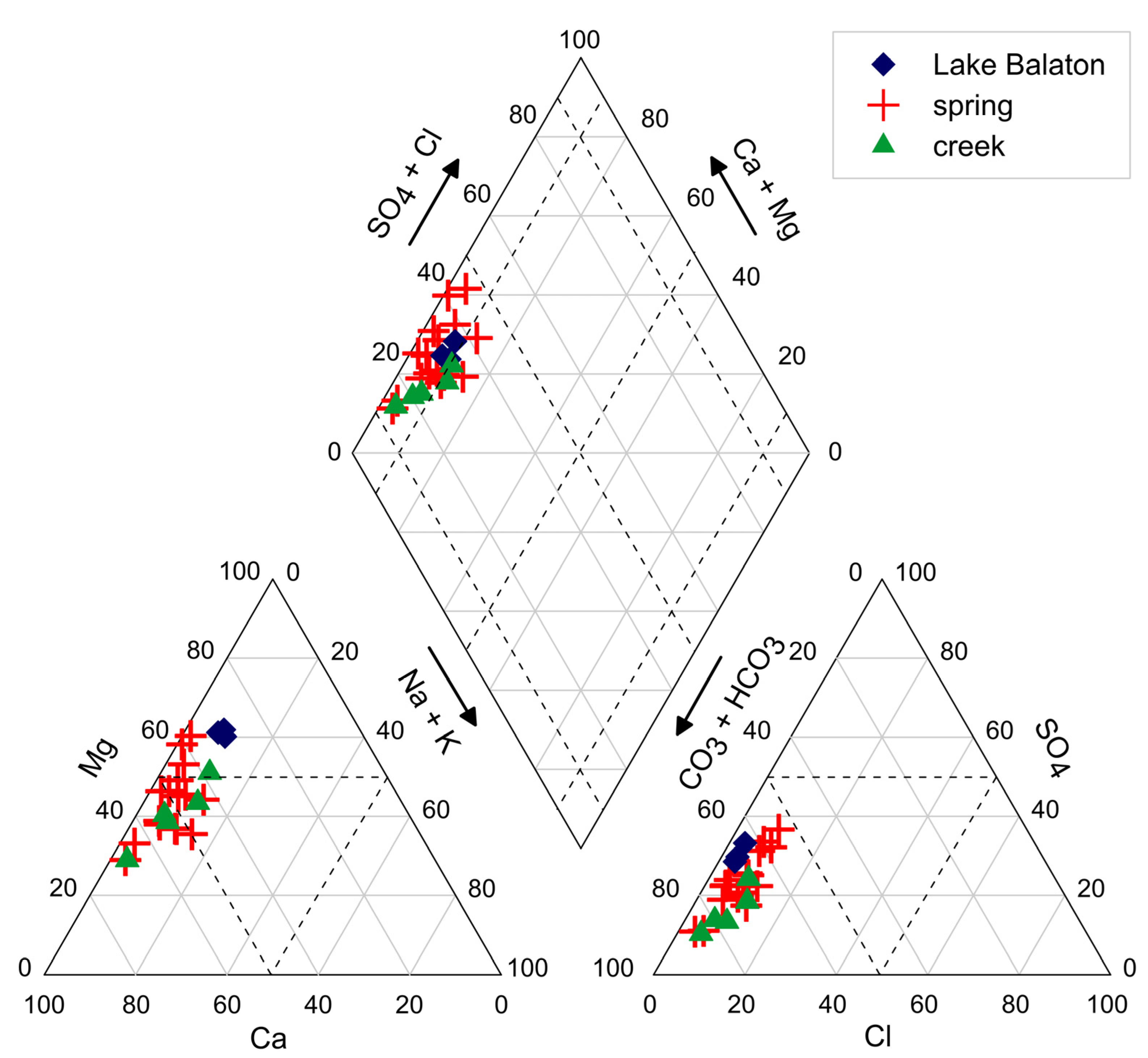
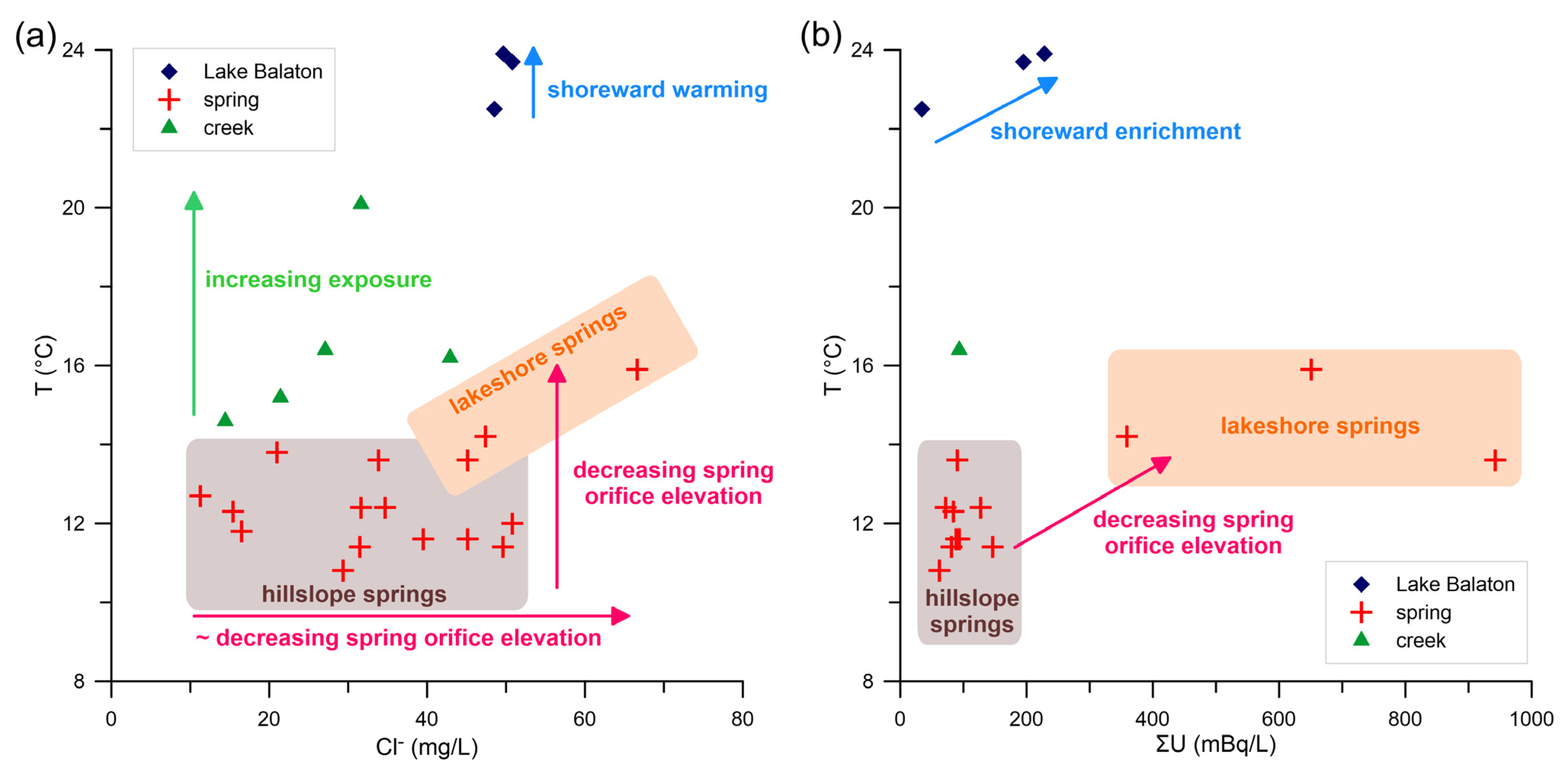
6. Hydrochemical Analyses
6.1. Methods and Materials
6.2. Results, Interpretation and Comparison
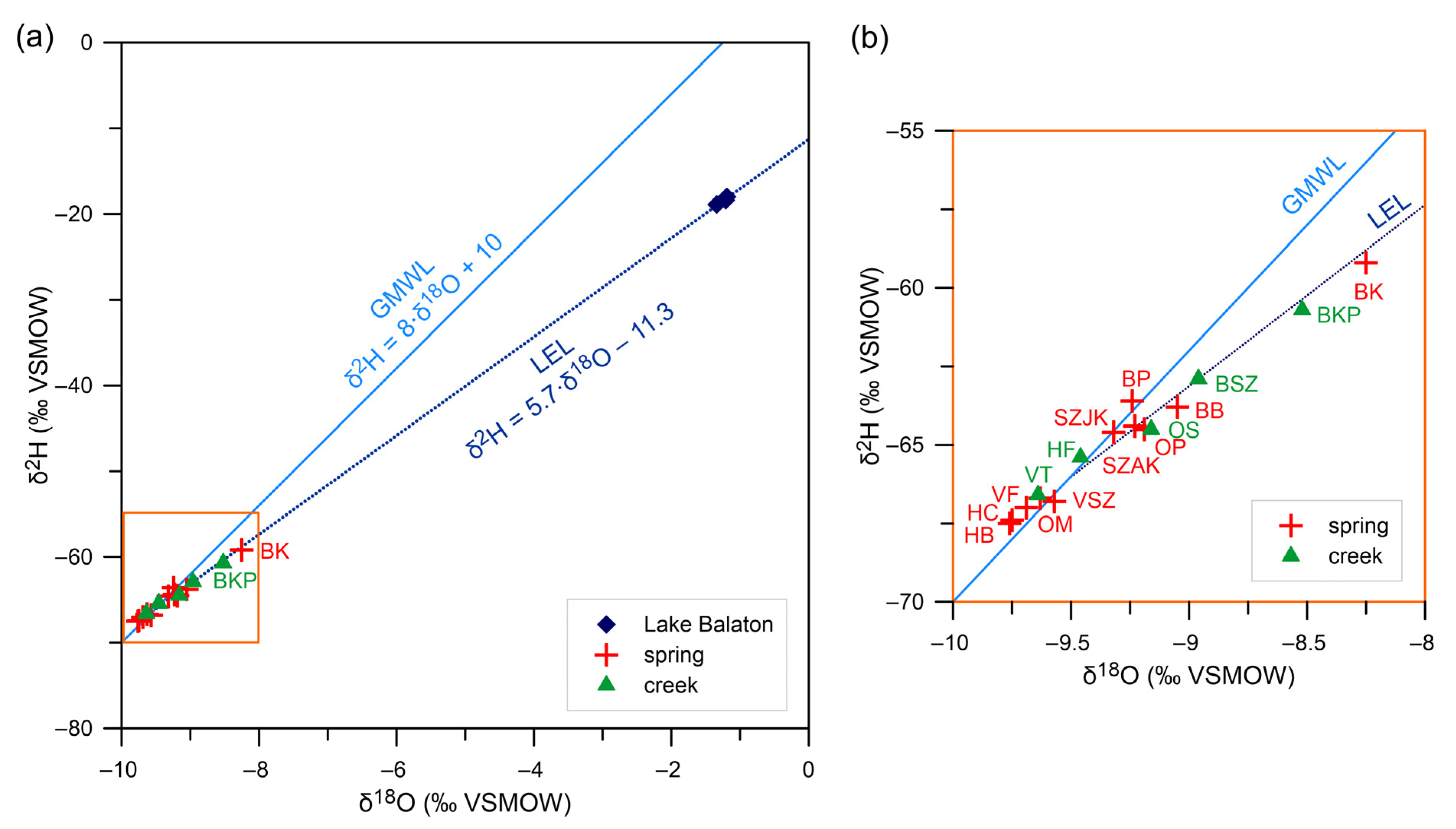
7. Stable Isotope Analysis
7.1. Methods and Materials
7.2. Results, Interpretation and Comparison
8. Numerical Simulation of Groundwater Flow and Heat Transport
8.1. Methods and Materials
8.2. Results, Interpretation and Comparison
9. Discussion
9.1. Surface Water–Groundwater Interaction and Hydraulic Processes of the Balaton Highland–Lake Balaton Region
9.2. Groundwater Contribution to Lake Balaton
10. Conclusions and Summary
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lorberer, Á. A Dunántúli-Középhegység Karsztvízszint-Térképei És a Főkarsztvíztároló Állapotellenőrzése [Karst Water Maps and Status Monitoring of the Karst Water Reservoir of Transdanubian Mountains]. In Proceedings of the Karsztvízkutatás Magyarországon; Vituki, Ed.; Felszín Alatti Vizekért Alapítvány—Vituki Rt Hidrológiai Intézet közös kiadása: Miskolc, Hungary, 2002; pp. 1–14. [Google Scholar]
- Mádl-Szőnyi, J.; Erőss, A.; Csondor, K.; Iván, V.; Tóth, Á. Hydrogeology of the Karst Regions in Hungary. In Cave and Karst Systems of Hungary; Veress, M., Leél-Őssy, S., Eds.; Springer: Cham, Switzerland, 2022; pp. 137–160. [Google Scholar]
- European Community. Directive 2000/60/EC of the European Parliament and of the Council of 23 October 2000 Establishing a Framework for Community Action in the Field of Water Policy; European Community: Brussels, Belgium, 2000. [Google Scholar]
- Rosenberry, D.O.; Lewandowski, J.; Meinikmann, K.; Nützmann, G. Groundwater—The Disregarded Component in Lake Water and Nutrient Budgets. Part 1: Effects of Groundwater on Hydrology. Hydrol. Process. 2015, 29, 2895–2921. [Google Scholar] [CrossRef]
- Rosenberry, D.O.; LaBaugh, J.W. Field Techniques for Estimating Water Fluxes between Surface Water and Ground Water; Geological Survey: Tuscaloosa, AL, USA, 2008.
- Hayashi, M.; Rosenberry, D.O. Effects of Groundwater Exchange on the Hydrology and Ecology of Surface Waters. Groundwater 2002, 40, 309–316. [Google Scholar] [CrossRef]
- Hood, J.L.; Roy, J.W.; Hayashi, M. Importance of Groundwater in the Water Balance of an Alpine Headwater Lake. Geophys. Res. Lett. 2006, 33, L13405. [Google Scholar] [CrossRef] [Green Version]
- Winter, T.C. Relation of Streams, Lakes, and Wetlands to Groundwater Flow Systems. Hydrogeol. J. 1999, 7, 28–45. [Google Scholar] [CrossRef]
- Winter, T.C.; Harvey, J.W.; Franke, O.L.; Alley, W.M. Ground Water and Surface Water: A Single Resource; USGS: Denver, CO, USA, 1998; Volume 1139, ISBN 0607893397.
- Ezugwu, C.N.; Apeh, S. Ground Water and Surface Water as One Resource: Connectivity and Interaction. IOSR J. Mech. Civ. Eng. 2017, 14, 54–59. [Google Scholar] [CrossRef]
- Baják, P.; Hegedűs-Csondor, K.; Tiljander, M.; Korkka-Niemi, K.; Surbeck, H.; Izsák, B.; Vargha, M.; Horváth, Á.; Pándics, T.; Erőss, A. Integration of a Shallow Soda Lake into the Groundwater Flow System by Using Hydraulic Evaluation and Environmental Tracers. Water 2022, 14, 951. [Google Scholar] [CrossRef]
- Central Transdanubian Water Management Directorate Balaton És a Tórészek Havi Vízháztartási Jellemzőinek Meghatározása, 2020 [Monthly Characteristics of the Water Budget of Lake Balaton, 2020]; Közép-Dunántúli Vízügyi Igazgatóság: Székesfehérvár, Hungary, 2021.
- Szádeczky-Kardoss, E. A Dunántúli-Középhegység Karsztvizének Néhány Problémájáról [On Some Issues of Karst Water of the Transdanubian Mountains]. Hidrológiai Közlöny 1941, 21, 67–92. [Google Scholar]
- Lóczy, L. A Balaton Környékének Geológiai Képződményei És Ezeknek Vidékek Szerinti Telepedése [Geological Formations around Lake Balaton and Their Settlement According to Regions]; Magyar Földrajzi Társaság Balaton-Bizottsága: Budapest, Hungary, 1913. [Google Scholar]
- Rádai, Ö. Módszerek, Lehetőségek a Felszín-Alatti Vízutánpótlódás (Fenék-Források) Helyének Lokalizálására a Balatonban [Techniques, Opportunities for the Localisation of Sublacustrine Replenishment in the Lake Balaton]; Vituki Témabeszámoló: Budapest, Hungary, 1982. [Google Scholar]
- Erdélyi, M. A Balaton Mélységi Vízforgalma [Groundwater Recharge to Lake Balaton]. Hidrológiai Közlöny 1983, 63, 429–476. [Google Scholar]
- Visnovitz, F.; Bodnár, T.; Tóth, Z.; Spiess, V.; Kudó, I.; Timár, G.; Horváth, F. Seismic Expressions of Shallow Gas in the Lacustrine Deposits of Lake Balaton, Hungary. Near Surf. Geophys. 2015, 13, 433–446. [Google Scholar] [CrossRef]
- Entz, B. Hevesek És Más Jégmentes Foltok a Befagyott Balatonon (Adatok a Téli Balaton Fiziográfiájának És Biológiájának Ismeretéhez) [“Heves” and Other Ice-Free Spots on the Frozen Lake Balaton (Data for Physiography and Biology of Lake Balaton in Winter)]. Annal. Biol. Tihany. 1960, 27, 41–53. [Google Scholar]
- Cholnoky, J. A Balaton Jege; Magyar Földrajzi Társaság: Budapest, Hungary, 1907; Volume 1. [Google Scholar]
- Csepregi, A. A karsztvíztermelés hatása a Dunántúli-középhegység vízháztartására [The effects of karst water production on the water budget of Transdanubian Mountains]. In Bányászati karsztvízszint-süllyesztés a Dunántúli-középhegységben; Alföldi, L., Kapolyi, L., Eds.; Hungarian Academy of Sciences: Budapest, Hungary, 2007; pp. 77–112. [Google Scholar]
- Alföldi, L.; Kapolyi, L. Bányászati Karsztvízszintsüllyesztés a Dunántúli-Középhegységben [The Mine Dewatering in the Transdanubian Mountains]; MTA FKI: Budapest, Hungary, 2007. [Google Scholar]
- Padisák, J.; Istvánovics, V. Differential Response of Blue-Green Algal Groups to Phosphorus Load Reduction in a Large Shallow Lake: Balaton, Hungary. SIL Proc. 1997, 26, 574–580. [Google Scholar] [CrossRef]
- Tóth, J. A Conceptual Model of the Groundwater Regime and the Hydrogeologic Environment. J. Hydrol. 1970, 10, 164–176. [Google Scholar] [CrossRef]
- Kocsis, K.; Horváth, G.; Keresztesi, Z.; Nemerkényi, Z. Magyarország nemzeti atlasza 2. kötet: Természeti környezet [National Atlas of Hungary, Volume 2: Natural environment]. In Magyarország nemzeti atlasza; Kocsis, K., Klinghammer, I., Horváth, G., Keresztesi, Z., Kovács, Z., Márton, M., Nemerkényi, Z., Zentai, L., Eds.; Magyar Tudományos Akadémia, Csillagászati és Földtudományi Kutatóközpont: Budapest, Hungary, 2018; p. 187. ISBN 9639545562. [Google Scholar]
- Stelczer, K. A Vízkészlet-Gazdálkodás Hidrológiai Alapjai: Egyetemi És Főiskolai Tankönyv [Hydrological Basics of Water Resources Management]; ELTE Eötvös Kiadó: Budapest, Hungary, 2000; ISBN 9634632491. [Google Scholar]
- Felméry, L.; Péczely, G.; Záchné Ruthner, M. Tanulmány a Bakony éghajlatáról [Study on the climate of Bakony Mountains]; Eötvös Loránd University: Budapest, Hungary, 1971. [Google Scholar]
- Beudant, F.-S. Voyage Minéralogique et Géologique En Hongrie Pendant l’année 1818 [Mineralogical and Geological Journey in Hungary during the Year 1818]; Verdière: Párizs, France, 1822. [Google Scholar]
- Budai, T.; Csillag, G.; Dudko, A.; Koloszár, L. A Balaton-Felvidék Földtani Térképe (1:50,000) [Geologic Map of the Balaton Highland (1:50,000)]; Magyar Állami Földtani Intézet: Budapest, Hungary, 1999. [Google Scholar]
- Budai, T.; Császár, G.; Csillag, G.; Dudko, A.; Koloszár, L.; Majoros, G. A Balaton-Felvidék Földtana [Geology of the Balaton Highland]; Magyar Állami Földtani Intézet Alkalmi kiadvány: Budapest, Hungary, 1999. [Google Scholar]
- Haas, J. Geology of Hungary; Springer Science & Business Media: Heidelberg, Germany, 2012; ISBN 3642219101. [Google Scholar]
- Szederkényi, T.; Kovács, S.; Haas, J.; Nagymarosy, A. Geology and History of Evolution of the ALCAPA Mega-Unit. In Geology of Hungary; Haas, J., Ed.; Springer: Heidelberg, Germany, 2012; pp. 1–102. [Google Scholar]
- Balla, Z.; Dudko, A. Large-Scale Tertiary Strike-Slip Displacements Recorded in the Structure of the Transdanubian Range. Geophys. Trans. 1989, 35, 3–63. [Google Scholar]
- Majoros, G. A Permi Üledékképződés Problémái a Dunántúli-Középhegységben: Egy Ősföldrajzi Modell És Néhány Következtetés [The Problems of Permian Sedimentation in the Transdanubian Mountains: A Paleogeographical Model and Some Conclusions]. Földtani Közlöny 1980, 110, 323–341. [Google Scholar]
- Haas, J.; Budai, T. Upper Permian-Triassic Facies Zones in the Transdanubian Range. Riv. Ital. Di Paleontol. E Stratigr. 1995, 101, 249–266. [Google Scholar]
- Broglio Loriga, C.; Góczán, F.; Haas, J.; Lenner, K.; Neri, C.; Oravecz Sheffer, A.; Posenato, R.; Szabó, I.; Tóth Makk, A. The Lower Triassic Sequences of the Dolomites (Italy) and Transdanubian Mid-Mountains (Hungary) and Their Correlation. Mem. Di Sci. Geol. 1990, 42, 41–103. [Google Scholar]
- Haas, J.; Budai, T. A Dunántúli-Középhegység Felső-Triász Képződményeinek Rétegtani- És Fácieskérdései [Stratigraphic and Facies Problems of the Upper Triassic in the Transdanubian Range]. Földtani Közlöny 2014, 144, 125–142. [Google Scholar]
- Magyar, I.; Geary, D.H.; Müller, P. Paleogeographic Evolution of the Late Miocene Lake Pannon in Central Europe. Palaeogeogr. Palaeoclimatol. Palaeoecol. 1999, 147, 151–167. [Google Scholar] [CrossRef]
- Tari, G.; Dövényi, P.; Dunkl, I.; Horváth, F.; Lenkey, L.; Stefanescu, M.; Szafián, P.; Tóth, T. Lithospheric Structure of the Pannonian Basin Derived from Seismic, Gravity and Geothermal Data. Geol. Soc. 1999, 156, 215–250. [Google Scholar] [CrossRef]
- Csicsek, L.Á.; Fodor, L. Középső-Triász Képződmények Pikkelyeződése a Bakonyban, Öskü Környékén [Imbrication of Middle Triassic Rocks near Öskü (Bakony Hills, Western Hungary)]. Földtani Közlöny 2016, 146, 355–370. [Google Scholar]
- Fodor, L. Mezozoos-kainozoos feszültségmezők és törésrendszerek a Pannon-medence ÉNy-i részén—Módszertan és szerkezeti elemzés [Mesozoic-Cenozoic Stress Fields and Fault Systems in the NW Part of the Pannon Basin—Methodology and Structural Analysis]; Budapest, Hungarian Academy of Sciences: Budapest, Hungary, 2010. [Google Scholar]
- Linzer, H.-G.; Tari, G. Structural Correlation between the Northern Calcareous Alps (Austria) and the Transdanubian Central Range (Hungary). In Tectonics and Sedimentation: Implications for Petroleum Systems: AAPG Memoir; Gao, D., Ed.; American Association of Petroleum Geologists: Tulsa, OK, USA, 2012; pp. 249–266. [Google Scholar]
- Maxey, G.B. Hydrostratigraphic Units. J. Hydrol. 1964, 2, 124–129. [Google Scholar] [CrossRef]
- Seaber, P.R. Hydrostratigraphic Units. Geol. N. Am. 1988, 2, 9–14. [Google Scholar]
- Császár, G. Magyarország Litosztratigráfiai Alapegységei [Lithostratigraphic Units of Hungary]; Magyar Állami Földtani Intézet: Budapest, Hungary, 1997. [Google Scholar]
- Gyalog, L. Magyarázó Magyarország Fedett Földtani Térképéhez (Az Egységek Rövid Leírása), 1:100.000 [Explanatory Book of the Surface Geological Map of Hungary (Brief Description of Units), 1:100.000]; Magyar Állami Földtani Intézet: Budapest, Hungary, 2005. [Google Scholar]
- Mádl-Szőnyi, J. Víztartó rendszerek sérülékenységi vizsgálata a dunántúli-középhegységi főkarsztvíztároló rendszer (DNy-i rész) példáján [Vulnerability assessment of aquifer systems with the example of main karst reservoir in the SW-Transdanubian Central Range]. Földtani Közlöny 1997, 127, 19–83. [Google Scholar]
- Mádl-Szőnyi, J.; Czauner, B.; Iván, V.; Tóth, Á.; Simon, S.; Erőss, A.; Bodor, P.; Havril, T.; Boncz, L.; Sőreg, V. Confined Carbonates–Regional Scale Hydraulic Interaction or Isolation? Mar. Pet. Geol. 2019, 107, 591–612. [Google Scholar] [CrossRef]
- Gondár, K.; Gondárné Sőregi, K. Hidrogeológia [Hydrogeology]. In A Balaton-felvidék földtana; Budai, T., Császár, G., Csillag, G., Dudko, A., Koloszár, L., Majoros, G., Eds.; Magyar Állami Földtani Intézet: Budapest, Hungary, 1999; pp. 151–162. [Google Scholar]
- Rman, N.; Tóth, G. Vízföldtani Koncepcionális Modell [Hydrogeological Conceptual Model]; T-JAM Projekt: Geotermikus Hasznosítások Számbavétele, a Hévízadók Értékelése és a Közös Hévízgazdálkodási Terv Előkészítése a Mura-Zala Medencében; Magyar Állami Földtani Intézet: Budapest, Hungary, 2011. [Google Scholar]
- Freeze, R.A.; Cherry, J.A. Groundwater; Printice-Hall Inc.: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Domenico, P.A.; Schwartz, F.W. Physical and Chemical Hydrogeology; John Wiley and Sons: New York, NY, USA, 1997. [Google Scholar]
- Brassington, R. Field Hydrogeology; John Wiley & Sons: Chichester, UK, 2017; ISBN 1118397363. [Google Scholar]
- Clark, S.P. Handbook of Physical Constants; Geological Society of America: New York, NY, USA, 1966; Volume 97, ISBN 0813710979. [Google Scholar]
- Sharma, P. Environmental and Engineering Geophysics; Cambridge University Press: Cambridge, UK, 1997; ISBN 0521576326. [Google Scholar]
- Beardsmore, G.R.; Cull, J.P. Crustal Heat Flow; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Eppelbaum, L.; Kutasov, I.; Pilchin, A. Investigating Deep Lithospheric Structures. In Applied Geothermics; Eppelbaum, L., Kutasov, I., Pilchin, A., Eds.; Springer: Heidelberg, Germany, 2014; pp. 269–391. [Google Scholar]
- Ogg, J.G.; Ogg, G.; Gradstein, F.M. A Concise Geologic Time Scale; Elsevier: Amszterdam, The Netherlands, 2016; ISBN 044459468X. [Google Scholar]
- Tóth, Á.; Kovács, S.; Kovács, J.; Mádl-Szőnyi, J. Springs Regarded as Hydraulic Features and Interpreted in the Context of Basin-Scale Groundwater Flow. J. Hydrol. 2022, 610, 127907. [Google Scholar] [CrossRef]
- Tóth, J. Gravitational Systems of Groundwater Flow: Theory, Evaluation, Utilization; Cambridge University Press: Cambridge, UK, 2009; ISBN 0521886384. [Google Scholar]
- Hubbert, K.M. The Theory of Ground-Water Motion. J. Geol. 1940, 48, 785–944. [Google Scholar] [CrossRef]
- Tóth, J.; Almási, I. Interpretation of Observed Fluid Potential Patterns in a Deep Sedimentary Basin under Tectonic Compression: Hungarian Great Plain, Pannonian Basin. Geofluids 2001, 1, 11–36. [Google Scholar] [CrossRef]
- Csondor, K.; Czauner, B.; Csobaji, L.; Győri, O.; Erőss, A. Characterization of the Regional Groundwater Flow Systems in South Transdanubia (Hungary) to Understand Karst Evolution and Development of Hydrocarbon and Geothermal Resources. Hydrogeol. J. 2020, 28, 2803–2820. [Google Scholar] [CrossRef]
- Czauner, B.; Mádl-Szőnyi, J. The Function of Faults in Hydraulic Hydrocarbon Entrapment: Theoretical Considerations and a Field Study from the Trans-Tisza Region, Hungary. Am. Assoc. Pet. Geol. Bull 2011, 95, 795–811. [Google Scholar] [CrossRef]
- Tóth, J. Hydraulic Continuity in Large Sedimentary Basins. Hydrogeol. J. 1995, 3, 4–16. [Google Scholar] [CrossRef]
- Izápy, G. Magyarország Forrásainak Katasztere [Natural Spring Cadastral of Hungary]; OVF-VITUKI Rt. Hidrológiai Intézete: Budapest, Hungary, 2002. [Google Scholar]
- Gondárné Sőregi, K.; Gondár, K. A Balaton-felvidék karsztvízföldtani vizsgálata [Karst hydrogeology investigation of the Balaton Highland]. Hidrológiai Közlöny 1988, 68, 348–355. [Google Scholar]
- Lorberer, Á. A Dunántúli-Középhegység Karsztvízszint Térképe (DNY-i Rész), 1950. Január 1-i Állapot (1:100,000) [Karst Water Level Map of the Transdanubian Mountains (SW Part), State of 1 January 1950 (1:100,000)]; OVF-VITUKI Rt. Hidrológiai Intézete: Budapest, Hungary, 1985. [Google Scholar]
- Singh, S.K.; Pahlow, M.; Booker, D.J.; Shankar, U.; Chamorro, A. Towards Baseflow Index Characterisation at National Scale in New Zealand. J. Hydrol. 2019, 568, 646–657. [Google Scholar] [CrossRef]
- Tallaksen, L.M. A Review of Baseflow Recession Analysis. J. Hydrol. 1995, 165, 349–370. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Muttiah, R.; Bernhardt, G. Automated Base Flow Separation and Recession Analysis Techniques. Ground Water 1995, 33, 1010–1018. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Automated Methods for Estimating Baseflow and Ground Water Recharge from Streamflow Records. J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
- Rantama, J. Aerial Thermal Infrared Imaging and Baseflow Filtering Analysis for River Baseflow Estimation in Lake Pyhäjärvi Catchment, SW Finland. Master’s Thesis, University of Helsinki, Helsinki, Finland, 2020. [Google Scholar]
- Nathan, R.J.; McMahon, T.A. Evaluation of Automated Techniques for Base Flow and Recession Analyses. Water Resour. Res. 1990, 26, 1465–1473. [Google Scholar] [CrossRef]
- Ladson, A.R.; Brown, R.; Neal, B.; Nathan, R. A Standard Approach to Baseflow Separation Using The Lyne and Hollick Filter. Australas. J. Water Resour. 2013, 17, 25–34. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; Miralles, D.G.; de Jeu, R.A.M.; Sampurno Bruijnzeel, L.A.; McVicar, T.R.; Schellekens, J. Global Patterns in Base Flow Index and Recession Based on Streamflow Observations from 3394 Catchments. Water Resour Res. 2013, 49, 7843–7863. [Google Scholar] [CrossRef] [Green Version]
- Back, W. Hydrochemical Facies and Ground-Water Flow Patterns in Northern Part of Atlantic Coastal Plain; USGS: Reston, VA, USA, 1966.
- Dong, H.; Gao, Z. Theoretical Progress of Groundwater Chemical Evolution Based on Tóthian Theory: A Review. Front. Mar. Sci. 2022, 1604. [Google Scholar] [CrossRef]
- Tóth, J. The Evolutionary Concepts and Practical Utilization of the Tóthian Theory of Regional Groundwater Flow. Int. J. Earth Environ. Sci. 2016, 111. [Google Scholar] [CrossRef] [Green Version]
- Piper, A.M. A Graphic Procedure in the Geochemical Interpretation of Water-analyses. Eos 1944, 25, 914–928. [Google Scholar] [CrossRef]
- Fetter, C.W. Applied Hydrogeology; Macmillan College Publishing Company: New York, NY, USA, 1994. [Google Scholar]
- Goldscheider, N.; Mádl-Szőnyi, J.; Erőss, A.; Schill, E. Thermal Water Resources in Carbonate Rock Aquifers. Hydrogeol. J. 2010, 18, 1303–1318. [Google Scholar] [CrossRef] [Green Version]
- Tóth, J. Groundwater as a Geologic Agent: An Overview of the Causes, Processes, and Manifestations. Hydrogeol. J. 1999, 7, 1–14. [Google Scholar] [CrossRef]
- Charette, M.A.; Moore, W.S.; Burnett, W.C. Chapter 5 Uranium- and Thorium-Series Nuclides as Tracers of Submarine Groundwater Discharge. Radioact. Environ. 2008, 13, 155–191. [Google Scholar]
- Erőss, A.; Surbeck, H.; Csondor, K.; Horváth, Á.; Mádl-Szőnyi, J.; Lénárt, L. Radionuclides in the Waters of the Bükk Region, Hungary. J. Radioanal. Nucl. Chem. 2014, 303, 2529–2533. [Google Scholar] [CrossRef]
- Erőss, A.; Mádl-Szőnyi, J.; Surbeck, H.; Horváth, Á.; Goldscheider, N.; Csoma, A.É. Radionuclides as Natural Tracers for the Characterization of Fluids in Regional Discharge Areas, Buda Thermal Karst, Hungary. J. Hydrol. 2012, 426, 124–137. [Google Scholar] [CrossRef]
- Gunn, J.; Bottrell, S.H.; Lowe, D.J.; Worthington, S.R.H. Deep Groundwater Flow and Geochemical Processes in Limestone Aquifers: Evidence from Thermal Waters in Derbyshire, England, UK. Hydrogeol. J. 2006, 14, 868–881. [Google Scholar] [CrossRef]
- An, R.; Jiang, X.-W.; Wang, J.-Z.; Wan, L.; Wang, X.-S.; Li, H. A Theoretical Analysis of Basin-Scale Groundwater Temperature Distribution. Hydrogeol. J 2015, 23, 397–404. [Google Scholar] [CrossRef]
- Bredehoeft, J.D.; Papaopulos, I.S. Rates of Vertical Groundwater Movement Estimated from the Earth’s Thermal Profile. Water Resour. Res. 1965, 1, 325–328. [Google Scholar] [CrossRef]
- Mádl-Szőnyi, J.; Tóth, Á. Basin-Scale Conceptual Groundwater Flow Model for an Unconfined and Confined Thick Carbonate Region. Hydrogeol. J. 2015, 23, 1359–1380. [Google Scholar] [CrossRef]
- Kiss, J.; Virágh, K. Urántartalmú Foszfátos Kõzet a Balatonfelvidéki (Pécsely) Triász Összletben [Uranium-Bearing Phosphatite Formation in the Triassic Succession at Balaton Highland (Pécsely)]. Földtani Közlöny 1959, 89, 85–97. [Google Scholar]
- Molnár, Z.; Kiss, G.; Dódony, I.; Zaccarini, F. Uranium and REE Enrichment of the Phosphatite Occurrence at Pécsely (Balaton Highland, Hungary). In Proceedings of the Acta Mineralogica-Petrographica, Abstract Series, Miskolc, Hungary, 20–24 September 2014; p. 90. [Google Scholar]
- Baják, P.; Csondor, K.; Pedretti, D.; Muniruzzaman, M.; Surbeck, H.; Izsák, B.; Vargha, M.; Horváth, Á.; Pándics, T.; Erőss, A. Refining the Conceptual Model for Radionuclide Mobility in Groundwater in the Vicinity of a Hungarian Granitic Complex Using Geochemical Modeling. Appl. Geochem. 2022, 137, 105201. [Google Scholar] [CrossRef]
- Surbeck, H. Alpha Spectrometry Sample Preparation Using Selectively Adsorbing Thin Films. Appl. Radiat. Isot. 2000, 53, 97–100. [Google Scholar] [CrossRef]
- Ilosvay, L. A Balaton Vizének Chemiai Viszonyai [The Chemical Conditions of Water in Lake Balaton]. In A Balaton tudományos tanulmányozásának eredményei; Lóczy, L., Ed.; Magyar Földrajzi Társaság: Budapest, Hungary, 1898; Volume I/6, pp. 1–27. [Google Scholar]
- Entz, B. Chemische Charakterisierung Der Gewässer in Der Umgebung Des Balatonsees (Plattensees) Und Chemische Verhältnisse Des Balatonwassers [Chemical Characterisation of Watercourses in the Vicinity of Lake Balaton and Chemical Conditions of Lake Balaton]. Annal. Biol. Tihany 1959, 26, 131–201. [Google Scholar]
- Schmidt, E.R. A Balatonkörnyéki Hévízfeltárási Lehetőségekről [On the Prospect of Thermal Water Exploration in the Vicinity of Lake Balaton]. Hidrológiai Tájékoztató 1967, 7, 54–57. [Google Scholar]
- Tompa, É.; Nyirő-Kósa, I.; Rostási, Á.; Cserny, T.; Pósfai, M. Distribution and Composition of Mg-Calcite and Dolomite in the Water and Sediments of Lake Balaton. Cent. Eur. Geol. 2014, 57, 113–136. [Google Scholar] [CrossRef] [Green Version]
- Kleb, B.; Török, E.; Zsilák, G.L. Vízföldtani Megfigyelések Balatongyörök Környékén [Hydrogeological Observations around Balatongyörök]. Hidrológiai Tájékoztató 1965, 5, 49–51. [Google Scholar]
- Tóth, Á. A Balaton-Felvidék Felszínalatti Vizeinek Hidraulikai Kapcsolata a Bakonnyal És a Balatonnal [Groundwater Flow Systems and Hydraulic Connection of the Bakony—Balaton Highland—Lake Balaton Region], Budapest, 2018. PhD Thesis, ELTE Eötvös Loránd University, Budapest, Hungary, 2018. [Google Scholar]
- Tsamos, P.; Kolias, P.; Lambropoulou, D.; Noli, F. Distribution and Temporal Variability of Uranium and Toxic Metal(Loid)s in Snow and Rainwater from an Oil Industry and Urban Area in Thessaloniki-Greece. Sci. Total Environ. 2022, 838, 155604. [Google Scholar] [CrossRef]
- Martin, P. Uranium and Thorium Series Radionuclides in Rainwater over Several Tropical Storms. J. Environ. Radioact. 2003, 65, 1–18. [Google Scholar] [CrossRef]
- Matsunami, T.; Mizohata, A.; Mamuro, T.; Tsujimoto, T. Detection of Uranium in Rain Water from Nuclear Explosions. Jpn. J. Health Phys. 1978, 13, 193–196. [Google Scholar] [CrossRef]
- Bodor, P.; Tóth, Á.; Kovács, J.; Mádl-Szőnyi, J. Multidimensional Data Analysis of Natural Springs in a Carbonate Region. In Proceedings of the First EAGE/TNO Workshop; Verweij, H., Ed.; European Association of Geoscientists & Engineers: Utrecht, The Netherlands, 2015; p. Th A03. [Google Scholar]
- Padisák, J.; Reynolds, C.S. Shallow Lakes: The Absolute, the Relative, the Functional and the Pragmatic. Hydrobiologia 2003, 506, 1–11. [Google Scholar] [CrossRef]
- Jasechko, S. Global Isotope Hydrogeology―Review. Rev. Geophys. 2019, 57, 835–965. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z.; Jiang, C. Run-off Analyses Using Isotopes and Hydrochemistry in Yushugou River Basin, Eastern Tianshan Mountains. J. Earth Syst. Sci. 2017, 126, 86. [Google Scholar] [CrossRef] [Green Version]
- Cao, X.; Wu, P.; Zhou, S.; Han, Z.; Tu, H.; Zhang, S. Seasonal Variability of Oxygen and Hydrogen Isotopes in a Wetland System of the Yunnan-Guizhou Plateau, Southwest China: A Quantitative Assessment of Groundwater Inflow Fluxes. Hydrogeol. J. 2018, 26, 215–231. [Google Scholar] [CrossRef]
- Turner, J.; Macpherson, D.K.; Stokes, R.A. The Mechanisms of Catchment Flow Processes Using Natural Variations in Deuterium and Oxygen-18. J. Hydrol. 1987, 94, 143–162. [Google Scholar] [CrossRef]
- Bolduc, C.; Lamoureux, S.F.; Franssen, J. Thermal and Isotopic Evidence for Surface and Subsurface Water Contributions to Baseflow in a High Arctic River. Hydrol. Process. 2018, 32, 602–616. [Google Scholar] [CrossRef]
- Craig, H. Standard for Reporting Concentrations of Deuterium and Oxygen-18 in Natural Waters. Science 1961, 133, 1833–1834. [Google Scholar] [CrossRef]
- Szőcs, T.; Frape, S.; Gwynne, R. Integrating Hydrogeochemical and Isotope Data in Studying Regional Groundwater Flow Systems in the Great Hungarian Plain. Procedia Earth Planet. Sci. 2015, 13, 177–180. [Google Scholar] [CrossRef] [Green Version]
- Babre, A.; Kalvāns, A.; Popovs, K.; Retiķe, I.; Dēliņa, A.; Vaikmäe, R.; Martma, T. Pleistocene Age Paleo-Groundwater Inferred from Water-Stable Isotope Values in the Central Part of the Baltic Artesian Basin. Isot. Environ. Health Stud. 2016, 52, 706–725. [Google Scholar] [CrossRef]
- Barna, G.; Fórizs, I. A Balaton Stabilizotóp-Hidrológiai Karakterisztikája [The Isotope Hydrologic Character of the Lake Balaton]. Hidrológiai Közlöny 2007, 87, 35–51. [Google Scholar]
- Koch, L. A Balatonfüredi Kossuth Lajos Gyógyforrás Vízföldtani Viszonyai És Felújítása [Hydrogeological Settings and Renovation of Kossuth Lajos Medicinal Spring in Balatonfüred]. Földtani Közlöny 1976, 106, 1–19. [Google Scholar]
- Kern, Z.; Hatvani, I.; Czuppon, G.; Fórizs, I.; Erdélyi, D.; Kanduč, T.; Palcsu, L.; Vreča, P. Isotopic ‘Altitude’ and ‘Continental’ Effects in Modern Precipitation across the Adriatic–Pannonian Region. Water 2020, 12, 1797. [Google Scholar] [CrossRef]
- Dansgaard, W. Stable Isotopes in Precipitation. Tellus 1964, 16, 436–468. [Google Scholar] [CrossRef]
- Fórizs, I.; Berecz, T.; Molnár, Z.; Süveges, M. Origin of Shallow Groundwater of Csepel Island (South of Budapest, Hungary, River Danube): Isotopic and Chemical Approach. Hydrol. Process. 2005, 19, 3299–3312. [Google Scholar] [CrossRef]
- Berecz, T.; Fórizs, I.; Deák, J. Felszín Alatti Vizek Környezeti Izotópos És Kémiai Vizsgálata a Duna-Tisza Köze Déli Részén [Stable Isotope and Chemical Investigation of Groundwaters in the Southern Danube-Tisza Interfluve Region]. Hidrológiai Közlöny 2001, 81, 118–124. [Google Scholar]
- Stute, M.; Deák, J. Environmental Isotope Study (14C, 13C, 18O, D, Noble Gases) on Deep Groundwater Circulation Systems in Hungary With Reference to Paleoclimate. Radiocarbon 1989, 31, 902–918. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Li, W. A Review of Regional Groundwater Flow Modeling. Geosci. Front. 2011, 2, 205–214. [Google Scholar] [CrossRef] [Green Version]
- Zimmerman, W.B. Multiphysics Modeling with Finite Element Methods; World Scientific Publishing Company: London, UK, 2006. [Google Scholar]
- Szijártó, M.; Galsa, A.; Tóth, Á.; Mádl-Szőnyi, J. Numerical Investigation of the Combined Effect of Forced and Free Thermal Convection in Synthetic Groundwater Basins. J. Hydrol. 2019, 572, 364–379. [Google Scholar] [CrossRef]
- Péczely, G. Éghajlattan [Climatology]; Nemzeti Tankönyvkiadó: Budapest, Hungary, 2009. [Google Scholar]
- Lenkey, L.; Mihályka, J.; Paróczi, P. Review of Geothermal Conditions of Hungary. Földtani Közlöny 2021, 151, 65–78. [Google Scholar] [CrossRef]
- Tóth, Á.; Galsa, A.; Mádl-Szőnyi, J. Significance of Basin Asymmetry and Regional Groundwater Flow Conditions in Preliminary Geothermal Potential Assessment–Implications on Extensional Geothermal Plays. Glob. Planet Chang. 2020, 195, 103344. [Google Scholar] [CrossRef]
- Békési, E.; Lenkey, L.; Limberger, J.; Porkoláb, K.; Balázs, A.; Bonté, D.; Vrijlandt, M.; Horváth, F.; Cloetingh, S.; van Wees, J.-D. Subsurface Temperature Model of the Hungarian Part of the Pannonian Basin. Glob. Planet Chang. 2018, 171, 48–64. [Google Scholar] [CrossRef]
- Lenkey, L.; Raáb, D.; Goetzl, G.; Lapanje, A.; Nádor, A.; Rajver, D.; Rotár-Szalkai, Á.; Svasta, J.; Zekiri, F. Lithospheric Scale 3D Thermal Model of the Alpine–Pannonian Transition Zone. Acta Geod. Geophys. 2017, 52, 161–182. [Google Scholar] [CrossRef] [Green Version]
- Stegena, L. Thermal Effect of Hydrogeology in Closed Basins. In Hydrogeological Regimes and Their Subsurface Thermal Effects; Beck, A.E., Garven, G., Stegena, L., Eds.; American Geophysical Union: Washington, DC, USA, 1987; pp. 81–86. ISBN 111866650X. [Google Scholar]
- Lenkey, L.; Dövényi, P.; Horváth, F.; Cloetingh, S. Geothermics of the Pannonian Basin and Its Bearing on the Neotectonics. EGU Stephan Mueller Spec. Publ. Ser. 2002, 3, 29–40. [Google Scholar] [CrossRef]
- Horváth, F.; Musitz, B.; Balázs, A.; Végh, A.; Uhrin, A.; Nádor, A.; Koroknai, B.; Pap, N.; Tóth, T.; Wórum, G. Evolution of the Pannonian Basin and Its Geothermal Resources. Geothermics 2015, 53, 328–352. [Google Scholar] [CrossRef]
- Korim, K. A Balaton Környéki Hévízfeltárás Helyzete És Jövője [The Present and Future of Thermal Water Exploraion in the Vicinity of Lake Balaton]. Hidrológiai Tájékoztató 1974, 14, 46–47. [Google Scholar]
- Gleeson, T.; Manning, A.H. Regional Groundwater Flow in Mountainous Terrain: Three-dimensional Simulations of Topographic and Hydrogeologic Controls. Water Resour. Res. 2008, 44, 1–16. [Google Scholar] [CrossRef]
- Central Transdanubian Water Management Directorate Vízgyűjtő-Gazdálkodási Terv—Balaton Részvízgyűjtő [Watershed Management Plan—Balaton Sub-Catchment] 2016. Available online: http://www.vizugy.hu/vizstrategia/documents/78C0BA65-F0E0-4B33-B77A-ACC6D9548482/Balaton_RVGT_aprilis.pdf (accessed on 5 March 2023).
- Central Transdanubian Water Management Directorate Vízgyűjtő-Gazdálkodási Terv—Balaton Közvetlen [Watershed Management Plan—Balaton Direct] 2016. Available online: http://www.vizugy.hu/vizstrategia/documents/FE0969DF-712C-4314-A8EF-6BEB5FAF973F/VGT2_4-2_Balaton_kozvetlen_vegleges.pdf (accessed on 5 March 2023).
- General Directorate of Water Management Vízgyűjtő-Gazdálkodási Terv—A Duna-Vízgyűjtő Magyarországi Része [Watershed Management Plan—The Hungarian Part of the Danube Watershed] 2016. Available online: http://www.vizugy.hu/vizstrategia/documents/E3E737A3-3EBC-4B6F-973C-5DD9B8A6DBAB/OVGT_foanyag_vegleges.pdf (accessed on 5 March 2023).
- Cholnoky, J. A Balaton Hidrográfiája [Hydrography of Lake Balaton]; Magyar Földrajzi Társaság: Budapest, Hungary, 1918; Volume I. [Google Scholar]
- Visnovitz, F. Gázok „szellemképe” a Balatoni Üledékekben [“Ghost Image” of Gases in the Balaton Sediments]. In A Balaton kutatása Lóczy Lajos nyomdokán; Babinszki, E., Horváth, F., Eds.; Magyarhoni Földtani Társulat: Budapest, Hungary, 2020; pp. 251–269. [Google Scholar]
- Lee, D.R. A Device for Measuring Seepage Flux in Lakes and Estuaries. Limnol. Oceanogr. 1977, 22, 140–147. [Google Scholar] [CrossRef]
- Rosenberry, D.O. Integrating Seepage Heterogeneity with the Use of Ganged Seepage Meters. Limnol. Oceanogr. Methods 2005, 3, 131–142. [Google Scholar] [CrossRef]
- Vallet-Coulomb, C.; Legesse, D.; Gasse, F.; Travi, Y.; Chernet, T. Lake Evaporation Estimates in Tropical Africa (Lake Ziway, Ethiopia). J. Hydrol. 2001, 245, 1–18. [Google Scholar] [CrossRef]
- Grannemann, N.; Hunt, R.; Nicholas, J.; Reilly, T.; Winter, T. The Importance of Ground Water in the Great Lakes Region; Geological Survey: Tuscaloosa, AL, USA, 2000.
- Varga, G. A Balaton Vízjárását Befolyásoló Tényezők [Factors Influencing the Water Cycle of Lake Balaton]. In A Balaton kutatása Lóczy Lajos nyomdokán; Babinszki, E., Horváth, F., Eds.; Magyarhoni Földtani Társulat: Budapest, Hungary, 2020; pp. 271–285. [Google Scholar]
- Lodge, D.M.; Krabbenhoft, D.P.; Striegl, R.G. A Positive Relationship between Groundwater Velocity and Submersed Macrophyte Biomass in Sparkling Lake Wisconsin. Limnol. Oceanogr. 1989, 34, 235–239. [Google Scholar] [CrossRef]
- Lewandowski, J.; Meinikmann, K.; Nützmann, G.; Rosenberry, D.O. Groundwater—The Disregarded Component in Lake Water and Nutrient Budgets. Part 2: Effects of Groundwater on Nutrients. Hydrol. Process. 2015, 29, 2922–2955. [Google Scholar] [CrossRef]
- Foster, S.; Koundouri, P.; Tuinhof, A.; Kemper, K.; Nanni, M.; Garduño, H. Groundwater Dependent Ecosystems: The Challenge of Balanced Assessment and Adequate Conservation; The World Bank: Washington, DC, USA, 2006. [Google Scholar]
- Eamus, D.; Fu, B.; Springer, A.E.; Stevens, L.E. Groundwater Dependent Ecosystems: Classification, Identification Techniques and Threats. In Integrated Groundwater Management; Jakeman, A.J., Barreteau, O., Hunt, R.J., Rinaudo, J.D., Ross, A., Eds.; Springer: Cham, Switzerland, 2016; pp. 313–346. [Google Scholar]

| Name of Stream | Start of Data Series | End of Data Series | Average Flow Rate (m3/s) | BFI (%) after 1st Pass | BFI (%) after 2nd Pass | BFI (%) after 3rd Pass | Average BFI (%) |
|---|---|---|---|---|---|---|---|
| Arácsi-séd | 1 January 1988 | 31 December 2020 | 0.014 | 86 | 79 | 75 | 80 |
| Burnót-patak | 1 July 1970 | 31 December 2020 | 0.129 | 72 | 58 | 50 | 60 |
| Fűzfői-séd | 1 January 1992 | 31 December 2020 | 0.017 | 69 | 56 | 49 | 58 |
| Kéki-séd | 1 January 1983 | 31 December 2020 | 0.038 | 83 | 76 | 71 | 76 |
| Örvényesi-séd | 1 July 1970 | 31 December 2020 | 0.073 | 88 | 82 | 78 | 83 |
| Tapolca-patak | 1 January 1986 | 31 December 2020 | 0.308 | 88 | 81 | 76 | 81 |
| River Zala | 1 July 1975 | 31 December 2020 | 7.17 | 82 | 71 | 64 | 73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tóth, Á.; Baják, P.; Szijártó, M.; Tiljander, M.; Korkka-Niemi, K.; Hendriksson, N.; Mádl-Szőnyi, J. Multimethodological Revisit of the Surface Water and Groundwater Interaction in the Balaton Highland Region—Implications for the Overlooked Groundwater Component of Lake Balaton, Hungary. Water 2023, 15, 1006. https://doi.org/10.3390/w15061006
Tóth Á, Baják P, Szijártó M, Tiljander M, Korkka-Niemi K, Hendriksson N, Mádl-Szőnyi J. Multimethodological Revisit of the Surface Water and Groundwater Interaction in the Balaton Highland Region—Implications for the Overlooked Groundwater Component of Lake Balaton, Hungary. Water. 2023; 15(6):1006. https://doi.org/10.3390/w15061006
Chicago/Turabian StyleTóth, Ádám, Petra Baják, Márk Szijártó, Mia Tiljander, Kirsti Korkka-Niemi, Nina Hendriksson, and Judit Mádl-Szőnyi. 2023. "Multimethodological Revisit of the Surface Water and Groundwater Interaction in the Balaton Highland Region—Implications for the Overlooked Groundwater Component of Lake Balaton, Hungary" Water 15, no. 6: 1006. https://doi.org/10.3390/w15061006
APA StyleTóth, Á., Baják, P., Szijártó, M., Tiljander, M., Korkka-Niemi, K., Hendriksson, N., & Mádl-Szőnyi, J. (2023). Multimethodological Revisit of the Surface Water and Groundwater Interaction in the Balaton Highland Region—Implications for the Overlooked Groundwater Component of Lake Balaton, Hungary. Water, 15(6), 1006. https://doi.org/10.3390/w15061006









