Successive-Station Streamflow Prediction and Precipitation Uncertainty Analysis in the Zarrineh River Basin Using a Machine Learning Technique
Abstract
:1. Introduction
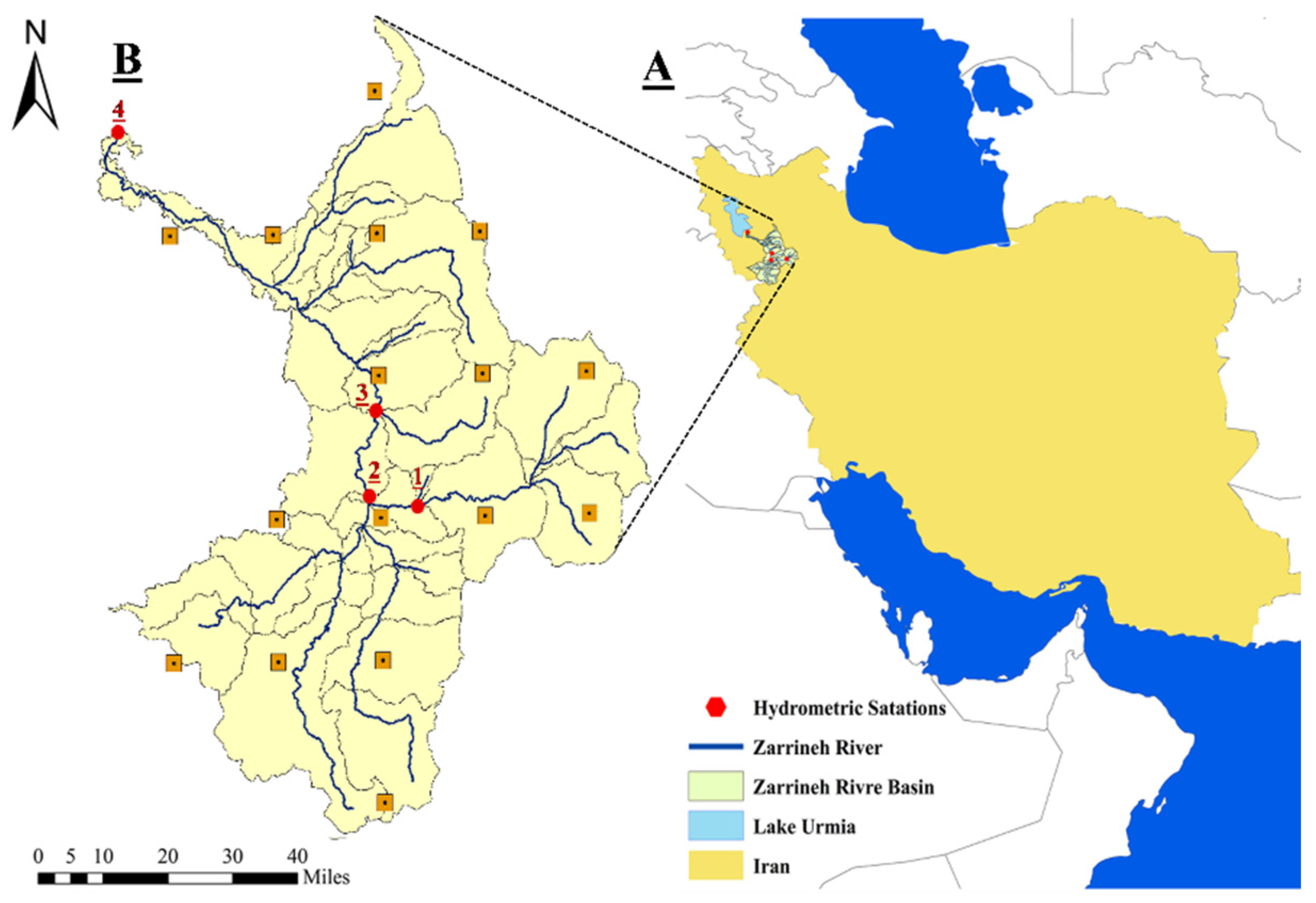
2. Study Area
3. Data Collection
4. Model Description
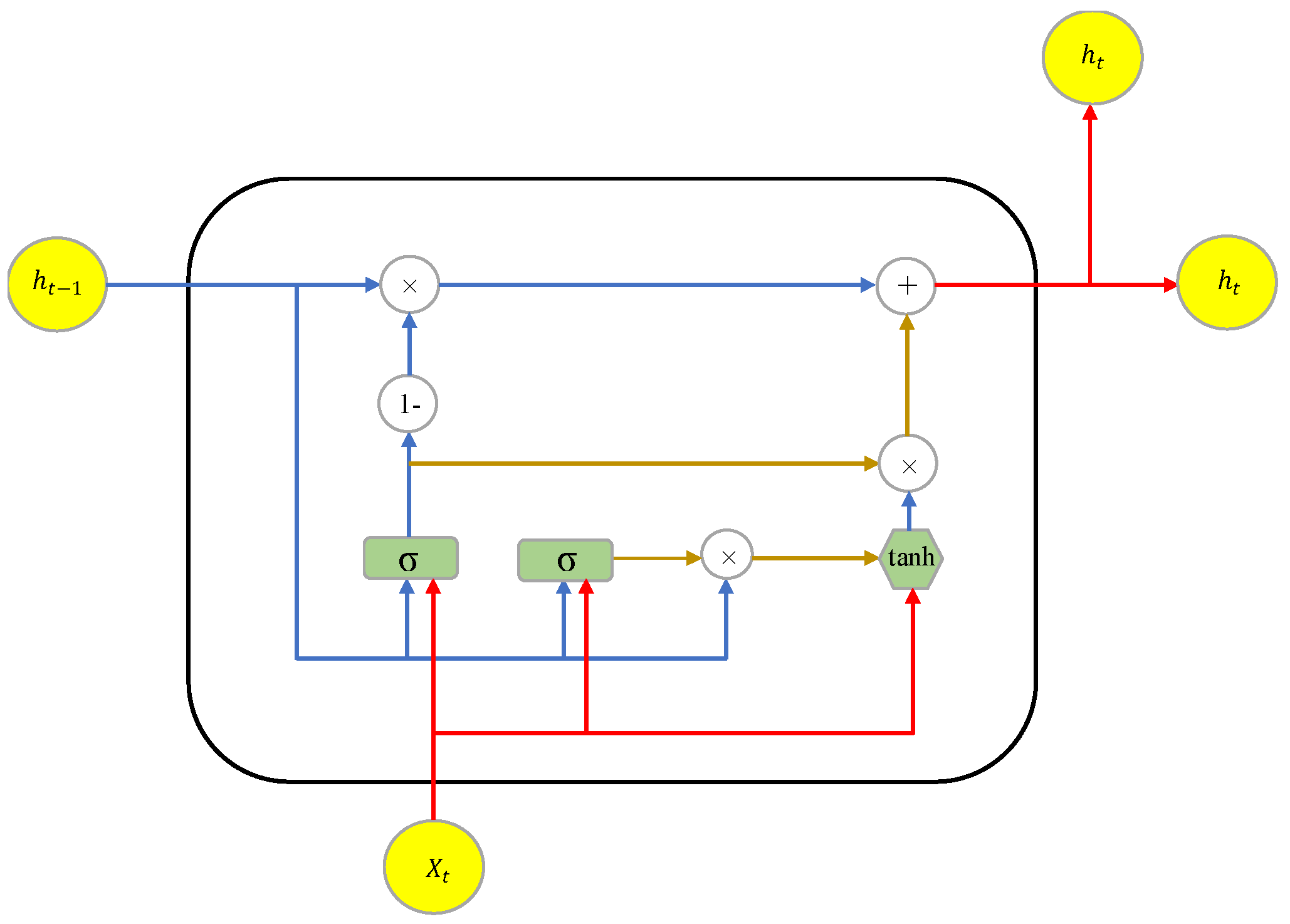
4.1. Gated Recurrent Unit (GRU) Cell Structure
4.2. GLUE Theory
5. Methodology
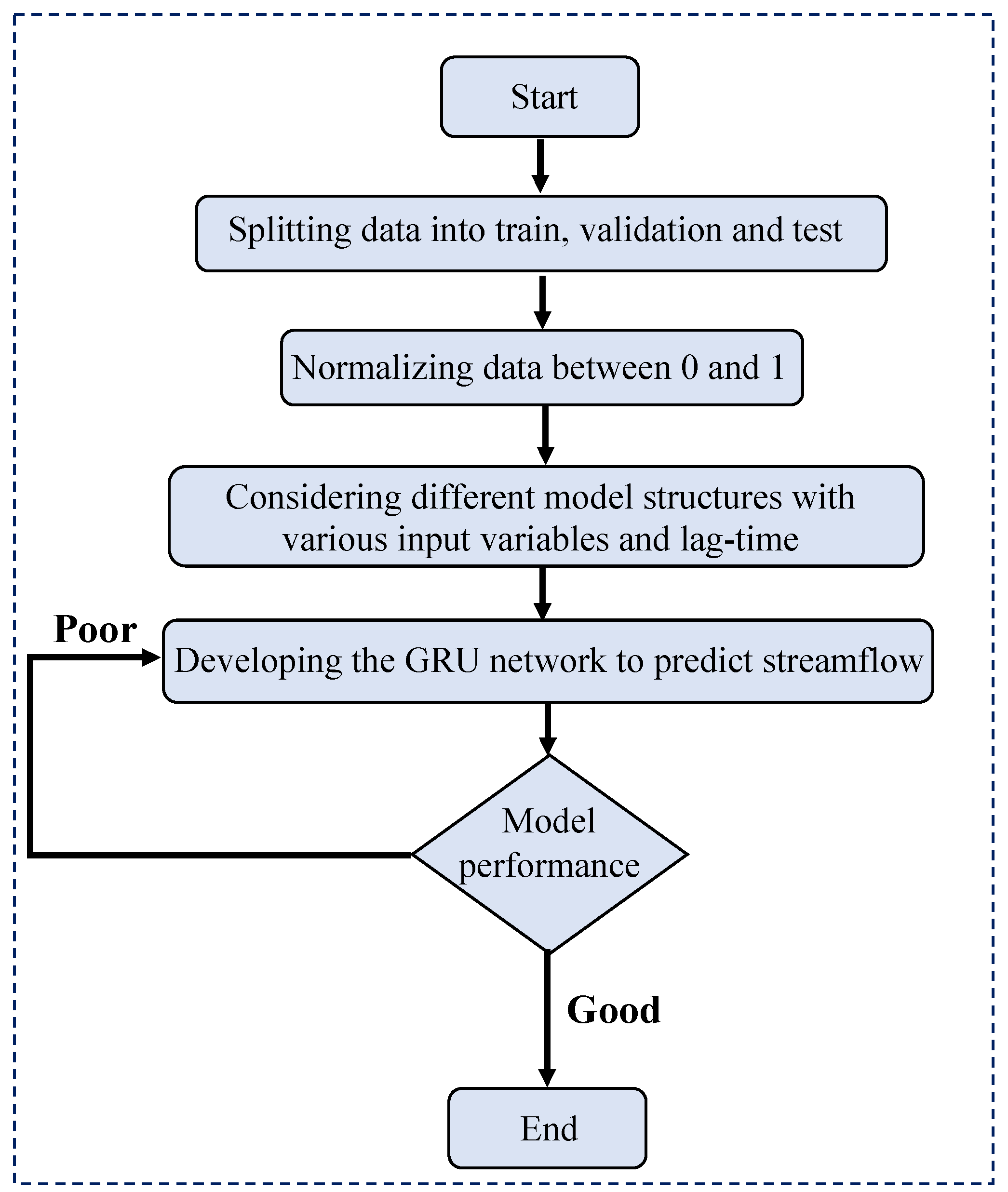
5.1. GRU Model Development
5.2. Data Normalization
5.3. Model Evaluation Criteria
5.4. Bias Correction Method
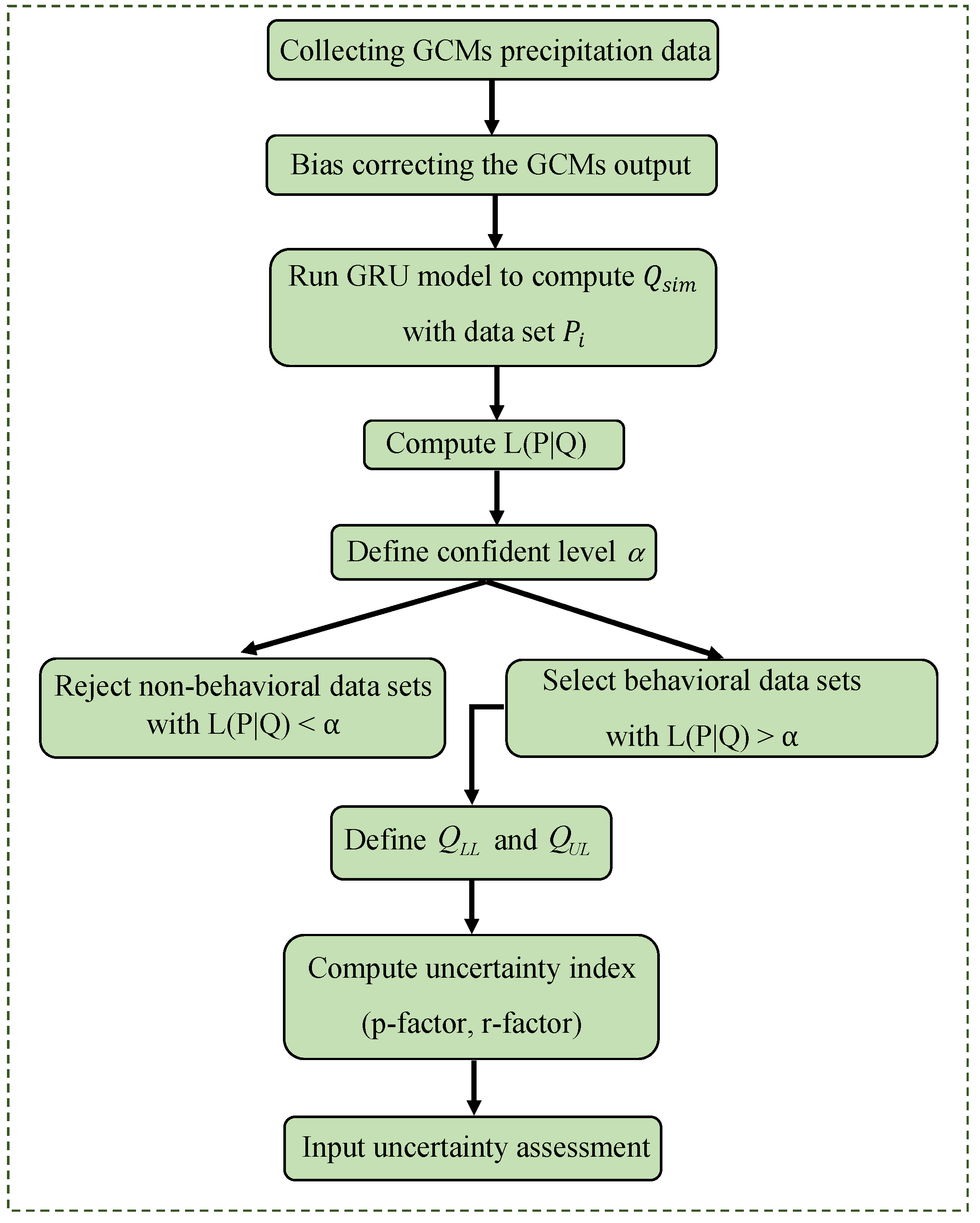
5.5. Quantification of Input Data Uncertainty Using GLUE
6. Results
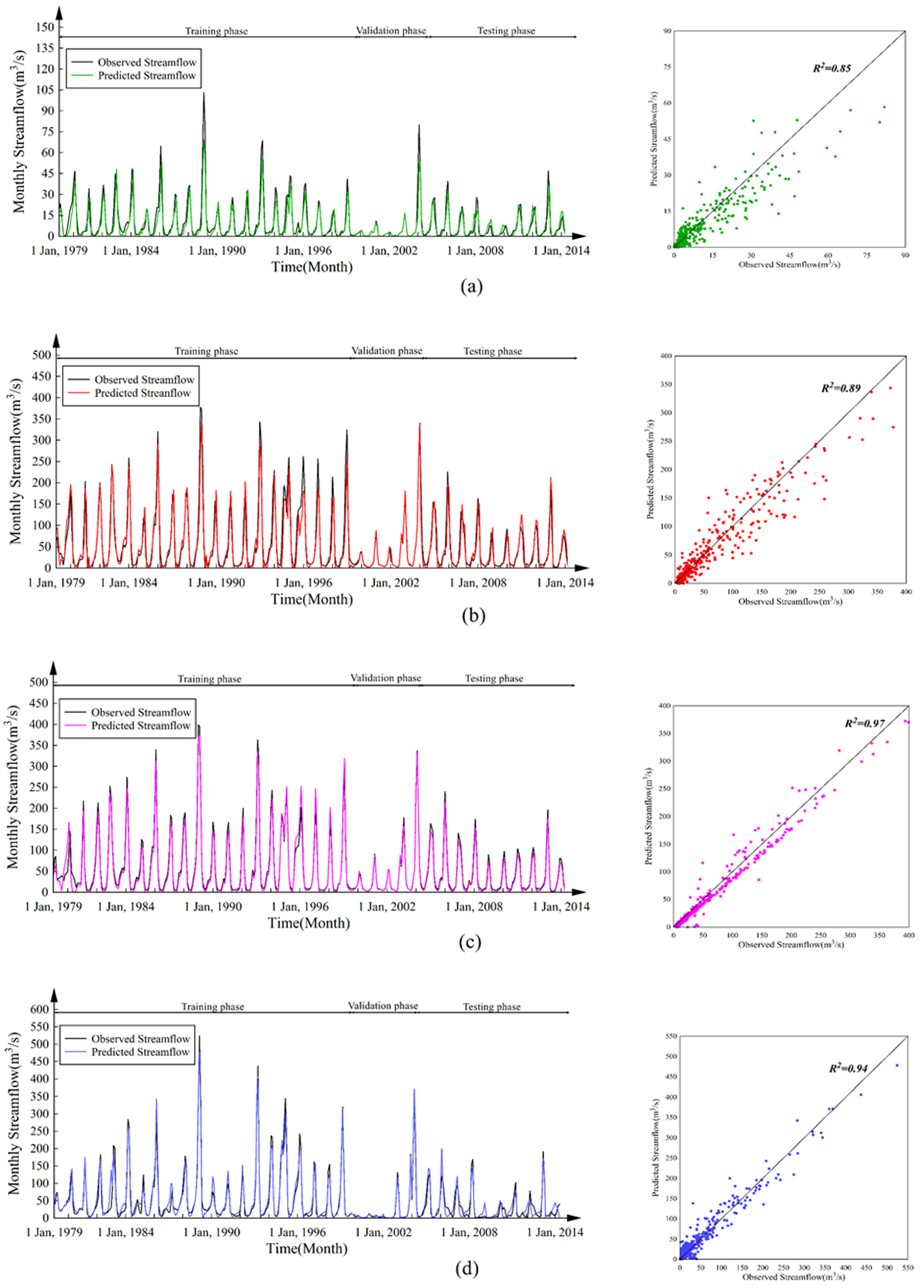
6.1. Evaluation of GRU Networks
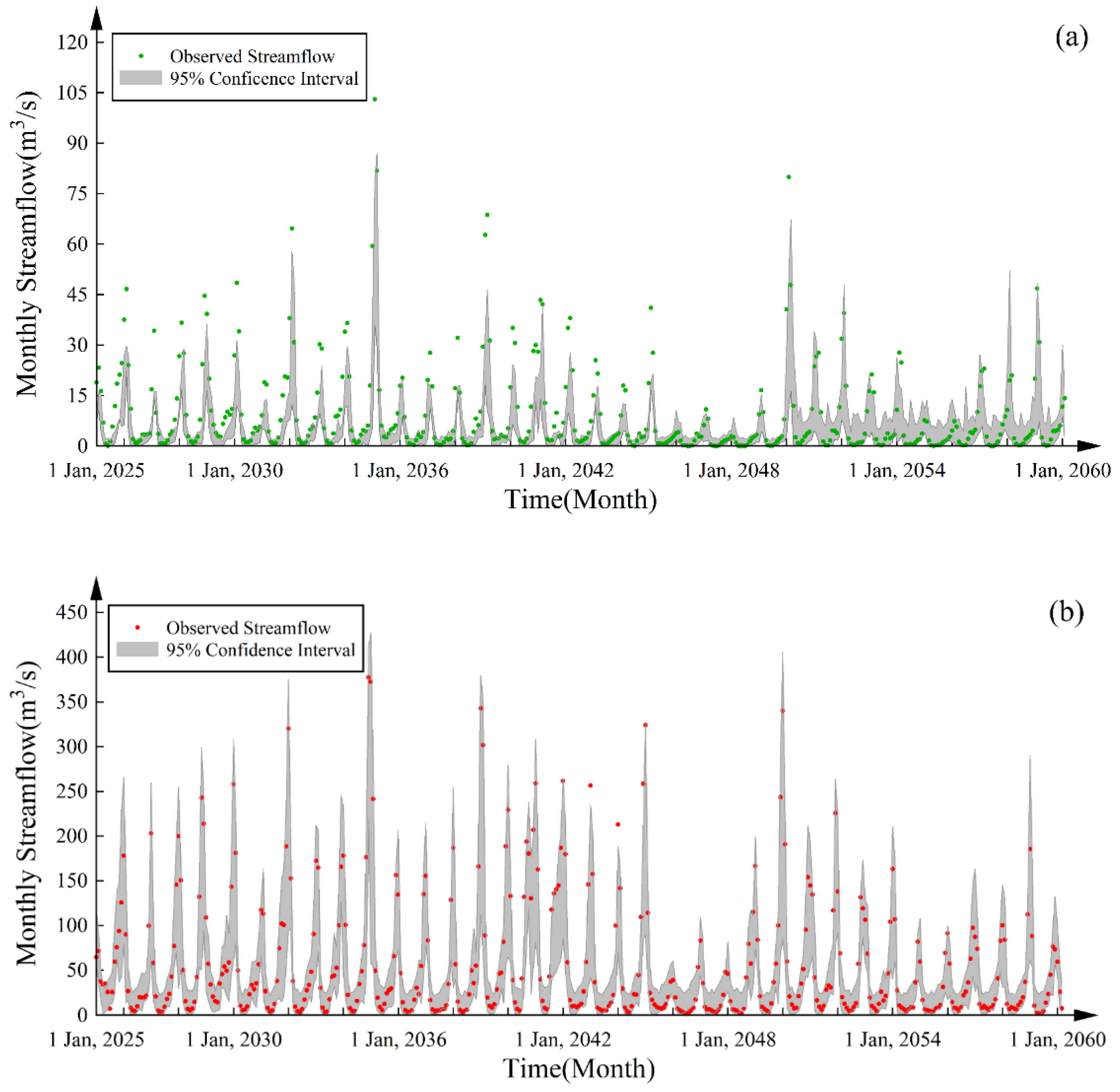
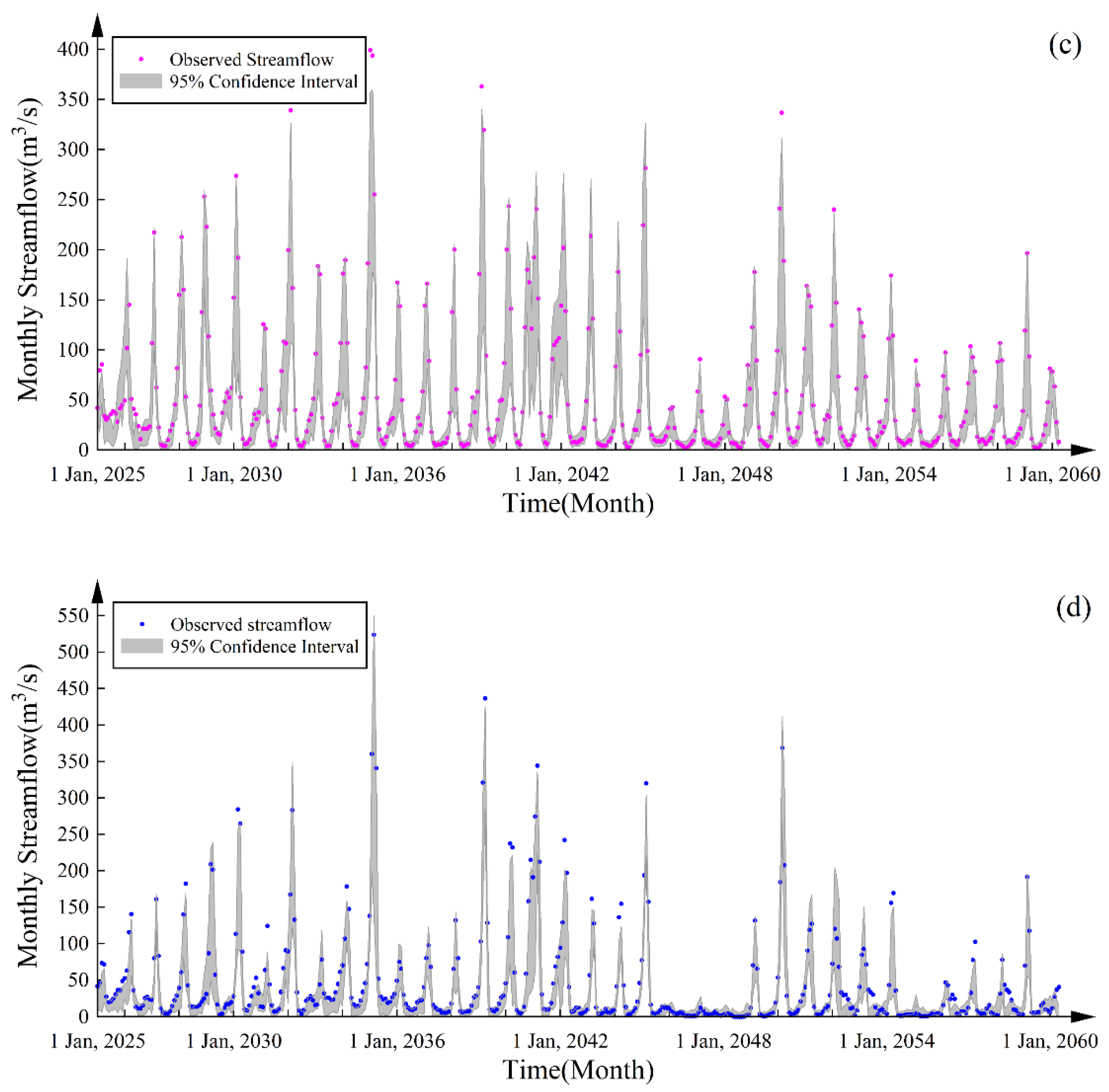
6.2. Uncertainty
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nakhaei, M.; Akrami, M.; Gheibi, M.; Coronado PD U, 2.0.0.4.; Hajiaghaei-Keshteli, M.; Mahlknecht, J. A novel framework for technical performance evaluation of water distribution networks based on the water-energy nexus concept. Energy Convers. Manag. 2022, 273, 116422. [Google Scholar] [CrossRef]
- Jalili, S.; Hamidi, S.A.; Namdar Ghanbari, R. Climate variability and anthropogenic effects on Lake Urmia water level fluctuations, northwestern Iran. Hydrol. Sci. J. 2016, 61, 1759–1769. [Google Scholar] [CrossRef] [Green Version]
- Yazdandoost, F.; Moradian, S.; Izadi, A. Evaluation of Water Sustainability under a Changing Climate in Zarrineh River Basin, Iran. Water Resour. Manag. 2020, 34, 4831–4846. [Google Scholar] [CrossRef]
- Farajzadeh, J.; Fard, A.F.; Lotfi, S. Modeling of monthly rainfall and runoff of Urmia lake basin using “feed-forward neural network” and “time series analysis” model. Water Resour. Ind. 2014, 7, 38–48. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.; Zhou, J.; Ye, L.; Meng, C. Streamflow estimation by support vector machine coupled with different methods of time series decomposition in the upper reaches of Yangtze River, China. Environ. Earth Sci. 2016, 75, 531. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Khan, A.; Zhang, Y.K.; Kuang, X.; Liang, X.; Nuttall, J. Daily runoff forecasting by deep recursive neural network. J. Hydrol. 2021, 596, 126067. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Adnan, R.M. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Ghadami, N.; Gheibi, M.; Kian, Z.; Faramarz, M.G.; Naghedi, R.; Eftekhari, M.; Fathollahi-Fard, A.M.; Dulebenets, M.A.; Tian, G. Implementation of solar energy in smart cities using an integration of artificial neural network, photovoltaic system and classical Delphi methods. Sustain. Cities Soc. 2021, 74, 103149. [Google Scholar] [CrossRef]
- Morovati, K.; Tian, F.; Kummu, M.; Shi, L.; Tudaji, M.; Nakhaei, P.; Olivares, M.A. Contributions from climate variation and human activities to flow regime change of Tonle Sap Lake from 2001 to 2020. J. Hydrol. 2023, 616, 128800. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Wu, H.; Chen, B. Evaluating uncertainty estimates in distributed hydrological modeling for the Wenjing River watershed in China by GLUE, SUFI-2, and ParaSol methods. Ecol. Eng. 2015, 76, 110–121. [Google Scholar] [CrossRef]
- Akbarian, H.; Jalali, F.M.; Gheibi, M.; Hajiaghaei-Keshteli, M.; Akrami, M.; Sarmah, A.K. A sustainable Decision Support System for soil bioremediation of toluene incorporating UN sustainable development goals. Environ. Pollut. 2022, 307, 119587. [Google Scholar] [CrossRef] [PubMed]
- Mousavi, S.J.; Nakhaei, P.; Sadollah, A.; Kim, J.H. Optimization of Hydropower Storage Projects Using Harmony Search Algorithm. In Harmony Search Algorithm, Proceedings of the 3rd International Conference on Harmony Search Algorithm (ICHSA 2017), Bilbao, Spain, 22–24 Februar 2017; Del Ser, J., Ed.; Springer: Singapore, 2017; Volume 514. [Google Scholar] [CrossRef]
- Talebidaloueia, M.; Mirbagheria, S.A.; Nakhaeib, P. Treatment prediction of sugar industry wastewater in moving-bed biofilm reactor using multi expression programming. Desalination Water Treat. 2020, 191, 82–92. [Google Scholar] [CrossRef]
- Gheibi, M.; Eftekhari, M.; Akrami, M.; Emrani, N.; Hajiaghaei-Keshteli, M.; Fathollahi-Fard, A.M.; Yazdani, M. A sustainable decision support system for drinking water systems: Resiliency improvement against cyanide contamination. Infrastructures 2022, 7, 88. [Google Scholar] [CrossRef]
- Bárdossy, A. Neural network-based modelling of the river Danube. J. Hydrol. 2008, 349, 88–100. [Google Scholar]
- Jang, D.; Kim, T.W.; Park, H. A Comparative Study of Machine Learning Methods for Streamflow Prediction of Unimpaired Rivers in the United States. Water 2016, 8, 438. [Google Scholar]
- Liu, J.; Yang, W.; Xiong, L.; He, X. Prediction of Daily Streamflow Using Random Forest Model. J. Hydrol. Eng. 2018, 23, 04018041. [Google Scholar]
- Xu, Z.; Xu, C.Y.; Song, J. A hybrid model based on Gaussian process regression and an improved differential evolution algorithm for river flow forecasting. J. Hydrol. 2016, 533, 143–153. [Google Scholar]
- Zhang, H.; Sun, Z.; Liu, C.; Zhang, J.; Zhang, B. LSTM-based streamflow forecasting for a river with multiple dams considering hydrologic similarity. J. Hydrol. 2019, 574, 697–710. [Google Scholar]
- Amiri, E. Forecasting daily river flows using nonlinear time series models. J. Hydrol. 2015, 527, 1054–1072. [Google Scholar] [CrossRef]
- Arab, M.; Akbarian, H.; Gheibi, M.; Akrami, M.; Fathollahi-Fard, A.M.; Hajiaghaei-Keshteli, M.; Tian, G. A soft-sensor for sustainable operation of coagulation and flocculation units. Eng. Appl. Artif. Intell. 2022, 115, 105315. [Google Scholar] [CrossRef]
- Hu, R.; Fang, F.; Pain, C.C.; Navon, I.M. Rapid spatio-temporal flood prediction and uncertainty quantification using a deep learning method. J. Hydrol. 2019, 575, 911–920. [Google Scholar] [CrossRef]
- Morovati, K.; Nakhaei, P.; Tian, F.; Tudaji, M.; Hou, S. A Machine Learning Framework to Predict Reverse Flow and Water Level: A Case Study of Tonle Sap Lake. J. Hydrol. 2021, 603, 127168. [Google Scholar] [CrossRef]
- Shahsavar, M.M.; Akrami, M.; Gheibi, M.; Kavianpour, B.; Fathollahi-Fard, A.M.; Behzadian, K. Constructing a smart framework for supplying the biogas energy in green buildings using an integration of response surface methodology, artificial intelligence and petri net modelling. Energy Convers. Manag. 2021, 248, 114794. [Google Scholar] [CrossRef]
- Raghu, M.; Poole, B.; Kleinberg, J.; Ganguli, S.; Sohl-Dickstein, J. On the expressive power of deep neural networks. In Proceedings of the International Conference on Machine Learning 2017, Sydney, Australia, 6–11 August 2017; pp. 2847–2854. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- Fu, R.; Zhang, Z.; Li, L. Using LSTM and GRU neural network methods for traffic flow prediction. In Proceedings of the 2016 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 11–13 November 2016; pp. 324–328. [Google Scholar] [CrossRef]
- Apaydin, H.; Feizi, H.; Sattari, M.T.; Colak, M.S.; Shamshirband, S.; Chau, K.W. Comparative analysis of recurrent neural network architectures for reservoir inflow forecasting. Water 2020, 12, 1500. [Google Scholar] [CrossRef]
- Zhu, S.; Heddam, S.; Nyarko, E.K.; Hadzima-Nyarko, M.; Piccolroaz, S.; Wu, S. Modeling daily water temperature for rivers: Comparison between adaptive neuro-fuzzy inference systems and artificial neural networks models. Environ. Sci. Pollut. Res. 2019, 26, 402–420. [Google Scholar] [CrossRef]
- Bae, D.H.; Trinh, H.L.; Nguyen, H.M. Uncertainty estimation of the SURR model parameters and input data for the Imjin River basin using the GLUE method. J. Hydro-Environ. Res. 2018, 20, 52–62. [Google Scholar] [CrossRef]
- Lee, H.; Balin, D.; Shrestha, R.R.; Rode, M. Streamflow prediction with uncertainty analysis, Weida catchment, Germany. KSCE J. Civ. Eng. 2010, 14, 413–420. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, J.; Wang, G.; Jin, J.; Liu, C.; Liu, Y.; Bao, Z. Uncertainty Analysis of SWAT Modeling in the Lancang River Basin Using Four Different Algorithms. Water 2021, 13, 341. [Google Scholar] [CrossRef]
- Zhang, C.; Yan, H.; Takase, K.; Oue, H. Comparison of the soil physical properties and hydrological processes in two different forest type catchments. Water Resour. 2016, 43, 225–237. [Google Scholar] [CrossRef]
- Her, Y.; Yoo, S.H.; Cho, J.; Hwang, S.; Jeong, J.; Seong, C. Uncertainty in hydrological analysis of climate change: Multi-parameter vs. multi-GCM ensemble predictions. Sci. Rep. 2019, 9, 4974. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fabry, F. Obstacles to the greater use of weather radar information. In Proceedings of the 6th International Symposium on Hydrological Applications of Weather Radar, Melbourne, Australia, 2–4 February 2004. [Google Scholar]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Diks, C.G.; Gupta, H.V.; Bouten, W.; Verstraten, J.M. Improved treatment of uncertainty in hydrologic modeling: Combining the strengths of global optimization and data assimilation. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Gupta, H.V.; Bouten, W.; Sorooshian, S. A Shuffled Complex Evolution Metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour. Res. 2003, 39, 1201. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.; Cai, Y.; Sun, L.; Wang, X.; Li, C.; Liu, Q. Sensitivity and uncertainty analysis for streamflow prediction based on multiple optimization algorithms in Yalong River Basin of southwestern China. J. Hydrol. 2021, 601, 126598. [Google Scholar] [CrossRef]
- Amini, A.; Ghazvinei, P.T.; Javan, M.; Saghafian, B. Evaluating the impacts of watershed management on runoff storage and peak flow in Gav-Darreh watershed, Kurdistan, Iran. Arab. J. Geosci. 2014, 7, 3271–3279. [Google Scholar] [CrossRef]
- Emami, F.; Koch, M. Agricultural water productivity-based hydro-economic modeling for optimal crop pattern and water resources planning in the Zarrine River Basin, Iran, in the wake of climate change. Sustainability 2018, 10, 3953. [Google Scholar] [CrossRef] [Green Version]
- Jubb, I.; Canadell, P.; Dix, M. Representative Concentration Pathways (RCPs); Australian Climate Change Science Program; Australian Government, Department of the Environment, Canberra: Canberra, Australia, 2013; pp. 5–7.
- Ramirez-Villegas, J.; Challinor, A.J.; Thornton, P.K.; Jarvis, A. Implications of regional improvement in global climate models for agricultural impact research. Environ. Res. Lett. 2013, 8, 024018. [Google Scholar] [CrossRef]
- Mengistu, A.G.; Woldesenbet, T.A.; Dile, Y.T. Evaluation of the performance of bias-corrected CORDEX regional climate models in reproducing Baro–Akobo basin climate. Theor. Appl. Climatol. 2021, 144, 751–767. [Google Scholar] [CrossRef]
- Kumar, P.S.; Praveen, T.V.; Prasad, M.A. Artificial Neural Network Model for Rainfall-Runoff—A Case Study. Int. J. Hybrid Inf. Technol. 2016, 9, 263–272. [Google Scholar] [CrossRef]
- Muhammad, A.U.; Li, X.; Feng, J. Using LSTM GRU and Hybrid Models for Streamflow Forecasting. In Machine Learning and Intelligent Communications, Proceedings of the 4th International Conference—MLICOM 2019, Nanjing, China, 24–25 August 2019; Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering; Zhai, X., Chen, B., Zhu, K., Eds.; Springer: Cham, Switzerland, 2019; Volume 294. [Google Scholar] [CrossRef]
- Hutter, F.; Hoos, H.; Leyton-Brown, K. An efficient approach for assessing hyperparameter importance. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 754–762. [Google Scholar]
- Liang, C.; Li, H.; Lei, M.; Du, Q. Dongting lake water level forecast and its relationship with the three gorges dam based on a long short-term memory network. Water 2018, 10, 1389. [Google Scholar] [CrossRef] [Green Version]
- Piani, C.; Weedon, G.P.; Best, M.; Gomes, S.M.; Viterbo, P.; Hagemann, S.; Haerter, J.O. Statistical bias correction of global simulated daily precipitation and temperature for the application of hydrological models. J. Hydrol. 2010, 395, 199–215. [Google Scholar] [CrossRef]
- Tieleman, T.; Hinton, G. Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural Netw. Mach. Learn. 2012, 4, 26–31. [Google Scholar]
- Kochenderfer, M.J.; Wheeler, T.A. Algorithms for Optimization; MIT Press: Cambridge, MA, USA, 2019; ISBN 978-0262039420. [Google Scholar]
- Mehan, S.; Neupane, R.P.; Kumar, S. Coupling of SUFI 2 and SWAT for Improving the Simulation of Streamflow in an Agricultural Watershed of South Dakota. Hydrol. Curr. Res. 2017, 8, 280. [Google Scholar] [CrossRef]
- Kiyan, A.; Gheibi, M.; Akrami, M.; Moezzi, R.; Behzadian, K. A Comprehensive Platform for Air Pollution Control System Operation in Smart Cities of Developing Countries: A Case Study of Tehran. Environ. Ind. Lett. 2023, 1, 10–27. [Google Scholar] [CrossRef]
- Kiyan, A.; Gheibi, M.; Akrami, M.; Moezzi, R.; Behzadian, K.; Taghavian, H. The Operation of Urban Water Treatment Plants: A Review of Smart Dashboard Frameworks. Environ. Ind. Lett. 2023, 1, 28–45. [Google Scholar] [CrossRef]
- Gheibi, M.; Chahkandi, B.; Behzadian, K.; Akrami, M.; Moezzi, R. Evaluation of Ceramic Water Filters’ Performance and Analysis of Managerial Insights by SWOT Matrix. Environ. Ind. Lett. 2023, 1, 1–9. [Google Scholar] [CrossRef]

| Name | Model Structure |
|---|---|
| S1 | |
| S2 | |
| S3 | |
| S4 | |
| S5 |
| Training Phase | Validation Phase | Testing Phase | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Station | Structure | NSE | R2 | RMSE | NSE | R2 | RMSE | NSE | R2 | RMSE |
| Safakhaneh (#1) | S1 | 0.34 | 0.35 | 13.9 | 0.49 | 0.34 | 15.1 | 0.46 | 0.29 | 12.3 |
| S2 | 0.53 | 0.66 | 10.2 | 0.52 | 0.63 | 11.1 | 0.54 | 0.57 | 8.1 | |
| S3 | 0.74 | 0.8 | 7.5 | 0.73 | 0.69 | 5.8 | 0.69 | 0.71 | 6.6 | |
| S4 | 0.75 | 0.86 | 5.8 | 0.75 | 0.78 | 6.7 | 0.8 | 0.8 | 5.3 | |
| S5 | 0.73 | 0.81 | 7.7 | 0.79 | 0.75 | 6.6 | 0.75 | 0.78 | 5.7 | |
| Boukan dam (#2) | S1 | −7.9 | 0.79 | 23.4 | −10.8 | 0.82 | 27.4 | −12.6 | 0.85 | 20.7 |
| S2 | 0.79 | 0.89 | 35.1 | 0.83 | 0.88 | 31.5 | 0.75 | 0.92 | 28.1 | |
| S3 | 0.8 | 0.81 | 35.5 | 0.73 | 0.76 | 27.7 | 0.78 | 0.81 | 25.9 | |
| S4 | 0.84 | 0.84 | 31.3 | 0.78 | 0.88 | 28.5 | 0.81 | 0.83 | 24.2 | |
| S5 | 0.88 | 0.89 | 26.8 | 0.88 | 0.89 | 23.5 | 0.85 | 0.86 | 20.7 | |
| Qezkorpi (#3) | S1 | 0.94 | 0.96 | 15.2 | 0.86 | 0.84 | 18.6 | 0.95 | 0.99 | 12.7 |
| S2 | 0.93 | 0.96 | 19.2 | 0.93 | 0.95 | 16.5 | 0.94 | 0.99 | 13.4 | |
| S3 | 0.95 | 0.96 | 15.9 | 0.92 | 0.94 | 11.4 | 0.96 | 0.99 | 10.2 | |
| S4 | 0.96 | 0.96 | 15.1 | 0.97 | 0.98 | 7.6 | 0.98 | 0.99 | 8.2 | |
| S5 | 0.94 | 0.95 | 18.7 | 0.91 | 0.94 | 14.1 | 0.94 | 0.99 | 12.6 | |
| Nezamabad (#4) | S1 | 0.72 | 0.72 | 42.3 | 0.66 | 0.72 | 34.7 | 0.71 | 0.77 | 27.7 |
| S2 | 0.81 | 0.85 | 34.8 | 0.84 | 0.87 | 26.3 | 0.79 | 0.82 | 23.7 | |
| S3 | 0.95 | 0.95 | 18.1 | 0.85 | 0.89 | 17.6 | 0.87 | 0.88 | 18.3 | |
| S4 | 0.94 | 0.94 | 18.7 | 0.89 | 0.93 | 22.4 | 0.85 | 0.88 | 19.8 | |
| S5 | 0.84 | 0.87 | 31.7 | 0.84 | 0.87 | 24.4 | 0.82 | 0.83 | 21.3 | |
| Station Names | p-Factor (%) | r-Factor | |
|---|---|---|---|
| Safakhaneh | 86 | 78.5 | 0.53 |
| Boukan dam | 89 | 89.3 | 0.57 |
| Qezkorpi | 91 | 86.6 | 0.52 |
| Nezam Abad | 85 | 61.6 | 0.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakhaei, M.; Ghazban, F.; Nakhaei, P.; Gheibi, M.; Wacławek, S.; Ahmadi, M. Successive-Station Streamflow Prediction and Precipitation Uncertainty Analysis in the Zarrineh River Basin Using a Machine Learning Technique. Water 2023, 15, 999. https://doi.org/10.3390/w15050999
Nakhaei M, Ghazban F, Nakhaei P, Gheibi M, Wacławek S, Ahmadi M. Successive-Station Streamflow Prediction and Precipitation Uncertainty Analysis in the Zarrineh River Basin Using a Machine Learning Technique. Water. 2023; 15(5):999. https://doi.org/10.3390/w15050999
Chicago/Turabian StyleNakhaei, Mahdi, Fereydoun Ghazban, Pouria Nakhaei, Mohammad Gheibi, Stanisław Wacławek, and Mehdi Ahmadi. 2023. "Successive-Station Streamflow Prediction and Precipitation Uncertainty Analysis in the Zarrineh River Basin Using a Machine Learning Technique" Water 15, no. 5: 999. https://doi.org/10.3390/w15050999







