Analysis of the Effect of Pore Water Pressure on a Small Radius Curve Section of a Fine Sand Layer under Cyclic Metro
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.1.1. Experimental Site Overview
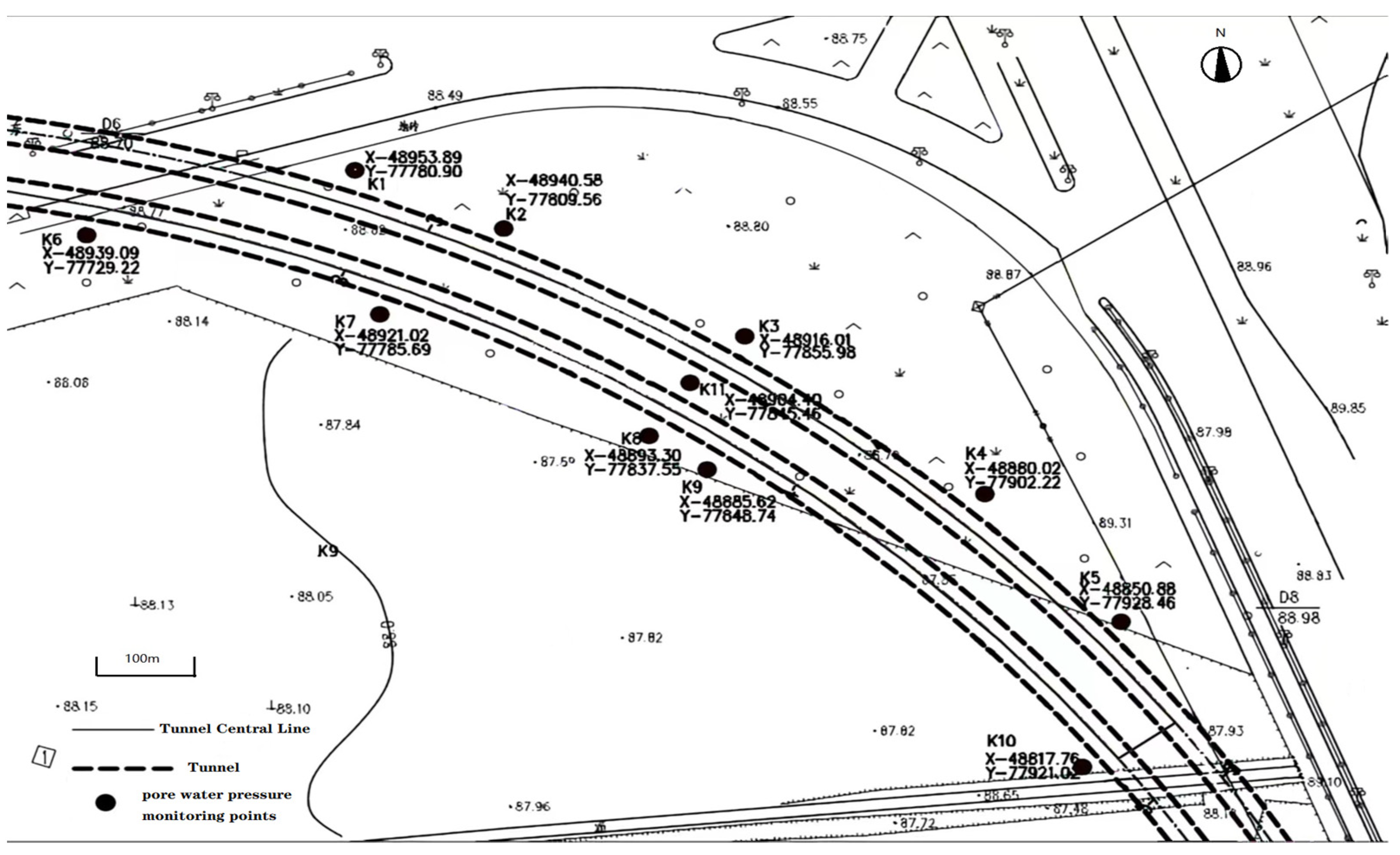
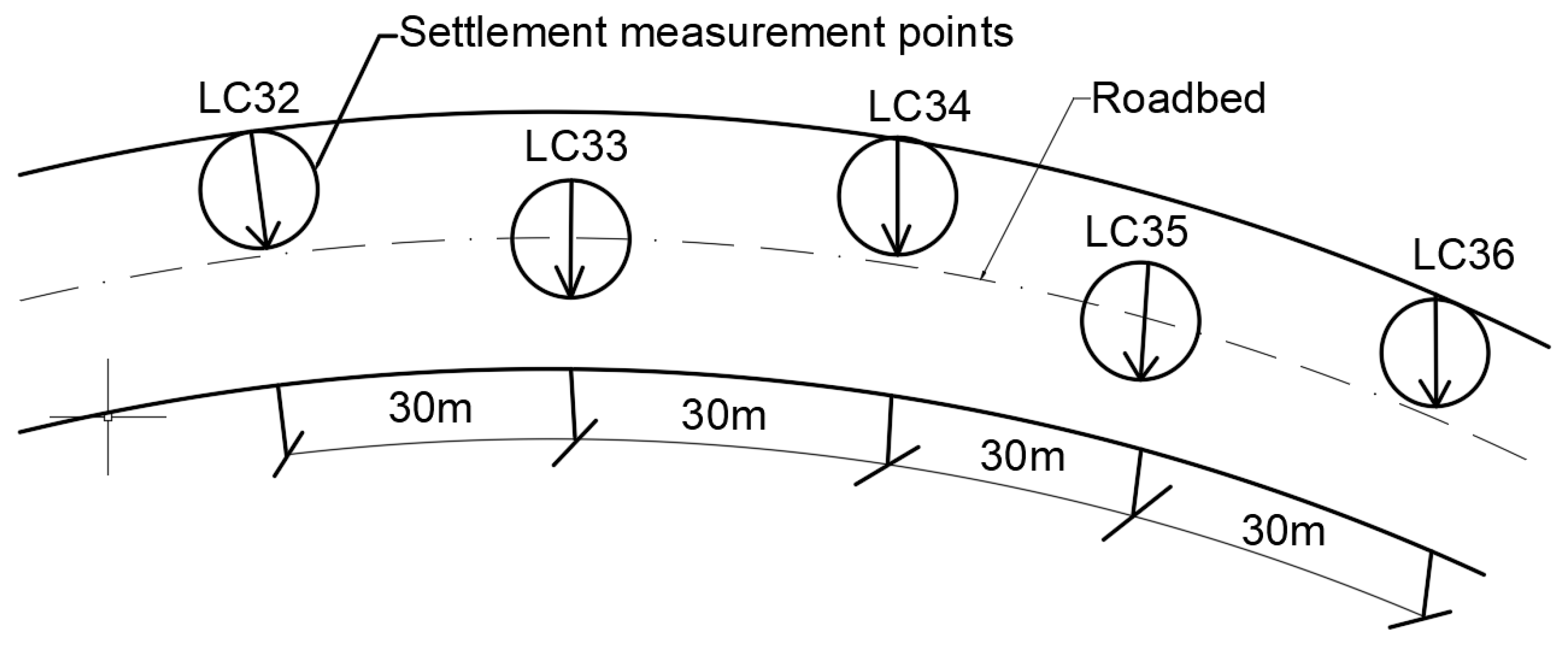
2.1.2. Experimental Measurement Point Layout
2.1.3. Experimental Content and Programme
2.2. Field Data Analysis
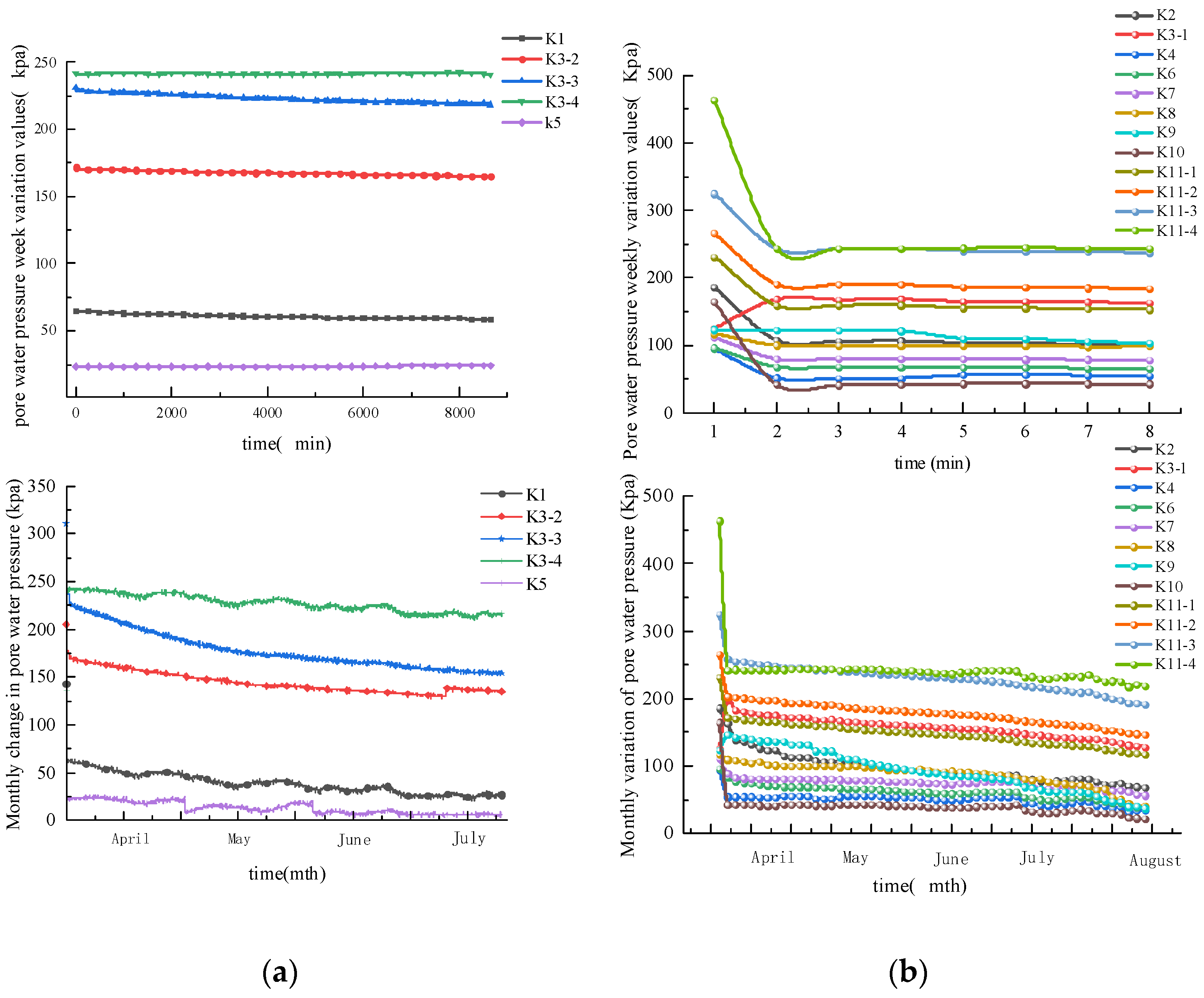
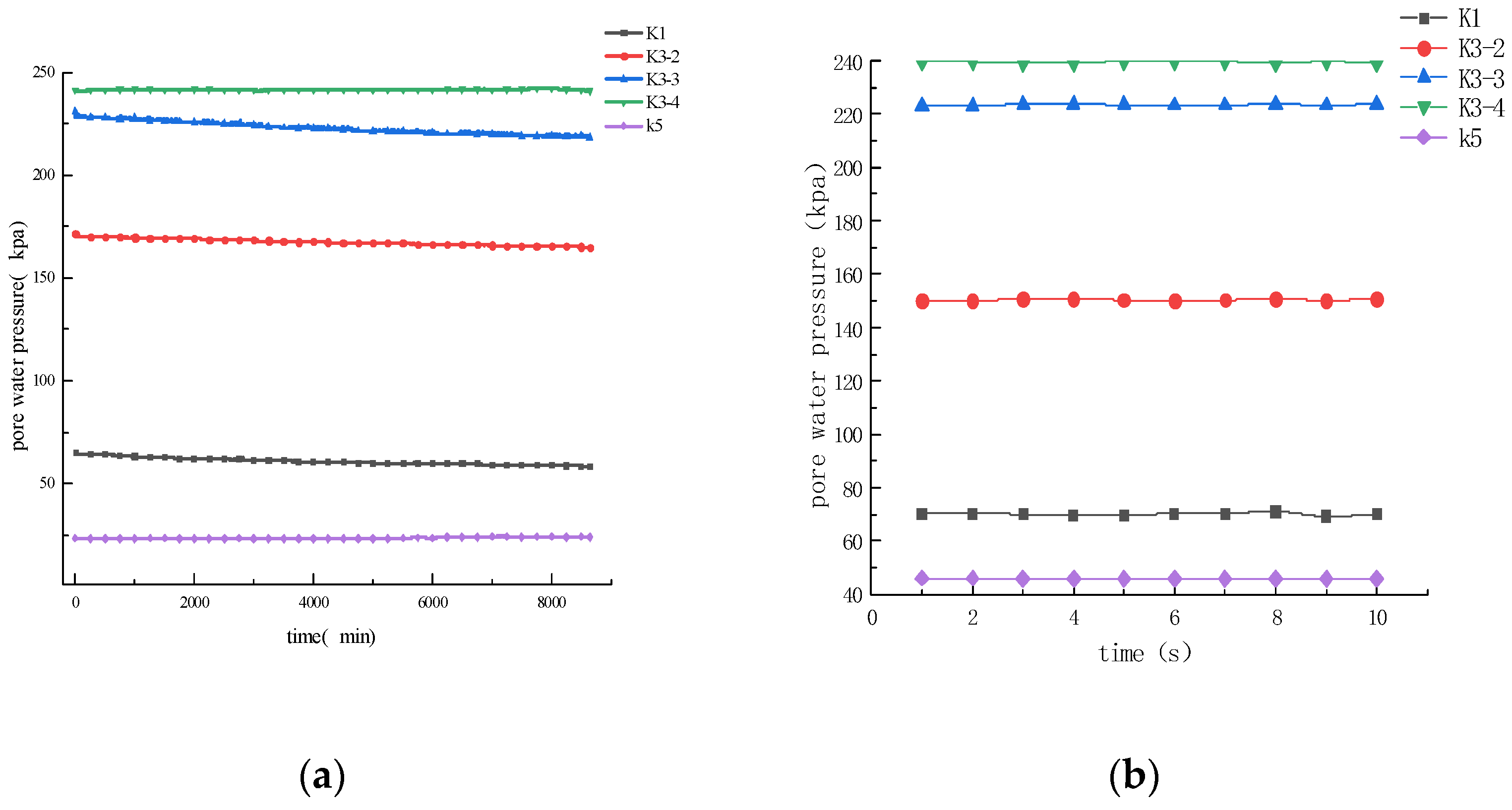
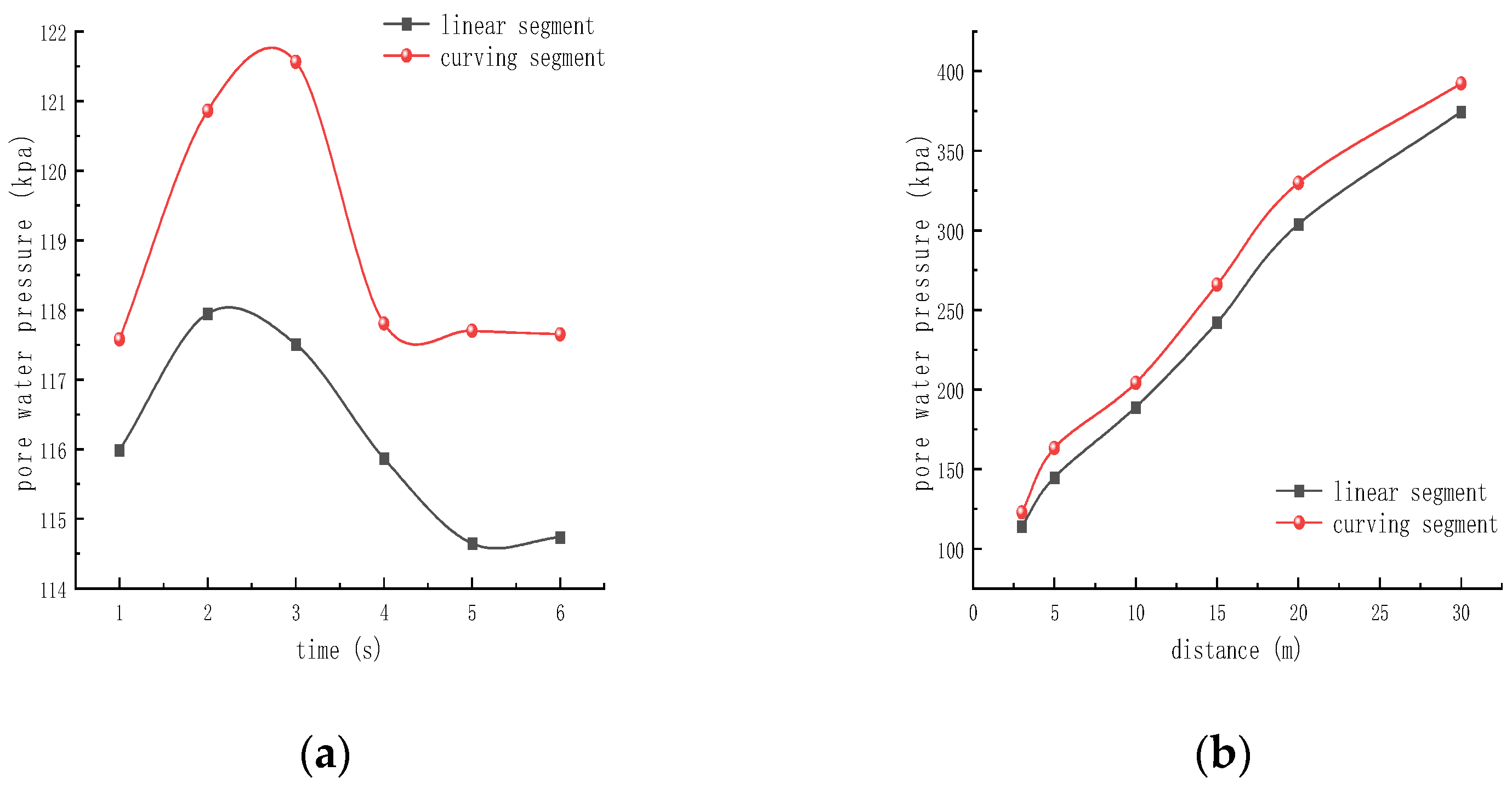
2.2.1. Pore Water Pressure Response Analysis under Cyclic Loading
2.2.2. Variation of Pore Water Pressure with Depth of Burial
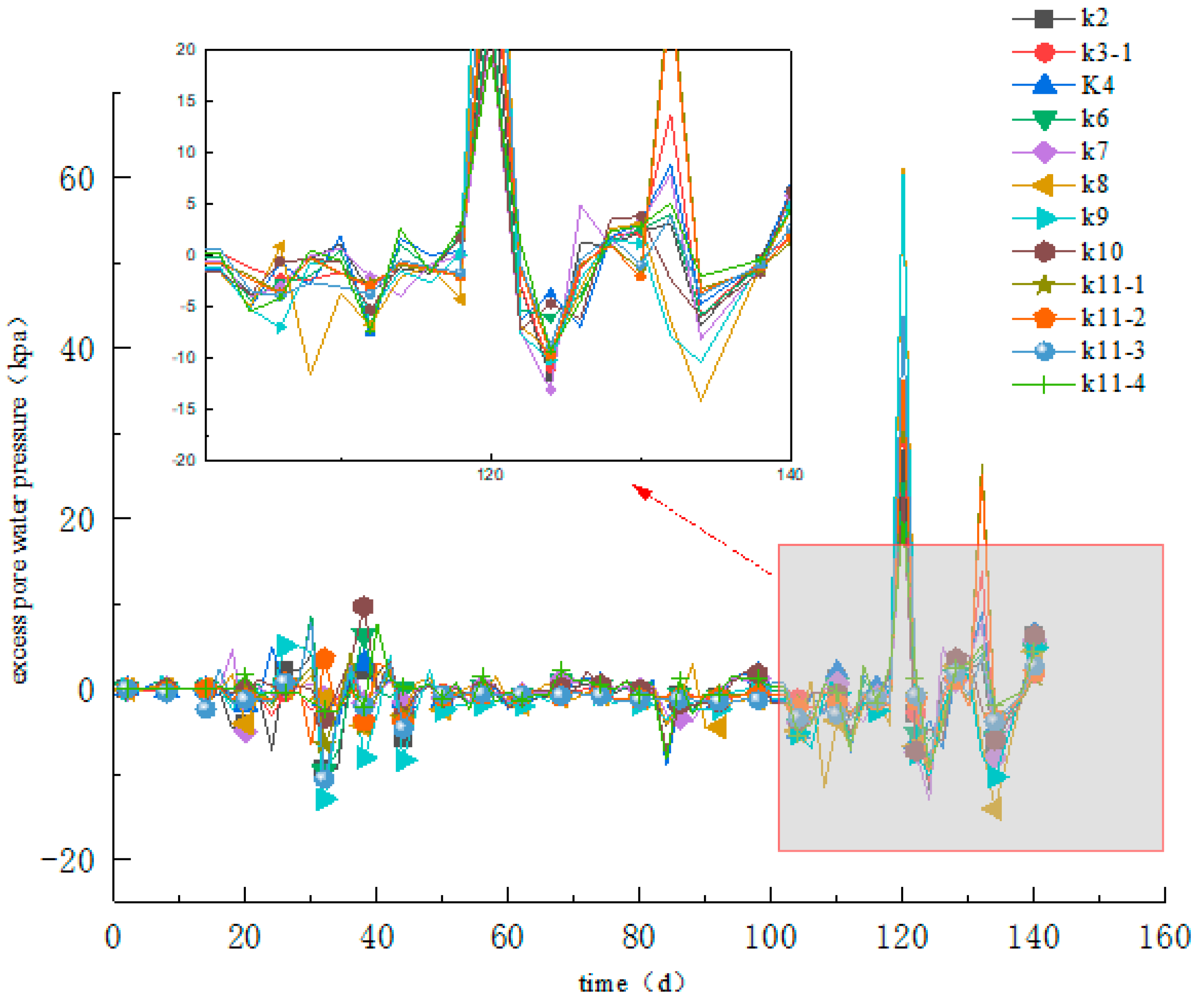
2.2.3. Excess Pore Water Pressure Response Analysis
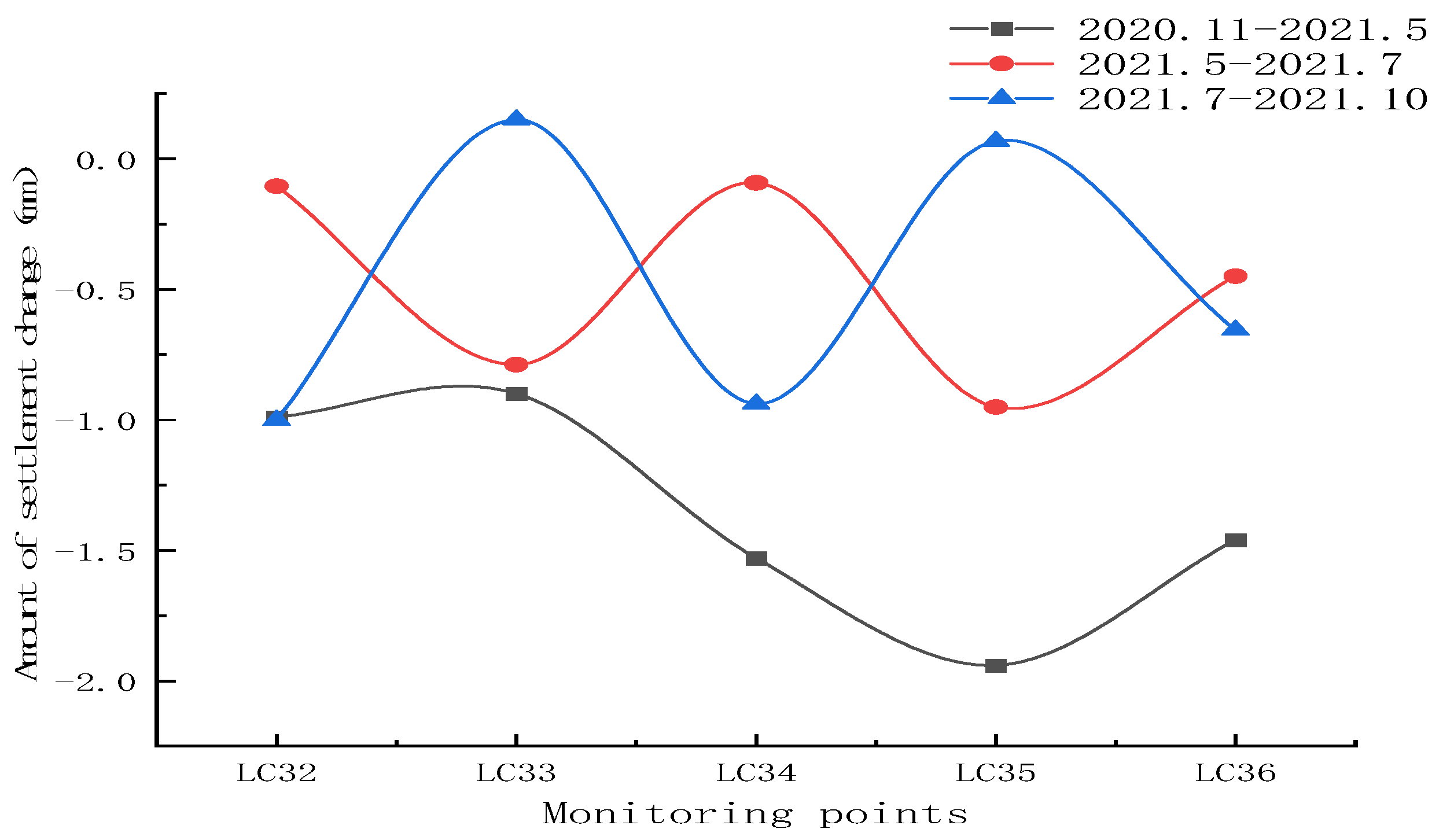
2.2.4. Ground Settlement Monitoring Analysis
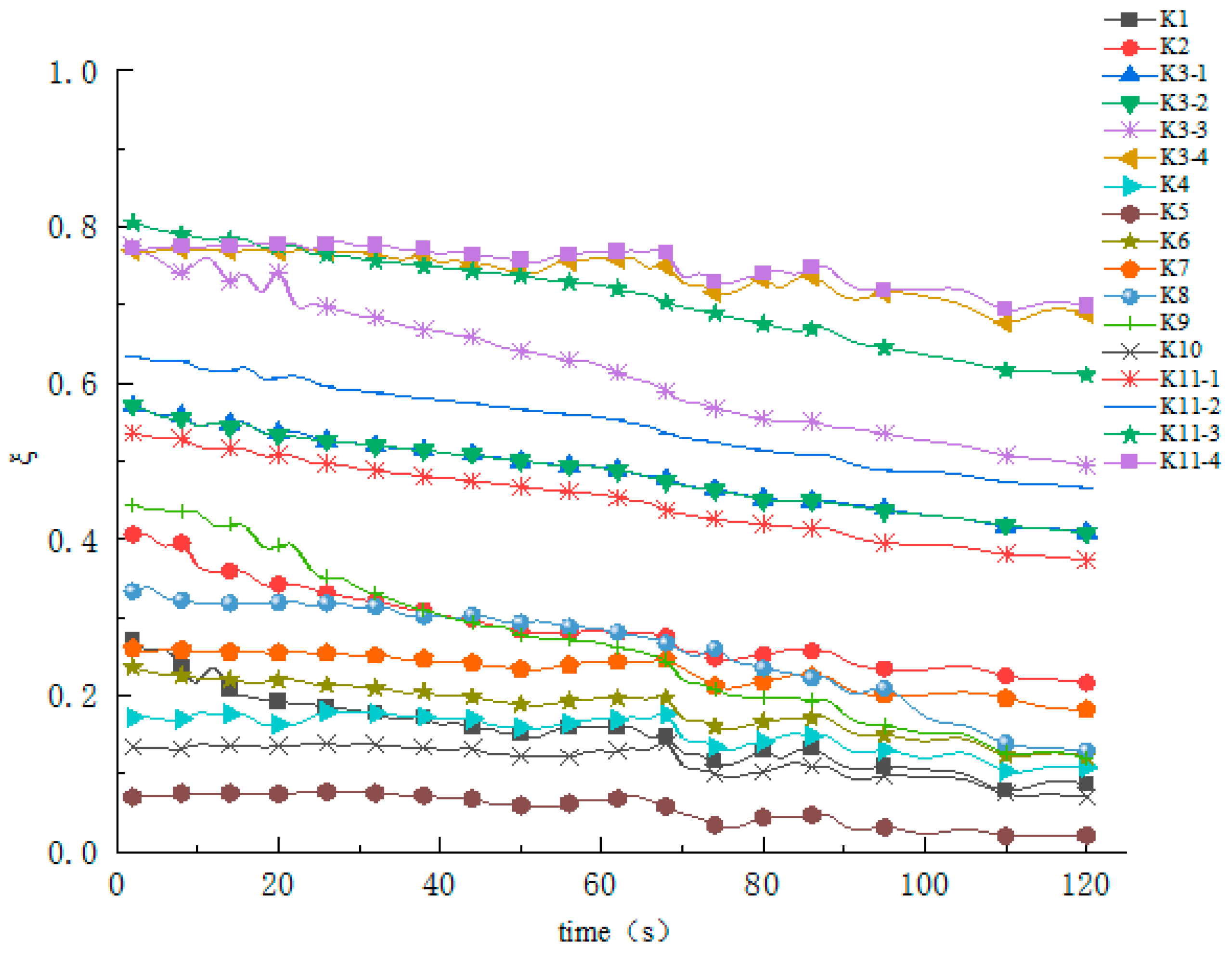
2.2.5. Liquefaction Predictions for Silty Soils
- (1)
- The ratio decreases under 0.8 for all monitoring points with increasing time, and the ratio decreases with increasing time for monitoring points with greater burial depths (e.g., K3-4, K11-4, K3-3, K11-3), indicating that the possibility of sand liquefaction is low.
- (2)
- Working conditions 1 and 2 represent K3-1 to K3-4 and K11-1 to K11-4, where the closer working condition 2 is to the tunnel, the greater the value found, which indicates that the closer to the tunnel the greater the dynamic response generated. At the same time, the ratio slowly increases and then decreases as the distance increases, remaining between 0.6 and 0.8, indicating that liquefaction is less likely to occur with increasing distance.
2.3. Constitutive Model
- (1)
- It is assumed that all soil bodies in the same rock formation are elastic-plastic, isotropic materials and conform to the Moore-Coulomb yielding criterion.
- (2)
- The construction phase group, consolidation analysis module, performs initial ground stress calculations considering only the effect of self-weight stresses and ignoring the effect of tectonic stresses.
- (3)
- The train is considered to be running at a constant speed.
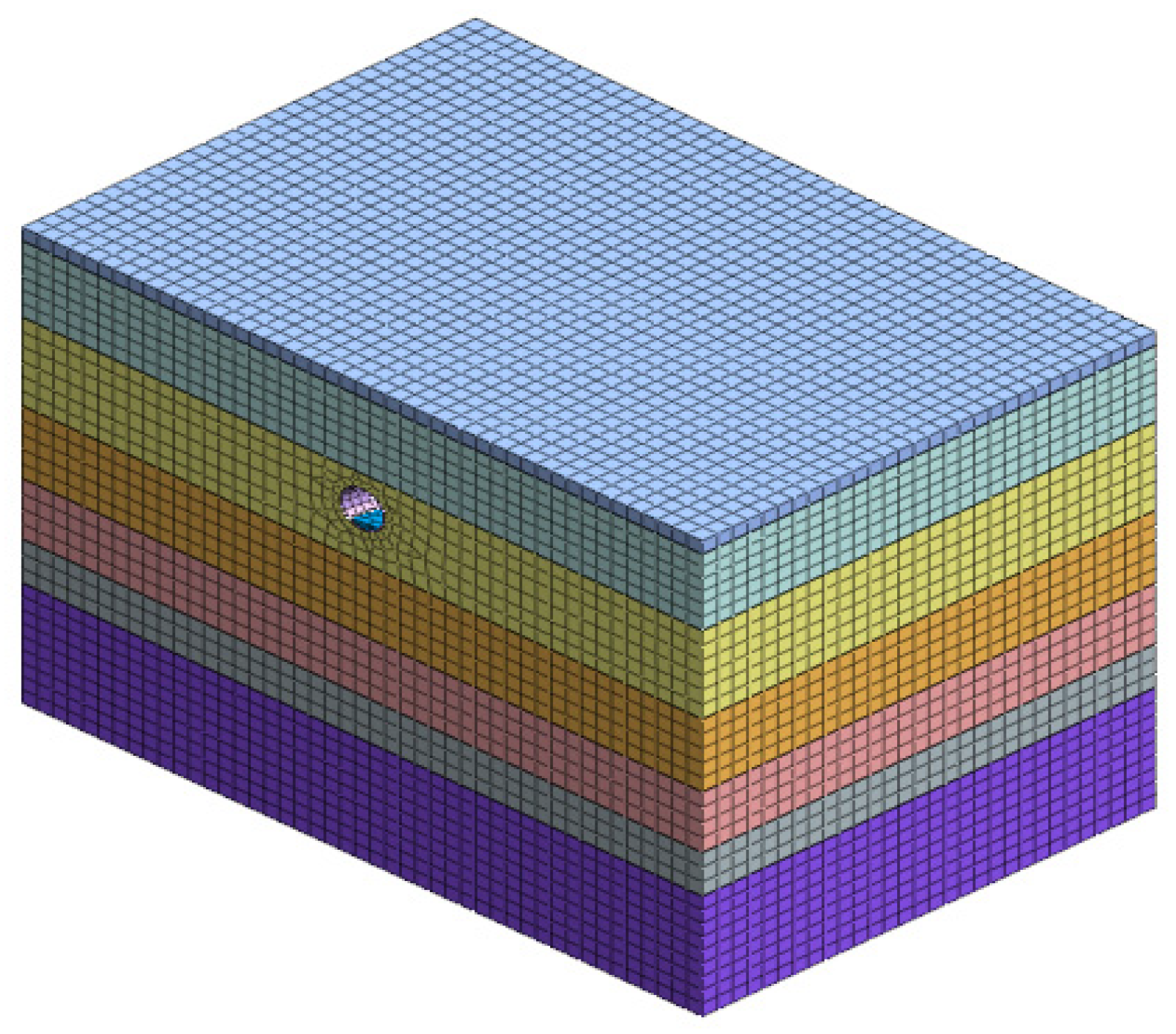
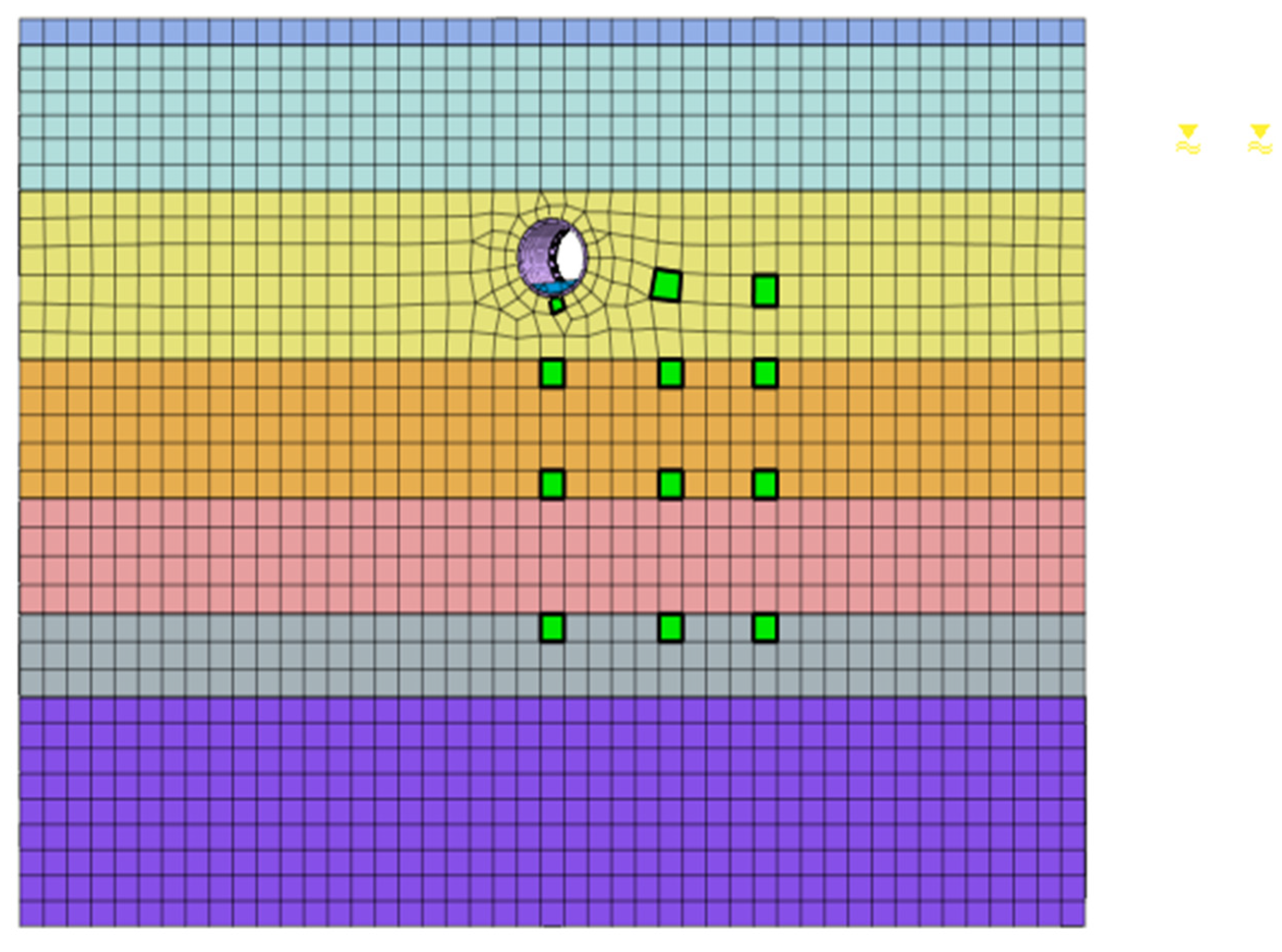
2.3.1. Numerical Model Development
2.3.2. Boundary Conditions and Model Parameters
- (1)
- Boundary conditions.
- (2)
- Model parameters
2.3.3. Determination of Vibration Loads
2.3.4. Calibration of the Model
3. Results and Discussion
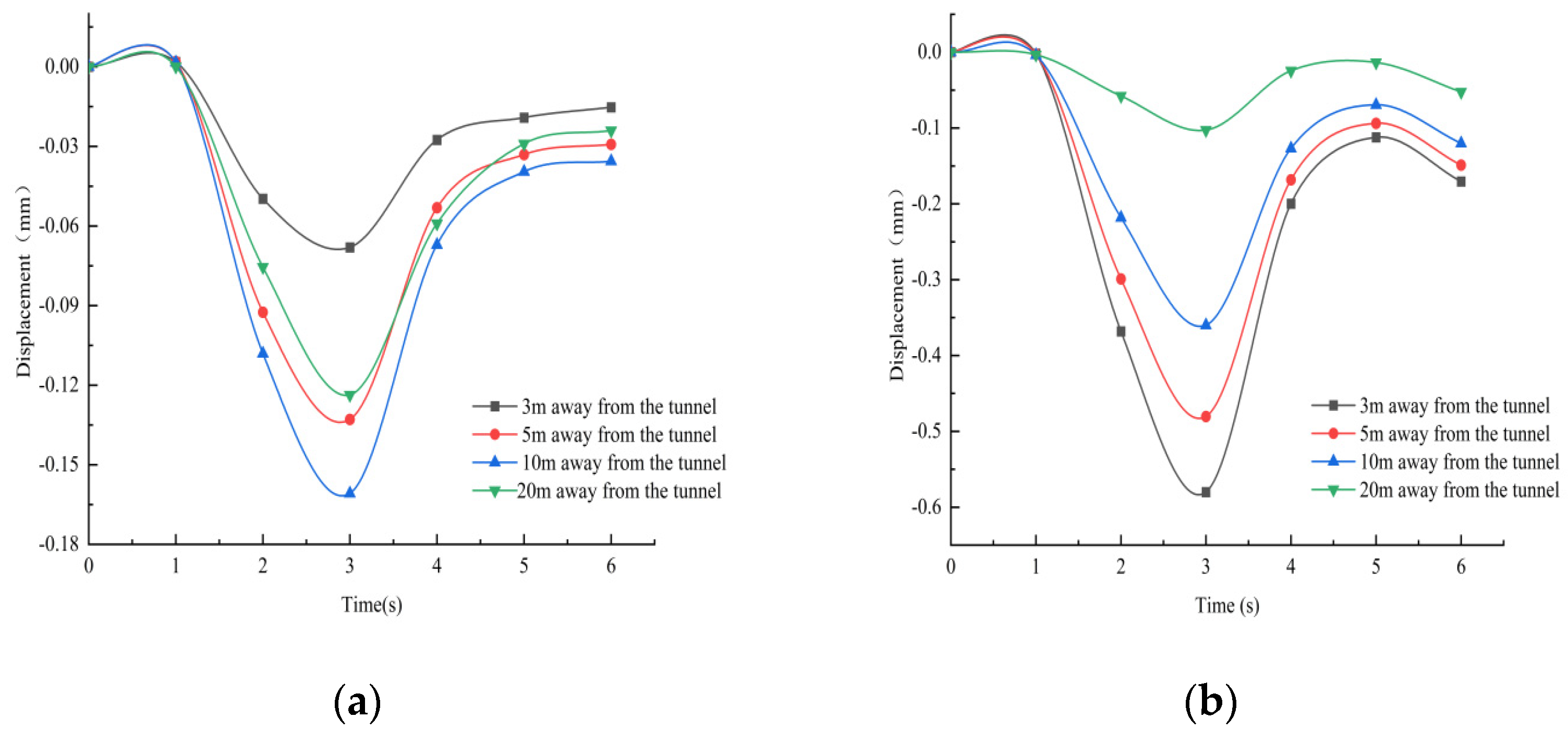
3.1. Excess Pore Water Pressure Response Pattern of the Soil at the Bottom of the Tunnel
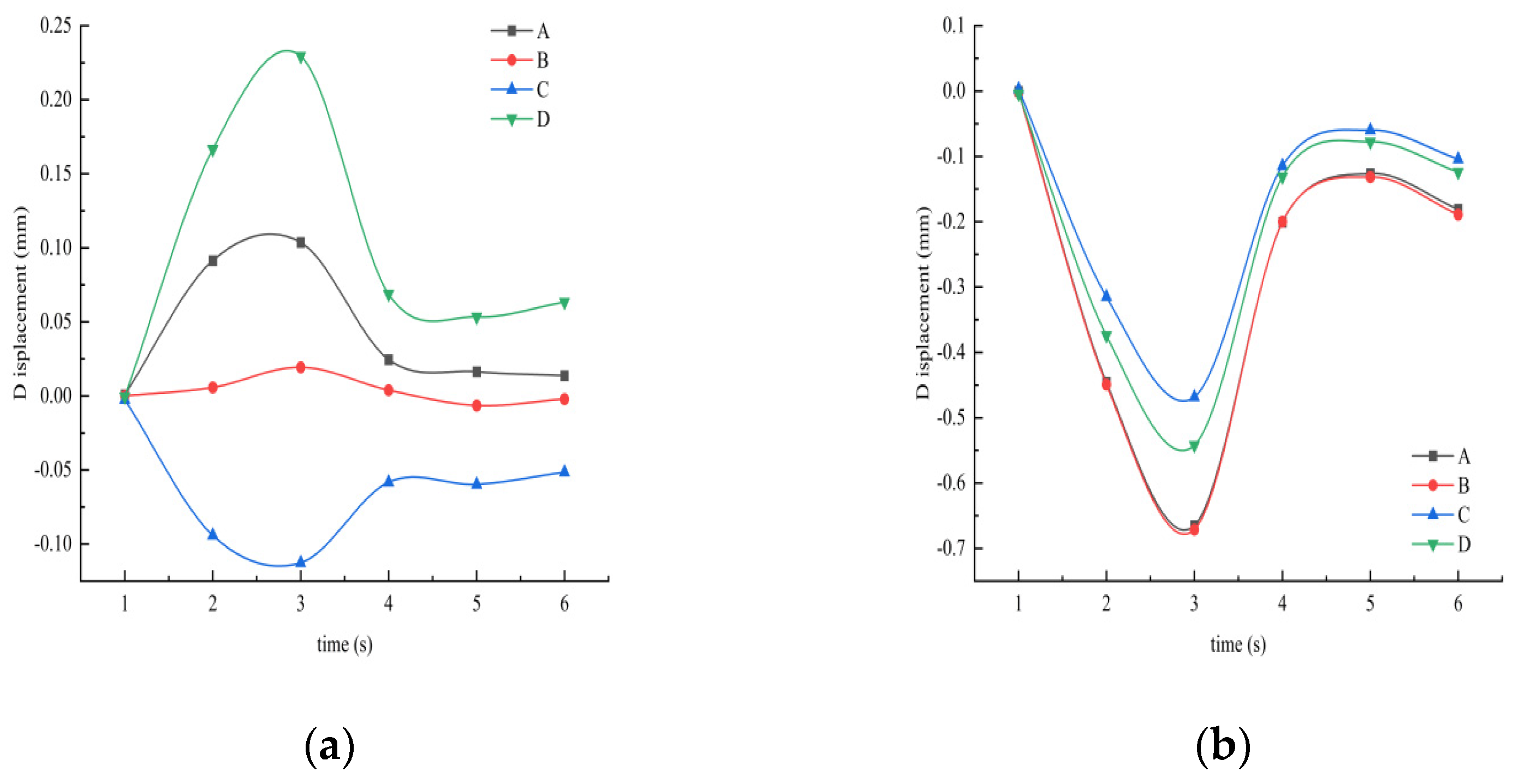
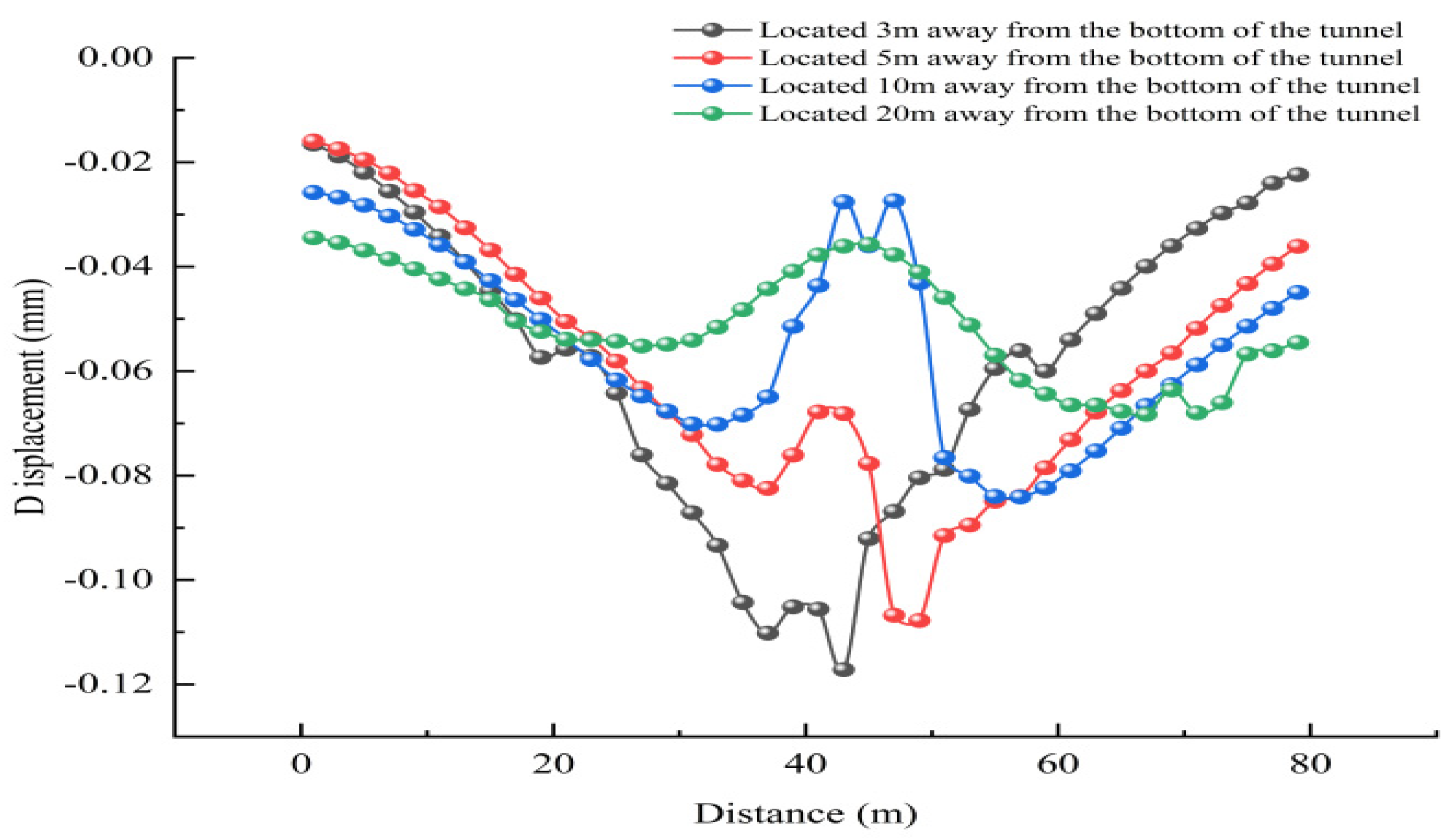
3.2. Soil Deformation Development Pattern during Train Operation
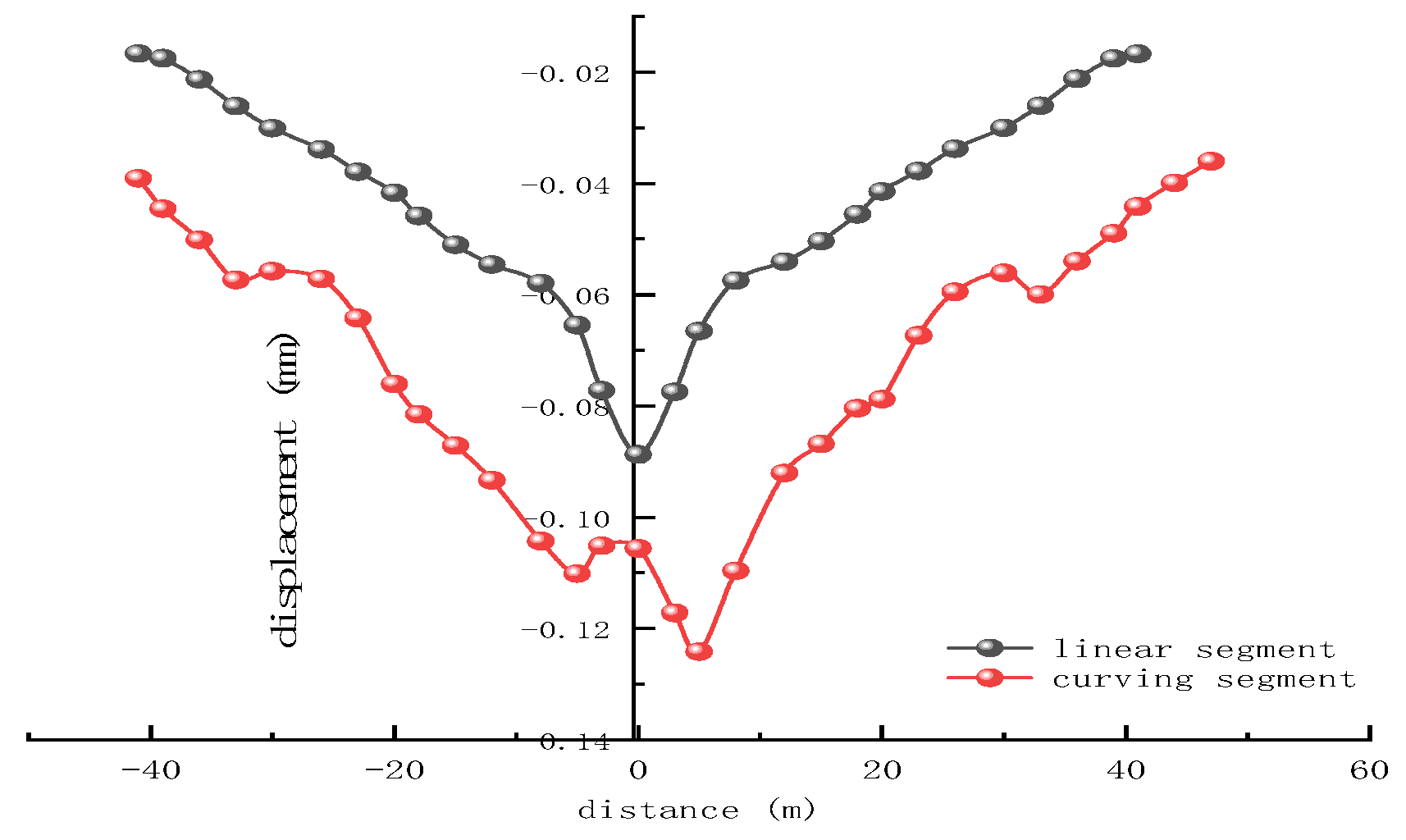
3.3. Analysis of Straight Versus Curved Sections
4. Conclusions and Discussion
- The pore water pressure and excess pore water pressure generated by the initial vibration of the train are not easily dissipated and transferred, resulting in a larger pore pressure in the silty sand layer at the beginning of the train operation. During this, the pore pressure fluctuates due to peak commuting periods and climatic problems, while the fine particles of the powdered sand soil have a small amount of cohesive particles, making the soil layer have a certain strength and cohesion. The pore pressure and excess pore water pressure gradually decrease and stabilise at a later stage under the action of the train vibration.
- Under the action of cyclic train load, the response of the powder sand soil around the tunnel to train vibration is closely related to the location. The closer to the tunnel, the more sensitive the response is. The upper part of the tunnel arch waist beyond a certain burial depth range with the disappearance of the vibration force pore pressure also decreases rapidly. The soil layer in the lower part of the tunnel arch waist with the disappearance of the vibration effect pore pressure in the short term is not easy to dissipate.
- Soil liquefaction is related to the type of soil and is less likely to occur in silty soils compared to other soil layers in this tunnel shield section.
- Under the action of cyclic loading, the greater the horizontal distance from the tunnel, the more slowly the super-pore water pressure decays, and along the vertical direction decays faster, indicating that the soil beneath the tunnel vibrates mainly in the vertical direction. The area where the soil settles more is mainly concentrated on the surface of the soil 3 m from the lining on the right side of the tunnel, in the silt layer on the upper side of the tunnel and 3 m at the bottom of the tunnel, mainly in a “V” shape; i.e., the displacement settlement is large in the middle and small at the ends.
- The tunnel settlement is reduced from 2 mm to 1 mm during train operation and the resulting track unevenness is more moderate. The deteriorating effect on wheel-rail dynamics is weaker, so the displacement caused by vibration is safe for vehicle operation.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmed, B.; Habib, T.; Hani, T. Analysis of soil settlement behind bridge abutments. Transp. Geotech. 2022, 36, 100812. [Google Scholar]
- Hyungjoon, S.; Yang, Z.; Cheng, C. Displacement Mapping of Point Clouds for Retaining Structure Considering Shape of Sheet Pile and Soil Fall Effects during Excavation. J. Geotech. Geoenviron. Eng. 2022, 148, 04022016. [Google Scholar]
- Shen, S.-L.; Wu, H.-N.; Cui, Y.-J.; Yin, Z.-Y. Long-term settlement behaviour of metro tunnels in the soft deposits of Shanghai. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2014, 40, 309–323. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, J.-L.; Dai, J.; Xu, C.-S.; Cui, C.-Y.; Meng, K. Study of Pore Water Pressure and Deformation Characteristics of Soil below Tunnel under Vibration Load of Metro Trains. Tunn. Constr. 2018, 38, 1785–1792. [Google Scholar]
- Lou, P.; Li, Y.; Xiao, H.; Zhang, Z.; Lu, S. Influence of Small Radius Curve Shield Tunneling on Settlement of Ground Surface and Mechanical Properties of Surrounding Rock and Segment. Appl. Sci. 2022, 12, 9119. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, S.; Ouyang, J.; Li, J.; Zhao, Y.; Lin, H.; Guo, P. Predicting Ground Surface Settlements Induced by Deep Excavation under Embankment Surcharge Load in Flood Detention Zone. Water 2022, 14, 3868. [Google Scholar] [CrossRef]
- Ma, C.-Y. The Dynamic Response Analysis of Liquefaction and Model Test about Underground Structure of Subway in Sand Stratum. Master’s Thesis, Xi’an University of Technology, Shaanxi, China, 2018. [Google Scholar]
- Cavallaro, A.; Capilleri, P.P.; Grasso, S. Site Characterization by Dynamic In Situ and Laboratory Tests for Liquefaction Potential Evaluation during Emilia Romagna Earthquake. Geosciences 2018, 8, 242. [Google Scholar] [CrossRef]
- Wang, Y.-G. Study on Dynamic Response and Long-Term Settlement of Curved Tunnel under Vibration on Load of Train in Silty Strata. Master’s Thesis, Henan University of Technology, Zhengzhou, China, 2020. [Google Scholar] [CrossRef]
- Khosravifar, A.; Dickenson, S.; Moug, D. Cyclic porewater pressure generation in intact silty soils. Soil Dyn. Earthq. Eng. 2022, 162, 107482. [Google Scholar] [CrossRef]
- Beiranvand, B.; Rajaee, T. Application of artificial intelligence-based single and hybrid models in predicting seepage and pore water pressure of dams: A state-of-the-art review. Adv. Eng. Softw. 2022, 173, 103268. [Google Scholar] [CrossRef]
- Singh, A.; Singh, D.; Chakraborty, M. Effect of various initial excess pore water pressure distributions on 1-D consolidation of clays. Int. J. Geotech. Eng. 2022, 16, 123–132. [Google Scholar] [CrossRef]
- Lachinani, H.; Jahanandish, M.; Ghahramani, A. Excess Pore Water Pressure Generation, Distribution and Dissipation in Self-boring Pressuremeter Test: Numerical Analysis. Int. J. Civ. Eng. 2022, 20, 1101–1114. [Google Scholar] [CrossRef]
- Luo, Q.; Liu, Y.; Zhou, Y.; Wu, J.; Yie, X. Research on Pore Water Pressure of Saturated Muck Soil Under Traffic Loading of Low Frequency. Am. J. Civ. Eng. 2016, 4, 149–158. [Google Scholar]
- Cary, C.E.; Zapata, C.E. Pore Water Pressure Response of Soil Subjected to Dynamic Loading under Saturated and Unsaturated Conditions. Int. J. Geomech. 2016, 16, D4016004. [Google Scholar] [CrossRef]
- Castelli, F.; Cavallaro, A.; Grasso, S.; Lentini, V. Undrained Cyclic Laboratory Behavior of Sandy Soils. Geosciences 2019, 9, 512. [Google Scholar] [CrossRef]
- Porcino, D.D. Recent advances in pore water pressure and liquefaction characteristics of low plasticity silty sands subjected to cyclic loading. IOP Conf. Ser. Earth Environ. Sci. 2019, 351, 012013. [Google Scholar] [CrossRef]
- Karakan, E.; Sezer, A.; Tanrinian, N. Evaluation of effect of limited pore water pressure development on cyclic behavior of a nonplastic silt. Soils Found. 2019, 59, 1302–1312. [Google Scholar] [CrossRef]
- Luo, J.; Miao, L. Research on dynamic creep strain and settlement prediction under the subway vibration loading. SpringerPlus 2016, 5, 1252. [Google Scholar] [CrossRef]
- Hou, C.Y.; Cui, Z.D. Quantitative Analysis of the Microstructures of Deep Silty Clay Subjected to Two Freezing–Thawing Cycles under Subway Vibration Loading. J. Cold Reg. Eng. 2021, 35, 04021012. [Google Scholar] [CrossRef]
- Gao, M.; Xu, X.; Chen, Q.S.; Wang, Y. Reduction of metro vibrations by honeycomb columns under the ballast: Field experiments. Soil Dyn. Earthq. Eng. 2020, 129, 105913. [Google Scholar] [CrossRef]
- Tang, Y.-Q.; Cui, Z.-D.; Zhang, X.; Zhao, S.-K. Dynamic response and pore pressure model of the saturated soft clay around the tunnel under vibration loading of Shanghai subway. Eng. Geol. 2008, 98, 126–132. [Google Scholar] [CrossRef]
- Ge, S.; Yao, X. Response characteristics of pore pressure in soils nearby metro tunnel due to train vibration loading. J. Eng. Geol. 2015, 23, 1093–1099. [Google Scholar]
- Wang, T.; Shi, B.; Ma, L.; Zhang, C.; Deng, Y. Dynamic response and long-term cumulative deformation of silty sand stratum induced by metro train vibration loads. J. Eng. Geol. 2020, 28, 1411–1418. [Google Scholar]
- Xiao, Z.-R.; Wang, Y.-G.; Zhang, W.-C.; Ren, L. Effect of train load in silt formation on the settlement of curved tunnel. J. Liaoning Tech. Univ. Nat. Sci. 2021, 40, 327–332. [Google Scholar]
- Wei, H. Study on Surface Subsidence and Environmental Impact Caused by Small Radius Curved Tunnel under Buildings. Master’s Thesis, Changzhou University, Changzhou, China, 2021. [Google Scholar] [CrossRef]
- Meng, Z.B.; Cui, S.C.; Zhao, T.F.; Jin, L.Q. The Finite Element Model Determination in the Loess Regions under Subway Vibration Loads. Adv. Mater. Res. 2011, 368–373, 2586–2590. [Google Scholar] [CrossRef]
- He, P.-P.; Cui, Z.-D. Dynamic response of a thawing soil around the tunnel under the vibration load of subway. Environ. Earth Sci. 2015, 73, 2473–2482. [Google Scholar] [CrossRef]
- Meng, Z.B.; Zhao, T.F.; Cui, S.C.; Jin, J. Dynamic Response Analysis under the Metro-Vibration Loading of Xi’an Bell Tower Timber Structure. Appl. Mech. Mater. 2012, 170–173, 1361–1366. [Google Scholar] [CrossRef]
- Shan, W.; Chen, H.-E.; Yuan, X.; Ma, W.; Li, H. Mechanism of pore water seepage in soil reinforced by step vacuum preloading. Bull. Eng. Geol. Environ. 2021, 80, 2777–2787. [Google Scholar] [CrossRef]
- Yang, Y.; Cai, R.; Zhang, G.; Su, S.; Liu, W. Evaluating and analyzing the stability of loess slope using intermittent rainfall and various rainfall patterns. Arab. J. Geosci. 2022, 15, 218. [Google Scholar] [CrossRef]
- Zhang, Z.-L.; Cui, Z.-D. Analysis of microscopic pore structures of the silty clay before and after freezing–thawing under the subway vibration loading. Environ. Earth Sci. 2017, 76, 528. [Google Scholar] [CrossRef]
- Duan, Z.; Li, Z.Y.; Wu, Y.B.; Niu, B.; Shen, R.J. Mechanical and microscopic properties of soil according to the rate of increase in pore water pressure. Soil Tillage Res. 2023, 225, 105530. [Google Scholar] [CrossRef]
- Wang, M.F. Dynamic Response of Saturated Silt Soil and Liquefaction by the Subway’s Vibration. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2009. [Google Scholar]
- Yuan, Y.; Liu, W.; Liu, W. Propagation law of ground vibration in the curve section of metro based on in-situ measurement. China Railw. Sci. 2012, 33, 133–138. [Google Scholar]
- Wang, L.H.; Lu, G.Y. Vehicle Type Selection for Zhengzhou Metro Line 1. Urban Rapid Rail Transit 2013, 26, 119–123. [Google Scholar]
- Wang, C.Y.; Zhao, J.Z.; Xu, X.; Kan, Q.H. Three-dimensional Finite Element Analysis of Wheel-rail Contact for Curved subway. J. Sichuan Univ. Sci. Eng. Nat. Sci. Ed. 2018, 31, 36–42. [Google Scholar]
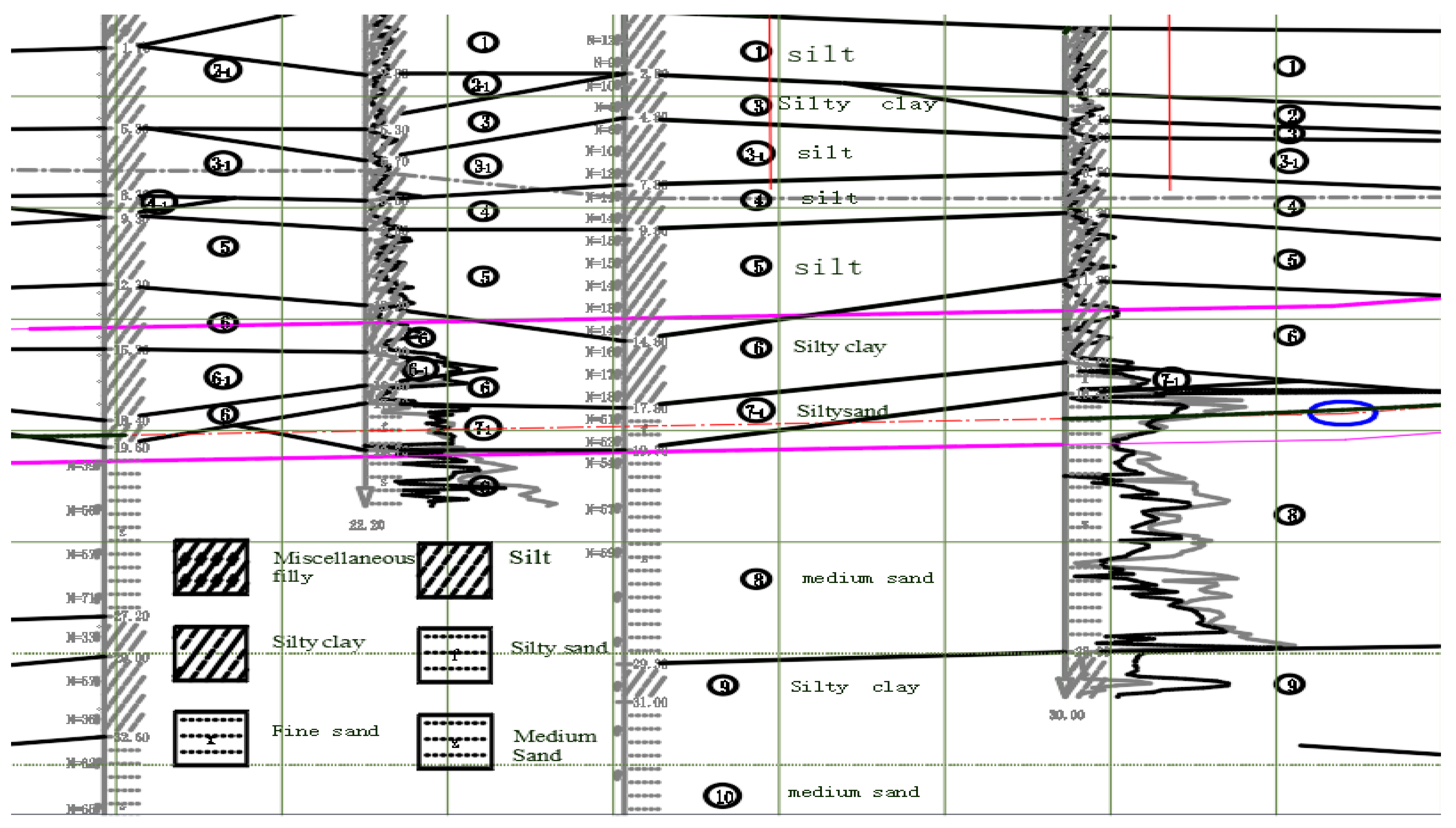





| Strata | GS | Moisture Content (w) | Porosity (e) | Clay Content (%) |
|---|---|---|---|---|
| silt | 2.7 | 17.8 | 0.703 | 15.9 |
| silt clay | 2.72 | 24.6 | 0.799 | 14.7 |
| silty sand | 2.63 | 23.2 | 0.68 | 14.7 |
| fine medium sand | 2.63 | 18.1 | 0.525 | 12.3 |
| Monitoring Points | Clearance of the Monitoring Point from the Outer Profile of the Interval Tunnel/m | Distance Between the Bottom of the Hole and the Tunnel Floor/m | Monitoring Points Borehole Depth/m | Monitoring Methods |
|---|---|---|---|---|
| K1 | 4.8 | 0.5 | 21.5 | Automatic |
| K2 | 3.6 | 0.9 | 21.5 | manual |
| K3-1 | 4.6 | 0.6 | 20 | manual |
| K3-2 | 4.6 | 3.6 | 23 | Automatic |
| K3-3 | 4.6 | 8.6 | 28 | Automatic |
| K3-4 | 4.6 | 18.6 | 38 | Automatic |
| K4 | 4.8 | 0.8 | 19 | manual |
| K5 | 3.3 | 0.8 | 18 | Automatic |
| K6 | 3.7 | 0.5 | 21.5 | manual |
| K7 | 3.9 | 0.9 | 21.5 | manual |
| K8 | 4.4 | 0.5 | 20 | manual |
| K9 | 3.8 | 0.6 | 19 | manual |
| K10 | 3.6 | 0.6 | 18 | manual |
| K11-1 | 4 | 0.5 | 20 | manual |
| K11-2 | 4 | 3.5 | 23 | manual |
| K11-3 | 4 | 8.5 | 28 | manual |
| K11-4 | 4 | 18.5 | 38 | manual |
| Strata | E (Mpa) | μ | γ (KN/M3) | Φ (°) | C (KN/M3) | K |
|---|---|---|---|---|---|---|
| Miscellaneous fill | / | 0.37 | 17 | 18 | 10 | 5.8 × 10−6 |
| Silt | 13.6 | 0.3 | 18.4 | 23 | 15 | 5.8 × 10−6 |
| Silty clay | 8.1 | 0.3 | 19 | 15 | 20 | 5.8 × 10−7 |
| Silty sand | 17 | 0.3 | 18 | 31.3 | 2 | 1.2 × 10−4 |
| Silt | 12 | 0.25 | 20.6 | 25 | 18 | 5.8 × 10−6 |
| Fine Medium Sand | 30.5 | 0.25 | 18 | 35.9 | 0 | 2.4 × 10−4 |
| Silty clay | 10.5 | 0.3 | 20.2 | 18 | 28 | 5.8 × 10−7 |
| Lining | 36,000 | 0.2 | 2500 | / | / | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Liu, X.; Lin, Y.; Tan, F. Analysis of the Effect of Pore Water Pressure on a Small Radius Curve Section of a Fine Sand Layer under Cyclic Metro. Water 2023, 15, 981. https://doi.org/10.3390/w15050981
Wang X, Liu X, Lin Y, Tan F. Analysis of the Effect of Pore Water Pressure on a Small Radius Curve Section of a Fine Sand Layer under Cyclic Metro. Water. 2023; 15(5):981. https://doi.org/10.3390/w15050981
Chicago/Turabian StyleWang, Xiaorui, Xu Liu, Yunhong Lin, and Fei Tan. 2023. "Analysis of the Effect of Pore Water Pressure on a Small Radius Curve Section of a Fine Sand Layer under Cyclic Metro" Water 15, no. 5: 981. https://doi.org/10.3390/w15050981
APA StyleWang, X., Liu, X., Lin, Y., & Tan, F. (2023). Analysis of the Effect of Pore Water Pressure on a Small Radius Curve Section of a Fine Sand Layer under Cyclic Metro. Water, 15(5), 981. https://doi.org/10.3390/w15050981






