Streamflow Estimation in a Mediterranean Watershed Using Neural Network Models: A Detailed Description of the Implementation and Optimization
Abstract
:1. Introduction
2. Materials and Methods
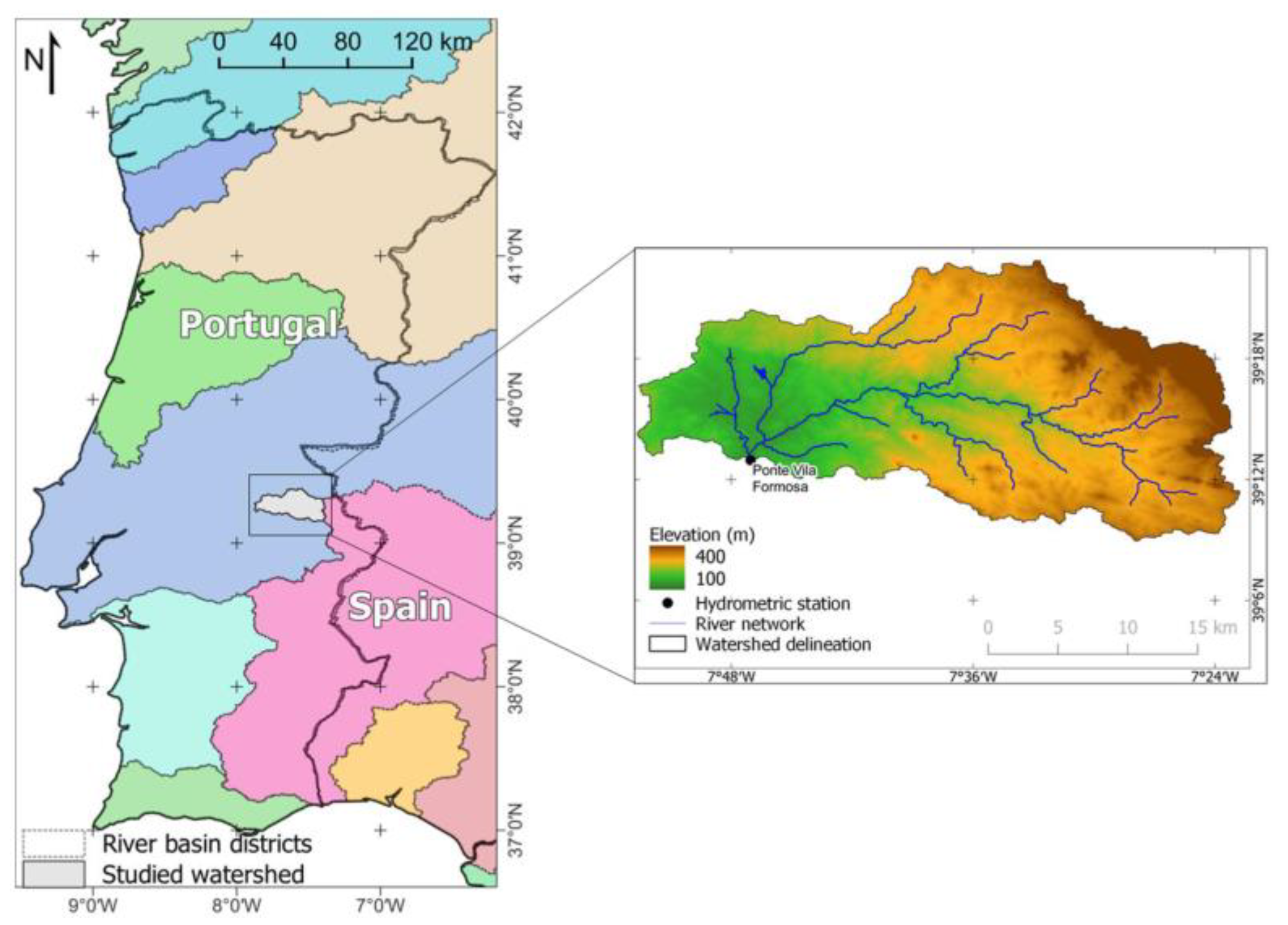
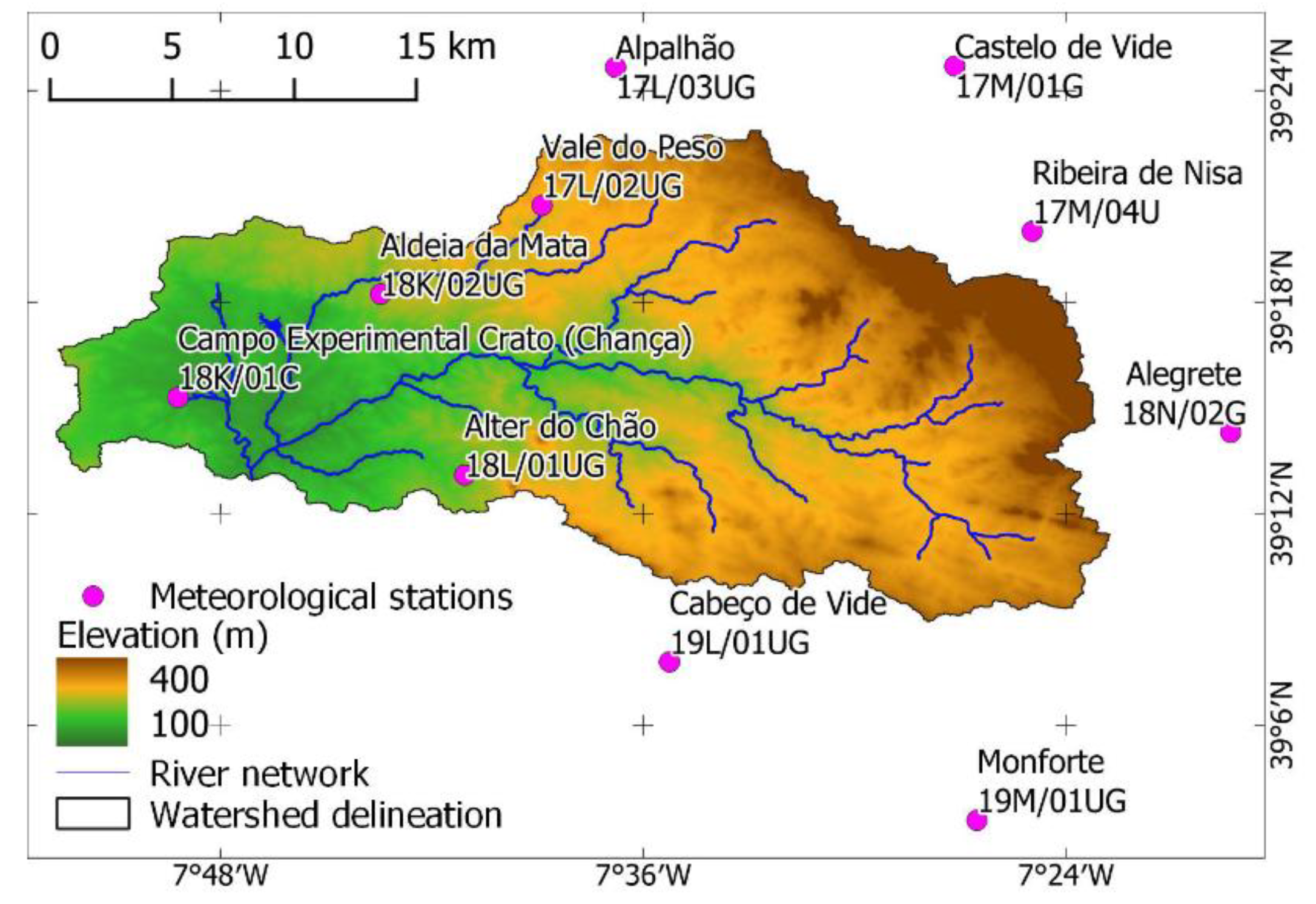
2.1. Description of the Study Area
2.2. Neural Network Models
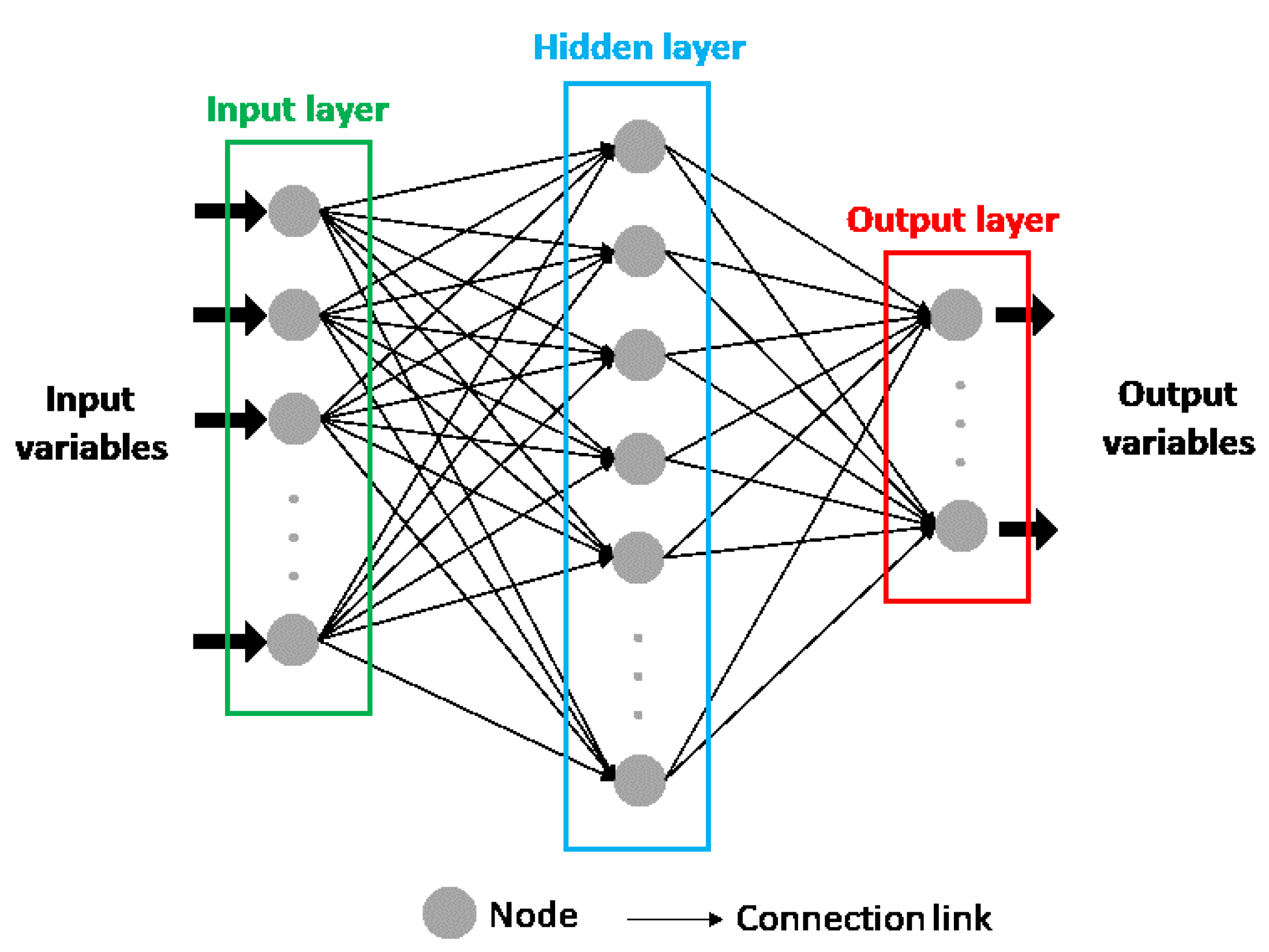
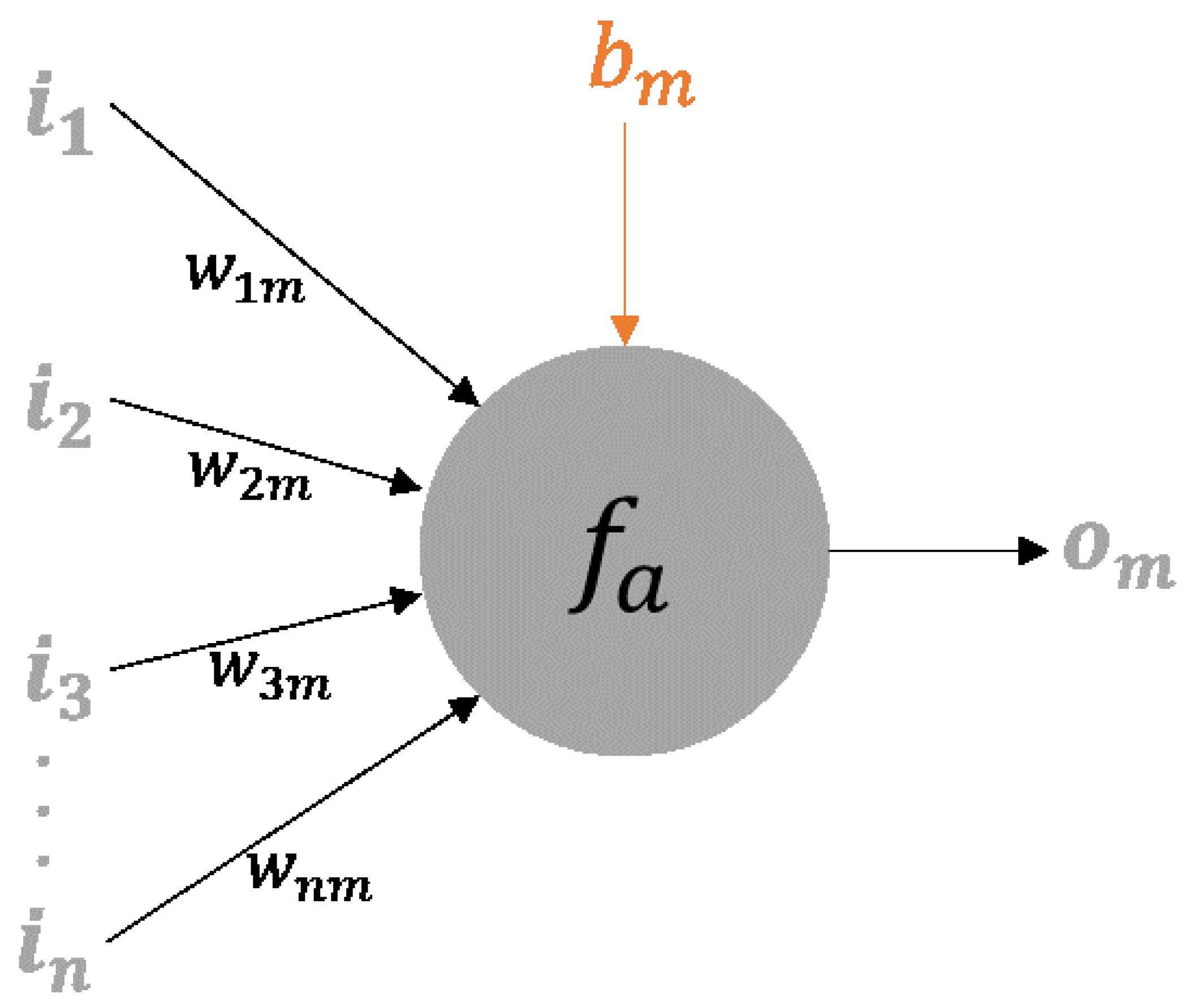
2.2.1. Artificial Neural Networks
2.2.2. Convolutional Neural Networks
2.2.3. Training Process
2.2.4. Input Variables
2.2.5. Tunning Parameters
2.3. Model Evaluation
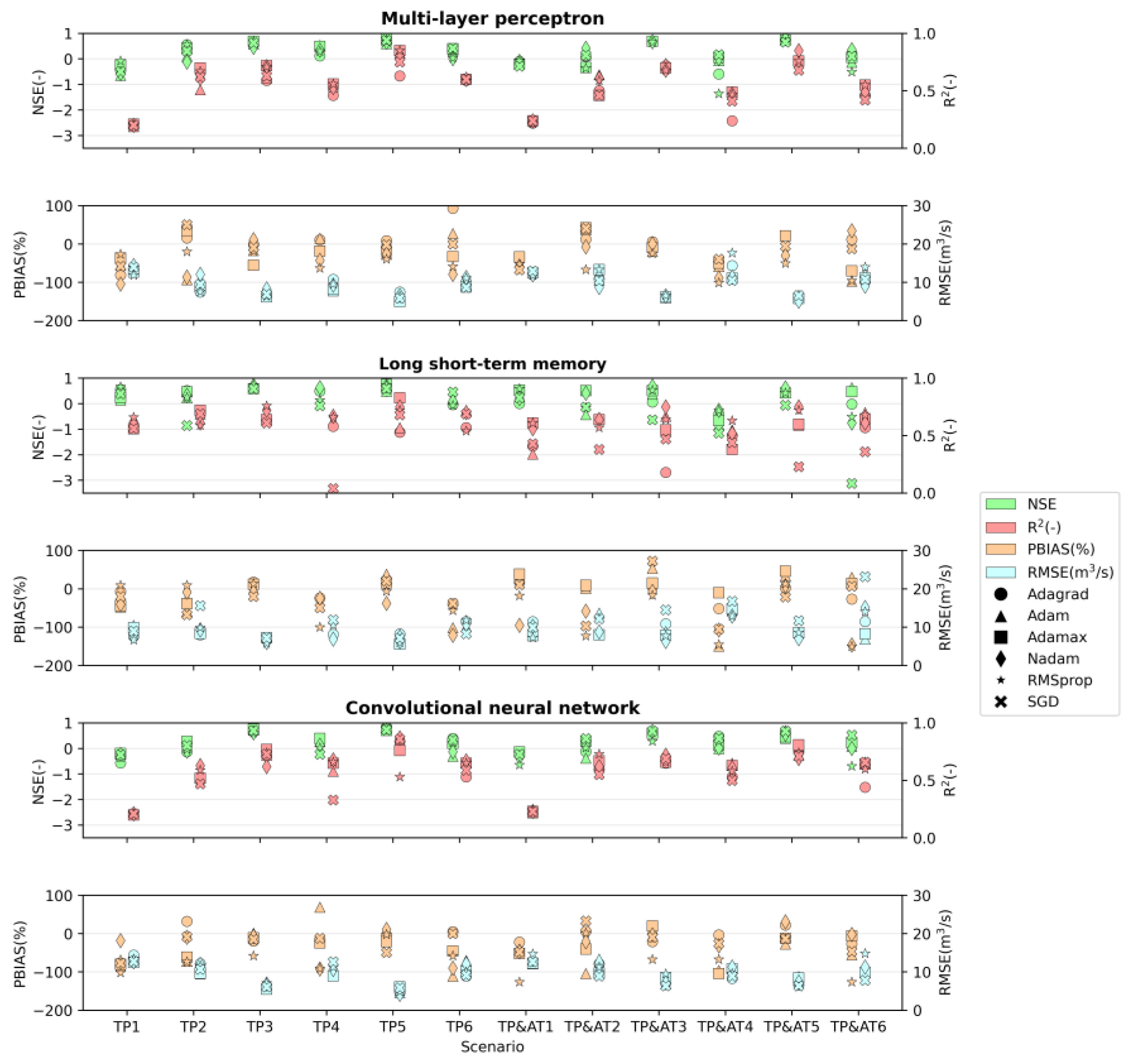
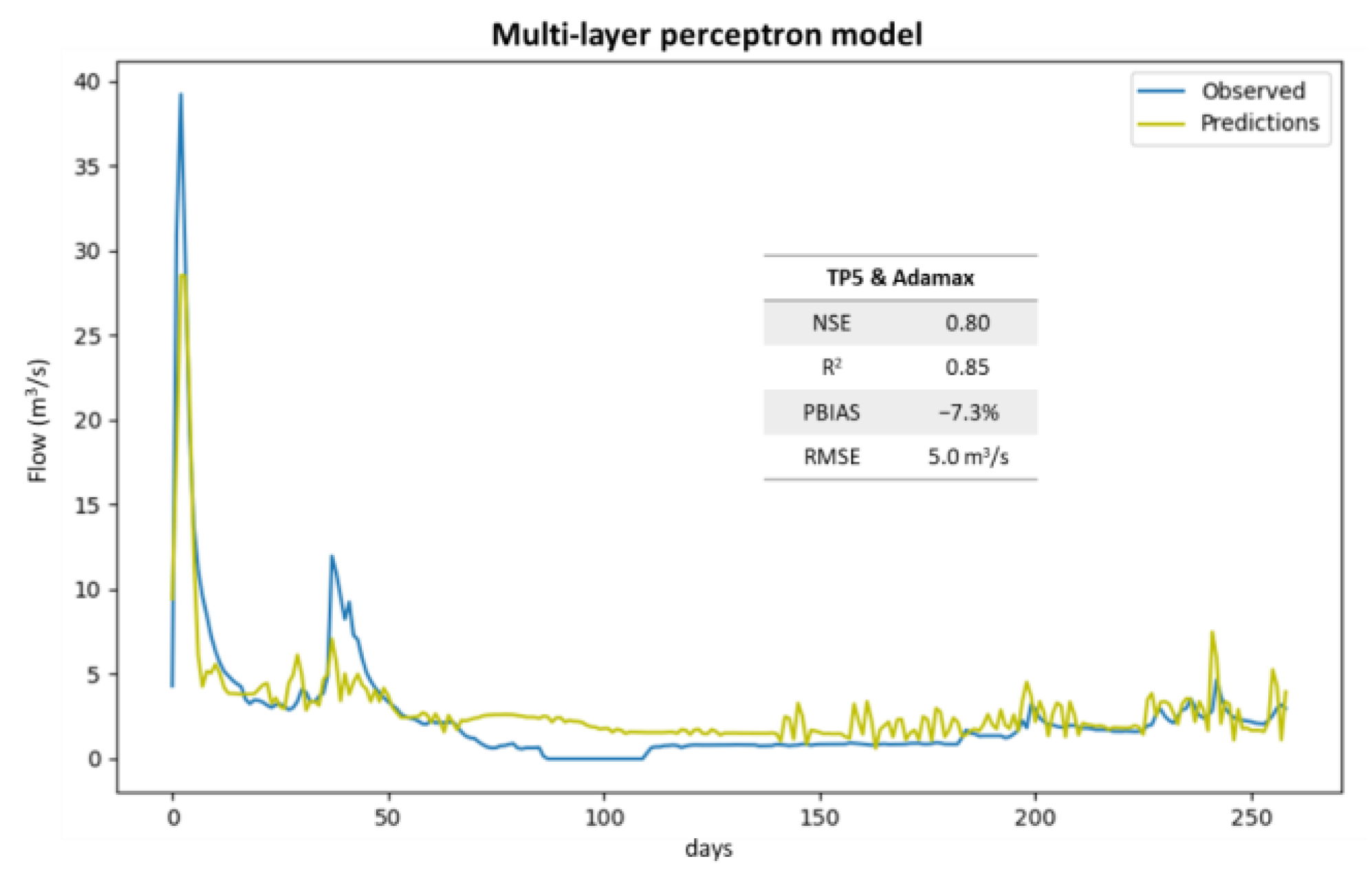
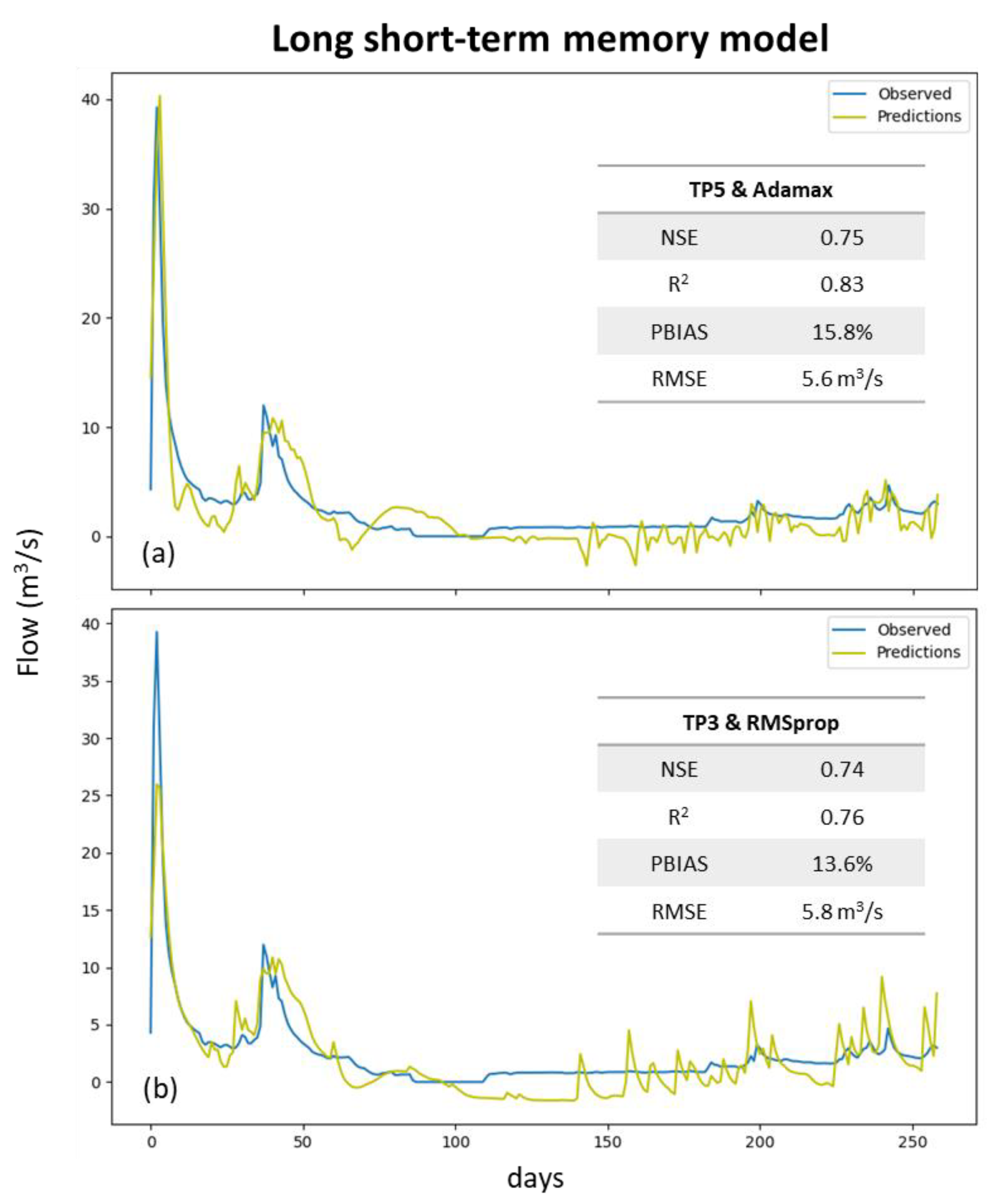
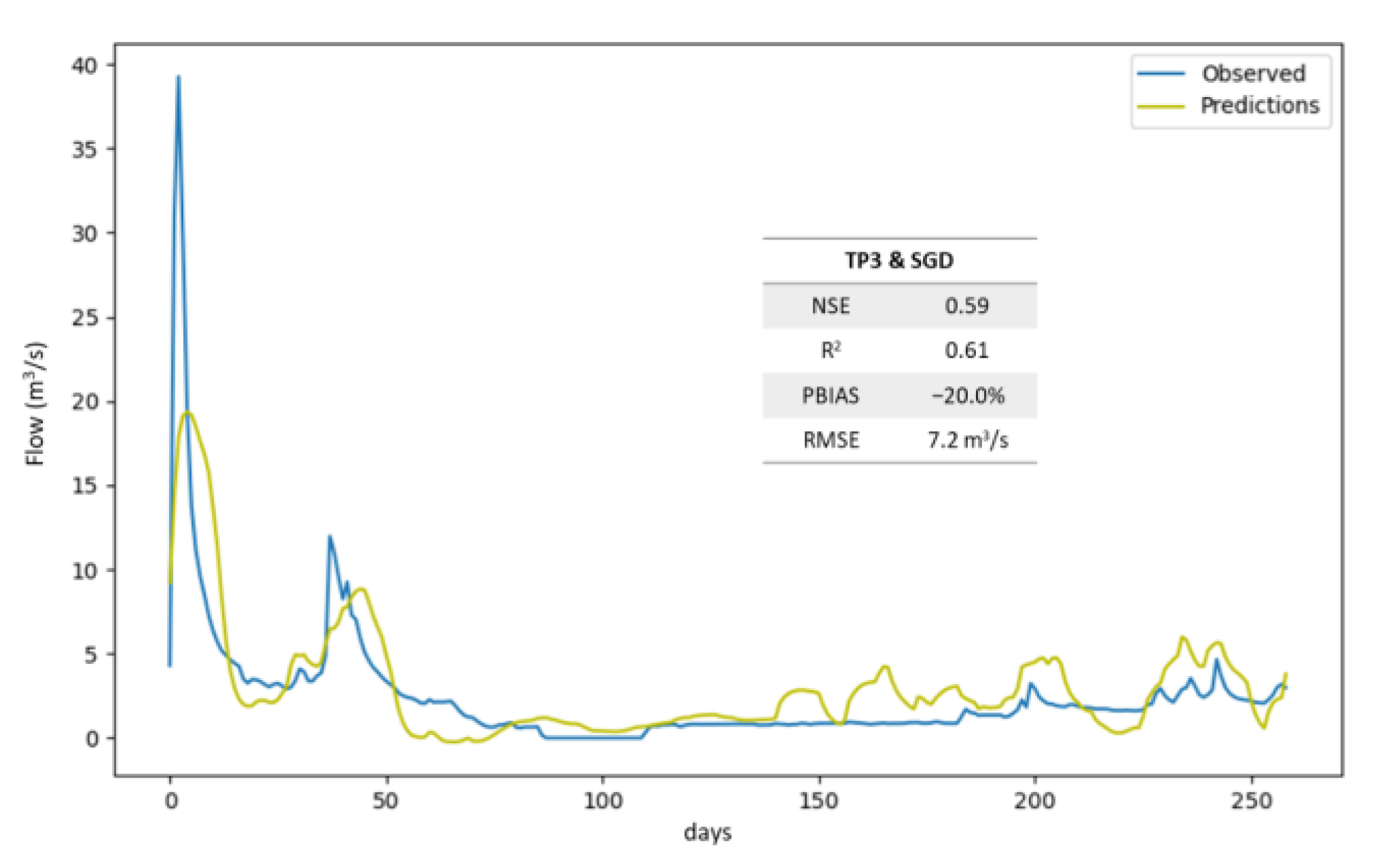
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bourdin, D.R.; Fleming, S.W.; Stull, R.B. Streamflow modelling: A primer on applications, approaches and challenges. Atmos. Ocean 2012, 50, 507–536. [Google Scholar] [CrossRef] [Green Version]
- Ni, L.; Wang, D.; Singh, V.P.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J. Streamflow and rainfall forecasting by two long short-term memory-based models. J. Hydrol. 2020, 583, 124296. [Google Scholar] [CrossRef]
- Humphrey, G.B.; Gibbs, M.S.; Dandy, G.C.; Maier, H.R. A hybrid approach to monthly streamflow forecasting: Integrating hydrological model outputs into a bayesian artificial neural network. J. Hydrol. 2016, 540, 623–640. [Google Scholar] [CrossRef]
- Besaw, L.E.; Rizzo, D.M.; Bierman, P.R.; Hackett, W.R. Advances in ungauged streamflow prediction using artificial neural networks. J. Hydrol. 2010, 386, 27–37. [Google Scholar] [CrossRef]
- Chiew, F.; McMahon, T. Application of the daily rainfall-runoff model MODHYDROLOG to 28 Australian catchments. J. Hydrol. 1994, 153, 383–416. [Google Scholar] [CrossRef]
- Jakeman, A.J.; Littlewood, I.G.; Whitehead, P.G. Computation of the instantaneous unit hydrograph and identifiable component flows with application to two small upland catchments. J. Hydrol. 1990, 117, 275–300. [Google Scholar] [CrossRef]
- Mehr, A.D.; Kahya, E.; Olyaie, E. Streamflow prediction using linear genetic programming in comparison with a neuro-wavelet technique. J. Hydrol. 2013, 505, 240–249. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, Y.; Zhang, C.; Wang, B. Are hybrid models integrated with data preprocessing techniques suitable for monthly streamflow forecasting? Some experiment evidences. J. Hydrol. 2015, 530, 137–152. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Chen, X.; Guan, Y. A multivariate conditional model for streamflow prediction and spatial precipitation refinement. J. Geophys. Res. 2015, 120, 10116–10129. [Google Scholar] [CrossRef] [Green Version]
- ASCE Task Committee on Application of Artificial Neural Networks in Hydrology. Artificial Neural Networks in Hydrology. I: Preliminary Concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Pham, Q.B.; Afan, H.A.; Mohammadi, B.; Ahmed, A.N.; Linh, N.T.T.; Vo, N.D.; Moazenzadeh, R.; Yu, P.-S.; El-Shafie, A. Hybrid model to improve the river streamflow forecasting utilizing multi-layer perceptron-based intelligent water drop optimization algorithm. Soft. Comput. 2020, 24, 18039–18056. [Google Scholar] [CrossRef]
- Hussain, D.; Khan, A.A. Machine learning techniques for monthly river flow forecasting of Hunza River, Pakistan. Earth Sci. Inform. 2020, 13, 939–949. [Google Scholar] [CrossRef]
- Sahoo, A.; Samantaray, S.; Ghose, D.K. Stream flow forecasting in Mahanadi River Basin using artificial neural networks. Procedia Comput. Sci. 2019, 157, 168–174. [Google Scholar] [CrossRef]
- Le, X.-H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) neural network for flood forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef] [Green Version]
- Hauswirth, S.M.; Bierkens, M.F.P.; Beijk, V.; Wanders, N. The potential of data driven approaches for quantifying hydrological extremes. Adv. Water Resour. 2021, 155, 104017. [Google Scholar] [CrossRef]
- Althoff, D.; Rodrigues, L.N.; Silva, D.D. Addressing hydrological modeling in watersheds under land cover change with deep learning. Adv. Water Resour. 2021, 154, 103965. [Google Scholar] [CrossRef]
- Shu, X.; Ding, W.; Peng, Y.; Wang, Z.; Wu, J.; Li, M. Monthly streamflow forecasting using convolutional neural network. Water Resour. Manag. 2021, 35, 5089–5104. [Google Scholar] [CrossRef]
- Wang, J.-H.; Lin, G.-F.; Chang, M.-J.; Huang, I.-H.; Chen, Y.-R. Real-time water-level forecasting using dilated causal convolutional neural networks. Water Resour. Manag. 2019, 33, 3759–3780. [Google Scholar] [CrossRef]
- Barino, F.O.; Silva, V.N.H.; Lopez-Barbero, A.P.; De Mello Honorio, L.; Santos, A.B.D. Correlated time-series in multi-day-ahead streamflow forecasting using convolutional networks. IEEE Access 2020, 8, 215748–215757. [Google Scholar] [CrossRef]
- Anderson, S.; Radić, V. Evaluation and interpretation of convolutional long short-term memory networks for regional hydrological modelling. Hydrol. Earth Syst. Sci. 2022, 26, 795–825. [Google Scholar] [CrossRef]
- SNIRH, n.d. Sistema Nacional de Informação de Recursos Hídricos. Available online: https://snirh.apambiente.pt/index.php?idMain= (accessed on 7 February 2021).
- Simionesei, L.; Ramos, T.B.; Palma, J.; Oliveira, A.R.; Neves, R. IrrigaSys: A web-based irrigation decision support system based on open source data and technology. Comput. Electron. Agric. 2020, 178, 105822. [Google Scholar] [CrossRef]
- Keras. GitHub. Available online: https://github.com/fchollet/keras (accessed on 19 November 2020).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI ’16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- O’Malley, T.; Bursztein, E.; Long, J.; Chollet, F.; Jin, H.; Invernizzi, L. Keras Tuner. Available online: https://github.com/keras-team/keras-tuner (accessed on 30 May 2021).
- Agencia Estatal de Meteorología (España). Atlas Climático Ibérico: Temperatura del Aire y Precipitación (1971–2000)=Atlas Climático Ibérico: Temperatura do ar e Precipitação (1971–2000)=Iberian Climate Atlas: Air Temperature and Precipitation (1971–2000); Instituto Nacional de Meteorología: Madrid, Spain, 2011. [Google Scholar]
- European Digital Elevation Model (EU-DEM), version 1.1., n.d. © European Union, Copernicus Land Monitoring Service 2019, European Environment Agency (EEA). Available online: https://land.copernicus.eu/pan-european/satellite-derived-products/eu-dem/eu-dem-v1.1/view (accessed on 15 May 2019).
- Panagos, P.; Van Liedekerke, M.; Jones, A.; Montanarella, L. European Soil Data Centre: Response to European policy support and public data requirements. Land Use Policy 2012, 29, 329–338. [Google Scholar] [CrossRef]
- Corine Land Cover 2012, n.d. © European Union, Copernicus Land Monitoring Service 2018, European Environment Agency (EEA). Available online: https://land.copernicus.eu/pan-european/corine-land-cover (accessed on 22 June 2019).
- ARBVS, n.d. Área Regada. Associação de Regantes e Beneficiários do Vale do Sorraia. Available online: https://www.arbvs.pt/index.php/culturas/area-regada (accessed on 18 October 2022).
- APA and ARH Tejo, 2012. Agência Portguesa do Ambiente and Administração da Região Hidrográfica Tejo. Plano de gestão da região hidrográfica do Tejo—Relatório técnico (Síntese). Available online: https://apambiente.pt/agua/1o-ciclo-de-planeamento-2010-2015 (accessed on 6 September 2022).
- Pörtner, H.-O.; Roberts, D.C.; Tignor, M.; Poloczanska, E.S.; Mintenbeck, K.; Alegría, A.; Craig, M.; Langsdorf, S.; Löschke, S.; Möller, V.; et al. IPCC, 2022: Climate Change 2022: Impacts, Adaptation and Vulnerability. In Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2022; p. 3068. [Google Scholar] [CrossRef]
- Almeida, C.; Ramos, T.; Segurado, P.; Branco, P.; Neves, R.; Proença de Oliveira, R. Water Quantity and Quality under Future Climate and Societal Scenarios: A Basin-Wide Approach Applied to the Sorraia River, Portugal. Water 2018, 10, 1186. [Google Scholar] [CrossRef] [Green Version]
- Lohani, A.K.; Kumar, R.; Singh, R.D. Hydrological time series modeling: A comparison between adaptive neuro-fuzzy, neural network and autoregressive techniques. J. Hydrol. 2012, 442–443, 23–35. [Google Scholar] [CrossRef]
- Dolling, O.R.; Varas, E.A. Artificial neural networks for streamflow prediction. J. Hydraul. Res. 2002, 40, 547–554. [Google Scholar] [CrossRef]
- Keras Documentation: Layer Activation Functions, n.d. Available online: https://keras.io/api/layers/activations/ (accessed on 14 October 2022).
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Cigizoglu, H.K. Estimation, forecasting and extrapolation of river flows by artificial neural networks. Hydrol. Sci. J. 2003, 48, 349–361. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Dobbins, R.W. Neural Network PC Tools. A Practical Guide; Academic Press: Cambridge, MA, USA, 1990. [Google Scholar] [CrossRef]
- Keras Documentation: Dropout Layer, n.d. Available online: https://keras.io/api/layers/regularization_layers/dropout/ (accessed on 14 October 2022).
- Elman, J.L. Finding structure in Time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. arXiv 2015. Available online: https://arxiv.org/abs/1506.00019 (accessed on 8 February 2023).
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural. Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural. Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Saon, G.; Picheny, M. Recent advances in conversational speech recognition using convolutional and recurrent neural networks. IBM J. Res. Dev. 2017, 61, 1:1–1:10. [Google Scholar] [CrossRef]
- Xu, W.; Jiang, Y.; Zhang, X.; Li, Y.; Zhang, R.; Fu, G. Using long short-term memory networks for river flow prediction. Hydrol. Res. 2020, 51, 1358–1376. [Google Scholar] [CrossRef]
- Shen, C. A transdisciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time-series. In The Handbook of Brain Theory and Neural Networks; Arbib, M.A., Ed.; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Chong, K.L.; Lai, S.H.; Yao, Y.; Ahmed, A.N.; Jaafar, W.Z.W.; El-Shafie, A. Performance enhancement model for rainfall forecasting utilizing integrated wavelet-convolutional neural network. Water Resour. Manag. 2020, 34, 2371–2387. [Google Scholar] [CrossRef]
- Bengio, Y. Learning Deep Architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Deng, L. A Tutorial Survey of Architectures, Algorithms, and Applications for Deep Learning. APSIPA Trans. Signal Inf. Process. 2014, 3, E2. [Google Scholar] [CrossRef] [Green Version]
- Tao, Q.; Liu, F.; Li, Y.; Sidorov, D. Air pollution forecasting using a deep learning model based on 1D convnets and bidirectional GRU. IEEE Access 2019, 7, 76690–76698. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, J.; Cao, L.; Wang, L.; Luo, X.; Wang, J.-H.; Bensoussan, A. Robust forecasting of river-flow based on convolutional neural network. IEEE Trans. Sustain. Comput. 2020, 5, 594–600. [Google Scholar] [CrossRef]
- Keras Documentation: Layer Weight Initializers, n.d. Available online: https://keras.io/api/layers/initializers/ (accessed on 2 December 2022).
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2017. Available online: https://arxiv.org/abs/1609.04747 (accessed on 8 February 2023).
- Ebert-Uphoff, I.; Lagerquist, R.; Hilburn, K.; Lee, Y.; Haynes, K.; Stock, J.; Kumler, C.; Stewart, J.Q. CIRA guide to custom loss functions for neural networks in environmental sciences—Version 1. arXiv 2021. Available online: https://arxiv.org/abs/2106.09757 (accessed on 8 February 2023).
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Wu, W.; Dandy, G.C.; Maier, H.R. Protocol for developing ANN models and its application to the assessment of the quality of the ANN model development process in drinking water quality modelling. Environ. Model. Softw. 2014, 54, 108–127. [Google Scholar] [CrossRef]
- Keras Documentation: Model Training APIs, n.d. Available online: https://keras.io/api/models/model_training_apis/ (accessed on 14 October 2022).
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic pptimization. arXiv 2017. Available online: https://arxiv.org/abs/1412.6980 (accessed on 8 February 2023).
- Reddi, S.J.; Kale, S.; Kumar, S. On the convergence of adam and beyond. arXiv 2019. Available online: https://arxiv.org/abs/1904.09237 (accessed on 8 February 2023).
- Dozat, T. Incorporating Nesterov Momentum into Adam. In Proceedings of the ICLR 2016 Workshop, San Juan, Puerto Rico, India, 2–4 May 2016. [Google Scholar]
- Juan, C.; Genxu, W.; Tianxu, M.; Xiangyang, S. ANN Model-based simulation of the runoff variation in response to climate change on the Qinghai-Tibet Plateau, China. Adv. Meteorol. 2017, 2017, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Nacar, S.; Hınıs, M.A.; Kankal, M. Forecasting daily streamflow discharges using various neural network models and training algorithms. KSCE J. Civ. Eng. 2018, 22, 3676–3685. [Google Scholar] [CrossRef]
- Riad, S.; Mania, J.; Bouchaou, L.; Najjar, Y. Rainfall-runoff model usingan artificial neural network approach. Math. Comput. Model. 2004, 40, 839–846. [Google Scholar] [CrossRef]
- Yang, S.; Yang, D.; Chen, J.; Zhao, B. Real-time reservoir operation using recurrent neural networks and inflow forecast from a distributed hydrological model. J. Hydrol. 2019, 579, 124229. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- McKinney, W. Data structures for statistical computing in Python. In Proceedings of the 9th Python in Science Conference 2010, Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar] [CrossRef] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Radiuk, P.M. Impact of training set batch size on the performance of convolutional neural networks for diverse datasets. Inf. Technol. Manag. 2017, 20, 20–24. [Google Scholar] [CrossRef]
- Airola, R.; Hager, K. Image Classification, Deep Learning and Convolutional Neural Networks: A Comparative Study of Machine Learning Frameworks. 2017. Thesis (BSc). Available online: https://www.diva-portal.org/smash/record.jsf?pid=diva2%3A1111144&dswid=341 (accessed on 16 October 2022).
- Afaq, S.; Rao, S. Significance of epochs on training a neural network. Int. J. Sci. Res. Sci. Eng. 2020, 9, 485–488. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. arXiv 2012. Available online: https://arxiv.org/abs/1206.2944 (accessed on 8 February 2023).
- Jin, Y.-F.; Yin, Z.-Y.; Zhou, W.-H.; Shao, J.-F. Bayesian model selection for sand with generalization ability evaluation. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 2305–2327. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Duan, S.; Ullrich, P.; Shu, L. Using convolutional neural networks for streamflow projection in California. Front. Water 2020, 2, 28. [Google Scholar] [CrossRef]
- Darbandi, S.; Pourhosseini, F.A. River flow simulation using a multilayer perceptron-firefly algorithm model. Appl. Water Sci. 2018, 8, 85. [Google Scholar] [CrossRef] [Green Version]
- Üneş, F.; Demirci, M.; Zelenakova, M.; Çalışıcı, M.; Taşar, B.; Vranay, F.; Kaya, Y.Z. River flow estimation using artificial intelligence and fuzzy techniques. Water 2020, 12, 2427. [Google Scholar] [CrossRef]
- Hu, Y.; Yan, L.; Hang, T.; Feng, J. Stream-flow forecasting of small rivers based on LSTM. arXiv 2020. Available online: https://arxiv.org/abs/2001.05681 (accessed on 8 February 2023).
- Lee, H.; Song, J. Introduction to convolutional neural network using Keras; an understanding from a statistician. Commun. Stat. Appl. Methods 2019, 26, 591–610. [Google Scholar] [CrossRef] [Green Version]
- Sit, M.; Demiray, B.; Demir, I. Short-Term Hourly Streamflow Prediction with Graph Convolutional GRU Networks. arXiv 2021. Available online: https://arxiv.org/abs/2107.07039 (accessed on 8 February 2023).
- Szczepanek, R. Daily Streamflow Forecasting in Mountainous Catchment Using XGBoost, LightGBM and CatBoost. Hydrology 2022, 9, 226. [Google Scholar] [CrossRef]
- Demir, I.; Xiang, Z.; Demiray, B.; Sit, M. WaterBench-Iowa: A large-scale benchmark dataset for data-driven streamflow forecasting. Earth Syst. Sci. Data 2022, 14, 5605–5616. [Google Scholar] [CrossRef]


| Station | Period | Annual Precipitation | |||
|---|---|---|---|---|---|
| Average (mm) | Minimum (mm) | Maximum (mm) | Number of Completed Years | ||
| Aldeia da Mata | 1979–2021 | 621 | 374 | 1056 | 26 |
| Alegrete | 1980–2021 | 794 | 457 | 1269 | 17 |
| Alpalhão | 1979–2021 | 717 | 365 | 1224 | 26 |
| Alter do Chão | 2011–2021 | 614 | 101 | 1081 | 90 |
| Cabeço de Vide | 1931–2021 | 668 | 352 | 1184 | 68 |
| Campo Experimental Crato (Chança) | 1971–2021 | 662 | 323 | 973 | 29 |
| Castelo de Vide | 1931–2021 | 824 | 46 | 1555 | 76 |
| Monforte | 1911–2020 | 516 | 256 | 1030 | 88 |
| Ribeira de Nisa | 1979–1985 | 673 | 452 | 962 | 5 |
| Vale do Peso | 1931–2021 | 757 | 401 | 1324 | 77 |
| Period | Streamflow | ||||
|---|---|---|---|---|---|
| Average (m3 s−1) | Minimum (m3 s−1) | Maximum (m3 s−1) | Std. Deviation (m3 s−1) | Number of Records | |
| 1 November 1979–6 March 2019 | 3.8 | 0 | 272.8 | 12.7 | 7703 |
| 25 July 2001–31 December 2008 | 3.8 | 0 | 160.1 | 9.0 | 2645 |
| Long Name | Activation Name | Equation |
|---|---|---|
| Linear | linear | |
| Exponential linear unit | elu | |
| Rectified linear unit | relu | |
| Softsign | softsign | |
| Hyperbolic tangent | tanh |
| Layers | Number of Layers | Number of Neurons | Activation Function | Dropout after Dense | Dropout Rate |
|---|---|---|---|---|---|
| Input dense | 1 | 1, 2, 3, 4, 5, 6 or training set size | Linear, elu or relu | Yes/No | 0.1 or 0.2 |
| Hidden dense | 0, 1, 2, 3 or 4 | 1, 2, 3, 4, 5, 6 or training set size | Softsign, linear, elu or relu | Yes/No (one by each hidden layer) | 0.1 or 0.2 |
| Output dense | 1 | 1 | Softsign or linear | - | - |
| Layers | Number of Layers | Number of Neurons | Activation Function |
|---|---|---|---|
| Input LSTM | 1 | 4, 8, 16 or 32 | tanh (by default) |
| Hidden LSTM | 0, 2 or 4 | If hidden layers = 2: 1st layer: 2 × ninput 2nd layer: ninput If hidden layers = 4: 1st layer: 2 × ninput 2nd layer: 3 × ninput 3rd layer: 2 × ninput 4th layer: ninput | tanh (by default) |
| Output dense | 1 | 1 | linear |
| Layers | N. of Layers | N. of Filters | Kernel Size | Pooling Size | N. of Neurons | Activation Function | Dropout after Dense | Dropout Rate |
|---|---|---|---|---|---|---|---|---|
| Input convolutional | 1 | 8, 16, or 32 | 1, 5, or 10 | - | - | None (by default) | - | - |
| MaxPooling1D | 1 | - | - | 1 or 2 | - | - | - | - |
| Hidden convolutional | 0 or 1 | 8, 16, or 32 | 8, 16, or 32 | - | - | None (by default) | - | - |
| MaxPooling1D | 1 | - | - | 1 or 2 | - | - | - | - |
| Flatten | 1 | - | - | - | - | - | - | - |
| Hidden dense | 0, 1, or 2 | - | - | - | 3, 5, or 10 | softsign, linear, elu, or relu | Yes/No (one by each hidden layer) | 0.1 or 0.2 |
| Output dense | 1 | - | - | - | 1 | softsign, linear, elu, or relu | - | - |
| Meteorological Variable | Average | Minimum | Maximum | Std. Deviation |
|---|---|---|---|---|
| Daily total precipitation (mm) | 1.59 | 0 | 45.50 | 4.24 |
| Daily air temperature (°C) | 16.09 | 1.77 | 34.74 | 6.46 |
| Scenario | Total Precipitation (TP) or Total Precipitation + Air Temperature (TP&AT) | |||||
|---|---|---|---|---|---|---|
| Time Lag (Days) | Acc. TP (Days) | Ave. AT (Days) | Training Set Size | Validation Set Size | Test Set Size | |
| TP1 | - | 1 | - | 1851 | 529 | 265 |
| TP2 | - | 1,2,3,4,5,10 | - | 1845 | 527 | 264 |
| TP3 | - | 10,30,60 | - | 1810 | 517 | 259 |
| TP4 | 1,2,3,4,5,6,7 | - | - | 1846 | 527 | 265 |
| TP5 | 1,2,3,4,5,6,7 | 1,2,3,4,5,10 | - | 1810 | 517 | 259 |
| TP6 | 1,2,3,4,5,6,7 | 10,30,60 | - | 1845 | 527 | 264 |
| TP&AT1 | - | 1 | 1 | 1851 | 529 | 265 |
| TP&AT2 | - | 1,2,3,4,5,10 | 1,2,3,4,5,10 | 1845 | 527 | 264 |
| TP&AT3 | - | 10,30,60 | 10,30,60 | 1810 | 517 | 259 |
| TP&AT4 | 1,2,3,4,5,6,7 | - | - | 1846 | 527 | 265 |
| TP&AT5 | 1,2,3,4,5,6,7 | 1,2,3,4,5,10 | 1,2,3,4,5,10 | 1810 | 517 | 259 |
| TP&AT6 | 1,2,3,4,5,6,7 | 10,30,60 | 10,30,60 | 1845 | 527 | 264 |
| Training Algorithm | Hyper-Parameters Optimized | |
|---|---|---|
| Possible Values Tested for Learning Rate | Possible Values Tested for ε | |
| SGD | 1 × 10−4, 1 × 10−3 or 1 × 10−2 | - |
| AdaGrad | - | 1 × 10−7 or 1 × 10−8 |
| RMSprop | - | |
| Adam | 1 × 10−4, 1 × 10−3 or 1 × 10−2 | |
| AdaMax | ||
| Nadam | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, A.R.; Ramos, T.B.; Neves, R. Streamflow Estimation in a Mediterranean Watershed Using Neural Network Models: A Detailed Description of the Implementation and Optimization. Water 2023, 15, 947. https://doi.org/10.3390/w15050947
Oliveira AR, Ramos TB, Neves R. Streamflow Estimation in a Mediterranean Watershed Using Neural Network Models: A Detailed Description of the Implementation and Optimization. Water. 2023; 15(5):947. https://doi.org/10.3390/w15050947
Chicago/Turabian StyleOliveira, Ana Ramos, Tiago Brito Ramos, and Ramiro Neves. 2023. "Streamflow Estimation in a Mediterranean Watershed Using Neural Network Models: A Detailed Description of the Implementation and Optimization" Water 15, no. 5: 947. https://doi.org/10.3390/w15050947






