1. Introduction
The hydraulic fracturing technique has been widely used in the development of unconventional reservoirs. During the fracturing process, fracture fluids are injected underground to crack the reservoir rocks. Such operations are usually fulfilled within hours to days. Considering the fast pace of the field operations, the real-time modeling of the hydraulic fracture operations is therefore of critical importance, as it visualizes the dynamic growth of downhole fractures and allows field engineers to adapt the operation parameters accordingly. The real-time simulation is challenging in two aspects. First, it requires the simulator to produce the numerical results fast enough. Secondly, it needs the simulator to interact with the hydraulic fracturing facilities, in order to pick up and interpret the real-time signals. Therefore, tremendous efforts are demanded in the development of such a program. In this paper, we will show the progress we have made in the above-mentioned regard.
The earliest trials of simulating the propagation of hydraulic fractures date back to the 1960s, when the PKN [
1,
2] model and the KGD [
3] model were developed. PKN and KGD models presume the shape of the fractures, which may not reflect the real conditions well. To conduct realistic simulation of fractures, more comprehensive numerical methods have been proposed. Among them, Finite Element Method (FEM) and its variants are the most widely used [
4,
5,
6,
7]. Classic FEM relies on re-meshing to track the propagating fracture, which increases the. computational load. To resolve such an issue, the Extended Finite Element Method (XFEM) [
8,
9,
10] has been developed. XFEM adopts ‘enriched’ basis functions to allow crack growth within an FEM element. Therefore, XFEM permits flexibility in handling 2D and 3D fracture growth. One potential drawback of XFEM lies in its huge computational cost, which prevents its wide application to the real-time simulation of field-scale problems.
The Discrete Element Method (DEM) [
11,
12,
13] is flexible in handing the discontinuities of fractures. DEM can also be coupled with damage mechanics and flow simulation [
14,
15,
16]. However, in most cases DEM is based on rigid body elements, which are known to have the ‘scaling’ issue [
17]. A hybrid finite-discrete element method [
18,
19,
20] has also been proposed, which adopts the discrete element method to simulate the fracture and adopts the finite element method to simulate the surrounding area in the vicinity of the fracture.
Wu and Olson [
21,
22] have adopted Discontinuous Discontinuity Method (DDM) for the simulation of multistage fractures. Based on Green’s theorem, DDM effectively reduces the simulation of the stress field to the boundary element, which makes it very convenient in tracking the propagation of complex fracture networks [
23]. Recently, DDM has been extended to inter-well interference [
24]. One potential drawback of DDM is that it is difficult to apply in heterogeneous problems. Besides discrete fracture (fracture planes) simulation, the propagation of complex fracture networks has also been investigated. Kresse et al. [
25], Weng [
26] and Weng et al. [
27] developed the Unconventional Fracture Model (UFM) to simulate the fracture growth in naturally fractured reservoirs in the ‘wiremesh’ manner. In such approaches, the fractures are not modeled distinctly but as a network, to account for the complex fracture-fracture interaction. The propagation of fractures is based on energy criteria. Recently, Li et al. [
28] investigated the hydrate-bearing wellbore stability with potential fracturing risks. Moreover, Li et al. [
29] studied the potential application of CO
2 as a fracturing fluid.
Although huge success has been achieved in the development of numerical models, a comprehensive simulator that accurately simulates the fracture propagation and proppant distribution while it maintains fast computational speed is still a challenge. In this work, we have developed a practical simulator, named FracCSM, based on combining the Integrated Finite Difference (IFD) and DDM methods. FracCSM is compositional, tracking the mitigation of every fluid and proppant component. The mass loss induced by fluid leakoff and energy loss caused by friction and thermal conduction have also been taken into consideration. We have integrated DDM with IFD. In our simulator, the DDM method is used to predict the fracture propagation, while IFD is used to simulate the fluid transport inside the fracture plane. The real practice of hydraulic fracturing operations demands the real-time monitoring of fracture growth underground. To fulfill such a goal, we have developed a novel framework for the real-time simulation of hydraulic fractures. In this framework, the program picks up and interprets the signal from the hydraulic fracturing facilities and sends it to the simulation engine for dynamic prediction, using the multi-process technique. Our approach has been used to conduct field-scale real-time hydraulic fracturing in the tight sandstone formations in Sulige gas field. This paper is arguably the first to document such advancement. Compared to previous works, the novelties of our work lie in the following aspects: the integration of DDM and IFD, the wellbore treatment and the real-time simulation framework.
This paper is organized as follows. In
Section 2, we present the mathematical model of FracCSM, including the transport model and the fracture mechanics model. In
Section 3, we describe the numerical approaches used in FracCSM, including the discretization scheme, combined framework and real-time simulation module. In
Section 4 and
Section 5, we present the validation and discuss the numerical results of FracCSM, respectively. In the last chapter, we conclude and summarize the work.
2. Mathematical Model
2.1. Fracture Initiation and Propagation
In this section, we present our fracture mechanics model, including the fracture extension criteria as well as the determination of the fracture width.
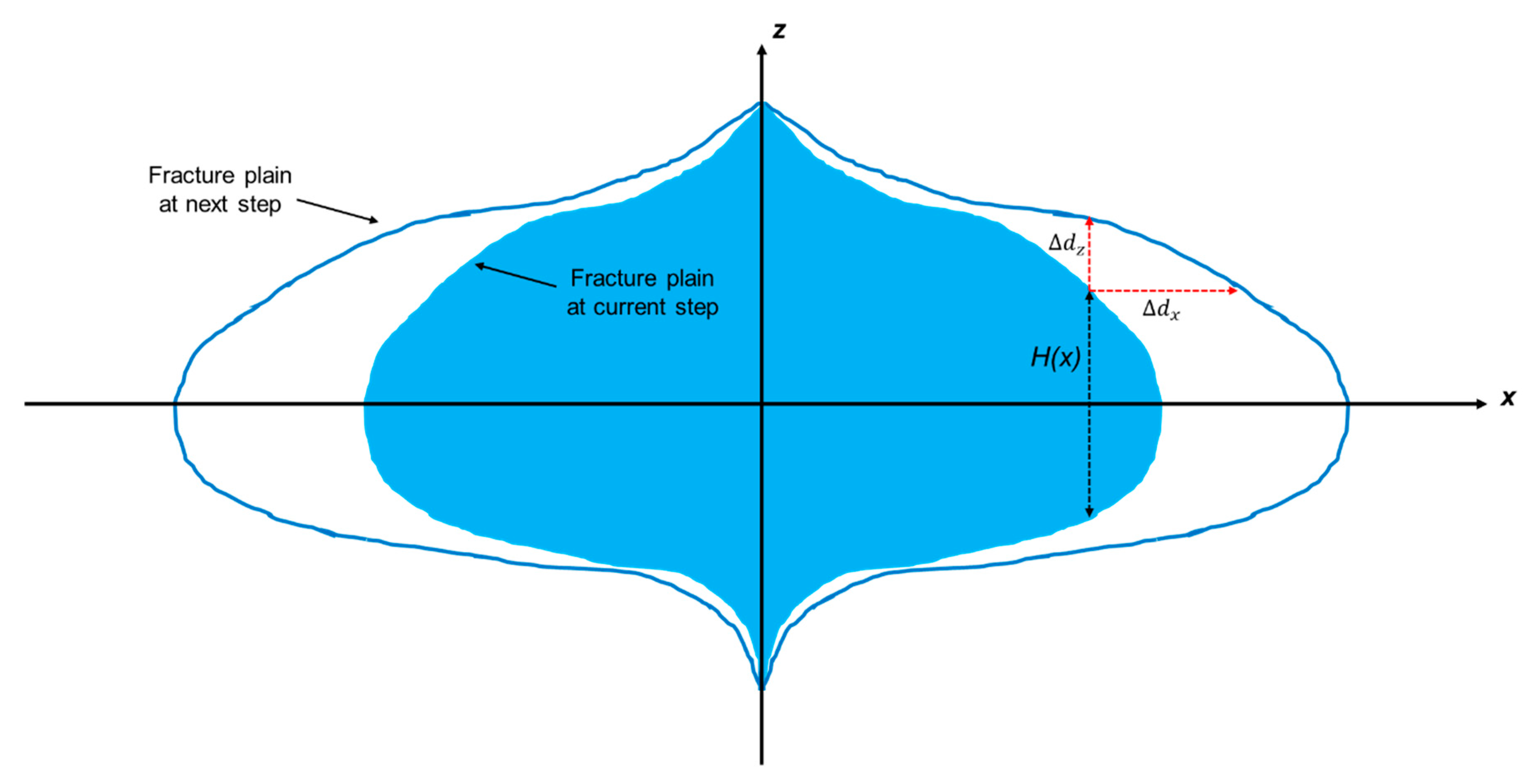
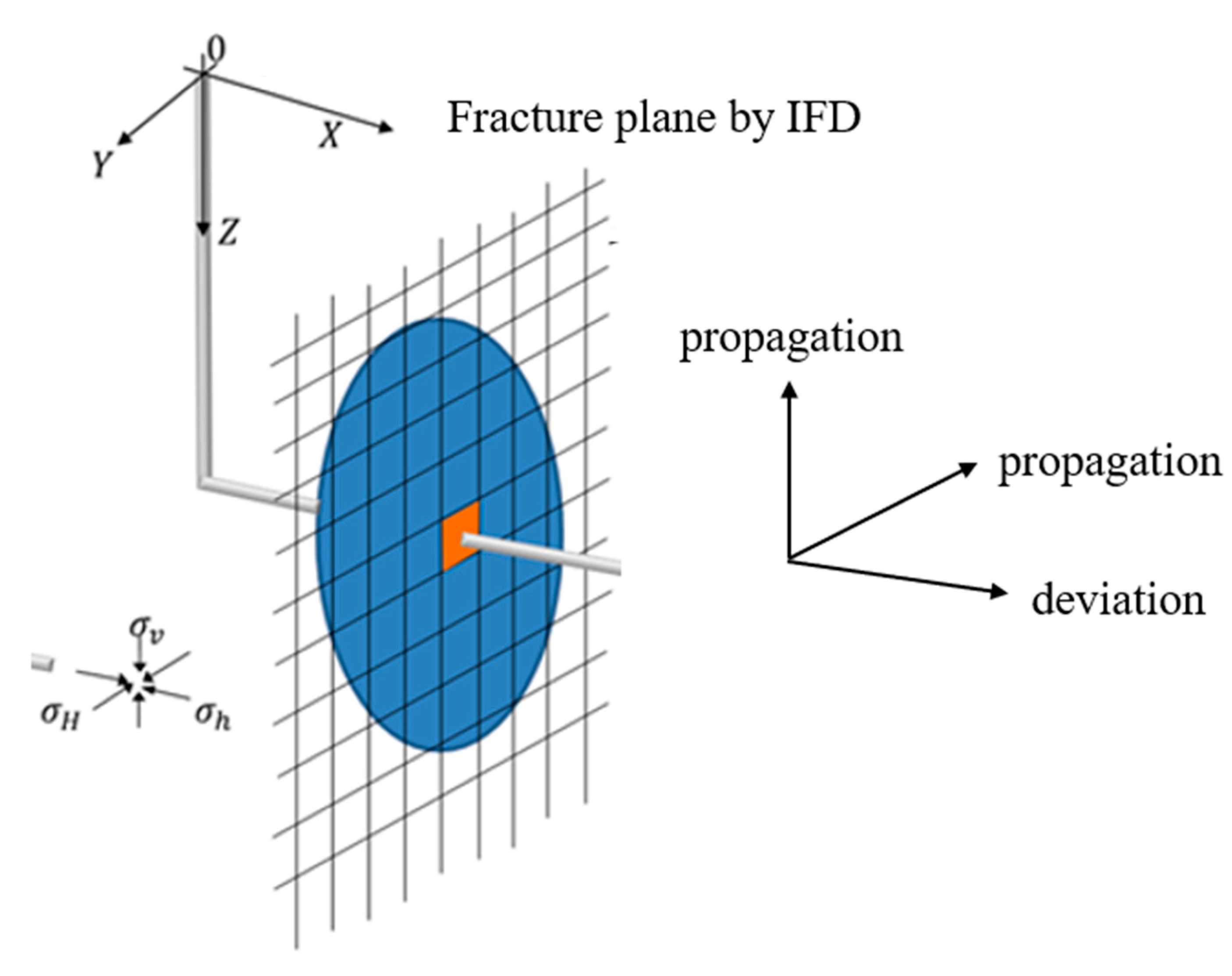
In FracCSM, the fracture is simulated on a dynamically growing rectangular grid. The fracture is allowed to propagate along the horizontal (x-direction) and vertical direction (z-direction). To account for the stress interference among fractures, we allow the fracture plane to deviate along the y-direction. The grid block size can be non-uniform, which will be explained in detail in
Section 3.1.
To describe the failure mechanism used in FracCSM, we start with the calculation of the stress intensity factor
for Mode-1 failure, as follows [
30]
where
denotes the normal displacement of the grid block at the fracture front, which is obtained by DDM as shown in
Section 3.2.
is the half length of the current fracture plane.
and
are the Young’s modulus and Poisson’s ratio, respectively. This correlation is also used in the work of Olson [
31] and Sheibani [
32]. We follow Mastrojannis’s approach [
33] to model the front propagation. We introduce the concept of front propagation velocity, which is the function of rock toughness
, as follows.
in which
Cext and
n are rock internal properties.
At each time step, we make a comparison between the stress intensity factor and the rock toughness. If the former is larger than the latter, the fracture front is allowed to propagate along the horizontal (x-) direction and the vertical (z-) direction. The formulation of the propagation distance is shown below
where
is the height of the fracture at position
x, as shown in
Figure 1.
and
are the grid block size along x- and z- direction, respectively. The grid system as well as the definition of x and z-direction will be explained in detail in
Section 3.1.
is the position of the grid block along z- direction.
is the time step length.
We use net pressure
to update the fracture width.
is calculated as
where
is the pressure inside the fracture. The solution is described in
Section 2.2.
is the minimum principal stress acting on the fracture plane, the calculation of which is fulfilled by the combination with DDM and is described in
Section 3.2.
The initiation of the fracture is subject to the breakdown pressure and the rock properties as well as the in-situ stress condition. The breakdown pressure
Pb is calculated as follows [
30].
where
is the tensile failure stress.
is the pore pressure of the formation.
is the pore pressure factor (treated as porosity in this work) [
34].
is Biot’s coefficient.
is the maximum principal stress.
2.2. Mass Transport Inside the Fracture
FracCSM has a comprehensive model to simulate the transport of mass and energy by tracking every mass component in the slurry. In FracCSM, the injected slurry is simulated with a compositional model, where it is modeled as a mixture of proppants and fluid components, including gel and additives. In our model, the velocity of all fluid components is assumed to be the same, set as
, while the velocity of proppants can differ from each other, subject to the settling effect and particle-wall interactions. The governing equations of both fluid components and proppant components are derived from the following mass conservation equation, as follows [
35].
where
,
and
are the density, velocity and fracture width, respectively. The fracture is set as a thin slit within the local
x-
z plane, ignoring the tortuosity.
For a system with
types of proppant components and
types of fluid components, the mass conservation equation within the fracture plane is as follows.
In the above equation, the first and second term represent the convective flow. The third term is the accumulation term and the last term is the leak-off rate. and are the concentration of the ith type of fluid and the ith type of proppant, respectively.
The mass conservation of the
ith type of proppant components satisfies the following equation.
To accurately simulate the mass transport of all components, the key lies in the calculation of the fluid component velocity and the proppant component velocity .
We define a slurry velocity
, which is the weighted summation of the fluid velocity and the proppant velocity, as follows [
35].
The velocity of the slurry is subject to the pressure gradient and the gravity effect, as below.
in which
γsl is the gravity acceleration term.
represents slurry viscosity. Based on Equation (9), the fluid component velocity
calculated as follows.
The above formulation is substituted into Equation (8) with the fluid pressure and the concentration as primary variables.
The proppant velocity consists horizontal component and vertical component .
is calculated by adding the slurry velocity with a settling velocity
is calculated by the Friehauf’s model [
36], as follows.
where
is Stoke’s velocity;
,which is the function of Reynold’s number
, represents the inertial effect,
quantifies the particle-particle interaction effect; and
, which is the function of particle diameter
and fracture width
, quantifies the particle-wall interaction effect. Their detailed formulations can be found in [
37,
38]
For the horizontal direction (x-direction), the proppant velocity
is calculated as [
35]
In the above equation, the parameter
is calculated as
and
where
is the particle diameter of the
ith type of proppant. Similarly to the treatment for fluid velocity, the proppant velocity is substituted into Equation (8) to solve the mass transport of proppants.
The viscosity of the slurry
is calculated by the power-law model [
27] as
where
is the maximum value of proppant concentration, beyond which the slurry will cease flowing.
is the power-law parameter.
and
are the viscosity and mole fraction of pure fluid component without proppants, respectively. The detailed formulation of the viscosity calculation can be found in [
34].
2.3. Leak-Off Rate Calculation
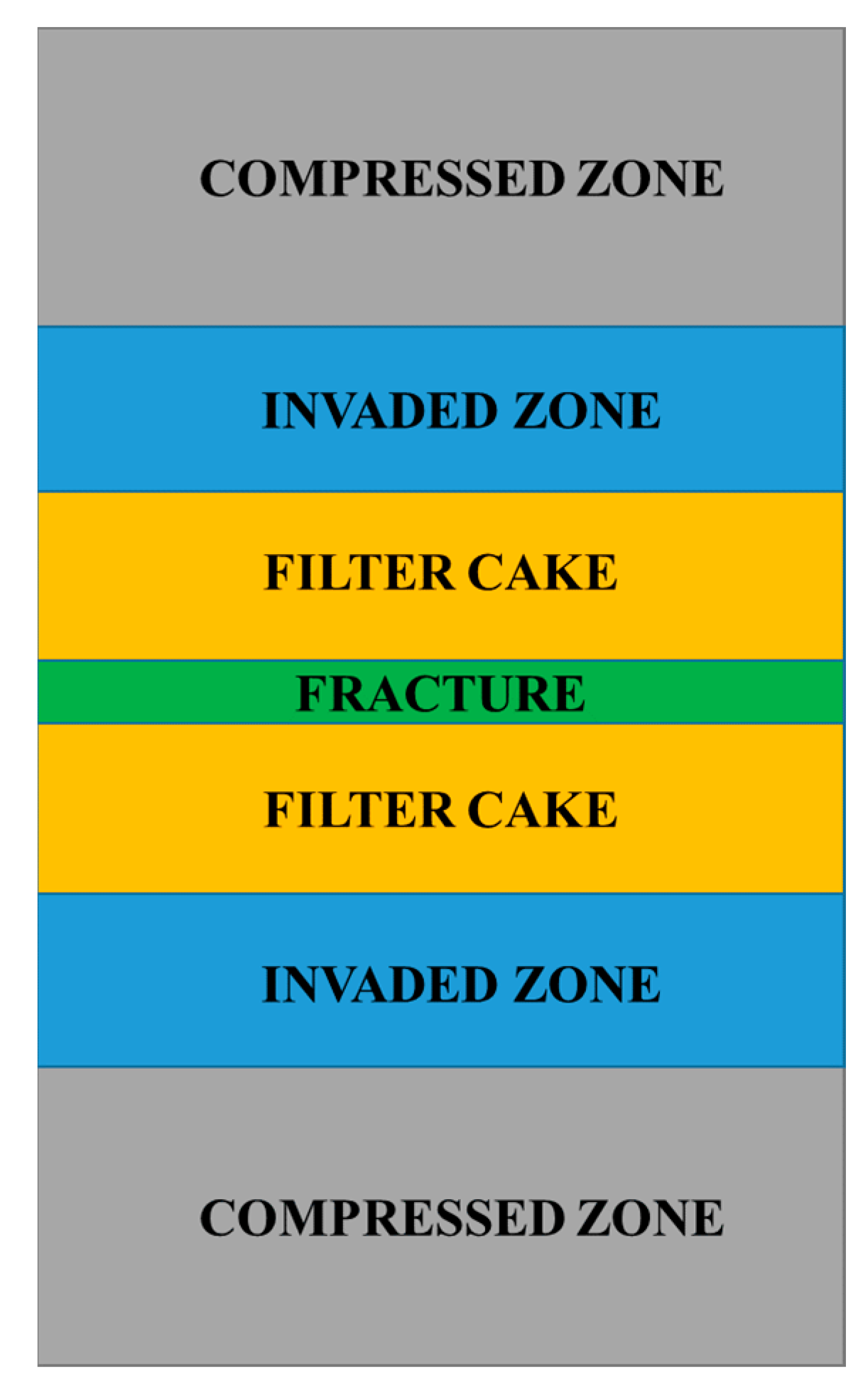
During the fracturing process, fracturing fluids leak into the formation, subject to the permeability of the formation rock, the fluid viscosity, and the pressure difference between the fracture and the formation. In FracCSM, the leak-off rate is calculated with the three-zone model, as introduced by Schechter [
39]. In the three-zone leak-off model, the formation surrounding the fracture is assumed to be sandwich-like, consisting of the filter cake zone, the invaded zone and the compressed formation fluids zone. The filter cake zone refers to the filter cake formed by slurry on the fracture face. The invaded zone is the zone in the vicinity of the fracture face that is (partly) invaded by the slurry. The compressed formation fluids zone refers to the formation that is relatively far away from the fracture and is impacted by the stress change induced by injection. A conceptual model of the three zones is shown in
Figure 2.
The fluid flow within the compressed formation fluids zone is modeled as the single-phase flow of a slightly compressible fluid in a semi-infinite medium. The fluid velocity,
vN, at the interface between the compressed formation fluids zone and the invaded zone can be calculated as follows [
40].
where
and
refer to the porosity, permeability of the reservoir rock, respectively.
and
are the compressibility and viscosity of the fluid.
τ is the time when leak-off commences.
and
are the pressure of the invaded zone and the compressed formation fluids zone, respectively.
is the overall leak-off coefficient of the compressed formation fluids zone.
For the invaded zone, the fluid velocity obeys Darcy’s law and the zone grows as fluid enters it. The fluid velocity in the invaded zone is given by:
where
Pcap is the capillary pressure between the invading fluid and the reservoir fluid.
is the pressure of the filter case zone.
is the overall leak-off coefficient of the invaded zone.
The fluid velocity between the fracture and the filter cake zone is calculated as
where
is the pressure inside the fracture and
is the overall leak-off coefficient of the filter cake zone.
is related to a laboratory-measured parameter
mw, which is the slope of a plot of filtrate volume with respect to the square root of time.
Since the velocities in Equations (18)–(20) are equal to each other, we can obtain an overall leak-off coefficient as
where
and
In the above equation, is the overall pressure drop.
2.4. Energy Transport Inside the Fracture
The general energy balance for a component that takes into account advection and conduction is
where
K is the thermal conductivity,
is the specific enthalpy,
is the specific internal energy, and
is the energy source/sink term. In FracCSM, the conduction term in the above equation is ignored, because of its relatively trivial contribution to the overall energy transport compared to the advection term. By integrating Equation (25) over the fracture width, we get
In the above equation, the specific enthalpy and internal energy can be calculated as
and
For each proppant or fluid component, the specific enthalpy and internal energy are assumed to be equal and can be calculated as
where
C is the specific heat capacity. The heat loss per unit area through the fracture faces is calculated as
where
Kres,
ρres and
Cres are the thermal conductivity, density and heat capacity of the reservoir formation, respectively.
τ is the starting time of the heat loss, as used in Carslaw and Jaeger [
41].
2.5. Mass/Energy Transport Inside the Wellbore
In this section, we present the mass and energy conservation equations of mass and energy transport inside the wellbore.
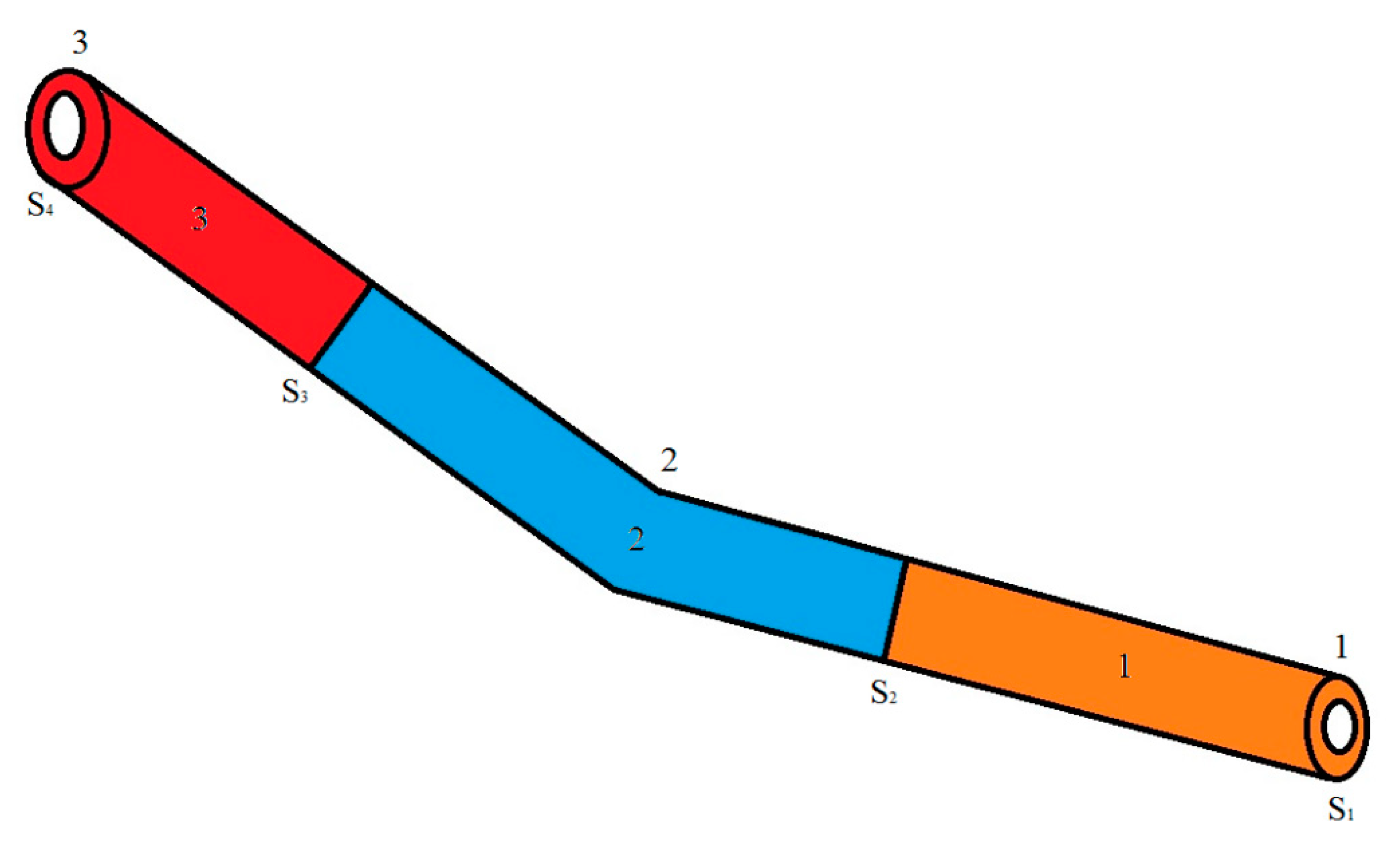
The wellbore is modeled as a series of connected well segments along the well trajectory. The slurry flow inside the wellbore is modeled as piston-like flow segments. The conceptual model of the well segments and the slurry segments are shown in
Figure 3. The properties of slurry, including density and viscosity, are calculated using the same approach as in the fracture.
We track the boundary of each slurry segment, which is denoted by Si, inside the wellbore during the simulation. The boundaries of the slurry segment are denoted by Si. The numbering of these slurry segment boundaries starts at one, the wellbore bottom, and increases as the wellbore is traversed toward the wellhead, with the last segment boundary being SN+1 (where N is the number of well segments) that is located at the wellhead. The slurry is injected into the wellbore at the wellhead and leaves the wellbore through perforations.
The mass conservation equation of the fluid and proppant components in slurry segment
i is
In the above equation, the subscripts p and f denote the fluid and the proppant components, respectively.
Aann is the annular area, x denotes component volume fraction, Tws is transmissibility per unit length for slurry loss to the surroundings, Pw and Psurr are the wellbore pressure and the surrounding pressure, respectively. qinj is rate of the injected slurry. The transmissibility per unit length for slurry loss to the surroundings is only non-zero along completed intervals.
The pressure along the wellbore is calculated as follows.
In the above equation,
g is the gravitational term and
S denotes wellbore trajectory.
Pw,fric is the frictional pressure, which is obtained as follows.
In the above equation,
Dh is the hydraulic diameter. The friction factor
f is calculated based on Reynolds number, as follows. For laminar flow, friction factor is 16/
NRe and in correlations for turbulent flow the friction factor is given by the following equation [
42].
The energy balance equation for a slurry segment is
where
qloss is the rate of heat loss per unit area from the slurry to the surroundings and
Do is the outer wellbore diameter for fluid flow. Heat loss from the slurry to the surroundings is modeled as heat flow through a uniform medium. In this work we derive the overall heat transfer coefficient for the medium based on the analytical solution of transient heat flow with a point heat source [
41].
The temperature profile for transient heat flow through a uniform infinite medium with a point heat source in the center is as follows
Based on the above equation, the heat flow,
Q profile is
In the above two equations, r denotes the radial distance to the center, while kth and αth are the thermal conductivity and the thermal diffusivity of the media, respectively. αth is thermal diffusivity, Q0 is the magnitude of the heat source (per unit length), t refers to time, τ is the time at which the heat source is activated, and Ei is the exponential integral function. Using Equations (36) and (37), the heat flow between the wellbore and the surroundings can be calculated.
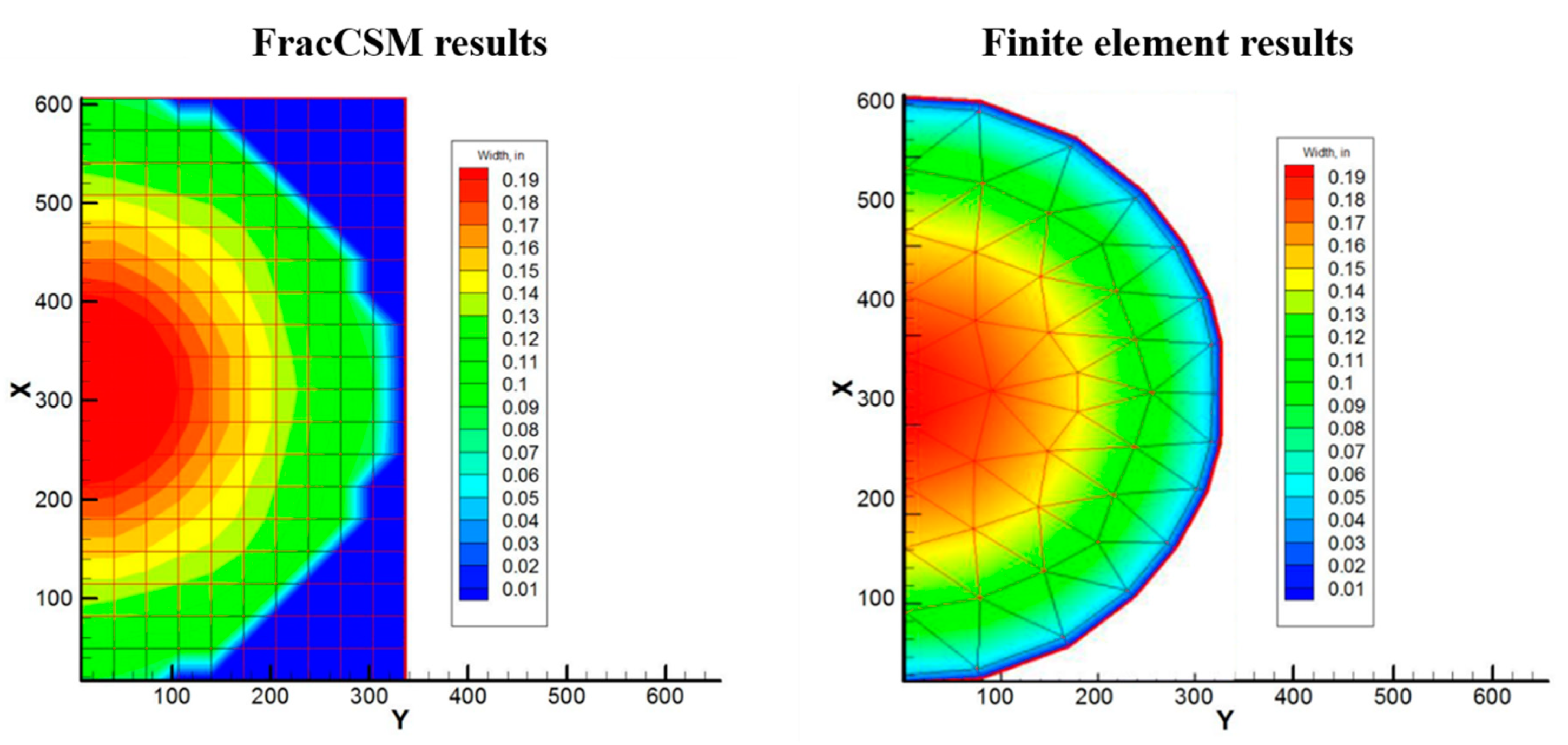
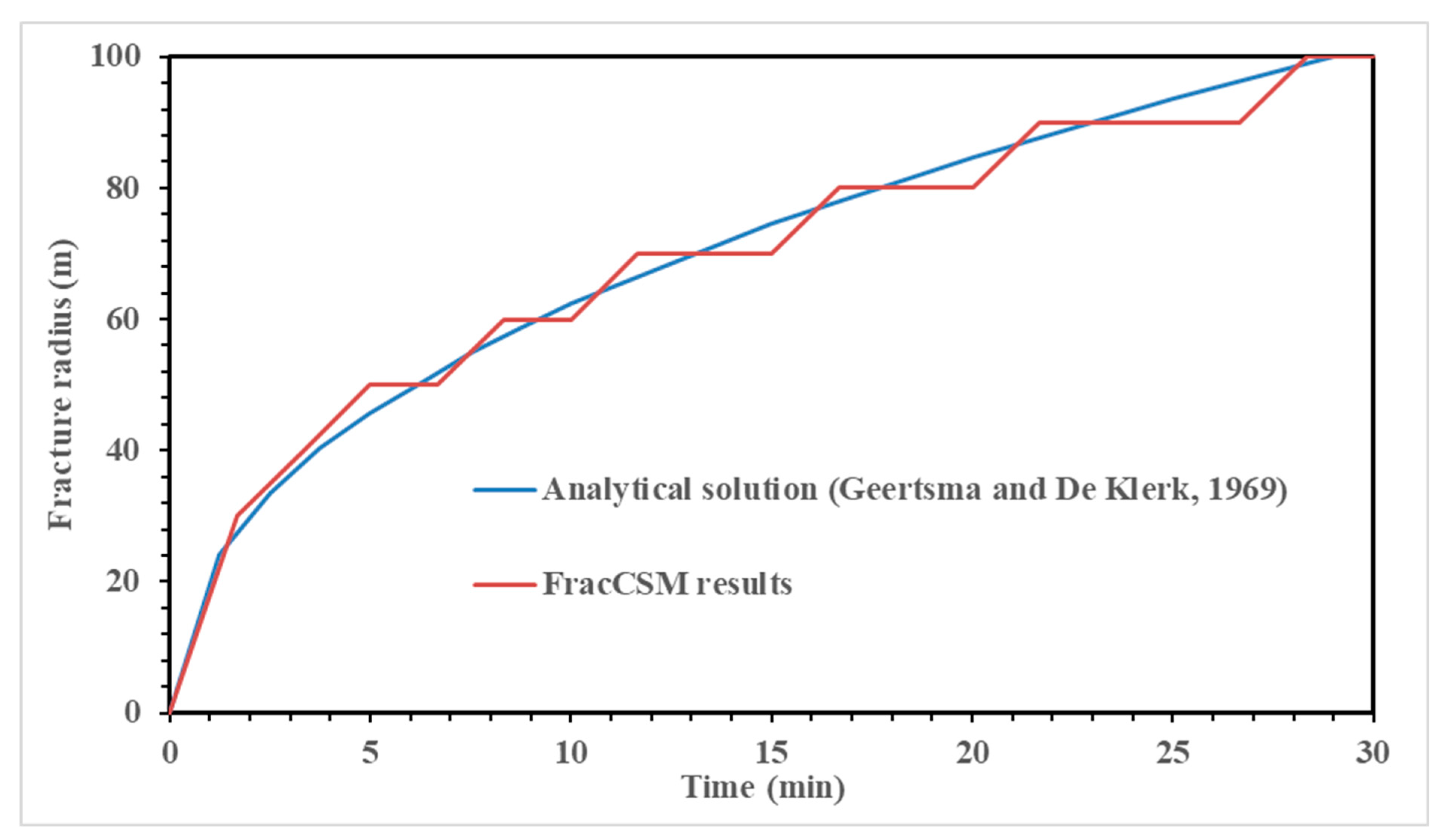
5. Results and Discussion
In this section, we present the applications of our program and discuss the numerical results.
5.1. Numerical Study of Single Fracture in Multi-Layer Reservoirs
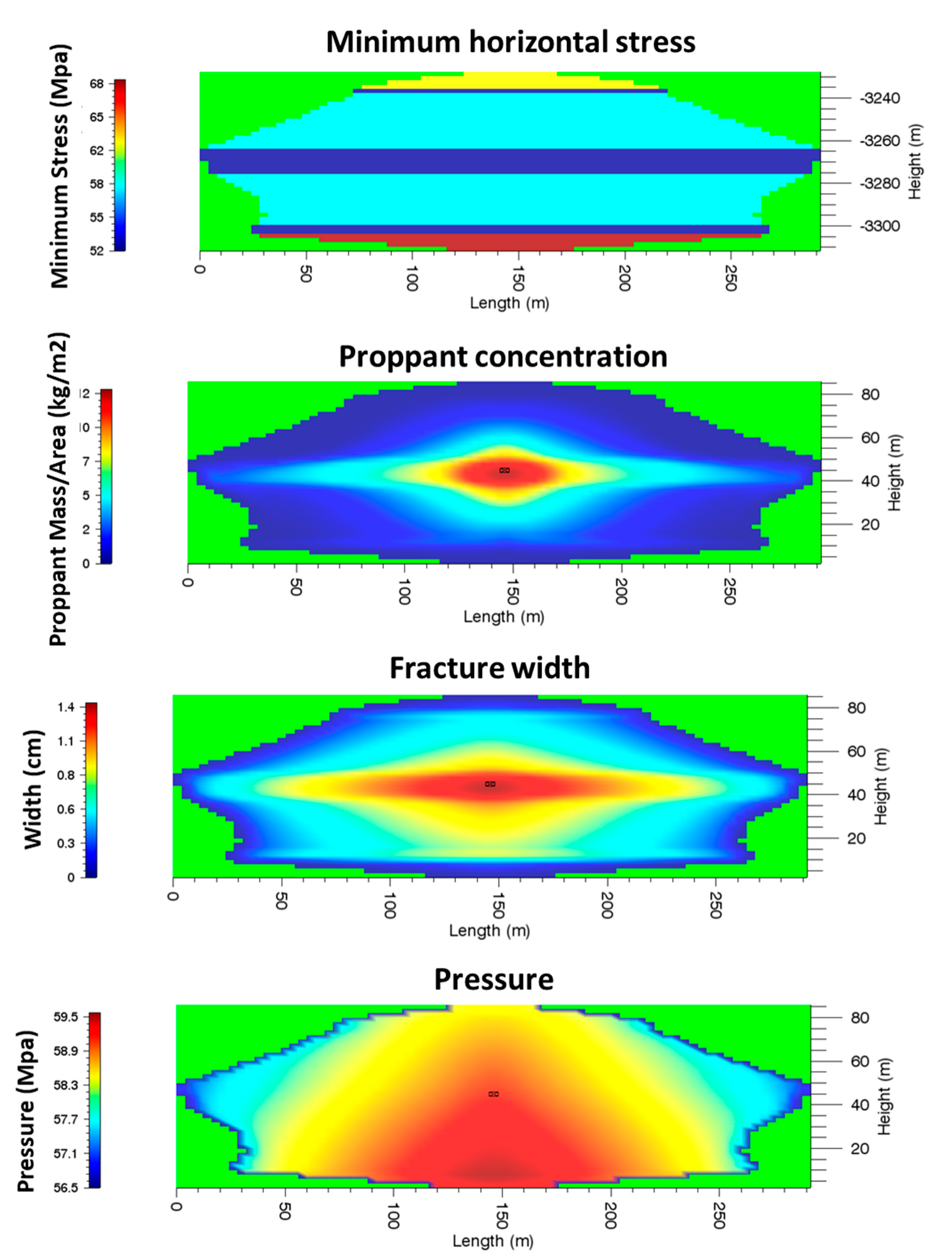
In this sub-section, we apply the developed program to five cases with multiple rock layers to investigate the stress offset impacts on fracture propagation. In these cases, high-permeable sandstone layers with different values of thickness are sandwiched by low-permeable shale layers, as shown in
Figure 10. The thickness of the sandstone layer is 12 m for all the five cases.
The thickness and stress of shale and sandstone layers of the five cases we run are listed in
Table 4. The properties of the rocks and other essential input parameters are listed in
Table 5. The pumping schedule of the five cases is listed in
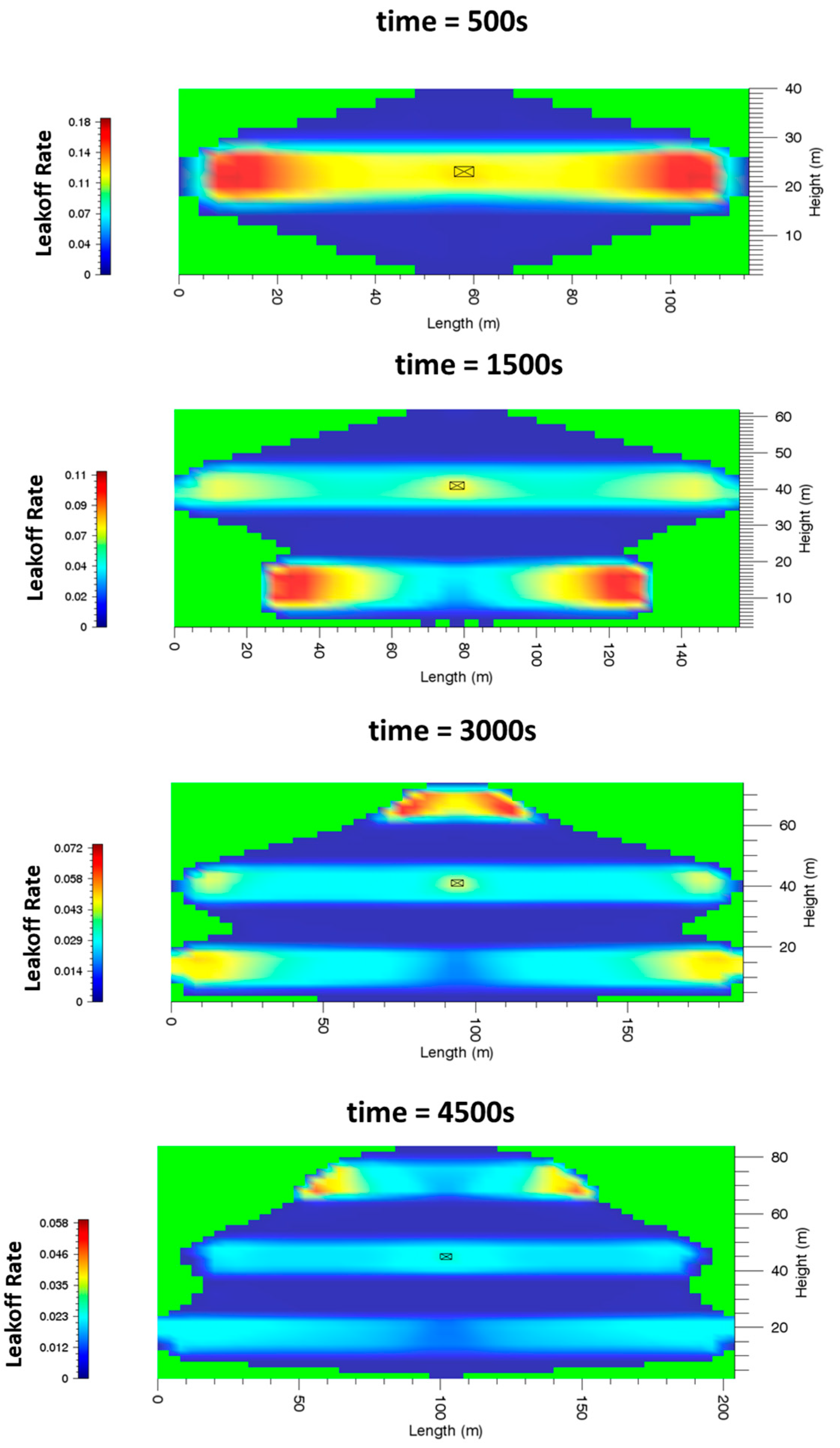
Table 6. The leak-off rate profiles across the fracture plane of Case 1 at different times are shown in
Figure 11. At the early stage, the leak-off rate is relatively higher, and leak-off occurs across the entire fracture. At the late stage of injection, the leak-off rate becomes very small, and leak off only occurs at the front of the fracture, which indicates that the tight sandstone formation will quickly get saturated because of the low permeability. As predicted by FracCSM, about 30% of fluids leaked into the formation, which is in accordance with field observations.
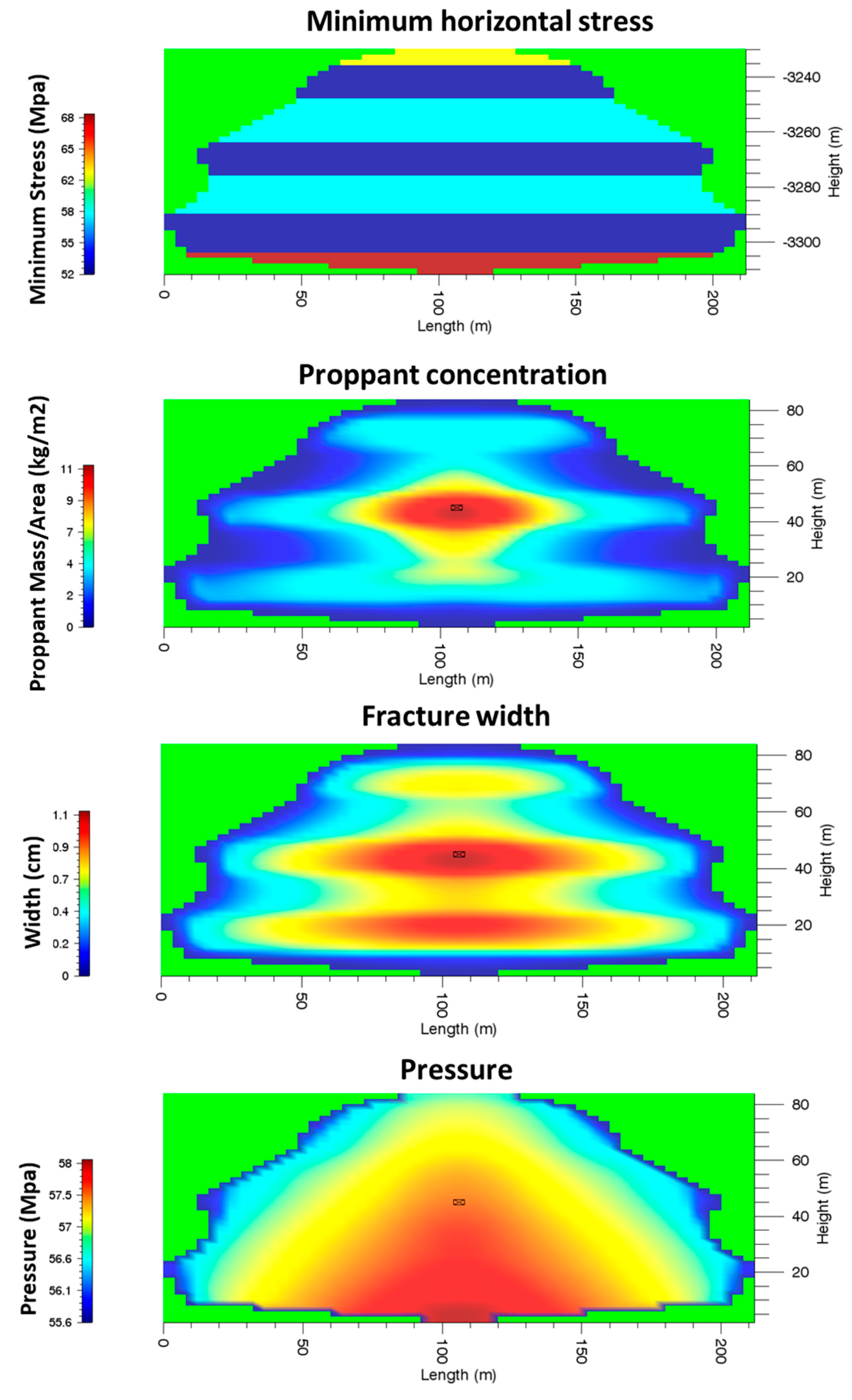
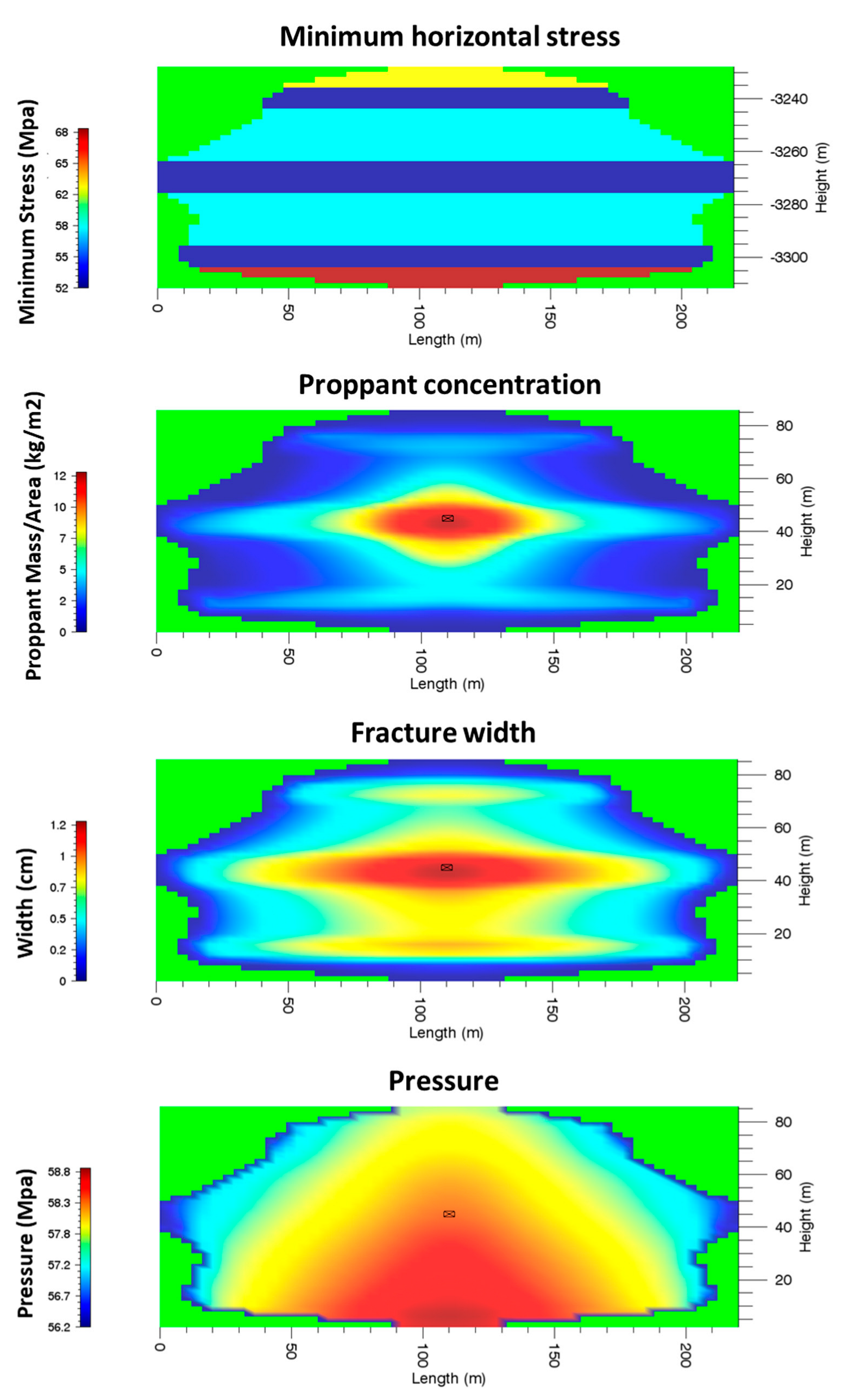
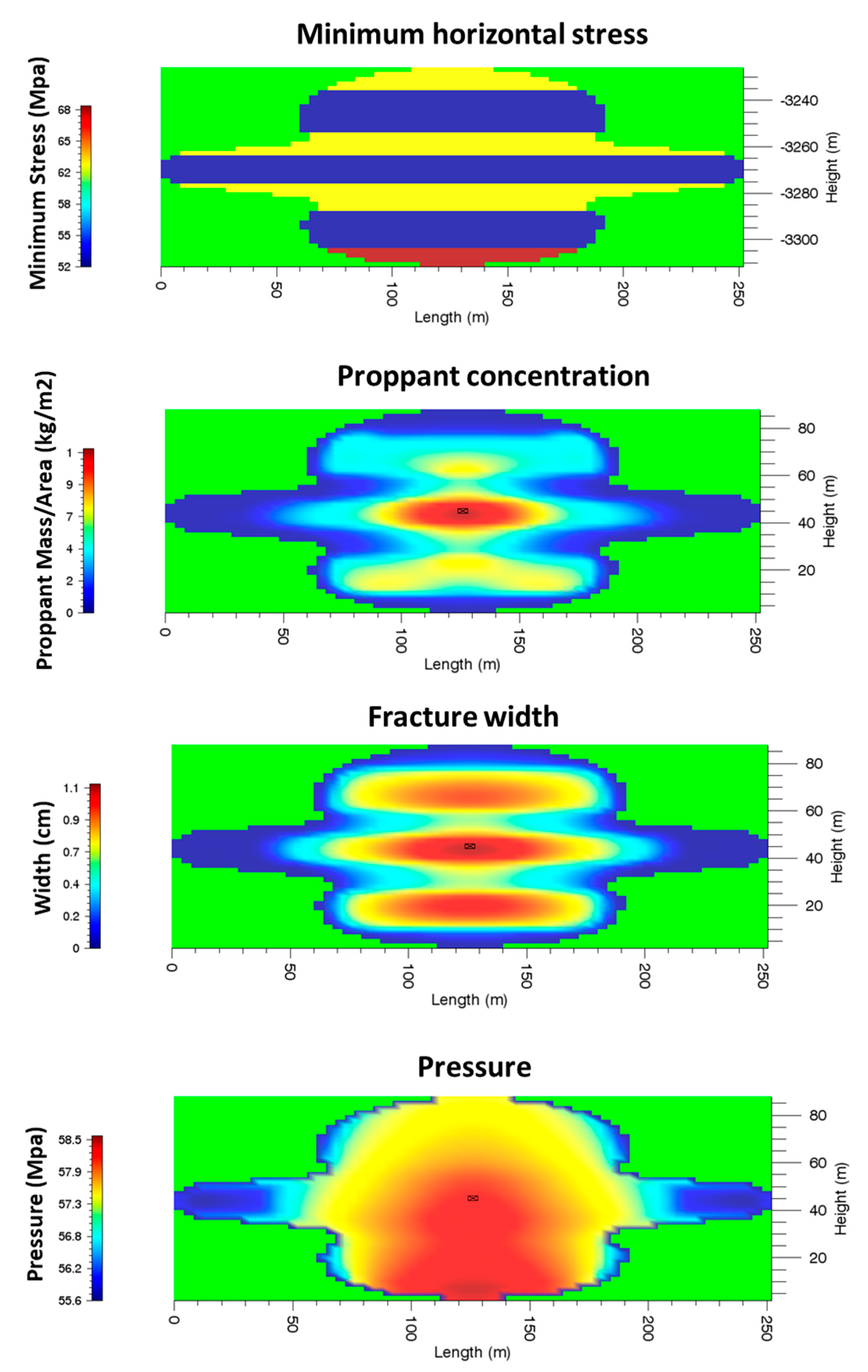
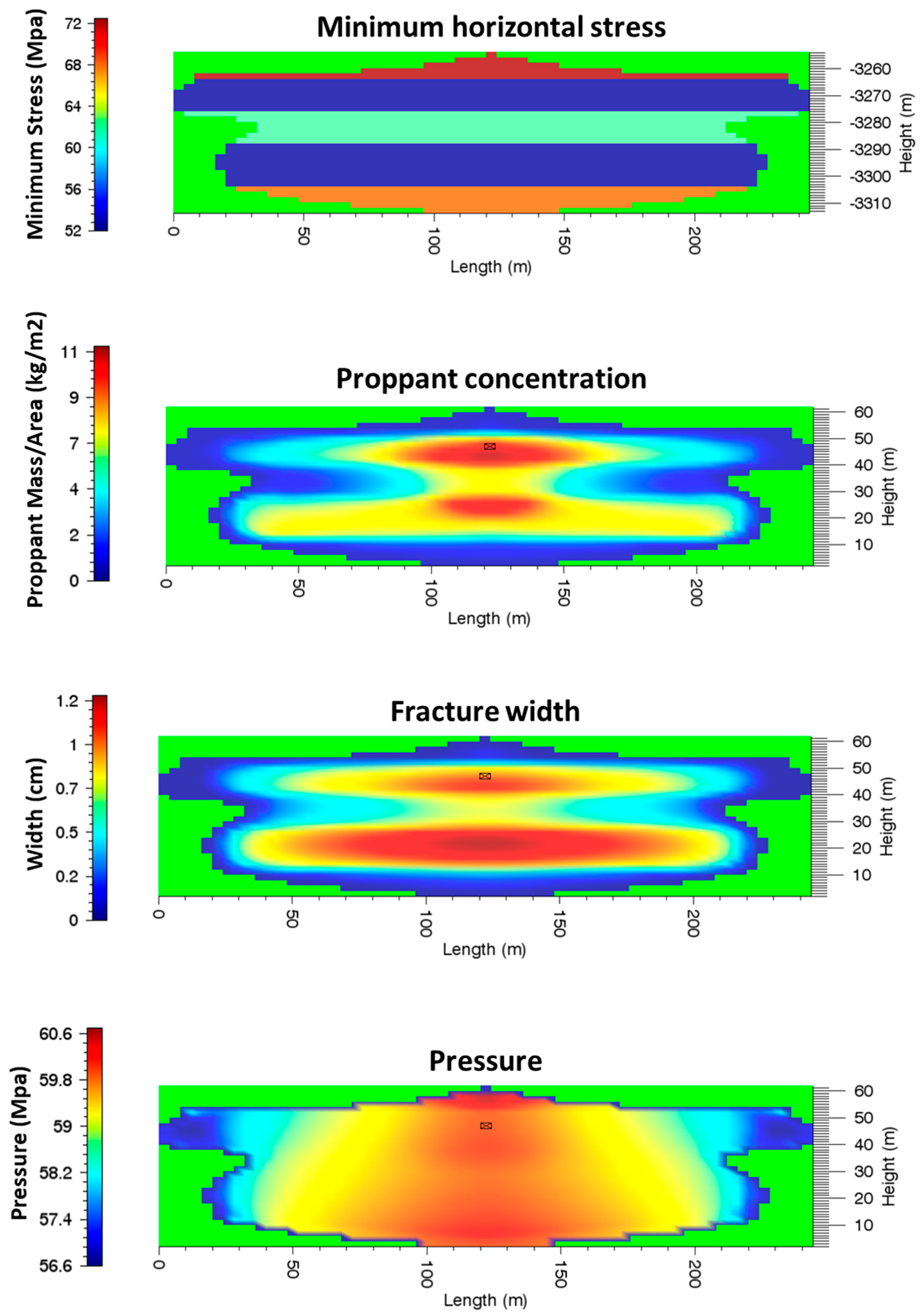
The stress profile and simulation results of Case 1 to Case 5 are shown in
Figure 12,
Figure 13,
Figure 14,
Figure 15 and
Figure 16, respectively. By comparing the results of Case 1 to 3, when the stress contrast between the shale interlayer and the tight sandstone layer is 6 MPa, the thickness of the neighboring shale interlayers should be at least 20 m to prevent the fracture from penetrating. This phenomenon is partly because the fracture toughness values of shale and tight sandstone in this reservoir are close to each other. It should be noted that, although the fracture propagates through the shale layers, the shale layers are not well-propped, because of the higher stress in these layers. The higher stress in the caprock layer will limit the height growth of the fracture, causing the fracture to be longer given the same amount of injected fluids. Meanwhile, the permeability of the formation plays an important role. When the permeability of the formation is higher, there are more fluids leaked off into the reservoirs. The loss of fluids in the fracture leads to higher viscosity of the proppant-bearing fluids, so that the proppant cannot be transported to certain layers. This phenomenon was largely ignored in the existing literature and we have used numerical experiments to examine it.
Compared to Cases 1 to 3, the minimum principal stress of Case 4 and Case 5 is higher, while the shale interlays are thinner, resulting in a different fracture geometry and proppant distribution. The thickness of the upper shale layers and the lower shale layer in Case 4 reduces to 10 m and 12 m, while the minimum principal stress of the shale layers increases. Although the upper and lower sandstone layer can be fractured, the fracture in the two layers is not long, as shown by the results.
5.2. Numerical Study of Multiple Fractures with Realistic Frictions
In this session, we present the numerical study of the simultaneous propagation of three fractures. The fractures are initiated from three neighboring perforations that locate 15 m from each other on a horizontal well (See
Figure 17). The horizontal well is drilled within a sandstone layer sandwiched by two shale layers (caprocks).
The rock properties used in this case are the same as those used in
Section 4.2, shown in
Table 5, except that the minimal principal stress of the sandstone layer and the shale layer is 52 MPa and 62 MPa, respectively. The pumping schedule is listed in
Table 7. We assume that all the three perforations are open; therefore, fractures can grow simultaneously.
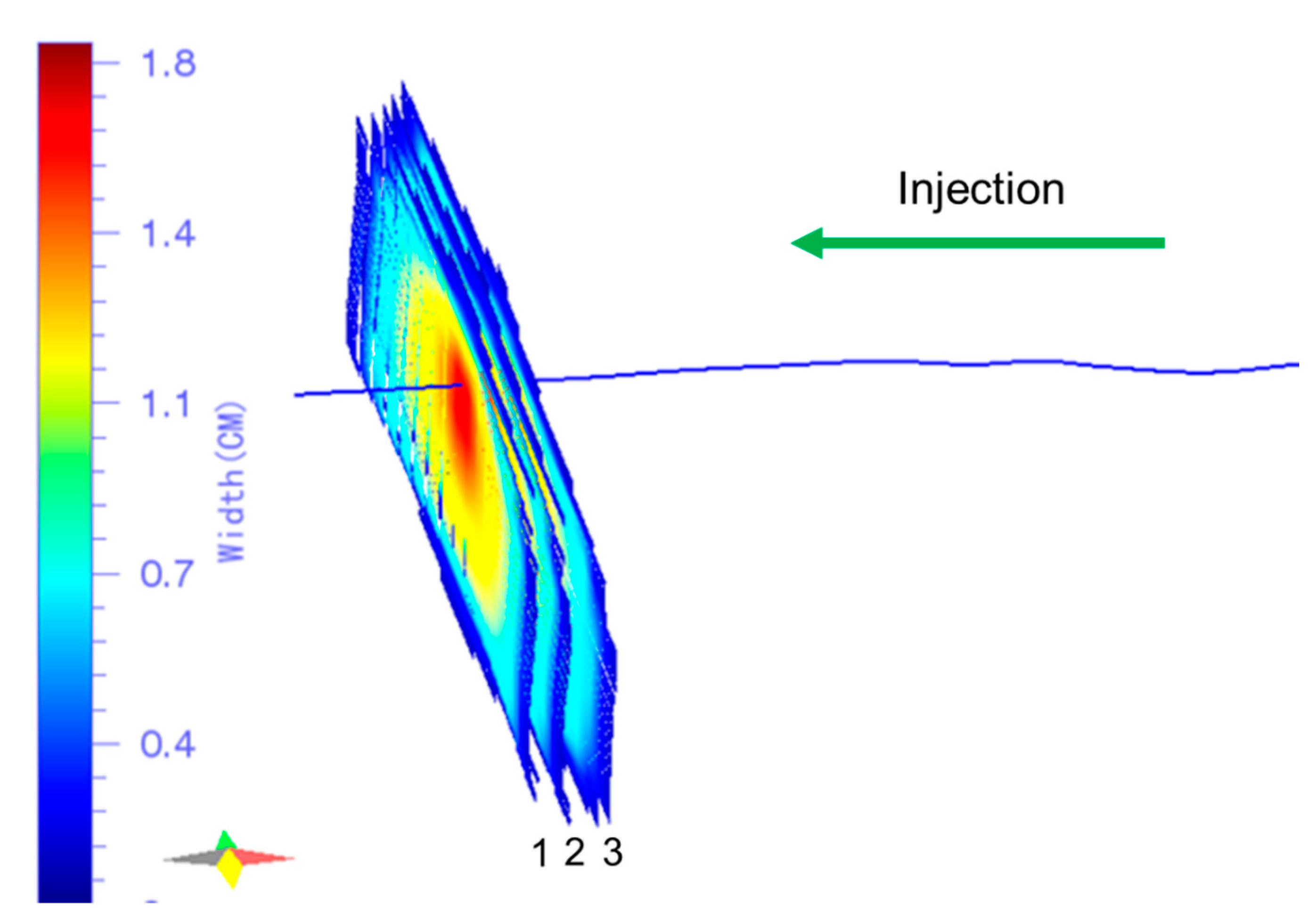
We use FracCSM to simulate this case and take the stress shadow effect into consideration. In this case, the friction along the wellbore is no more ignored. The 3D view of the resulting three fractures is shown in
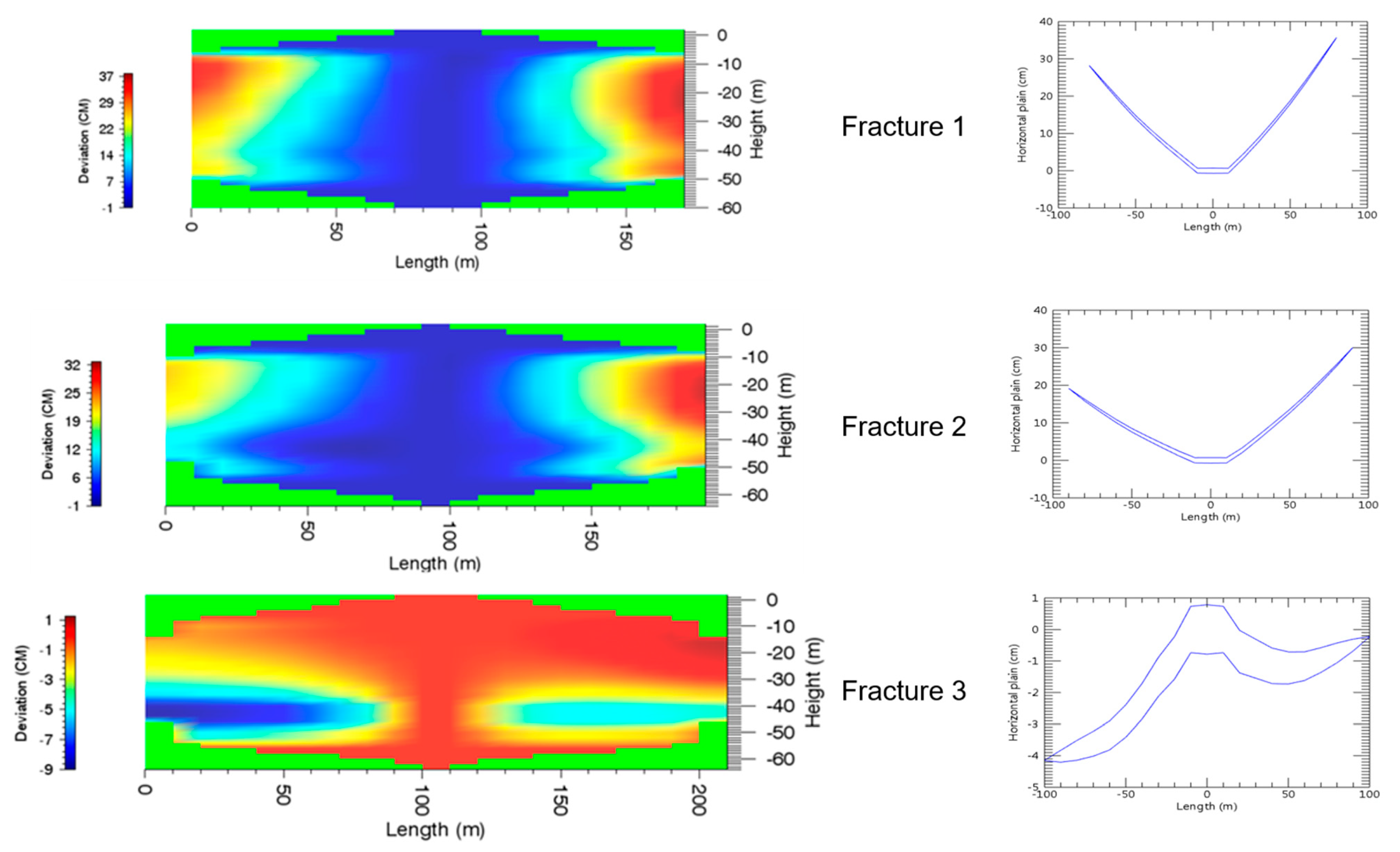
Figure 18. The deviation profiles of the three fractures are shown in
Figure 19. According to the results, with realist frictional force taken into consideration, the multiple simulated fractures are not symmetric, not like that observed in [
21,
49]. Fracture 3 is longer than Fracture 1 and Fracture 2, because it is in the upstream direction of the injected slurry. The slurry that flows into Fracture 3 has relatively higher energy. This also results in Fracture 3 having less deviation. The comparison of the fracture length with and without the friction within the wellbore is shown in
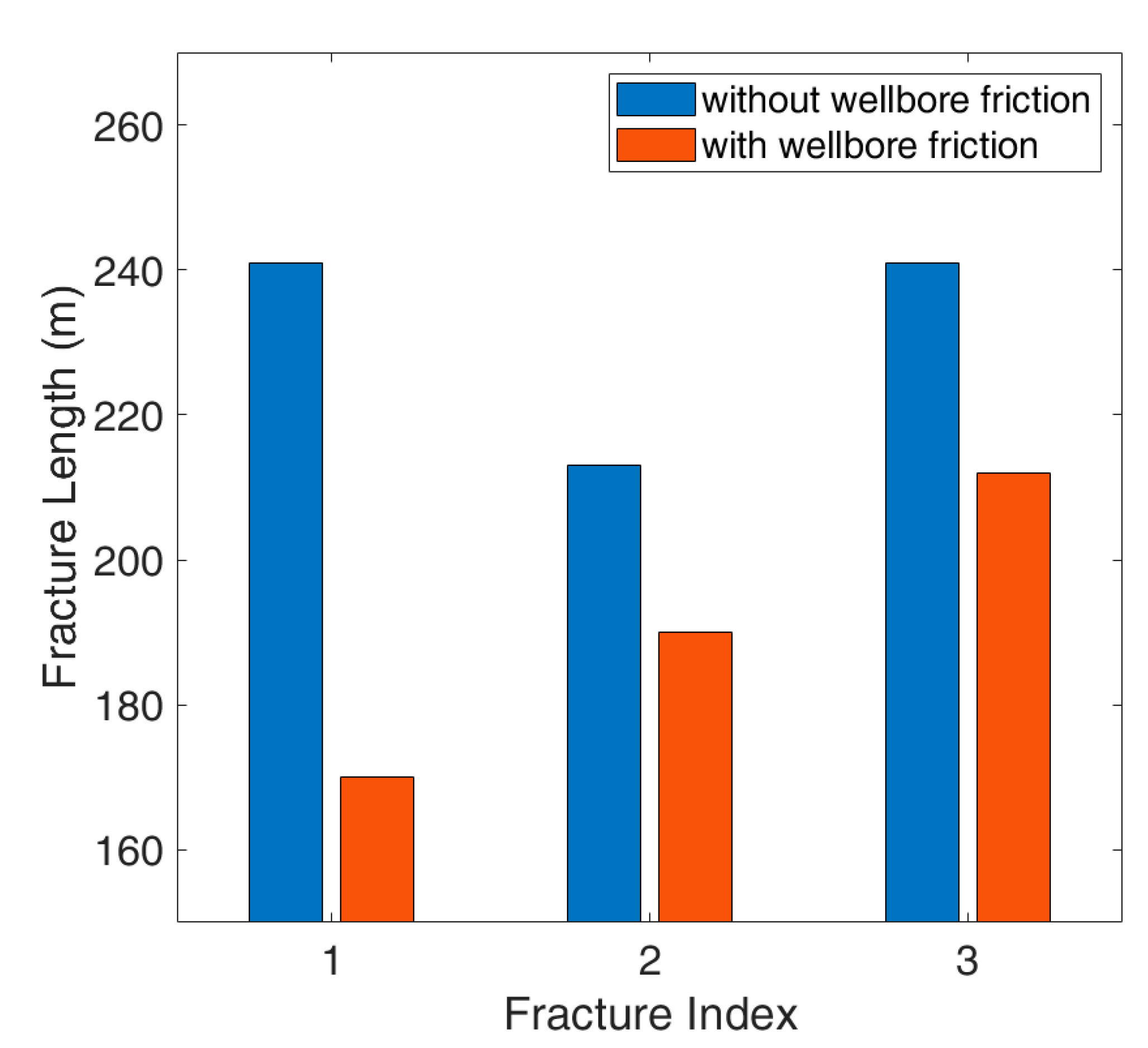
Figure 20, according to which the frictional loss plays an important role in the propagation of multiple fractures.
5.3. Field Application Results
The real-time simulation module of FracCSM has been successfully applied in Sulige gas field, a tight sandstone gas field in Changqing Reservoir, China.
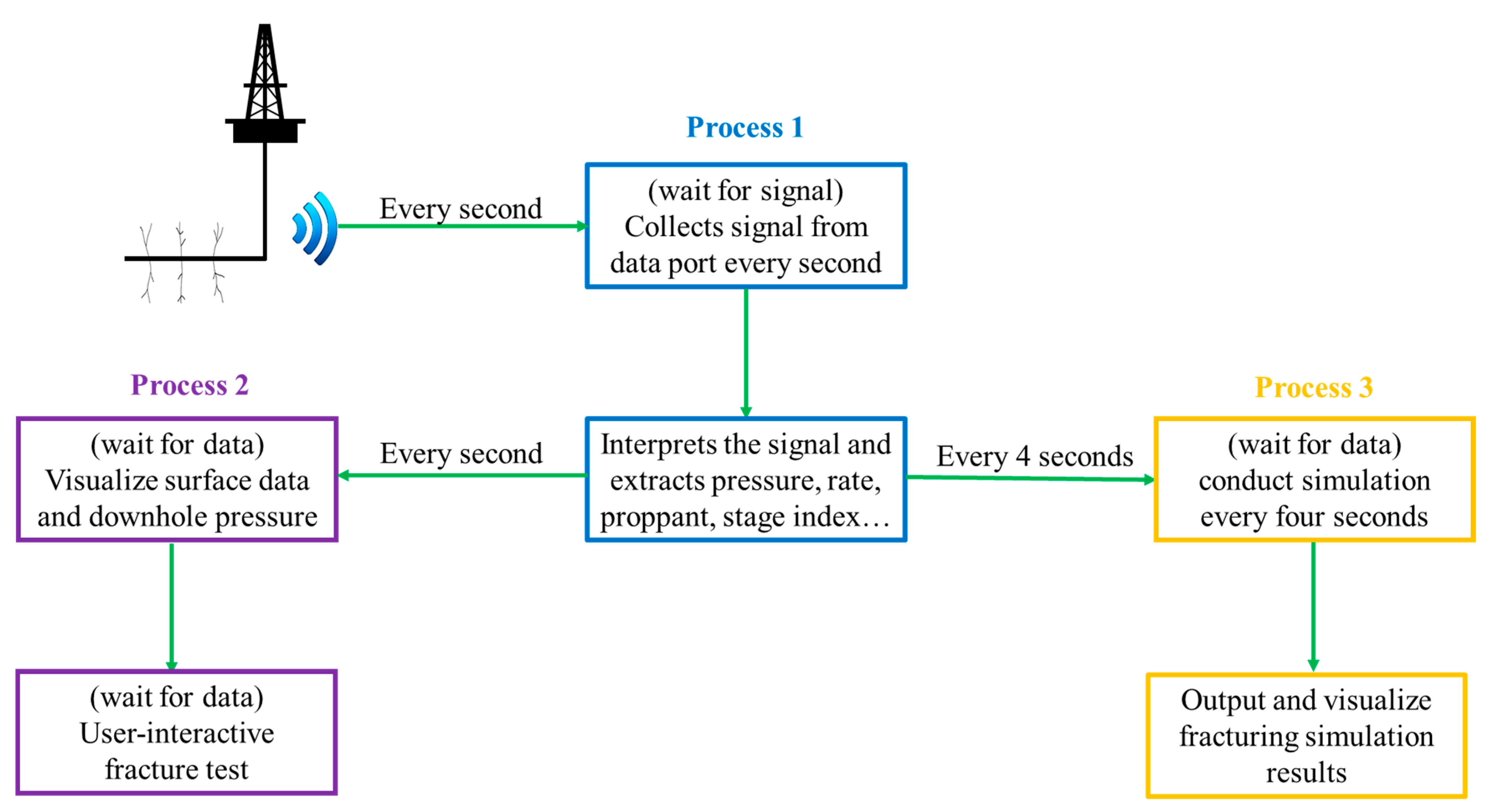
The hydraulic fracturing facility emits signals every second. The signal is passed to FracCSM through an RS232 data port. FracCSM picks up and interprets the signal to obtain the real-time injection rate, surface pressure, stage index and temperature.
The type of the proppant and the fluid used within each stage is determined by a pre-set pumping schedule input by the user. FracCSM then searches in the database for the properties of the proppant and the fluid. Based on the collected real-time data, FracCSM conducts simulation every four seconds and updates the fracture geometry in the user interface.
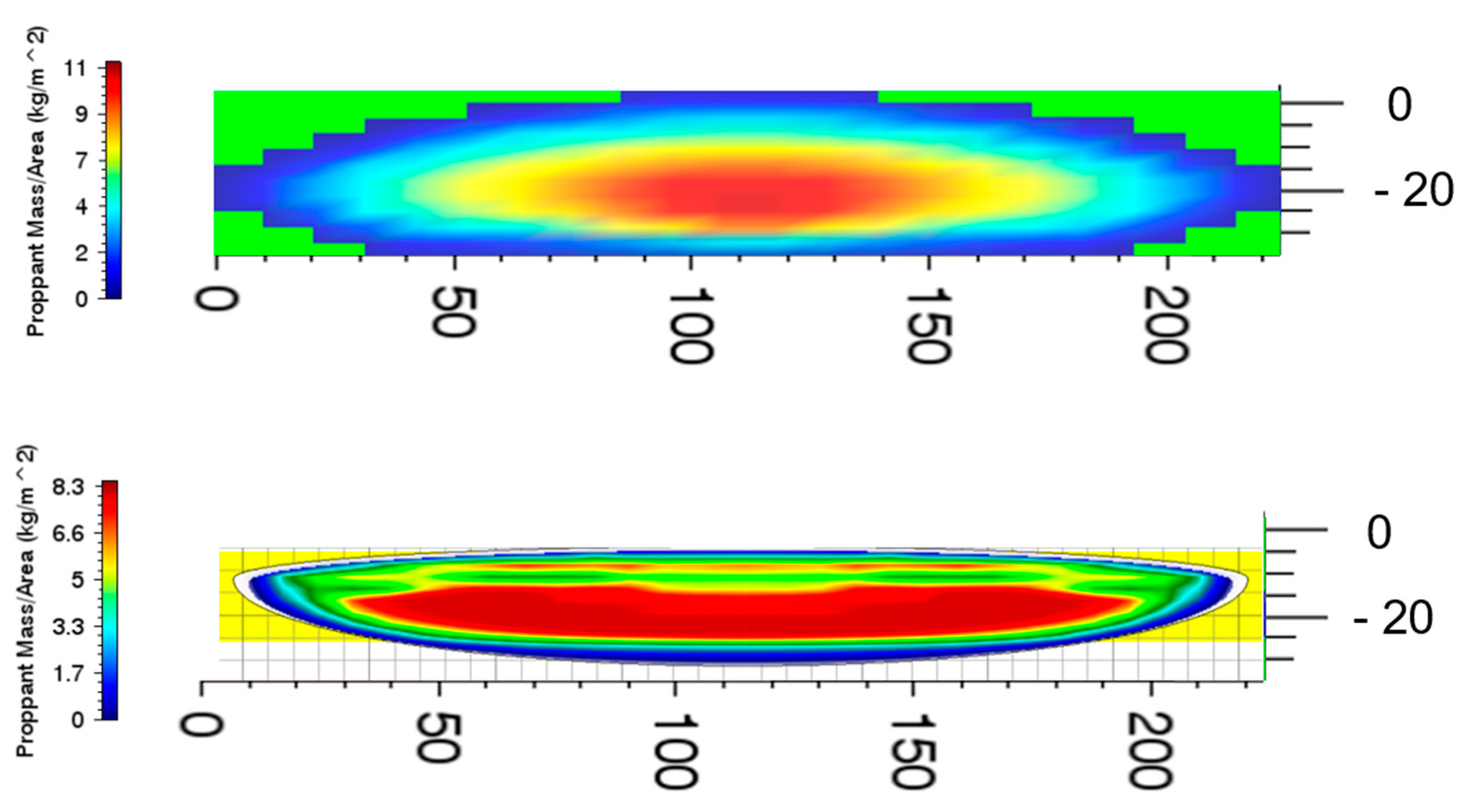
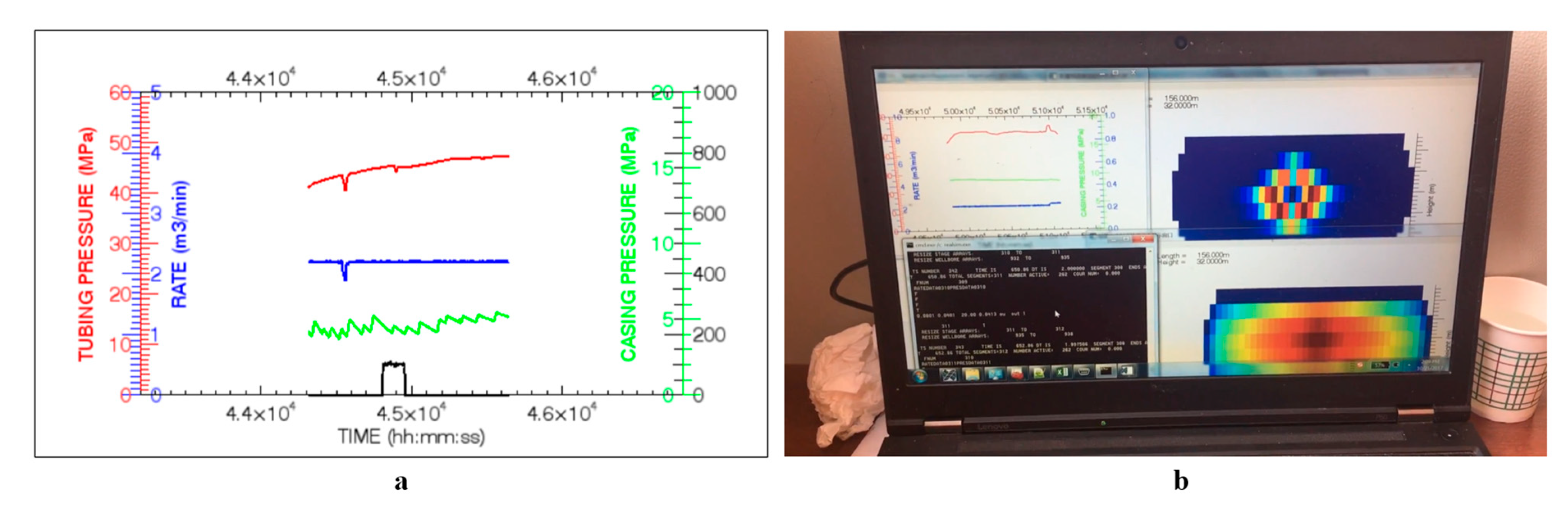
FracCSM has been successfully applied to 8 wells in Sulige gas field. The grid block dimension used is 2 m by 1 m. The time lag between the simulation and downhole operations is less than 2 s, which guarantees the early detection of screen-out. For one of the wells, the recorded surface data profile as real-time visualization of the fracture geometry of a slug of proppant is shown in
Figure 21. According to the figure, FracCSM captures the transient variation of fracture geometry as well as the variation of proppant distribution. The corresponding video has been uploaded as a
Supplementary Material of this paper.
The results indicate that FracCSM is able to conduct real-time fracturing simulation smoothly and accurately. Moreover, the net pressure predicted by FracCSM matches real observations well.
5.4. Discussion
We have successfully applied the developed program to both synthetic and real-world cases, which demonstrates the accuracy as well as the flexibility of the proposed approach. Through the numerical experiments, we found that:
The wellbore friction has a considerable impact on the hydraulic length of the fracture.
The stress interference effect as well as the leak-off effect both affect the propped length of the fracture, via affecting the fracture width and the proppant-carrying capability of the slurry.
The multi-process framework shows sound flexibility in dealing with real-time simulations.
In addition to hydraulic fracturing in tight reservoirs, our program also has the potential to be applied to the stimulation of geothermal reservoirs. Moreover, the multi-process framework can also be utilized in other engineering areas where the simulation engine needs to interact with real-time signals.
Admittedly, our program still possesses certain limitations. First of all, our program cannot deal with the interaction between hydraulic fractures with pre-existing natural fractures/joints. Secondly, the proppant transport model is empirical. Recent research [
52] has shown that the proppant transport within hydraulic fractures also has the bridging effect. Thirdly, the speed of the program has room to improve. We are working on the parallelization of the simulation engine.
6. Summary and Conclusions
In this work, we have developed a comprehensive simulator FracCSM for practical simulation of hydraulic fracturing operations. This simulator is based on an Integrated Finite Difference and Discontinuous Displacement Method and has been validated by both research code and commercial software. We have formulated a comprehensive model for the mass/energy transport in the wellbore and inside the fracture, including the proppant settling, fluid leak-off and frictional loss effect. We have developed a novel framework to combine IFD and DDM, which suitably takes the advantages of each method. The combined algorithm avoids the discretization of the entire reservoir, which significantly improves its computational speed, enabling it to conduct real-time simulation.
From the numerical study, we can draw the following conclusions:
Stress offset along with permeability distribution not only affects the fracture propagation, but also the proppant distribution inside the fracture plane. Ignoring the impact of proppant concentration on the fluid flow may lead to overestimation of the propped height.
The energy loss induced by friction and heat conduction within the wellbore and the formation plays an important role in the simulation of hydraulic fractures. The mass/energy transport must be comprehensively simulated to obtain realistic resutls of single as well as multiple fracture propagation.
In general, the hydraulic fracturing operations involve complex thermal-hydraulic-mechanical processes, and thus multiphysical simulation techniques are crucial in real practice.
Our program and its results have already been adopted by the users to guide the hydraulic fracturing operations in Sulige gas field. Our program can be further applied to the recovery of unconventional oil/gas reservoirs [
53,
54].