Effects of Wave Height, Period and Sea Level on Barred Beach Profile Evolution: Revisiting the Roller Slope in a Beach Morphodynamic Model
Abstract
1. Introduction
2. Methodology
2.1. Process-Based Numerical Model
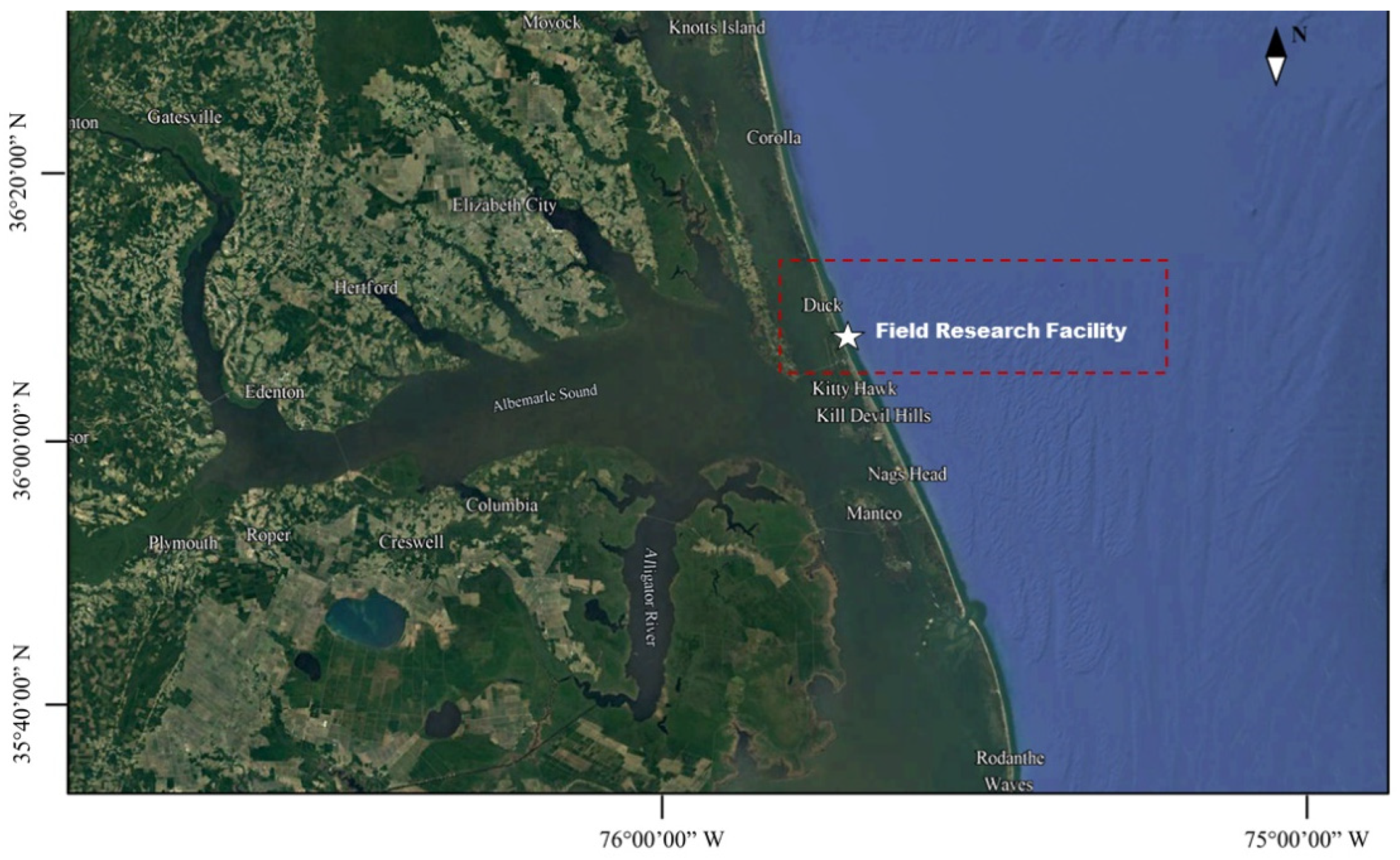
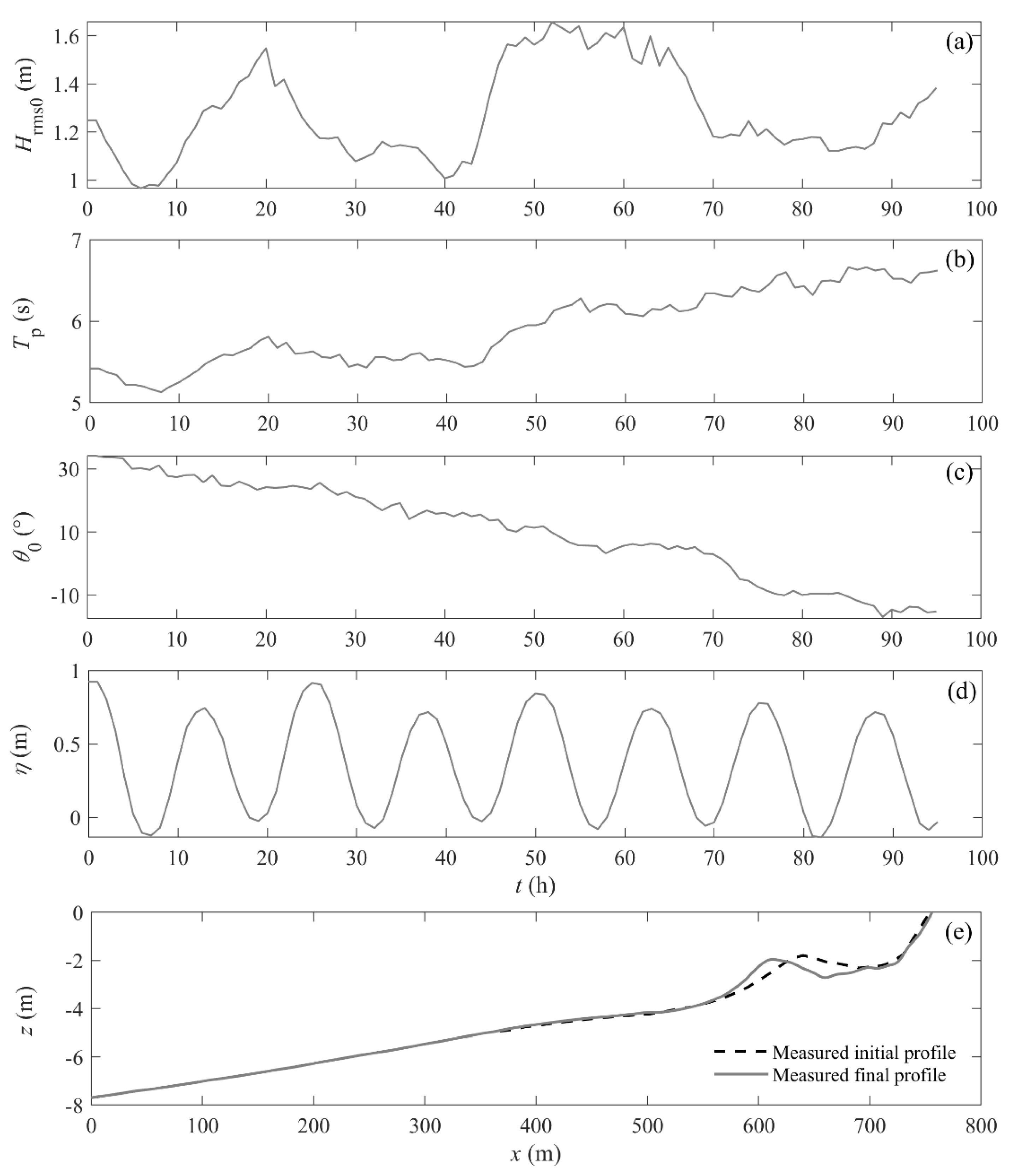
2.2. Field Data
3. Results and Discussion
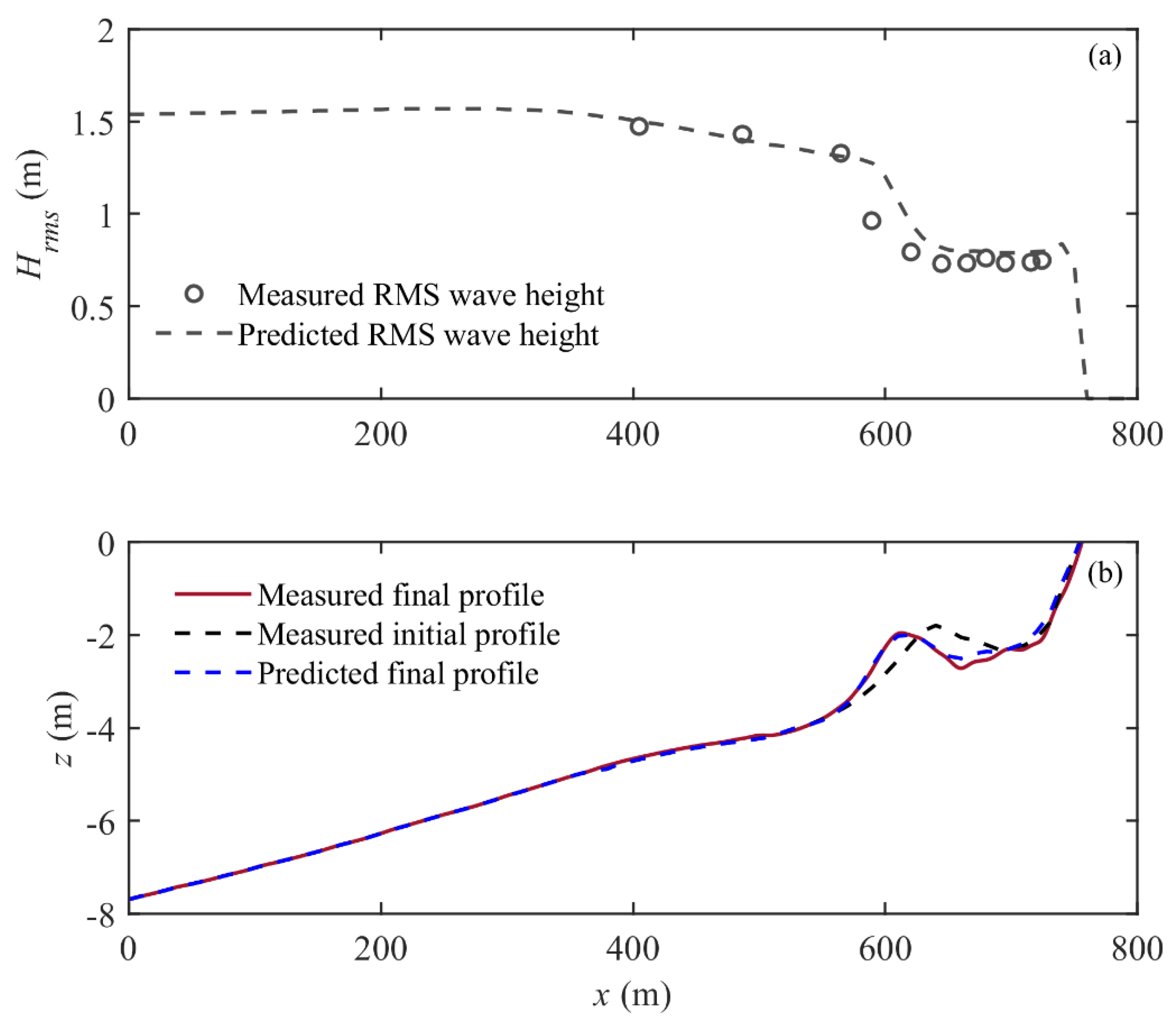
3.1. Model Calibration with Constant Roller Slope
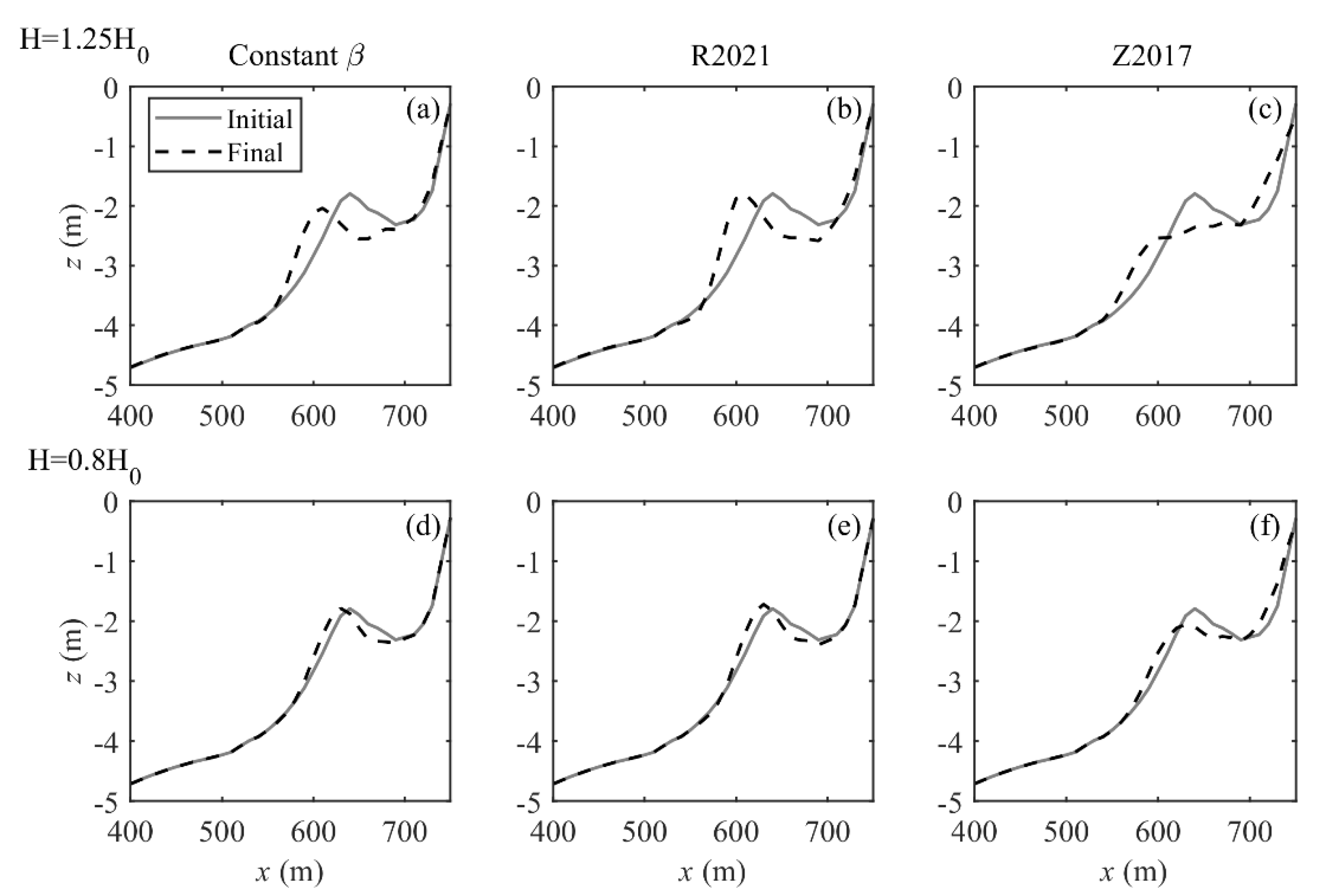
3.2. Model Calibration with Varying Roller Slope
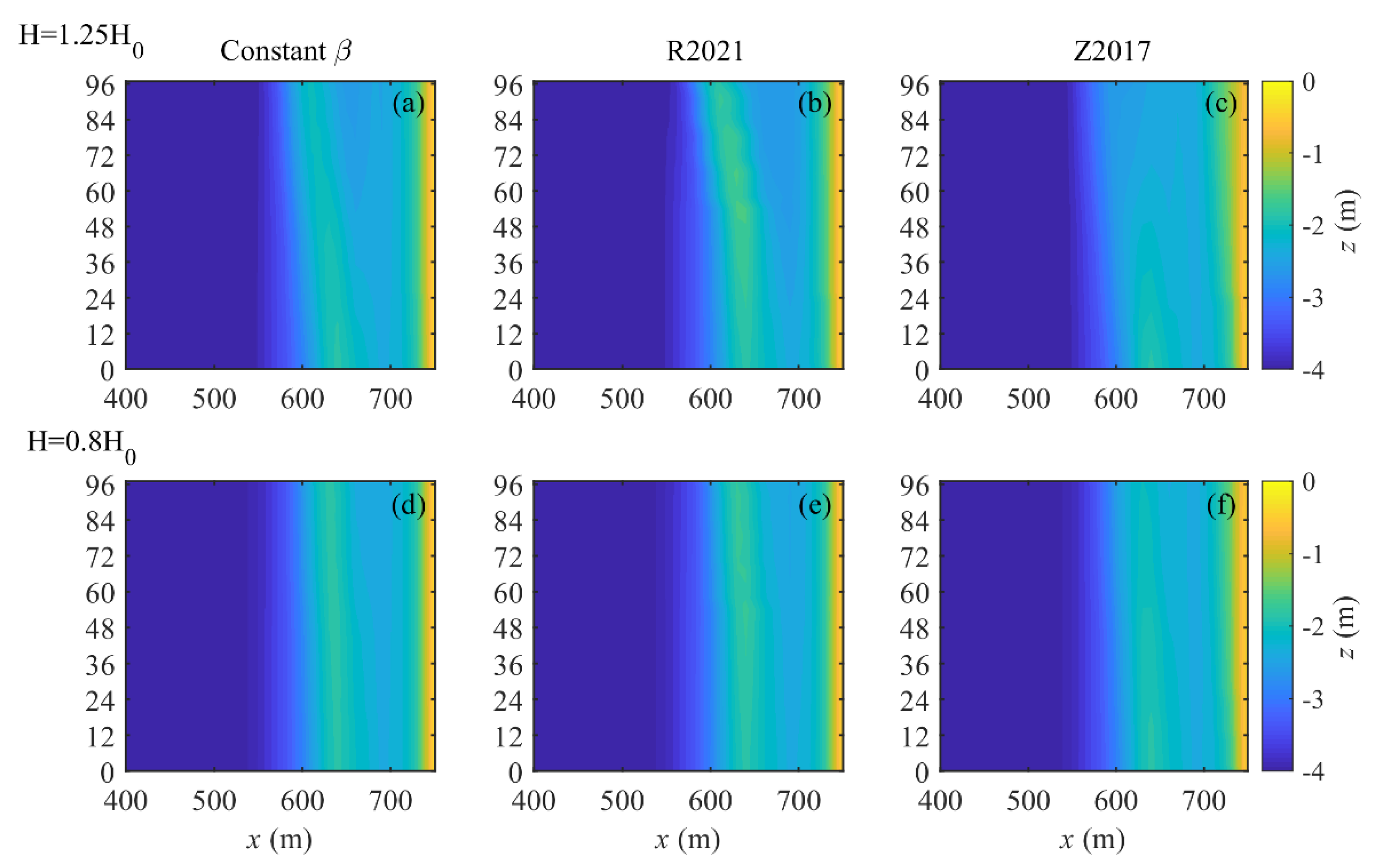
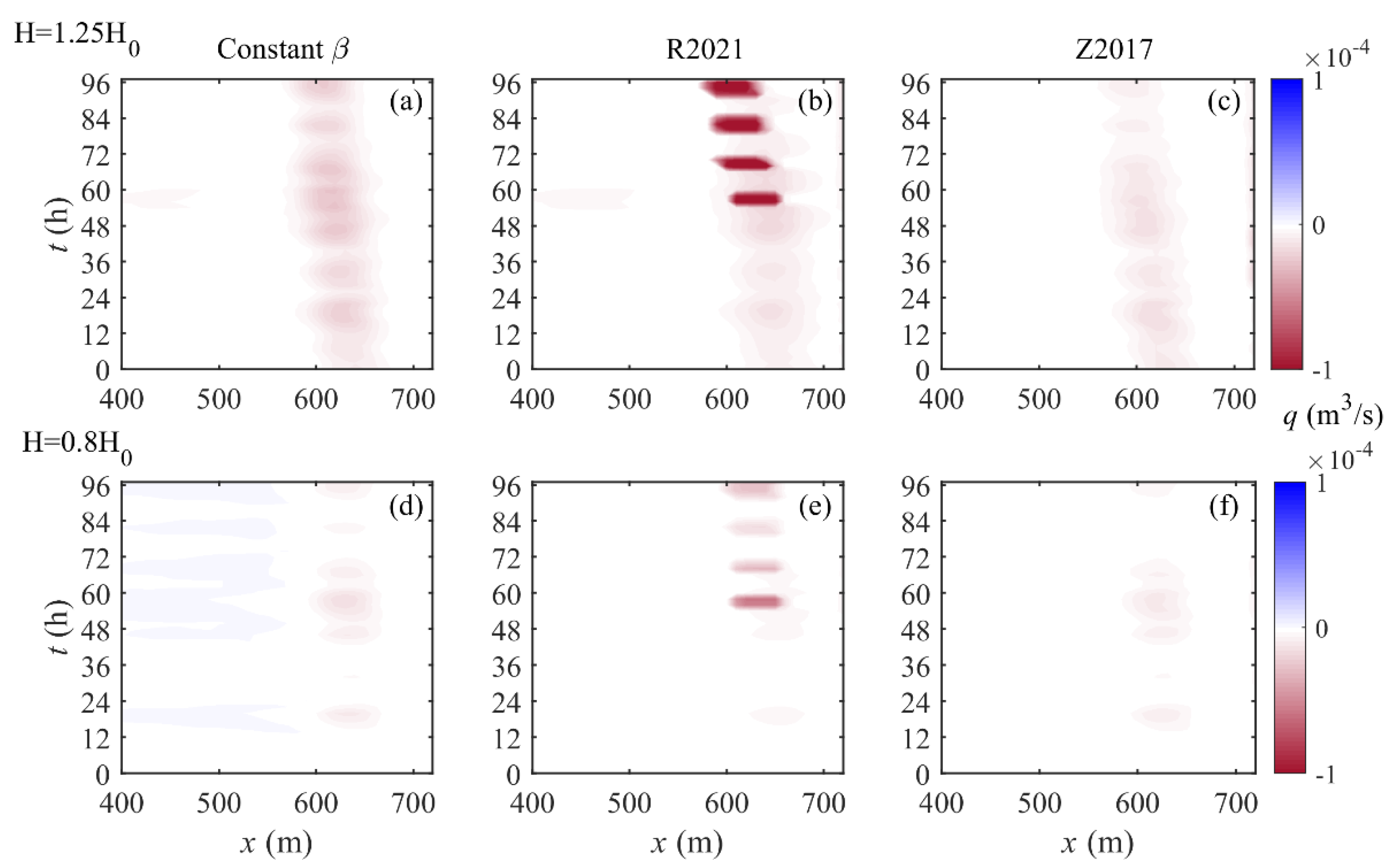
3.3. Effect of Wave Height on Sandbar Evolution
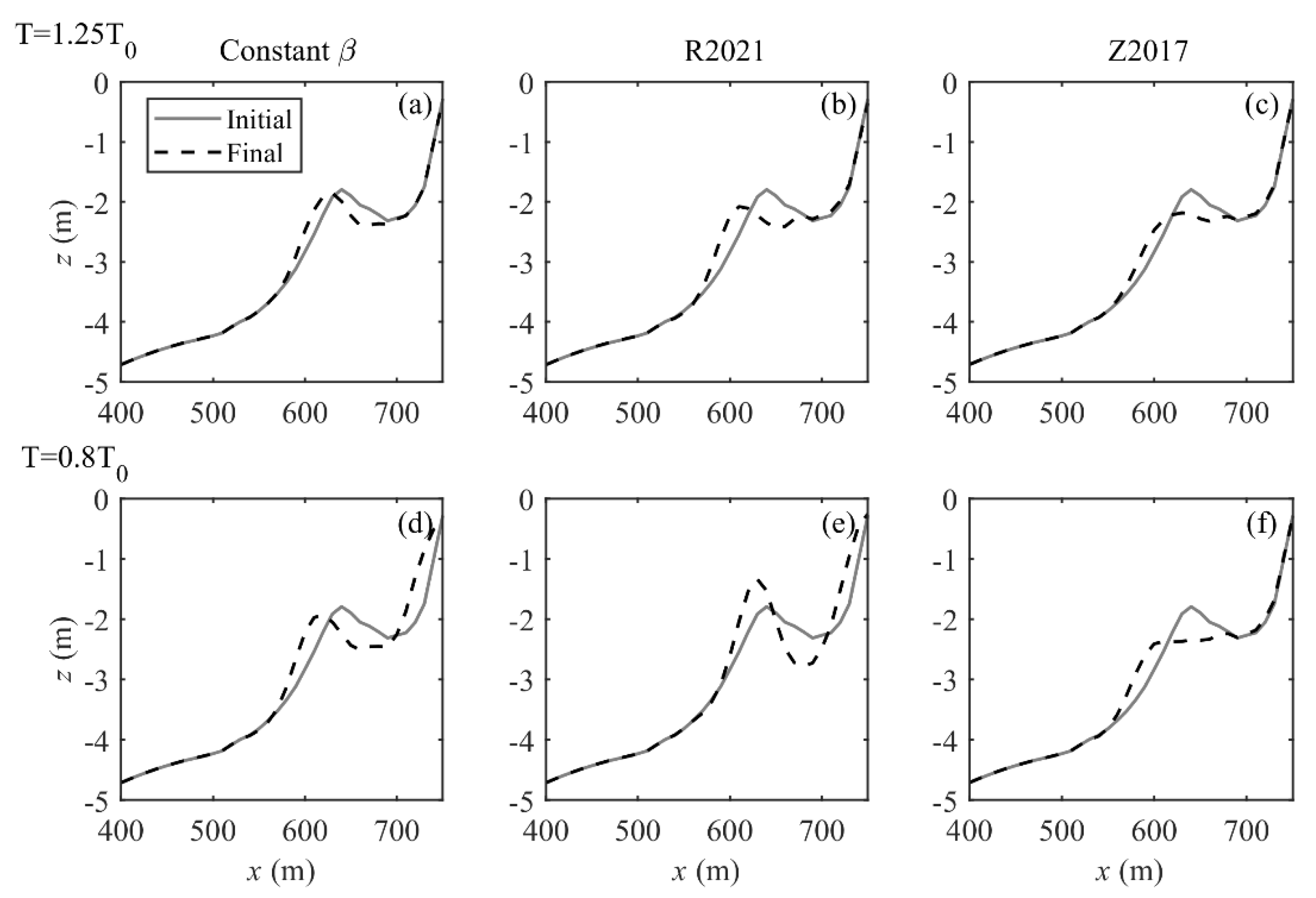
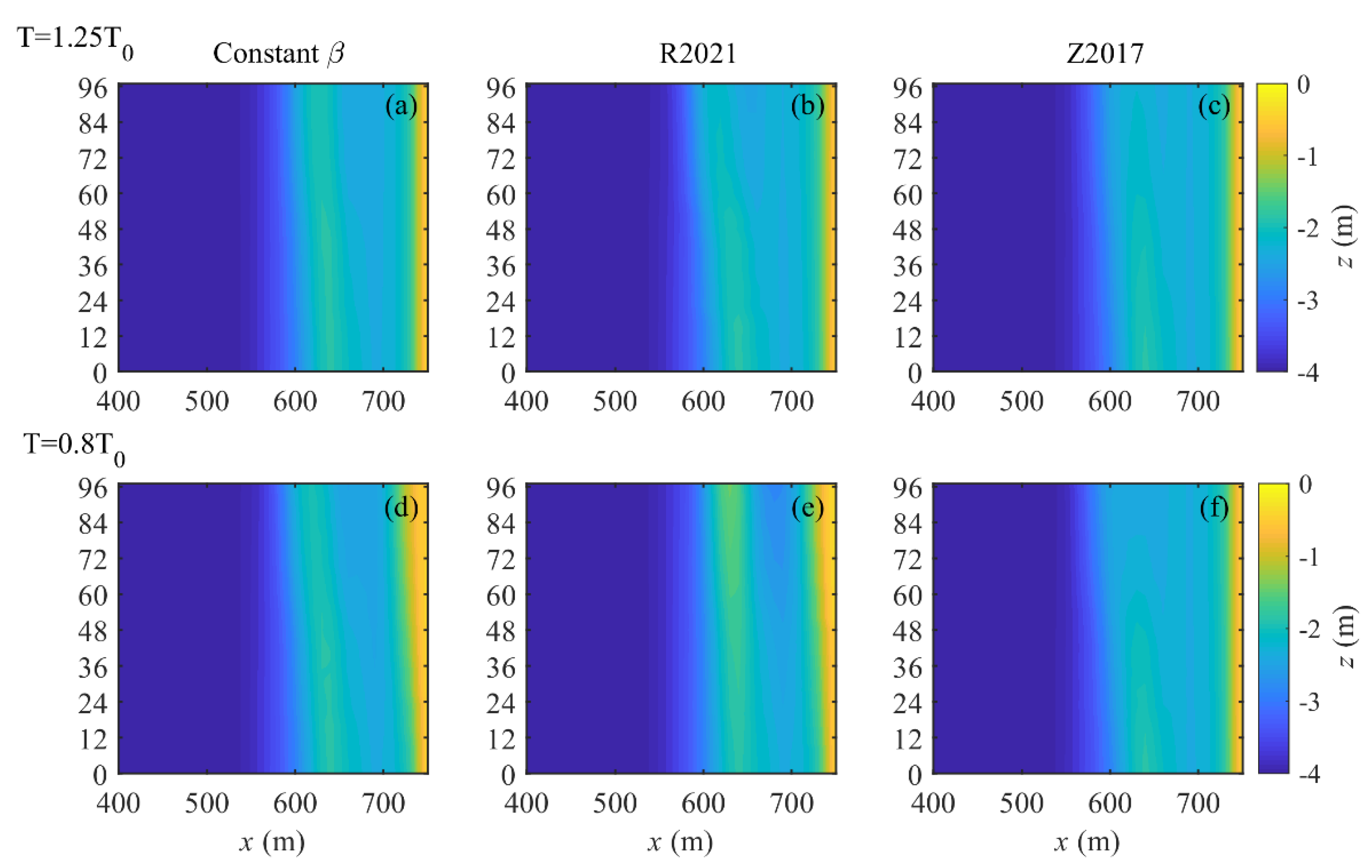
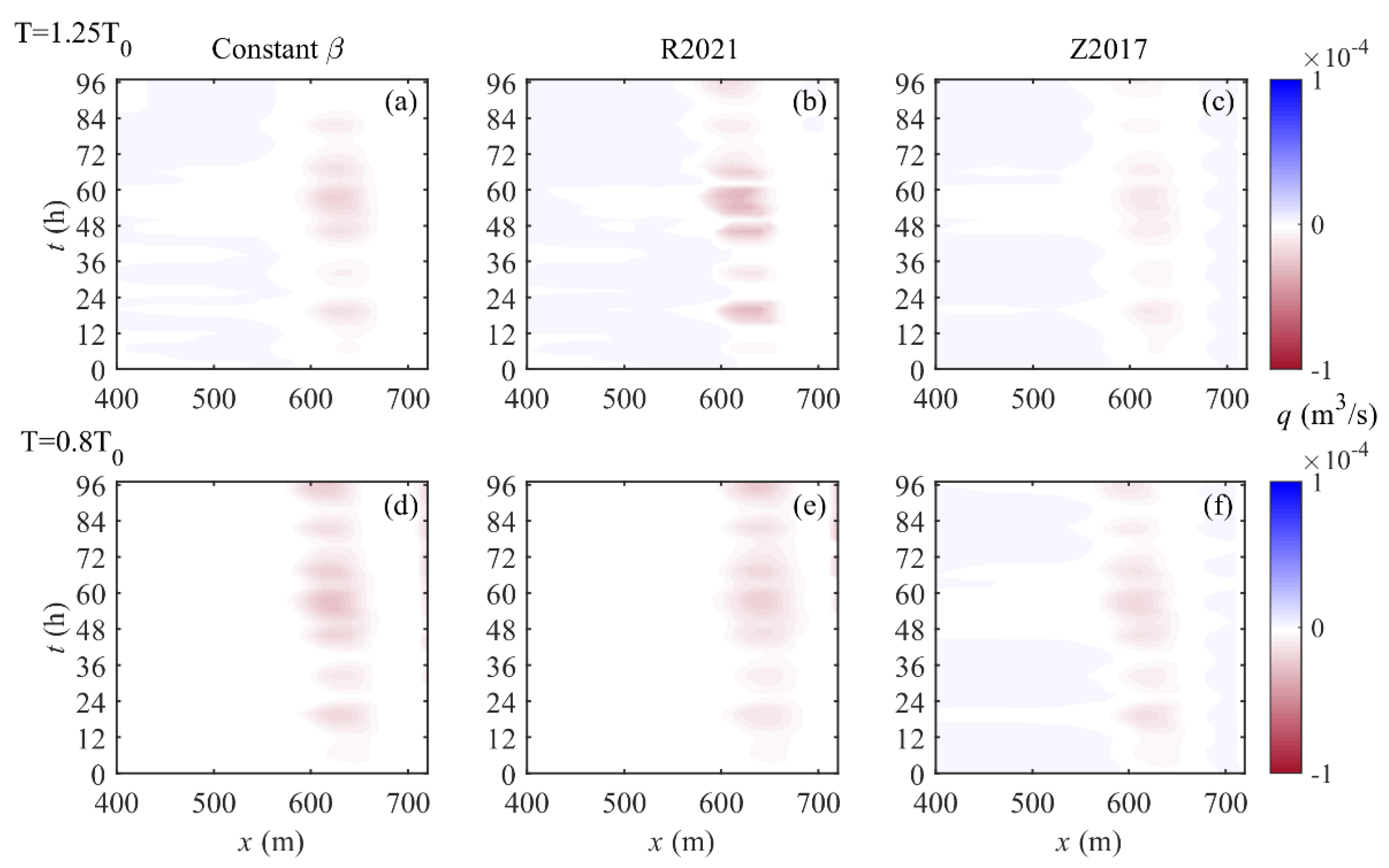
3.4. Effect of Wave Period on Sandbar Migration
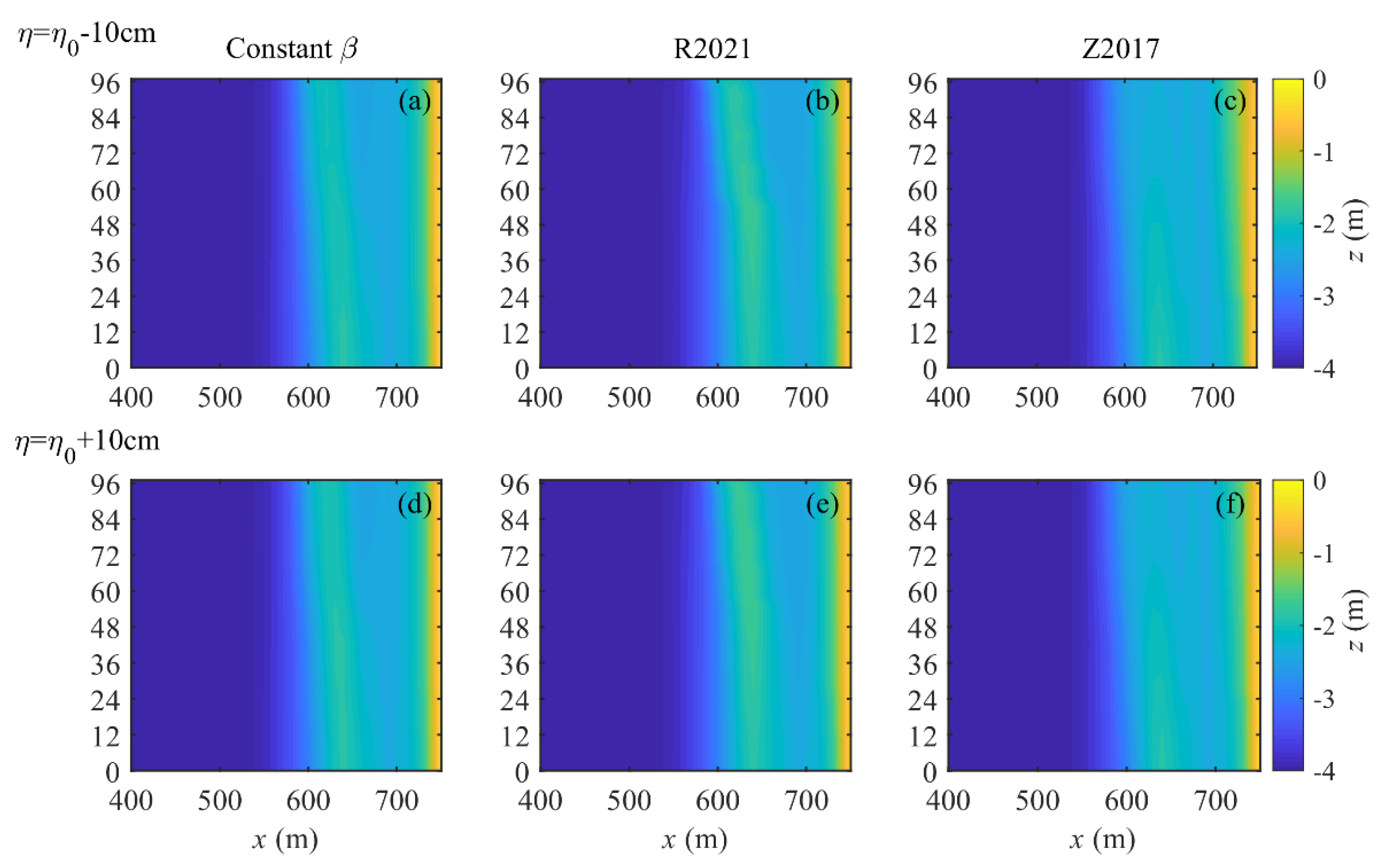
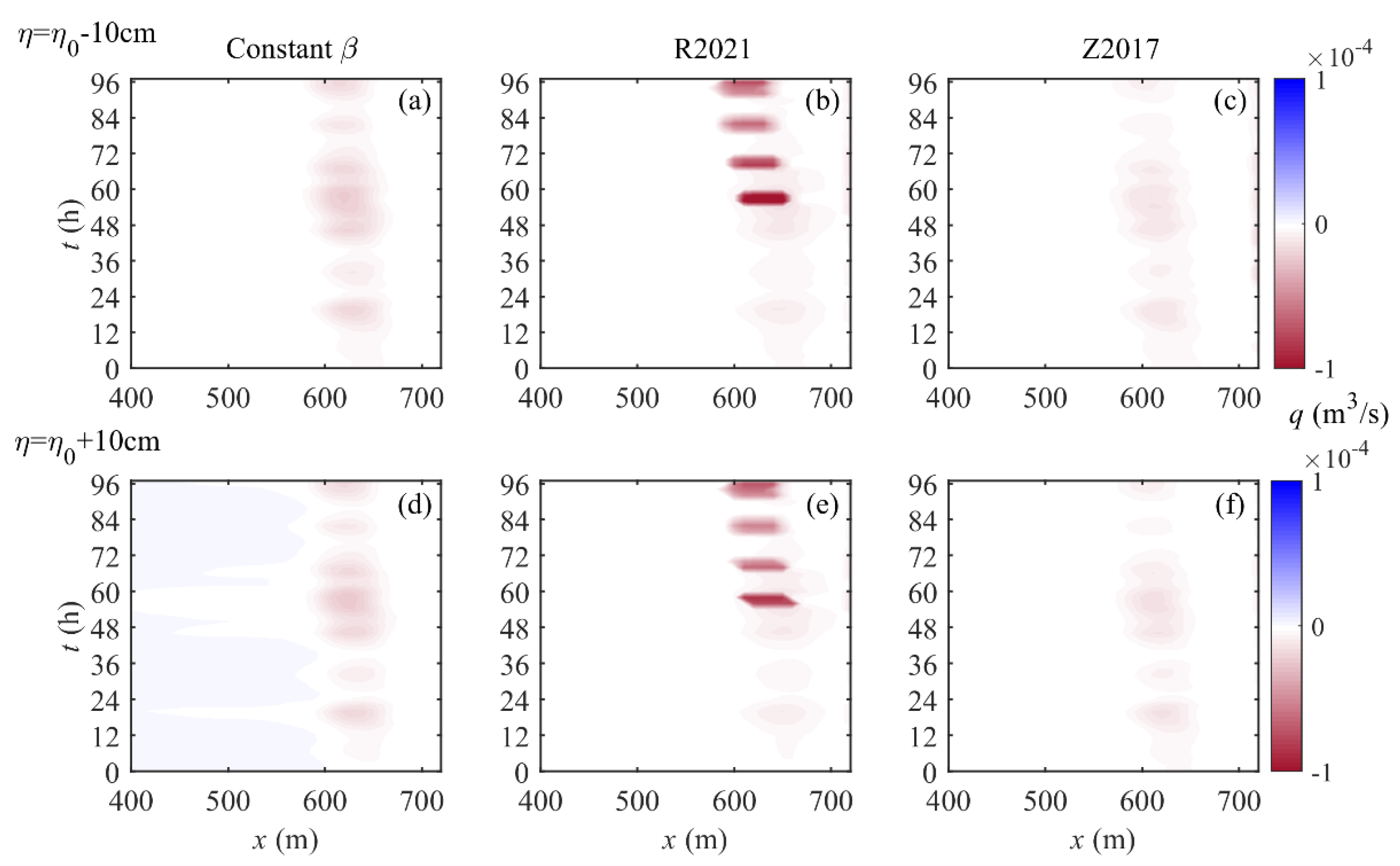
3.5. Effect of Sea Level on Sandbar Migration
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cai, F.; Cao, C.; Qi, H.; Su, X.; Lei, G.; Liu, J.; Zhao, S.; Liu, G.; Zhu, K. Rapid Migration of Mainland China’s Coastal Erosion Vulnerability Due to Anthropogenic Changes. J. Environ. Manag. 2022, 319, 115632. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhang, J.; Zheng, J. Coastal Hydrodynamics and Morphodynamics, 2nd ed.; China Communications Press: Beijing, China, 2022. [Google Scholar]
- Li, Y.; Zhang, C.; Chen, D.; Zheng, J.; Sun, J.; Wang, P. Barred Beach Profile Equilibrium Investigated with a Process-Based Numerical Model. Cont. Shelf Res. 2021, 222, 104432. [Google Scholar] [CrossRef]
- Wang, P.; Davis, R.A. A Beach Profile Model for a Barred Coast: Case Study from Sand Key, West-Central Florida. J. Coast. Res. 1998, 14, 981–991. [Google Scholar]
- Jacobsen, N.G.; Fredsøe, J. Cross-Shore Redistribution of Nourished Sand near a Breaker Bar. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 125–134. [Google Scholar] [CrossRef]
- Lesser, G.; Roelvink, J.; van Kester, J.; Stelling, G. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; Van Dongeren, A.; van Thiel De Vries, J.; McCall, R.; Lescinski, J. Modelling storm impacts on beaches, dunes and barrier islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- Ruessink, G.; Kuriyama, Y.; Reniers, A.; Roelvink, J.A.; Walstra, D.J.R. Modeling cross-shore sandbar behavior on the timescale of weeks. J. Geophys. Res. Atmos. 2007, 112, 1–15. [Google Scholar] [CrossRef]
- Tong, L.; Liu, P.L.F. Transient Wave-Induced Pore-Water-Pressure and Soil Responses in a Shallow Unsaturated Poroelastic Seabed. J. Fluid Mech. 2022, 938, A36. [Google Scholar] [CrossRef]
- Zhang, J.; Larson, M. A Numerical Model for Offshore Mound Evolution. J. Mar. Sci. Eng. 2020, 8, 160. [Google Scholar] [CrossRef]
- Zheng, J.; Zhang, C.; Demirbilek, Z.; Lin, L. Numerical Study of Sandbar Migration under Wave-Undertow Interaction. J. Waterw. Port Coast. Ocean Eng. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Reniers, A.; Thornton, E.; Stanton, T.; Roelvink, J. Vertical flow structure during Sandy Duck: Observations and modeling. Coast. Eng. 2004, 51, 237–260. [Google Scholar] [CrossRef]
- Rafati, Y.; Hsu, T.-J.; Elgar, S.; Raubenheimer, B.; Quataert, E.; van Dongeren, A. Modeling the hydrodynamics and morphodynamics of sandbar migration events. Coast. Eng. 2021, 166, 103885. [Google Scholar] [CrossRef]
- Walstra, D.J.R.; Mocke, G.P.; Smit, F. Roller Contributions as Inferred from Inverse Modelling Techniques. In Coastal Engineering Proceedings; Amer Society of Civil Engineers: Orlando, FL, USA, 1996; pp. 1205–1218. [Google Scholar]
- Wang, A.; Wu, X.; Bi, N.; Ralston, D.K.; Wang, C.; Wang, H. Combined Effects of Waves and Tides on Bottom Sediment Resuspension in the Southern Yellow Sea. Mar. Geol. 2022, 452, 106892. [Google Scholar] [CrossRef]
- Zhang, Y.; Hong, X.; Qiu, T.; Liu, X.; Sun, Y.; Xu, G. Tidal and wave modulation of rip current dynamics. Cont. Shelf Res. 2022, 243, 104764. [Google Scholar] [CrossRef]
- Chi, S.-H.; Zhang, C.; Sui, T.-T.; Cao, Z.-B.; Zheng, J.-H.; Fan, J.-S. Field observation of wave overtopping at sea dike using shore-based video images. J. Hydrodyn. 2021, 33, 657–672. [Google Scholar] [CrossRef]
- Zhang, J.; Larson, M.; Ge, Z.P. Numerical Model of Beach Profile Evolution in the Nearshore. J. Coast. Res. 2020, 36, 506. [Google Scholar] [CrossRef]
- Pan, Y.; Yin, S.; Chen, Y.P.; Yang, Y.B.; Xu, C.Y.; Xu, Z.S. An experimental study on the evolution of a submerged berm under the effects of regular waves in low-energy conditions. Coast. Eng. 2022, 176, 104169. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Cai, Y.; Xie, M.; Qi, H.; Wang, Y. Wave Dissipation and Sediment Transport Patterns during Shoreface Nourishment towards Equilibrium. J. Mar. Sci. Eng. 2021, 9, 535. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Dai, W.; Chen, D.; Sui, T.; Xie, M.; Chen, S. Laboratory investigation on morphology response of submerged artificial sandbar and its impact on beach evolution under storm wave condition. Mar. Geol. 2021, 443, 106668. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Q.; Zheng, J.; Demirbilek, Z. Parameterization of nearshore wave front slope. Coast. Eng. 2017, 127, 80–87. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Zheng, J.; Xie, M.; Shi, J.; Wang, G. Parametric modelling of nearshore wave reflection. Coast. Eng. 2021, 169, 103978. [Google Scholar] [CrossRef]
- Baldock, T.E.; Holmes, P.; Bunker, S.; Van Weert, P. Cross-Shore Hydrodynamics within an Unsaturated Surf Zone. Coast. Eng. 1998, 34, 173–196. [Google Scholar] [CrossRef]
- Thornton, E.B.; Guza, R.T. Transformation of Wave Height Distribution. J. Geophys. Res. 1983, 88, 5925–5938. [Google Scholar] [CrossRef]
- Janssen, T.T.; Battjes, J.A. A Note on Wave Energy Dissipation over Steep Beaches. Coast. Eng. 2007, 54, 711–716. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Cai, Y.; Shi, J.; Zheng, J.; Cai, F.; Qi, H. Parameterization of Nearshore Wave Breaker Index. Coast. Eng. 2021, 168, 103914. [Google Scholar] [CrossRef]
- Apotsos, A.; Raubenheimer, B.; Elgar, S.; Guza, R.T.; Smith, J.A. Effects of wave rollers and bottom stress on wave setup. J. Geophys. Res. 2007, 112, C02003. [Google Scholar] [CrossRef]
- Dally, W.R.; Brown, C.A. A modelling investigation of the breaking wave roller with application to cross-shore currents. J. Geophys. Res. 1995, 100, 24873–24883. [Google Scholar] [CrossRef]
- Dong, G.; Chen, H.; Ma, Y. Parameterization of Nonlinear Shallow Water Waves over Sloping Bottoms. Coast. Eng. 2014, 94, 23–32. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Chen, S.; Sui, T.; Chen, D.; Qi, H. Influence of Artificial Sandbar on Nonlinear Wave Transformation: Experimental Investigation and Parameterizations. Ocean Eng. 2022, 257, 111540. [Google Scholar] [CrossRef]
- Zheng, J.; Yao, Y.; Chen, S.; Chen, S.; Zhang, Q. Laboratory study on wave-induced setup and wave-driven current in a 2DH reef-lagoon-channel system. Coast. Eng. 2020, 162, 103772. [Google Scholar] [CrossRef]
- Feddersen, F.; Guza, R.T.; Elgar, S.; Herbers, T.H.C. Alongshore momentum balances in the nearshore. J. Geophys. Res. Ocean. 1998, 103, 15667–15676. [Google Scholar] [CrossRef]
- Gallagher, E.L.; Elgar, S.; Guza, R.T. Observations of Sand Bar Evolution on a Natural Beach. J. Geophys. Res. Ocean. 1998, 103, 3203–3215. [Google Scholar] [CrossRef]
- Long, C.E. Index and Bulk Parameters for Frequency-Direction Spectra Measured at CERC Field Research Facility, June 1994 to August 1995. Misc. Pap. CERC-96-6. 1996. Available online: https://onlinebooks.library.upenn.edu/webbin/book/lookupid?key=ha102348778 (accessed on 10 November 2021).
- Zhang, J.; Larson, M. Decadal-Scale Subaerial Beach and Dune Evolution at Duck, North Carolina. Mar. Geol. 2021, 440, 106576. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Chi, S.-H.; Yang, Y.-H.; Shi, J.; Sui, T.-T. Numerical test of scale relations for modelling coastal sandbar migration and inspiration to physical model design. J. Hydrodyn. 2022, 34, 700–711. [Google Scholar] [CrossRef]
- Zhao, S.H.; Cai, F.; Qi, H.S.; Zhu, J.; Zhou, X.; Lei, G.; Zheng, J.X. Contrasting sand-mud transition migrations of estuarine and bay beaches and their potential morphological responses. Geomorphology 2020, 365, 107243. [Google Scholar] [CrossRef]
- Zhao, S.H.; Qi, H.S.; Cai, F.; Zhu, J.; Zhou, X.; Lei, G. Morphological and sedimentary features of sandy-muddy transitional beaches in estuaries and bays along mesotidal to macrotidal coasts. Earth Surf. Process. Landf. 2020, 45, 1660–1676. [Google Scholar] [CrossRef]
- van Rijn, L.C.; Walstra, D.J.R.; Grasmeijer, B.; Sutherland, J.; Pan, S.; Sierra, J. The predictability of cross-shore bed evolution of sandy beaches at the time scale of storms and seasons using process-based profile models. Coast. Eng. 2003, 47, 295–327. [Google Scholar] [CrossRef]
- Roelvink, J.A.; Stive, M.J.F. Bar-Generating Cross-Shore Flow Mechanisms on a Beach. J. Geophys. Res. Ocean. 1989, 94, 4785–4800. [Google Scholar] [CrossRef]
- Sanchez-Arcilla, A.; Caceres, I. An Analysis of Nearshore Profile and Bar Development under Large Scale Erosive and Accretive Waves. J. Hydraul. Res. 2017, 56, 231–244. [Google Scholar] [CrossRef]
- Kuang, C.; Mao, X.; Gu, J.; Niu, H.; Ma, Y.; Yang, Y.; Qiu, R.; Zhang, J. Morphological processes of two artificial submerged shore-parallel sandbars for beach nourishment in a nearshore zone. Ocean Coast. Manag. 2019, 179, 104870. [Google Scholar] [CrossRef]
- Kuang, C.; Ma, Y.; Han, X.; Pan, S.; Zhu, L. Experimental Observation on Beach Evolution Process with Presence of Artificial Submerged Sand Bar and Reef. J. Mar. Sci. Eng. 2020, 8, 1019. [Google Scholar] [CrossRef]
- Kuang, C.; Han, X.; Zhang, J.; Zou, Q.; Dong, B. Morphodynamic Evolution of a Nourished Beach with Artificial Sandbars: Field Observations and Numerical Modeling. J. Mar. Sci. Eng. 2021, 9, 245. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Zang, J.; Dong, G.; Ma, X.; Zhu, Y.; Zhou, L. Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 2020, 158, 103670. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Zhao, S.; Cai, F.; Liu, Z.; Cao, C.; Qi, H. Disturbed Climate Changes Preserved in Terrigenous Sediments Associated with Anthropogenic Activities During the Last Century in the Taiwan Strait, East Asia. Mar. Geol. 2021, 437, 106499. [Google Scholar] [CrossRef]
- Shafiei, H.; Chauchat, J.; Bonamy, C.; Marchesiello, P. Adaptation of the Santoss Transport Formula for 3d Nearshore Models: Application to Cross-Shore Sandbar Migration. Ocean Model. 2022, 181, 102138. [Google Scholar] [CrossRef]
- Marchesiello, P.; Chauchat, J.; Shafiei, H.; Almar, R.; Benshila, R.; Dumas, F.; Debreu, L. 3D wave-resolving simulation of sandbar migration. Ocean Model. 2022, 180, 102127. [Google Scholar] [CrossRef]
- Fang, K.; Yi, F.; Liu, J.; Sun, J. Laboratory study on the effect of an artificial sandbar on nourished beach profile evolution. Int. J. Offshore Polar Eng. 2022, 32, 218–226. [Google Scholar] [CrossRef]


| Case ID | Wave Height | Wave Period | Sea Level |
|---|---|---|---|
| 1 | 1.25H0 | T0 | η0 |
| 2 | 0.8H0 | T0 | η0 |
| 3 | H0 | 1.25T0 | η0 |
| 4 | H0 | 0.8T0 | η0 |
| 5 | H0 | T0 | η0 − 10 cm |
| 6 | H0 | T0 | η0 + 10 cm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Li, Y.; Zhang, C.; Wang, Z.; Dai, W.; Chi, S. Effects of Wave Height, Period and Sea Level on Barred Beach Profile Evolution: Revisiting the Roller Slope in a Beach Morphodynamic Model. Water 2023, 15, 923. https://doi.org/10.3390/w15050923
Wang G, Li Y, Zhang C, Wang Z, Dai W, Chi S. Effects of Wave Height, Period and Sea Level on Barred Beach Profile Evolution: Revisiting the Roller Slope in a Beach Morphodynamic Model. Water. 2023; 15(5):923. https://doi.org/10.3390/w15050923
Chicago/Turabian StyleWang, Guangsheng, Yuan Li, Chi Zhang, Zilin Wang, Weiqi Dai, and Shanhang Chi. 2023. "Effects of Wave Height, Period and Sea Level on Barred Beach Profile Evolution: Revisiting the Roller Slope in a Beach Morphodynamic Model" Water 15, no. 5: 923. https://doi.org/10.3390/w15050923
APA StyleWang, G., Li, Y., Zhang, C., Wang, Z., Dai, W., & Chi, S. (2023). Effects of Wave Height, Period and Sea Level on Barred Beach Profile Evolution: Revisiting the Roller Slope in a Beach Morphodynamic Model. Water, 15(5), 923. https://doi.org/10.3390/w15050923







