Abstract
The role of groundwater (GW) discharge on surface water (SW) quantity, quality and temperature is known to be important. Moreover, the effect of GW contributions to river thermal budgets is critical in natural rivers considering that water temperature plays a vital role in fish survival during extreme heat events. The identification of zones with GW input in rivers can, thus, help river management plans. However, detecting these zones at the watershed scale can be a challenge. This work combines thermal infrared (TIR) imagery of rivers and water sampling for radon measurements for better documentation of GW in rivers. The Sainte-Marguerite and Berard Rivers, both located in Quebec, Canada, are known for their abundance of salmonids. Their water temperature profiles were plotted using TIR imagery, and five cooling zones in the Berard River and two for the Sainte-Marguerite River were identified in which notable GW–SW exchange was the suspected cause. Radon concentrations measured within the cooling zones showed clear GW contribution to SW. TIR imagery is an effective and fast way to identify GW seepage at the watershed scale. Radon can be used as a complementary natural tracer of GW in rivers at finer scales. The combination of both methods was shown to be reliable for the identification of GW in rivers. This can help for a better anticipation of GW effects in management plans to deal with extreme heat waves that are predicted to occur more frequently under future climate change scenarios.
1. Introduction
Groundwater exchanges in rivers deliver base flow, affect water quality, mitigate water temperature, and provide thermal refuge for fish [1]. Heat has been used as a tracer for the identification of groundwater–surface water (GW–SW) exchange [2]. Groundwater (GW) temperature varies less throughout the year compared to surface water (SW), such that it can influence a river’s temperature profile, providing cool water to rivers during summer and warm water during winter. Over the winter, warm water is important for survival of fish from eggs to alevin [3,4]. During summer when river water temperature goes above thermal optimal for fish and other ectotherms, they seek shelter in zones of GW seepage known as thermal refuges [5,6,7]. In the context of climate change, extreme temperature events are expected to occur more frequently in the future [8,9,10]. Therefore, it is important to study the effects of GW in rivers to better understand temperature regimes and evaluate the impact on fish habitats [11,12]. This calls for GW-related studies to be considered for a better freshwater fishery management plan.
Thermal infrared (TIR) imagery is an effective monitoring tool for the identification of spatiotemporal variability of discrete thermal refuges and larger scale cooling zones in rivers [13,14,15]. In addition to the identification of thermal refuges and cooling zones, understanding the sources of these cool water patches is important to better understand their potential response to climate change. Thermal refuges can be classified based on their location and shape in the river and, accordingly, their source (either SW or GW) can be identified [16,17]. In addition to these discrete thermal refuges, rivers can often exhibit larger-scale ‘diffuse’ cooling zones [5]. The source of cold water for these larger-scale river cooling zones can be from small or large tributaries that enter the main stem or from GW seepage.
Identifying the exact source of cold water for these larger cooling zones by relying on TIR imagery alone can be difficult [18], and the exact sources of cooling water inputs have rarely been the subject of previous TIR-based studies (e.g., [15,19]). Thus, the hypothesis of consistently higher GW seepage in large cooling zones remains unverified. The present study combines the use of 222Rn (henceforward referred as radon) as a natural tracer for the detection of GW in the river cooling zones to overcome the limits of the TIR imagery method in validating this hypothesis.
Naturally dissolved radon in water was proven to be a reliable tracer for GW–SW interaction investigation during the last two to three decades [20,21,22]. Radon has a short half-life of 3.8 days, and when in water, it tends to attach to air bubbles that can escape to the atmosphere via gas exchange. Consequently, its concentration in GW is one or more orders of magnitude higher than SW [20,21]. Therefore, where radon concentration in the river is high, an active exfiltration of radon-bearing GW is present [23,24]. Radon measurement in SW and GW can be used for the identification of GW flow paths near SW bodies, its recharge or discharge [23,25] and quantification of this infiltration or exfiltration rate [20,21,22,26,27,28,29]. The objective of this study was, therefore, to verify the presence of GW in the identified cooling zones with TIR imagery and estimate the GW seepage rate into the river within these zones by measuring the radon concentration in SW and GW. Similar studies have been carried out for marine environments (e.g., [30]) and lakes (e.g., [31]), but are limited for rivers (e.g., [32]).
2. Study Area
The two rivers selected for this study are the Sainte-Marguerite River, which drains into the Saguenay River about 12 km from the Sacre-Coeur municipality in the Côte-Nord region of the Quebec Province, and the Berard River, which discharges into Ungava Bay in the northern village of Tasiujaq in Nunavik, northern Quebec (Figure 1).
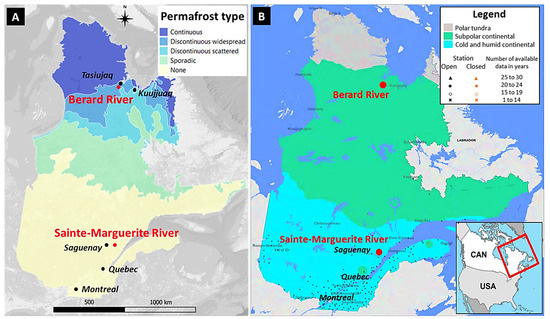
Figure 1.
Location of the two studied rivers on permafrost distribution map ((A) adapted from [34]) and Köppen climate classification map ((B) [35]) of the Quebec Province.
The Sainte-Marguerite River is in the south of the province, without permafrost (Figure 1A) and in a continental cold and humid climate (Figure 1B) with an annual average temperature of 3 °C and an average annual precipitation of 980 mm. The Berard River is in the northern part of the province, in a discontinuous permafrost zone (Figure 1A) and in a continental subpolar climate (Figure 1B) with an annual average temperature of −5.2 °C and an average annual precipitation of 447 mm [33].
The studied section of the Sainte-Marguerite River is from the junction of the main branch with the north-east branch for a length of ~40 km (Figure 2). At the Sainte-Marguerite River study site, the bedrock geology consists of metamorphic rocks, mostly gneiss, migmatite, and orthopyroxene granitoids such as charnockite, mangerite, jotunite and hypersthene syenite (Figure 2). The shallow aquifer under and adjacent to the Sainte-Marguerite River is made of fine sand and sandy silt material, which is recent and ancient river terrace alluvial deposit with a variable thickness of 1–30 m, underlaid with less permeable deltaic and prodeltaic glaciomarine sediment [36]. However, based on field observations, the near-surface riverbed material of the Sainte-Marguerite River is highly permeable recent river deposits made of coarse sand, gravel and boulders with a thickness of <5 m.
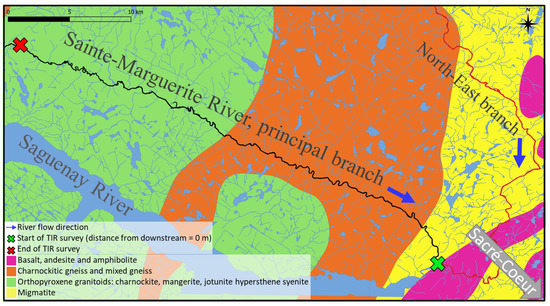
Figure 2.
Bedrock geology across the Sainte-Marguerite River (based on [36]).
The Berard River study site covers 17.5 km downstream of Berard Lake to the river’s mouth in Ungava Bay (Figure 3). The bedrock geology across the Berard River is a mix of sedimentary rocks dominantly made of conglomerate, sandstone, siltstone, mudrock, wacke and quartz arenite. Near the bay and further from the river valley, igneous rocks dominantly made of gabbro, diorite, quartz diorite, gabbronorite, anorthosite, granite and granodiorite are also present (Figure 3). Some bedrock formations contain a considerable amount of iron (orange in Figure 3). Based on field observation, the shallow aquifer below the Berard River is made of recent alluvium. From 0 to about 0.75 m depth, a hardpan with boulders and rocks with a diameter of 1 cm to >50 cm is present. Low-permeability deep-water fine-grained glaciomarine sediment is present underneath the shallow alluvial aquifer [36].
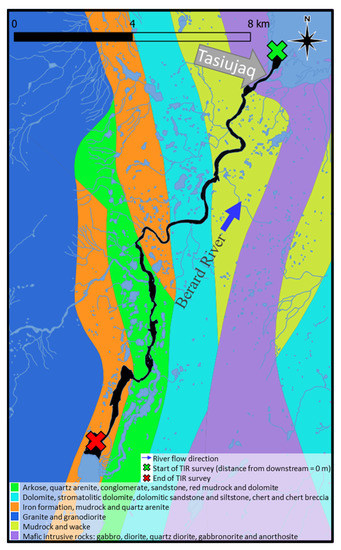
Figure 3.
Bedrock geology across the Berard River (based on [36]).
3. Materials and Methods
3.1. Aerial TIR Imagery
The details about the acquisition method and equipment regarding TIR image acquisition can be found in [16,17], but information specific to this study is presented here. The thermal imagery of the rivers was acquired with an FLIR SC660 camera attached to a helicopter. Imagery was acquired in mid-September (the low flow season of the studied rivers), during a warm sunny day near midday with air temperature around 20 °C. This ensures maximum contrast between river water temperature and GW-fed cooling zones, for ease of their identification. Flights were conducted at an altitude of approximately 400 m above ground, which resulted in a thermal image resolution of ~25 cm. Additionally, the low ground speed of the helicopter lead to a good image overlap (more than 75%). RGB images (3 cm resolution) were collected at the same time to provide visual context for the thermal images.
River temperature profiles were generated by plotting mean river water temperature against distance downstream. The mean river temperature of each thermal image was calculated by averaging the temperature of three points in the river central line (details in [18]). TIR-derived temperatures were validated using Onset HOBO MX2201 Pendant temperature loggers installed in the river, following the approaches detailed in [16,17].
The asymptotic warming paradigm [37] states that river water temperature should increase when moving from upstream to downstream as a function of energy exchanges at the air–water interface. However, temperature long profiles rarely follow this trend in nature, due partially to advection from either SW or GW exchanges. As such, large-scale cooling zones in the order of 100–1000 m are often present in a river’s temperature profile. For the purposes of this study, we defined a cooling zone as a section of profile with a sustained temperature decrease of 0.25 °C or greater. Areas of the river temperature profile that exhibited a temperature decrease greater than this magnitude were, thus, used to identify the presence and length of a cooling zone. Since GW seepage can be the source of cold water, the cooling zone’s existence is expected to be temporally persistent. Therefore, these cooling zones were selected for further investigation regarding the presence of GW in the rivers.
3.2. Radon Measurements
Radon is naturally produced from the decay of background uranium in soil, rock and water. Therefore, its presence in GW depends on the lithology and aquifer geochemistry [21,38]. Thus, bedrock type has been considered for the interpretation of radon sampling results. Additionally, water sampling was avoided during or after rainy days when the water level was high, since radon concentration in rain is very low and dilutes the radon level in SW and GW.
Nine sampling points on each river were considered. Selected sampling points for radon measurement correspond to the identified cooling zones from TIR imagery analysis. One or more sampling points inside the cooling zone were selected and one point before or after cooling zones. The radon sampling points were selected at the center of the river, since river temperature profile is based on three measurements points on the river center line. In addition, as the aim was to verify the presence of GW seepage, sampling points were located as close as possible to the bottom of the river. Radon can escape from the water samples via gas exchange, so the samples were taken by submerging the bottles and closing the cap under water. Moreover, samples from two shallow piezometers (depth of about 2 m from the ground surface), installed close to the river, were also collected to verify the difference in radon concentration in GW and SW. GW samples were collected by the use of a peristaltic pump set to a low flow to avoid air bubbles entering the samples. One duplicate (representing 10% of samples collected) from GW samples and one for SW samples at each studied river were analyzed to validate the accuracy of the sampling and measurements.
Water samples were analyzed within 24 h of the sampling period to avoid radon complete decay before its analysis. Radon concentration was measured by the use of an AB-5R portable radiation monitor device [39]. Radon was first extracted into cells designed for AB-5R by the use of a WG-1001 device [39]. The AB-5R device then counted the emitted alpha particles from radon decay inside the cell. For each sample, five 5 min counting cycles were considered. The counts were later translated to radon concentration in Bq/L by applying a correction factor considering the time between the sampling event and the analysis.
The GW flow pattern can be verified by having radon concentration in the installed piezometers at different locations in the studied section of the river. Few SW samples were collected near the piezometers to estimate the GW flow path [25].
Moreover, by using the mass conservation theory (Equation (1)), the fraction of GW in the river (f), which is the ratio of GW seepage flow rate () (m3/s) to river discharge () (m3/s), can be approximated by Equation (2), where radon concentration in GW and in SW at the study site are (Bq/L) and (Bq/L), respectively, and (Bq/L) is background concentration, which is the concentration in SW upstream of the study area [20].
The mass balance theory is solved for a selected area of the river by selecting an upstream and a downstream section. The radon concentrations used in Equation (2) should be calibrated considering the loss of radon by gas exchange and radioactive decay [20]. The gas exchange correction factor is applied to take into account the loss of radon via gas exchange between the upstream and downstream section. If the flow in between the upstream and downstream section is not turbulent, the gas exchange within the zone is negligible. The radioactive decay correction factor is to adjust the radon concentration loss for the sampling time difference between upstream and downstream sections. If the sampling of these two sections is carried out relatively simultaneously, the correction factor is very small and the results are not different from the case if the two samples are taken at the same time at the upstream and downstream sections. Therefore, calibration factors were not applied in this study as a simplification. Instead, we considered as the radon concentration in the upstream warming zone, as the radon concentration in the cooling zone (average if multiple sampling within the zone is present) and as the average radon concentration in the shallow piezometers on shore.
The results of GW seepage flow rates from radon mass balance methods were then compared to GW seepage measured by seepage meters in the Sainte-Marguerite River (Figure 4). Seepage meters measure the amount of GW gained or lost from the isolated section of the riverbed by the barrel. Several seepage meters were installed on the riverbed close to the location of piezometers for a duration of 6 to 24 h. By knowing the amount of water in the plastic bags (V) (m3), the duration of the measurement (t) (s) and area of the barrel (A) (m2), the vertical GW flow rate (q) (m/s) into the river can be calculated from Equation (3) [40].
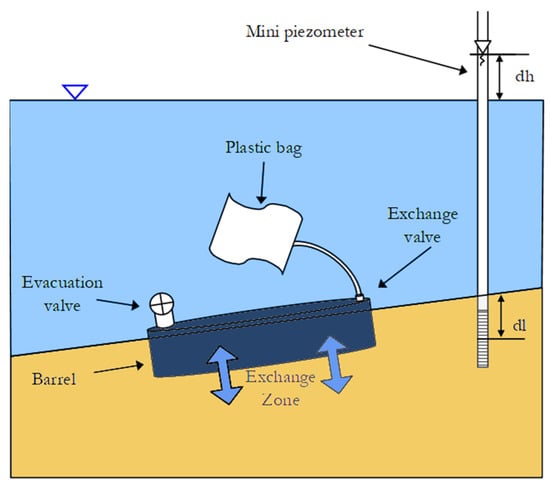
Figure 4.
Schematic of the seepage meter device.
Moreover, the horizontal GW flow rate can be calculated by using the mean hydraulic conductivity (k) (m/s) of the riverbank material from slug tests in the piezometers close to the river shore and the hydraulic gradient (i) (m/m) between the piezometer and river water levels with the Darcy equation (Equation (4)).
4. Results
4.1. River Temperature Profile
The river temperature profile from TIR imagery of the Sainte-Marguerite River shows two cooling zones, named S1 and S2, which have a length of two and seven kilometers, respectively. These cooling zones cover approximately 22.5% of the studied river length (Figure 5).
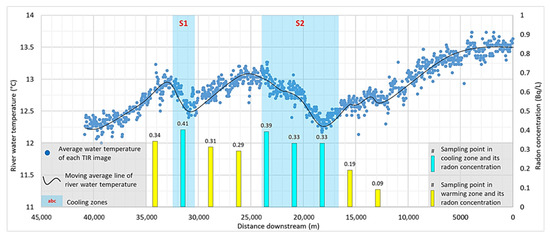
Figure 5.
Scatter plot showing temperature profile of Sainte-Marguerite River and columns showing location of radon sampling and measured concentration.
The Berard River temperature profile shows five cooling zones with a length varying between 665 m and 2365 m and a total length of 7.8 km, which is 46% of the total studied length of the river (Figure 6).
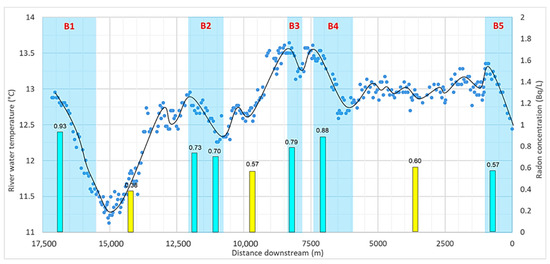
Figure 6.
Scatter plot showing temperature profile of Berard River and columns showing location of radon sampling and measured concentration (labels same as Figure 5).
4.2. Radon Measurements
Four of the nine sampling points on the Sainte-Marguerite River were in cooling zones and five in warming (or temperature stable) zones. The identified cooling zones in this river are lengthy, thus, multiple sampling points in them were selected to have at least one point for every two kilometers. The measured radon concentration in the cooling zones varies between 0.33 Bq/L and 0.41 Bq/L, with an average of 0.35 Bq/L, while for the warming zones, the concentration range was 0.09 Bq/L to 0.34 Bq/L with an average of 0.25 Bq/L (Figure 7). This difference in average values was meaningful based on t-tests (Figure 8). The average radon concentration for GW samples of the Sainte-Marguerite River was 6.23 Bq/L.
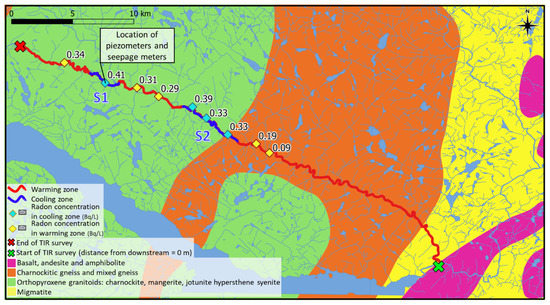
Figure 7.
Cooling zones and radon sampling points of Saint-Marguerite River.
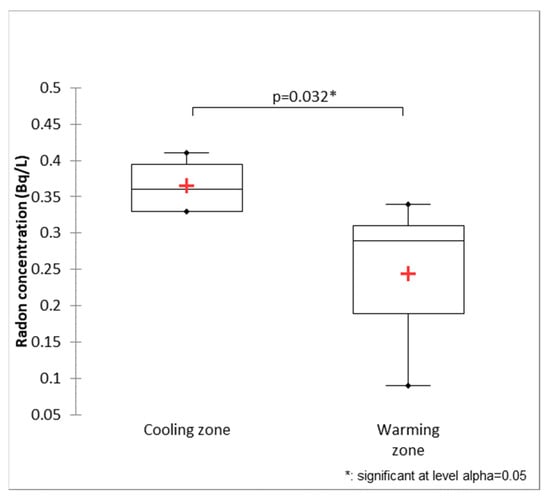
Figure 8.
Box and whisker plot of radon concentration for cooling and warming zones of Sainte-Marguerite River showing significant difference at 95% confidence level t-test.
Six sampling points are located in the cooling zones of the Berard River and three in warming or stable zones. One sampling point in each cooling zone and one in each warming zone in between the cooling zones were selected. However, in B2 (second most downstream zone), two sampling points were selected, one before and one after the entrance of the large tributary to the main stem. This aids in the assessment of the effect of mixing of the tributary and the main stem water on the measured radon concentration. The radon concentration for points in cooling zones ranges between 0.57 Bq/L and 0.93 Bq/L, and the average was 0.76 Bq/L, while the concentration of points in warming zones has a range between 0.38 Bq/L and 0.60 Bq/L, with an average of 0.51 Bq/L (Figure 9). This difference in average values was significant based on t-tests (Figure 10). The GW samples had an average radon concentration of 10.85 Bq/L.
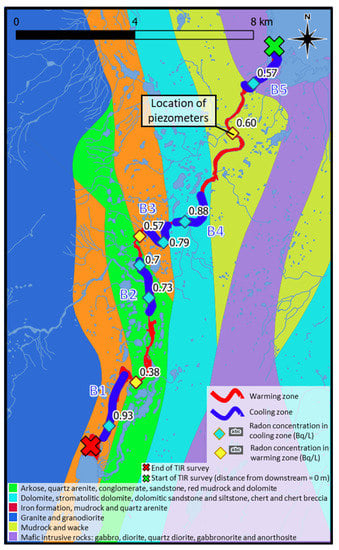
Figure 9.
Cooling zones and radon sampling points of Berard River.
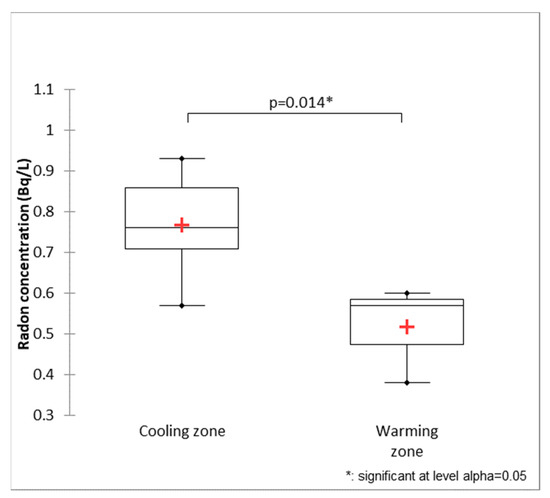
Figure 10.
Box and whisker plot of radon concentration for cooling and warming zones of Berard River showing significant difference at 95% confidence level t-test.
The radon concentration in the piezometers and river were compared to identify GW seepage into the rivers. For the Sainte-Marguerite River, the piezometers are located in a large-scale cooling zone of the river (S1) on the north-east (left) bank of the river, where GW seepage to the river was expected due to the slope of the riverbank (Figure 11). The geometric average hydraulic conductivity (k) of riverbank materials based on slug tests in the two piezometers is about 0.0011 m/s (0.002 m/s for PS1 and 0.0006 m/s for PS2). The pressure head difference between these two piezometers was about 7 cm at the time of measurements, considering the distance between two piezometers of 13 m the horizontal hydraulic gradient (i) was 0.0054 m/m. The GW temperature was about 5 °C, while the river water temperature was about 12 °C.
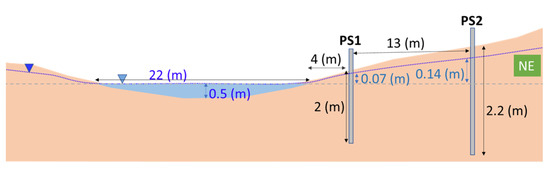
Figure 11.
Cross section of Sainte-Marguerite River at location of piezometers.
The radon concentration in the piezometer further from the river (PS2 in Figure 12) was higher than the one close to the river (PS1 in Figure 12), which is prone to dilution and mixing with SW. Moreover, the radon concentration in the river from SS1 to SS3 decreases. This shows that GW seepage reduces by moving from the left riverbank to the right riverbank.
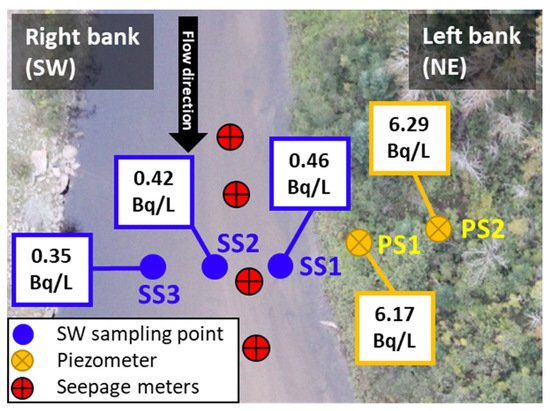
Figure 12.
Radon concentration of Sainte-Marguerite River piezometers and SW.
Piezometers on the Berard River were installed in a warming zone on the left (south-west) bank of the river (Figure 13). However, this location was a cold GW-fed side channel, which was identified through TIR imaging (Figure 14A). The hydraulic conductivity of riverbank material is about 0.003 m/s based on slug tests in piezometer PB1. PB2 was not used for hydraulic conductivity measurements since it is located on a sand and gravel bar in between the main stem and side channel and is not representative of riverbank material. The GW level in PB1 was 1 cm higher than the SW level at the time of measurements. Considering the distance between PB1 and side channel shoreline, 5 m, the horizontal hydraulic gradient was 0.002 m/m. The GW temperature was about 1 °C, while the river water temperature was about 11 °C in the main branch and 7 °C in the side channel. GW seepage is more noticeable in the upstream section, and the temperature difference with the main stem is about 5 °C, while the difference is lower and near 3.5 °C further downstream (Figure 14A). To confirm the effect of radon on sampling location, several SW and GW samples were collected from piezometers at this site (Figure 14B). Radon concentration in the main stem was 0.60 Bq/L and within the range of other SW measurements of the river. However, the concentration in GW of the piezometers and side channel was more than ten times higher. The concentration upstream of the side channel, where GW discharges, was 19.33 Bq/L, which is close to the measured value of 21.27 Bq/L in piezometers at the shore of the river at a depth of about 1.8 m below ground level. This confirms that the source of cold water in this channel is GW. The radon concentration at the downstream section of the side channel was 8.30 Bq/L. The measured radon concentration in the piezometer located between the side channel and the main stem (PB2 in Figure 14B) was 15.44 Bq/L.
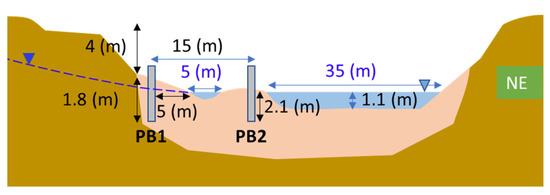
Figure 13.
Cross section of Berard River at location of piezometers.
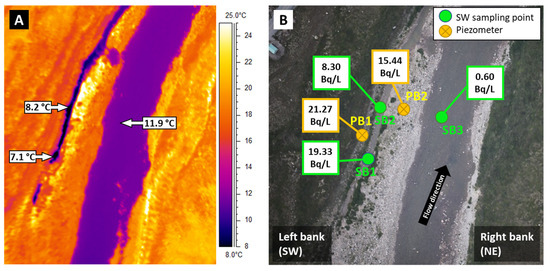
Figure 14.
Water temperature of the side channel and main stem from TIR imaging (A) and radon concentration in Berard River piezometers and SW (B).
Based on Equation (2) and simplifications mentioned in the methodology section, the fraction of GW in the river was calculated for the identified cooling zones (Table 1), except for the first and last cooling zones of the Berard River (B1 and B5). The upstream (background) concentration for B1 was not measured due to difficulty of sampling in the deep lake. The radon concentration in the B5 cooling zone is lower than the upstream hotter section, and Equation (2) considers this section a GW-losing section.

Table 1.
Calculated fraction of GW in the identified cooling sections of the rivers.
The average GW seepage compared to river discharge is about 1% and 2.75% for the studied section of the Sainte-Marguerite River and Berard River, respectively.
The river flow rate was 6.5 m3/s in the first cooling zone of the Saint-Marguerite River. Thus, a 1.1% GW fraction translates into a 0.07 m3/s GW flow through the riverbed between the two most upstream sampling sites in this river (values of 0.34 Bq/L and 0.41 Bq/L in Figure 7). The length of the river between these two sampling points is about 5.75 km, and the average width of the river is 18 m, which gives a GW seepage velocity of 6.9 × 10−7 m/s through the riverbed sediments in this section. This GW seepage velocity is very close to the measured GW seepage with seepage meters of 6.45 × 10−7 m/s. This value is an extrapolation of the measured GW discharge by seepage meters to the same river reach.
The river flow rate of the Berard River a bit downstream of piezometer installation site was about 18.5 m3/s. Considering the same flow rate for the B4 cooling zone, the 3% GW fraction results in a GW seepage rate of 6.2 × 10−6 m/s, which is a rough estimation due to the simplifications.
Verification of the GW seepage fraction with seepage meters was only carried out for the first cooling zone of the Sainte-Marguerite River. Installation of seepage meters for other cooling zones of the Berard and Sainte-Marguerite Rivers was not possible due to accessibility issues, high water depth and the riverbed being covered with pebbles and boulders. However, the horizontal GW flow toward the river was calculated with the Darcy equation (Equation (4)). The calculated Darcy flow (q) was 5.9 × 10−6 m/s and 6 × 10−6 m/s for the Sainte-Marguerite and Berard River, respectively.
5. Discussion
5.1. TIR Imaging Method
TIR imaging analysis is a fast and reliable method for evaluating river temperature profiles (e.g., [41]) over large spatial scales, compared to in-river techniques such as fiber-optic DTS (e.g., [42]). River temperature profiles clearly showed large-scale cooling zones in rivers. However, the exact source of cool water (GW or SW) cannot be detected in some cases. For example, the first cooling zone of the Berard River is located after a lake, and so its presence could ostensibly have been attributed to this; similarly, a large tributary (1 °C colder) enters the main stem in the middle of second cooling zone, potentially obfuscating the source of this cooling zone. Conversely, other small tributaries in the Berard River were clearly not the source of cooling zones as the lack of riparian vegetation meant that these tributaries, clearly visible in TIR images at a temperature similar to the main stem, were not responsible for cooling of the observed magnitude. On the other hand, the same observation could not be made for the Sainte-Marguerite River, since the riparian canopy renders small tributaries almost invisible in TIR images. While measuring the temperature of each individual tributary entering the main stem is a possible solution to verify if they provide cool water to the main stem, as is the installation of piezometers along the river to measure GW temperature, these options are time consuming, difficult to achieve depending on accessibility and partially negate the benefits of using TIR. Therefore, while TIR (and, more broadly, temperature) can be useful as a tracer for identifying the source of cool zones in rivers (e.g., [15,18,19,43]), it cannot conclusively highlight GW–SW exchanges. Therefore, comparison and combination with another method such as radon measurement is advantageous.
5.2. Radon Measurements
The average radon concentration of cooling zones was higher than the average radon concentration in warming zones for both the Sainte-Marguerite and Berard Rivers. The difference was significant based on 0.05 significance level t-tests, and the calculated p values were 0.032 and 0.014 for the Sainte-Marguerite and Berard Rivers, respectively. Additionally, radon concentration was generally higher in cooling zones compared to neighboring warming zones. The only exception is the concentration in the last cooling zones of the Berard River near the bay (B5 in Figure 6), which could be due to different reasons such as the influence of sea water that can lower radon concentration or the influence of igneous rock underlying this section with lower radon potential. Moreover, by looking at Figure 6, it can be seen that the measured 0.60 Bq/L radon concentration is not actually in a warming zone and rather in a zone with constant temperature (zone between B4 and B5), which can be a sign of GW seepage in this section that offsets the atmospheric warming of the river channel. Higher radon concentration can be a proof that the assumption of higher GW seepage in cooling zones was correct and the identified cooling zones were GW-fed.
The timing of sampling was shown to be very important, as it was observed in previous studies that radon concentration can change depending on the season and river water level (e.g., [25,26]). In this study, two sets of samples were collected for both the Sainte-Marguerite and Berard Rivers. The first set was collected in a relatively high flow rate after rainy days. The radon concentrations in these samples were very low and almost not detected since radon concentration in rain water is almost zero. The results from these samples were not used for further analysis and are not presented in this article. Sampling after rainy days should be avoided since the water in the river will be mainly runoff and the GW effect in the river cannot be detected with radon concentration. This is also true for TIR surveying, which should not be carried out after rainy days.
The assumption was that a higher measured radon concentration is present in the cooling zone since there is a discharge of radon/uranium-rich GW with a lower temperature. However, the higher measured radon concentration could be due to a higher radon content in the bedrock [44,45]. To verify if this was not the case, the type of bedrock at each sampling point in the river was evaluated.
Water samples from the Sainte-Marguerite River were collected in a metamorphic bedrock setting with six samples on orthopyroxene granitoids (light green in Figure 7) and three downstream on gneiss (orange in Figure 7). These bedrock units are a mix of several rock types. Orthopyroxene granitoids contain mangerite and monzonite, which are igneous intrusive rocks with a moderate silica content. The higher the silica content in bedrock, the higher the potential for this type of rock to be a radon source [46]. High silica content tends to precipitate uranium in the bedrock, and the uranium will emit radon during its decay. In the Canadian Shield, 69 dwellings that were built over monzonite were sampled for radon concentration in air of their basement. The average radon concentration of these indoor radon measurements was 0.28 Bq/L, which highlighted monzonite as a major radon source in Quebec [46]. Gneiss is acidic-granitic bedrock and might be associated with a high level of radon. Based on this information, it is possible to have more radon in a gneiss unit than in monzonite. However, this effect was not clear in the Sainte-Marguerite River case. The two sampling locations downstream have very low radon concentrations. The effect of bedrock is limited since the water level was very low and concentration loss can occur by gas exchange.
It was complicated to estimate if a bedrock unit is prone to radon emission for the Berard River, since multiple rock types are merged together into larger bedrock units in the available geological maps (Figure 9). However, the results of radon measurements at the selected study site on the Berard River showed that the depth and location of piezometers can reveal interesting results about GW seepage and mixing with SW. The measured radon concentration in the piezometer located between the side channel and the main stem (PB2 in Figure 14B) was lower than the one measured in the piezometer on the riverbank (PB1 in Figure 14B) and upstream of the side channel (SB1 in Figure 14B). This could be the result of GW mixing with SW of the main stem in the hyporheic zone below the ground surface.
The inferred fraction of GW in the rivers of this study using the radon concentration method seems low (<3%). However, it did not seem out of range and close to the lower calculated value in similar studies [20,21,26,27,28,29]. Methods with natural tracers such as radon for the quantification of GW–SW exchange can have large uncertainties [47]. In this study, the shallow depth of sampling for both GW and SW, human error, the presence of air bubbles in samples and lack of correction factors can be reasons for the low measured values. The shallow depth of piezometers means water at this depth is in contact with the unsaturated zone (i.e., air) and can lose radon through gas exchange. At the river sampling locations, the rivers were shallow, although the samples were taken close to the riverbed. As a consequence, it is possible for radon to escape due to gas exchange. Samples were taken by submerging the bottles in water and closing the cap, which can introduce errors if samples were not airtight or air bubbles were present. Therefore, to minimize the impact of such potential errors, we focused on the identification of GW in rivers by comparing radon concentration at different locations instead of quantifying the exchange rate with a radon mass balance calculation. The quantification of the fraction of GW in the river is accurate when all required measurements needed for the calculation of correction factors are feasible (i.e., when it is possible to have a reliable evaluation of the thickness of the stagnant film, the average depth of the stream and the velocity of the stream water at location of each SW sampling point for radon [20]). Nonetheless, the calculated GW seepage rate with radon mass balance was not far from the seepage meter measurements extrapolated to the same river reach for the cooling zone in the Sainte-Marguerite River where the seepage meters were installed. However, the calculated GW discharge rate with radon mass balance and seepage meters was lower than the calculated flow with the Darcy equation at the river cross section of both rivers where piezometers were located. The calculated GW flow for the Berard River from the radon mass balance (6.2 × 10−6 m/s) and Darcy equation (6 × 10−6 m/s) are relatively close and in the same order of magnitude. The GW flow for the Sainte-Marguerite River from radon mass balance (6.9 × 10−7 m/s) and seepage meters (6.45 × 10−7 m/s) were close, but they were one order of magnitude lower than the GW flow calculated with the Darcy equation (5.9 × 10−6 m/s). The riverbed material at the Sainte-Marguerite River study site was shown to be anisotropic, with ten times higher horizontal hydraulic conductivity compared to vertical hydraulic conductivity. A higher GW flow of one order of magnitude when calculated with the Darcy equation and piezometric data characteristics of horizontal flow compared to seepage meters providing vertical flux measurements is not unrealistic. Moreover, the location of the piezometers was known to be an optimal GW discharge zone, either based on TIR imagery or hydrodynamics of the river cross section (sloped riverbank and presence of permeable material). Additionally, the piezometers were placed in a location with loose material to facilitate the manual installation. As a result, the measured hydraulic conductivity with slug tests was relatively high for the material intercepted by the piezometers. Thus, the calculated Darcy flow with this method is likely overestimated since maximum parameters are considered for a section in which there can be important subsurface heterogeneities. Therefore, we suggest the use of seepage meters, which give a direct seepage rate of the riverbed at different locations, for validation of the flow rate from radon mass balance. Moreover, the installation of seepage meters can be easier than piezometers. This appears to be a better alternative than calculating the Darcy flow from limited piezometer data, which may have overestimated the GW flow in our study cases. Installing seepage meters in different locations within the cooling zone is suggested for better and complete validation of the radon mass balance method, although it is time consuming.
This study was focused on the shallow GW system close to the river since sampling points for GW were in piezometers at about 2 m depth. Shallow piezometers next to rivers have been used in previous similar studies to show the GW–SW exchange (e.g., [23,25]). Choosing this depth of investigation for GW was appropriate because the recorded water level with pressure loggers inside piezometers was above the river water level and the screens of piezometers were in the saturated zone. Therefore, the samples collected from piezometers were representative of GW. Moreover, since the alluvial aquifer below these rivers is not deep and is underlaid by a low permeable layer, there is limited connection of the river to the deep GW system. However, deep observation wells would be required for better characterization of the GW to the river and the consideration of the deep GW system expected to supply radon.
The AB-5R radon measurement device is portable and allowed us to analyze the samples in the field without the need for fast shipment of samples for laboratory analysis, which is required to avoid radon decay in collected samples before analysis. However, the number of required cells for the AB-5R device was limited (three). Each cell should be cleaned by air and rest for 24 h before the next use. The resulting analysis time for water samples was about 3 days. A larger number of samples would imply a longer period between the first and last sample measurements, which could result in different weather and river flow conditions. The weather and river flow conditions were almost the same by limiting the sampling of the river to three consecutive days, which allowed us to better compare radon concentration along the river. In any cases, having more GW and SW samples can improve our interpretation of GW–SW exchange with a better spatial resolution. This would require either more AB-5R cells or sending samples to an external lab for analysis. Furthermore, repeating radon measurement at the same locations can provide better reliability and may reveal a temporal variability of GW seepage into the river [25].
6. Conclusions
TIR imaging is effective and fast in identifying river temperature anomalies and a useful tool for generating river temperature profiles. Simple sampling requirements and fast analysis (with proper equipment) associated with radon measurements make it an efficient method for application to large-scale studies. Radon measurements can, therefore, constitute a useful complementary technique for TIR to verify if GW is the source of cool water in a river. Based on results of radon measurements, it was verified that all cooling zones were the result of GW seepage. Combining the TIR and radon measurements for pinpointing the sampling locations that show more interest regarding GW influence can be effective since SW sampling at various points of rivers can be difficult due to limited accessibility and difficulty of analysis of a high number of samples. Unlike TIR imagery, which gives indicative results, radon measurements can provide quantitative measures of GW–SW exchange. In this study, the river discharge was not measured at different sampling sites and the exact GW seepage flow cannot be calculated. Nevertheless, calculated values give an approximation of GW flow to the river compared to river discharge or hyporheic exchange. The combination of TIR imagery and radon measurements can give reliable results for the identification of zones with high potential of GW–SW interaction. To obtain better results from radon mass balance calculation and improve the future implementation of this method, it would be ideal to have measurement of river flow at different cross sections of a cooling zone (at least two at the start and the end), installation of several seepage meters within the cooling zone and installation of piezometers next to the river at different locations of the studied river reach. In this way, the correction factors that were not used in this study could also be taken into account. Moreover, the GW–SW exchange rate could be calculated with a thermal budget analysis by installation of piezometers with temperature data loggers next to the river at different locations for different sections of rivers, providing another comparative method. These steps were not applicable in this study due to the nature of the selected rivers. Deep water and high flows made a wide-scale installation of seepage meters impossible. The presence of hardpan with boulder and rocks in the top soil prevented the manual installation of piezometers. The remoteness of the rivers and lack of drilling equipment did not allow deep observation wells. In such difficult environments for field instrumentation, modeling can be a solution for better understanding of GW–SW interaction. Models can be built based on available data and can then be calibrated based on field measurements. In future works, a coupled GW–SW model of flow and heat transfer for the studied rivers will be built to quantify the GW–SW exchange rate and its spatiotemporal variation to anticipate the changes in river water temperature and the effects on fish species, which are important for local communities.
Author Contributions
Conceptualization, M.F., J.R. and R.M.; methodology, M.F.; formal analysis, M.F.; data curation, M.F.; writing—original draft preparation, M.F.; writing—review and editing, M.F., J.R., R.M., J.-P.D., S.J.D. and N.B.; visualization, M.F. All authors have read and agreed to the published version of the manuscript.
Funding
This project was funded by Environment and Climate Change Canada’s Environmental Damages Fund (EDF-PQ- 2017 J002). The authors also would like to acknowledge the financial support from CREATE-TEDGIEER program, National Sciences and Engineering Research Council of Canada (NSERC); Grant number- 498017-2017.
Data Availability Statement
The data are not publicly available, since parts of the data were obtained from indigenous communities’ category 1 and 2 lands of northern Quebec, but are available from the corresponding author with the permission of the Northern Village Office and Landholding of Tasiujaq.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Power, G.; Brown, R.S.; Imhof, J.G. Groundwater and fish—Insights from northern North America. Hydrol. Process. 1999, 13, 401–422. [Google Scholar] [CrossRef]
- Anderson, M.P. Heat as a Ground Water Tracer. Groundwater 2005, 43, 951–968. [Google Scholar] [CrossRef]
- Geist, D.R.; Dauble, D.D. Redd site selection and spawning habitat use by fall chinook salmon: The importance of geomorphic features in large rivers. Environ. Manage. 1998, 22, 655–669. [Google Scholar] [CrossRef]
- Baxter, C.V.; Hauer, F.R. Geomorphology, hyporheic exchange, and selection of spawning habitat by bull trout (Salvelinus confluentus). Can. J. Fish. Aquat. Sci. 2000, 57, 1470–1481. [Google Scholar] [CrossRef]
- Dugdale, S.J.; Franssen, J.; Corey, E.; Bergeron, N.E.; Lapointe, M.; Cunjak, R.A. Main stem movement of Atlantic salmon parr in response to high river temperature. Ecol. Freshw. Fish 2015, 25, 429–445. [Google Scholar] [CrossRef]
- Frechette, D.M.; Dugdale, S.J.; Dodson, J.J.; Bergeron, N.E. Understanding summertime thermal refuge use by adult Atlantic salmon using remote sensing, river temperature monitoring, and acoustic telemetry1. Can. J. Fish. Aquat. Sci. 2018, 75, 1999–2010. [Google Scholar] [CrossRef]
- Ebersole, J.L.; Liss, W.J.; Frissell, C.A. Cold water patches in warm streams: Physicochemical characteristics and the influence of shading. J. Am. Water Resour. Assoc. 2003, 39, 355–368. [Google Scholar] [CrossRef]
- Colombo, A.F.; Etkin, D.; Karney, B.W. Climate Variability and the Frequency of Extreme Temperature Events for Nine Sites across Canada: Implications for Power Usage. J. Clim. 1999, 12, 2490–2502. [Google Scholar] [CrossRef]
- Fortin, G.; Acquaotta, F.; Fratianni, S. The evolution of temperature extremes in the Gaspé Peninsula, Quebec, Canada (1974–2013). Theor. Appl. Climatol. 2017, 130, 163–172. [Google Scholar] [CrossRef]
- Breton, M.-P.; Cloutier, G.; Waygood, E.O.D. QUEBEC. In Climate Risks and Adaptation Practices for the Canadian Transportation Sector 2016; Government of Canada: Ottawa, ON, Canada, 2017; pp. 181–216. [Google Scholar]
- Gunn, J.; Snucins, E. Brook charr mortalities during extreme temperature events in Sutton River, Hudson Bay Lowlands, Canada. Hydrobiologia 2010, 650, 79–84. [Google Scholar] [CrossRef]
- Poesch, M.S.; Chavarie, L.; Chu, C.; Pandit, S.N.; Tonn, W. Climate Change Impacts on Freshwater Fishes: A Canadian Perspective. Fisheries 2016, 41, 385–391. [Google Scholar] [CrossRef]
- Willms, T.; Whitworth, G. Mapping of Critical Summer Thermal Refuge Habitats for Chinook Salmon, Coho Salmon, Steelhead and Bull Trout in the Nicola River Watershed—2016; Report submitted to Habitat Stewardship Program for Species at Risk project reference number: 2016HSP7592; Fraser Basin Council: Kamloops, BC, Canada, 2016. [Google Scholar]
- Torgersen, C.; Ebersole, J. Primer for Identifying Cold-Water Refuges to Protect and Restore Thermal Diversity in Riverine Landscapes; Report prepared for region 10, Washington report number: EPA 910-C-12-001; U.S. Environmental Protection Agency: Seattle, DC, USA, 2012. [Google Scholar]
- Mejia, F.H.; Torgersen, C.E.; Berntsen, E.K.; Maroney, J.R.; Connor, J.M.; Fullerton, A.H.; Ebersole, J.L.; Lorang, M.S. Longitudinal, Lateral, Vertical, and Temporal Thermal Heterogeneity in a Large Impounded River: Implications for Cold-Water Refuges. Remote Sens. 2020, 12, 1386. [Google Scholar] [CrossRef]
- Dugdale, S.J.; Bergeron, N.E.; St-Hilaire, A. Spatial distribution of thermal refuges analysed in relation to riverscape hydromorphology using airborne thermal infrared imagery. Remote Sens. Environ. 2015, 160, 43–55. [Google Scholar] [CrossRef]
- Dugdale, S.J.; Bergeron, N.E.; St-Hilaire, A. Temporal variability of thermal refuges and water temperature patterns in an Atlantic salmon river. Remote Sens. Environ. 2013, 136, 358–373. [Google Scholar] [CrossRef]
- Fakhari, M.; Raymond, J.; Martel, R.; Dugdale, S.J.; Bergeron, N. Identification of Thermal Refuges and Water Temperature Patterns in Salmonid-Bearing Subarctic Rivers of Northern Quebec. Geographies 2022, 2, 528–548. [Google Scholar] [CrossRef]
- Wawrzyniak, V.; Piégay, H.; Poirel, A. Longitudinal and temporal thermal patterns of the French Rhône River using Landsat ETM+ thermal infrared images. Aquat. Sci. 2011, 74, 405–414. [Google Scholar] [CrossRef]
- Wu, Y.; Wen, X.; Zhang, Y. Analysis of the exchange of groundwater and river water by using Radon-222 in the middle Heihe Basin of northwestern China. Environ. Geol. 2004, 45, 647–653. [Google Scholar] [CrossRef]
- Ortega, L.; Manzano, M.; Custodio, E.; Hornero, J.; Rodríguez-Arévalo, J. Using 222Rn to identify and quantify groundwater inflows to the Mundo River (SE Spain). Chem. Geol. 2015, 395, 67–79. [Google Scholar] [CrossRef]
- Berth, C.; Bourg, A.C.M. Radon-222 and Chloride as Natural Tracers of the Infiltration of River Water into an Alluvial Aquifer in Which There. Environ. Sci. Technol. 1994, 1994, 794–798. [Google Scholar]
- Hoehn, E.; Von Gunten, H.R. Radon in groundwater: A tool to assess infiltration from surface waters to aquifers. Water Resour. Res. 1989, 25, 1795–1803. [Google Scholar] [CrossRef]
- Rogers, S. Physical Behavior and Geologic Control of Radon in Mountain Streams; Experimental and theoretical geophysics. U.S. Geological Survey. Bulletin 1052-E., Prepared on behalf of the U.S. Atomic Energy Commission; United State Government Printing Office: Washington, DC, USA, 1958. [Google Scholar]
- Schubert, M.; Knoeller, K.; Treutler, H.-C.; Weiss, H.; Dehnert, J. 222Rn as a tracer for the estimation of infiltration of surface waters into aquifers. Radioact. Environ. 2006, 8, 326–334. [Google Scholar]
- Yi, P.; Luo, H.; Chen, L.; Yu, Z.; Jin, H.; Chen, X.; Wan, C.; Ale, A.; Zheng, M.; Hu, Q. Evaluation of groundwater discharge into surface water by using Radon-222 in the Source Area of the Yellow River, Qinghai-Tibet Plateau. J. Environ. Radioact. 2018, 192, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Cook, P.G.; Lamontagne, S.; Berhane, D.; Clark, J.F. Quantifying groundwater discharge to Cockburn River, southeastern Australia, using dissolved gas tracers 222Rn and SF6. Water Resour. Res. 2006, 42, 1–12. [Google Scholar] [CrossRef]
- Corbett, D.R.; Burnett, W.C.; Cable, P.H.; Clark, S.B. Radon tracing of groundwater input into Par Pond, Savannah River Site. J. Hydrol. 1997, 203, 209–227. [Google Scholar] [CrossRef]
- Burnett, W.C.; Peterson, R.N.; Santos, I.R.; Hicks, R.W. Use of automated radon measurements for rapid assessment of groundwater flow into Florida streams. J. Hydrol. 2010, 380, 298–304. [Google Scholar] [CrossRef]
- Kelly, J.L.; Dulai, H.; Glenn, C.R.; Lucey, P.G. Integration of aerial infrared thermography and in situ radon-222 to investigate submarine groundwater discharge to Pearl Harbor, Hawaii, USA. Limnol. Oceanogr. 2019, 64, 238–257. [Google Scholar] [CrossRef]
- Wilson, J.; Rocha, C. A combined remote sensing and multi-tracer approach for localising and assessing groundwater-lake interactions. Int. J. Appl. Earth Obs. Geoinf. 2016, 44, 195–204. [Google Scholar] [CrossRef]
- Malard, F.; Tockner, K.; Ward, J.V. Shifting dominance of subcatchment water sources and flow paths in a glacial floodplain, Val Roseg, Switzerland. Arct. Antarct. Alp. Res. 1999, 31, 135–150. [Google Scholar] [CrossRef]
- ClimateData.ca. Environment and Climate Change Canada Data Servers End-use Licence. Available online: https://eccc-msc.github.io/open-data/licence/readme_en/ (accessed on 1 September 2021).
- Lemieux, J.M.; Fortier, R.; Talbot-Poulin, M.C.; Molson, J.; Therrien, R.; Ouellet, M.; Banvil, D. Occurrence of groundwater in cold environments: Examples from Nunavik, Canada. Hydrogeol. J. 2016, 24, 1497–1513. [Google Scholar] [CrossRef]
- Gouvernement du Québec, “Climate Normals 1981–2010,” Ministère De l’Environnement et de la Lutte Contre les Changements Climatiques. 2021. Available online: https://www.environnement.gouv.qc.ca/climat/normales/climat-qc.htm (accessed on 20 March 2019).
- SIGÉOM. Surface Deposits Map. Système D’information Géominière du Quebec. 2020. Available online: https://sigeom.mines.gouv.qc.ca/signet/classes/I1108_afchCarteIntr (accessed on 3 June 2021).
- Fullerton, A.H.; Torgersen, C.E.; Lawler, J.J.; Faux, R.N.; Steel, E.A.; Beechie, T.J. Rethinking the longitudinal stream temperature paradigm: Region-wide comparison of thermal infrared imagery reveals unexpected complexity of river temperatures. Hydrol. Process. 2015, 29, 4719–4737. [Google Scholar] [CrossRef]
- Elzain, A.A. Measurement of Radon-222 concentration levels in water samples in Sudan. Adv. Appl. Sci. Res. 2014, 5, 229–234. [Google Scholar]
- Pylon. Pylon AB5 Portable Radiation Monitor. Pylon Electronic Inc. 2022. Available online: https://pylonelectronics-radon.com/wp-content/uploads/2019/08/DS138R2-AB7.pdf (accessed on 10 December 2022).
- Rosenberry, D.O.; LaBaugh, J.W. Field Techniques for Estimating Water Fluxes Between Surface Water and Ground Water Techniques and Methods 4—D2; U.S. Geological Survey: Reston, VA, USA, 2008. [Google Scholar]
- Faux, R.N.; Maus, P.; Lachowski, H.; Torgersen, C.E.; Boyd, M.S. New Approaches for Monitoring Stream Temperature: Airborne Thermal Infrared Remote Sensing; US Department of Agriculture Forest Service Engineering, Remote Sensing Applications Center: Salt Lake City, UT, USA, 2001. [Google Scholar]
- Kaandorp, V.P.; Doornenbal, P.J.; Kooi, H.; Broers, H.P.; de Louw, P.G. Temperature buffering by groundwater in ecologically valuable lowland streams under current and future climate conditions. J. Hydrol. X 2019, 3, 100031. [Google Scholar] [CrossRef]
- Dugdale, S.J.; Kelleher, C.A.; Malcolm, I.A.; Caldwell, S.; Hannah, D.M. Assessing the potential of drone-based thermal infrared imagery for quantifying river temperature heterogeneity. Hydrol. Process. 2019, 33, 1152–1163. [Google Scholar] [CrossRef]
- Hahn, E.J.; Gokun, Y.; Andrews Jr, W.M.; Overfield, B.L.; Robertson, H.; Wiggins, A.; Rayens, M.K. Radon potential, geologic formations, and lung cancer risk. Prev. Med. Rep. 2015, 2, 342–346. [Google Scholar] [CrossRef] [PubMed]
- Ershaidat, N.M.; Al-Bataina, B.A.; Al-Shereideh, S.A. Characteristics of soil radon transport in different geological formations. Environ. Geol. 2007, 55, 29–35. [Google Scholar] [CrossRef]
- Drolet, J.-P.; Martel, R.; Poulin, P.; Dessau, J.-C.; Lavoie, D.; Parent, M.; Lévesque, B. An approach to define potential radon emission level maps using indoor radon concentration measurements and radiogeochemical data positive proportion relationships. J. Environ. Radioact. 2013, 124, 57–67. [Google Scholar] [CrossRef]
- Xie, Y.; Cook, P.G.; Shanafield, M.; Simmons, C.T.; Zheng, C. Uncertainty of natural tracer methods for quantifying river-aquifer interaction in a large river. J. Hydrol. 2016, 535, 135–147. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).