Hydrological Vulnerability Assessment of Riverine Bridges: The Bajo Grau Bridge Case Study
Abstract
:1. Introduction
2. Materials and Methods
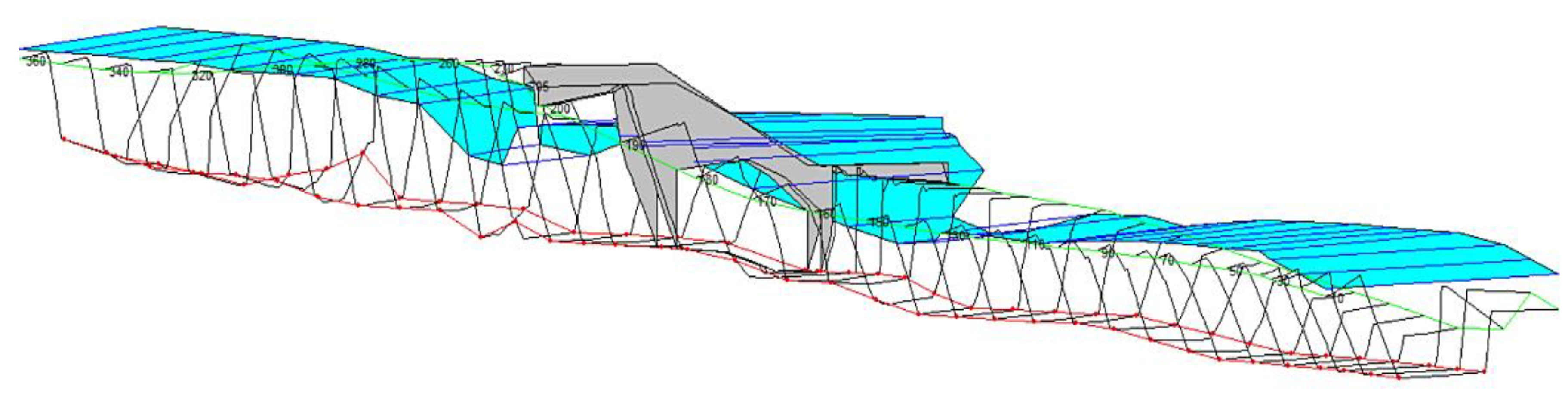
2.1. Topological Study
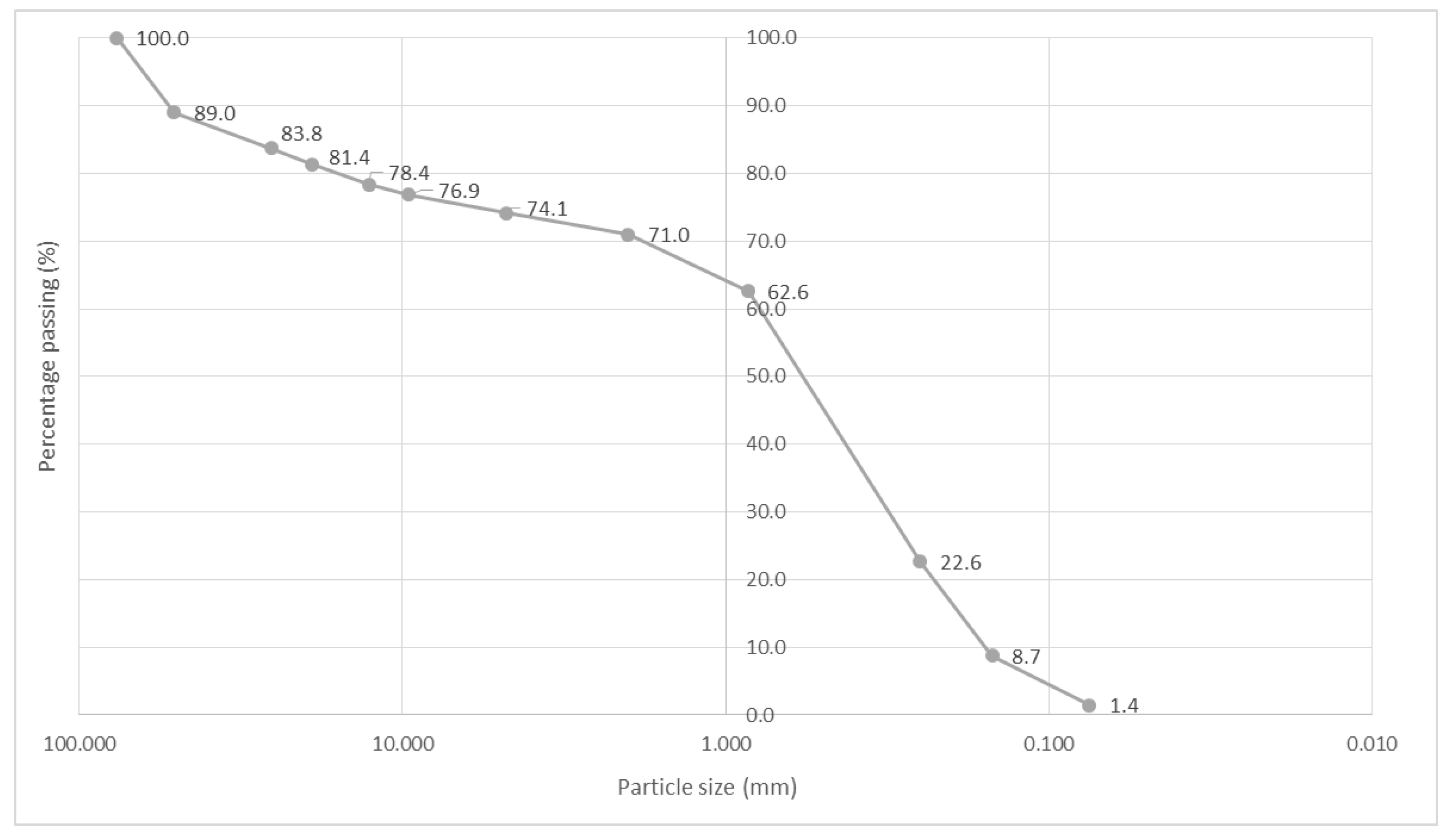
2.2. Soil Mechanics Study
3. Results
3.1. Hydrological Statistic and Scenarios Proposition
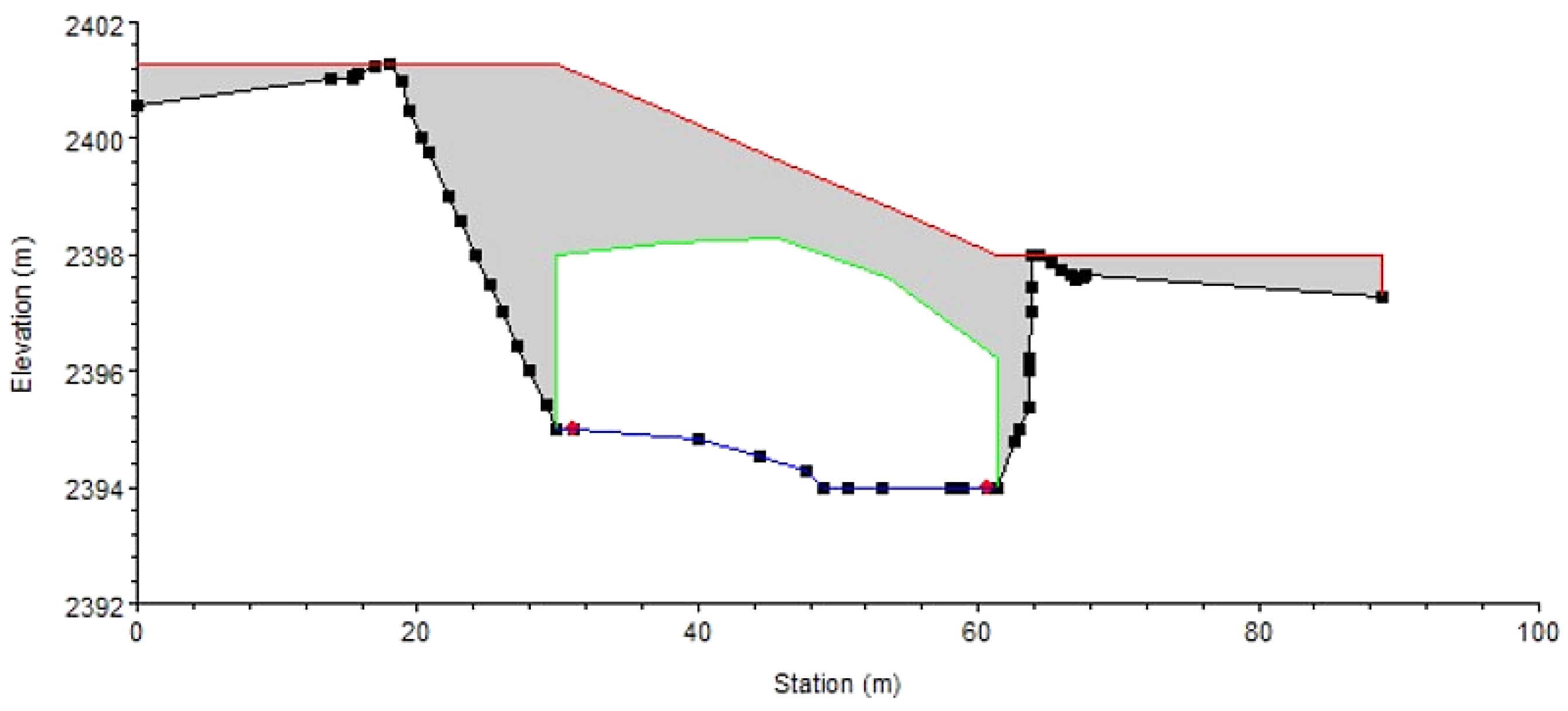
3.2. Hydraulic Aspects
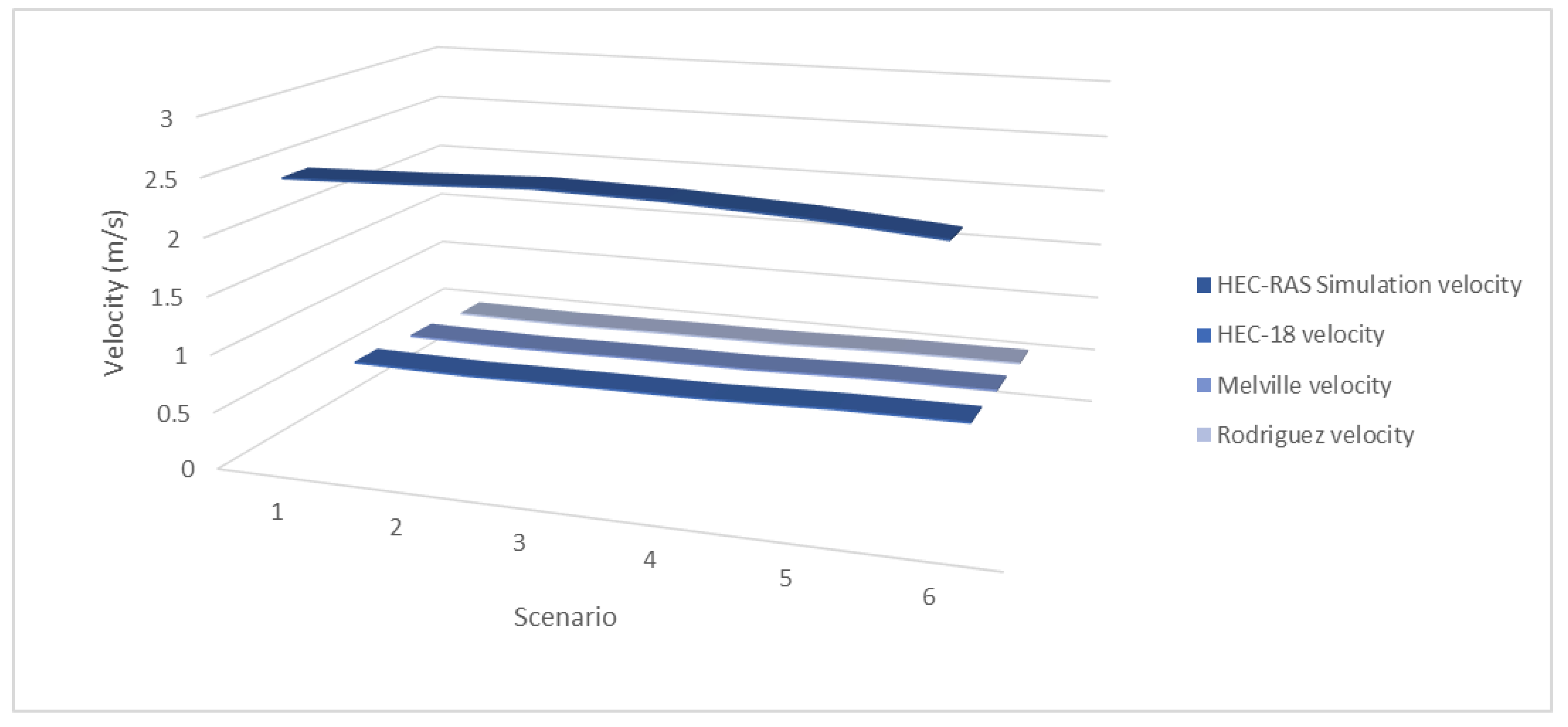
3.3. Scouring Study
4. Hydrological Vulnerability Assessment
5. Environmental Vulnerability (EV)
5.1. Flow Rate Variability
5.2. Water Quality and Composition
6. Physical Vulnerability (PV)
6.1. Building Material Used
6.2. Location
6.3. Soil Quality
6.4. Geometric Characteristics of the Bridge
6.5. Erosion on the Deck
6.6. Protection against Scouring
6.7. Overflow and Flooding
6.8. Regulations Compliance
7. Hydrological Vulnerability (HV)
8. Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Proske, D. Comparison of the collapse frequency and the probability of failure of bridges. Proc. Inst. Civ. Eng.-Bridge Eng. 2019, 172, 27–40. [Google Scholar] [CrossRef]
- Shirhole, A.; Holt, R. Planning for a comprehensive bridge safety program. Transp. Res. Rec. 1991, 1290, 39–50. [Google Scholar]
- Wardhana, K.; Hadipriono, F.C. Analysis of recent bridge failures in the United States. J. Perform. Constr. Facil. 2003, 17, 144–150. [Google Scholar] [CrossRef] [Green Version]
- Mondoro, A.; Frangopol, D.M.; Liu, L. Bridge Adaptation and Management under Climate Change Uncertainties: A Review. Nat. Hazards Rev. 2018, 19, 04017023. [Google Scholar] [CrossRef]
- Smith, D. Bridge failures. Proc. Inst. Civ. Eng. 1976, 60, 367–382. [Google Scholar] [CrossRef]
- Pregnolato, M.; Winter, A.O.; Mascarenas, D.; Sen, A.D.; Bates, P.; Motley, M.R. Assessing flooding impact to riverine bridges: An integrated analysis. Nat. Hazards Earth Syst. Sci. Discuss. 2020, 2020, 1–18. [Google Scholar] [CrossRef]
- Bastidas-Arteaga, E.; Stewart, M.G. Damage risks and economic assessment of climate adaptation strategies for design of new concrete structures subject to chloride-induced corrosion. Struct. Saf. 2015, 52, 40–53. [Google Scholar] [CrossRef] [Green Version]
- Kosič, M.; Anžlin, A.; Bau’, V. Flood Vulnerability Study of a Roadway Bridge Subjected to Hydrodynamic Actions, Local Scour and Wood Debris Accumulation. Water 2023, 15, 129. [Google Scholar] [CrossRef]
- Rowan, E.; Evans, C.; Riley-Gilbert, M.; Hyman, R.; Kafalenos, R.; Beucler, B.; Rodehorst, B.; Choate, A.; Schultz, P. Assessing the Sensitivity of Transportation Assets to Extreme Weather Events and Climate Change. Transp. Res. Rec. 2013, 2326, 16–23. [Google Scholar] [CrossRef]
- La Republica. Cierran tres puentes ante posible desborde del río Chili en Arequipa. La Republica, 2019. [Google Scholar]
- Méndez, R. Cierran Puentes en Arequipa por Incremento del Caudal del río Chili. Andina. 2012. Available online: https://andina.pe/agencia/noticia-cierran-puentes-arequipa-incremento-del-caudal-del-rio-chili-399604.aspx (accessed on 11 January 2023).
- Riva, R. Cierran Tres Puentes Ante Posible Desborde del río Chili en Arequipa. RPP. 2011. Available online: https://rpp.pe/peru/actualidad/cierran-tres-puentes-ante-posible-desborde-del-rio-chili-en-arequipa-noticia-339102 (accessed on 11 January 2023).
- Gharbi, M.; Soualmia, A.; Dartus, D.; Masbernat, L. Comparison of 1D and 2D hydraulic models for floods simulation on the Medjerda Riverin Tunisia. J. Mater. Environ. Sci. 2016, 7, 3017–3026. Available online: https://scholar.google.com/scholar_lookup?hl=en&volume=7%288%29&publication_year=2016&pages=3017-3026&author=M.+Gharbi&author=A.+Soualmia&author=D.+Dartus&author=L.+Masbernat&title=Comparison+of+1D+and+2D+hydraulic+models+for+floods+simulation+on+the+medjerda+river+in+tunisia (accessed on 11 January 2023).
- Anees, M.T.; Abdullah, K.; Nawawi, M.N.M.; Ab Rahman, N.N.; Piah, A.R.; Zakaria, N.A.; Syakir, M.I.; Omar, A.K. Numerical modeling techniques for flood analysis. J. Afr. Earth Sci. 2016, 124, 478–486. [Google Scholar] [CrossRef]
- Papaioannou, G.; Loukas, A.; Vasiliades, L.; Aronica, G.T. Flood inundation mapping sensitivity to riverine spatial resolution and modelling approach. Nat. Hazards 2016, 83, 117–132. [Google Scholar] [CrossRef]
- Timbadiya, P.V.; Patel, P.L.; Porey, P.D. HEC-RAS based hydrodynamic model in prediction of stages of lower Tapi River. ISH J. Hydraul. Eng. 2011, 17, 110–117. [Google Scholar] [CrossRef]
- Popescu, C.; Bărbulescu, A. Floods Simulation on the Vedea River (Romania) Using Hydraulic Modeling and GIS Software: A Case Study. Water 2023, 15, 483. [Google Scholar] [CrossRef]
- Merkuryeva, G.; Merkuryev, Y.; Sokolov, B.V.; Potryasaev, S.; Zelentsov, V.A.; Lektauers, A. Advanced river flood monitoring, modelling and forecasting. J. Comput. Sci. 2015, 10, 77–85. [Google Scholar] [CrossRef]
- Ghimire, E.; Sharma, S.; Lamichhane, N. Evaluation of one-dimensional and two-dimensional HEC-RAS models to predict flood travel time and inundation area for flood warning system. ISH J. Hydraul. Eng. 2022, 28, 110–126. [Google Scholar] [CrossRef]
- Ahmad, B.; Kaleem, M.S.; Butt, M.J.; Dahri, Z.H. Hydrological modelling and flood hazard mapping of Nullah Lai. Proc. Pak. Acad. Sci. 2010, 47, 215–226. [Google Scholar]
- Cook, A.; Merwade, V. Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J. Hydrol. 2009, 377, 131–142. [Google Scholar] [CrossRef]
- Deng, L.; Cai, C.S. Bridge Scour: Prediction, Modeling, Monitoring, and Countermeasures—Review. Pract. Period. Struct. Des. Constr. 2010, 15, 125–134. [Google Scholar] [CrossRef] [Green Version]
- Garg, V.; Setia, B.; Singh, V.; Kumar, A. Scour protection around bridge pier and two-piers-in-tandem arrangement. ISH J. Hydraul. Eng. 2022, 28, 251–263. [Google Scholar] [CrossRef]
- Khalid, M.; Muzzammil, M.; Alam, J. A reliability-based assessment of live bed scour at bridge piers. ISH J. Hydraul. Eng. 2021, 27, 105–112. [Google Scholar] [CrossRef]
- Bathrellos, G.D.; Karymbalis, E.; Skilodimou, H.D.; Gaki-Papanastassiou, K.; Baltas, E.A. Urban flood hazard assessment in the basin of Athens Metropolitan city, Greece. Environ. Earth Sci. 2016, 75, 319. [Google Scholar] [CrossRef]
- Mani, P.; Chatterjee, C.; Kumar, R. Flood hazard assessment with multiparameter approach derived from coupled 1D and 2D hydrodynamic flow model. Nat. Hazards 2014, 70, 1553–1574. [Google Scholar] [CrossRef]
- Akay, H.; Baduna Koçyiğit, M. Hydrologic assessment approach for river bridges in western Black Sea basin, Turkey. J. Perform. Constr. Facil. 2020, 34, 04019090. [Google Scholar] [CrossRef]
- Liu, W.-C.; Hsieh, T.-H.; Liu, H.-M. Flood Risk Assessment in Urban Areas of Southern Taiwan. Sustainability 2021, 13, 3180. [Google Scholar] [CrossRef]
- Geng, Y.; Zheng, X.; Wang, Z.; Wang, Z. Flood risk assessment in Quzhou City (China) using a coupled hydrodynamic model and fuzzy comprehensive evaluation (FCE). Nat. Hazards 2020, 100, 133–149. [Google Scholar] [CrossRef] [Green Version]
- Glas, H.; De Maeyer, P.; Merisier, S.; Deruyter, G. Development of a low-cost methodology for data acquisition and flood risk assessment in the floodplain of the river Moustiques in Haiti. J. Flood Risk Manag. 2020, 13, e12608. [Google Scholar] [CrossRef]
- Garrote, J.; Díez-Herrero, A.; Escudero, C.; García, I. A Framework Proposal for Regional-Scale Flood-Risk Assessment of Cultural Heritage Sites and Application to the Castile and León Region (Central Spain). Water 2020, 12, 329. [Google Scholar] [CrossRef] [Green Version]
- Mitoulis, S.A.; Argyroudis, S.A.; Loli, M.; Imam, B. Restoration models for quantifying flood resilience of bridges. Eng. Struct. 2021, 238, 112180. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Banerjee, S. Retrofit Optimization for Resilience Enhancement of Bridges under Multihazard Scenario. J. Struct. Eng. 2016, 142, C4015012. [Google Scholar] [CrossRef]
- Dong, Y.; Frangopol, D.M. Probabilistic Time-Dependent Multihazard Life-Cycle Assessment and Resilience of Bridges Considering Climate Change. J. Perform. Constr. Facil. 2016, 30, 04016034. [Google Scholar] [CrossRef]
- Patel, D.A.; Lad, V.H.; Chauhan, K.A.; Patel, K.A. Development of Bridge Resilience Index Using Multicriteria Decision-Making Techniques. J. Bridge Eng. 2020, 25, 04020090. [Google Scholar] [CrossRef]
- Lad, V.H.; Patel, D.A.; Chauhan, K.A.; Patel, K.A. Development of Fuzzy System Dynamics Model to Forecast Bridge Resilience. J. Bridge Eng. 2022, 27, 04022114. [Google Scholar] [CrossRef]
- Lad, V.; Patel, D.; Chauhan, K.; Patel, K. Development of causal loop diagram for bridge resilience. In Proceedings of the 37th Annual Association of Research in Construction Management Conference, Glasgow, UK, 6–7 September 2021; pp. 137–146. [Google Scholar]
- Concha, C.J.; Miranda, A.G. Análisis del Riesgo de Inundación de la Cuencia del Río Chili en el Tramo de Chilina a Uchumayo-Arequipa; Universidad Católica de Santa María: Arequipa, Peru, 2016. [Google Scholar]
- Paredes Pinto, J.C. Gestión de Riesgos Bajo el Enfoque del PMI en Obras Viales Existentes–Caso: Puente Bajo Grau, Arequipa. Master’s Thesis, Universidad Católica de Santa María, Arequipa, Peru, 2019. [Google Scholar]
- INDECI. Manual Básico Para la Estimación de Riesgo/Basic Manual for Risk Estimation; Dirección Nacional de Prevención—Instituto Nacional de Defensa Civil: Lima, Peru, 2006. [Google Scholar]
- MTC in English: Ministry of Transport and Communications. Peruvian Code. Title in English: Bridge Manual. Lima, Peru. Available online: https://portal.mtc.gob.pe/transportes/caminos/normas_carreteras/documentos/manuales/MANUAL%20DE%20PUENTES%20PDF.pdf (accessed on 13 February 2023).
- ANA in English: Water National Authority. Peruvian Guideline. Title in English: Water Resources Management Plan of the Quica-Chili Basin. Available online: https://repositorio.ana.gob.pe/handle/20.500.12543/10 (accessed on 13 February 2023).
- AUTODEMA in English: Autonomous Authority of Majes. Peruvuan Guideline. Title English: Chili System Water Movement. Available online: https://www.autodema.gob.pe/movimiento-hidrico (accessed on 13 February 2023).
- MTC in English: Ministry of Transport and Communications. Peruvian Code. Title in English: Manual of Hidrology, Hydraulics and Drainage. Lima, Peru. Available online: http://transparencia.mtc.gob.pe/idm_docs/normas_legales/1_0_2950.pdf (accessed on 13 February 2023).
- Kottegoda, N.T.; Rosso, R. Statistics, Probability, and Reliability for Civil and Environmental Engineers; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Chereque Morán, W. Hidrología: Para Estudiantes de Ingeniería Civil; Pontificia Universidad Católica del Perú: Lima, Peru, 1989. [Google Scholar]
- Aparicio Mijares, F.J. Fundamentos de Hidrología de Superficie; Limusa: Mexico City, Mexico, 1989. [Google Scholar]
- Te Chow, V.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Brunner, G.W. HEC-RAS River Analysis System Version 4.1. 2010, US Army Corps of Engineers, Institute of Water Resources, Hydrologic Engineering Center (HEC). Available online: https://www.hec.usace.army.mil/software/hec-ras/documentation/HEC-RAS_4.1_Users_Manual.pdf (accessed on 14 February 2023).
- Cowan, W.L. Estimating hydraulic roughness coefficients. Agric. Eng. 1956, 37, 473–475. [Google Scholar]
- Marcus, W.A.; Roberts, K.; Harvey, L.; Tackman, G. An Evaluation of Methods for Estimating Manning’s n in Small Mountain Streams. Mt. Res. Dev. 1992, 12, 227. [Google Scholar] [CrossRef]
- Rodríguez Díaz, H.A. Hidráulica fluvial. Fundamentos y Aplicaciones. Socavación. Colombia. 2010. Available online: https://repositorio.escuelaing.edu.co/handle/001/1728?show=full (accessed on 14 February 2023).
- Lamb, M.P.; Dietrich, W.E.; Venditti, J.G. Is the critical Shields stress for incipient sediment motion dependent on channel-bed slope? J. Geophys. Res. 2008, 113, F02008. [Google Scholar] [CrossRef] [Green Version]
- Melville, B.W.; Coleman, S.E. Bridge Scour; Water Resources Publication: Highlands Ranch, CO, USA, 2000. [Google Scholar]
- Richardson, E.V.; Davis, S.R. Evaluating Scour at Bridges; Federal Highway Administration, Office of Bridge Technology: Washington, DC, USA, 2001. [Google Scholar]
- Lischtvan, L.; Lebediev, V. Gidrologia I Gidraulika v Mostovom Doroshnom, Straitielvie. Hydrology and Hydraulics in Bridge and Road Building; Gidrometeoizdat: Leningrad, USSR, 1959. [Google Scholar]
- Juarez, E.; Rico, A. Mecánica de suelos; Flujo de Agua en suelos. tomo III. Mexico. 1984. Available online: https://www.academia.edu/34972391/Mec%C3%A1nica_de_suelos_Tomo_III_Eulalio_Ju%C3%A1rez_Badillo_y_Alfonso_Rico_Rodr%C3%ADguez (accessed on 14 February 2023).
- Schreider, M.; Scacchi, G.; Franco, F.; Fuentes, R.; Moreno, C. Aplicación del método de Lischtvan y Lebediev al cálculo de la erosión general. Tecnol. Y Cienc. Del Agua 2001, 16, 15–26. [Google Scholar]
- Froehlich, D.C. Local scour at bridge abutments. In Proceedings of the 1989 National Conference on Hydraulic Engineering, New Orleans, LA, USA, 14–18 August 1989; pp. 13–18. [Google Scholar]
- Simons, D.; Lewis, G.; Field, W. Embankment protection at river constrictions. In Proceedings of the Colorado State University, Bridge Engineering Conference, Fort Collins, CO, USA, 1970. [Google Scholar]
- Liu, H.-K.; Chang, F.M.; Skinner, M.M. Effect of Bridge Constriction on Scour and Backwater; Colorado State University: Fort Collins, CO, USA, 1961; Available online: https://hdl.handle.net/10217/186161 (accessed on 14 February 2023).
- Salazar Pinto, B.; Cutipa Luque, J.; Ramírez Valverde, G.; Juyo Salazar, R.; Paredes Fuentes, J.; Villanueva Salas, J. Estudio de la contaminación por cromo (Cr) en el río chili y parque industrial de río seco (PIRS), Arequipa—Perú 2015–2016. Veritas 2017, 16, 43–46. [Google Scholar] [CrossRef]
- Dueñas Mejia, A.L.; Astoyauri Chipana, F.F. Problema de la Contaminación del río Chili Vulnera el Principio Constitucional de Protección de la Salud Arequipa 2021. Moquegua, Peru. 2022. Available online: https://hdl.handle.net/20.500.12819/1720 (accessed on 14 February 2023).
- Ministry of Economy and Finance. Economic Transparency—Expenditure Execution Consultation; Ministry of Economy and Finance, 2022. Available online: https://www.mef.gob.pe/es/?option=com_content&language=es-ES&Itemid=100944&lang=es-ES&view=article&id=504 (accessed on 13 February 2023).
- CGP. Effectiveness of Public Investment at the Regional and Local Levels during the Period 2009 to 2014 (EFECTIVIDAD de la inversión Pública a Nivel Regional y Local durante el Período 2009 al 2014). Lima, Peru. 2016. Available online: http://doc.contraloria.gob.pe/estudios-especiales/estudio/2016/Estudio_Inversion_Publica.pdf (accessed on 14 February 2023).
- Bonifaz, J.L.; Urrunaga, R.; Aguirre, J.; Quequezana, P.; Pastor, C.; Brichetti, J.P. Infrastructure Gap in Peru (Brecha de Infraestructura en el Perú); Inter-American Development Bank: Washington, DC, USA, 2019. [Google Scholar]
- Mignot, E.; Dewals, B. Hydraulic modelling of inland urban flooding: Recent advances. J. Hydrol. 2022, 609, 127763. [Google Scholar] [CrossRef]
- Rong, Y.; Zhang, T.; Zheng, Y.; Hu, C.; Peng, L.; Feng, P. Three-dimensional urban flood inundation simulation based on digital aerial photogrammetry. J. Hydrol. 2020, 584, 124308. [Google Scholar] [CrossRef]
- Seo, J.; Hu, J.W.; Lee, J. Summary review of structural health monitoring applications for highway bridges. J. Perform. Constr. Facil. 2016, 30, 04015072. [Google Scholar] [CrossRef]
- Prendergast, L.J.; Limongelli, M.P.; Ademovic, N.; Anžlin, A.; Gavin, K.; Zanini, M. Structural Health Monitoring for Performance Assessment of Bridges under Flooding and Seismic Actions. Struct. Eng. Int. 2018, 28, 296–307. [Google Scholar] [CrossRef] [Green Version]



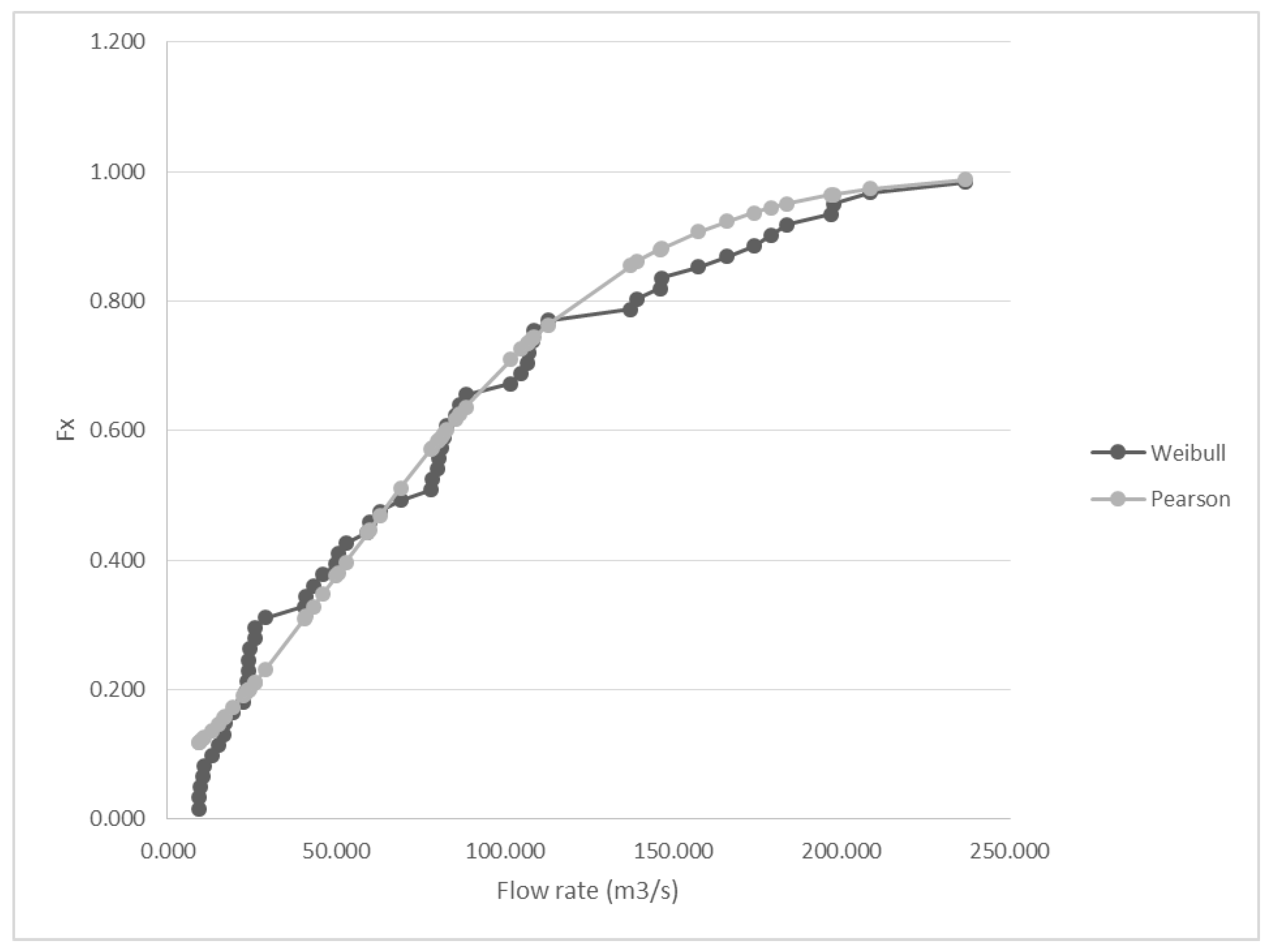
| Empirical Model | Theoretical Model | Max Delta (D) | Tabular Delta (d) |
|---|---|---|---|
| California | Normal | 0.121 | 0.176 |
| Log Normal | 0.142 | ||
| Gumbel | 0.111 | ||
| Pearson III | 0.118 | ||
| Weibull | Normal | 0.110 | |
| Log Normal | 0.133 | ||
| Gumbel | 0.122 | ||
| Pearson III | 0.101 | ||
| Gringorten | Normal | 0.112 | |
| Log Normal | 0.133 | ||
| Gumbel | 0.119 | ||
| Pearson III | 0.108 | ||
| Blom | Normal | 0.111 | |
| Log Normal | 0.133 | ||
| Gumbel | 0.120 | ||
| Pearson III | 0.107 |
| Scenario | T (Years) | Q (m3/s) |
|---|---|---|
| 1 | 100 | 251.74 |
| 2 | 200 | 276.45 |
| 3 | 400 | 325.87 |
| 4 | 500 | 350.57 |
| 5 | 1000 | 474.11 |
| 6 | - | 500.00 |
| Scenario | Return Period | Flow Rate (m3/s) | Min. Elevation (m) | Normal Flow Depth Elevation (m) | Critical Flow Depth Elevation (m) | Velocity (m/s) | Flow Area (m2) | Water Mirror (m) | Froude Number |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 100 | 251.74 | 2393.99 | 2397.49 | 2396.30 | 2.47 | 112.31 | 52.22 | 0.46 |
| 2 | 200 | 276.45 | 2393.99 | 2397.72 | 2396.41 | 2.50 | 125.64 | 65.14 | 0.45 |
| 3 | 400 | 325.87 | 2393.99 | 2398.16 | 2396.62 | 2.54 | 155.35 | 68.23 | 0.43 |
| 4 | 500 | 350.57 | 2393.99 | 2398.38 | 2396.72 | 2.52 | 170.14 | 68.67 | 0.41 |
| 5 | 1000 | 474.11 | 2393.99 | 2399.39 | 2397.19 | 2.47 | 240.67 | 70.09 | 0.36 |
| 6 | 1104 | 500.00 | 2393.99 | 2399.71 | 2397.29 | 2.39 | 263.19 | 70.37 | 0.34 |
| Scenario | T (Years) | Inferior Deck Height (m) | Real EMWL Height (m) | Code EMWL Height (m) | Heights Difference (m) | Result |
|---|---|---|---|---|---|---|
| 1 | 100 | 2396.24 | 2397.32 | 2394.24 | 3.08 | Failure |
| 2 | 200 | 2396.24 | 2397.51 | 2394.24 | 3.27 | Failure |
| 3 | 400 | 2396.24 | 2397.87 | 2394.24 | 3.63 | Failure |
| 4 | 500 | 2396.24 | 2398.02 | 2394.24 | 3.78 | Failure |
| 5 | 1000 | 2396.24 | 2399.00 | 2394.24 | 4.76 | Failure |
| 6 | - | 2396.24 | 2399.71 | 2394.24 | 5.47 | Failure |
| Variable | Low—1 | Medium—2 | High—3 | Very high—4 |
|---|---|---|---|---|
| Environmental Vulnerability (EV) Levels | ||||
| Flow rates variability | Average levels | Levels slightly higher than the average | Levels higher than the average | Levels much higher than the average |
| Water quality and composition | Low pollution levels | Medium pollution levels | High pollution levels | Very high pollution levels |
| Physical Vulnerability (PV) Levels | ||||
| Building material used | Concrete, steel or similar resilient materials in a good state | Concrete, steel, wood or similar materials in a regular state | Wood or adobe without structural reinforcements in a bad state | Adobe, reed and minor resistance materials in precarious state |
| Location: proximity to a populated centre | Far, >5 Km. | Moderately close, 1–5 km | Close, 0.2–1 km, | Very close, 0.2–0 km |
| Soil quality along the riverbed | Good conditions, without obstructions and/or variability | Regular conditions, without many obstructions and/or variability | Bad conditions, with obstructions and variability | Very bad conditions, with obstructions and great variability |
| Geometric characteristics—Bridge height | The height allows the water to flow without inconvenience. It has more than 2 m of variance between the water surface and the deck underside | The height allows the water to flow without inconvenience. It has less than 2 m of variance between the water surface and the deck underside | The height does not allow the water to flow normally. The water level reaches the deck | The height does not allow water to flow normally. The water level surpasses the deck |
| Erosion on the deck | The deck is not reached by the water flow | The deck is reached in the underside by the water flow, causing erosion | The deck is reached in a bigger area by the water flow, causing further erosion | The whole deck is reached by the water flow. It causes erosion in the upper section too |
| Protection against scouring | The abutments are protected against the flow | The abutments are moderately protected against the flow | The abutments are poorly protected against the flow | The abutments are unprotected against the flow |
| Overflow and flooding | The flow does not exceed the deck height and does not overflow | The flow reaches the deck height, but does not overflow | The flow reaches the deck height and overflows | The flow exceeds the deck height, causing overflow and flooding |
| Regulations compliance | Strictly compliance of the code | Moderately compliance of the code | Low compliance of the code | Without compliance of the code |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espinoza Vigil, A.J.; Booker, J. Hydrological Vulnerability Assessment of Riverine Bridges: The Bajo Grau Bridge Case Study. Water 2023, 15, 846. https://doi.org/10.3390/w15050846
Espinoza Vigil AJ, Booker J. Hydrological Vulnerability Assessment of Riverine Bridges: The Bajo Grau Bridge Case Study. Water. 2023; 15(5):846. https://doi.org/10.3390/w15050846
Chicago/Turabian StyleEspinoza Vigil, Alain Jorge, and Julian Booker. 2023. "Hydrological Vulnerability Assessment of Riverine Bridges: The Bajo Grau Bridge Case Study" Water 15, no. 5: 846. https://doi.org/10.3390/w15050846







