Predicting Groundwater Level Based on Machine Learning: A Case Study of the Hebei Plain
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.3. Methods
2.3.1. Support Vector Machine
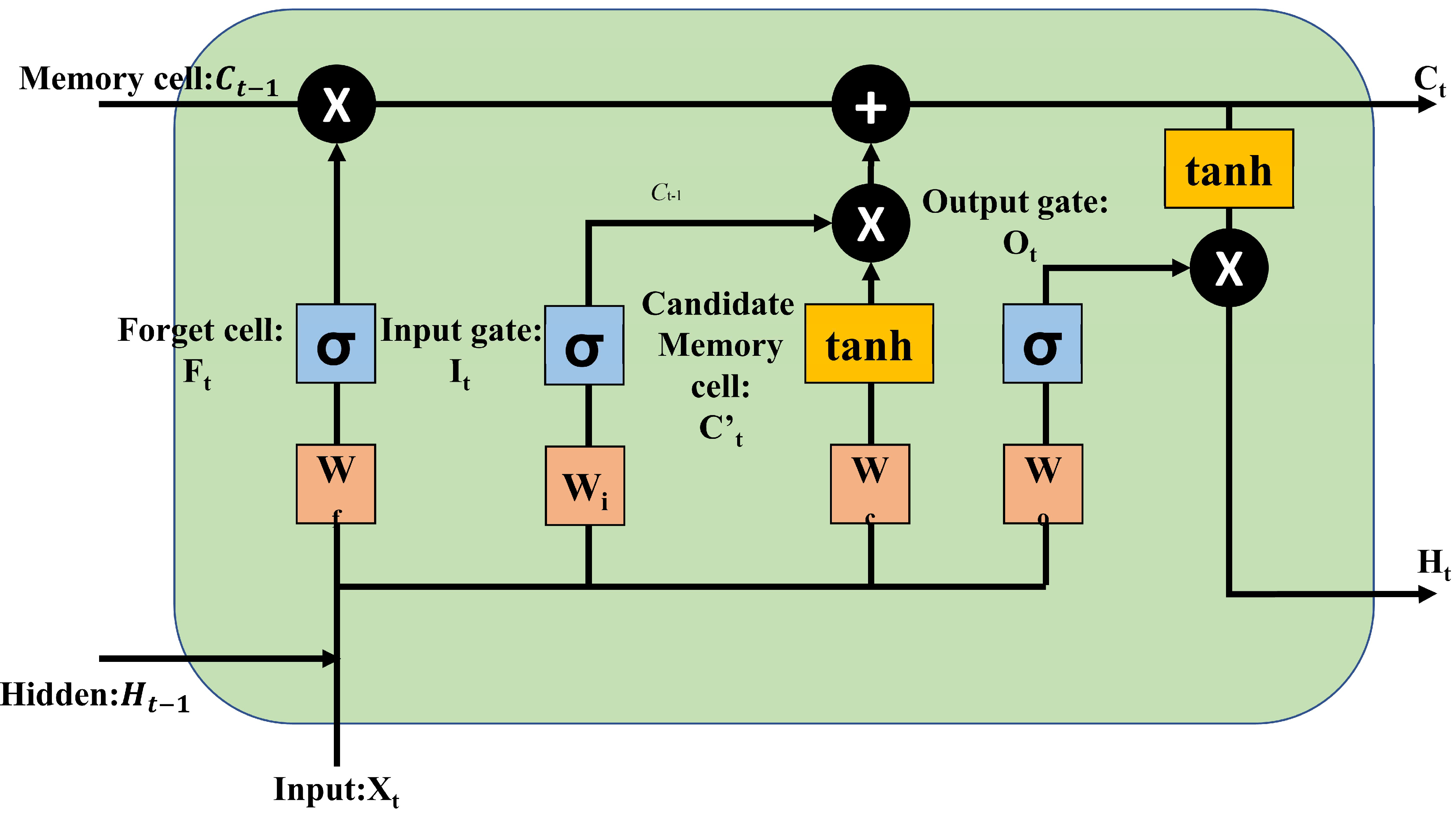
2.3.2. Long-Short Term Memory
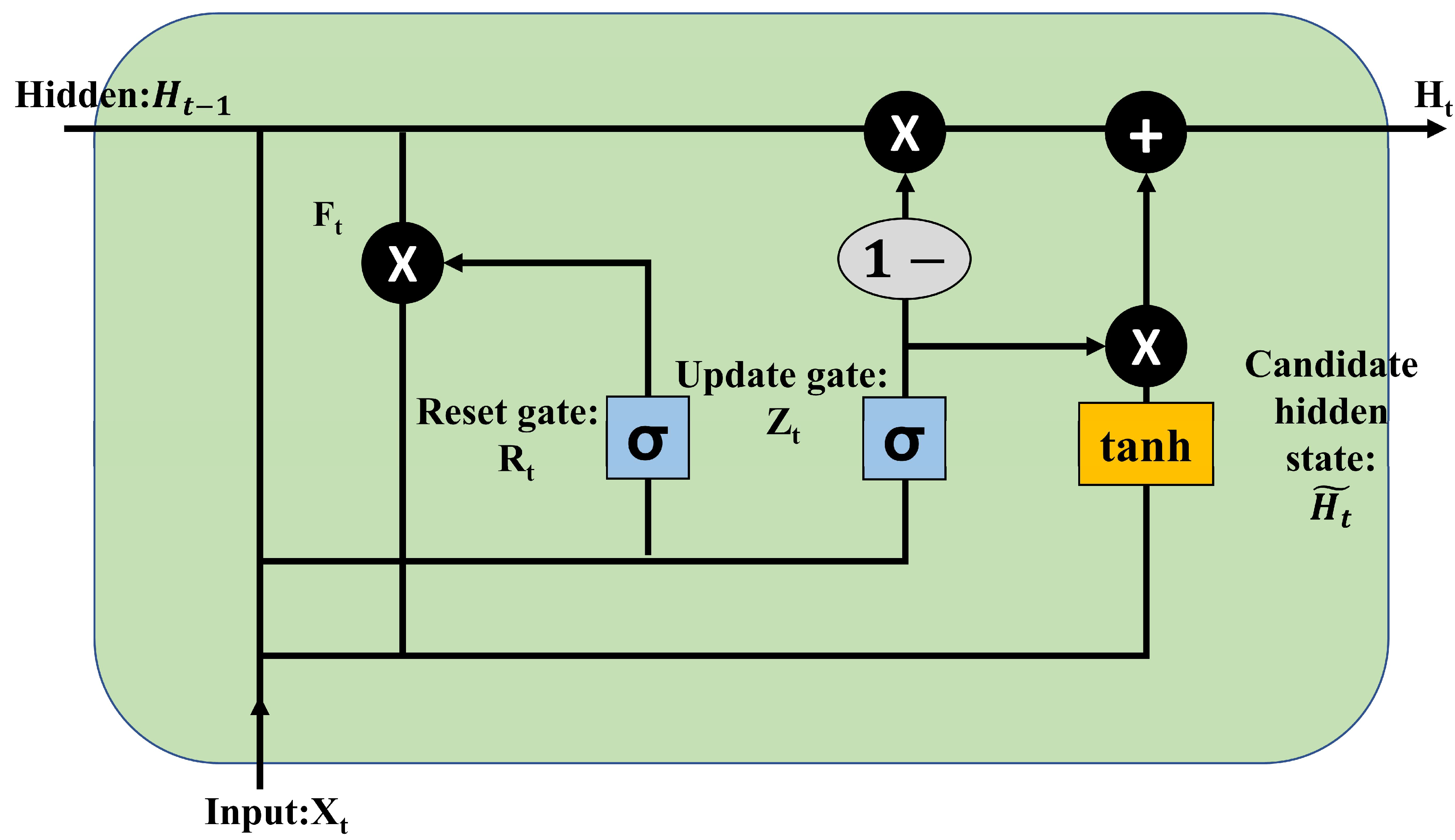
2.3.3. Gated Recurrent Units
2.3.4. Multi-Layer Perceptron
2.4. Performance Evaluation of Models
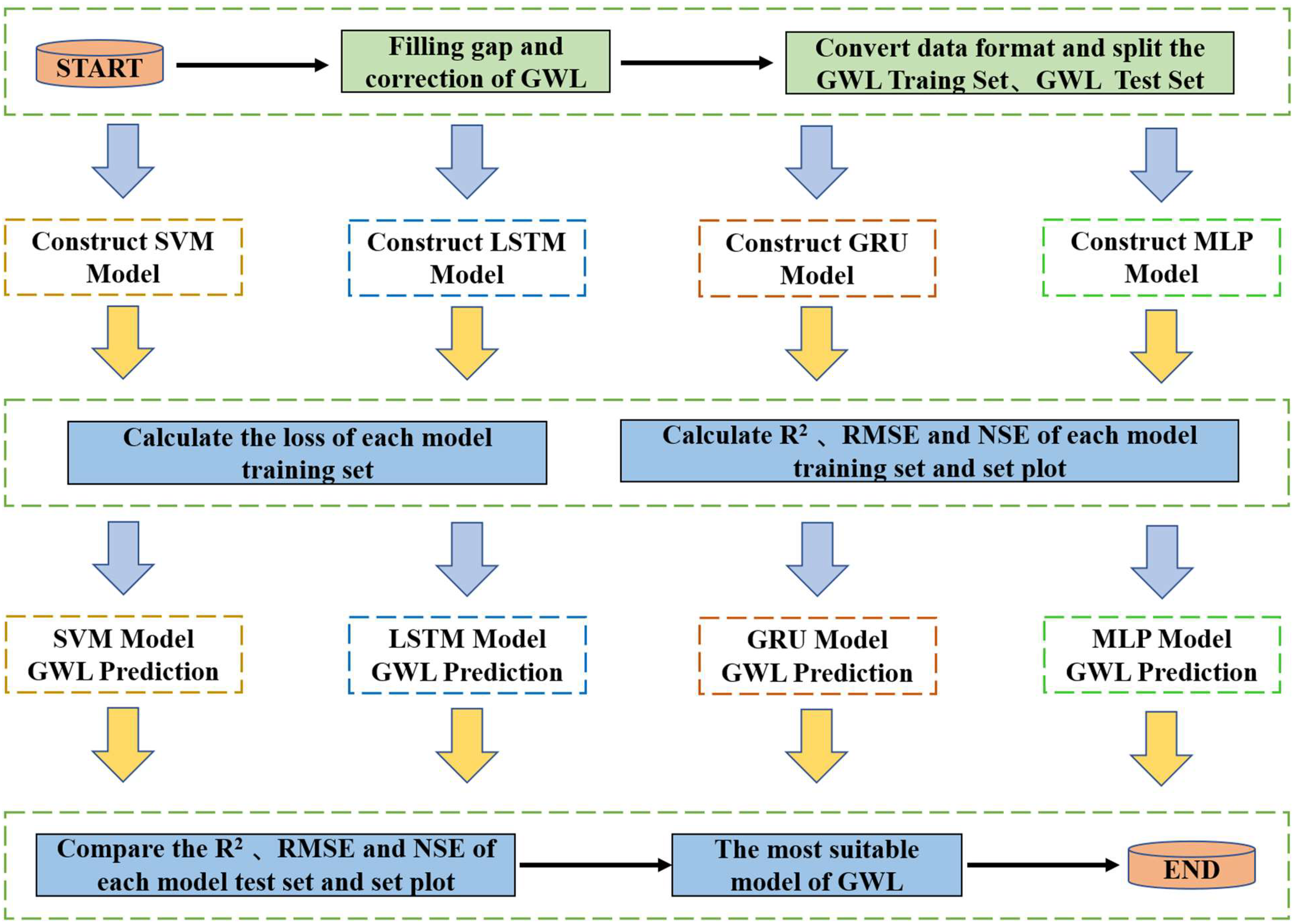
2.5. Groundwater Level Prediction Methodology
3. Results and Discussion
3.1. GWL Prediction Using SVM Model
3.2. GWL Prediction Using the LSTM Model
3.3. GWL Prediction Using the MLP Model
3.4. GWL Prediction Using the GRU Model
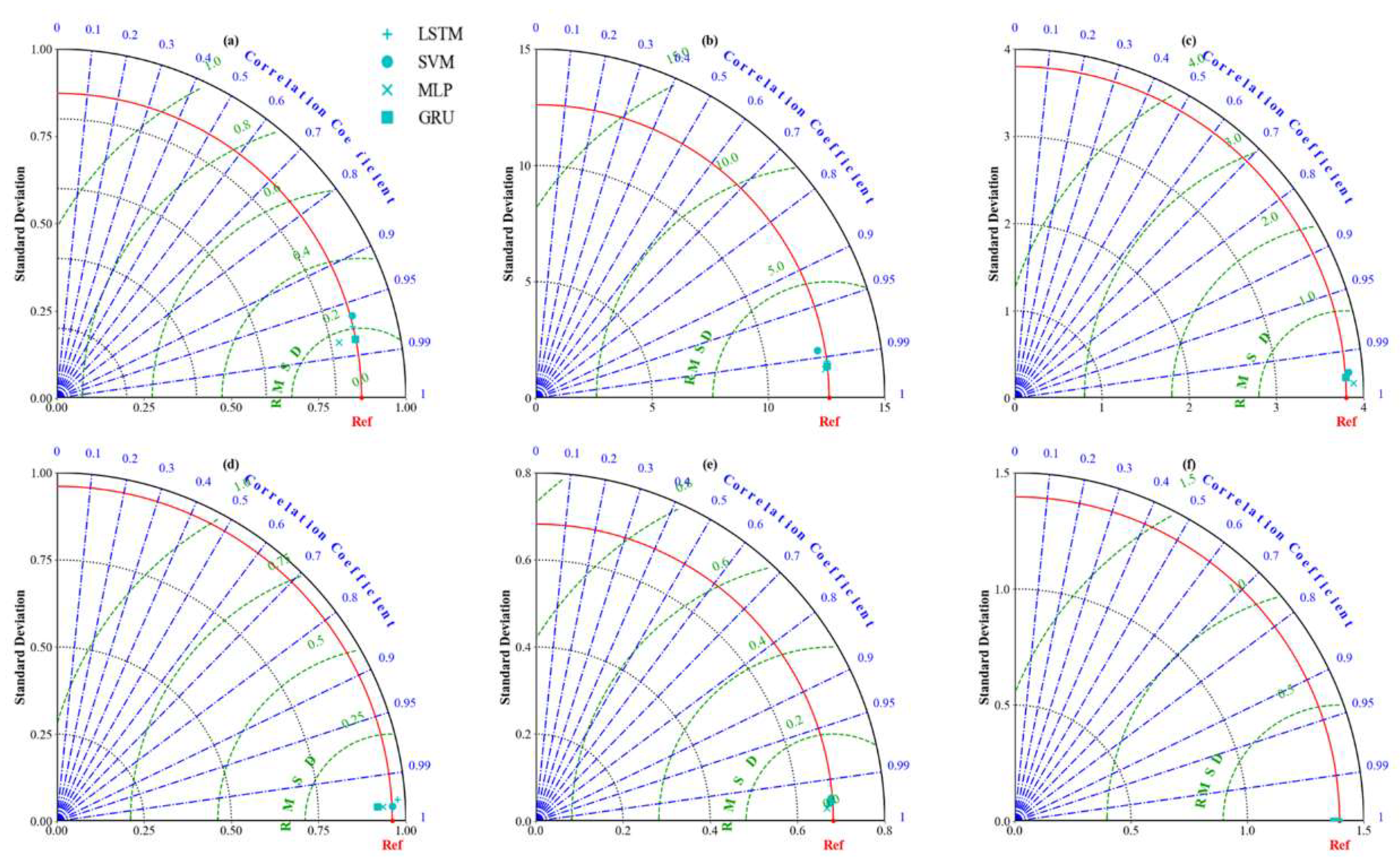
3.5. Model Comparison
4. Conclusions
- (1)
- By comparing the RMSE, R2, and NSE indicators, we discovered that the GRU model performed the best for dynamically fluctuating and dynamically increasing stations, while the MLP model performed the best for dynamically decreasing stations. The update gate in the GRU model acquired previous moment state information in the current state, which assisted in capturing long-term dependencies in the time series and solved the problem of overfitting to some extent. Moreover, the GRU model not only showed good performance in predicting trends, but it was also better than the other models regarding the training time and capturing extreme values, thus making it the most suitable model for predicting the GWL in the Hebei Plain.
- (2)
- Apart from the different principles of each model, the differences in the simulation results can be attributed to factors such as data segmentation during the modeling process, the length of subsequences, and the uncertainty of model parameters. Moreover, the influence of the different activation functions on the GWL in the different models should also be considered. Furthermore, the training frequency of each model in this study was the same, and adaptive improvements should be made for each model in subsequent studies.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wei, Y.; Sun, B. Optimizing Water Use Structures in Resource-Based Water-Deficient Regions Using Water Resources Input–Output Analysis: A Case Study in Hebei Province, China. Sustainability 2021, 13, 3939. [Google Scholar] [CrossRef]
- Currell, M.J.; Han, D.; Chen, Z.; Cartwright, I. Sustainability of groundwater usage in northern China: Dependence on palaeowaters and effects on water quality, quantity and ecosystem health. Hydrol. Process. 2012, 26, 4050–4066. [Google Scholar] [CrossRef]
- Niu, J.; Zhu, X.G.; Parry, M.A.J.; Kang, S.; Du, T.; Tong, L.; Ding, R. Environmental burdens of groundwater extraction for irrigation over an inland river basin in Northwest China. J. Clean. Prod. 2019, 222, 182–192. [Google Scholar] [CrossRef] [Green Version]
- Gupta, B.B.; Nema, A.K.; Mittal, A.K.; Maurya, N.S. Modeling of Groundwater Systems: Problems and Pitfalls. Available online: https://www.researchgate.net/profile/Atul-Mittal-3/publication/261758986_Modeling_of_Groundwater_Systems_Problems_and_Pitfalls/links/00b495356b45d3464c000000/Modeling-of-Groundwater-Systems-Problems-and-Pitfalls.pdf (accessed on 2 December 2022).
- Ahmadi, S.H.; Sedghamiz, A. Geostatistical analysis of spatial and temporal variations of groundwater level. Environ. Monit. Assess. 2007, 129, 277–294. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhang, W.; Nie, N.; Guo, Y. Long-term groundwater storage variations estimated in the Songhua River Basin by using GRACE products, land surface models, and in-situ observations. Sci. Total Environ. 2019, 649, 372–387. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, S.; Russo, T.A.; Elliott, J.; Foster, I. Machine learning algorithms for modeling groundwater level changes in agricultural regions of the US. Water Resour. Res. 2017, 53, 3878–3895. [Google Scholar] [CrossRef] [Green Version]
- Yadav, B.; Ch, S.; Mathur, S.; Adamowski, J. Assessing the suitability of extreme learning machines (ELM) for groundwater level prediction. J. Water Land Dev. 2017, 32, 103–112. [Google Scholar] [CrossRef]
- Xiong, J.; Guo, S.; Kinouchi, T. Leveraging machine learning methods to quantify 50 years of dwindling groundwater in India. Sci. Total Environ. 2022, 835, 155474. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0048969722025700 (accessed on 3 December 2022). [CrossRef]
- Pratoomchai, W.; Kazama, S.; Hanasaki, N.; Ekkawatpanit, C.; Komori, D. A projection of groundwater resources in the Upper Chao Phraya River basin in Thailand. Hydrol. Res. Lett. 2014, 8, 20–26. [Google Scholar]
- Thomas, B.F.; Famiglietti, J.S.; Landerer, F.W.; Wiese, D.N.; Molotch, N.P.; Argus, D.F. GRACE groundwater drought index: Evaluation of California Central Valley groundwater drought. Remote Sens. Environ. 2017, 198, 384–392. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; p. 314. [Google Scholar]
- Scholkoff, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002; p. 648. [Google Scholar]
- Asefa, T.; Kemblowski, M.W.; Urroz, G.; McKee, M.; Khalil, A. Support vectors–based groundwater head observation networks design. Water Resour. Res. 2004, 40, 11. Available online: https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2004WR003304 (accessed on 3 December 2022). [CrossRef] [Green Version]
- Yoon, H.; Jun, S.C.; Hyun, Y.; Bae, G.-O.; Lee, K.-K. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer. J. Hydrol. 2011, 396, 128–138. [Google Scholar] [CrossRef]
- Tapak, L.; Rahmani, A.R.; Moghimbeigi, A. Prediction the groundwater level of Hamadan-Bahar plain, west of Iran using support vector machines. J. Res. Health Sci. 2013, 14, 82–87. [Google Scholar]
- Sudheer, C.; Maheswaran, R.; Panigrahi, B.K.; Mathur, S. A hybrid SVM-PSO model for forecasting monthly streamflow. Neural Comput. Appl. 2014, 24, 1381–1389. [Google Scholar] [CrossRef]
- Wang, W.; Xu, D.; Chau, K.; Chen, S. Improved annual rainfall-runoff forecasting using PSO–SVM model based on EEMD. J. Hydroinformatics 2013, 15, 1377–1390. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Vu, M.T.; Jardani, A.; Massei, N.; Fournier, M. Reconstruction of missing groundwater level data by using Long Short-Term Memory (LSTM) deep neural network. J. Hydrol. 2021, 597, 125776. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Groundwater level forecasting with artificial neural networks: A comparison of long short-term memory (LSTM), convolutional neural networks (CNNs), and non-linear autoregressive networks with exogenous input (NARX). Hydrol. Earth Syst. Sci. 2021, 25, 1671–1687. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3/E; Pearson Education India: New Delhi, India, 2009; Available online: https://www.pearson.com/en-us/subject-catalog/p/neural-networks-and-learning-machines/P200000003278 (accessed on 4 December 2022).
- Foddis, M.L.; Montisci, A.; Trabelsi, F.; Uras, G. An MLP-ANN-based approach for assessing nitrate contamination. Water Supply 2019, 19, 1911–1917. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Deo, R.C.; Karimi, V.; Yaseen, Z.M.; Terzi, O. Implementation of a hybrid MLP-FFA model for water level prediction of Lake Egirdir, Turkey. Stoch. Environ. Res. Risk Assess. 2018, 32, 1683–1697. [Google Scholar] [CrossRef]
- Singh, A.; Imtiyaz, M.; Isaac, R.K.; Denis, D.M. Comparison of soil and water assessment tool (SWAT) and multilayer perceptron (MLP) artificial neural network for predicting sediment yield in the Nagwa agricultural watershed in Jharkhand, India. Agric. Water Manag. 2012, 104, 113–120. [Google Scholar] [CrossRef]
- Jia, X.; Cao, Y.; O’Connor, D.; Zhu, J.; Tsang, D.C.; Zou, B.; Hou, D. Mapping soil pollution by using drone image recognition and machine learning at an arsenic-contaminated agricultural field. Environ. Pollut. 2021, 270, 116281. [Google Scholar] [CrossRef] [PubMed]
- Ijlil, S.; Essahlaoui, A.; Mohajane, M.; Essahlaoui, N.; Mili, E.M.; Van Rompaey, A. Machine Learning Algorithms for Modeling and Mapping of Groundwater Pollution Risk: A Study to Reach Water Security and Sustainable Development (Sdg) Goals in a Mediterranean Aquifer System. Remote Sens. 2022, 14, 2379. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. Available online: https://arxiv.org/abs/1406.1078 (accessed on 4 December 2022).
- Jeong, J.; Park, E. Comparative applications of data-driven models representing water table fluctuations. J. Hydrol. 2019, 572, 261–273. [Google Scholar] [CrossRef]
- Zhang, D.; Lindholm, G.; Ratnaweera, H. Use long short-term memory to enhance Internet of Things for combined sewer overflow monitoring. J. Hydrol. 2018, 556, 409–418. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, G.; Huang, X.; Chen, K.; Hou, J.; Zhou, J. Development of a surrogate method of groundwater modeling using gated recurrent unit to improve the efficiency of parameter auto-calibration and global sensitivity analysis. J. Hydrol. 2021, 598, 125726. [Google Scholar] [CrossRef]

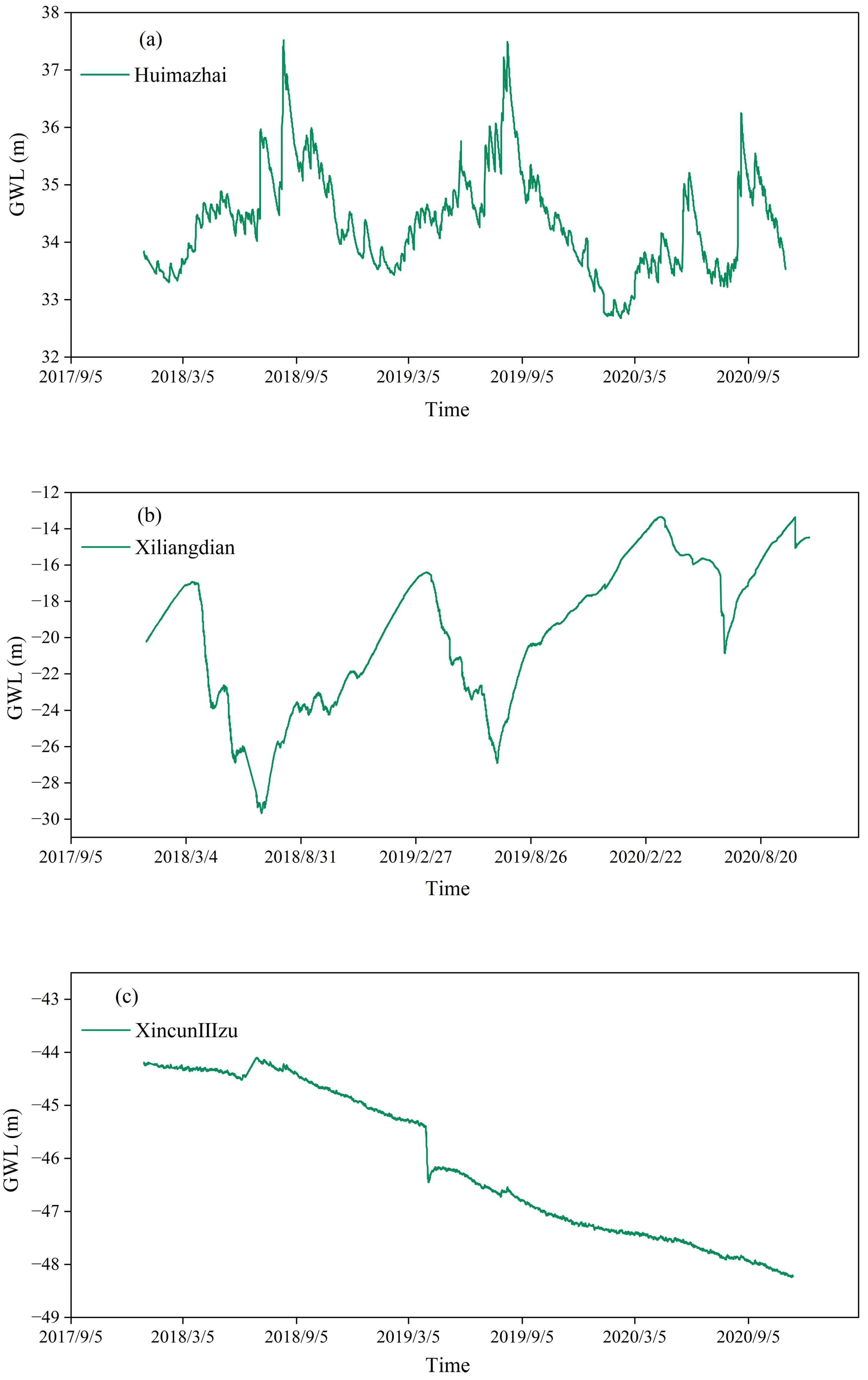

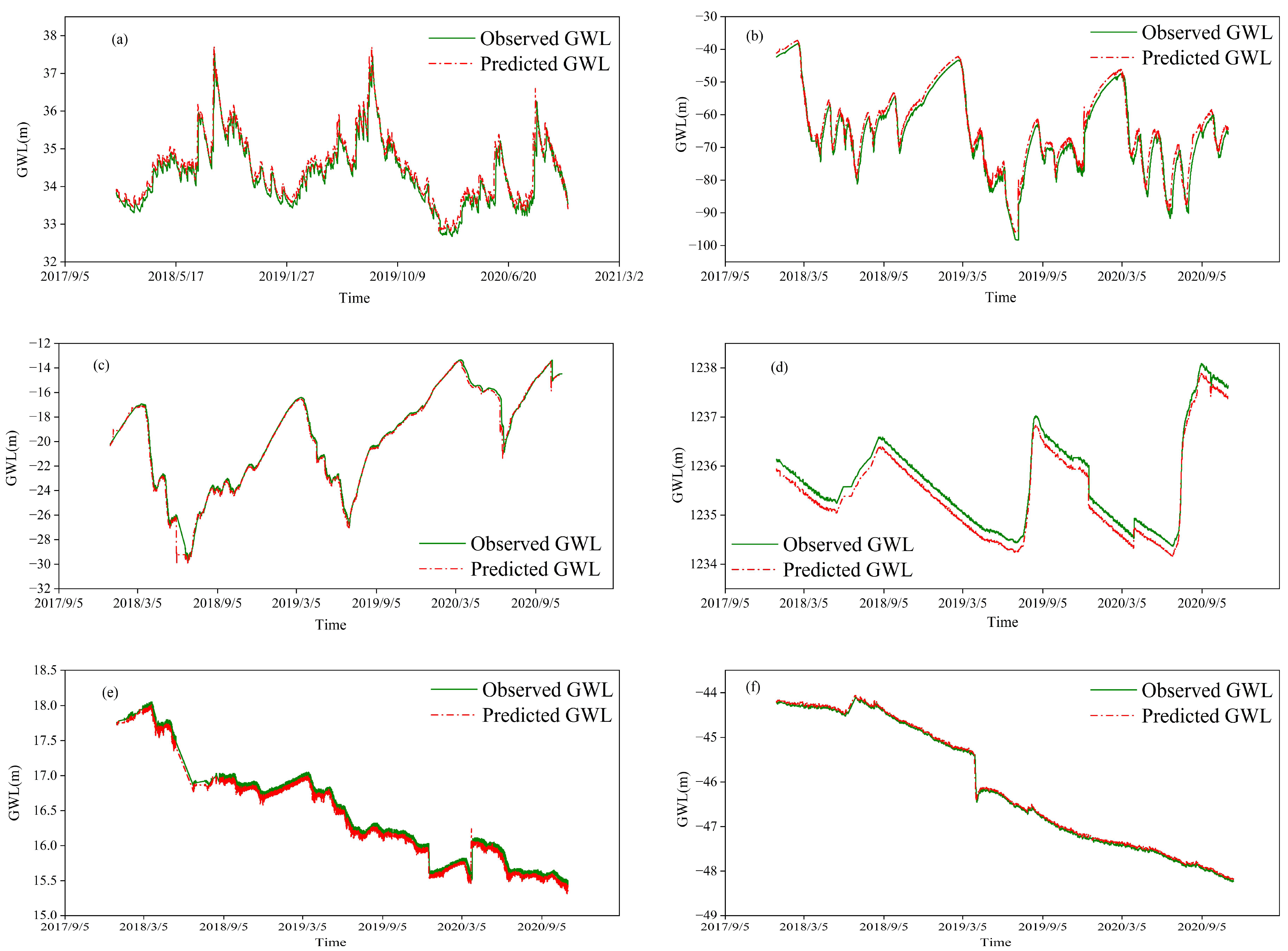
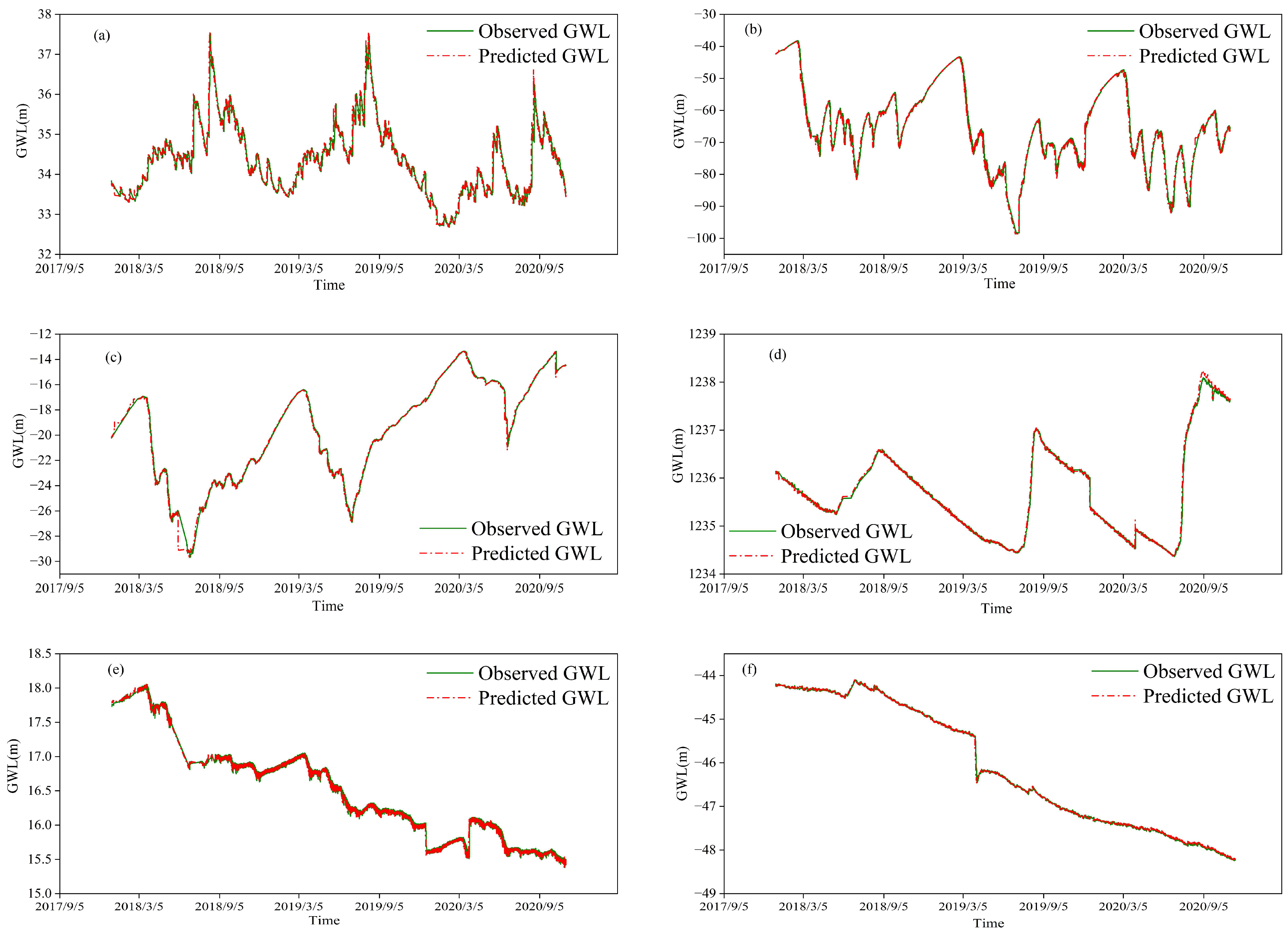
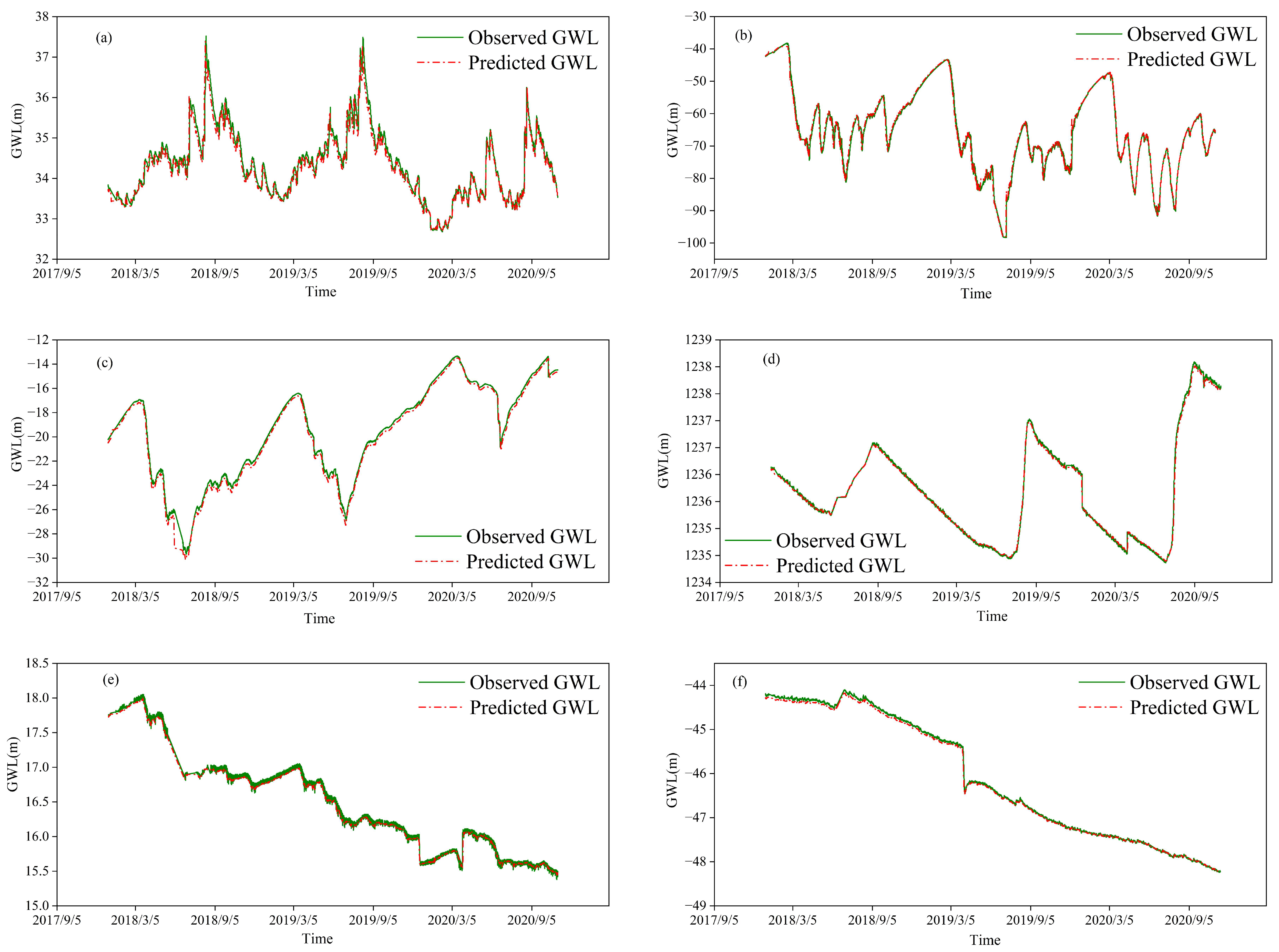


| Number | Type | Station | City | GWL | Sequence Length (Day) |
|---|---|---|---|---|---|
| 1 | dynamic fluctuations | Huimazhai | Qinhuangdao | 33.83 | 5480 |
| 2 | Hongmiao | Xingtai | 17.74 | 5480 | |
| 3 | dynamic increase | Xiliangdian | Baoding | −20.23 | 5480 |
| 4 | Yanmeidong | Baoding | 1236.14 | 5480 | |
| 5 | dynamic decrease | Wangduxiancheng | Baoding | −42.33 | 5480 |
| 6 | XincunIIIzu | Huanghua | −44.21 | 5480 |
| Station | Training | Testing | ||||
|---|---|---|---|---|---|---|
| RMSE | R2 | NSE | RMSE | R2 | NSE | |
| Huimazhai | 0.253 | 0.953 | 0.921 | 0.396 | 0.757 | 0.691 |
| Hongmiao | 2.299 | 0.98 | 0.967 | 3.823 | 0.867 | 0.804 |
| Xiliangdian | 0.298 | 0.995 | 0.994 | 0.511 | 0.915 | 0.908 |
| Yanmeidong | 0.204 | 0.998 | 0.909 | 0.193 | 0.998 | 0.984 |
| Wangduxiancheng | 0.076 | 0.992 | 0.985 | 0.071 | 0.929 | 0.808 |
| XincunIIIzu | 0.052 | 0.999 | 0.998 | 0.045 | 0.990 | 0.940 |
| Station | Training | Testing | ||||
|---|---|---|---|---|---|---|
| RMSE | R2 | NSE | RMSE | R2 | NSE | |
| Huimazhai | 0.192 | 0.955 | 0.955 | 0.263 | 0.868 | 0.864 |
| Hongmiao | 1.581 | 0.985 | 0.984 | 1.771 | 0.958 | 0.958 |
| Xiliangdian | 0.244 | 0.996 | 0.996 | 0.338 | 0.961 | 0.96 |
| Yanmeidong | 0.053 | 0.994 | 0.994 | 0.116 | 0.996 | 0.994 |
| Wangduxiancheng | 0.049 | 0.994 | 0.994 | 0.036 | 0.953 | 0.95 |
| XincunIIIzu | 0.037 | 0.999 | 0.999 | 0.028 | 0.987 | 0.976 |
| Station | Training | Testing | ||||
|---|---|---|---|---|---|---|
| RMSE | R2 | NSE | RMSE | R2 | NSE | |
| Huimazhai | 0.201 | 0.959 | 0.95 | 0.128 | 0.979 | 0.968 |
| Hongmiao | 1.419 | 0.988 | 0.987 | 0.514 | 0.997 | 0.996 |
| Xiliangdian | 0.347 | 0.999 | 0.991 | 0.295 | 0.987 | 0.969 |
| Yanmeidong | 0.033 | 0.998 | 0.998 | 0.08 | 0.998 | 0.997 |
| Wangduxiancheng | 0.041 | 0.997 | 0.996 | 0.028 | 0.969 | 0.97 |
| XincunIIIzu | 0.051 | 0.999 | 0.998 | 0.014 | 0.995 | 0.994 |
| Station | Training | Testing | ||||
|---|---|---|---|---|---|---|
| RMSE | R2 | NSE | RMSE | R2 | NSE | |
| Huimazhai | 0.182 | 0.959 | 0.959 | 0.08 | 0.988 | 0.987 |
| Hongmiao | 1.449 | 0.987 | 0.987 | 0.518 | 0.996 | 0.996 |
| Xiliangdian | 0.229 | 0.996 | 0.996 | 0.123 | 0.995 | 0.995 |
| Yanmeidong | 0.04 | 0.998 | 0.996 | 0.098 | 0.998 | 0.996 |
| Wangduxiancheng | 0.041 | 0.996 | 0.996 | 0.033 | 0.961 | 0.96 |
| XincunIIIzu | 0.081 | 0.999 | 0.996 | 0.027 | 0.995 | 0.978 |
| Model | SVM | LSTM | GRU | MLP |
|---|---|---|---|---|
| Time (min) | 1081 | 1660 | 1251 | 2694 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Lu, C.; Sun, Q.; Lu, W.; He, X.; Qin, T.; Yan, L.; Wu, C. Predicting Groundwater Level Based on Machine Learning: A Case Study of the Hebei Plain. Water 2023, 15, 823. https://doi.org/10.3390/w15040823
Wu Z, Lu C, Sun Q, Lu W, He X, Qin T, Yan L, Wu C. Predicting Groundwater Level Based on Machine Learning: A Case Study of the Hebei Plain. Water. 2023; 15(4):823. https://doi.org/10.3390/w15040823
Chicago/Turabian StyleWu, Zhenjiang, Chuiyu Lu, Qingyan Sun, Wen Lu, Xin He, Tao Qin, Lingjia Yan, and Chu Wu. 2023. "Predicting Groundwater Level Based on Machine Learning: A Case Study of the Hebei Plain" Water 15, no. 4: 823. https://doi.org/10.3390/w15040823
APA StyleWu, Z., Lu, C., Sun, Q., Lu, W., He, X., Qin, T., Yan, L., & Wu, C. (2023). Predicting Groundwater Level Based on Machine Learning: A Case Study of the Hebei Plain. Water, 15(4), 823. https://doi.org/10.3390/w15040823













