Multi-Scale Wake Characteristics of the Flow over a Cylinder with Different V-Groove Numbers
Abstract
:1. Introduction
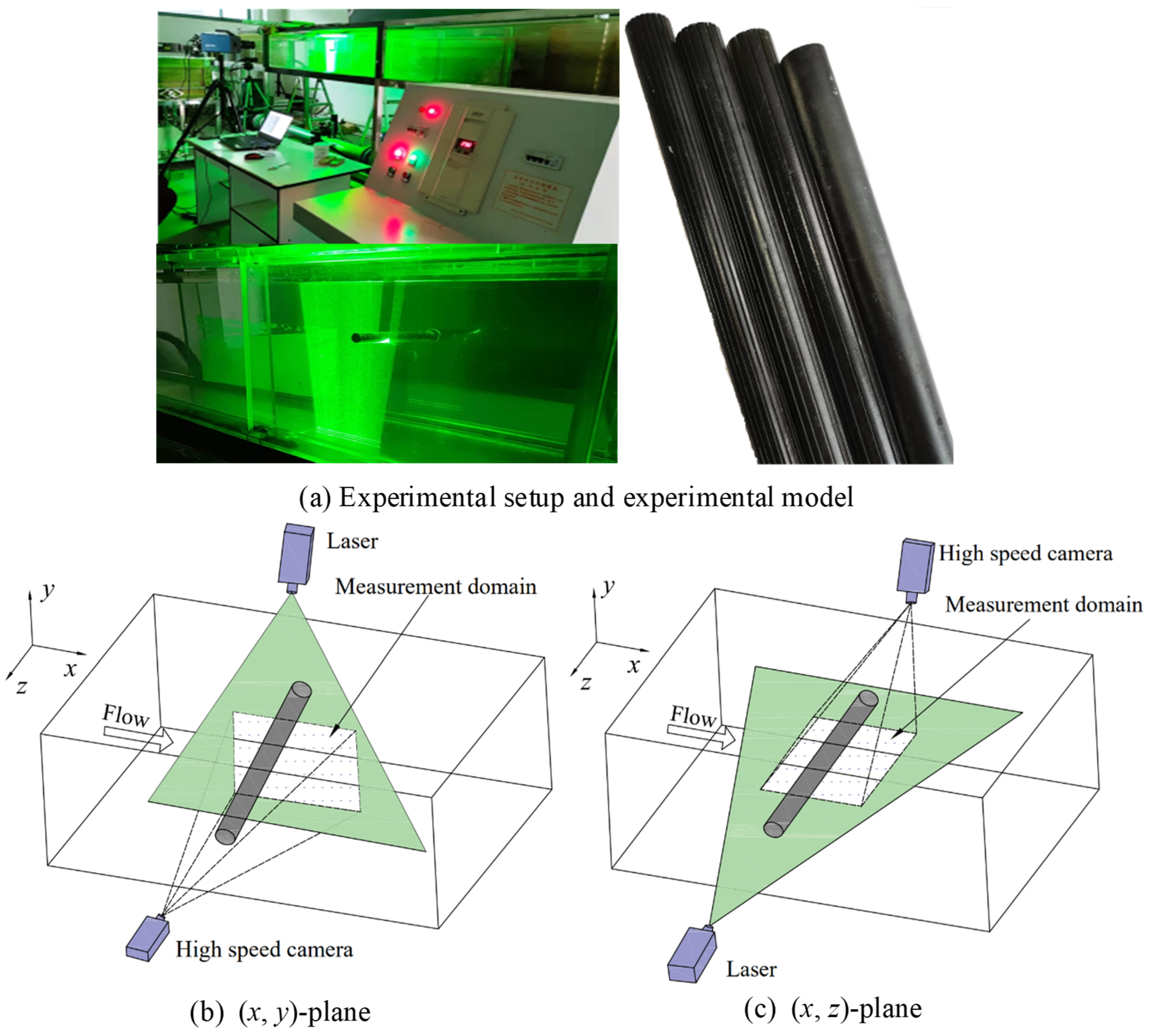
2. Experimental Methods
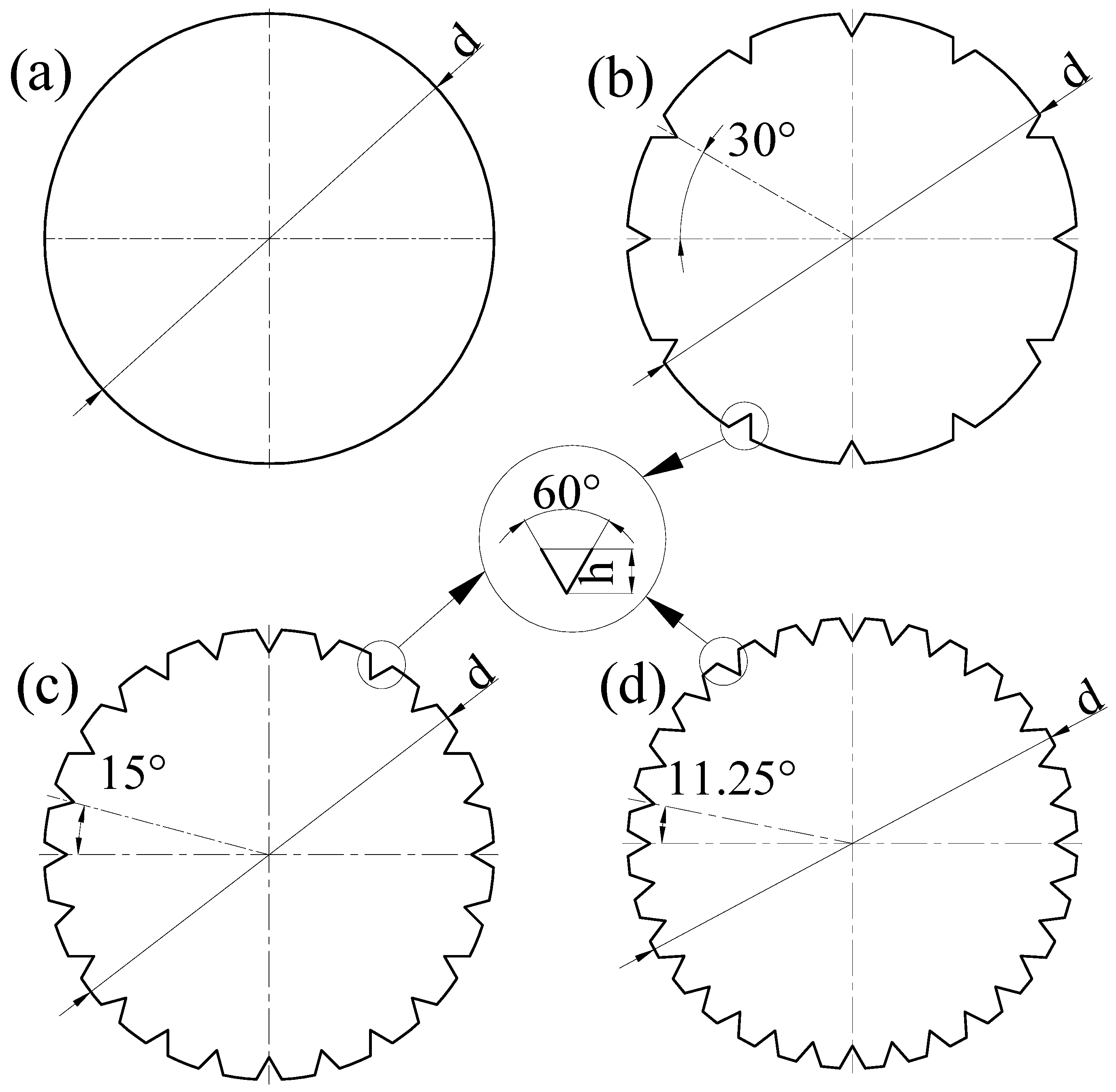
2.1. Experimental Models
2.2. High-Speed PIV Measurement
2.3. Orthogonal Wavelet Multi-Resolution Procedure
3. Experimental Results and Discussion
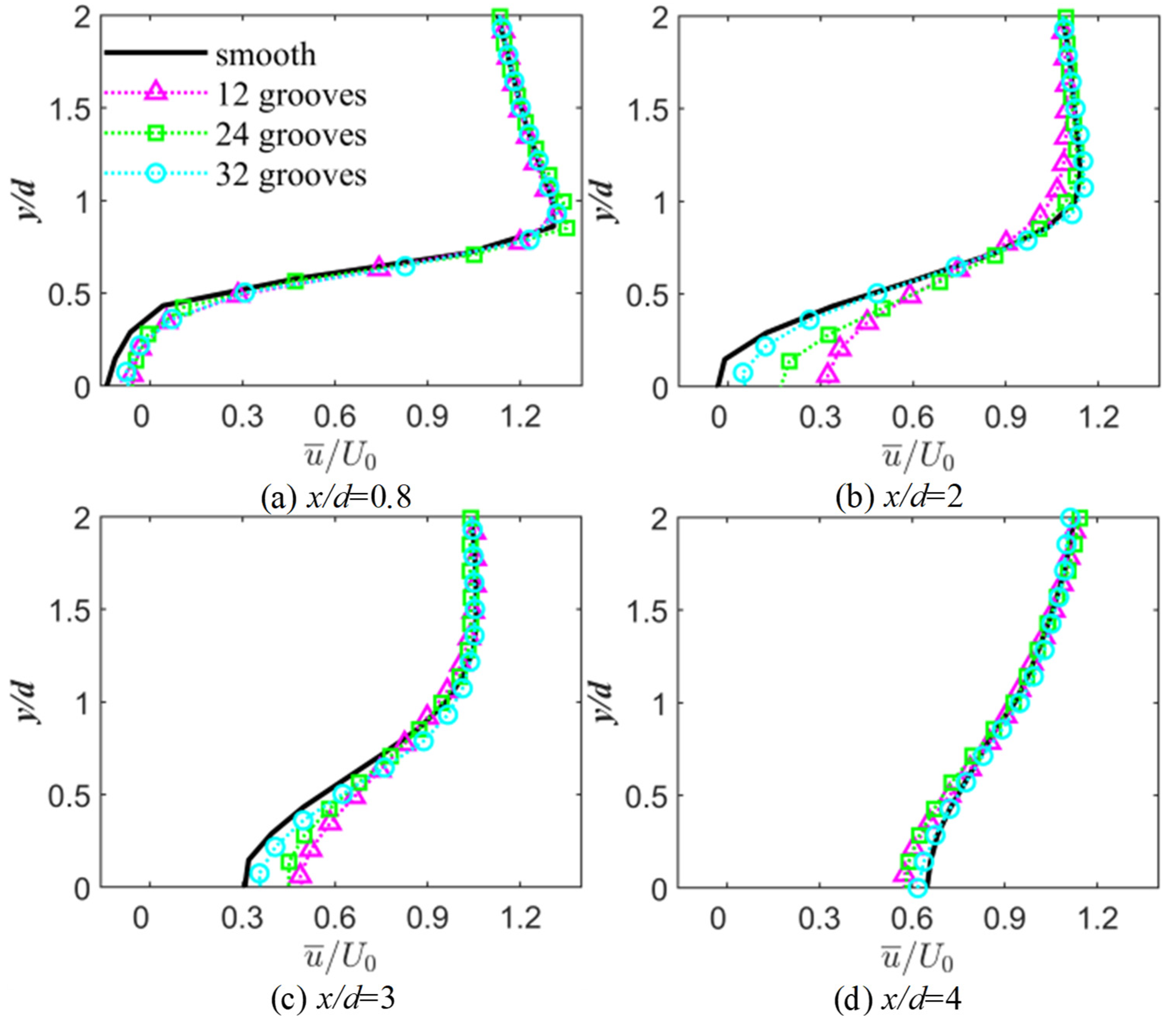
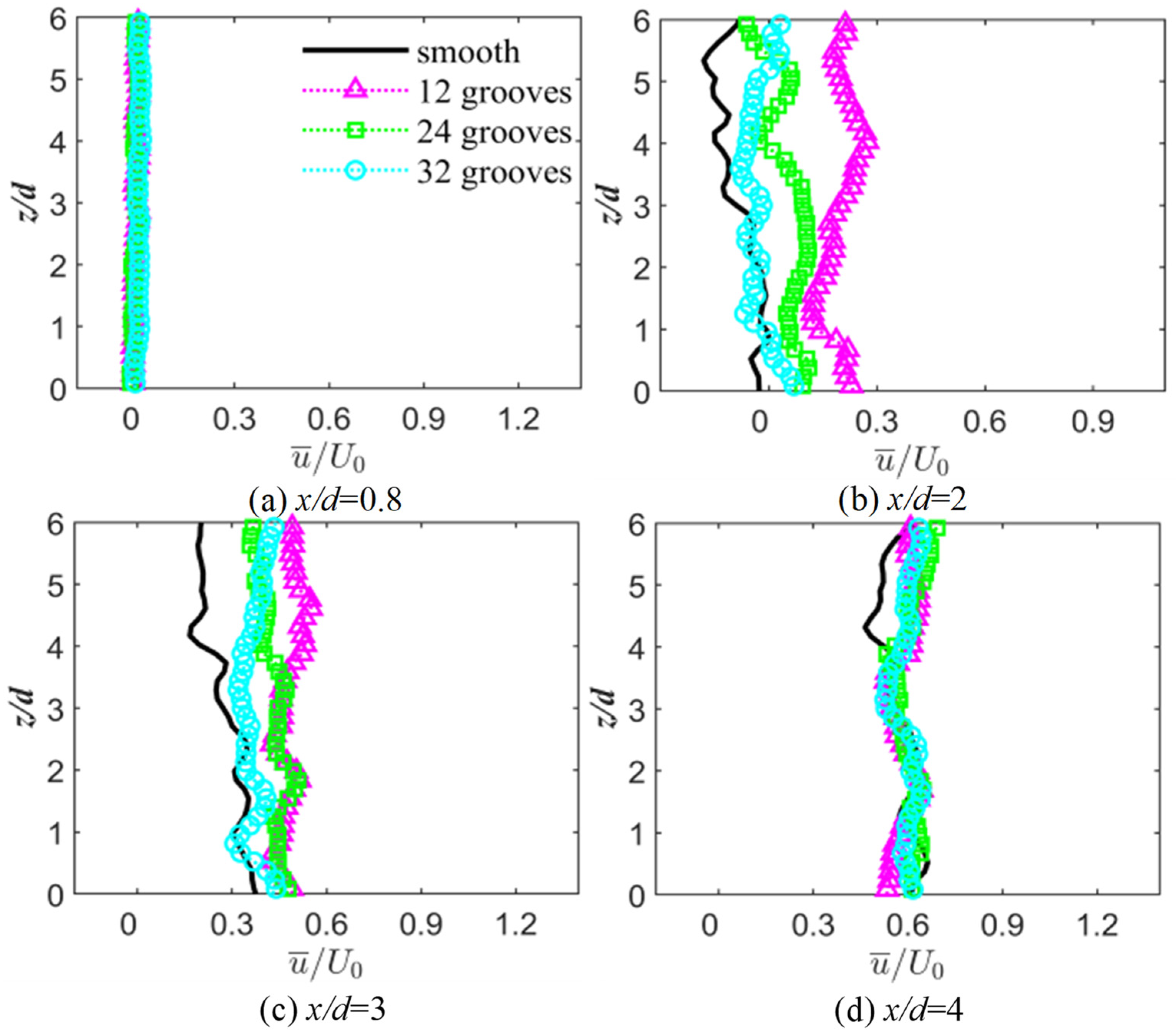
3.1. Profiles of Mean Velocity
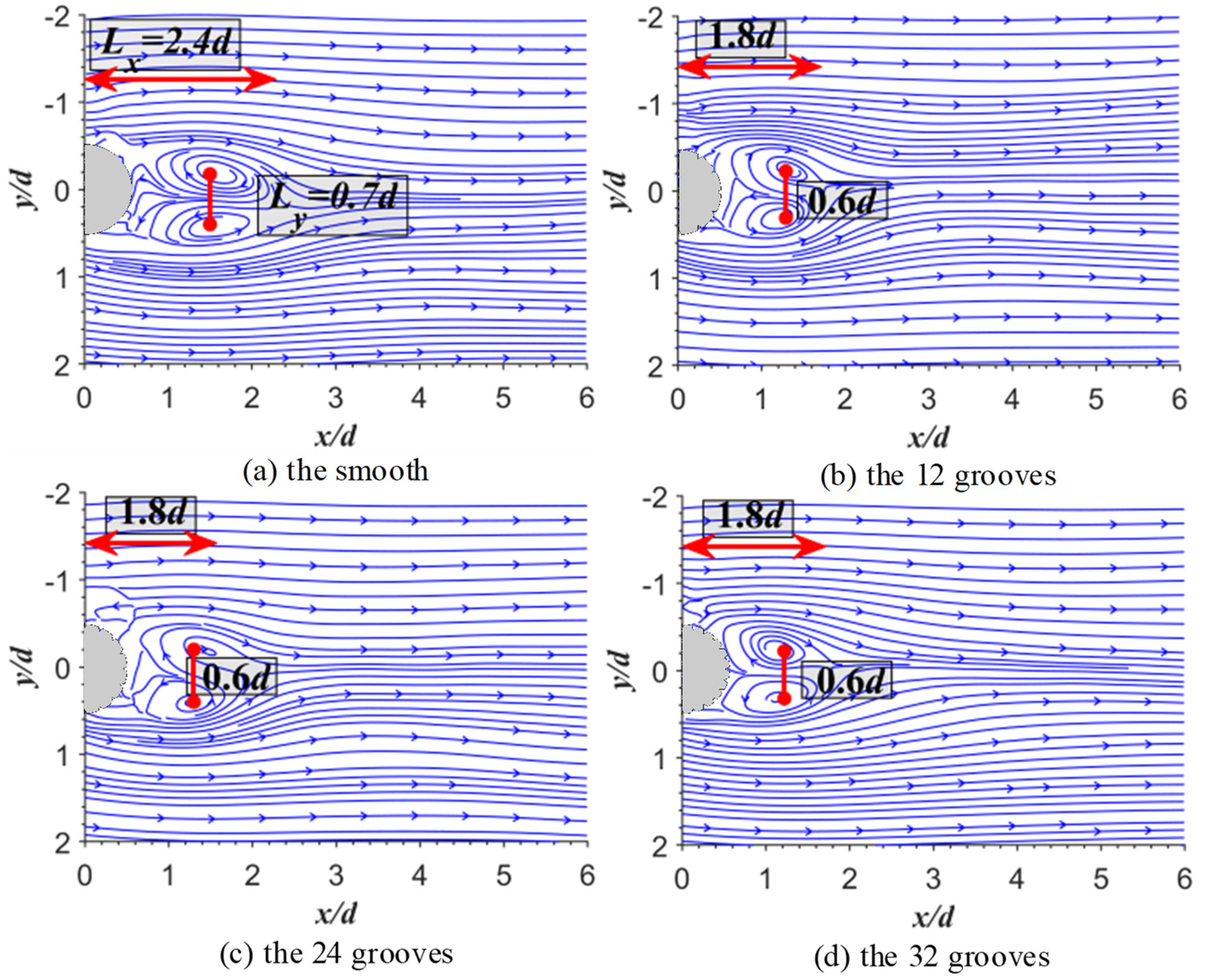
3.2. Time-Averaged Streamlines and Recirculation Region
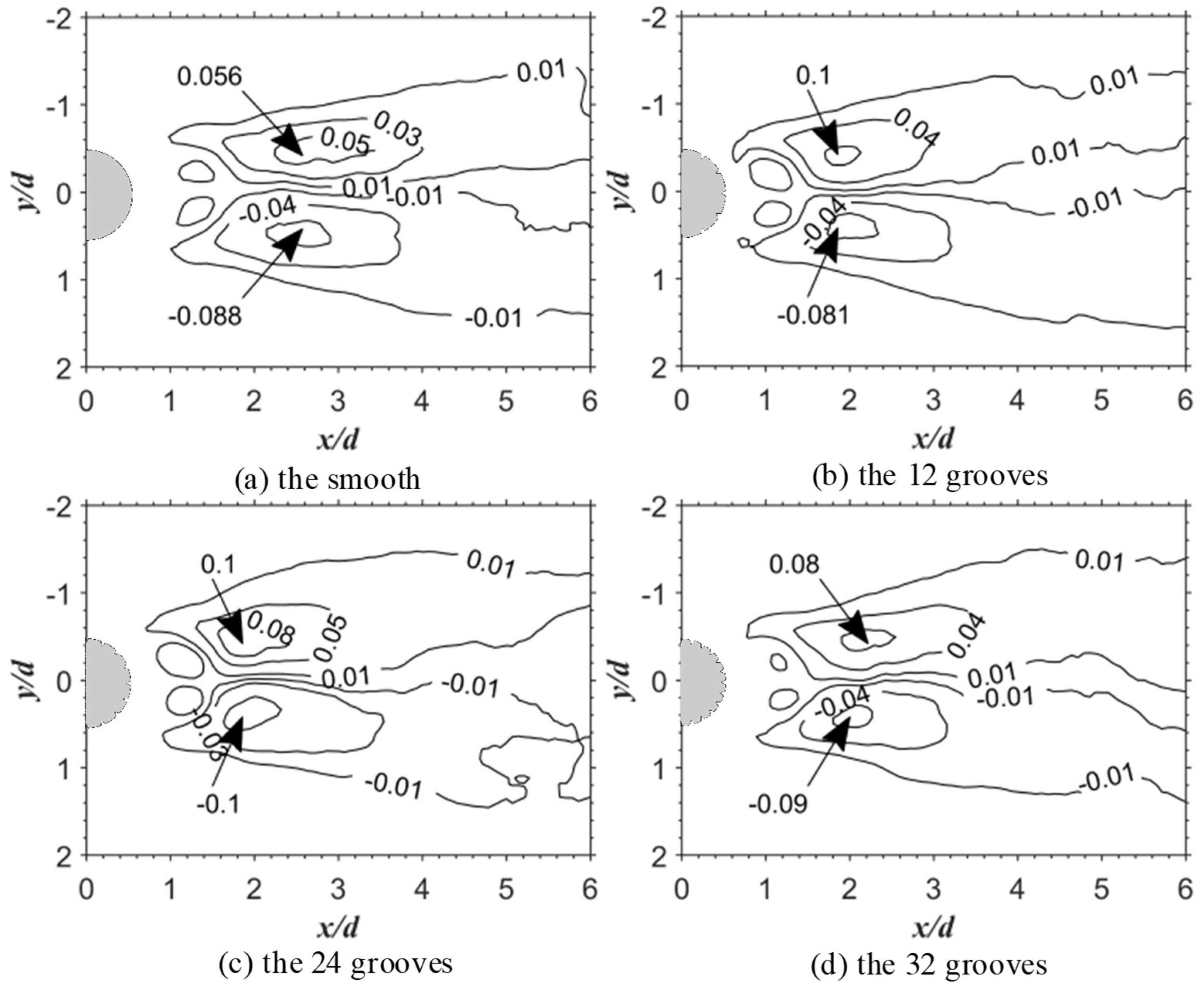
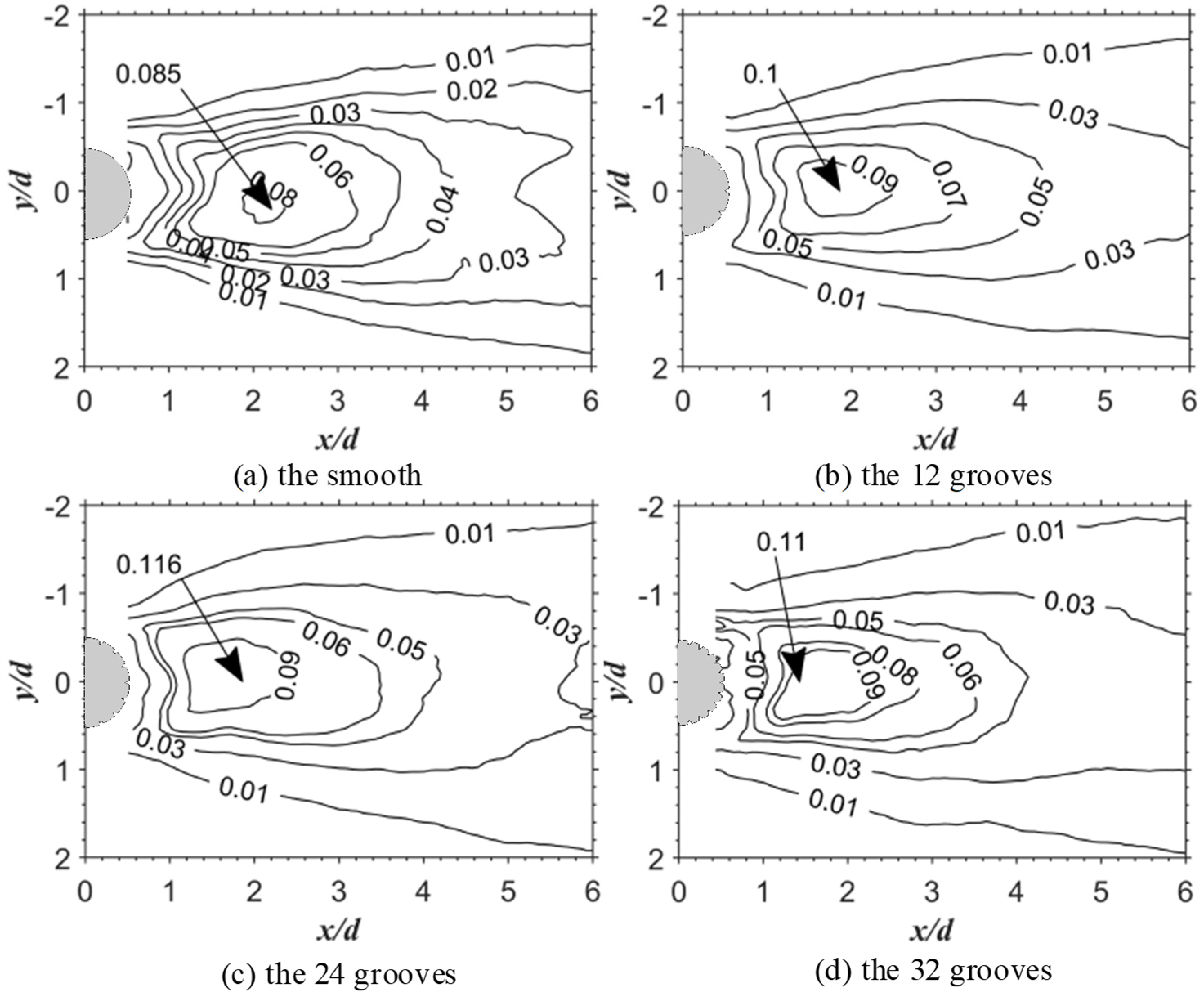
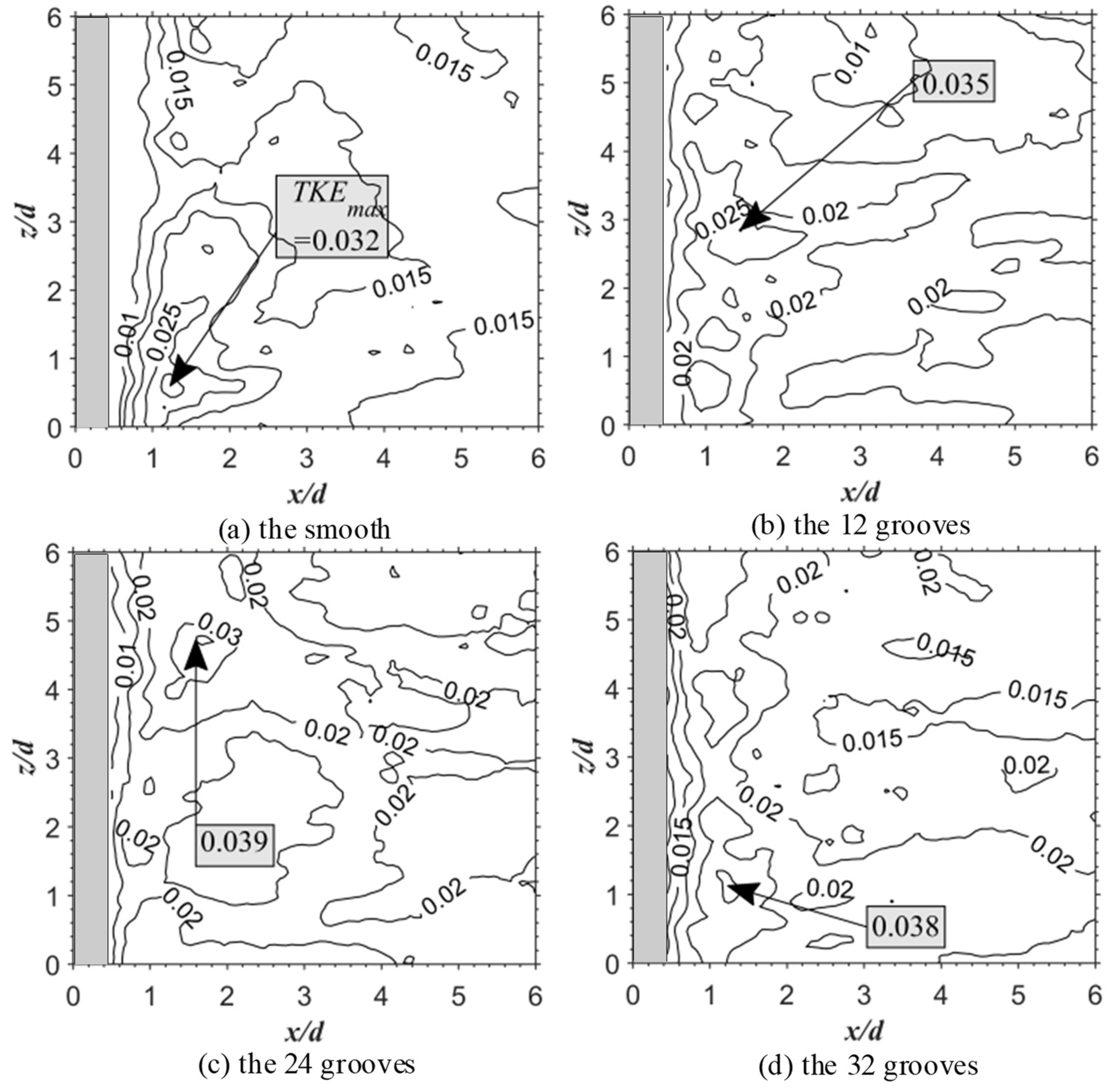
3.3. Reynolds Stress and Turbulent Kinetic Energy
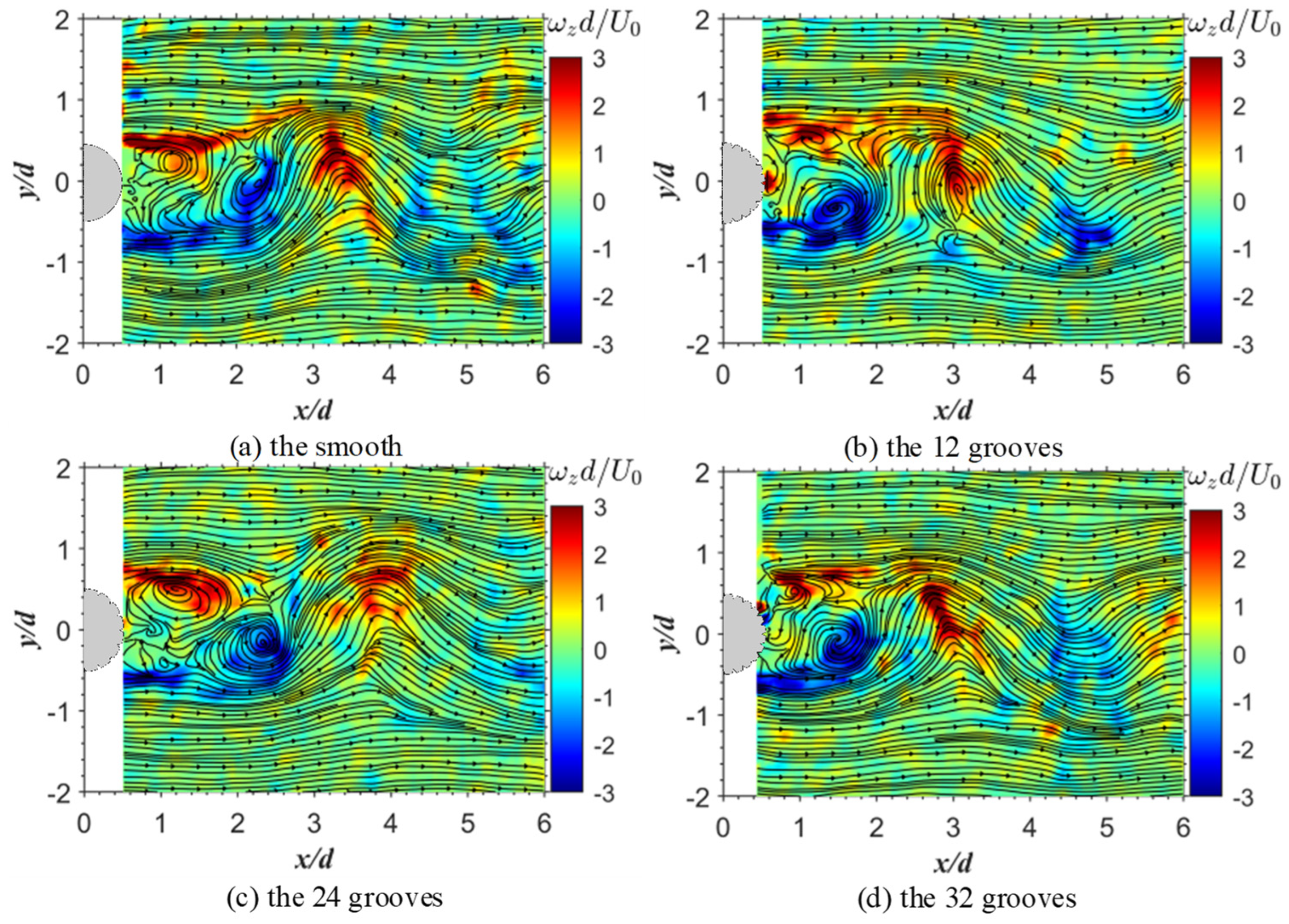
3.4. Instantaneous Flow Structures
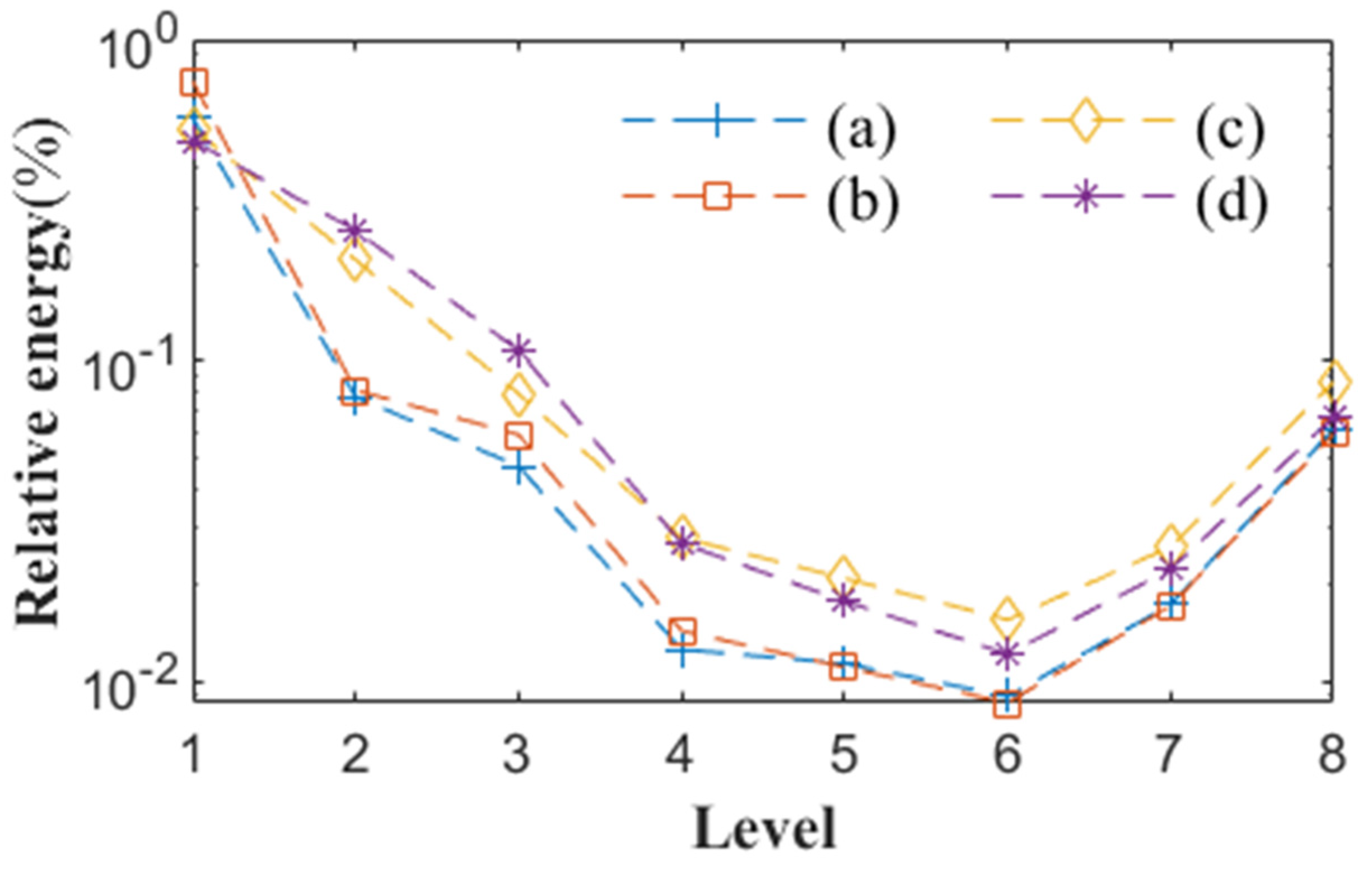
3.5. Select Wavelet Components Based on Relative Energy Percentage
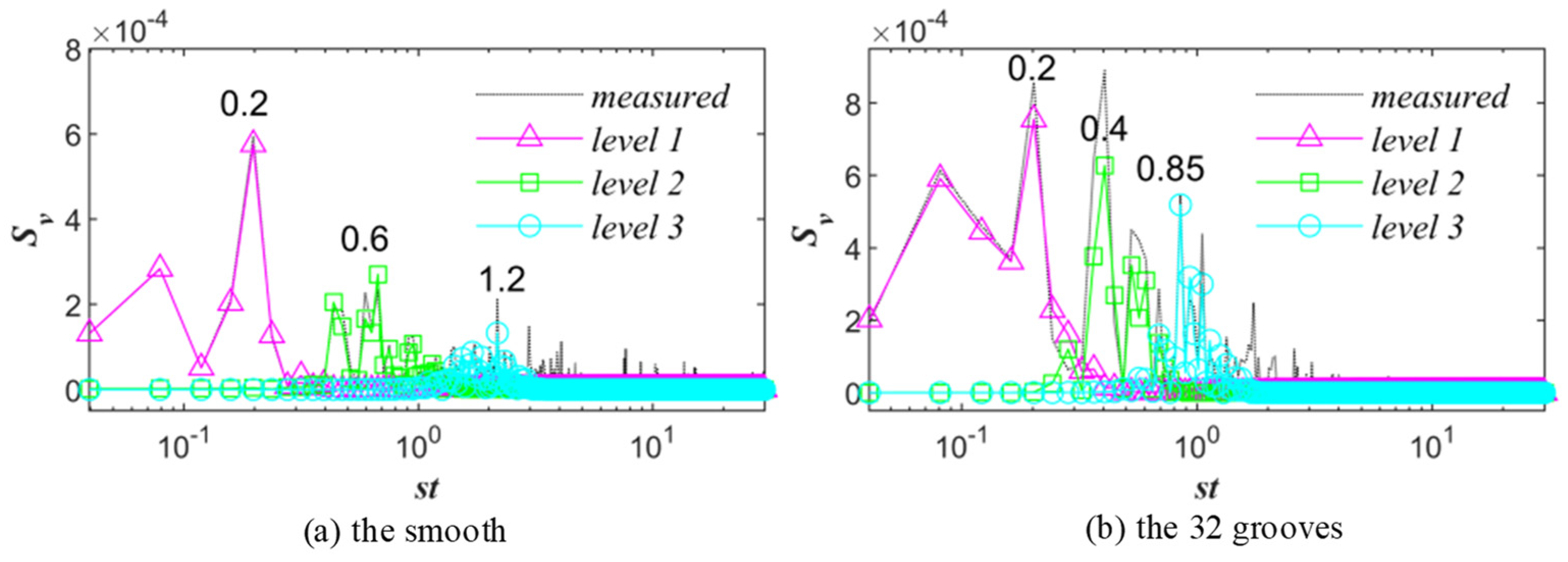
3.6. Spectral Analysis Calculation of Vortex Frequency
3.7. Instantaneous Vorticity Contours of Different Scales
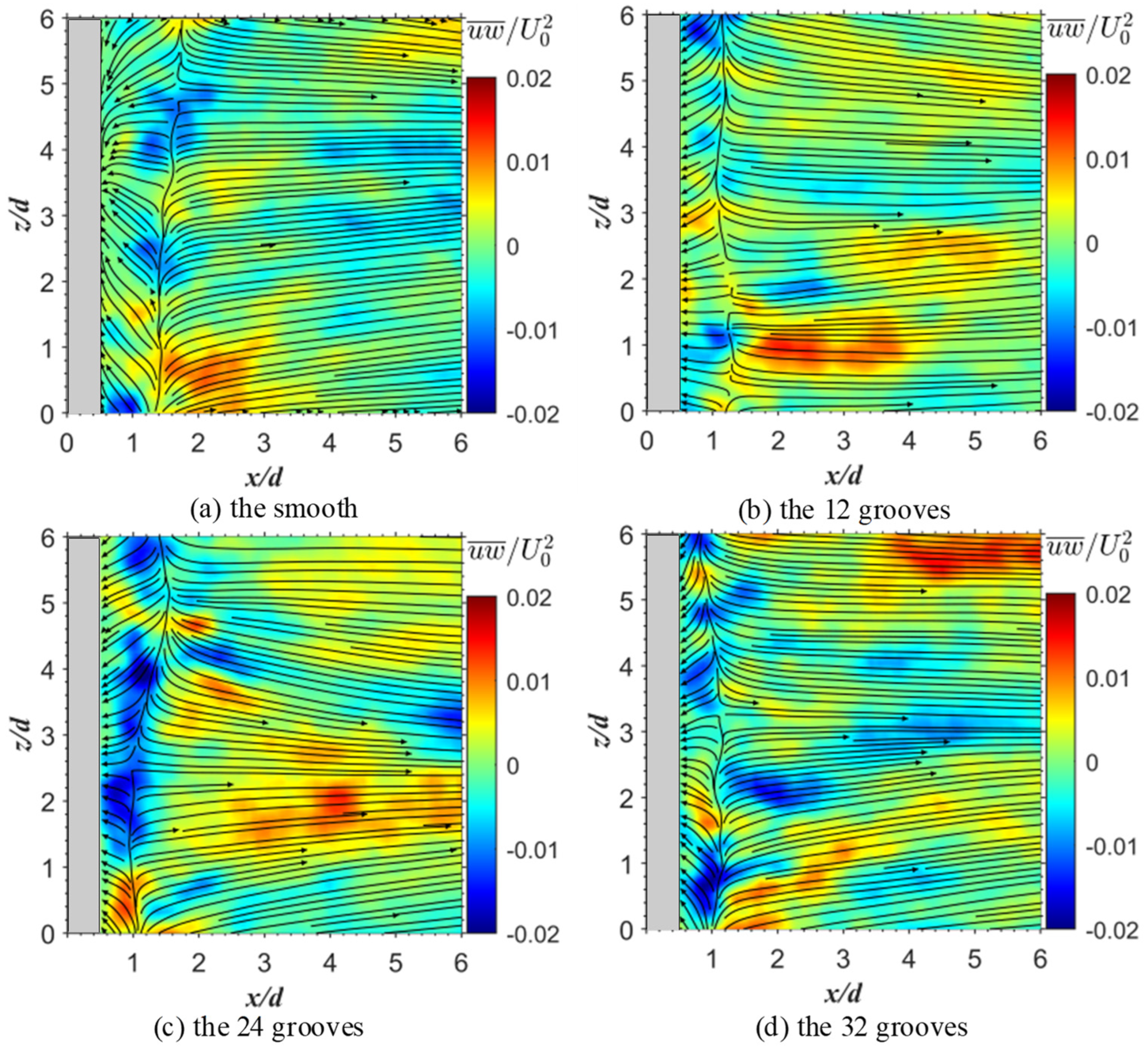
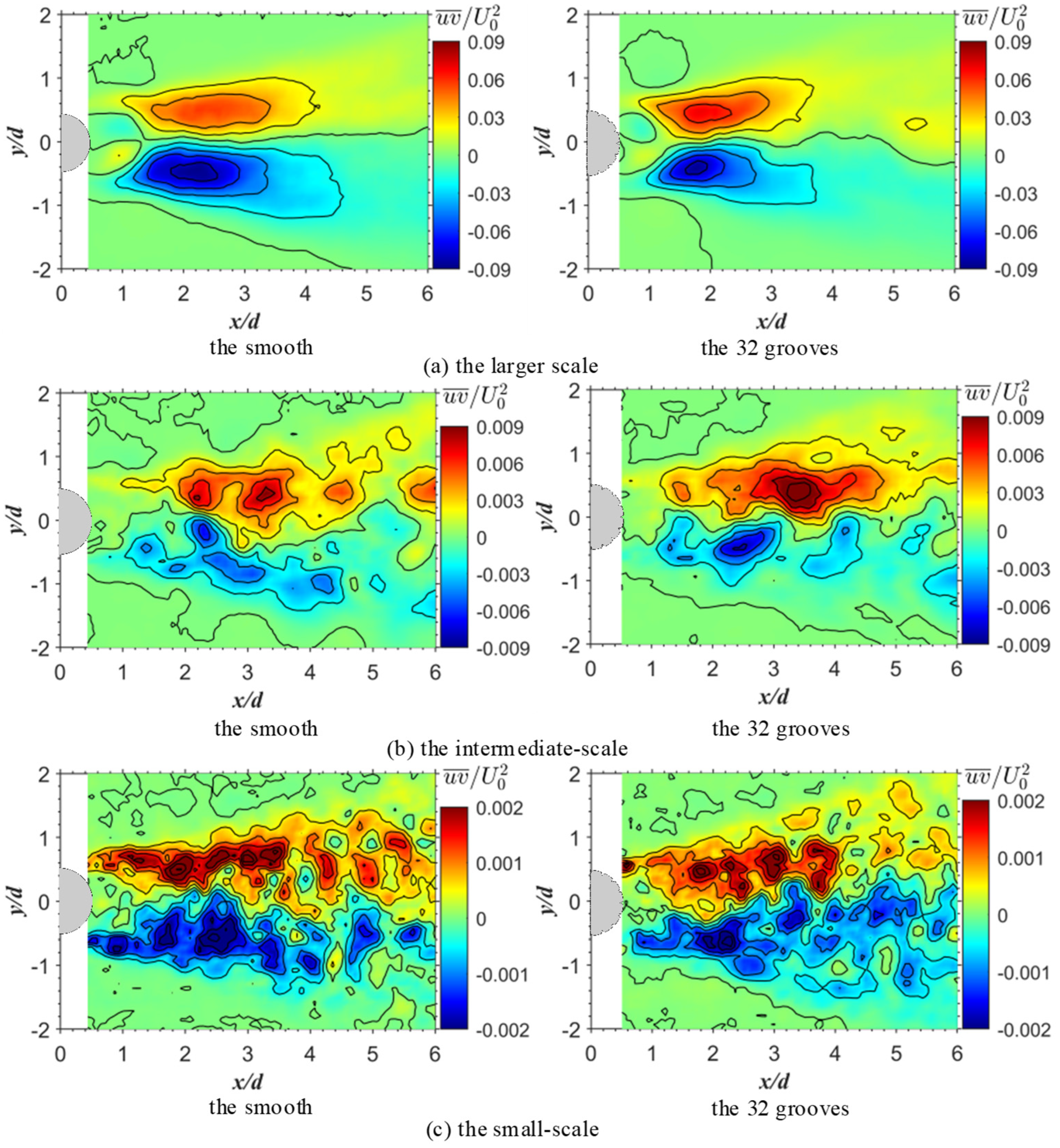
3.8. Reynold Shear Stress Contour of Different Scales
4. Conclusions
- (1)
- The results of the time-averaged velocity profile showed that the v-groove can reduce the width of the reflux section and the velocity gradient. The v-groove can reduce the recirculation region, increase the Reynolds shear stress and the turbulent kinetic energy, and prevent the formation of Karman-like vortices. The number of grooves does not affect the recirculation region.
- (2)
- When comparing the smooth and 32-groove cylinders at different scales of vorticity, it was observed that at the large scale, the Karman-like vortices of the grooves were closer to the trailing edge of the cylinder. At the intermediate scale, there were more vortices behind the 32-groove cylinder, whereas at the small scale, strong vortex oscillations were observed behind the grooved cylinder.
- (3)
- When comparing the smooth and 32-groove cylinders at different shear stress scales, it was confirmed that at the large scale, the v-groove surface can reduce the recirculation region. At the intermediate and small scales, the shear layer instability creates vortices, increasing the turbulent kinetic energy and narrowing the wake region.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| d | the diameter of the smooth cylinder | the low-frequency coefficients | |
| the center frequency | s | the area of the cross-section | |
| h | the height of the v-groove | st | the Strouhal number |
| L | the length of the smooth cylinder | TKE | the turbulent kinetic energy |
| the length of two vortices | the maximum turbulent kinetic energy | ||
| the width between the two foci points | the flow velocity | ||
| the wavelet basis matrix | the horizontal velocities | ||
| p | the distance between two measured points | the flow-fluctuating velocities at different levels | |
| the permutation matrices | the fluctuation velocity | ||
| Q | the quantity of flow | the normalized time-averaged stream-wise velocity | |
| Re | the Reynolds number | the normalized Reynolds stress | |
| the spatial correlation coefficient | the longitudinal velocities | ||
| the integral length scale | the wavelet analysis matrix | ||
| the relative energy | the wall-normal velocities | ||
| the length from the reference point to the space point | the normalized vorticity | ||
| S | the wavelet coefficient matrix | the referenced point |
References
- Hwang, J.Y.; Yang, K.S. Drag reduction on a circular cylinder using dual detached splitter plates. J. Wind Eng. Ind. Aerodyn. 2007, 95, 551–564. [Google Scholar] [CrossRef]
- Liu, K.; Deng, J.; Mei, M. Experimental study on the confined flow over a circular cylinder with a splitter plate. Flow Meas. Instrum. 2016, 51, 95–104. [Google Scholar] [CrossRef]
- Zhou, T.; Razali, S.; Hao, Z.; Cheng, L. On the study of vortex-induced vibration of a cylinder with helical strakes. J. Fluids Struct. 2011, 27, 903–917. [Google Scholar] [CrossRef]
- Yang, Y.; Laima, S. Three-dimensional effects for flow past a wavy cylinder at low Reynolds numbers. Ocean Eng. 2022, 263, 112427. [Google Scholar] [CrossRef]
- Ying, Z.L.; Liu, L.S.; Yu, J. TR-PIV measurement of the wake behind a grooved cylinder at low Reynolds number. J. Fluids Struct. 2011, 27, 394–407. [Google Scholar] [CrossRef]
- Yamagishi, Y.; Oki, M. Effect of the number of grooves on flow characteristics around a circular cylinder with triangular grooves. J. Vis. 2005, 8, 57–64. [Google Scholar] [CrossRef]
- Quintavalla, S.J.; Angilella, A.J.; Smits, A.J. Drag reduction on grooved cylinders in the critical Reynolds number regime. Exp. Therm. Fluid Sci. 2013, 48, 15–18. [Google Scholar] [CrossRef]
- Qi, J.; Qi, Y.; Chen, Q.; Yan, F. A Study of Drag Reduction on Cylinders with Different V-Groove Depths on the Surface. Water 2022, 14, 36. [Google Scholar] [CrossRef]
- Williamson, C. The natural and forced formation of spot-like “vortex dislocations” in the transition wake. J. Fluid Mech. 1992, 243, 393–441. [Google Scholar] [CrossRef]
- Naghib-Lahouti, A.; Lavoie, P.; Hangan, H. Wake instabilities of a blunt trailing edge profiled body at intermediate Reyn-olds numbers. Exp. Fluids 2014, 55, 1–15. [Google Scholar] [CrossRef]
- De, A.K.; Sarkar, S. Wake events during early three-dimensional transition of a circular cylinder placed in shear flow. Phys. Fluids 2020, 32, 053603. [Google Scholar] [CrossRef]
- Talley, S.; Iaccarino, G.; Mungal, G.; Mansour, N. An experimental and computational investigation of flow past cacti. Annu. Res. Briefs Cent. Turbul. Res. NASA AmesStanford Univ. 2001, 51–63. [Google Scholar]
- Fujisawa, N.; Hirabayashi, K.; Yamagata, T. Aerodynamic noise reduction of circular cylinder by longitudinal grooves. J. Wind Eng. Ind. Aerodyn. 2020, 199, 104129. [Google Scholar] [CrossRef]
- Addison, P.S.; Murray, K.B.; Watson, J.N. Wavelet transform analysis of open channel wake flows. J. Eng. Mech. 2001, 127, 58–70. [Google Scholar] [CrossRef]
- Fujimoto, S.; Rinoshika, A. Wavelet multi-resolution analysis on turbulent wakes of asymmetric bluff body. Int. J. Mech. Sci. 2015, 92, 121–132. [Google Scholar] [CrossRef]
- Rinoshika, A.; Omori, H. Orthogonal wavelet analysis of turbulent wakes behind various bluff bodies. Exp. Therm. Fluid Sci. 2011, 35, 1231–1238. [Google Scholar] [CrossRef]
- Yan, Z.A.; Lin, D.; Arc, D. Multi-scale wake structures around the dune. Exp. Therm. Fluid Sci. 2019, 104, 209–220. [Google Scholar] [CrossRef]
- Rinoshika, A.; Zhou, Y.U. Orthogonal wavelet multi-resolution analysis of a turbulent cylinder wake. J. Fluid Mech. 2005, 524, 229–248. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.; Zhou, T.; An, H.; Zhu, H.; Cheng, L. Experimental studies on wake structures of a circular cylinder with different surface roughness heights. Int. J. Heat Fluid Flow 2022, 94, 108941. [Google Scholar] [CrossRef]
- Lim, H.C.; Lee, S.J. PIV measurements of near wake behind a U-grooved cylinder. J. Fluids Struct. 2004, 18, 119–130. [Google Scholar] [CrossRef]
- Lee, S.J.; Lim, H.C.; Han, M.; Lee, S.S. Flow control of circular cylinder with a V-grooved micro-riblet film. Fluid Dyn. Res. 2005, 37, 246–266. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, X.; Guo, W.; Gho, W.M.; Tan, S.K. Experimental study on flow past a circular cylinder with rough surface. Ocean Eng. 2015, 109, 7–13. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, S.; Yan, F.; Zhang, J.; Song, B. Multi-Scale Wake Characteristics of the Flow over a Cylinder with Different V-Groove Numbers. Water 2023, 15, 805. https://doi.org/10.3390/w15040805
Jiang S, Yan F, Zhang J, Song B. Multi-Scale Wake Characteristics of the Flow over a Cylinder with Different V-Groove Numbers. Water. 2023; 15(4):805. https://doi.org/10.3390/w15040805
Chicago/Turabian StyleJiang, Suyu, Fei Yan, Jian Zhang, and Bo Song. 2023. "Multi-Scale Wake Characteristics of the Flow over a Cylinder with Different V-Groove Numbers" Water 15, no. 4: 805. https://doi.org/10.3390/w15040805




