2.2. Analysis of Interactions of Key Stakeholders
The purpose of this study was to investigate the decision evolution behavior of EPEs and MEs. Therefore, we considered the EPEs and MEs the two key stakeholders in this evolutionary game.
Municipal enterprises (MEs): Although the MEs in various regions are state-owned, they all depend on their revenue. MEs generally need a large amount of water, but the price of municipal water is generally higher than that of tap water. The price of urban water supply in China is classified. According to the nature of use, urban water can be divided into five categories: residential, industrial, administrative, business service and special water. The prices of all types of water are determined by the local people’s government and the administrative department of water supply in considering the actual situation. However, municipal water belongs to the category of non-residential water in all provinces and cities, the price of which is higher than that of tap water. Taking 10 cities in Jilin Province as an example (
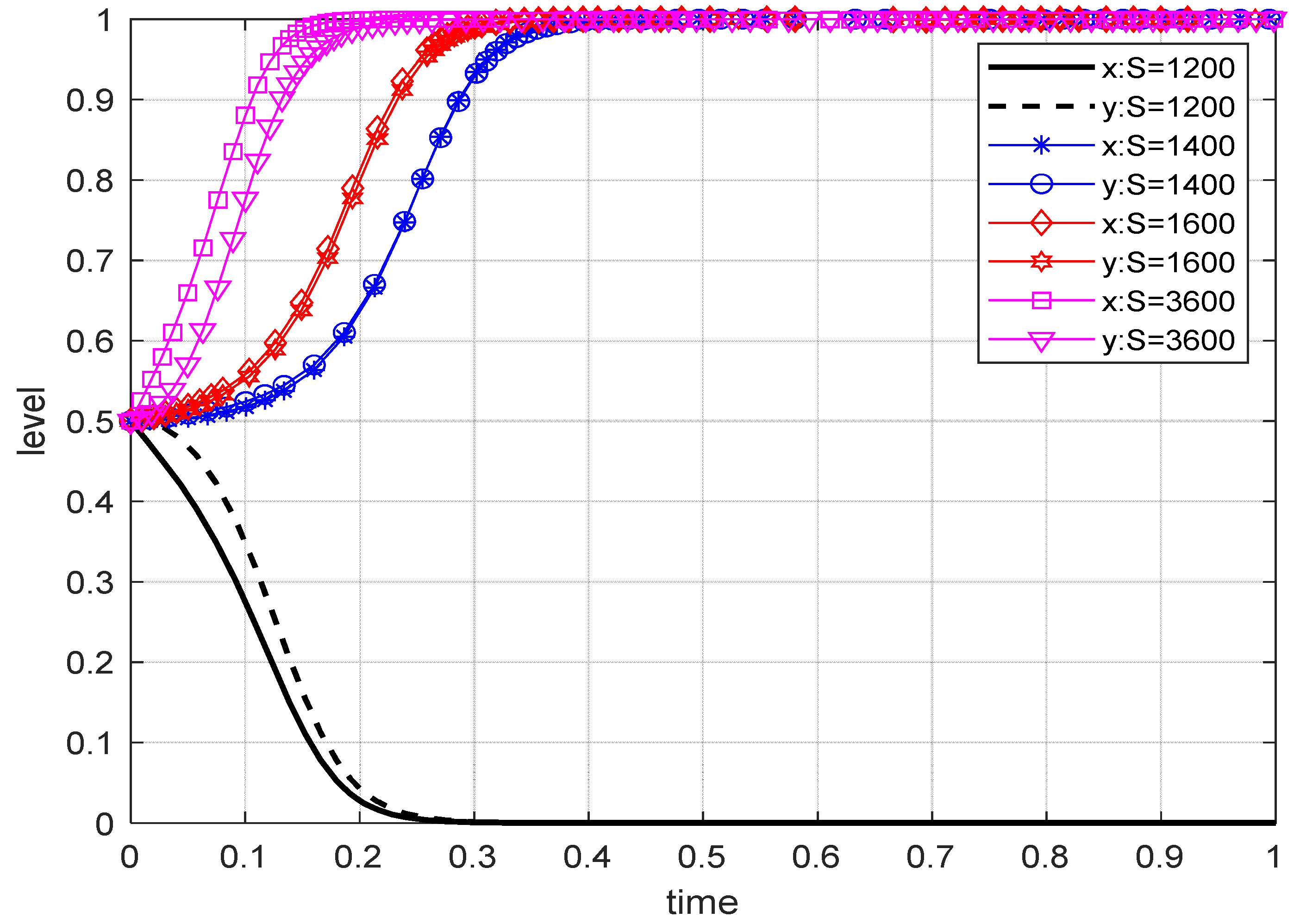
Appendix A), municipal water in each city is approximately 10–15% higher than the price of tap water. MEs are more willing to actively look for alternatives. Both government departments and MEs are willing to motivate EPEs through subsidies and other incentive measures to attract more EPEs to recycle rainwater, to promote the increase in rainwater trading volume (RWTV). However, subsidies cannot be blindly increased, which will lead to increased costs for MEs. Therefore, the government can consider whether some incentive policies are useful or to increase others.
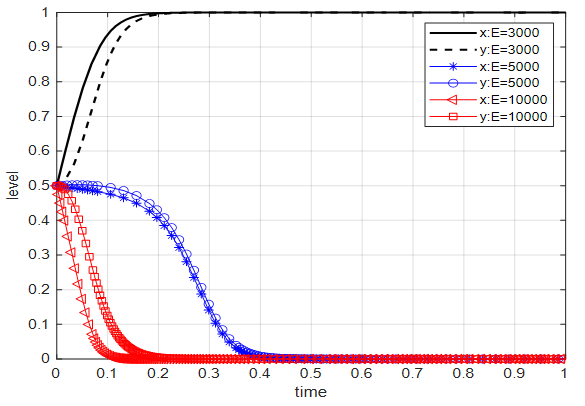
Environmental protection enterprises (EPEs): Economic benefits are the ultimate pursuit of any enterprise [
38]. Companies are free to decide whether to recycle and trade rainwater, which is not currently mandated by the government, even though rainwater recycling plays a crucial role in promoting SCCSs. Although some EPEs have begun trading rainwater, many are still dubious, fearing that the additional expense of treating stormwater may not be justified by the absence of long-term execution of the agreement. Therefore, many EPEs are willing to cooperate with MEs in the case of incentive policies. However, when incentive policies are insufficient, they will choose to cooperate with enterprises with lower water quality requirements.
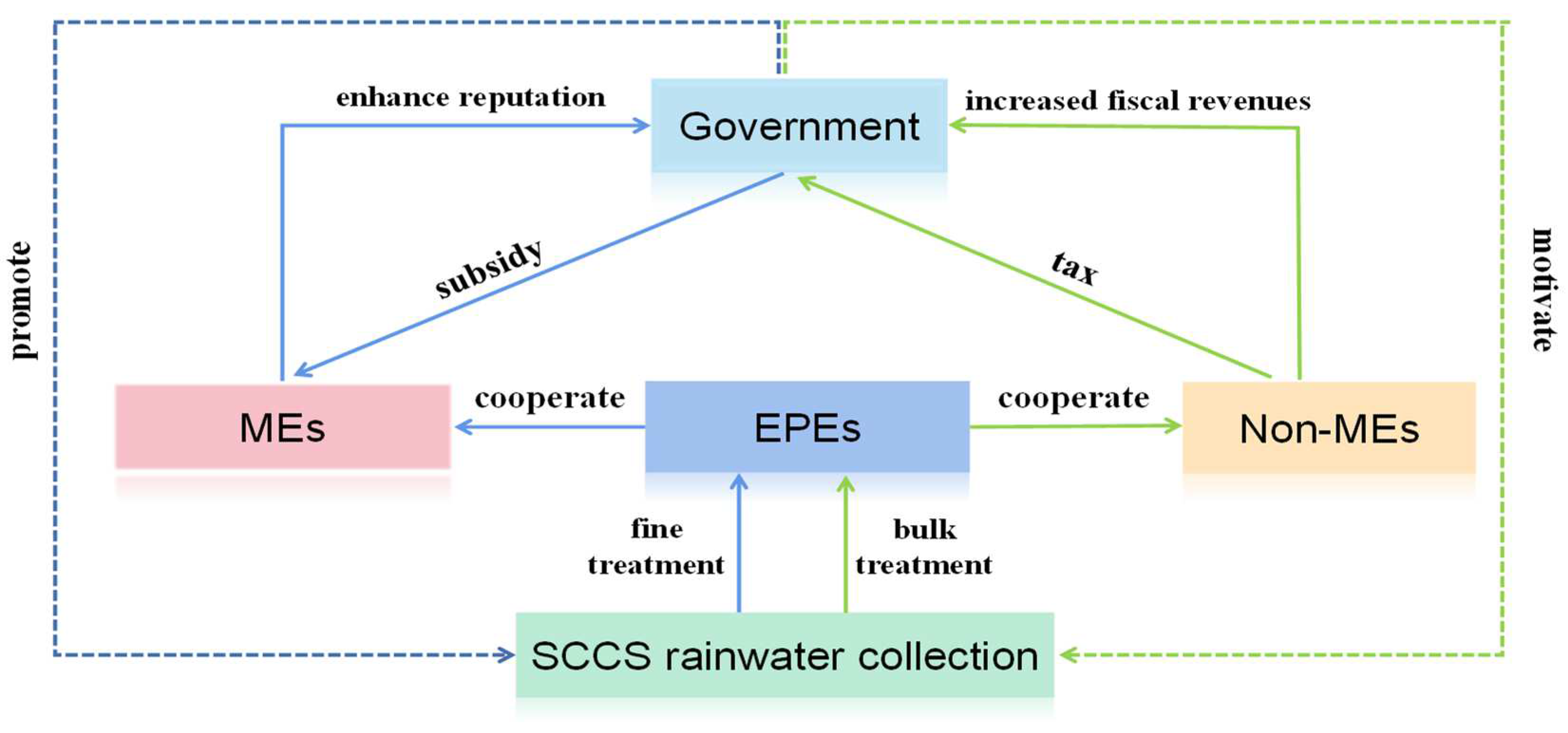
The interests of EPEs and MEs are mutually affected in the RWT that promotes sponge cities.
Figure 2 shows the interactions between the two stakeholders. The goal in this study was to determine the equilibrium point on the basis of the EGT between the EPEs and MEs if EPEs are willing to participate in the SCCS and recycle rainwater. Under the incentive policy, EPEs cooperate with MEs. The income of EPEs comes from transaction income, subsidies, and incremental revenue to attract more enterprises to buy, and the expenditures are costs and taxes. MEs benefit from the money they save by trading rainwater instead of the high cost of buying tap water, the benefits of attracting more EPEs to increase rainwater trading, and the increased prestige. However, parameters do not all simultaneously arise in the same case.
2.3. Evolutionary Game Modeling between EPEs and MEs
With the establishment of a rainwater management system in the context of SCCSs, the lost rainwater resources are treated by EPEs to meet the urban miscellaneous water standards. The purchase cost of rainwater is much lower than that from water supply companies. Under the concept of sustainable development, if the EPEs process the collected rainwater and then sell it to the MEs, it will create economic and environmental benefits. If is sold to the non-MEs, the EPEs can also obtain a relatively appreciable profit. In this case, the EPEs need to pay taxes to the government. To effectively understand the cooperative evolution mechanism among the relevant participants in the RWT process and reveal the influence of different factors on the decision-making behavior of the game players, we constructed a two-party evolutionary game model of two stakeholders: MEs and EPEs.
2.3.1. Model Assumption
Hypothesis 1 (H1): Both sides of the game are rationally bounded. They can all learn and adapt to dynamic environmental changes and optimize their strategies in the process of water rights trading in the context of sponge cities.
Hypothesis 2 (H2): When EPEs cooperate with non-MEs in the RWT, the cost of EPEs (the cost of water treatment for agriculture, forestry, animal husbandry, fishery, etc., which do not require high water quality) CE, tax T is paid to the government, and revenue RE is obtained. If MEs choose the negative strategy, EPEs cooperate with non-MEs and adopt a series of preferential policies to attract additional sales revenue E. If EPEs cooperate with MEs, additional costs will be incurred (recreational, ornamental landscape environmental water, green pouring of roads, and other high water quality requirements) CE ( > 0), in this case, the increased revenue is RE ( > 0), and financial subsidy S is received.
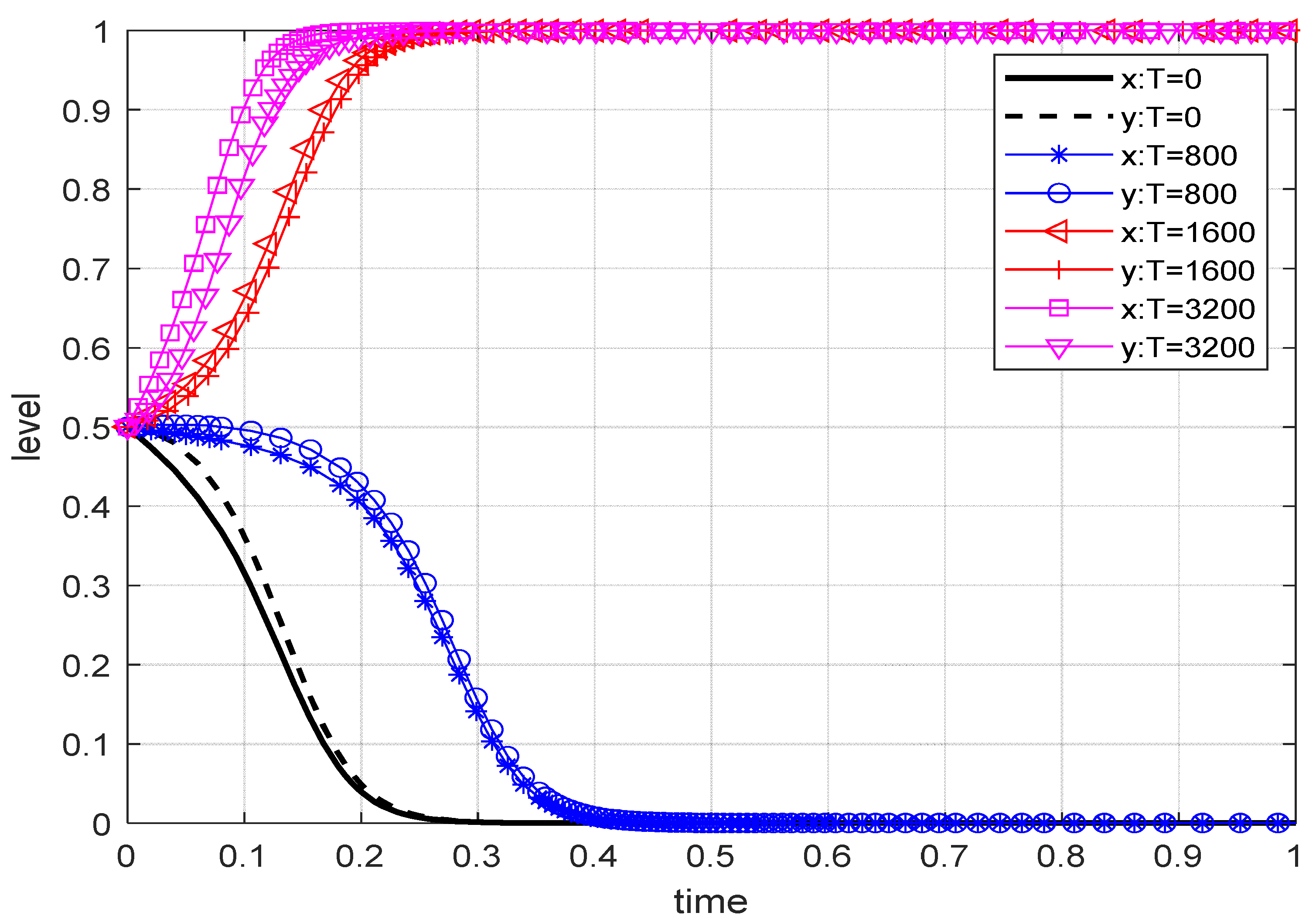
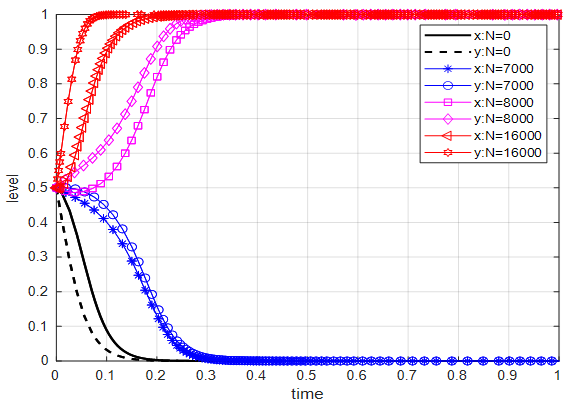
Hypothesis 3 (H3): If MEs choose the negative strategy in the RWT, the cost for MEs to buy tap water is CM, and the gain is RM. If MEs choose the positive strategy, the additional cost is CM ( > 0), the increased-revenue is RM ( > 0), attracting more EPEs to join and increasing RWT revenue N. If EPEs choose to cooperate with non-MEs, MEs adopt positive strategies to introduce a series of preferential subsidy policies and win the recognition of superior government departments, which will lead to subsidy income T ( > 0).
2.3.2. Parameters and Income Matrix
Assuming that the probability of EPEs adopting cooperation with MEs is x (0 ≤ x ≤ 1), the probability of EPEs adopting cooperation with non-MEs is 1 − x. The probability of MEs choosing the positive strategy is y (0 ≤ y ≤ 1); the probability of MEs choosing the negative strategy is 1 − y. Based on the assumptions in
Section 2.3.1, the payoff matrix of EPEs and Mes is as shown in
Table 1.
2.3.3. Stakeholder Replication Dynamic Equation
Let U
11 represent the expected payoff of the EPEs if they cooperate with Mes, and let U
12 represent the expected payoff of the EPEs if they cooperate with non-Mes. U
1 represents the average expected payoff of the EPEs. U
11, U
12, and U
1 can be expressed as:
Therefore, the replicator dynamics equation of the EPEs can be written as:
Similarly, U
21 represents the expected payoff of the MEs if they choose positive strategies, and U
22 represents the expected payoff of the MEs if they choose negative strategies. U
2 represents the average expected payoff of the MEs. U
21, U
22, and U
2 can be expressed as:
Therefore, the replicator dynamics equation of the MEs can be written as (8):
The replicator dynamic equations of EPEs and MEs constitute a two-dimensional dynamic system I, as shown in Equation (9):
2.3.4. Equilibrium Point and Stability Analysis
- (i).
Equilibrium point
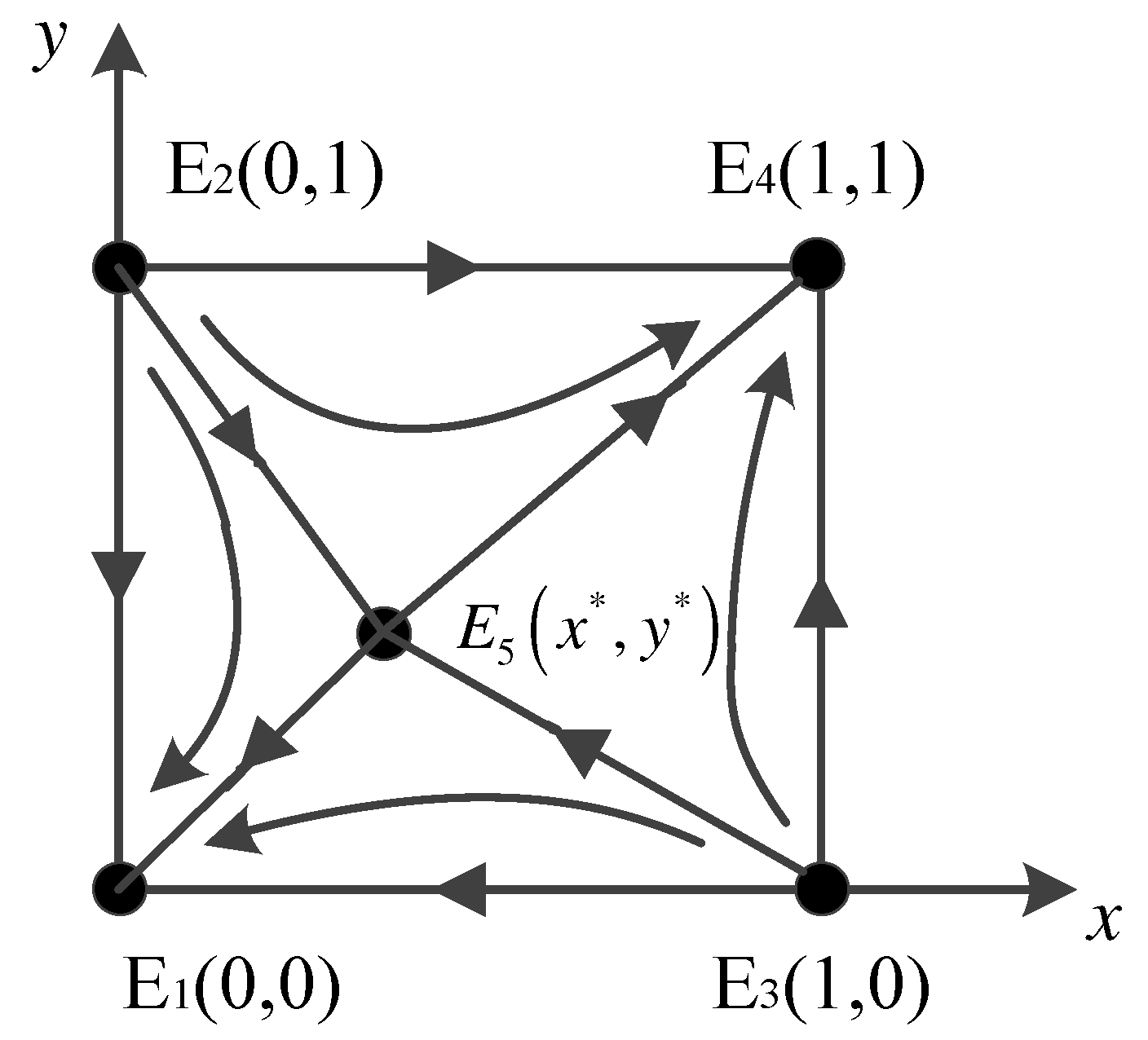
In system I, when four local equilibrium points of two-species adopting pure strategies can be obtained: E1(0, 0), E2(0, 1), E3(1, 0), and E4(1, 1) and a mixed strategy equilibrium point may exist in in system I: E5(x*, y*), where x* = and y* = .
- (ii).
Stability analysis of equilibrium point
If the EPEs meet the condition of stability, when , , then . If is the stable state boundary, when y > y*, then , , which indicates that EPEs choose to cooperate with MEs as the stable state; When y < y*, then , , indicating that EPEs choose to cooperate with Non-MEs as the stable state.
If the MEs meet the condition of stability, when , , then, . If , is the stable state boundary, when x > x*, then , , indicating that MEs choose positive strategies as the stable state; when x < x*, then , , indicating that MEs choose negative strategies as the stable state.
In
Figure 3, the point (x*, y*) is the saddle point of this evolutionary game. The square in the coordinate is divided into four parts by the five points donated as E
1(0, 0), E
2(0, 1), E
4(1, 1), E
3(1, 0), and E
5(x*, y*). For an unstable initial situation with a specific value of (x*, y*), the evolutionary trend shows a convergence from point E
5(x*, y*) to E
1(0, 0) or E
4(1, 1). The trend is expressed by the arrows in
Figure 3. The arrow represents the two evolutionary results of EPEs and MEs after a long-term game in the RWT. E
4(1, 1) is an ideal evolutionary game stable strategy. It means that EPEs choose to cooperate with MEs for more profit, and MEs choose positive strategies to gain social reputation or recognition from superior departments. In this case, the two sides jointly promoted the construction and maintenance of sponge cities.
2.4. ESS Analysis between EPEs and MEs
As the stability of the group’s dynamic equilibrium points systemically ascribed by differential equations can be obtained through the Jacobian matrix partial stability, the partial stability of the system can be explored using the Jacobian matrix to analyze the final evolutionary stability. The Jacobi matrix was established, as shown in Equation (10):
Based on the matrix, its determinant (
) and trace (
) were also obtained (Equations (11) and (12)):
Regarding the equilibrium point of the model, if and only if the Jacobian matrix fits (1) If
,
, then the point is in a partially asymptotic stability, that is, an evolutionarily stable strategy ESS [
39]; (2) If
,
, then the corresponding equilibrium point is unstable fixed point; (3) If
,
, then the corresponding equilibrium point is the saddle point. When
,
,
, E
5 is not the ESS. Based on the above equations,
Table 2 displays
and
for each equilibrium point.
Table 2 shows that four expressions—a, b, c, and d—are related to the stability of the system. They each stand for the relative benefit of a strategy’s payoff. If it is positive, the first strategy has a comparative advantage; if it is negative, the second strategy does. As a result, 16 situations could be created using the symbols for the four expressions, as shown in
Table 3.
The stability of equilibrium points and replicator dynamic replicator results in 16 situations are provided in
Table 4 based on the aforementioned investigation. The four equilibrium points of the interaction strategy between EPEs and MEs are listed in the first column of the table as E
1(0, 0), E
2(0, 1), E
3(1, 0), and E
4(1, 1). In scenarios 1–16, the first and second columns represent
and
, respectively, while the third column represents the states at the four equilibrium points.
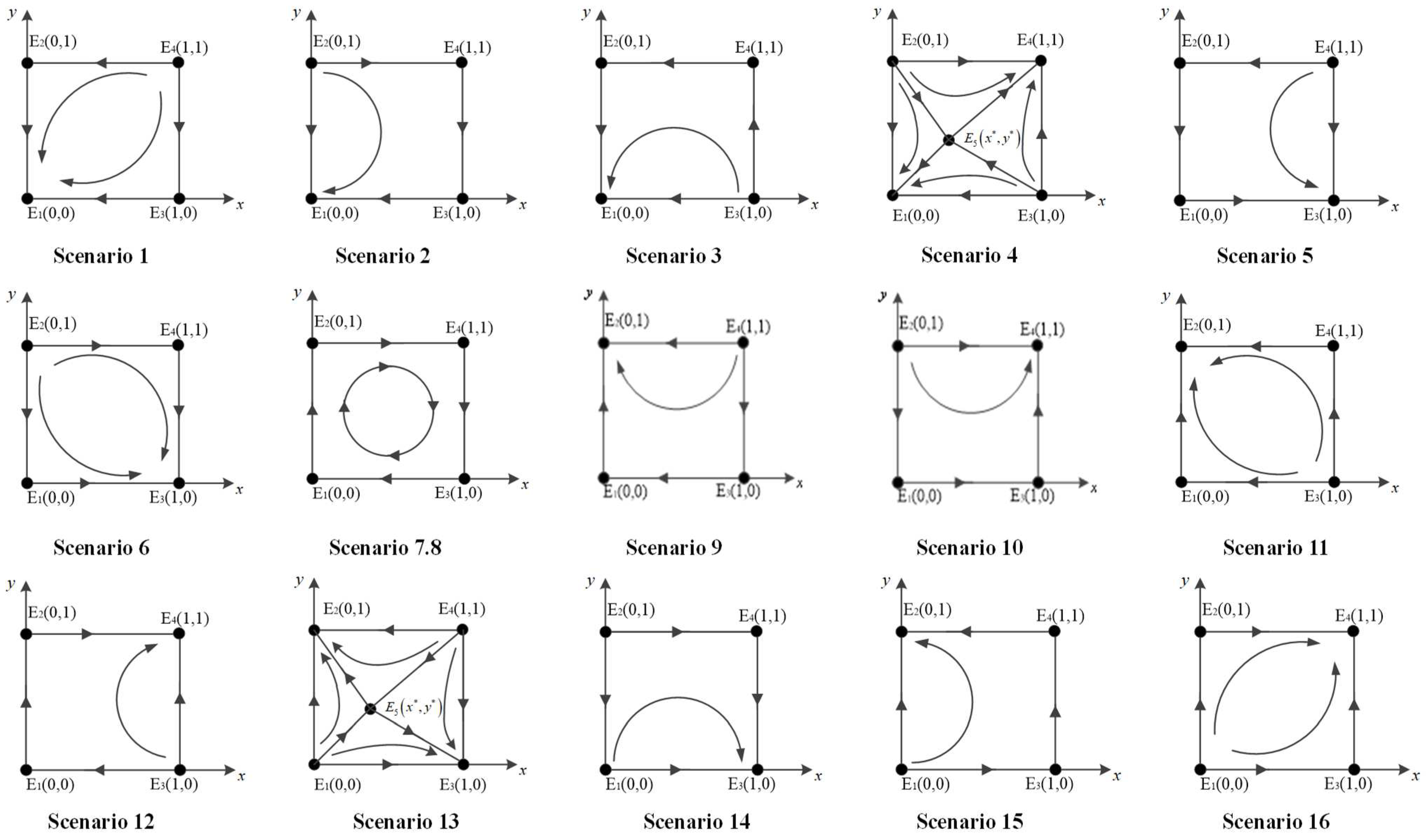
Figure 4 depicts the evolutionary path and equilibrium stability of EPE-ME strategic interaction under 16 different scenarios. Scenario 1 shows convergence evolution from E
4(willing to cooperate) to E
1(unwilling to cooperate); when a < 0, the improvement in MEs reputation is less than the increased cost of choosing a positive strategy after EPEs choose to cooperate with non-MEs; when b < 0, the net profit value of EPEs cooperating with MEs is less than the increase in sales value attracted by cooperation with non-MEs; when c < 0, EPEs cooperate with MEs, and after MEs adopt the positive strategy, the benefit of attracting more EPEs to join is less than the cost of MEs choosing the positive strategy; when d < 0, it means that when EPEs choose to cooperate with the non-MEs, and the tax paid is less than the net cost of EPEs choosing to cooperate with MEs. To summarize, if EPEs gain more profit from cooperating with non-MEs than from cooperating with MEs and pay less taxes than the net cost of cooperating with MEs, then EPEs’ strategies will change from “Cooperating with MEs” to “Cooperating with Non-MEs”. However, when the income of MEs is less than the increased cost of the MEs’ positive strategies, the MEs’ strategies will change from “positive strategy” to “negative strategy”. The evolutionary game system converges to E
1(0, 0). Conversely, in scenario 16, the initial strategy equilibrium point would converge at E
4(1, 1). This is the expected outcome of the eventual evolution of the two parties.
In scenarios 2 and 3, the ultimate point of equilibrium would converge at E1(0, 0); In scenario 5, the ultimate point of equilibrium would converge at E1(1, 0); in scenario 9, the ultimate point of equilibrium would converge at E1(0, 1). To summarize, we concluded that if only one party gains when changing the strategy, the two parties will not reach cooperation in the long-term evolution process, and thus the ultimate point of equilibrium would converge at (0, 0); if the external benefits (subsidies, etc.) directly obtained by the EPEs and MEs are greater than the benefits generated by the cooperation between the two parties, no matter whether the other party chooses cooperation, the evolutional game path of the party with benefits tends to be 1.
In scenario 11, the ultimate point of equilibrium would converge at E2(0, 1), suggesting that regardless of the strategy chosen by the EPEs, the benefits of the MEs will not be affected, so the result of the final evolutionary game of the MEs tends to 1; similarly, in scenario 6, the ultimate point of equilibrium would converge at E3(1, 0), and the final evolutionary game result of EPEs also tends to be 1.
In scenario 10, the ultimate point of equilibrium would converge at E4(1, 1), and in scenario 14, the ultimate point of equilibrium would converge at E3(1, 0), suggesting that the strategy choice of EPEs in this evolutionary game tends toward cooperation with MEs, If the MEs choose the active strategy, the evolutionary game system converges to E4(1, 1), conversely, it converges toward E3(1, 0). Similarly, in scenario 12, the ultimate point of equilibrium would converge at E4(1, 1); in scenario 15, the ultimate point of equilibrium would converge at E2(0, 1), suggesting that the strategy choice of MEs in evolutionary game tends toward cooperation with MEs. If the MEs choose the active strategy, the evolutionary game system converges to E4(1, 1), suggesting that the MEs choose an active strategy. If the EPEs choose to cooperate with the MEs, the ultimate point of equilibrium would converge at E4(1, 1), otherwise the ultimate point of equilibrium would converge at E2(0, 1).
As shown in scenarios 7 and 8, uncertain system evolution results from the strategic evolution process between EPEs and MEs being so cyclical that a stable state is never reached.
As shown in scenario 4, E
1(0, 0) and E
4(1, 1) are the two equilibrium points; in scenario 13, E
1(1, 1) is an ideal evolutionary game stable strategy. The choice of system evolution strategy depends on the area of quadrangle
and
; if
, the likelihood is higher that the ultimate point of equilibrium would converge at (0,0); if
, the likelihood is higher that the ultimate point of equilibrium would converge at (1, 1); if
, the final equilibrium point has the same probability of converging at two points. Therefore, the factors influencing the final strategy of the evolutionary game are the parameters that determine the area of
.
Equation (13) shows that , , , , , , , , , and all affect the area of . Next, we analyzed the sensitivity of each parameter.