1. Introduction
Water is one of the most important natural resources for all life on Earth. It has always been important to consider the availability and quality of water when selecting not only where people will live but also how joyful those lives will be. India’s entire usable water supply, which has been calculated to be around 1124 Billion Cubic Metres (BCM), is just 28% of the water generated through precipitation (692 BCM from surface and 435 BCM from ground) [
1]. Approximately 87% (689 BCM) of water use is diverted for irrigation, and by 2050, that percentage may rise to 1072 BCM. Groundwater is a significant irrigation supply [
2].
1.1. Utilization of Water in Various Sectors
Fresh water is used commercially for establishments including hotels, restaurants, offices, motels, other commercial buildings, and both civilian and military institutions. The majority of people’s daily water use is primarily for domestic purposes. Water used for daily household chores, including drinking, eating, cooking, cleaning, bathing, laundry, washing dishes and watering lawns and landscapes, is referred to as domestic use [
3].
The nation’s businesses use industrial water as a crucial resource for things such as processing, sanitation, conveyance, attenuation and cooling in manufacturing plants. Chemical, steel and petroleum refining are a few of the major water-consuming sectors [
1]. The same water is frequently used by industries multiple times for different reasons.
Water for irrigation is the water that is used for agricultural, vineyard, pasture, and horticultural crops. It is also used to irrigate pastures, prevent frost and freezing damage, apply chemicals, cool crops, harvest them and remove salts from the root zone of crops. The extraction of natural deposits, substances such as anthracite coal and mineral products, solvents such as crude oil and gases such as natural energy resources all include using water. As a subset of mining activity, this category comprises quarrying, milling (including trouncing, screenings, washing and flotation) and other processes. About 34% of the water utilized for mining is saline, which is a sizable percentage [
3].
1.2. Categorization of Wastewater
With utilization of water in various domains as discussed above, wastewater is also produced. The categorization of wastewater is given below:
Human excreta (faeces and urine), which is frequently combined with old toilet paper or wipes, can be the source of wastewater. If this waste is collected by flushing toilets, it is referred to as “blackwater” [
4].
Washing water (for one’s own clothing, dishes, floors, and other items), commonly referred to as greywater or sullage.
Excess domestically produced liquids (drinks, cooking leftovers, insecticides, lubrication oil, paint, cleaning agents, etc.).
Urban rainwater runoff from roads, parking lots, roofs, walkways and pavements (contains lubricants, animal droppings, garbage, gasoline or diesel, rubber remnants from tyres, soap scum, metals from vehicle exhausts, etc.).
Highway runoff, including lubricants, anti-icing chemicals and rubber remnants, notably from tyres, and storm sewers (trash included) [
5].
Liquids made by humans (pesticides dumped illegally, used oils, etc.).
Agriculture discharge (pesticides and other chemicals get mixed with the water).
Carbon discharge from the coal and oil industry and their byproducts.
Industrial plant discharge (loam, sand, alkali and chemical byproducts) and industrial waste, etc.) [
6].
As the wastewater is produced, it is processed at Wastewater Treatment Plants (WWTPs) that remove numerous particles and chemicals that are hazardous [
7]. As a result, WWTPs play a significant role in influencing both urban and rural settings. Growth in a region’s population causes a rise in water consumption, and a continual rise in water use leads to an increase in the amount of wastewater the area produces [
8]. In order to satisfy the demand for effluent (processed) water, the wastewater treatment plants must work effectively [
5,
9]. Their operational efficiency is enabled by cost- effective utilization of diverse resources which can be ensured by knowing in advance the quality parameters of the wastewater entering (influent) the WWTP and processed/treated water (effluent) leaving the WWTP.
In this paper, we predict influent and effluent quality parameters of one of the largest UASB-based Wastewater Treatment Plants in Uttar Pradesh and the second largest in Asia, namely the Bharwara Wastewater Treatment Plant. A brief description of the plant is given below.
1.3. Bharwara Wastewater Treatment Plant
The Bharwara Wastewater Treatment Plant (WWTP) situated in Lucknow, as shown in
Figure 1, is the second largest UASB-based wastewater treatment plant in Asia and can operate and process 345 MLD (million litres per day) on average with the capacity to handle a peak load of 517 MLD of sewage, which is processed from three different inlet chambers: A, B and C as shown in the
Figure 1. A detailed description of the plant is presented in [
10].
Bharwara WWTP has five zones, namely preliminary treatment, UASB reactor, polishing pond, pre-aeration tank and sludge drying beds as shown in
Figure 1. Different parameters of water quality were recorded from the inlet chamber, the outlet of the UASB reactor, the polishing pond, the outlet of chlorine contact tank and the primary sludge as shown in
Table 1.
Table 1 presents the location as well as the parameters of each zone of the plant.
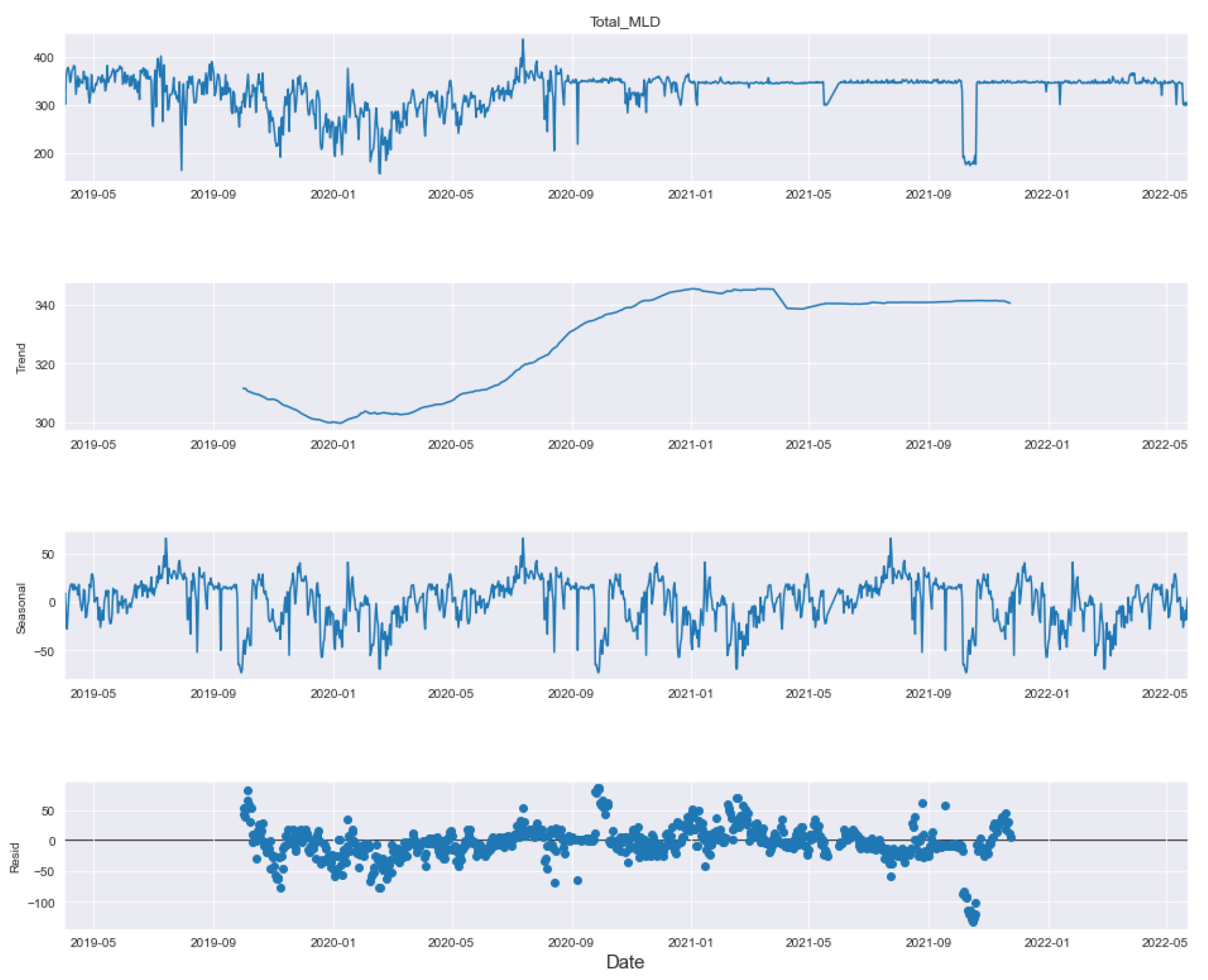
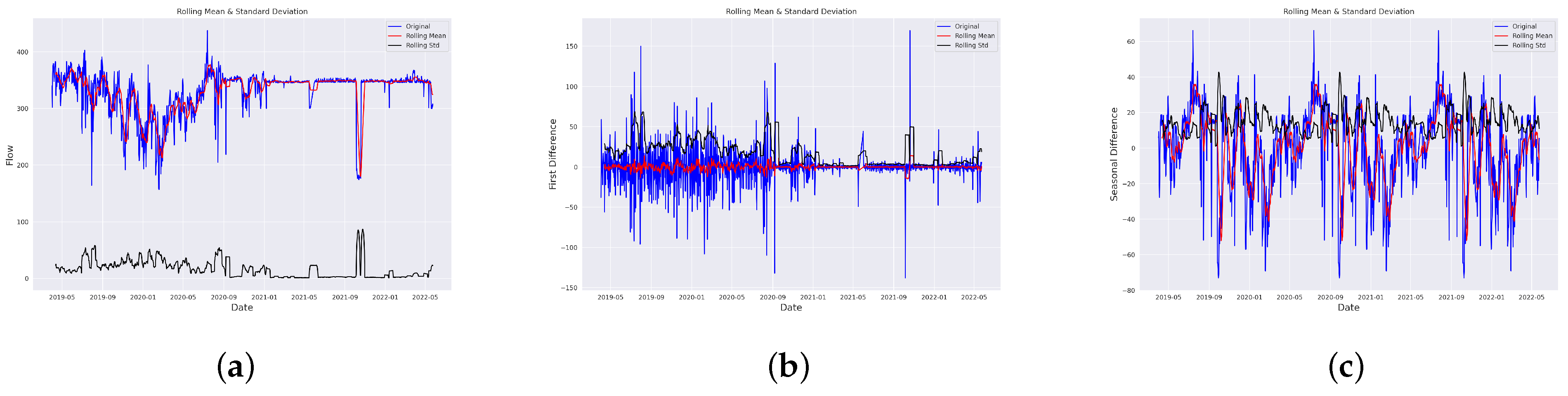
In this paper, we analyze the flow of influent as well as the quality parameters of effluent, namely pH value (pH), dissolved oxygen (DO), chemical oxygen demand (COD), total suspended solids (TSSs), biochemical oxygen demand (BOD) and myeloproliferative neoplasms (MPN) at the Bharwara WWTP and propose a novel model to predict these quality parameters of influent and effluent. The range and units of these parameters are shown in
Table 2.
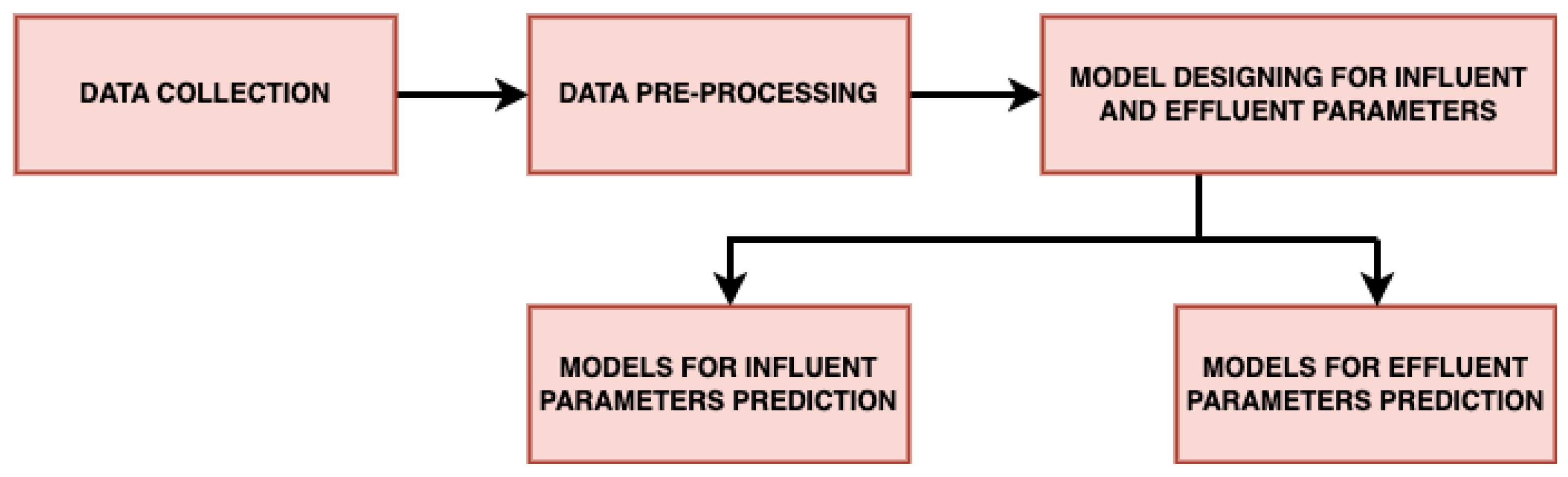
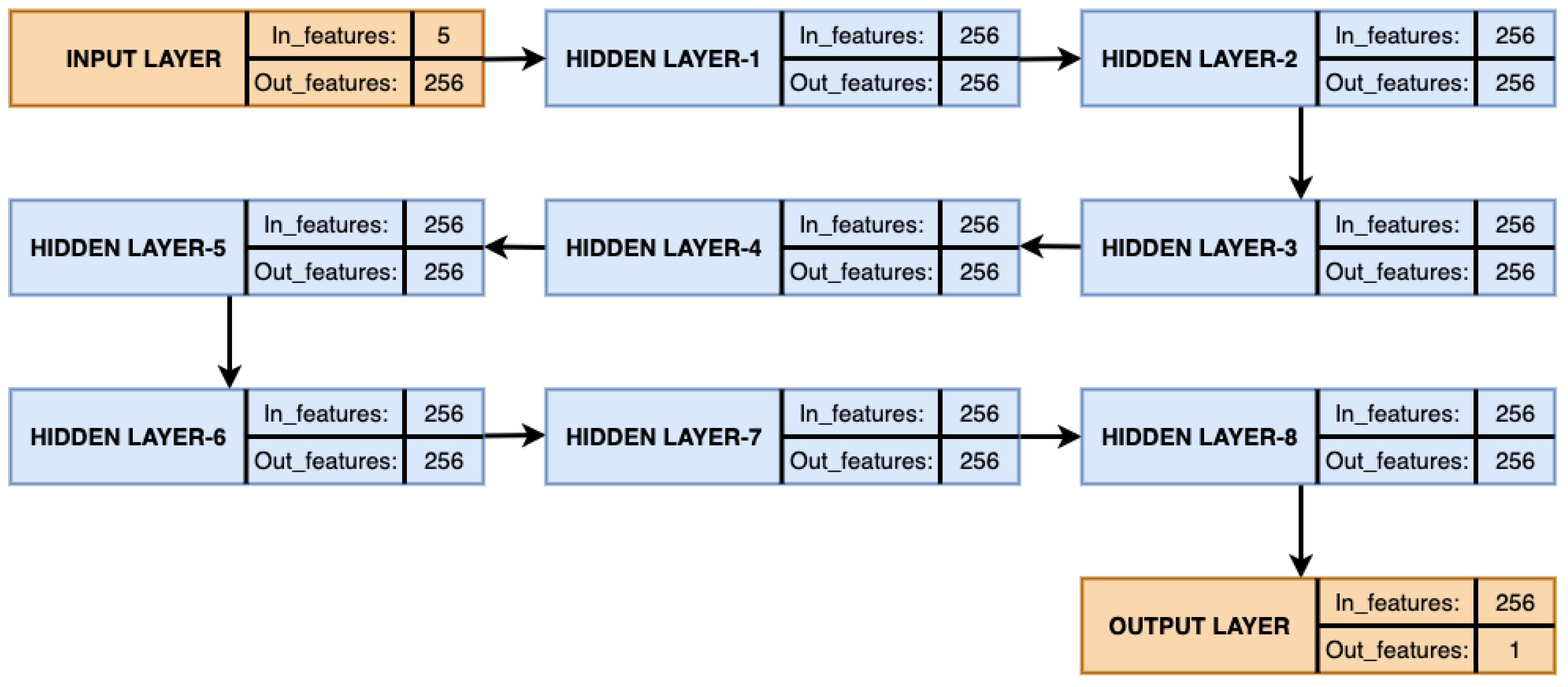
The novelty of this paper is to propose and implement a machine-learning-based model named
wPred to predict influent and effluent quality parameters. The proposed model provides centralized monitoring of WWTP operations and processes. By understanding the influent and effluent quality parameters in advance, the model proposed in this paper enables cost-effective utilization of various resources at wastewater treatment plants. Another highlight of the paper is that in the proposed novel model we have collected real-time data which are taken from the various locations at the plant and trained the model using the data. These locations and parameters are given in
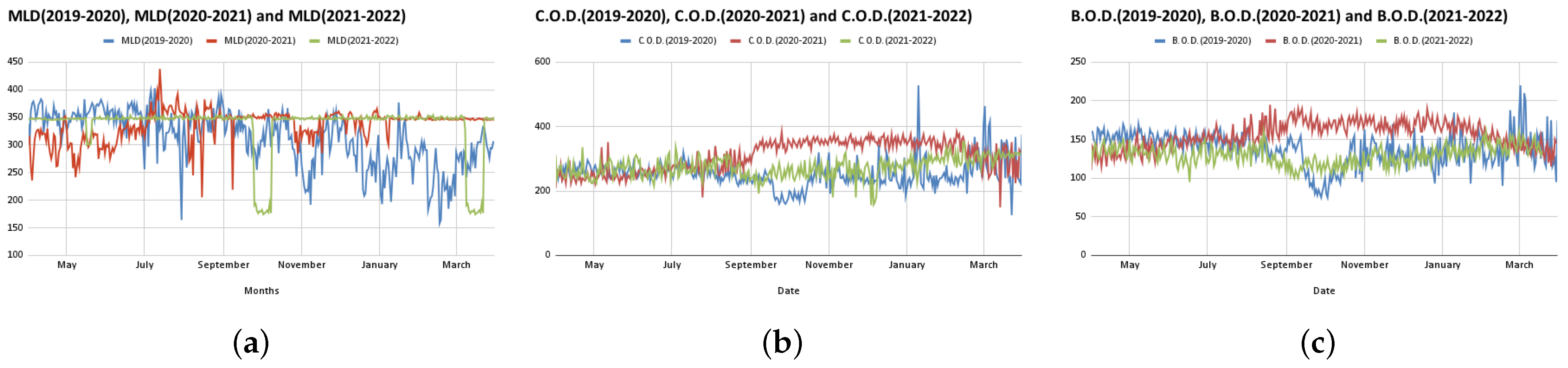
Table 1. The total duration of the data collected for analysis purposes was from April 2019 to May 2022—a total of 38 months pre-, during and post-COVID-19 [
10].
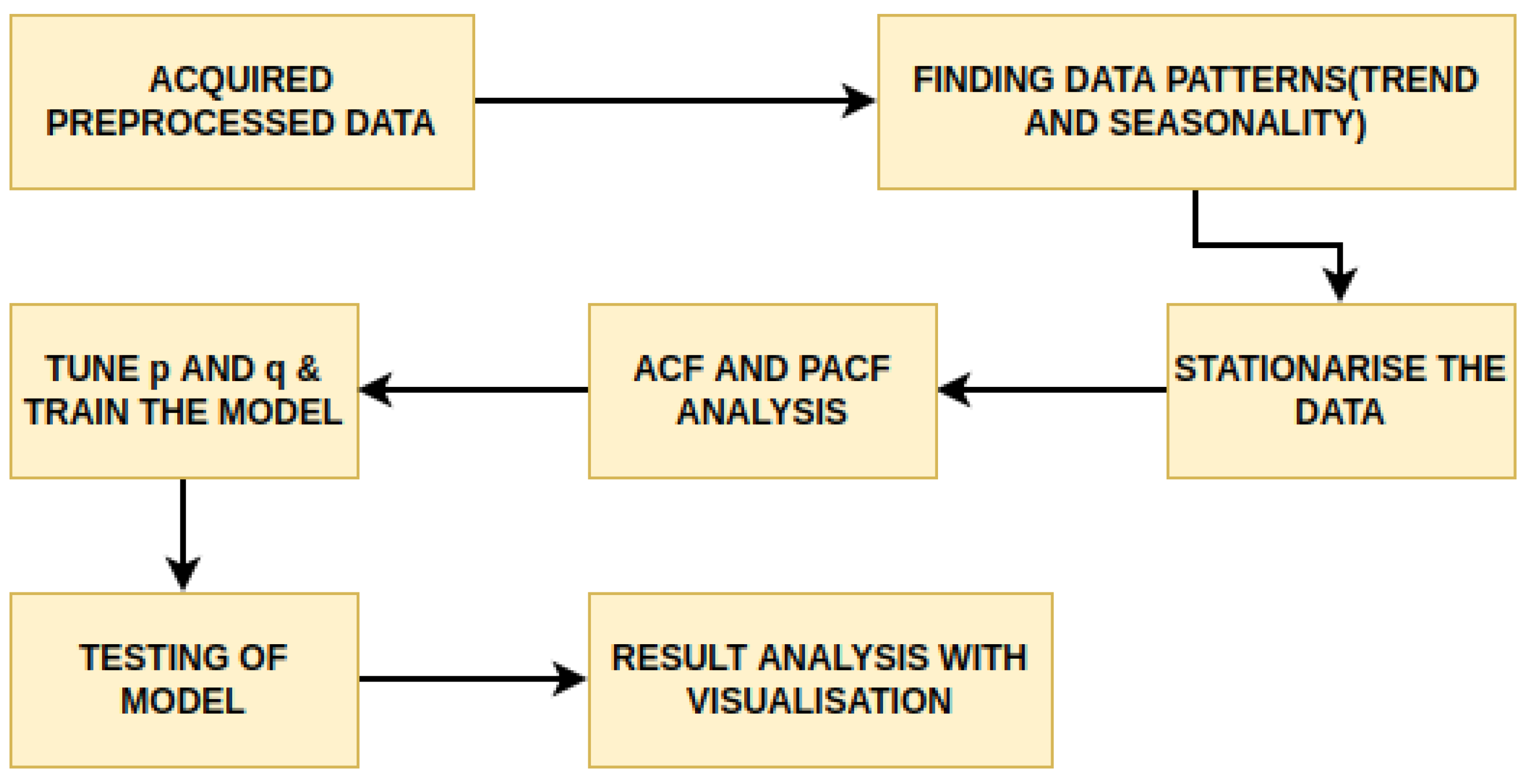
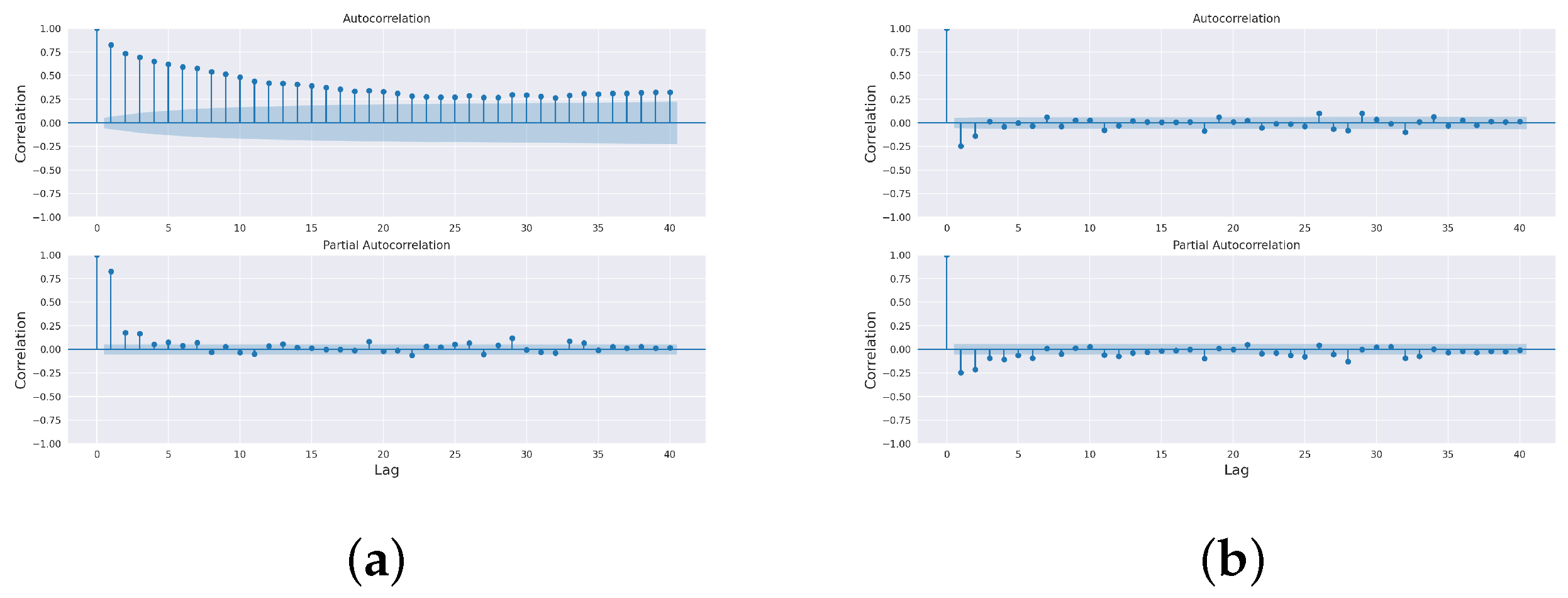
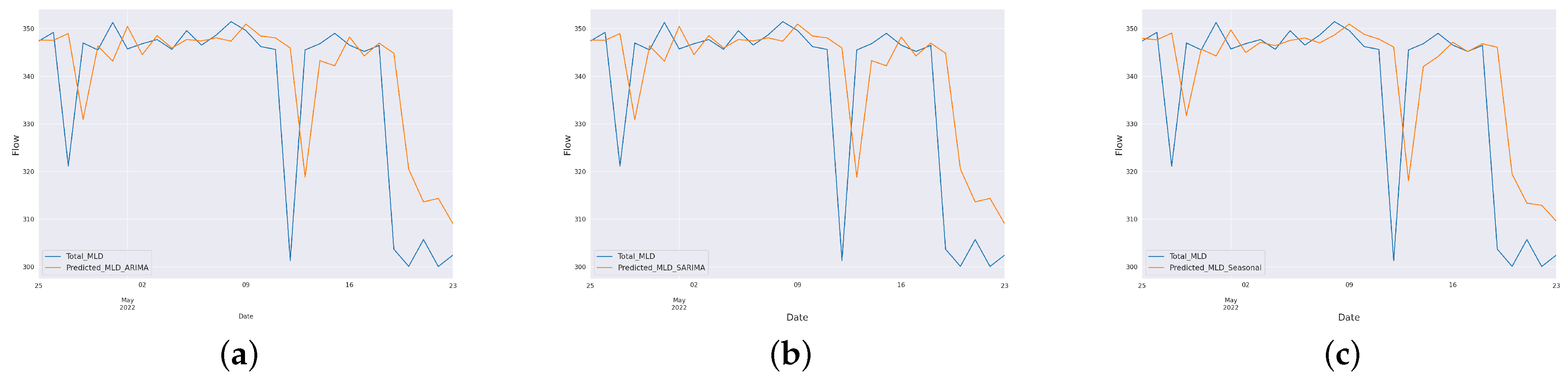
The paper aimed to predict the influent and effluent quality parameters of the WWTP using different machine learning models, namely ARIMA [
11], SARIMA [
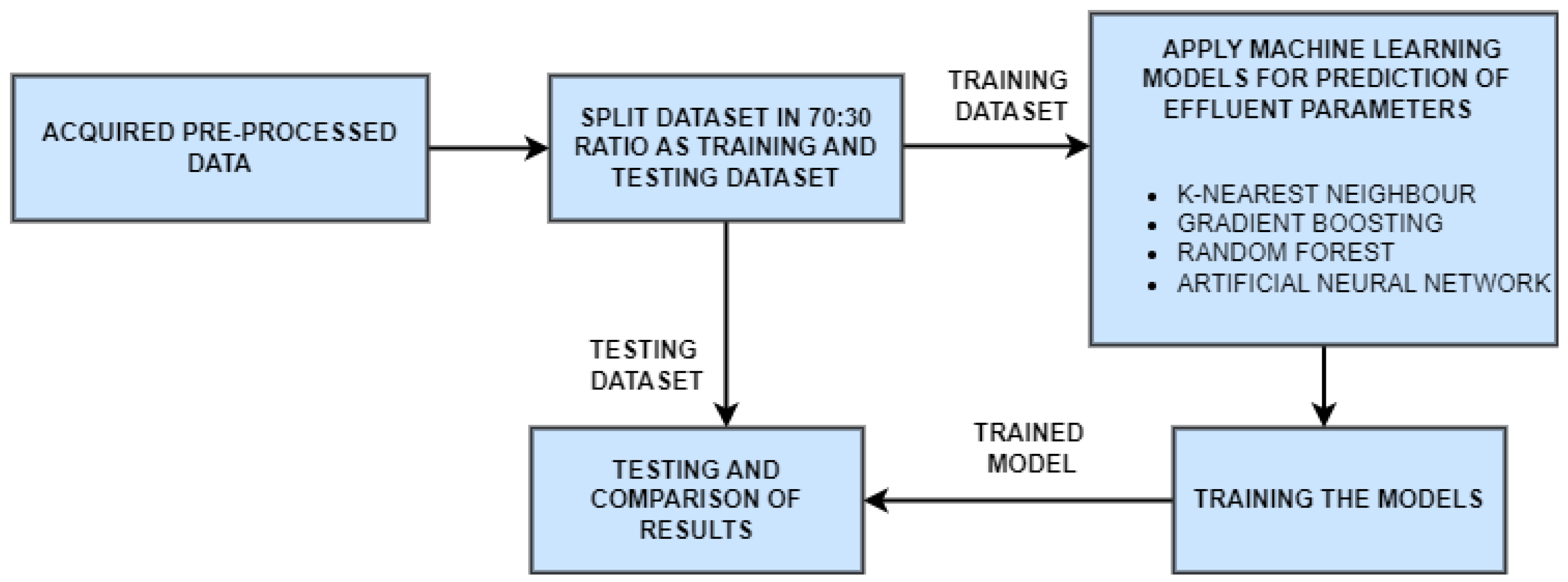
12] and the proposed SARIMA with seasonal order. Among these models, the proposed SARIMA with seasonal order gave better predictions of influent parameters. For effluent parameter prediction, we used kNN [
13], gradient boosting [
14], random forest [
15] and a proposed artificial neural network (ANN) [
16] model. Among these, the proposed ANN outperformed the others. The proposed SARIMA with seasonal order and proposed artificial neural network models are the important components of the proposed model
wPred which is elaborated in detail in
Section 3.
The model
wPred presented in this paper is specifically designed and implemented for the Bharwara WWTP. However, with a specific training component or perhaps after minor model improvements, the implemented model will be suitable for any wastewater treatment facility that is based on the UASB. This paper is organized as follows:
Section 2 includes the related works in the field followed by methodology in
Section 3, and the experimental findings are summarized with visualisation in
Section 4.
Section 5 discusses the conclusions and future works.
2. Related Works
This section outlines recent studies that have been conducted on the issue of wastewater treatment and parameter prediction. In [
17], the authors explain the input parameters COD, BOD and TSS, based on an artificial neural network to propose a model for the prediction of TSS. For the Konya Wastewater treatment facility, model performance was shown using MSE and R value/correlation coefficient. With the use of neural networks with different hidden layers, the proposed model produced good results, with the training set’s correlation coefficient rising to 0.99.
In order to forecast the total nitrogen (T-N) concentration in the plant, ANN and SVM models were used in [
18]. The
value, relative efficiency and Nash–Sutcliff efficiency [
19] criteria were applied to the model’s evaluation. Latin hypercube one factor at a time (LH-OAT) [
20] and a pattern search method were used in a sensitivity analysis, which revealed that the ANN model outperformed the SVM model [
16].
In [
21], a study on rainwater discharge and a methodology for estimating BOD, TSS, COD and TDS in wastewater were also presented. Modeling was conducted using the support vector analysis and regression tree algorithms, and performance was measured using the
value and the root-mean-squared error. The SVR model outperformed the regression tree for TSS, COD and TDS, while the regression tree outperformed SVR for BOD.
Online monitoring of wastewater quality was demonstrated in [
22]. The concentrations of TSS, O&G and COD were monitored using a turbidimeter and UV/VIS spectroscopy. The signals from the two sensors were combined using a sensor fusion technique. The model was created using the boosting-partial least squares (boosting-PLS) method, which uses fused data to forecast wastewater quality.
In [
23], the influent quality was predicted using four machine learning techniques: linear regression [
24], ridge [
25], ElasticNet [
26], and lasso. Different techniques showed good accuracy for predicting influent parameters for various conditions. The outcomes reported in the reference made use of these models as warning modules to help with WWTP daily operations.
Ref. [
27] explains the efficiency of the treatment plant for the removal of effluent particles, namely nitrogen was predicted by a model based on artificial intelligence. An SVM [
28], ANFIS trapezoidal MF model [
29], and an ANFIS Gbell MF model [
29] were separate models created in Matlab. Parameters pH,
, nitrogen, free ammonia and Kjeldahl
were measured as influence parameters. By using the RMSE, NSE and correlation coefficient, performance was evaluated (R). An SVM networks model produced good outcomes.
The monitoring of intake and output parameters as well as the evaluation of STP’s efficacy were the main objectives in [
30]. In order to identify similar sites, the cluster analysis technique was used to discover some connections between the present site and other sites. Measurements of the amounts of sulfate, nitrates, chloride, phosphate and bicarbonates revealed that STP efficiency was not up to par.
As the population increases rapidly, huge consumption of water is being recorded, leading to a drastic increase in the generation of wastewater; hence efficient wastewater treatment plants are needed. The authors in [
17,
18,
22,
23,
27,
30] have worked on the problem but their solutions are specific to their plants which are situated in different geographical locations. Therefore, a model is required for efficient utilization of a UASB-based wastewater treatment plant. The methodology for the proposed model is explained in the following section.
5. Conclusions and Future Works
In this paper, we have designed and implemented a novel model wPred to predict/forecast wastewater (influent) parameters, namely incoming load (total MLD), and effluent parameters, namely MPN, BOD, COD, DO, TSS and pH for the real-time data obtained pre-, during and post-COVID-19 period from a UASB-based Bharwara WWTP in Asia. The categorization of influent and effluent model design wPred further divides the problem into two sub-problems, where the influent total MLD value is forecasted using ARIMA and seasonal ARIMA models, whereas the effluent parameters are predicted and compared using four machine learning models: kNN, random forest, gradient boosting regression and the proposed artificial neural network model. Forecasting the incoming load gives promising results with an extremely low symmetric mean absolute prediction error of 2.59% indicating high prediction accuracy in the proposed model wPred. Moreover, the estimation of effluent parameters with the help of the proposed ANN model results in a significant rise in accuracy compared to the existing machine learning models, as high as 74.55% (for effluent pH), a significantly low mean squared error (0.014 for effluent BOD), and a strong correlation (R-value) up to 0.99 (for effluent DO) in the proposed model wPred. The results of the proposed model wPred provide a way forward in reducing the manual effort of recording the wastewater quality parameters and also helps in forecasting the incoming load based on seasonal variations effectively. Future works include the addition of a larger dataset which would more clearly explain how different parameters affect one another. We also plan to design a more generalized model applicable for a large class of UASB-based WWTPs.