Analysis of Long-Term Trend of Stream Flow and Interaction Effect of Land Use and Land Cover on Water Yield by SWAT Model and Statistical Learning in Part of Urmia Lake Basin, Northwest of Iran
Abstract
:1. Introduction
2. Materials and Methods
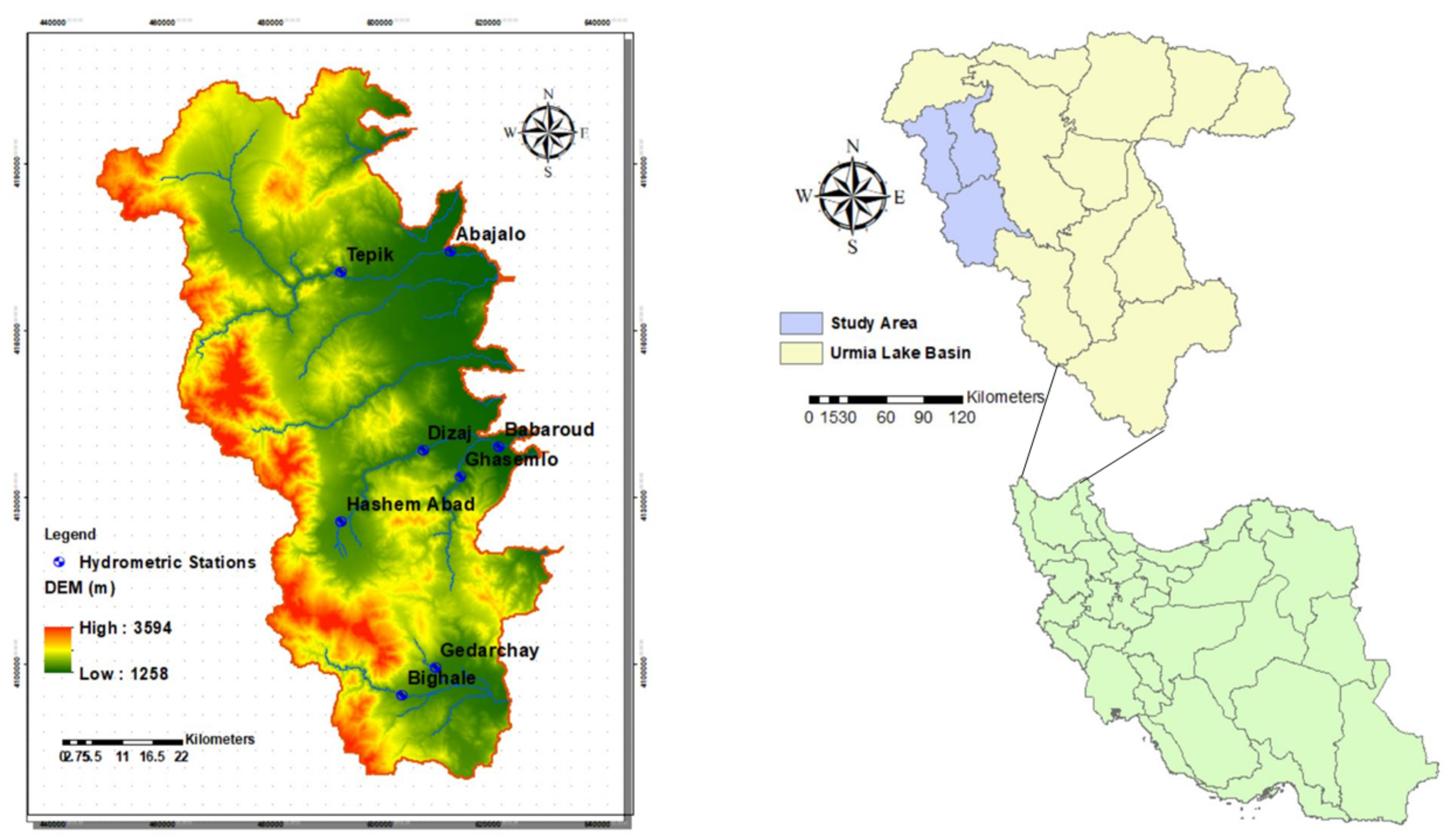
2.1. Study Area
2.2. Trend and Change Point Analysis
2.3. Hydrologic Simulation by SWAT Model
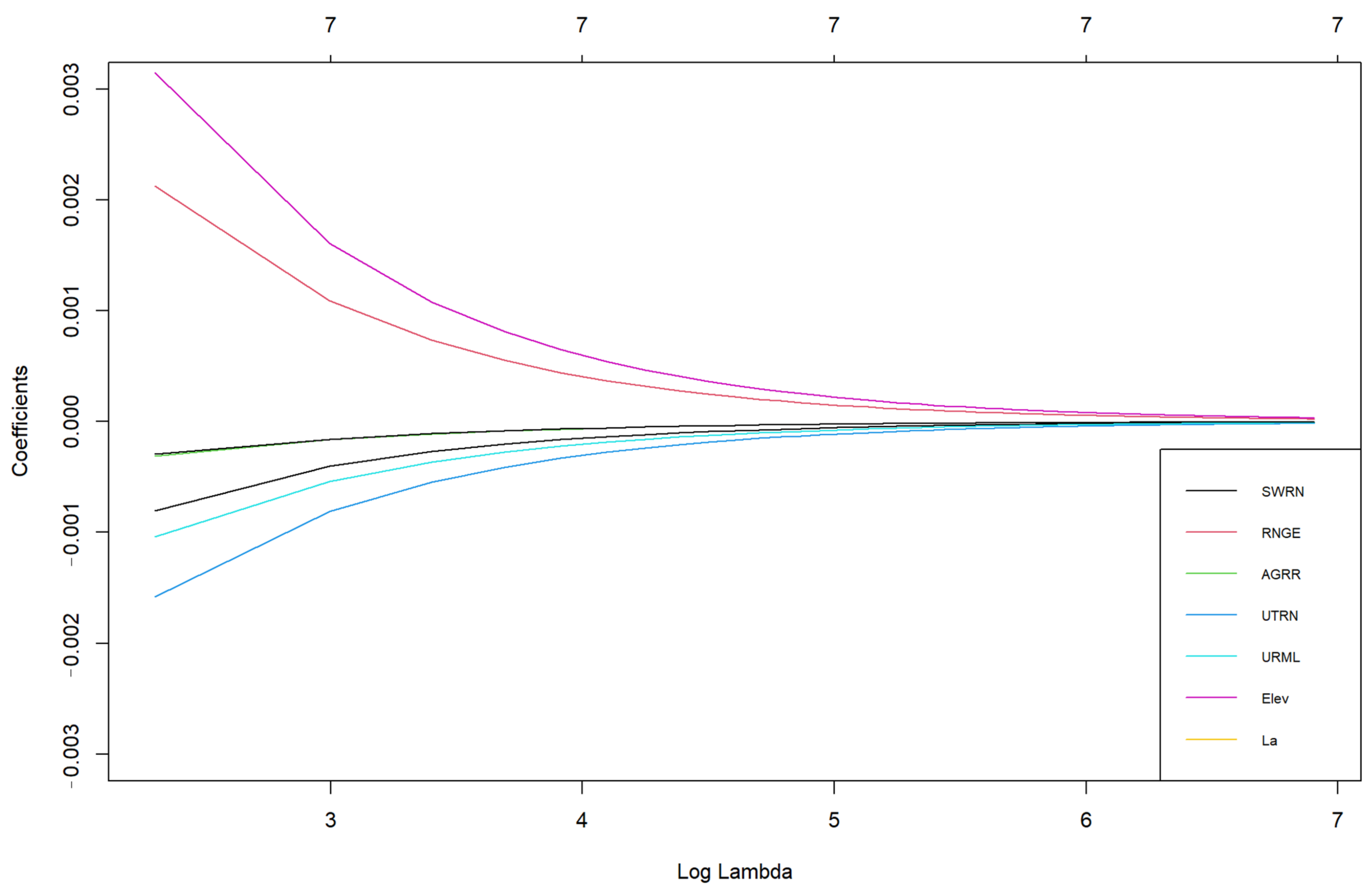
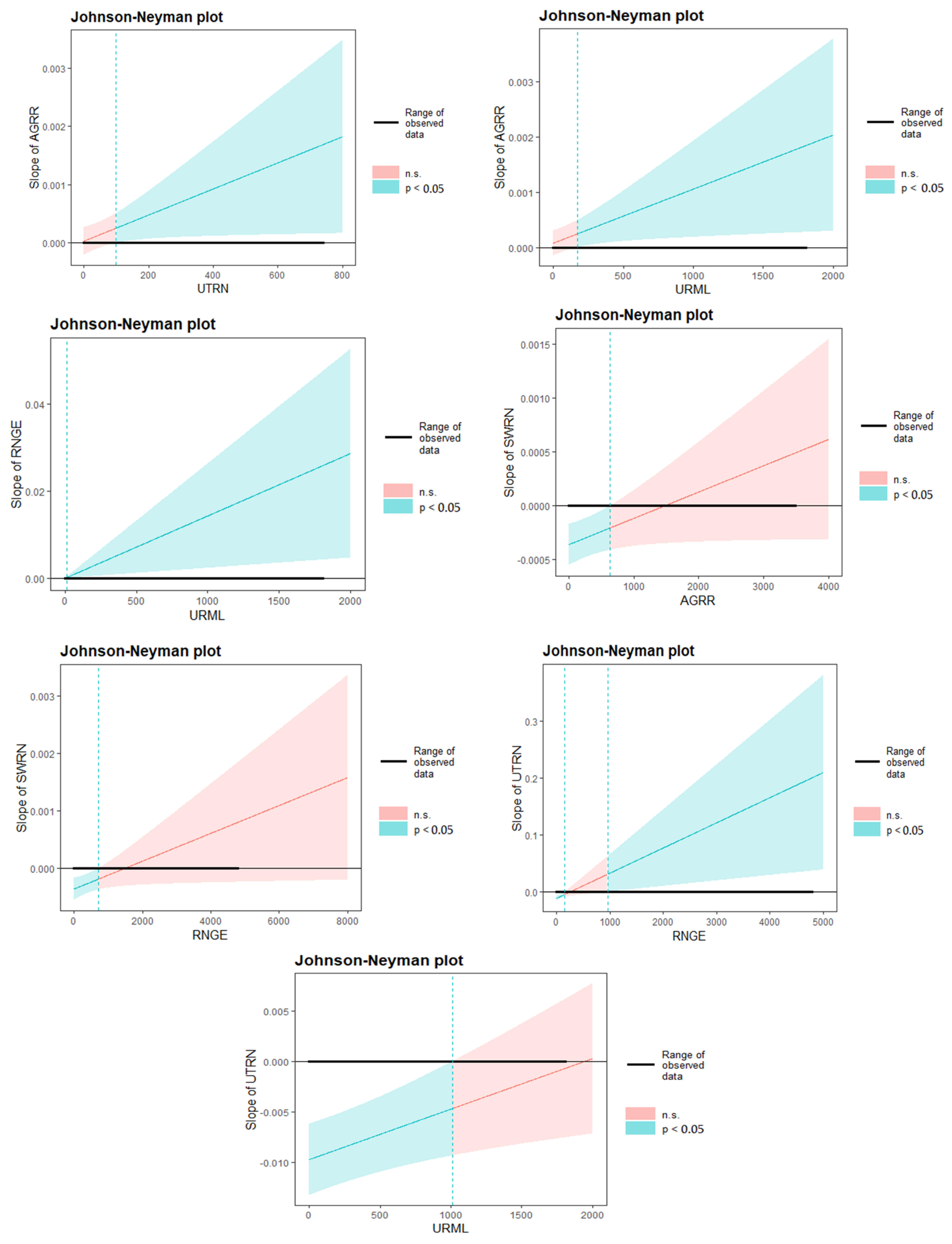
2.4. Multiple Linear Regression and Johnson–Neyman Interaction Analysis
3. Results and Discussion
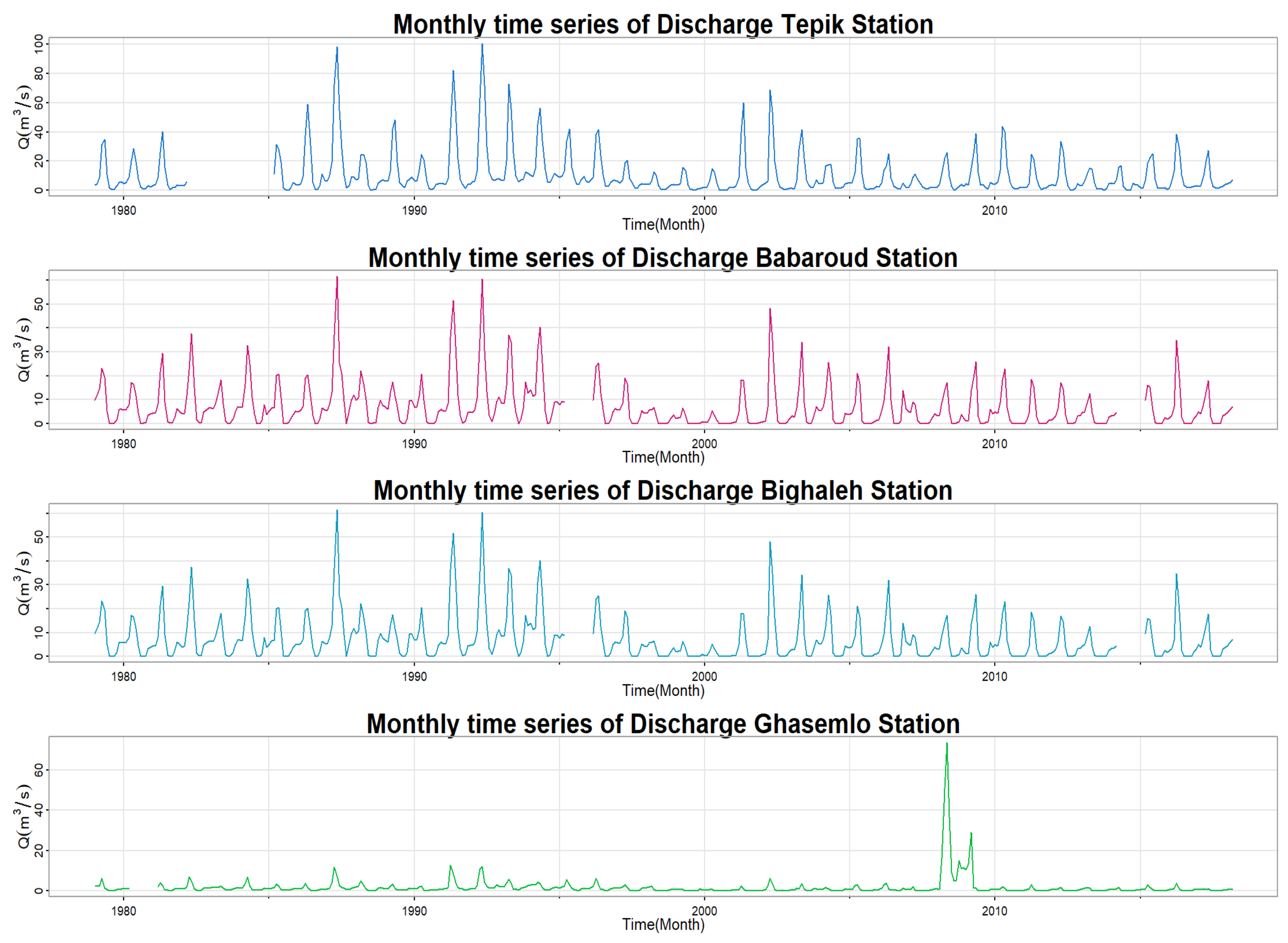
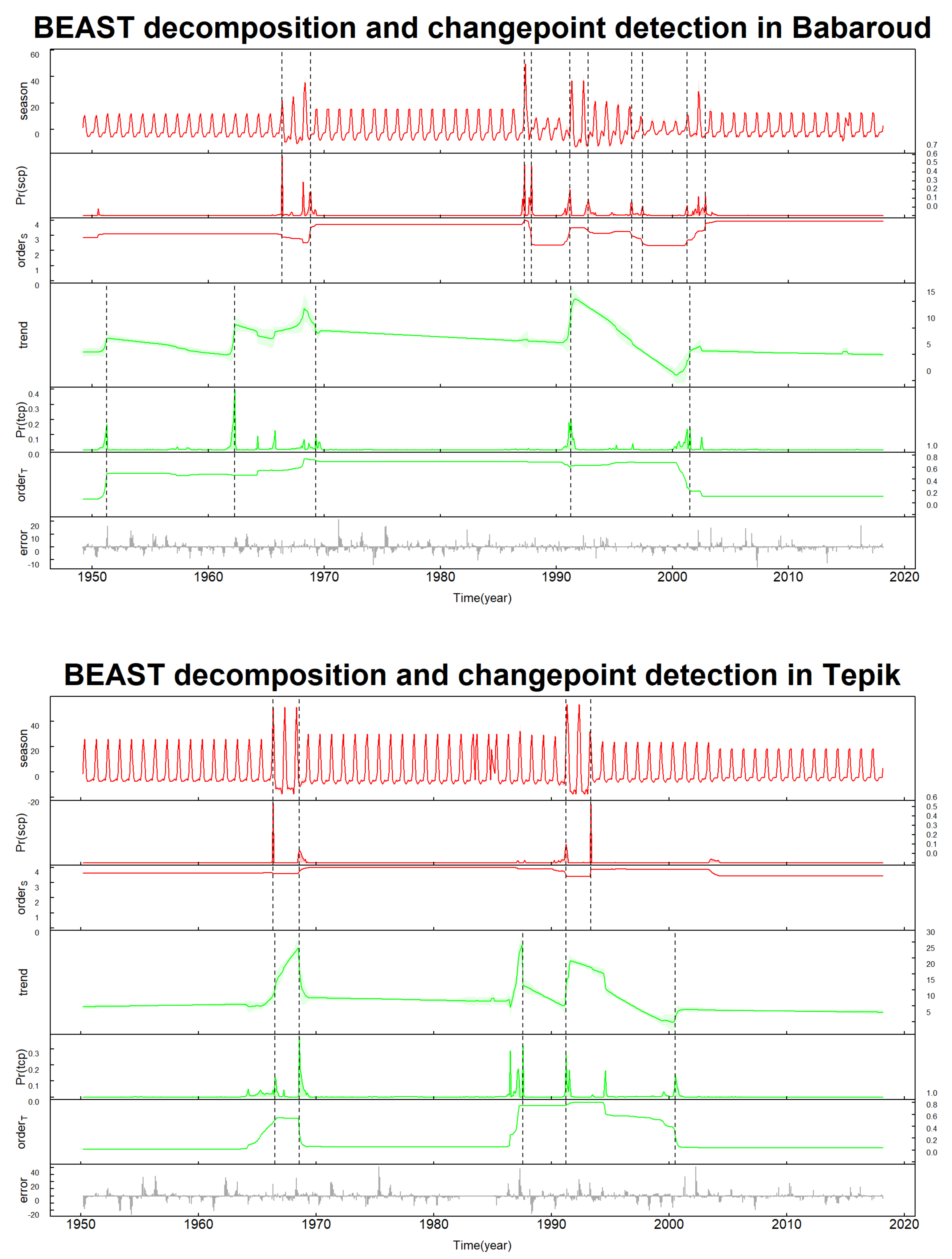
3.1. Trend Analysis of Stream Flow
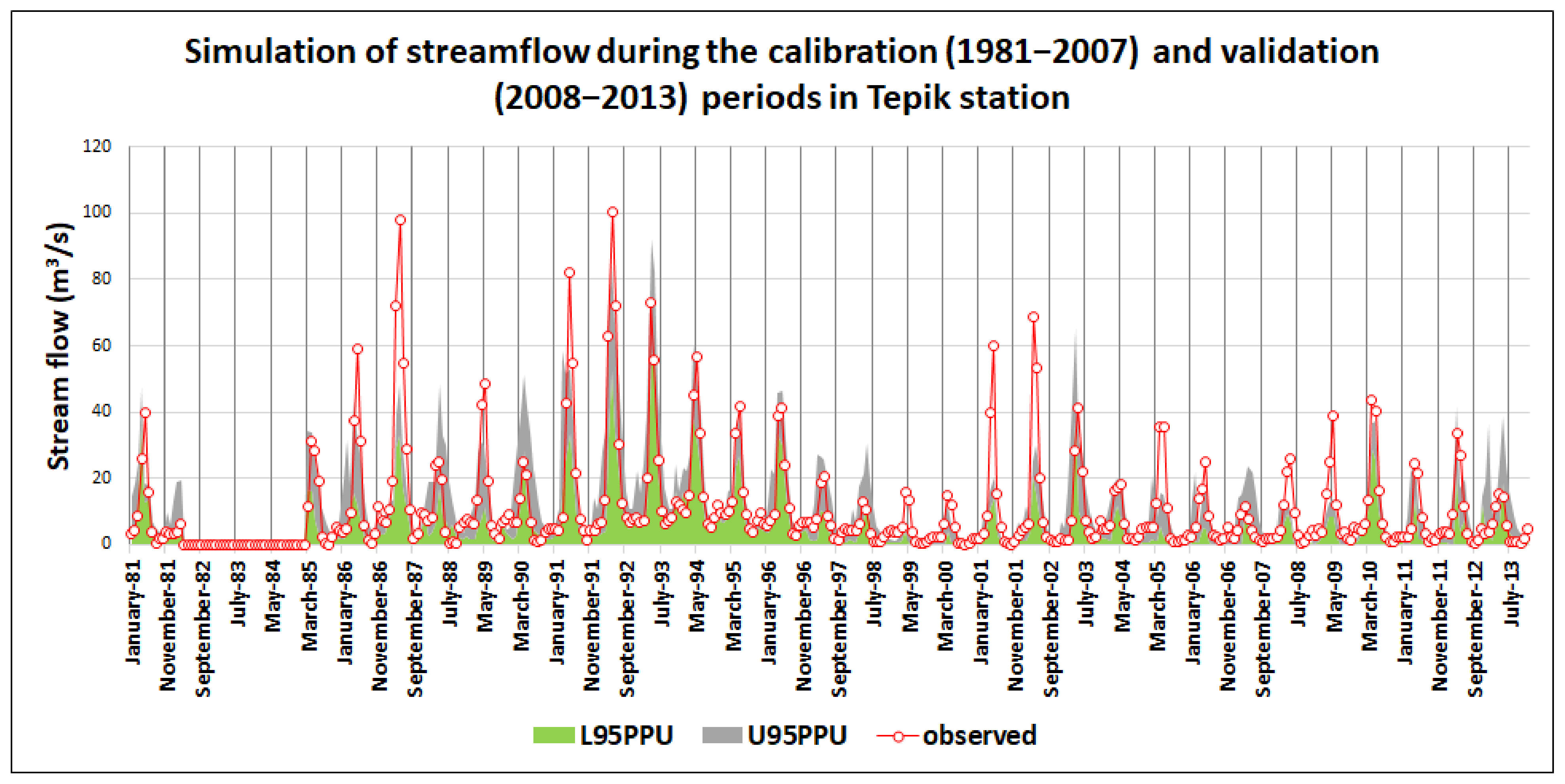
3.2. Water Yield Estimation by the SWAT Model
3.3. Main and Interaction Effects of LULCs on Water Yield
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1984. [Google Scholar]
- Neeti, N.; Eastman, J.R. A contextual Mann-Kendall approach for the assessment of trend significance in image time series. Trans. GIS 2011, 15, 599–611. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. J. Roy. Stat. Soc. C App. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Zhao, K.; Wulder, M.A.; Hu, T.; Bright, R.; Wu, Q.; Qin, H.; Li, Y.; Toman, E.; Mallick, B.; Zhang, X.; et al. Detecting change-point, trend, and seasonality in satellite time series data to track abrupt changes and nonlinear dynamics: A Bayesian ensemble algorithm. Remote Sens. Environ. 2019, 232, 111181. [Google Scholar] [CrossRef]
- He, Z.; Yao, J.; Lu, Y.; Guo, D. Detecting and explaining long-term changes in river water quality in south-eastern Australia. Hydrol. Process. 2022, 36, e14741. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, L.; Qiu, J.; Yan, J.; Wan, L.; Wang, P.; Hu, N.; Cheng, W.; Fu, B. Spatially explicit quantification of the interactions among ecosystem services. Landsc. Ecol. 2017, 32, 1181–1199. [Google Scholar] [CrossRef]
- Francesconi, W.; Srinivasan, R.; Pérez-Miñana, E.; Willcock, S.P.; Quintero, M. Using the Soil and Water Assessment Tool (SWAT) to model ecosystem services: A systematic review. J. Hydrol. 2016, 535, 625–636. [Google Scholar] [CrossRef]
- Anand, J.; Gosain, A.K.; Khosa, R. Prediction of land use changes based on Land Change Modeler and attribution of changes in the water balance of Ganga basin to land use change using the SWAT model. Sci. Total Environ. 2018, 644, 503–519. [Google Scholar] [CrossRef]
- Balist, J.; Malekmohammadi, B.; Jafari, H.R.; Nohegar, A.; Geneletti, D. Detecting land use and climate impacts on water yield ecosystem service in arid and semi-arid areas. A study in Sirvan River Basin-Iran. Appl. Water Sci. 2022, 12, 1–14. [Google Scholar] [CrossRef]
- Roushangar, K.; Alami, M.T.; Golmohammadi, H. Modeling the effects of land use/land cover changes on water requirements of Urmia Lake basin using CA-Markov and NETWAT models. Model. Earth Syst. Environ. 2022, 1–13. [Google Scholar] [CrossRef]
- Zaman, M.R.; Morid, S.; Delavar, M. Evaluating climate adaptation strategies on agricultural production in the Siminehrud catchment and inflow into Lake Urmia, Iran using SWAT within an OECD framework. Agric. Syst. 2016, 147, 98–110. [Google Scholar] [CrossRef]
- Samal, D.R.; Gedam, S. Assessing the impacts of land use and land cover change on water resources in the Upper Bhima river basin, India. Environ. Chall. 2021, 5, 100251. [Google Scholar] [CrossRef]
- de Oliveira Serrão, E.A.; Silva, M.T.; Ferreira, T.R.; de Ataide, L.C.P.; dos Santos, C.A.; de Lima, A.M.M.; da Silva, V.D.P.R.; de Sousa, F.D.A.S.; Gomes, D.J.C. Impacts of land use and land cover changes on hydrological processes and sediment yield determined using the SWAT model. Int. J. Sediment Res. 2022, 37, 54–69. [Google Scholar] [CrossRef]
- Guder, A.C.; Demissie, T.A.; Ahmed, D.T. Evaluation of hydrological impacts of land use/land cover changes of Holota Watershed, Upper Awash Sub-basin, Ethiopia. J. Sediment. Environ. 2022, 2022, 1–17. [Google Scholar] [CrossRef]
- Bauer, D.J.; Curran, P.J. Probing interactions in fixed and multilevel regression: Inferential and graphical techniques. Multivar. Behav. Res. 2005, 40, 373–400. [Google Scholar] [CrossRef] [PubMed]
- Thiessen, E.D.; Pavlik, P.I., Jr. iMinerva: A mathematical model of distributional statistical learning. Cogn. Sci. 2013, 37, 310–343. [Google Scholar] [CrossRef] [PubMed]
- Fathian, F.; Morid, S.; Kahya, E. Identification of trends in hydrological and climatic variables in Urmia Lake basin, Iran. Theor. Appl. Climatol. 2015, 119, 443–464. [Google Scholar] [CrossRef]
- Nazeri Tahroudi, M.; Ramezani, Y.; Ahmadi, F. Investigating the trend and time of precipitation and river flow rate changes in Lake Urmia basin, Iran. Arab. J. Geosci. 2019, 12, 1–13. [Google Scholar] [CrossRef]
- Nikbakht, J.; Tabari, H.; Talaee, P.H. Streamflow drought severity analysis by percent of normal index (PNI) in northwest Iran. Theor. Appl. Climatol. 2013, 112, 565–573. [Google Scholar] [CrossRef]
- Vaheddoost, B.; Aksoy, H. Interaction of groundwater with Lake Urmia in Iran. Hydrol. Process. 2018, 32, 3283–3295. [Google Scholar] [CrossRef]
- Hu, T.; Toman, E.M.; Chen, G.; Shao, G.; Zhou, Y.; Li, Y.; Zhao, K.; Feng, Y. Mapping fine-scale human disturbances in a working landscape with Landsat time series on Google Earth Engine. ISPRS J. Photogramm. 2021, 176, 250–261. [Google Scholar] [CrossRef]
- Zhao, K.; Valle, D.; Popescu, S.; Zhang, X.; Mallick, B. Hyperspectral remote sensing of plant biochemistry using Bayesian model averaging with variable and band selection. Remote Sens. Environ. 2013, 132, 102–119. [Google Scholar] [CrossRef]
- Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R.; Haney, E.B.; Neitsch, S.L. Chapter 13: SWAT INPUT DATA: CST. In SWAT 2012 Input/Output Documentation; Texas Water Resources Institute: College Station, TX, USA, 2013; pp. 179–186. [Google Scholar]
- Milewski, A.; Sultan, M.; Yan, E.; Becker, R.; Abdeldayem, A.W.; Gelil, K.A. Remote sensing solutions for estimating runoff and recharge in arid environments. J. Hydrol. 2009, 373, 1–14. [Google Scholar] [CrossRef]
- Astuti, I.; Kamalakanta, S.; Milewski, A.; Mishra, D. Impact of Land Use/Land Cover (LULC) change on surface runoff in an increasingly urbanized tropical watershed. Water Resour. Manag. 2019, 33, 4087–4103. [Google Scholar] [CrossRef]
- Milewski, A.; Seyoum, W.; Elkadiri, R.; Durham, M. Multi-scale hydrologic sensitivity to climatic and anthropogenic changes in Morocco. Geosciences 2020, 10, 13. [Google Scholar] [CrossRef]
- USDA Soil Conservation Service. National Engineering Handbook; Hydrology Section 4 (Chapters 4–10); United States Department of Agriculture: Washington, DC, USA, 1972. [Google Scholar]
- White, E.D.; Feyereisen, G.W.; Veith, T.L.; Bosch, D.D. Improving daily water yield estimates in the Little River watershed: SWAT adjustments. Trans. ASABE 2009, 52, 69–79. [Google Scholar] [CrossRef]
- Oeurng, C.; Sauvage, S.; Sánchez-Pérez, J.M. Assessment of hydrology, sediment and particulate organic carbon yield in a large agricultural catchment using the SWAT model. J. Hydrol. 2011, 401, 145–153. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: Temple, TX, USA, 2011. [Google Scholar]
- Ayivi, F.; Jha, M.K. Estimation of water balance and water yield in the Reedy Fork-Buffalo Creek Watershed in North Carolina using SWAT. Int. Soil Water Conserv. Res. 2018, 6, 203–213. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Pai, N.; Steiner, J.L.; Gowda, P.H.; Winchell, M.; Rathjens, H.; Starks, P.J.; Verser, J.A. SWAT-LUT: A desktop graphical user interface for updating land use in SWAT. J. Am. Water Resour. Assoc. 2019, 55, 1102–1115. [Google Scholar] [CrossRef] [Green Version]
- Abbaspour, K.C. SWAT Calibration and Uncertainty Programs. A User Manual; Swiss Federal Institute of Aquatic Science and Technology: Duebendorf, Switzerland, 2015; pp. 17–66. [Google Scholar]
- Kumar, S.; Merwade, V. Impact of watershed subdivision and soil data resolution on SWAT model calibration and parameter uncertainty. J. Am. Water Resour. Assoc. 2009, 45, 1179–1196. [Google Scholar] [CrossRef]
- Grusson, Y.; Sun, X.; Gascoin, S.; Sauvage, S.; Raghavan, S.; Anctil, F.; Sáchez-Pérez, J.M. Assessing the capability of the SWAT model to simulate snow, snow melt and streamflow dynamics over an alpine watershed. J. Hydrol. 2015, 531, 574–588. [Google Scholar] [CrossRef]
- Dhami, B.; Himanshu, S.K.; Pandey, A.; Gautam, A.K. Evaluation of the SWAT model for water balance study of a mountainous snowfed river basin of Nepal. Environ. Earth Sci. 2018, 77, 1–20. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Vejdani, M.; Haghighat, S. SWAT-CUP calibration and uncertainty programs for SWAT. In Proceedings of the Modsim 2007: International Congress on Modelling and Simulation: Land Water and Environmental Management: Integrated Systems for Sustainability, Christchurch, New Zealand, 10–13 December 2007. [Google Scholar]
- Narsimlu, B.; Gosain, A.K.; Chahar, B.R.; Singh, S.K.; Srivastava, P.K. SWAT model calibration and uncertainty analysis for streamflow prediction in the Kunwari River Basin, India, using sequential uncertainty fitting. Environ. Process. 2015, 2, 79–95. [Google Scholar] [CrossRef]
- Zhuang, D.F.; Liu, J.Y. Study on the model of regional differentiation of land use degree in China. J. Nat. Resour. 1997, 12, 105–111. [Google Scholar]
- Long, J.A. Interactions: Comprehensive, User-Friendly Toolkit for Probing Interactions. R Package Version 1.1.0. 2019. Available online: https://cran.r-project.org/package=interactions (accessed on 21 September 2022).
- Shadkam, S.; Ludwig, F.; van Oel, P.; Kirmit, Ç.; Kabat, P. Impacts of climate change and water resources development on the declining inflow into Iran’s Urmia Lake. J. Great Lakes Res. 2016, 42, 942–952. [Google Scholar] [CrossRef]
- Khazaei, B.; Khatami, S.; Alemohammad, S.H.; Rashidi, L.; Wu, C.; Madani, K.; Kalantari, Z.; Destouni, G.; Aghakouchak, A. Climatic or regionally induced by humans? Tracing hydro-climatic and land-use changes to better understand the Lake Urmia tragedy. J. Hydrol. 2019, 569, 203–217. [Google Scholar] [CrossRef]
- Pang, S.; Wang, X.; Melching, C.S.; Feger, K.H. Development and testing of a modified SWAT model based on slope condition and precipitation intensity. J. Hydrol. 2020, 588, 125098. [Google Scholar] [CrossRef]
- Li, M.; Di, Z.; Duan, Q. Effect of sensitivity analysis on parameter optimization: Case study based on streamflow simulations using the SWAT model in China. J. Hydrol. 2021, 603, 126896. [Google Scholar] [CrossRef]
- Wu, L.; Liu, X.; Chen, J.; Yu, Y.; Ma, X. Overcoming equifinality: Time-varying analysis of sensitivity and identifiability of SWAT runoff and sediment parameters in an arid and semiarid watershed. Environ. Sci. Pollut. Res. 2022, 29, 31631–31645. [Google Scholar] [CrossRef] [PubMed]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’ sensitivity analysis of a complex environmental model. Environ. Model. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]
- Kushwaha, A.; Jain, M.K. Hydrological simulation in a forest dominated watershed in Himalayan region using SWAT model. Water Resour. Manag. 2013, 27, 3005–3023. [Google Scholar] [CrossRef]
- Xueman, Y.; Wenxi, L.; Yongkai, A.; Dong, W. Assessment of parameter uncertainty for non-point source pollution mechanism modeling: A Bayesian-based approach. Environ. Pollut. 2020, 263, 114570. [Google Scholar] [CrossRef] [PubMed]
- Kumar, N.; Singh, S.K.; Srivastava, P.K.; Narsimlu, B. SWAT Model calibration and uncertainty analysis for streamflow prediction of the Tons River Basin, India, using Sequential Uncertainty Fitting (SUFI-2) algorithm. Model. Earth Syst. Environ. 2017, 3, 1–13. [Google Scholar] [CrossRef]
- Gareth, J.; Daniela, W.; Trevor, H.; Robert, T. An Introduction to Statistical Learning: With Applications in R; Springer: Los Angeles, CA, USA, 2013. [Google Scholar]
- Field, A.; Miles, J.; Field, Z. Discovering Statistics Using R; Sage Publications: Thousand Oaks, CA, USA, 2012. [Google Scholar]
- Li, C.; Sun, G.; Caldwell, P.V.; Cohen, E.; Fang, Y.; Zhang, Y.; Oudin, L.; Sanchez, G.M.; Meentemeyer, R.K. Impacts of urbanization on watershed water balances across the conterminous United States. Water Resour. Res. 2020, 56, e2019WR026574. [Google Scholar] [CrossRef]
- Thompson, C.G.; Kim, R.S.; Aloe, A.M.; Becker, B.J. Extracting the variance inflation factor and other multicollinearity diagnostics from typical regression results. Basic Appl. Soc. Psychol. 2017, 39, 81–90. [Google Scholar] [CrossRef]
- Nahib, I.; Ambarwulan, W.; Rahadiati, A.; Munajati, S.L.; Prihanto, Y.; Suryanta, J.; Turmudi, T.; Nuswantoro, A.C. Assessment of the impacts of climate and LULC changes on the water yield in the Citarum River Basin, West Java Province, Indonesia. Sustainability 2021, 13, 3919. [Google Scholar] [CrossRef]
- Lee, D.; Derrible, S. Predicting residential water demand with machine-based statistical learning. J. Water Resour. Plan. Manag. 2020, 146, 04019067. [Google Scholar] [CrossRef]
- Redhead, J.W.; Stratford, C.; Sharps, K.; Jones, L.; Ziv, G.; Clarke, D.; Oliver, T.H.; Bullock, J.M. Empirical validation of the InVEST water yield ecosystem service model at a national scale. Sci. Total Environ. 2016, 569, 1418–1426. [Google Scholar] [CrossRef]
- Guo, M.; Ma, S.; Wang, L.J.; Lin, C. Impacts of future climate change and different management scenarios on water-related ecosystem services: A case study in the Jianghuai ecological economic Zone, China. Ecol. Indic. 2021, 127, 107732. [Google Scholar] [CrossRef]
- Wang, X.; Liu, G.; Lin, D.; Lin, Y.; Lu, Y.; Xiang, A.; Xiao, S. Water yield service influence by climate and land use change based on InVEST model in the monsoon hilly watershed in South China. Geomat. Nat. Hazards Risk 2022, 13, 2024–2048. [Google Scholar] [CrossRef]
- Dennedy-Frank, P.J.; Muenich, R.L.; Chaubey, I.; Ziv, G. Comparing two tools for ecosystem service assessments regarding water resources decisions. J. Environ. Manag. 2016, 177, 331–340. [Google Scholar] [CrossRef]
- Li, S.; Yang, H.; Lacayo, M.; Liu, J.; Lei, G. Impacts of land-use and land-cover changes on water yield: A case study in Jing-Jin-Ji, China. Sustainability 2018, 10, 960. [Google Scholar] [CrossRef]
- Miller, J.W.; Stromeyer, W.R.; Schwieterman, M.A. Extensions of the Johnson-Neyman technique to linear models with curvilinear effects: Derivations and analytical tools. Multivar. Behav. Res. 2013, 48, 267–300. [Google Scholar] [CrossRef]
- Seekell, D.A.; Byström, P.; Karlsson, J. Lake morphometry moderates the relationship between water color and fish biomass in small boreal lakes. Limnol. Oceanogr. 2018, 63, 2171–2178. [Google Scholar] [CrossRef]
- Freire, Y.A.; Cabral, L.L.P.; Browne, R.A.V.; Vlietstra, L.; Waters, D.L.; Duhamel, T.A.; Costa, E.C. Daily step volume and intensity moderate the association of sedentary time and cardiometabolic disease risk in community-dwelling older adults: A cross-sectional study. Exp. Gerontol. 2022, 170, 111989. [Google Scholar] [CrossRef] [PubMed]
- Xiong, X.; Grunwald, S.; Myers, D.B.; Ross, C.W.; Harris, W.G.; Comerford, N.B. Interaction effects of climate and land use/land cover change on soil organic carbon sequestration. Sci. Total Environ. 2014, 493, 974–982. [Google Scholar] [CrossRef]
- Molina, A.; Govers, G.; Vanacker, V.; Poesen, J.; Zeelmaekers, E.; Cisneros, F. Runoff generation in a degraded Andean ecosystem: Interaction of vegetation cover and land use. Catena 2007, 71, 357–370. [Google Scholar] [CrossRef]


| Parameter Types | Description | Unit | Min | Max | Fitted Value |
|---|---|---|---|---|---|
| Surface flow parameters | |||||
| r__SOL_K | Saturated hydraulic conductivity | mm/h | −0.8 | 0.8 | varied over watershed |
| r__SOL_BD | Moist bulk density | g/cm3 | −0.3 | 0.3 | varied over watershed |
| r__SOL_AWC | Available water capacity of soil top layer | mm H2O/mm soil | 0 | 3 | varied over watershed |
| r__HRU_SLP | Average slope steepness | m/m | −0.5 | 3 | varied over watershed |
| r__OV_N | Manning’s “n” value for overland flow | - | −0.5 | 3 | varied over watershed |
| r__SLSUBBSN | Average slope length | m | −0.2 | 0.2 | varied over watershed |
| r__CN2 | Initial SCS runoff curve number for moisture condition II | - | −0.3 | 0.3 | varied over watershed |
| v__ESCO | Soil evaporation compensation factor | - | 0 | 1 | varied over watershed |
| Groundwater flow parameters | |||||
| v__GWQMN | Threshold depth of water in shallow aquifer required for return flow to occur | mm | 500 | 5000 | varied over watershed |
| v__GW_REVAP | Groundwater “revap” coefficient | - | 0.02 | 0.2 | varied over watershed |
| v__REVAPMN | Threshold depth of water in shallow aquifer required for percolation to deep aquifer to occur | mm | 0 | 500 | varied over watershed |
| v__GW_DELAY | Groundwater delay time | days | 0 | 100 | varied over watershed |
| v__RCHRG_DP | Deep aquifer percolation fraction | - | 0 | 0.5 | varied over watershed |
| v__ALPHA_BF | Baseflow recession constant | 1/days | 0 | 0.2 | varied over watershed |
| Snowmelt parameters | |||||
| v__SFTMP | Snowfall temperature | °C | −5 | 5 | −0.46 |
| v__SMTMP | Snowmelt base temperature | °C | −5 | 5 | 2.5 |
| v__SMFMX | Maximum melt rate for snow during year | mm H2O/°C-day | 0 | 5 | 3.13 |
| v__SMFMN | Minimum melt rate for snow during the year | mm H2O/°C-day | 0 | 5 | 0.35 |
| v__TIMP | Snow pack temperature lag factor | - | 0 | 1 | 0.79 |
| Elevation band parameters | |||||
| v__TLAPS | Temperature lapse rate | °C/km | −8 | −4 | −5.15 |
| v__PLAPS | Precipitation lapse rate | mm H2O/km | 0 | 100 | 7.03 |
| Babaroud Station | Tepik Station | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| trend change points | seasonal change points | trend change points | seasonal change points | ||||||||
| prob(cpPr) | time(year) (cp) | #scp | prob(cpPr) | time(year) (cp) | #scp | prob(cpPr) | time(year) (cp) | #scp | prob(cpPr) | time (cp) | #scp |
| 0.978 | 1991.25 | 1 | 0.923 | 1987.66 | 1 | 0.99 | 1968.58 | 1 | 0.724 | 1993.3 | 1 |
| 0.753 | 2000.50 | 2 | 0.847 | 1950.50 | 2 | 0.65 | 1991.58 | 2 | 0.501 | 1991.2 | 2 |
| 0.653 | 1969.25 | 3 | 0.695 | 1990.75 | 3 | 0.43 | 2000.50 | 3 | 0.438 | 1987.8 | 3 |
| 0.611 | 1958.25 | 4 | 0.562 | 1966.33 | 4 | 0.41 | 1987.25 | 4 | 0.435 | 1987.1 | 4 |
| 0.550 | 1964.25 | 5 | 0.493 | 1969.16 | 5 | 0.35 | 1965.25 | 5 | 0.355 | 1954.5 | 5 |
| 0.453 | 1992.58 | 6 | 0.331 | 1966.3 | 6 | ||||||
| 0.440 | 2002.75 | 7 | 0.247 | 1968.8 | 7 | ||||||
| 0.375 | 2002.16 | 8 | 0.236 | 1990.0 | 8 | ||||||
| 0.341 | 1996.50 | 9 | 0.101 | 1996.6 | 9 | ||||||
| 0.318 | 1997.41 | 10 | 0.093 | 1961.5 | 10 | ||||||
| Validation | Calibration | Gauging Stations | ||||||
|---|---|---|---|---|---|---|---|---|
| r-Factor | p-Factor | NS | R2 | r-Factor | p-Factor | NS | R2 | |
| 0.46 | 0.49 | 0.55 | 0.62 | 0.63 | 0.64 | 0.68 | 0.68 | Abajalo |
| 0.61 | 0.27 | 0.37 | 0.49 | 0.76 | 0.30 | 0.49 | 0.65 | Tepik |
| 0.47 | 0.29 | 0.61 | 0.72 | 0.51 | 0.41 | 0.66 | 0.67 | Dizaj |
| 0.34 | 0.40 | 0.70 | 0.73 | 0.44 | 0.51 | 0.53 | 0.64 | Hashem Abad |
| 1.13 | 0.39 | 0.52 | 0.66 | 1.02 | 0.46 | 0.47 | 0.57 | Gedarchay |
| 0.72 | 0.50 | 0.71 | 0.73 | 0.81 | 0.57 | 0.74 | 0.75 | Bighaleh |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakizadeh, M.; Milewski, A.; Sattari, M.T. Analysis of Long-Term Trend of Stream Flow and Interaction Effect of Land Use and Land Cover on Water Yield by SWAT Model and Statistical Learning in Part of Urmia Lake Basin, Northwest of Iran. Water 2023, 15, 690. https://doi.org/10.3390/w15040690
Sakizadeh M, Milewski A, Sattari MT. Analysis of Long-Term Trend of Stream Flow and Interaction Effect of Land Use and Land Cover on Water Yield by SWAT Model and Statistical Learning in Part of Urmia Lake Basin, Northwest of Iran. Water. 2023; 15(4):690. https://doi.org/10.3390/w15040690
Chicago/Turabian StyleSakizadeh, Mohamad, Adam Milewski, and Mohammad Taghi Sattari. 2023. "Analysis of Long-Term Trend of Stream Flow and Interaction Effect of Land Use and Land Cover on Water Yield by SWAT Model and Statistical Learning in Part of Urmia Lake Basin, Northwest of Iran" Water 15, no. 4: 690. https://doi.org/10.3390/w15040690
APA StyleSakizadeh, M., Milewski, A., & Sattari, M. T. (2023). Analysis of Long-Term Trend of Stream Flow and Interaction Effect of Land Use and Land Cover on Water Yield by SWAT Model and Statistical Learning in Part of Urmia Lake Basin, Northwest of Iran. Water, 15(4), 690. https://doi.org/10.3390/w15040690









