Experimental and Numerical Study on Flow Control Using 3-Array Submerged Vane in Laboratory Channel Bend
Abstract
:1. Introduction
2. Materials and Methods
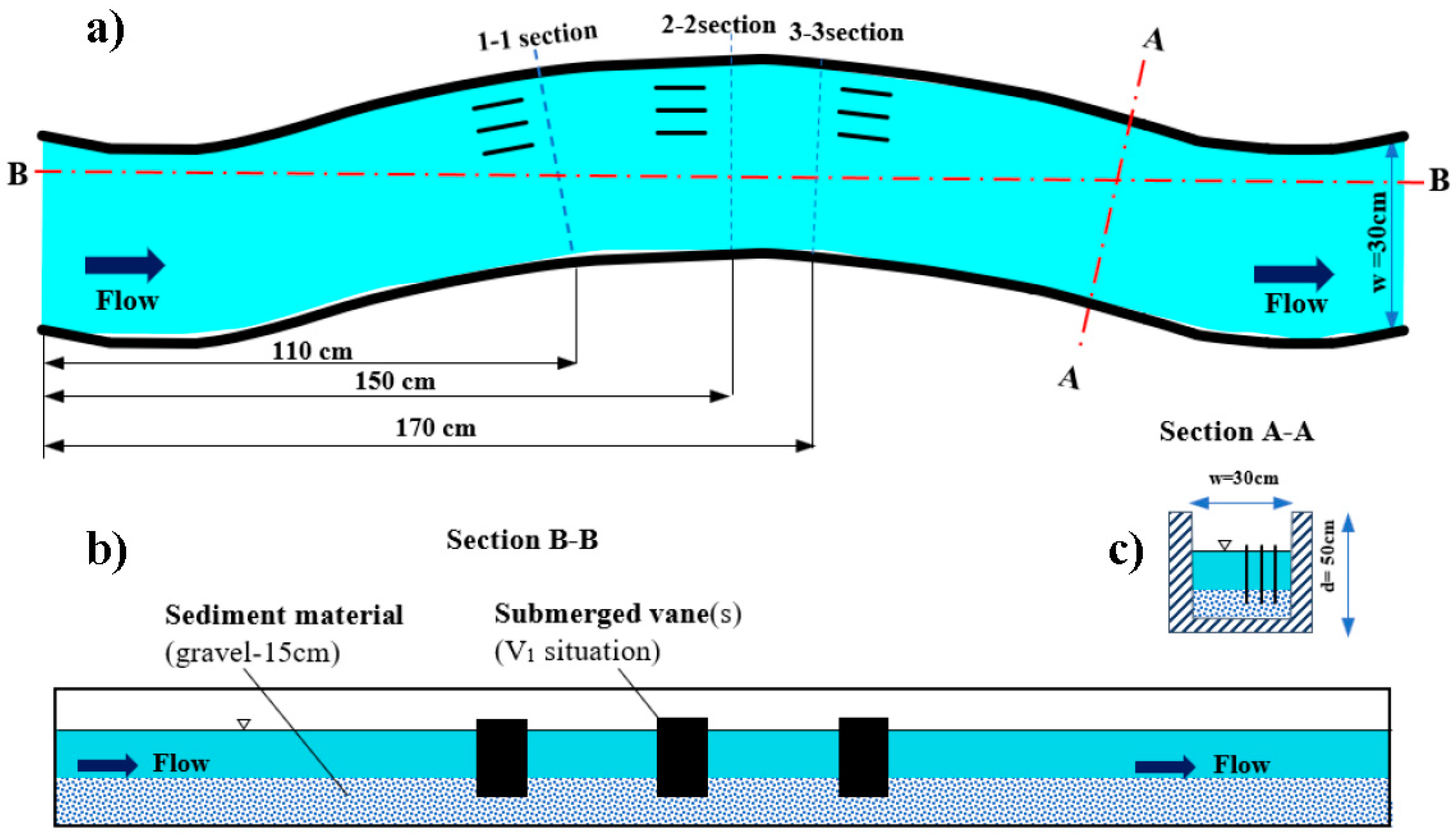
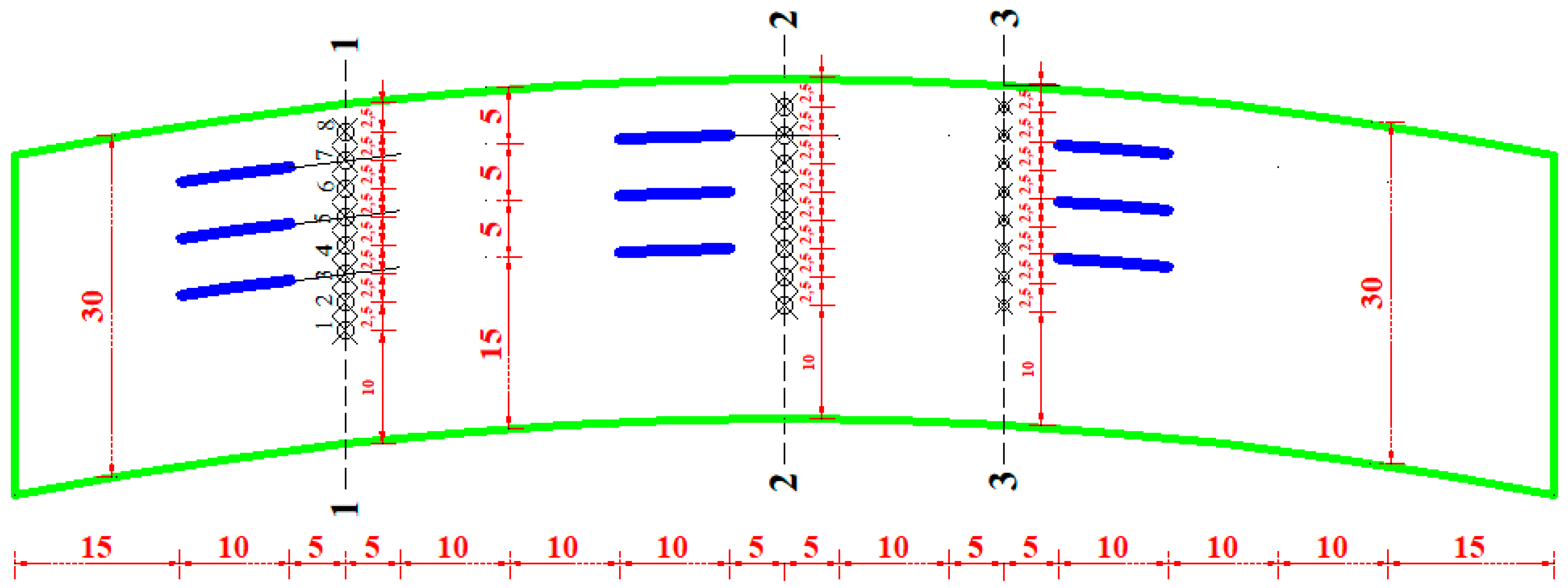
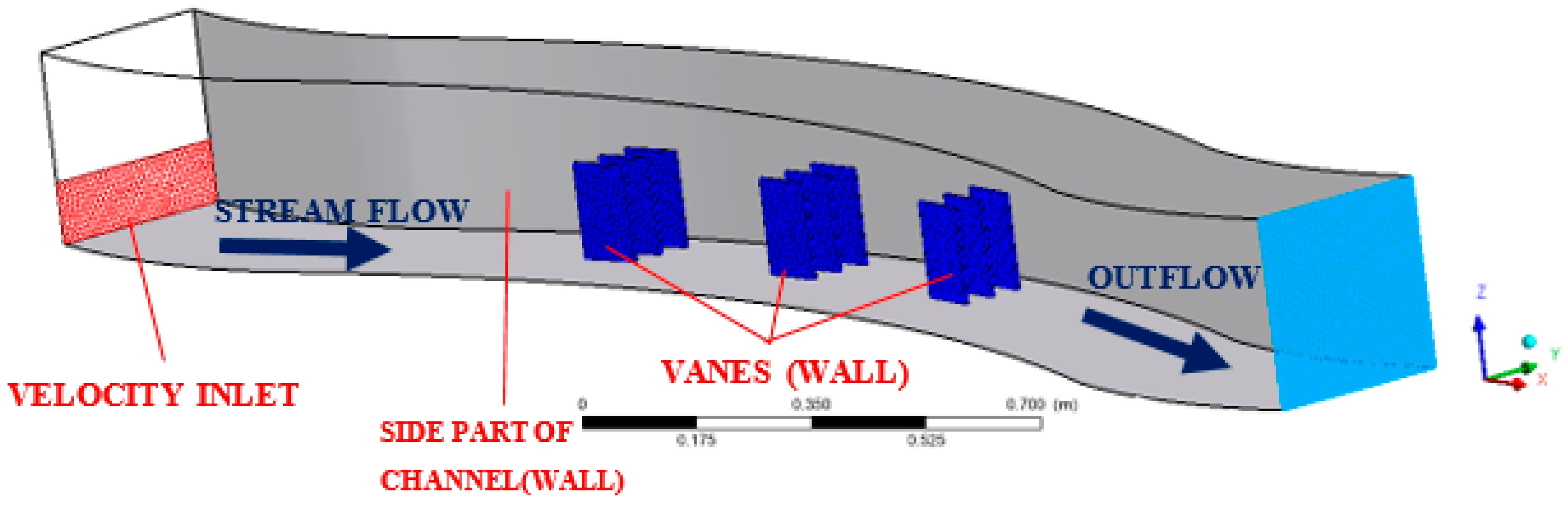
2.1. Experimental Set-Up
2.2. Mathematical Model
2.2.1. Basic Equations
2.2.2. Boundary Conditions for Submerged Vanes
2.2.3. Meshing-Grid Information
2.2.4. Numerical Solver
3. Results and Discussion
4. Conclusions
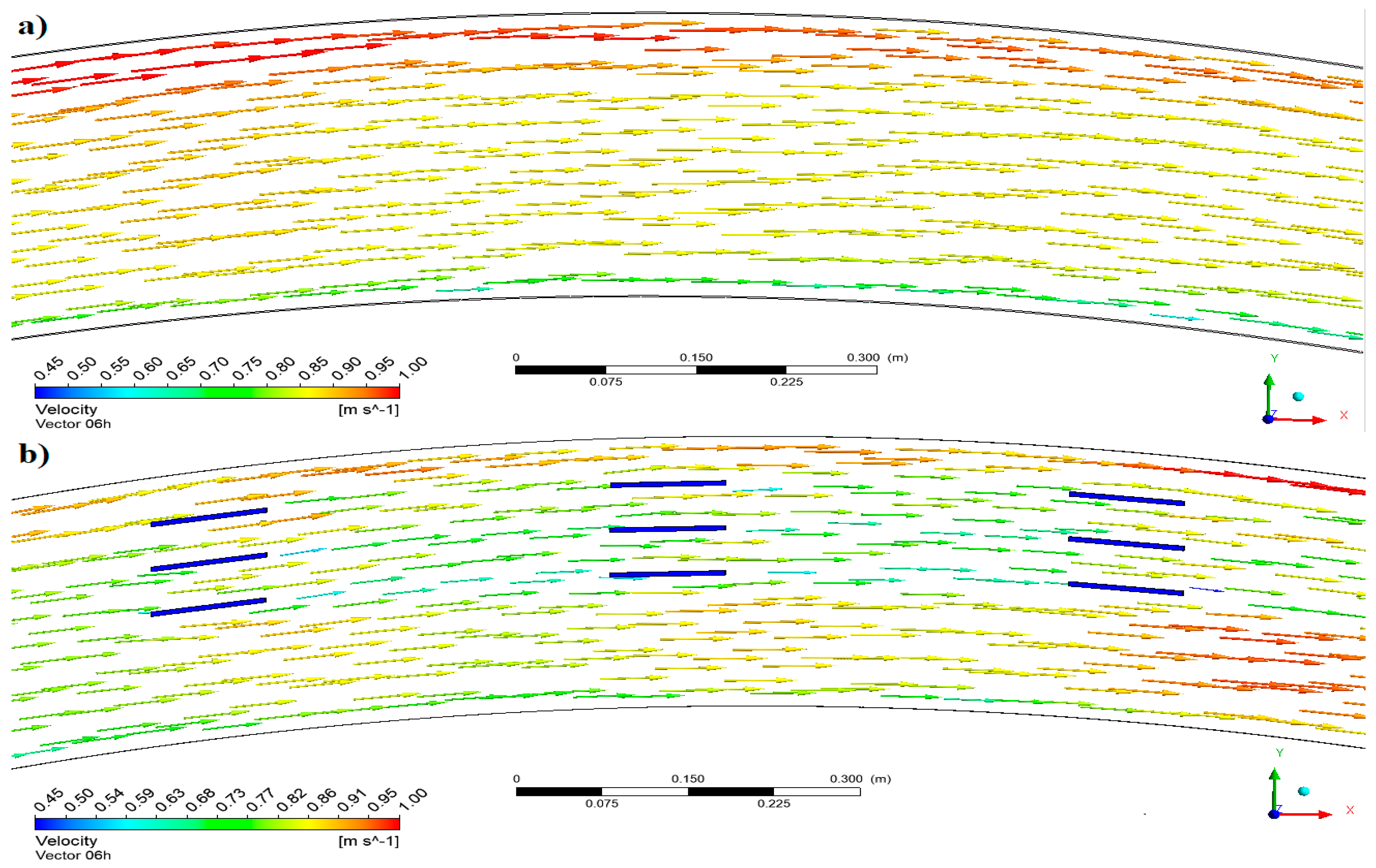
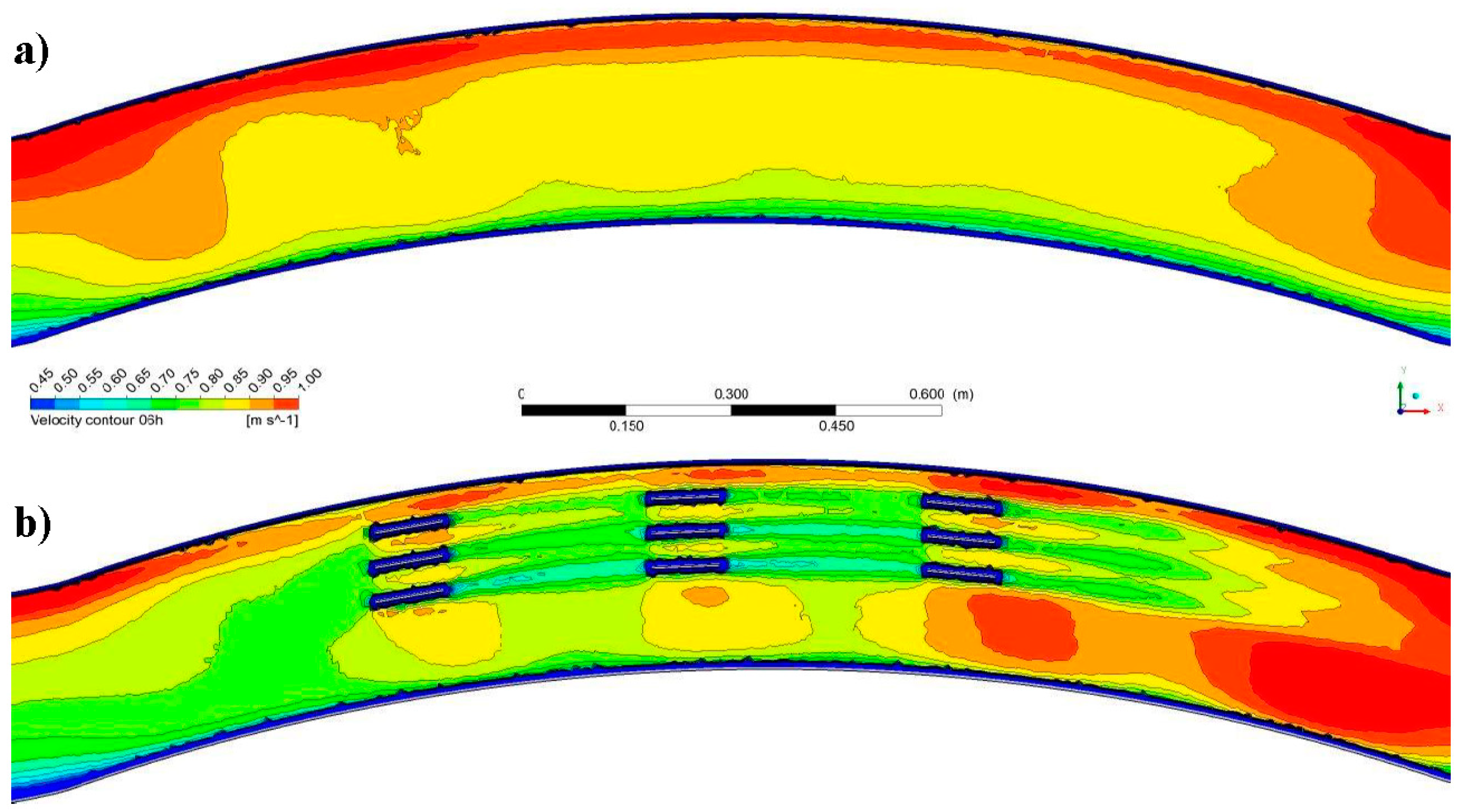
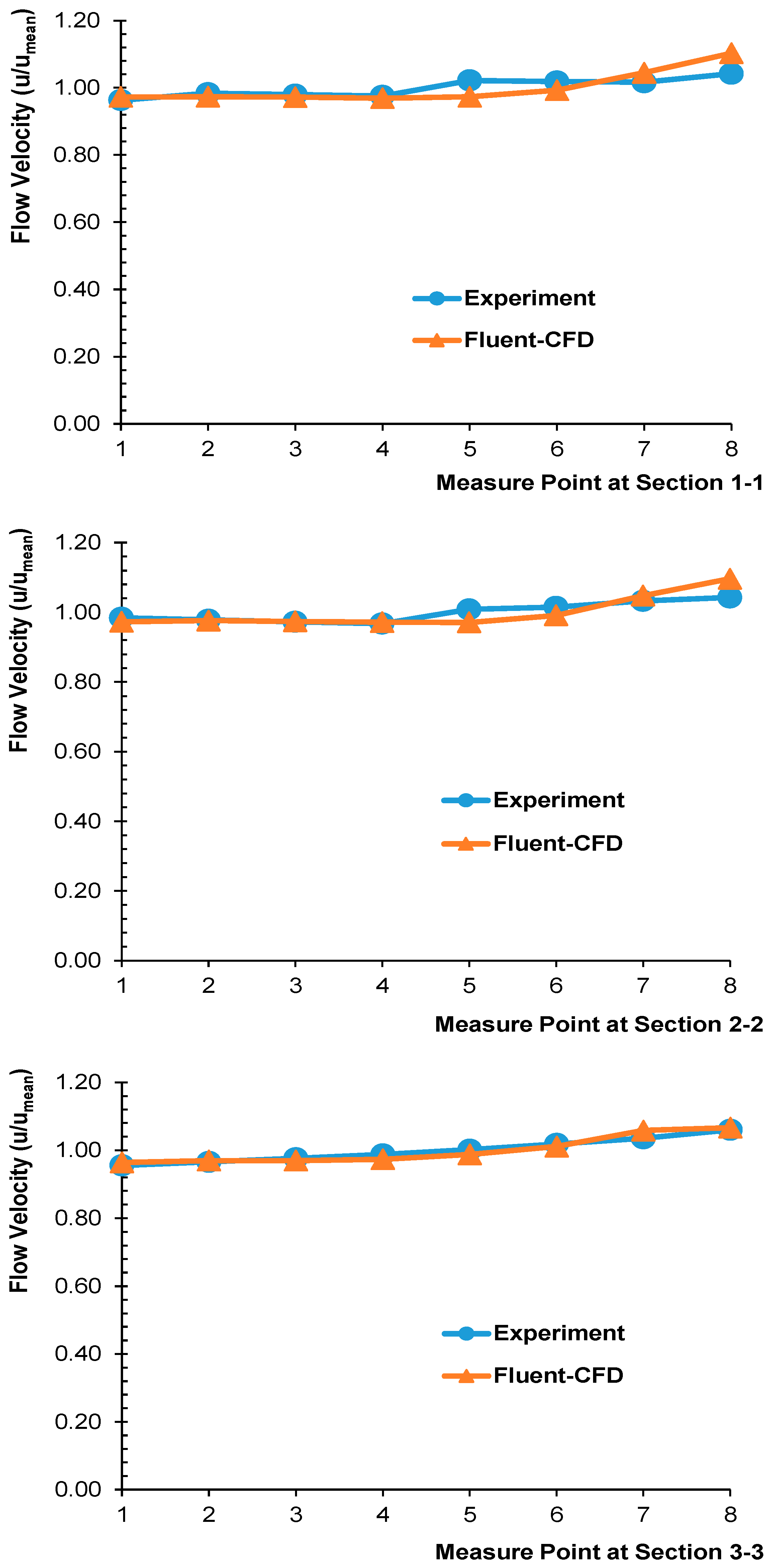
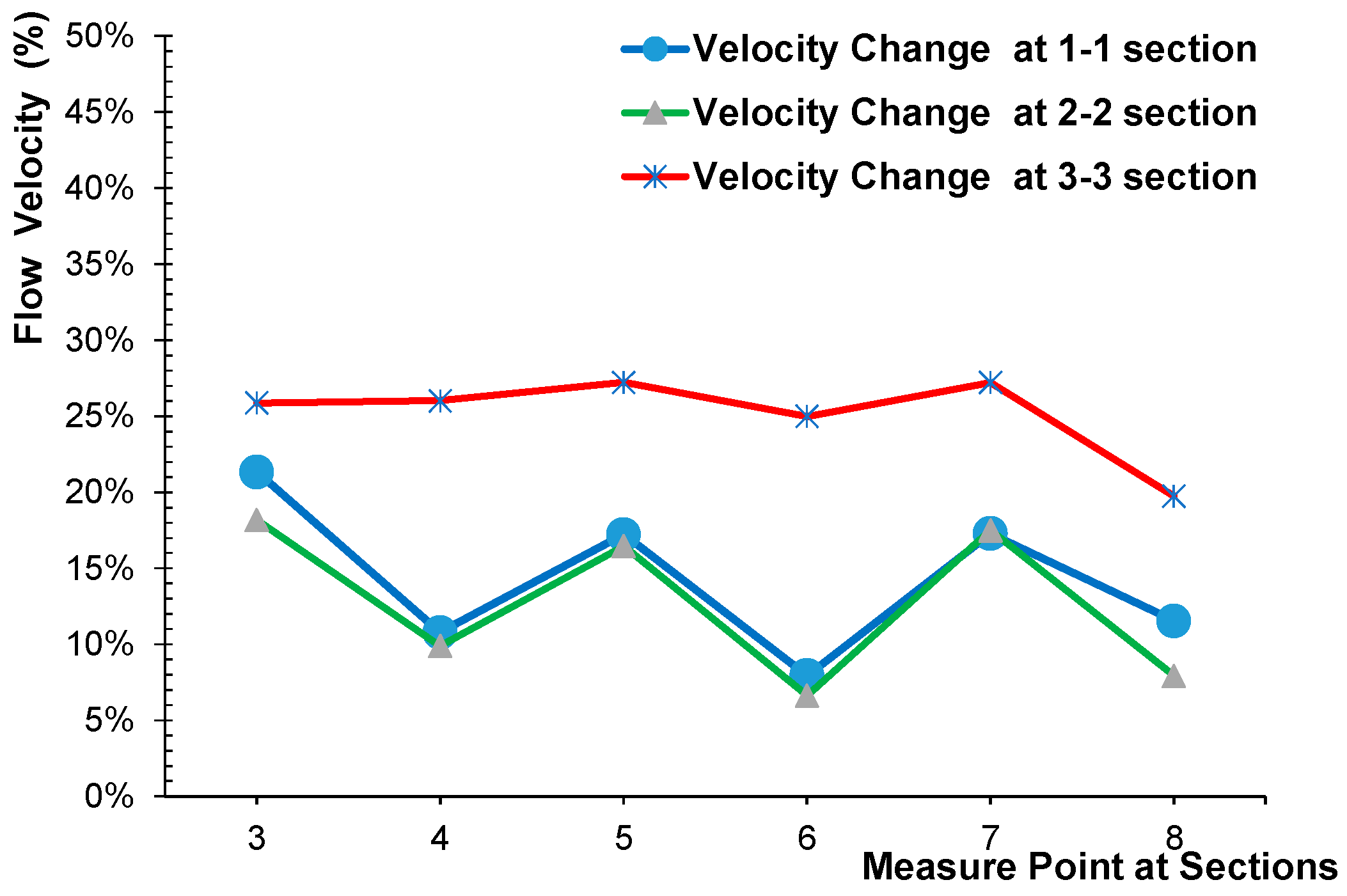
- The simulated CFD velocity for the without vane and 9 (3 × 3) vane cases were compared with the measured data. If the results of the experiments are examined in accordance with the CFD simulation results, a lower error has been detected. Figure 1. Flow velocity changes for ‘with vanes’ situation at sections; 1-1, 2-2 and 3-3. When the experimental and CFD results were examined, the maximum error was observed as 6.32%.
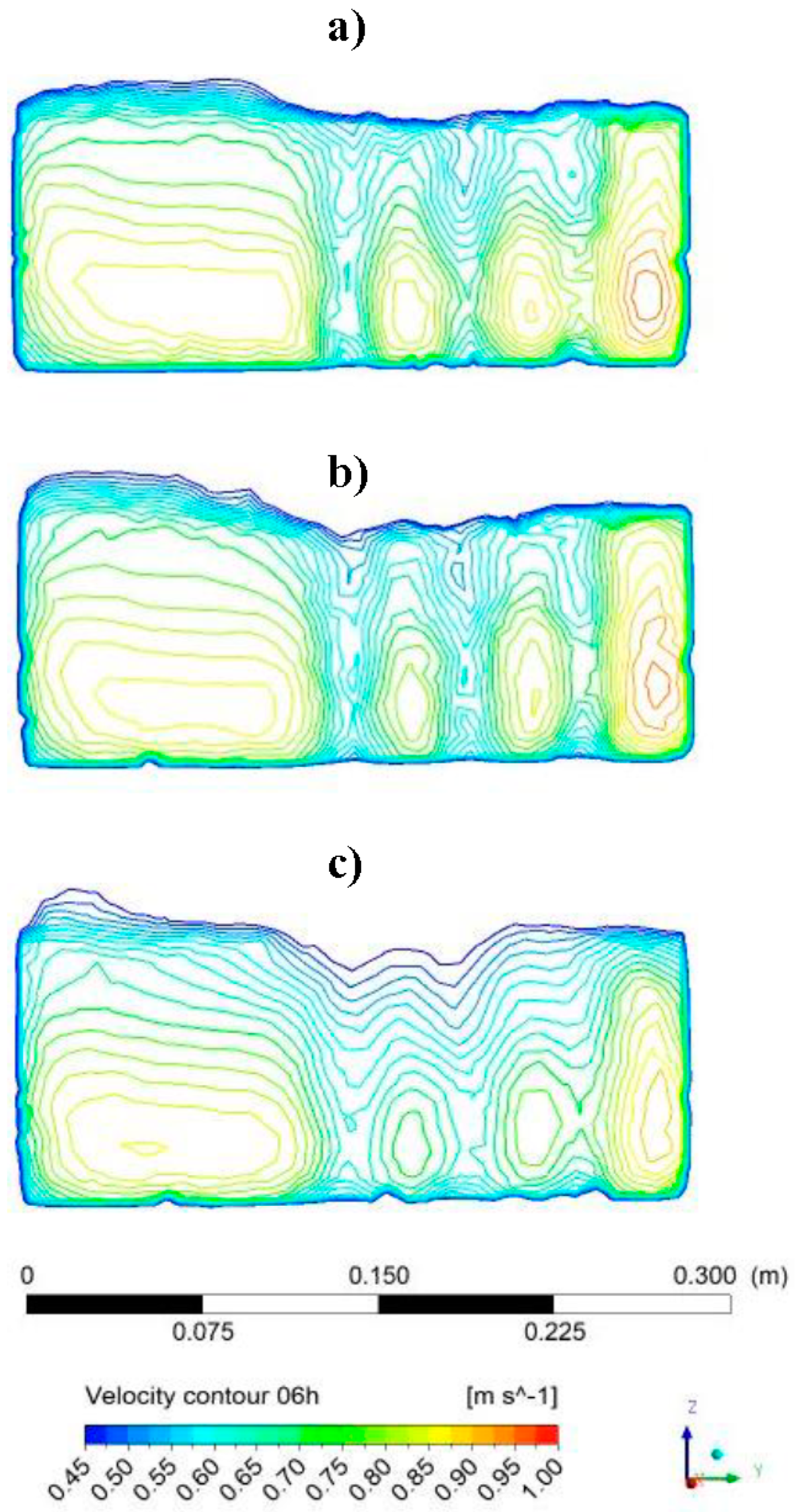
- It was found that 3 vane structures in 3-array affect the mean flow velocity by 27% and minimum flow velocity by 16% at 0.6 d.
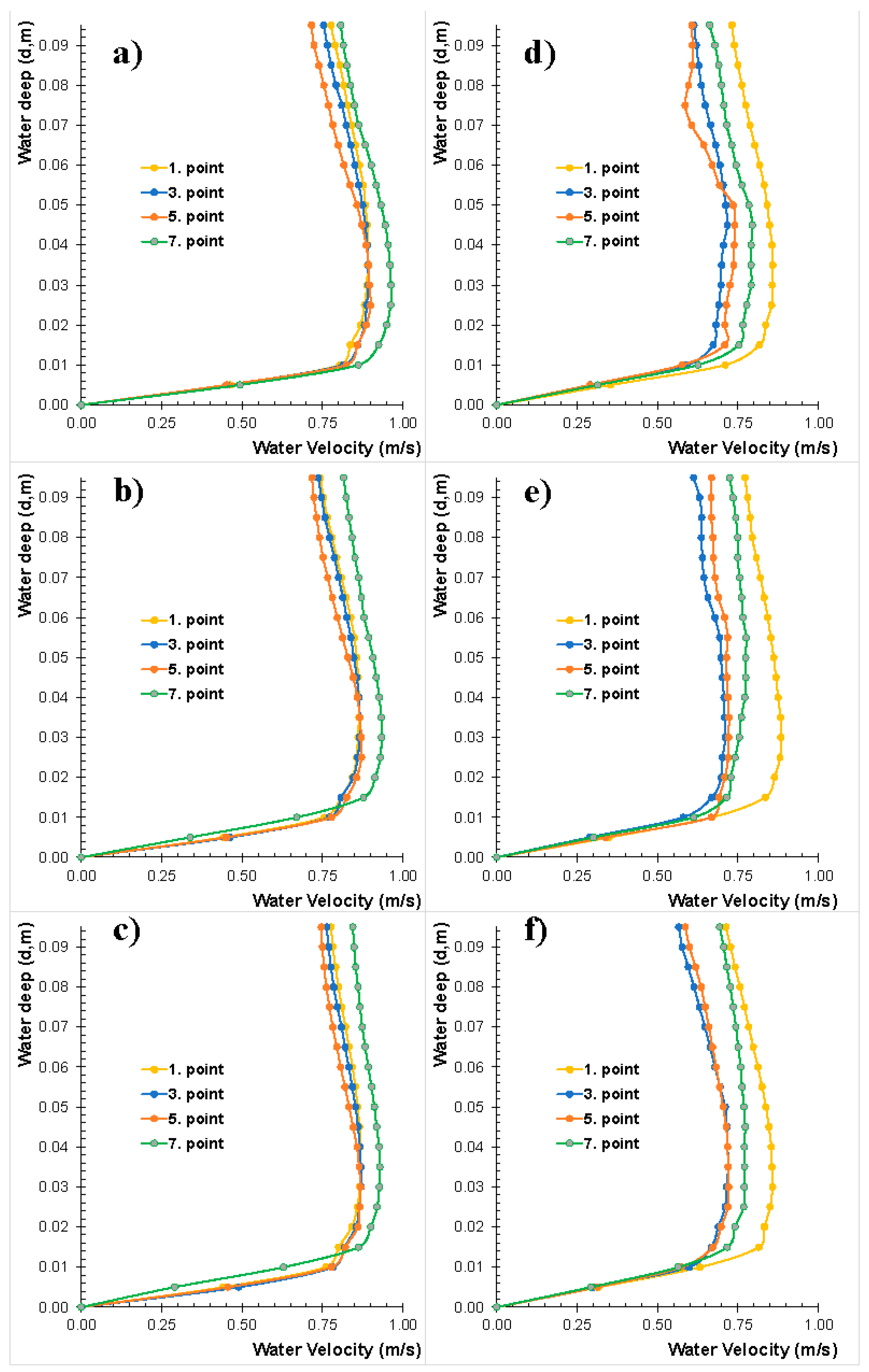
- The flow velocities were investigated along with depth using the CFD and found that the mean velocity was reduced by 14–21% along the depth.
- Submerged vane structures balance the flow of water depth on the inner bank with the water depth on the outer bank within open channel flows. It reduced the flow velocity by directing the water depth and flow velocity from the outer bank to the inner bank.
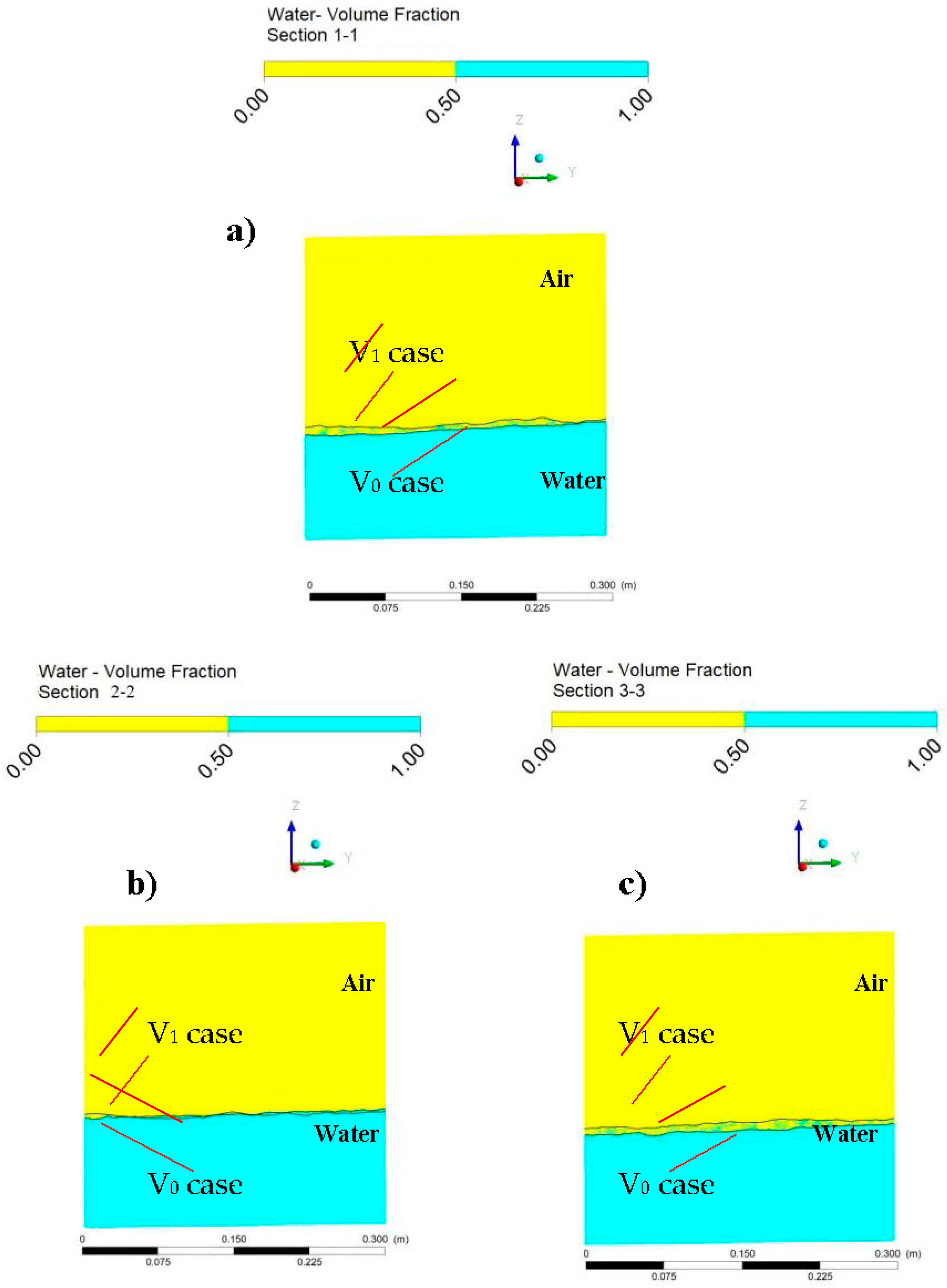
- When the depth changes in sections are examined, it is observed that generally submerged vanes increase the water depth. In the sections, the water depth increased by about 6–8% in the V1 case compared to the V0 case.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Odgaard, A.J.; Kennedy, J.F. Analysis of Sacramento River Bend Flows, and Development of a New Method for Bank Protection; The University of Iowa: Iowa City, IA, USA, 1982; Available online: http://www2.iihr.uiowa.edu/wp-content/uploads/2013/06/IIHR241.pdf (accessed on 27 December 2022).
- Odgaard, A.J.; Kennedy, J.F. River-Bend Bank Protection by Submerged Vanes. J. Hydraul. Eng. 1983, 109, 1161–1173. [Google Scholar] [CrossRef]
- Odgaard, A.J.; Lee, H.Y.E. Submerged Vanes for Flow Control and Bank Protection in Streams; Iowa Institute of Hydraulic Research, the University of Iowa: Iowa City, IA, USA, 1984; Available online: https://agris.fao.org/agris-search/search.do?recordID=US874929288 (accessed on 27 December 2022).
- Odgaard, A.J. Streambank Erosion along Two Rivers in Iowa. Water Resour. Res. 1987, 23, 1225–1236. [Google Scholar] [CrossRef]
- Marelius, F.; Sinha, S.K. Experimental Investigation of Flow Past Submerged Vanes. J. Hydraul. Eng. 1998, 124, 542–545. [Google Scholar] [CrossRef]
- Voisin, A.; Townsend, R.D. Model Testing of Submerged Vanes in Strongly Curved Narrow Channel Bends. Can. J. Civ. Eng. 2002, 29, 37–49. [Google Scholar] [CrossRef]
- Gemici, E. Açık Kanallarda Batık Kanatlarla Akım Yönetimi; Erciyes Üniversity: Kayseri, Turkish, 2015. [Google Scholar]
- Mohammadiun, S.; Salehi Neyshabouri, S.A.A.; Naser, G.; Vahabi, H. Numerical Investigation of Submerged Vane Effects on Flow Pattern in a 90° Junction of Straight and Bend Open Channels. Iran. J. Sci. Technol. Trans. Civ. Eng. 2016, 40, 349–365. [Google Scholar] [CrossRef]
- Fathi, A.; Zomorodian, S.M.A. Effect of Submerged Vanes on Scour Around a Bridge Abutment. KSCE J. Civ. Eng. 2018, 22, 2281–2289. [Google Scholar] [CrossRef]
- Kalathil, S.T.; Wuppukondur, A.; Balakrishnan, R.K.; Chandra, V. Control of Sediment Inflow into a Trapezoidal Intake Canal Using Submerged Vanes. Port Coast. Ocean. Eng. 2018, 144, 04018020. [Google Scholar] [CrossRef]
- Zarei, E.; Vaghefi, M.; Hashemi, S.S. Bed Topography Variations in Bend by Simultaneous Installation of Submerged Vanes and Single Bridge Pier. Arab. J. Geosci. 2019, 12, 178. [Google Scholar] [CrossRef]
- Lake, R.W.; Shaeri, S.; Senevirathna, S.T.M.L.D. Design of Submerged Vane Matrices to Accompany a River Intake in Australia. J. Environ. Eng. Sci. 2021, 16, 58–65. [Google Scholar] [CrossRef]
- Gumgum, F.; Cardoso, A.H. Optimizing the Desilting Efficiency of Submerged Vane Fields at Lateral Diversions. J. Hydraul. Eng. 2022, 149, 04022031. [Google Scholar] [CrossRef]
- Bor, A. Experimental Investigation of 90° Intake Flow Patterns with and without Submerged Vanes under Sediment Feeding Conditions. Can. J. Civ. Eng. 2021, 49, 452–463. [Google Scholar] [CrossRef]
- Üneş, F. Investigation of Density Flow in Dam Reservoirs Using a Three-Dimensional Mathematical Model Including Coriolis Effect. Comput. Fluids 2008, 37, 1170–1192. [Google Scholar] [CrossRef]
- Ünes, F. Prediction of Density Flow Plunging Depth in Dam Reservoirs: An Artificial Neural Network Approach. Clean 2010, 38, 296–308. [Google Scholar] [CrossRef]
- Üneş, F.; Demirci, M.; Varçin, H. 3-D Numerical Simulation of a Real Dam Reservoir: Thermal Stratified Flow. Springer Water 2016, 377–394. [Google Scholar] [CrossRef]
- Üneş, F.; Varçin, H. Investigation of Seasonal Thermal Flow in a Real Dam Reservoir Using 3-D Numerical Modeling. J. Hydrol. Hydromech. 2015, 63, 38–46. [Google Scholar] [CrossRef]
- Odgaard, A.J. River Training and Sediment Management with Submerged Vanes. River Train. Sediment Manag. Submerg. Vanes 2009. [Google Scholar] [CrossRef]
- Turhan, E.; Ozmen-Cagatay, H.; Kocaman, S. Experimental and Numerical Investigation of Shock Wave Propagation Due to Dam-Break Over a Wet Channel. Pol. J. Environ. Stud. 2019, 28, 2877–2898. [Google Scholar] [CrossRef]
- Ozmen-Cagatay, H.; Turhan, E.; Kocaman, S. An Experimental Investigation of Dam-Break Induced Flood Waves for Different Density Fluids. Ocean Eng. 2022, 243, 110227. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. Mathematical Models of Turbulence; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Kim, H.; Nanjundan, P.; Lee, Y.W. Numerical Study on the Sloshing Flows in a Prismatic Tank Using Natural Frequency of the Prismatic Shapes. Prog. Comput. Fluid Dyn. 2021, 21, 152–160. [Google Scholar] [CrossRef]
- Simsek, O.; Akoz, M.S.; Soydan, N.G. Numerical Validation of Open Channel Flow over a Curvilinear Broad-Crested Weir. Prog. Comput. Fluid Dyn. 2016, 16, 364–378. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- ANSYS Analysis Systems Fluid Simulation Software. Available online: https://www.ansys.com/products/fluids (accessed on 27 December 2022).
- Salim, S.M.; Ariff, M.; Cheah, S.C. Wall Y+ Approach for Dealing with Turbulent Flows over a Wall Mounted Cube. Prog. Comput. Fluid Dyn. 2010, 10, 341–351. [Google Scholar] [CrossRef]
- Gerasimov, A. Modeling Turbulent Flows with Fluent. Available online: http://www.ae.metu.edu.tr/seminar/Turbulence_Seminar/Modelling_turbulent_flows_with_FLUENT.pdf (accessed on 27 December 2022).
- Unes, F.; Varcin, H. 3-D Real Dam Reservoir Model for Seasonal Thermal Density Flow. Environ. Eng. Manag. J. 2017, 16, 2009–2024. [Google Scholar] [CrossRef]
- Biswas, P.; Barbhuiya, A.K. Effect of Submerged Vane on Three Dimensional Flow Dynamics and Bed Morphology in River Bend. River Res. Appl. 2019, 35, 301–312. [Google Scholar] [CrossRef]





| Q (m3 s−1) | B (m) | d (m) | A (m2) | T (m) | Rh (m) | Vmean (m s−1) (m s−1) | Fr |
|---|---|---|---|---|---|---|---|
| 0.025 | 0.300 | 0.095 | 0.0285 | 0.490 | 0.058 | 0.900 | 0.94 |
| Presented Study | Odgaard [19] | |
|---|---|---|
| Vane height/length (cm) | 10/10 | 7.4/15.2 |
| Meander angle (°) | 30 | 90 |
| Bend radius (m) | 3.60 | 11.89 |
| Flow discharge (m3/s) | 0.025 | 0.11–0.15 |
| Mean velocity (m/s) | 0.900 | 0.396 |
| Water surface slope | 0.0003 | 0.00064 |
| Mean flow depth (cm) | 11 (V0 case), 12 (V1 case) | 17.4 and 18.2 |
| Solver Set | Solver | Pressure Based |
|---|---|---|
| Space-Time | 3D, Unsteady | |
| Model | Multiphase Model | VOF |
| Viscous Model | k-ε | |
| Phase | Primary Phase | Air |
| Secondary Phase | water | |
| Discretization | Pressure | Presto |
| Momentum | Second order upwind | |
| Pressure-Velocity Coupling | Method | Coupled |
| Convergence Criterion | Residuals | 0.001 (Continuity) |
| 0.001 (Momentum) |
| Section No | Point No | Location at x Direction (m) | Location at y Direction (m) | Experiment Results | Fluent CFD Results | Error (%) |
|---|---|---|---|---|---|---|
| 1-1 | 1 | 1.10 | 0.247 | 0.96 | 0.97 | 0.97 |
| 2 | 1.10 | 0.272 | 0.98 | 0.97 | 1.08 | |
| 3 | 1.10 | 0.297 | 0.98 | 0.97 | 0.74 | |
| 4 | 1.10 | 0.322 | 0.98 | 0.97 | 0.67 | |
| 5 | 1.10 | 0.347 | 1.02 | 0.97 | 4.77 | |
| 6 | 1.10 | 0.372 | 1.02 | 0.99 | 2.53 | |
| 7 | 1.10 | 0.397 | 1.02 | 1.04 | 2.78 | |
| 8 | 1.10 | 0.422 | 1.04 | 1.10 | 5.89 | |
| 2-2 | 1 | 1.50 | 0.247 | 0.98 | 0.97 | 1.11 |
| 2 | 1.50 | 0.272 | 0.98 | 0.98 | 0.21 | |
| 3 | 1.50 | 0.297 | 0.97 | 0.97 | 0.08 | |
| 4 | 1.50 | 0.322 | 0.97 | 0.97 | 0.44 | |
| 5 | 1.50 | 0.347 | 1.01 | 0.97 | 3.68 | |
| 6 | 1.50 | 0.372 | 1.01 | 0.99 | 2.36 | |
| 7 | 1.50 | 0.397 | 1.03 | 1.05 | 1.45 | |
| 8 | 1.50 | 0.422 | 1.04 | 1.10 | 5.17 | |
| 3-3 | 1 | 1.70 | 0.247 | 0.96 | 0.96 | 0.90 |
| 2 | 1.70 | 0.272 | 0.97 | 0.97 | 0.42 | |
| 3 | 1.70 | 0.297 | 0.98 | 0.97 | 0.67 | |
| 4 | 1.70 | 0.322 | 0.99 | 0.97 | 1.44 | |
| 5 | 1.70 | 0.347 | 1.00 | 0.99 | 1.40 | |
| 6 | 1.70 | 0.372 | 1.02 | 1.01 | 0.72 | |
| 7 | 1.70 | 0.397 | 1.04 | 1.06 | 2.21 | |
| 8 | 1.70 | 0.422 | 1.06 | 1.07 | 0.60 |
| Section No | Point No | Location at x Direction (m) | Location at y Direction (m) | Experiment Results | Fluent CFD Results | Error (%) |
|---|---|---|---|---|---|---|
| 1-1 | 1 | 1.10 | 0.247 | 1.10 | 1.07 | 2.81 |
| 2 | 1.10 | 0.272 | 1.07 | 1.03 | 4.08 | |
| 3 | 1.10 | 0.297 | 0.88 | 0.87 | 0.83 | |
| 4 | 1.10 | 0.322 | 0.98 | 0.98 | 0.91 | |
| 5 | 1.10 | 0.347 | 0.90 | 0.92 | 2.08 | |
| 6 | 1.10 | 0.372 | 1.01 | 1.04 | 3.28 | |
| 7 | 1.10 | 0.397 | 0.97 | 0.98 | 1.46 | |
| 8 | 1.10 | 0.422 | 1.10 | 1.11 | 0.63 | |
| 2-2 | 1 | 1.50 | 0.247 | 1.05 | 1.10 | 4.53 |
| 2 | 1.50 | 0.272 | 1.06 | 1.03 | 3.10 | |
| 3 | 1.50 | 0.297 | 0.91 | 0.89 | 2.31 | |
| 4 | 1.50 | 0.322 | 0.95 | 0.97 | 1.96 | |
| 5 | 1.50 | 0.347 | 0.92 | 0.90 | 1.93 | |
| 6 | 1.50 | 0.372 | 1.00 | 1.03 | 3.17 | |
| 7 | 1.50 | 0.397 | 0.97 | 0.96 | 0.71 | |
| 8 | 1.50 | 0.422 | 1.14 | 1.12 | 1.70 | |
| 3-3 | 1 | 1.70 | 0.247 | 1.08 | 1.10 | 2.35 |
| 2 | 1.70 | 0.272 | 1.03 | 1.03 | 0.32 | |
| 3 | 1.70 | 0.297 | 0.99 | 0.93 | 6.32 | |
| 4 | 1.70 | 0.322 | 0.94 | 0.93 | 0.75 | |
| 5 | 1.70 | 0.347 | 0.93 | 0.93 | 0.37 | |
| 6 | 1.70 | 0.372 | 0.95 | 0.98 | 2.77 | |
| 7 | 1.70 | 0.397 | 1.03 | 1.00 | 3.48 | |
| 8 | 1.70 | 0.422 | 1.05 | 1.11 | 5.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taşar, B.; Üneş, F.; Gemici, E.; Zelenakova, M. Experimental and Numerical Study on Flow Control Using 3-Array Submerged Vane in Laboratory Channel Bend. Water 2023, 15, 659. https://doi.org/10.3390/w15040659
Taşar B, Üneş F, Gemici E, Zelenakova M. Experimental and Numerical Study on Flow Control Using 3-Array Submerged Vane in Laboratory Channel Bend. Water. 2023; 15(4):659. https://doi.org/10.3390/w15040659
Chicago/Turabian StyleTaşar, Bestami, Fatih Üneş, Ercan Gemici, and Martina Zelenakova. 2023. "Experimental and Numerical Study on Flow Control Using 3-Array Submerged Vane in Laboratory Channel Bend" Water 15, no. 4: 659. https://doi.org/10.3390/w15040659





