A Non-Hydrostatic Model for Simulating Weakly Dispersive Landslide-Generated Waves
Abstract
:1. Introduction
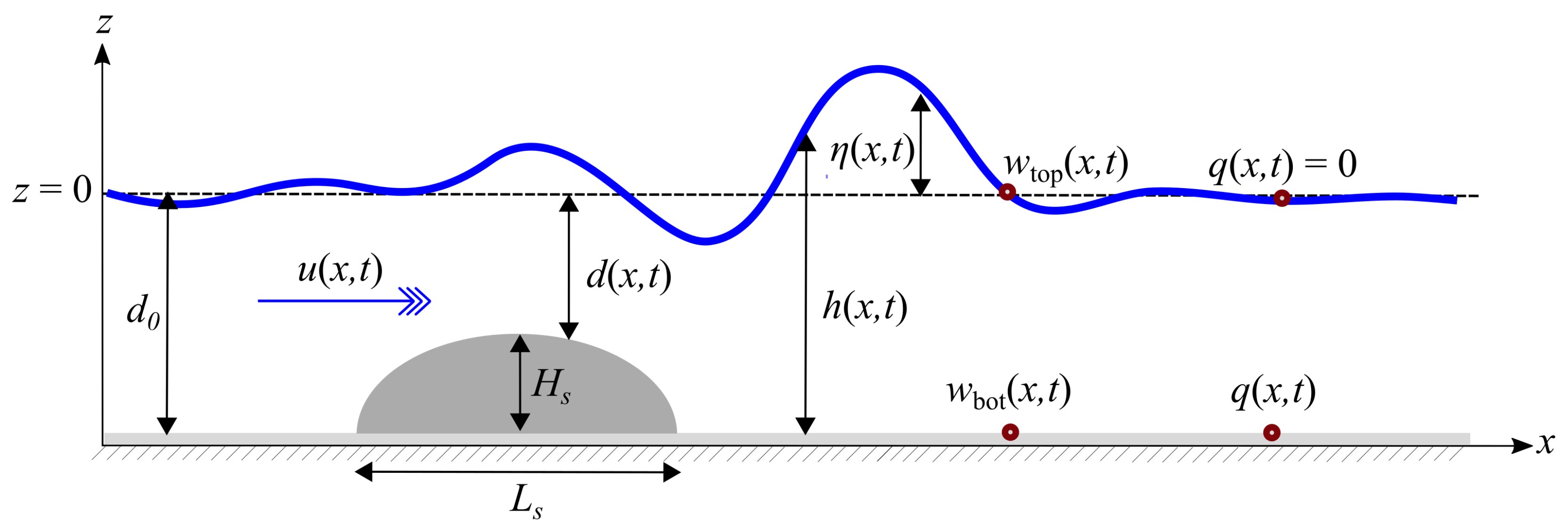
2. Governing Equations and the NH-1L Scheme
- Calculate from Equation (8); then the free surface is .
- Calculate using Equation (9), where the non-hydrostatic pressure term is neglected.
- Solve the linear system of Equation (16) to obtain .
- Calculate using Equation (12).
- Calculate the corrected values of using Equation (19).
- Calculate using Equation (10).
3. Model Validation
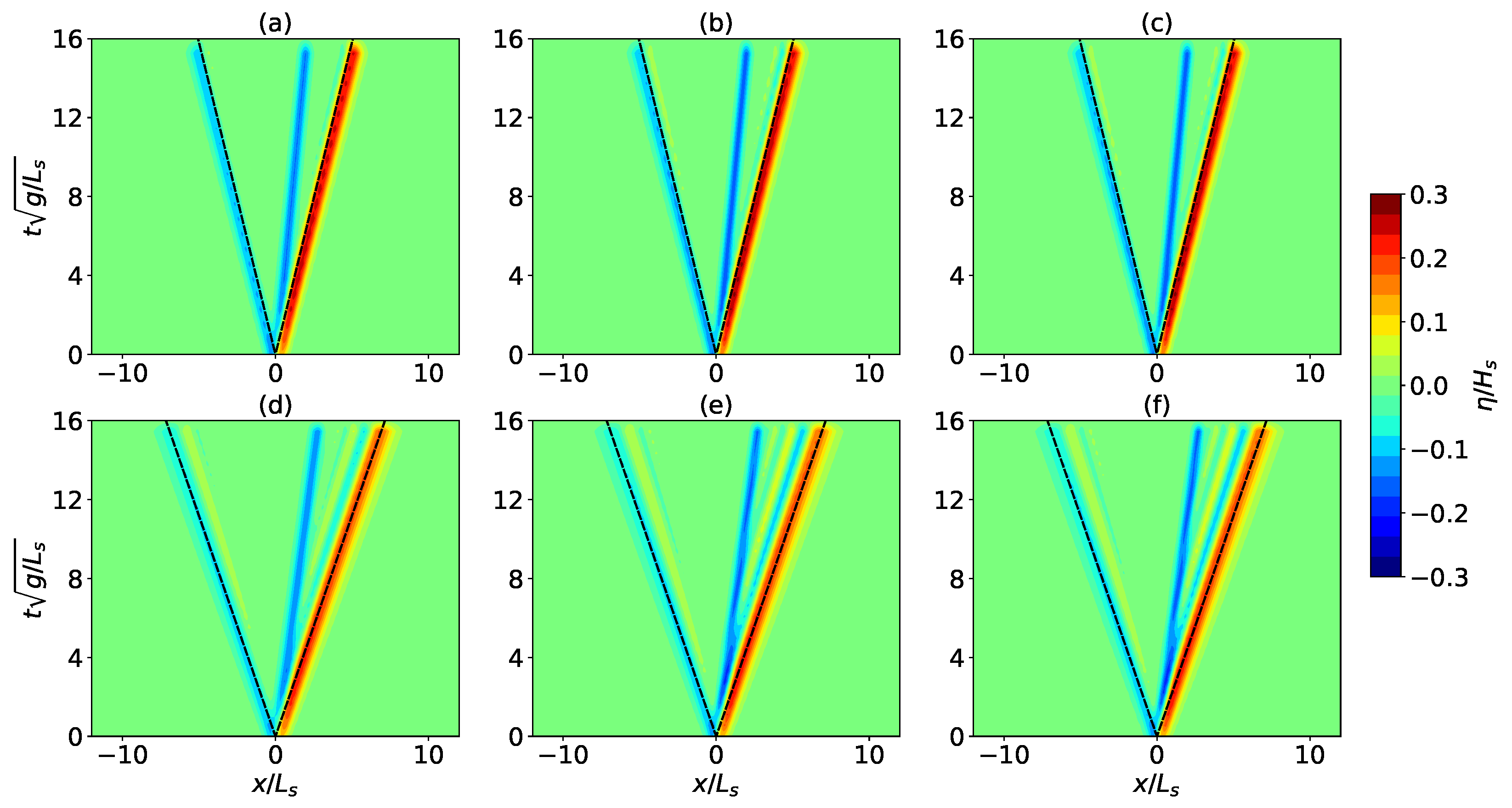
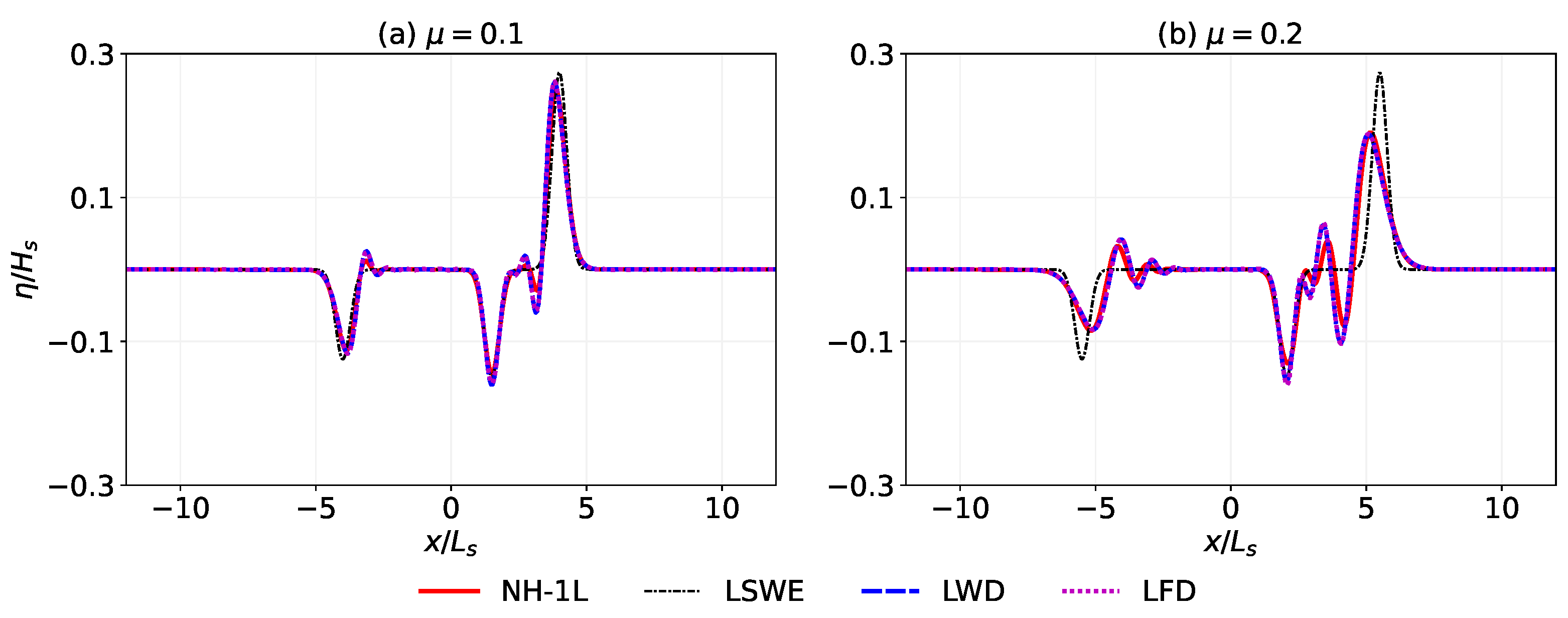
3.1. Waves Generated by Landslide with Constant Speed
3.2. Waves Generated by Landslide with Acceleration
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harbitz, C.B.; Løvholt, F.; Bungum, H. Submarine landslide tsunamis: How extreme and how likely? Nat. Hazards 2014, 72, 1341–1374. [Google Scholar] [CrossRef]
- Pakoksung, K.; Suppasri, A.; Imamura, F.; Athanasius, C.; Omang, A.; Muhari, A. Simulation of the Submarine Landslide Tsunami on 28 September 2018 in Palu Bay, Sulawesi Island, Indonesia, Using a Two-Layer Model. Pure Appl. Geophys. 2019, 176, 3323–3350. [Google Scholar] [CrossRef]
- González-Vida, J.M.; Macías, J.; Castro, M.J.; Sánchez-Linares, C.; de la Asunción, M.; Ortega-Acosta, S.; Arcas, D. The Lituya Bay landslide-generated mega-tsunami—Numerical simulation and sensitivity analysis. Nat. Hazards Earth Syst. Sci. 2019, 19, 369–388. [Google Scholar] [CrossRef]
- Paris, A.; Heinrich, P.; Paris, R.; Abadie, S. The December 22, 2018 Anak Krakatau, Indonesia, Landslide and Tsunami: Preliminary Modeling Results. Pure Appl. Geophys. 2020, 177, 571–590. [Google Scholar] [CrossRef]
- Liu, Q.; Pan, M.; Wang, X.; An, Y. A two-layer model for landslide generated impulse wave: Simulation of the 1958 Lituya bay landslide impact wave from generation to long–duration transport. Adv. Water Resour. 2021, 154, 103989. [Google Scholar] [CrossRef]
- Mungkasi, S.; Magdalena, I.; Pudjaprasetya, S.R.; Wiryanto, L.H.; Roberts, S.G. A staggered method for the shallow water equations involving varying channel width and topography. Int. J. Multiscale Comput. Eng. 2018, 16, 231–244. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Jilani, A.N. A higher-order Boussinesq-type model with moving bottom boundary: Applications to submarine landslide tsunami waves. Int. J. Numer. Methods Fluids 2007, 53, 1019–1048. [Google Scholar] [CrossRef]
- Fuhrman, D.R.; Madsen, P.A. Tsunami generation, propagation, and run-up with a high-order Boussinesq model. Coast. Eng. 2009, 56, 747–758. [Google Scholar] [CrossRef]
- Fang, K.; Liu, Z.; Sun, J.; Xie, Z.; Zheng, Z. Development and validation of a two-layer Boussinesq model for simulating free surface waves generated by bottom motion. Appl. Ocean. Res. 2020, 94, 101977. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Zang, J.; Dong, G.; Ma, X.; Zhu, Y.; Zhou, L. Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 2020, 158, 103670. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Grilli, S.T.; Watts, P. Modeling of waves generated by a moving submerged body. Applications to underwater landslides. Eng. Anal. Bound. Elem. 1999, 23, 645–656. [Google Scholar] [CrossRef]
- Grilli, S.T.; Vogelmann, S.; Watts, P. Development of a 3D numerical wave tank for modeling tsunami generation by underwater landslides. Eng. Anal. Bound. Elem. 2002, 26, 301–313. [Google Scholar] [CrossRef]
- Grilli, S.T.; Watts, P. Tsunami Generation by Submarine Mass Failure. I: Modeling, Experimental Validation, and Sensitivity Analyses. J. Waterw. Port Coastal Ocean. Eng. 2005, 131, 283–297. [Google Scholar] [CrossRef]
- Ai, C.; Ma, Y.; Yuan, C.; Xie, Z.; Dong, G. A three-dimensional non-hydrostatic model for tsunami waves generated by submarine landslides. Appl. Math. Model. 2021, 96, 1–19. [Google Scholar] [CrossRef]
- Abadie, S.; Morichon, D.; Grilli, S.; Glockner, S. Numerical simulation of waves generated by landslides using a multiple-fluid Navier–Stokes model. Coast. Eng. 2010, 57, 779–794. [Google Scholar] [CrossRef]
- Mao, J.; Zhao, L.; Liu, X.; Cheng, J.; Avital, E. A three-phases model for the simulation of landslide-generated waves using the improved conservative level set method. Comput. Fluids 2017, 159, 243–253. [Google Scholar] [CrossRef]
- Li, G.; Chen, G.; Li, P.; Jing, H. Efficient and Accurate 3-D Numerical Modelling of Landslide Tsunami. Water 2019, 11, 2033. [Google Scholar] [CrossRef]
- Paris, A.; Heinrich, P.; Abadie, S. Landslide tsunamis: Comparison between depth-averaged and Navier–Stokes models. Coast. Eng. 2021, 170, 104022. [Google Scholar] [CrossRef]
- Kirby, J.T.; Grilli, S.T.; Horrillo, J.; Liu, P.L.F.; Nicolsky, D.; Abadie, S.; Ataie-Ashtiani, B.; Castro, M.J.; Clous, L.; Escalante, C.; et al. Validation and inter-comparison of models for landslide tsunami generation. Ocean. Model. 2022, 170, 101943. [Google Scholar] [CrossRef]
- Ma, G.; Shi, F.; Kirby, J.T. Shock-capturing non-hydrostatic model for fully dispersive surface wave processes. Ocean. Model. 2012, 43–44, 22–35. [Google Scholar] [CrossRef]
- Ma, G.; Kirby, J.T.; Hsu, T.J.; Shi, F. A two-layer granular landslide model for tsunami wave generation: Theory and computation. Ocean. Model. 2015, 93, 40–55. [Google Scholar] [CrossRef]
- Young, C.C.; Wu, C.H.; Hsu, T.W. The Role of Non-Hydrostatic Effects in Nonlinear Dispersive Wave Modeling. Water 2020, 12, 3513. [Google Scholar] [CrossRef]
- Zhang, C.; Kirby, J.T.; Shi, F.; Ma, G.; Grilli, S.T. A two-layer non-hydrostatic landslide model for tsunami generation on irregular bathymetry. 2. Numerical discretization and model validation. Ocean. Model. 2021, 160, 101769. [Google Scholar] [CrossRef]
- Macías, J.; Escalante, C.; Castro, M.J. Multilayer-HySEA model validation for landslide-generated tsunamis—Part 1: Rigid slides. Nat. Hazards Earth Syst. Sci. 2021, 21, 775–789. [Google Scholar] [CrossRef]
- Stelling, G.; Zijlema, M. An accurate and efficient finite-difference algorithm for non-hydrostatic free-surface flow with application to wave propagation. Int. J. Numer. Methods Fluids 2003, 43, 1–23. [Google Scholar] [CrossRef]
- Bai, Y.; Cheung, K.F. Depth-integrated free-surface flow with parameterized non-hydrostatic pressure. Int. J. Numer. Methods Fluids 2013, 71, 403–421. [Google Scholar] [CrossRef]
- Cui, H.; Pietrzak, J.D.; Stelling, G.S. Optimal dispersion with minimized Poisson equations for non-hydrostatic free surface flows. Ocean. Model. 2014, 81, 1–12. [Google Scholar] [CrossRef]
- Tarwidi, D.; Pudjaprasetya, S.R.; Adytia, D. A reduced two-layer non-hydrostatic model for submarine landslide-generated tsunamis. Appl. Ocean. Res. 2022, 127, 103306. [Google Scholar] [CrossRef]
- Walters, R.A. A semi-implicit finite element model for non-hydrostatic (dispersive) surface waves. Int. J. Numer. Methods Fluids 2005, 49, 721–737. [Google Scholar] [CrossRef]
- Pudjaprasetya, S.R.; Magdalena, I.; Tjandra, S.S. A Nonhydrostatic Two-Layer Staggered Scheme for Transient Waves due to Anti-Symmetric Seabed Thrust. J. Earthq. Tsunami 2017, 11, 1740002. [Google Scholar] [CrossRef]
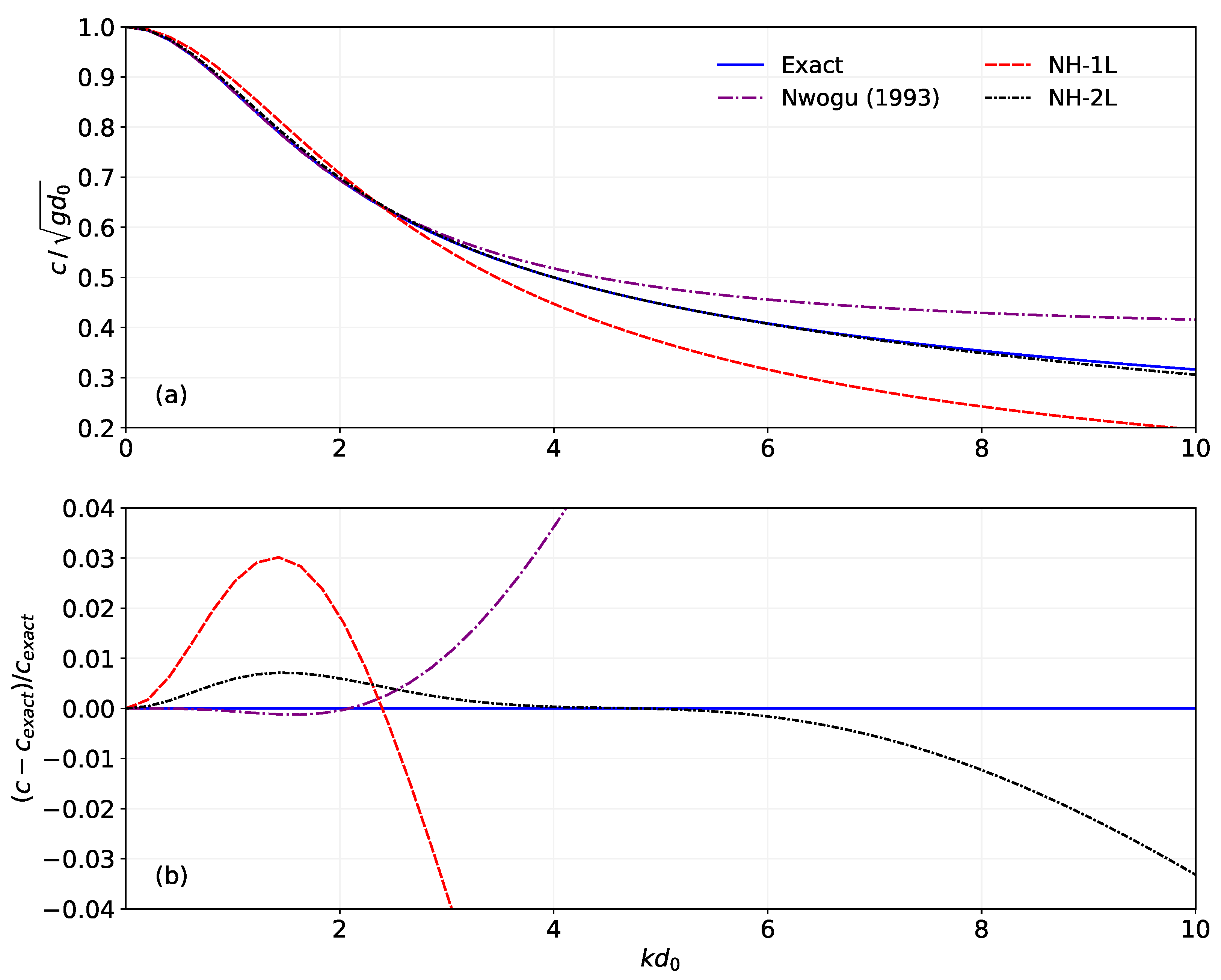
- Nwogu, O. Alternative Form of Boussinesq Equations for Nearshore Wave Propagation. J. Waterw. Port Coastal Ocean. Eng. 1993, 119, 618–638. [Google Scholar] [CrossRef]
- Lo, H.Y.; Liu, P.L.F. On the analytical solutions for water waves generated by a prescribed landslide. J. Fluid Mech. 2017, 821, 85–116. [Google Scholar] [CrossRef]
- Whittaker, C.; Nokes, R.; Davidson, M. Tsunami forcing by a low Froude number landslide. Environ. Fluid Mech. 2015, 15, 1215–1239. [Google Scholar] [CrossRef]
- Jing, H.; Chen, G.; Liu, C.; Wang, W.; Zuo, J. Dispersive effects of water waves generated by submerged landslide. Nat. Hazards 2020, 103, 1917–1941. [Google Scholar] [CrossRef]

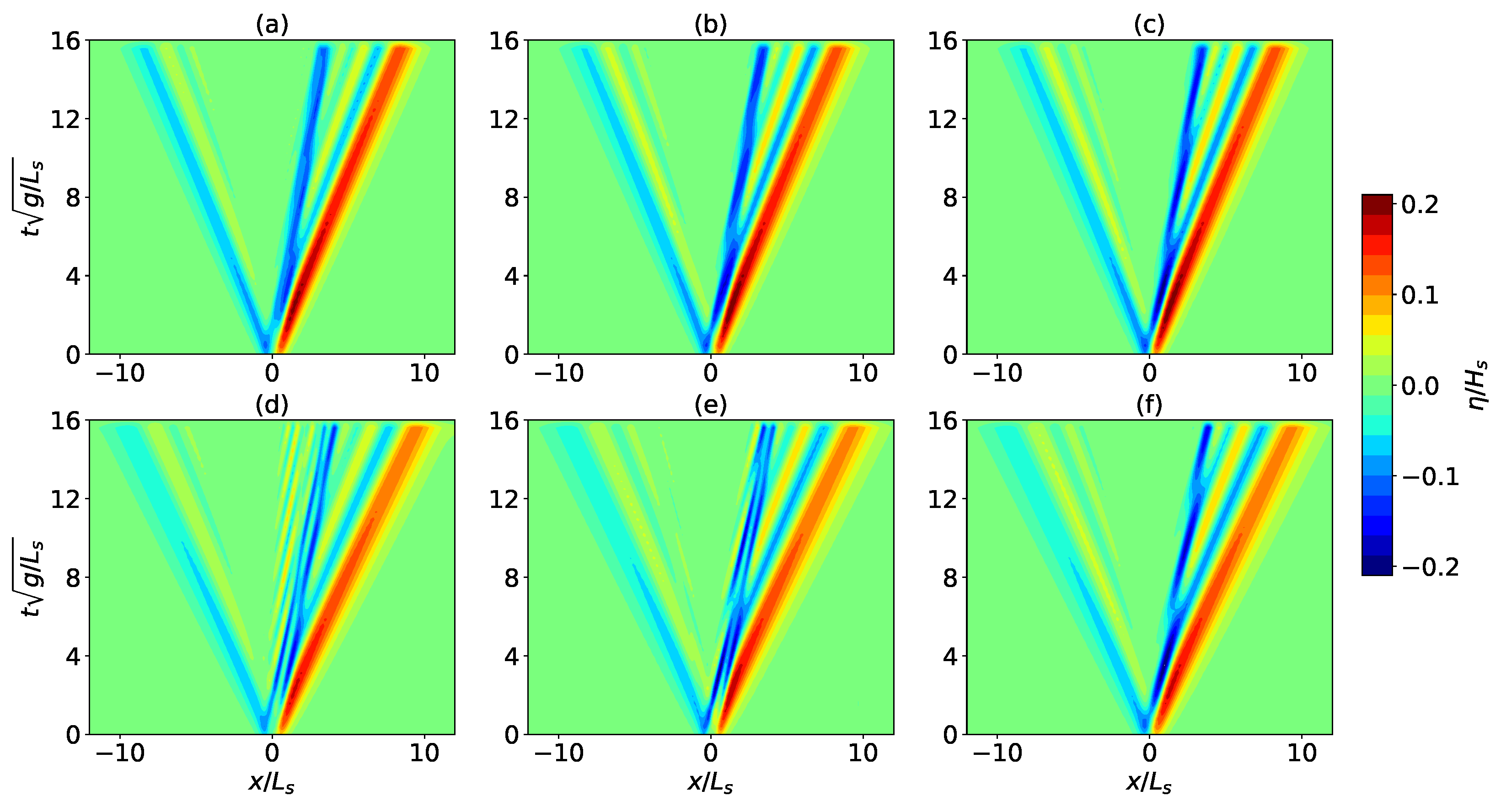
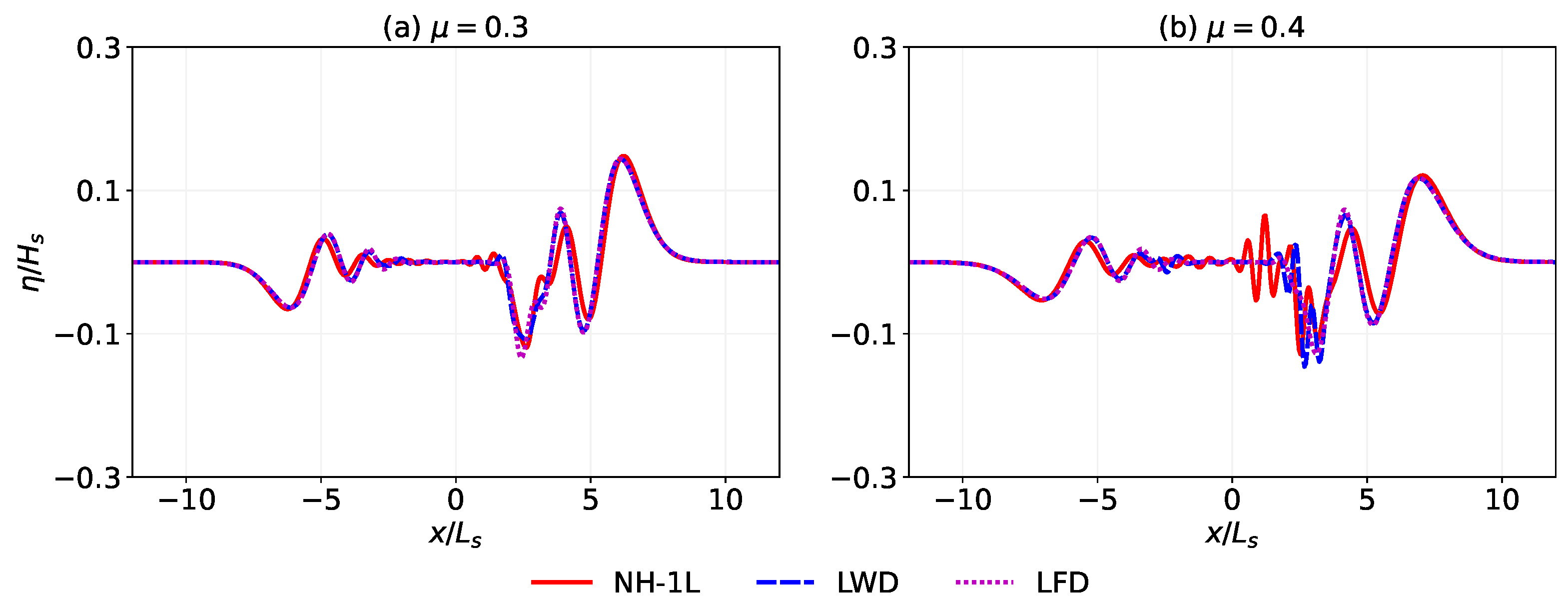


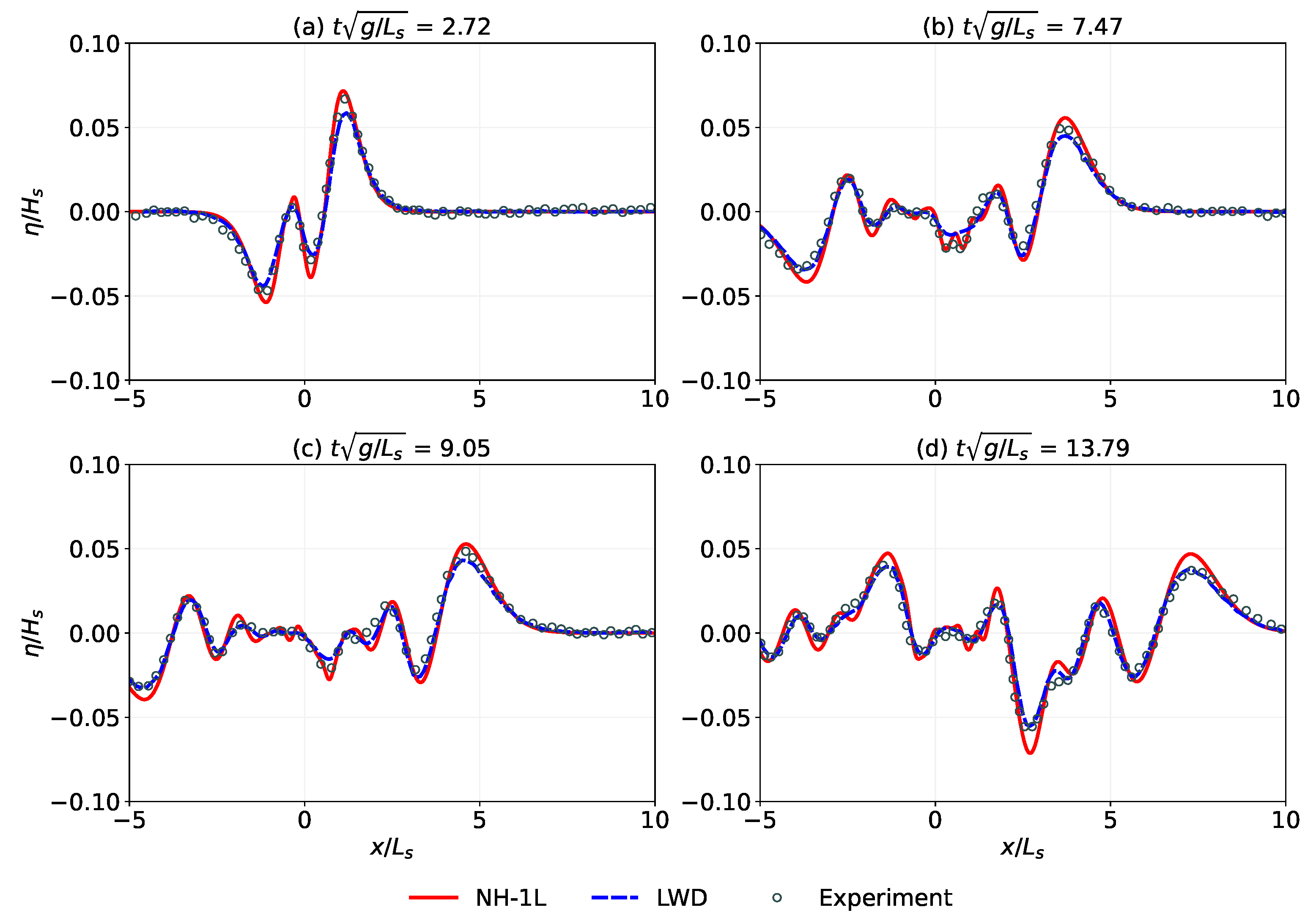
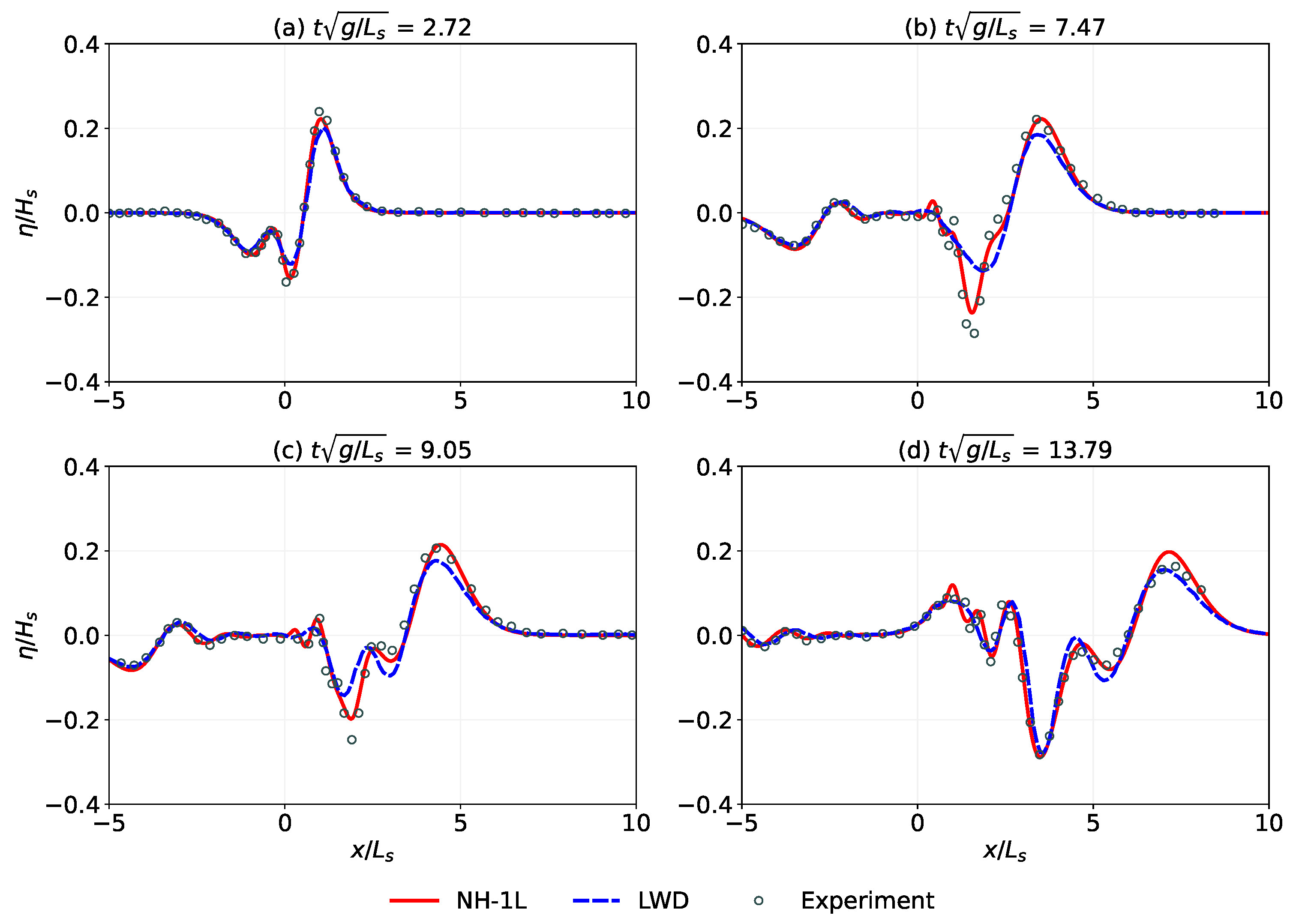
| Run | |||
|---|---|---|---|
| 21 | 0.153 | 0.125 | 0.35 |
| 23 | 0.153 | 0.375 | 0.35 |
| 12 | 0.102 | 0.500 | 0.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarwidi, D.; Pudjaprasetya, S.R.; Tjandra, S.S. A Non-Hydrostatic Model for Simulating Weakly Dispersive Landslide-Generated Waves. Water 2023, 15, 652. https://doi.org/10.3390/w15040652
Tarwidi D, Pudjaprasetya SR, Tjandra SS. A Non-Hydrostatic Model for Simulating Weakly Dispersive Landslide-Generated Waves. Water. 2023; 15(4):652. https://doi.org/10.3390/w15040652
Chicago/Turabian StyleTarwidi, Dede, Sri Redjeki Pudjaprasetya, and Sugih Sudharma Tjandra. 2023. "A Non-Hydrostatic Model for Simulating Weakly Dispersive Landslide-Generated Waves" Water 15, no. 4: 652. https://doi.org/10.3390/w15040652





