Flow–Solid Coupling Analysis of Ice–Concrete Collision Nonlinear Problems in the Yellow River Basin
Abstract
:1. Introduction
2. Numerical Simulation
2.1. Display Time Integration Principle
2.2. Fluid–Solid Coupling Method
3. Modelling of Tunnel Impact by Drift Ice
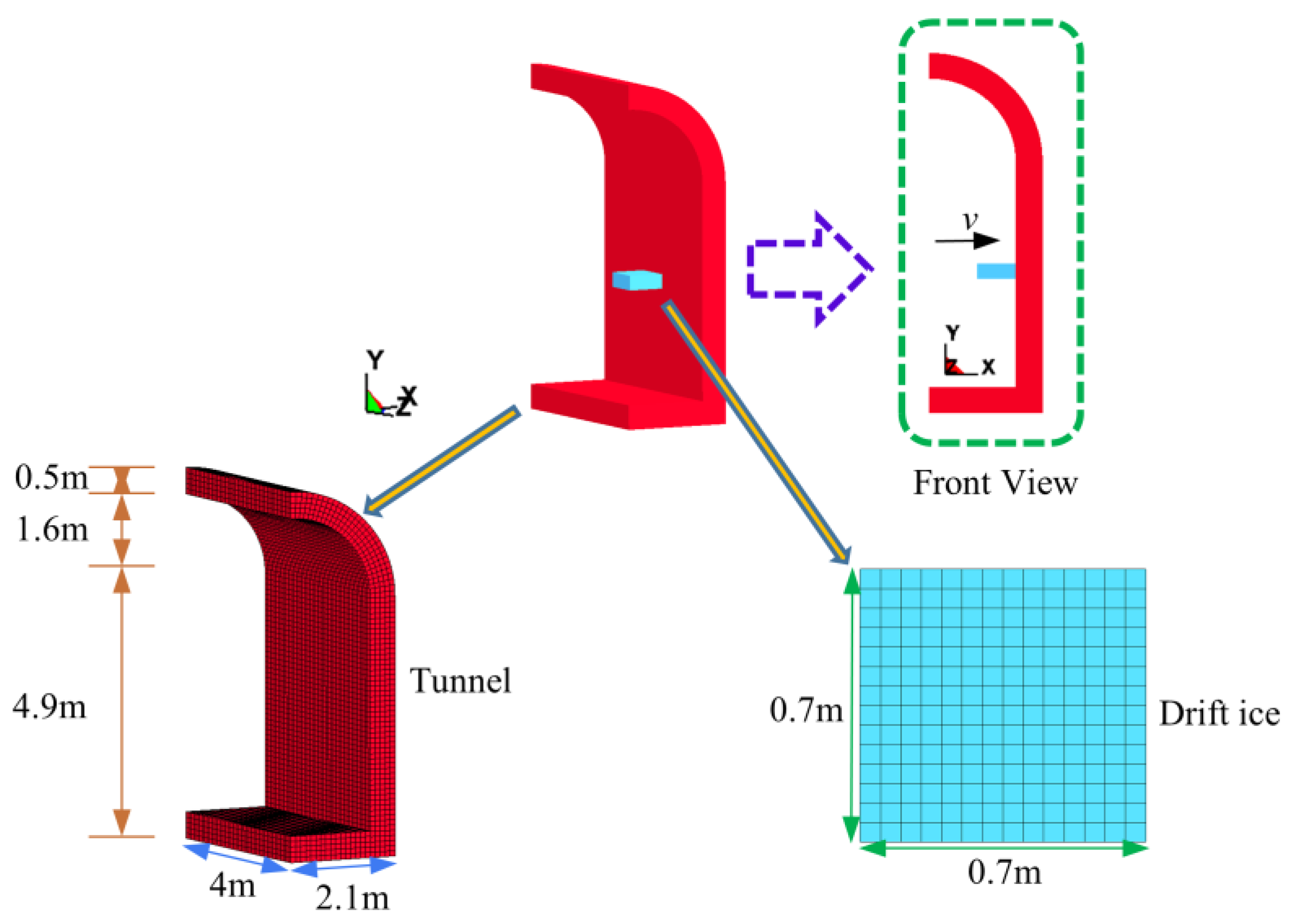
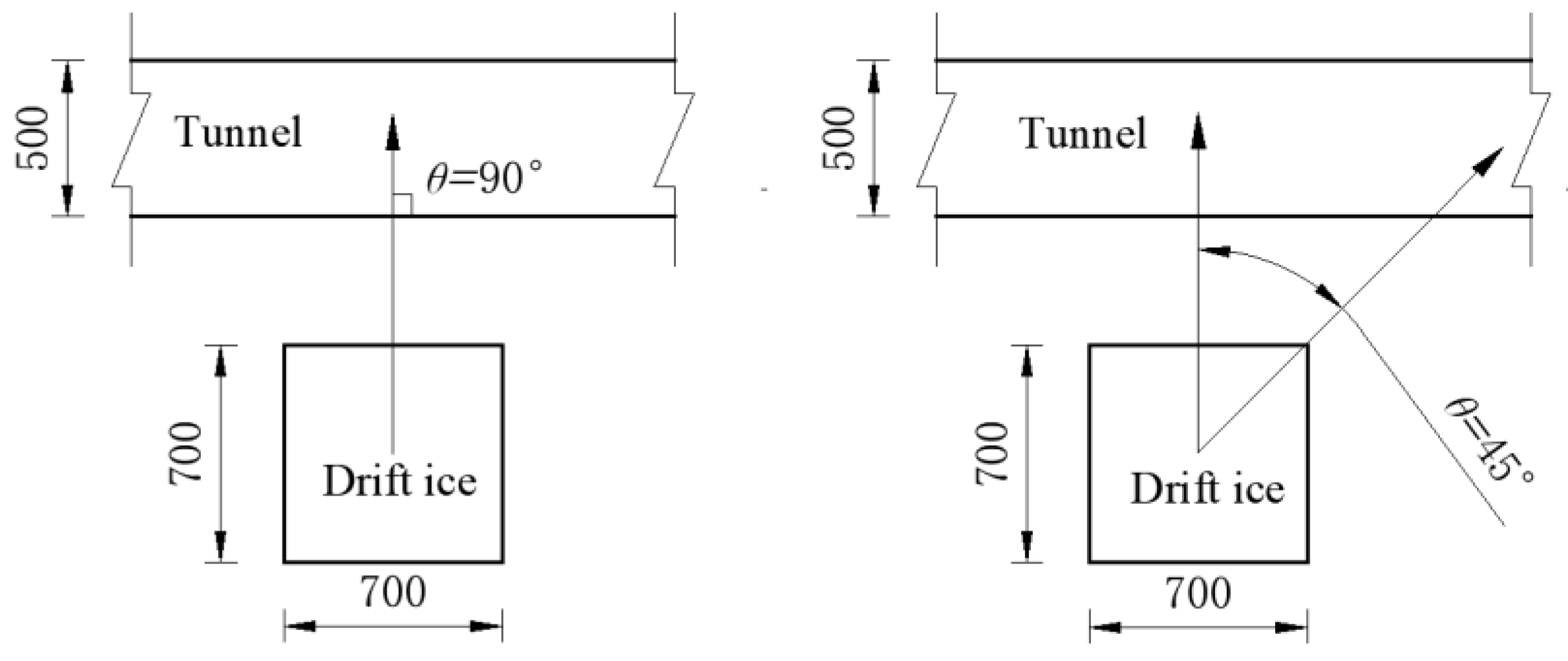
3.1. Engineering Examples
3.2. Selection of Model Material Parameters
- (1)
- Drift ice material model: At present, the research on ice materials is mainly focused on sea ice, while the research on river ice materials is relatively scarce. The drift ice in the river shows different mechanical properties under conditions of different temperature and strain rate. In this paper, the ice material is combined with the uniaxial compression test of river ice carried out in [23]. The plastic material related to strain rate (* MAT_STRAIN_RATE_DEPENDENT_PLASTICITY) is selected to simulate the characteristics of drift ice. The parameters of ice material model are shown in Table 1.
- (2)
- Tunnel material model: In the process of ice–tunnel collision, the tunnel lining will be damaged and deformed, so selection of tunnel lining materials should undergo plastic deformation. The concrete material model is CSCM-CONCRETE model developed by FHA Company [24]. The parameters used in the concrete material model are shown in Table 2.
- (3)
- Water and air media models: The constitutive model and equation of state are often used in LS-DYNA software to describe fluid materials (water, air). Therefore, the blank material Null was chosen to simulate water and air [25] with the parameters shown in Table 3. The equation of state is defined by the polynomial equation and the Gruneisen equation [26] for water and air media, respectively, and the parameters of both equations of state are shown in Table 3.
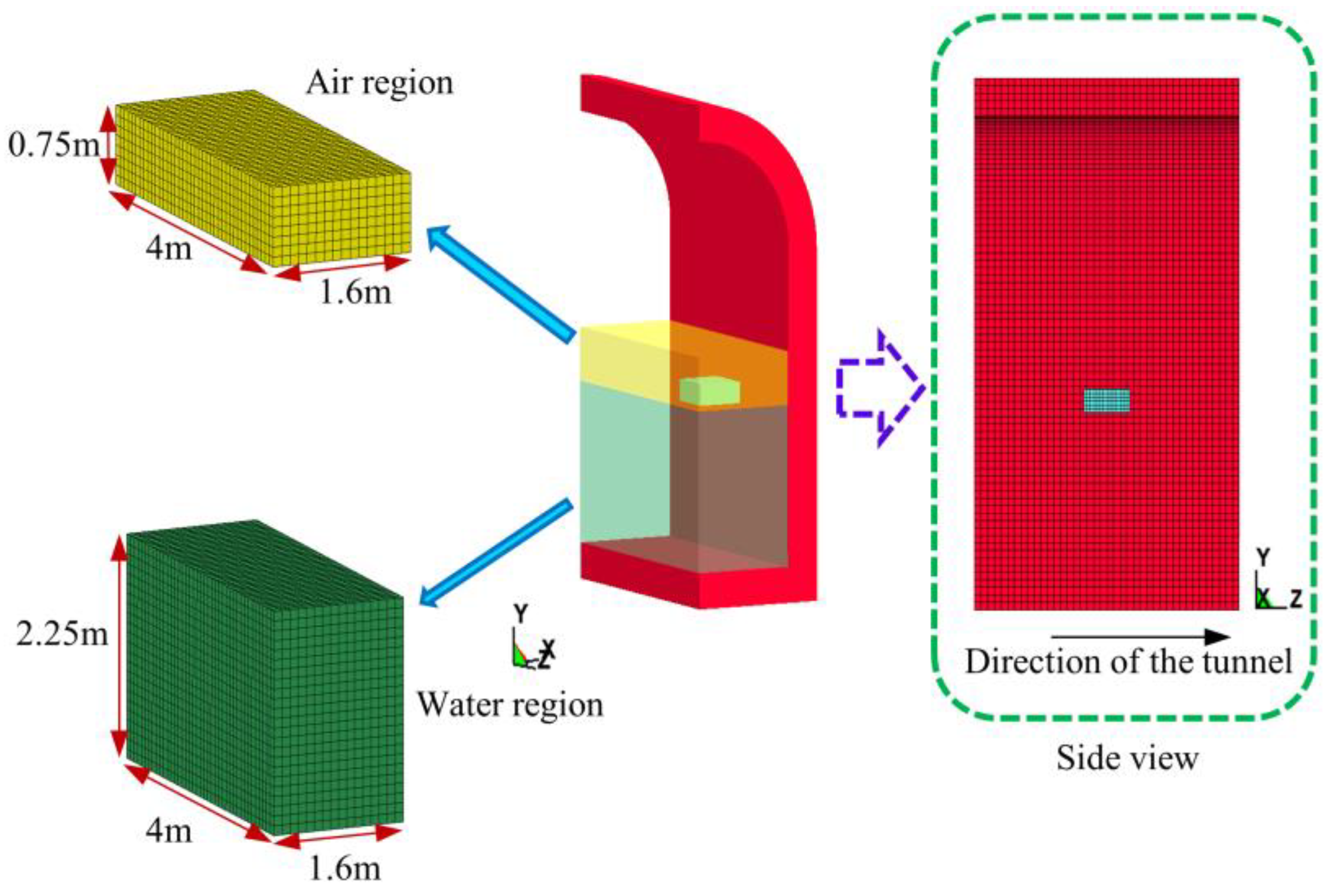
3.3. Model Building
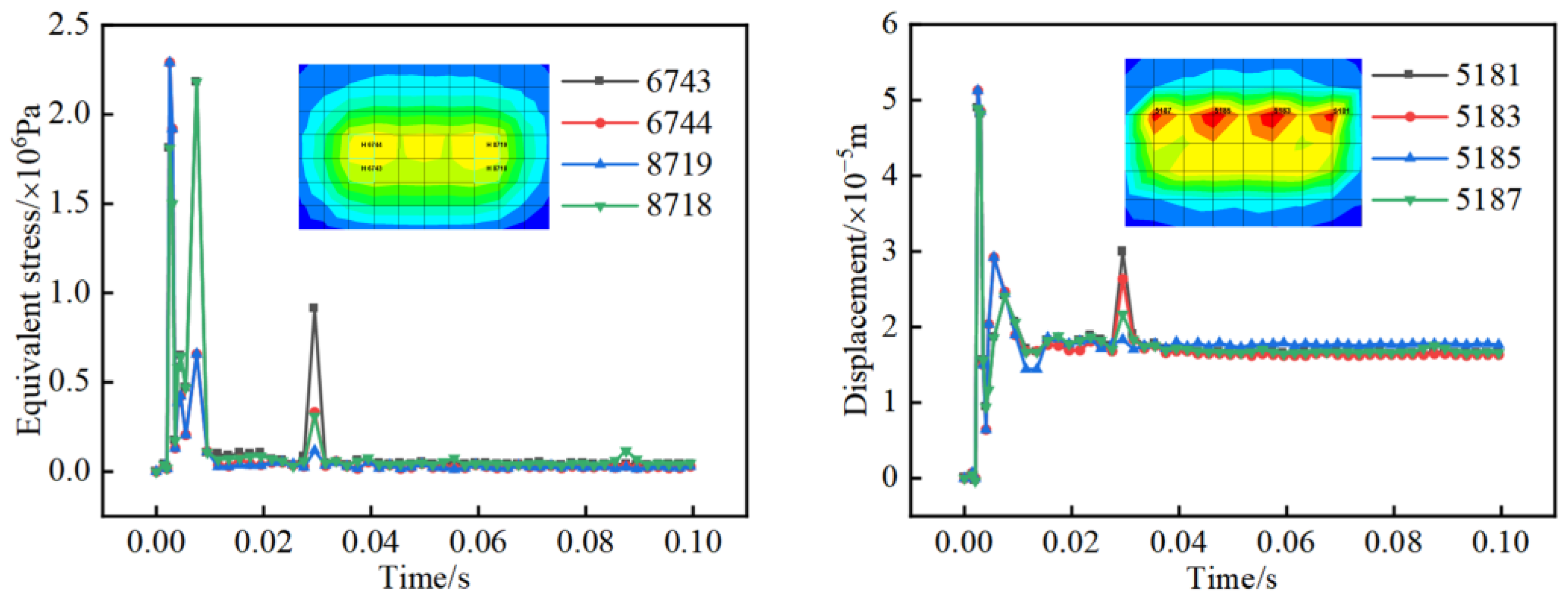
3.4. Mesh Sensitivity Study
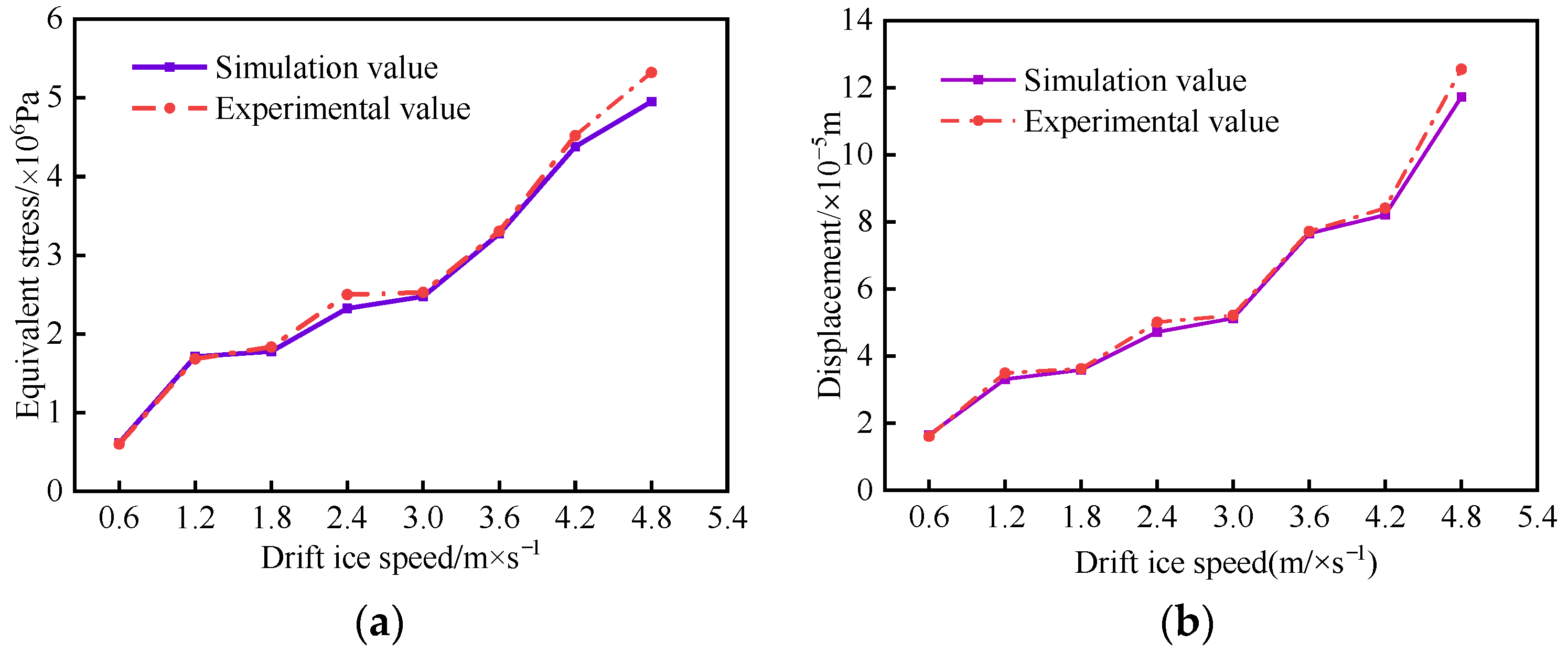
3.5. Test Verification
4. Numerical Simulation Results and Analysis
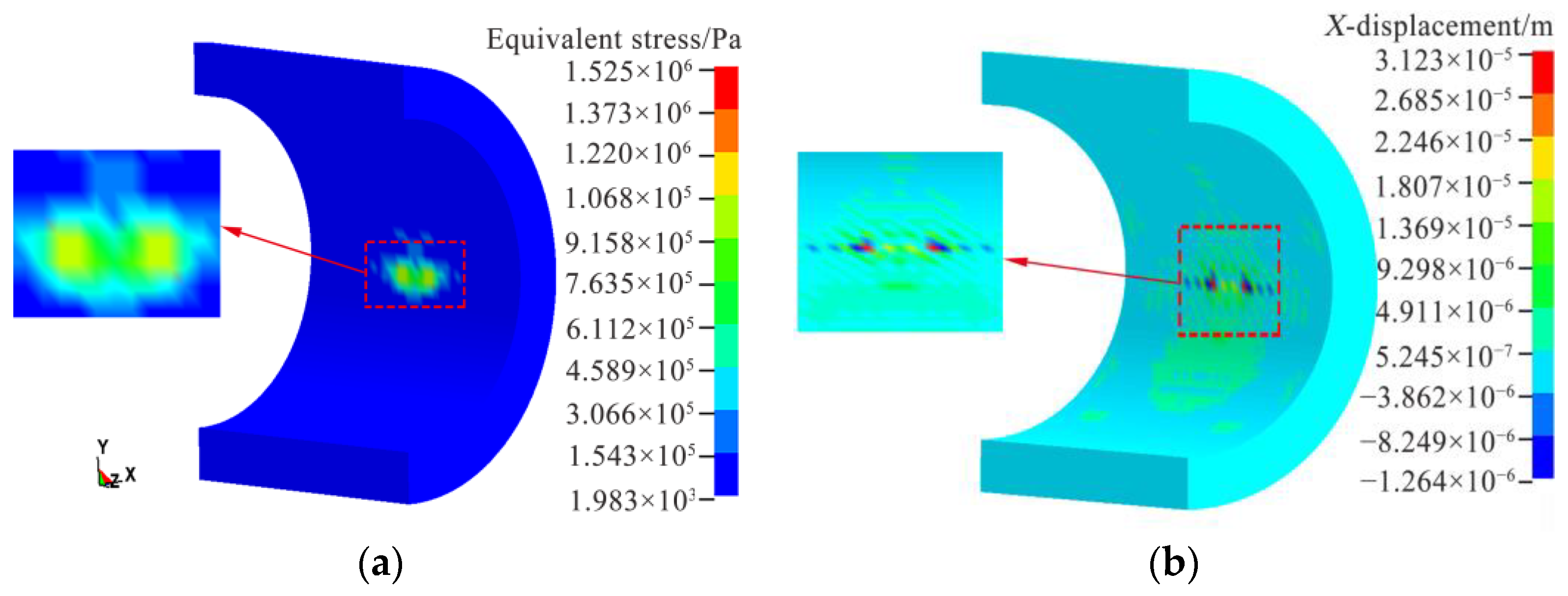
4.1. Simulation Results under Typical Operating Conditions
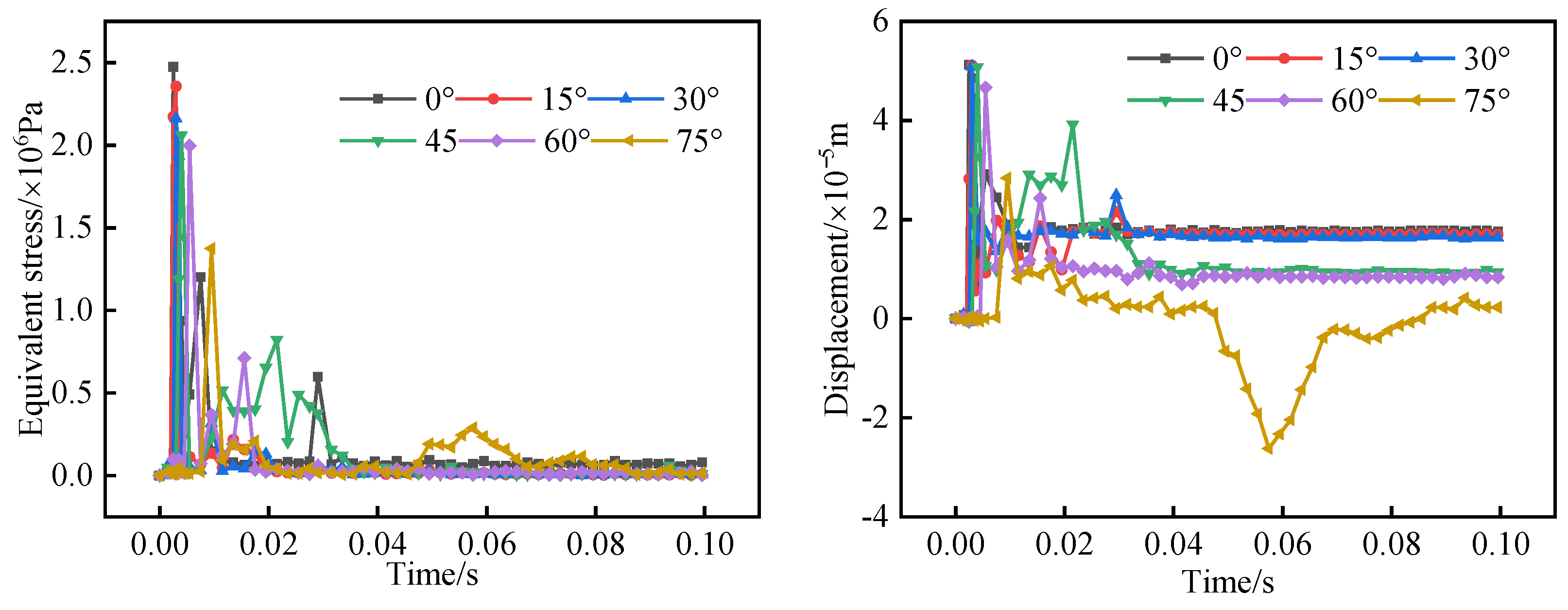
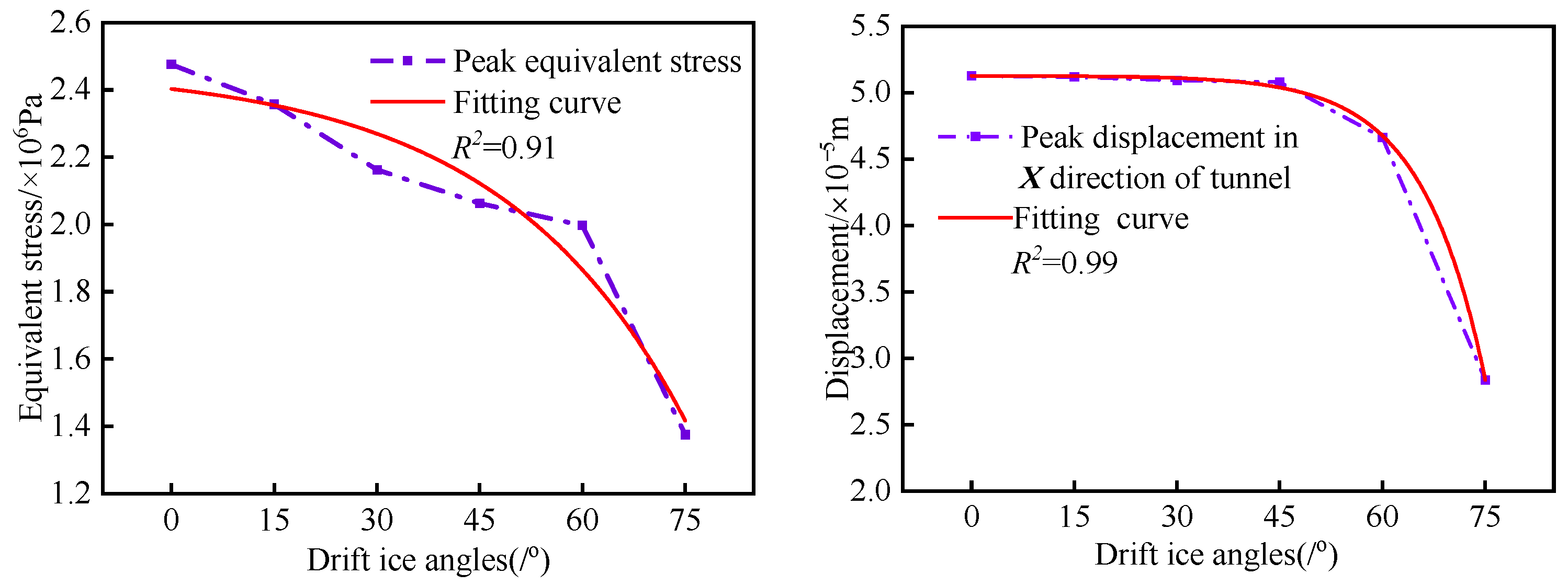
4.2. Simulation Results for Different Ice Flow Angles
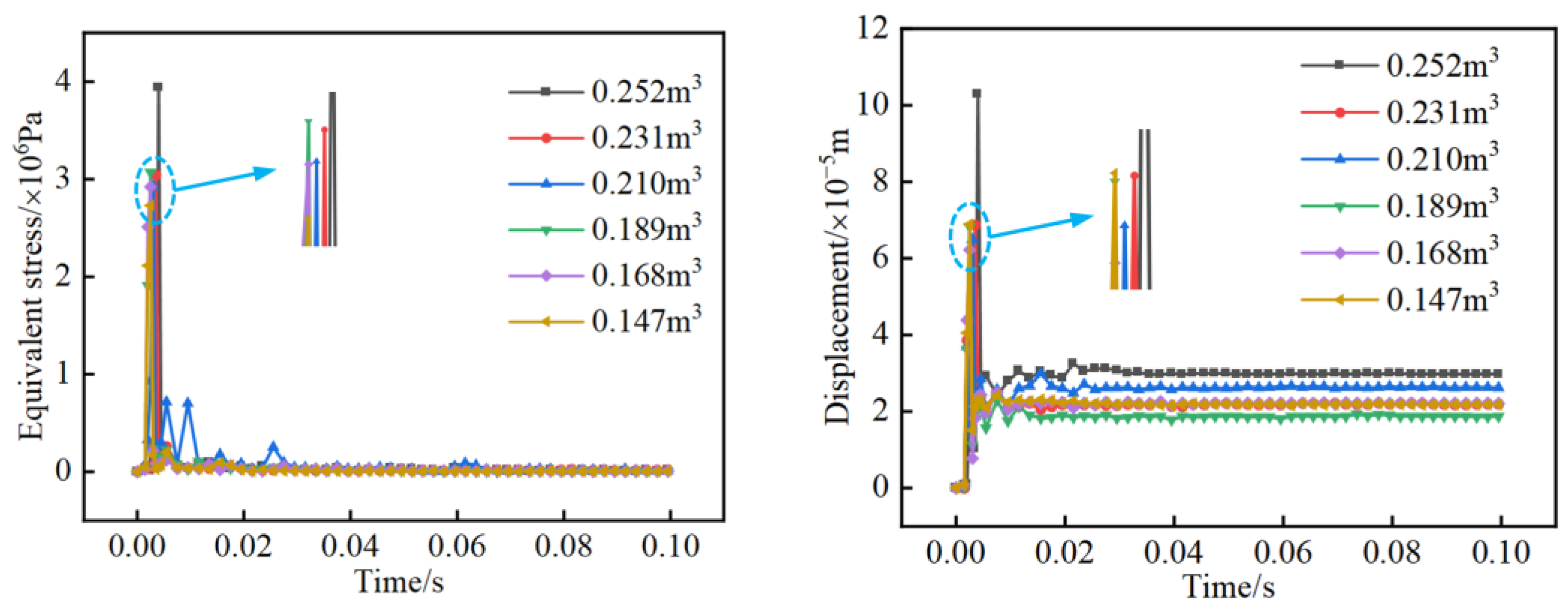
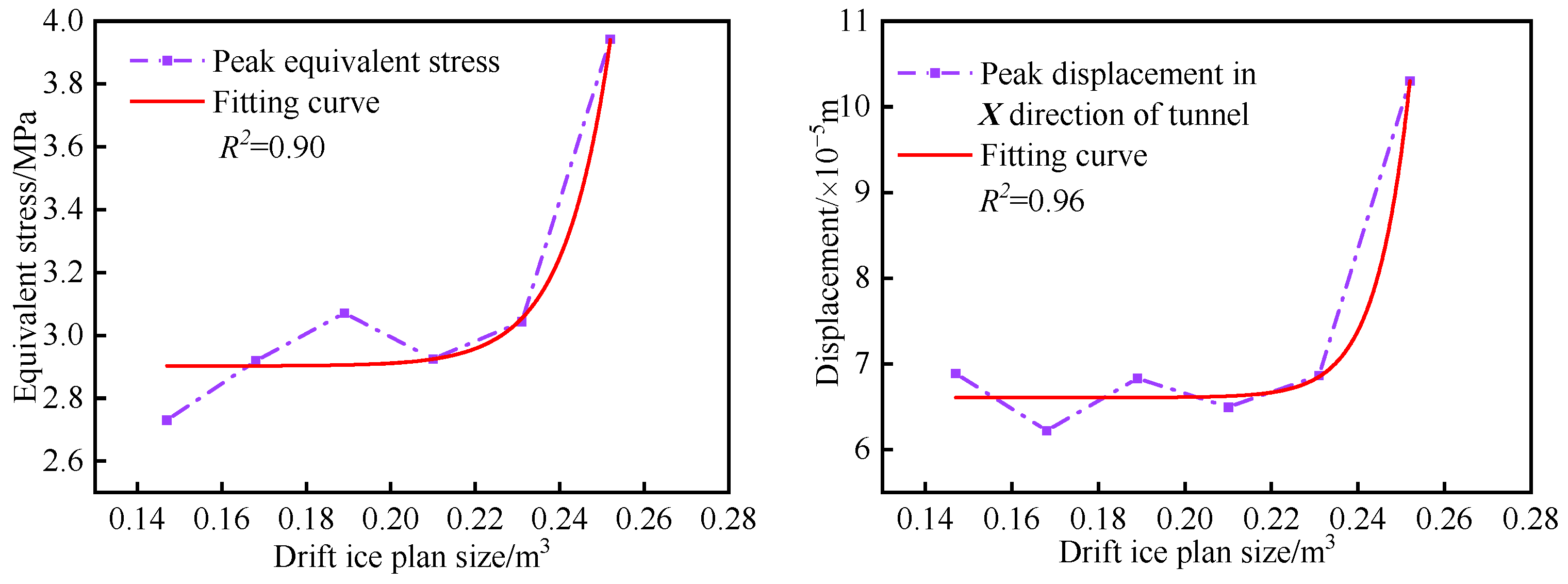
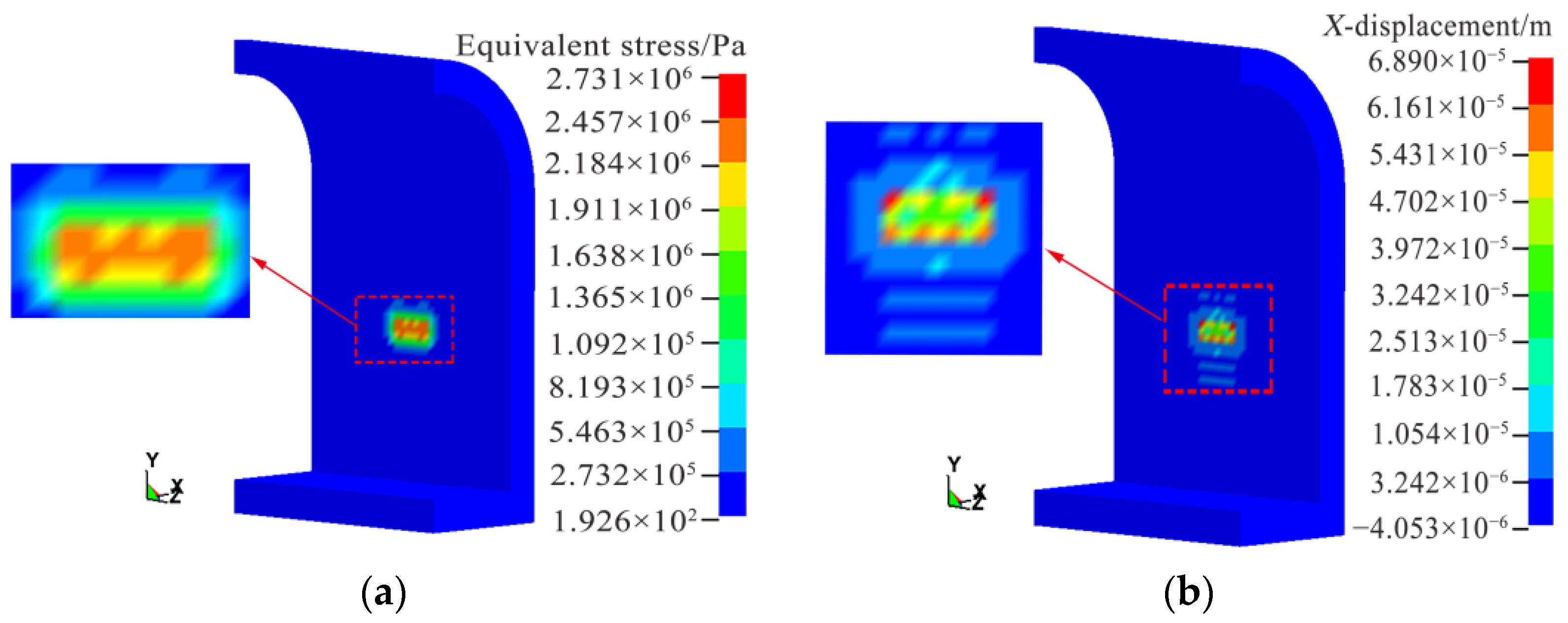
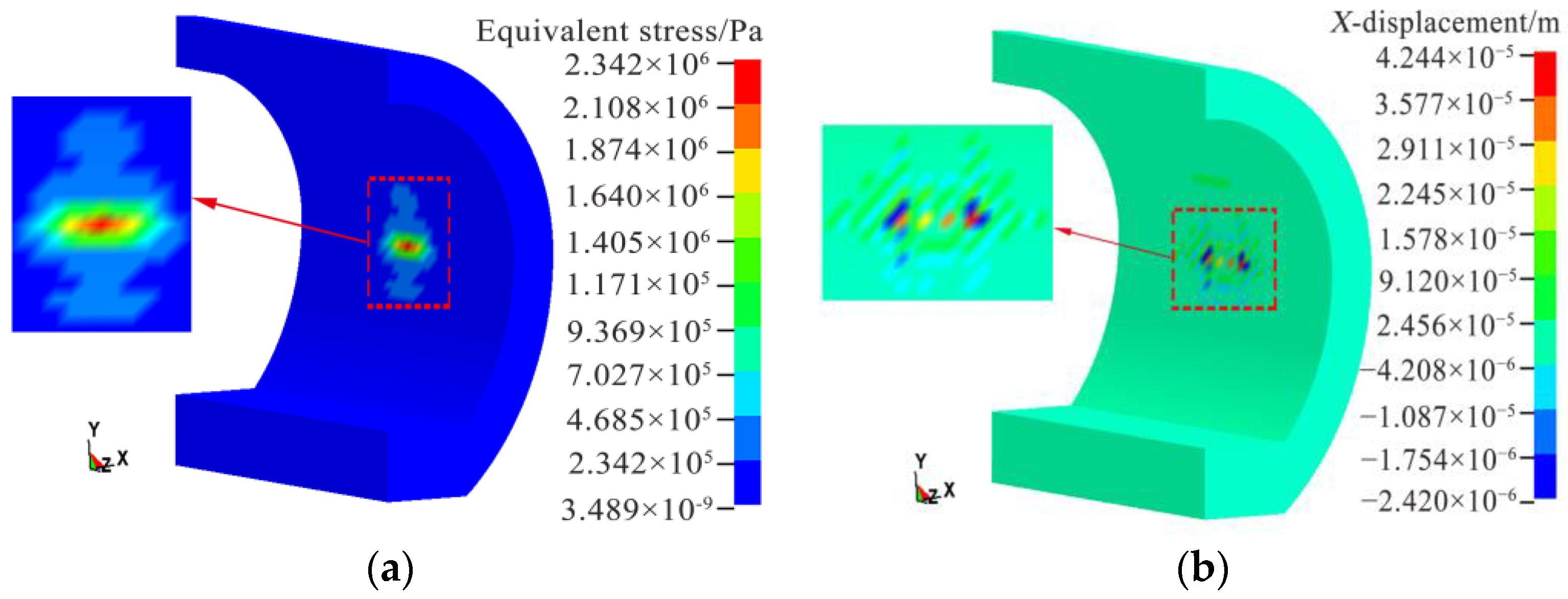
4.3. Simulation Results for Different Drift Ice Sizes
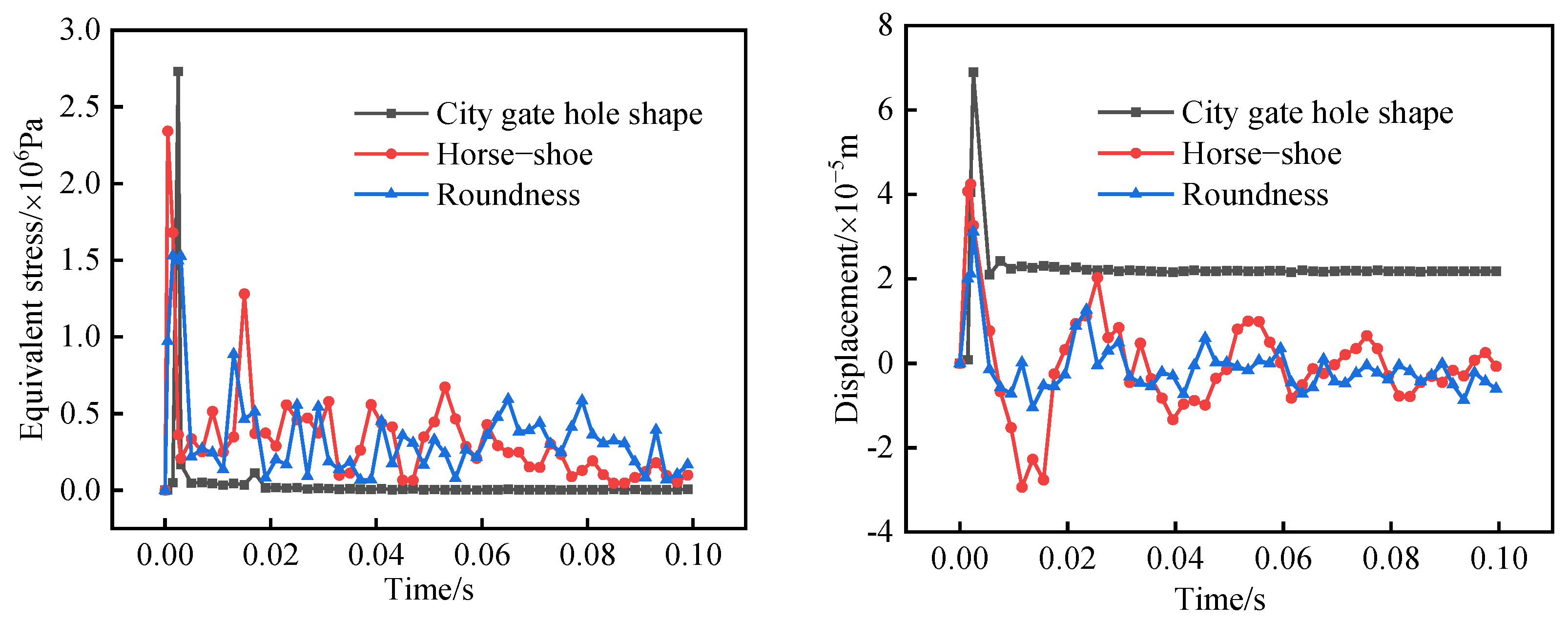
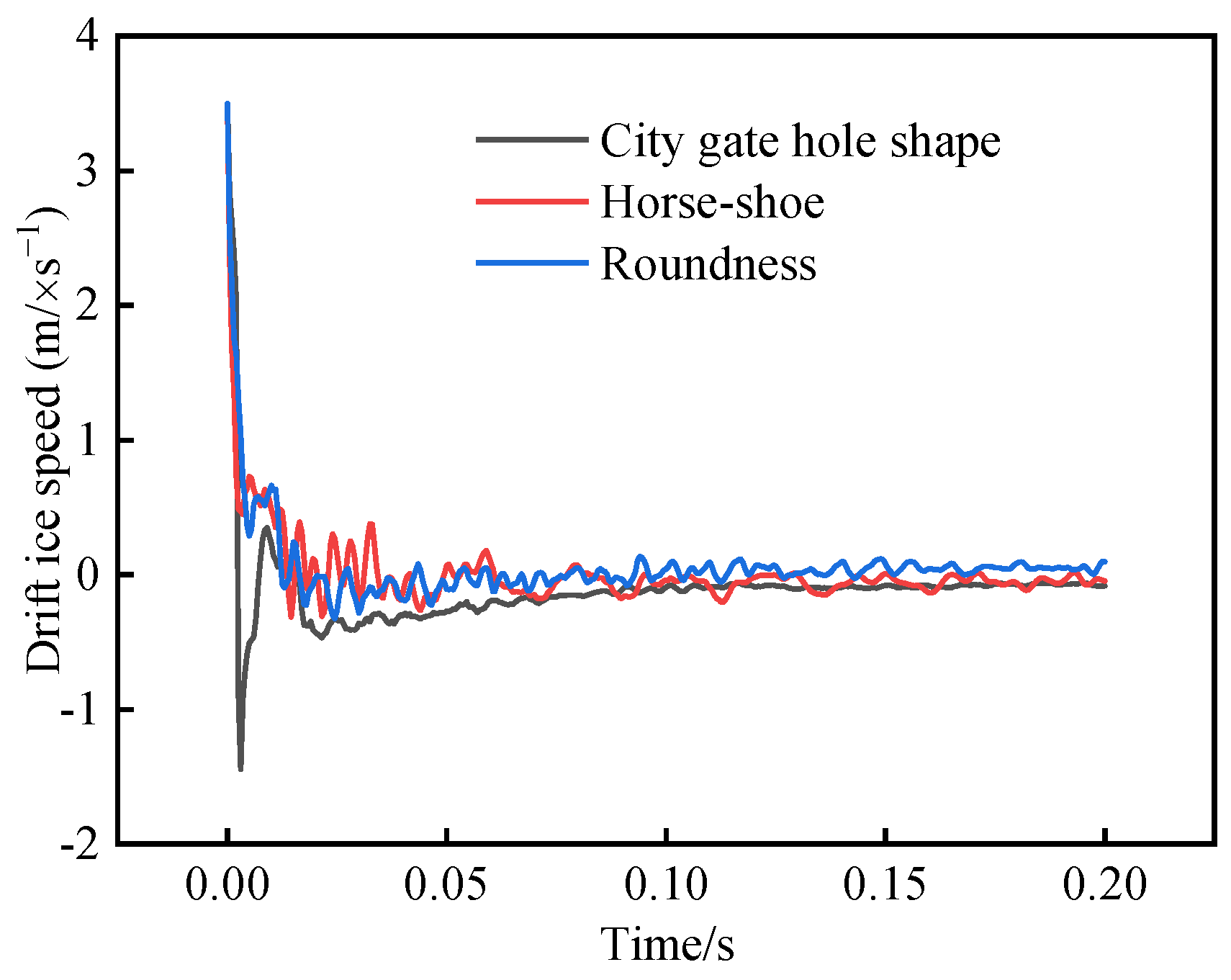
4.4. Simulation Results for Different Tunnel Cross-Sections
5. Conclusions
- (1)
- The experimental values of maximum equivalent stress and X-directional displacement show the same trend as the simulated values by comparing with the experimental results of the model of impact of drift ice on the water transfer tunnel, both of which show an increasing trend with an increase in drift ice velocity. This also indicates that the ice material model parameters, ALE algorithm, and grid size used in this paper can simulate the impact of drift ice on the water transfer tunnel more accurately. In addition, it is found that, when the ice velocity is greater than 3.0 m/s, the impact of drift ice on the water transfer tunnel is obvious, so engineers should fully consider the impact of drift ice velocity on a tunnel when designing the tunnel.
- (2)
- Comprehensive analysis of the different drift ice conditions simulated in this study shows that, as drift ice collision angle and drift ice size increase, the fitted curves of equivalent stress and peak displacement in X-direction all show an exponential function. The difference is that equivalent stress and peak displacement in X-direction keep decreasing as drift ice collision angle increases, while the most obvious effect of positive drift ice collision on the tunnel lining is found. However, as size of drift ice increases, peak equivalent stress and X-directional displacement show different trends, and peak equivalent stress and X-directional displacement decrease in the range of 0.189–0.210 m3, indicating that the “size effect” of drift ice and the influence of water medium on the ice–tunnel collision process are obvious. When the drift ice size is larger than 0.210 m3, the peaks all increase with an increase in drift ice size, indicating that “size effect” and water medium have a significantly lower influence at this time. In the case of changing only the tunnel section form, both the peak equivalent stress and peak displacement in the X-direction in the tunnel lining impact zone decrease as the curvature of the tunnel structure increases, indicating that, the greater the curvature of the tunnel structure, the better its crashworthiness. In addition, a comparative analysis of the effect on tunnel lining under different drift ice sizes and tunnel section forms was carried out and it was found that the average peak equivalent stress when the drift ice size changes is 1.53 times higher than the average peak value of different tunnel section forms and 1.41 times higher than the average peak X-directional displacement. Therefore, regional drift ice disaster characteristics in the engineering design should fully consider drift ice collision angle, drift ice size, and tunnel cross-section form on the impact of a water transmission tunnel.
- (3)
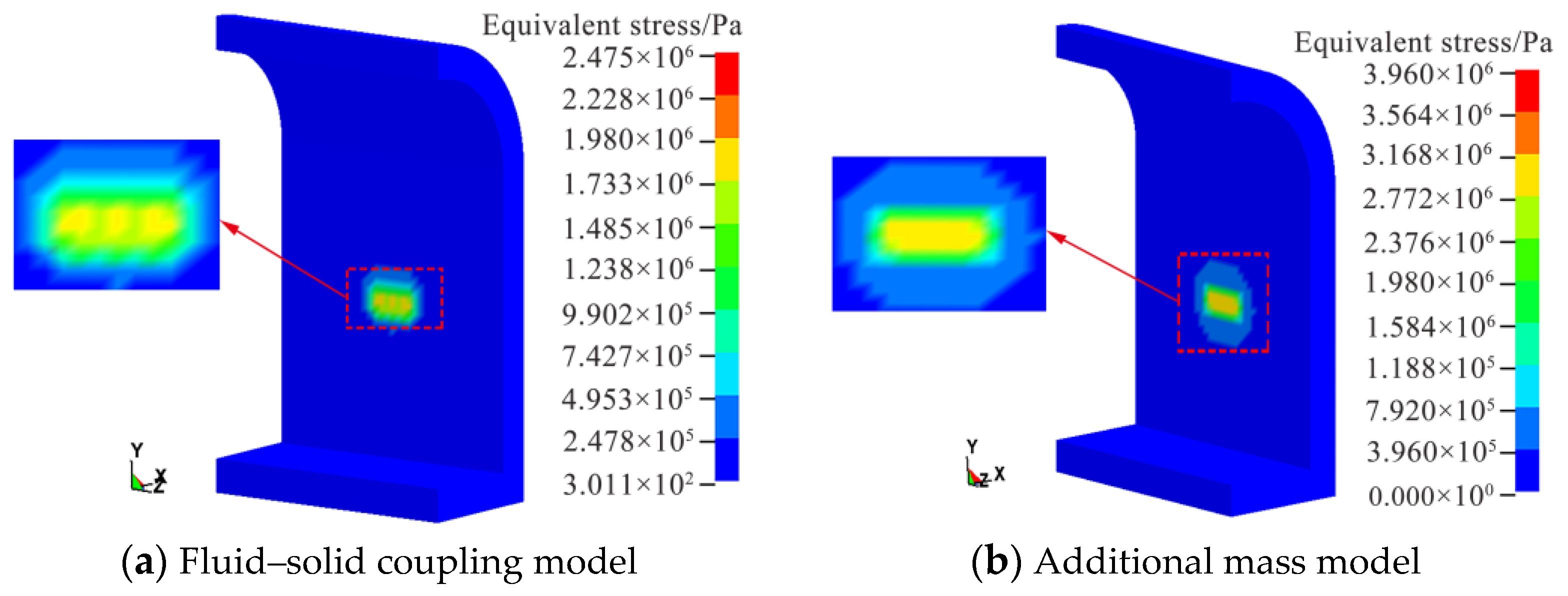
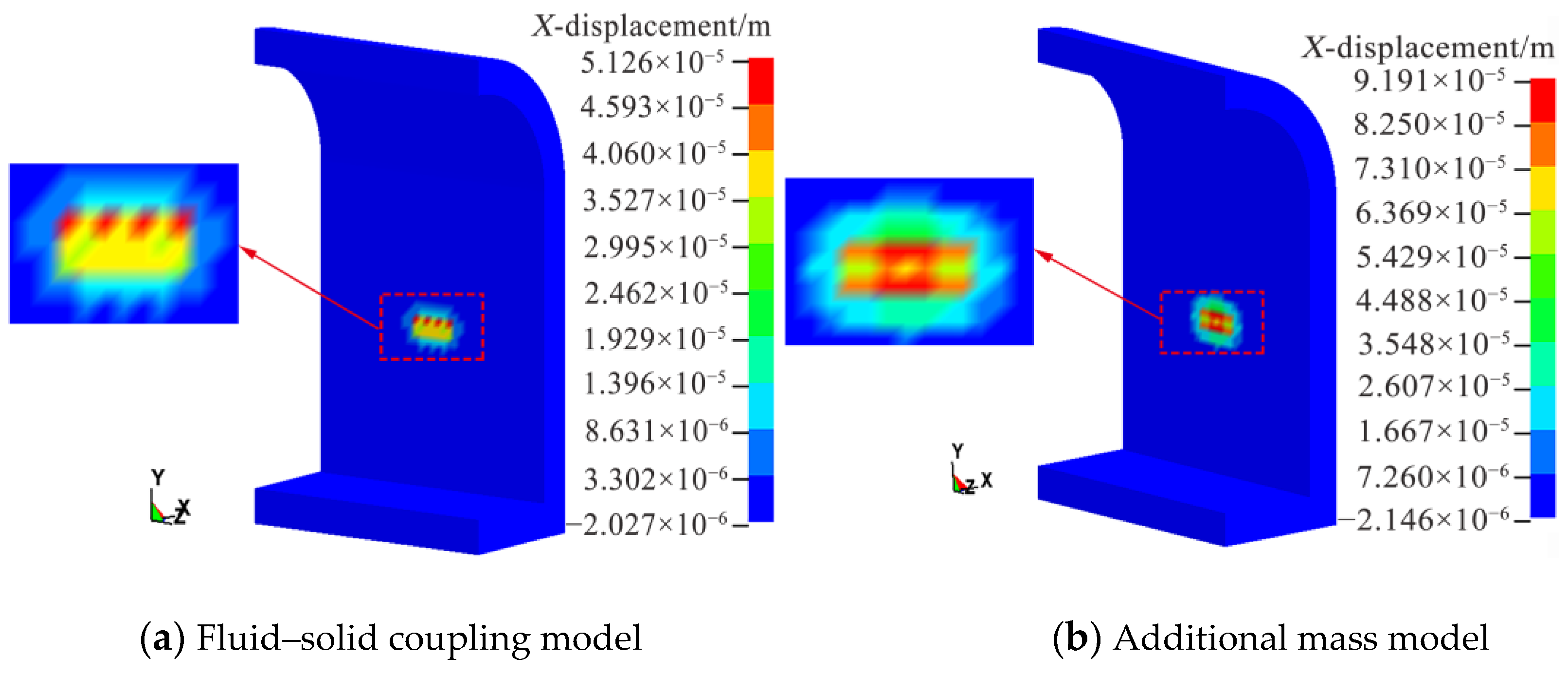
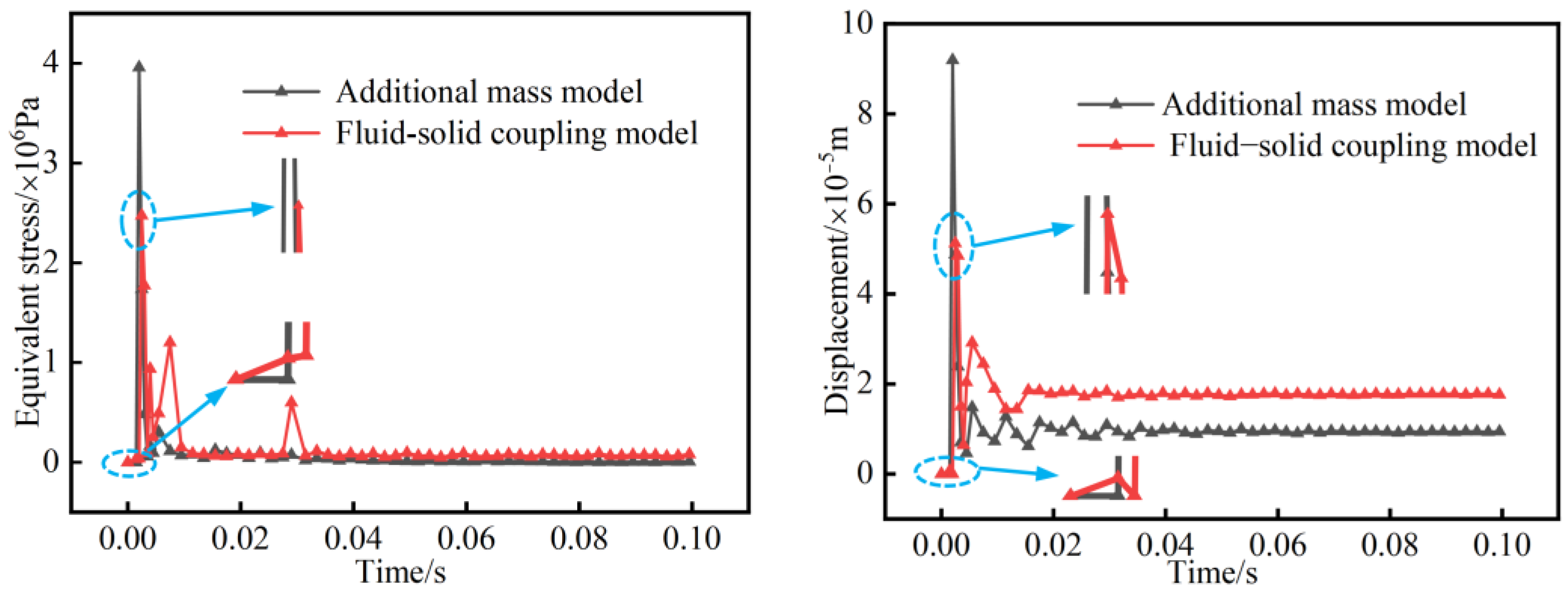
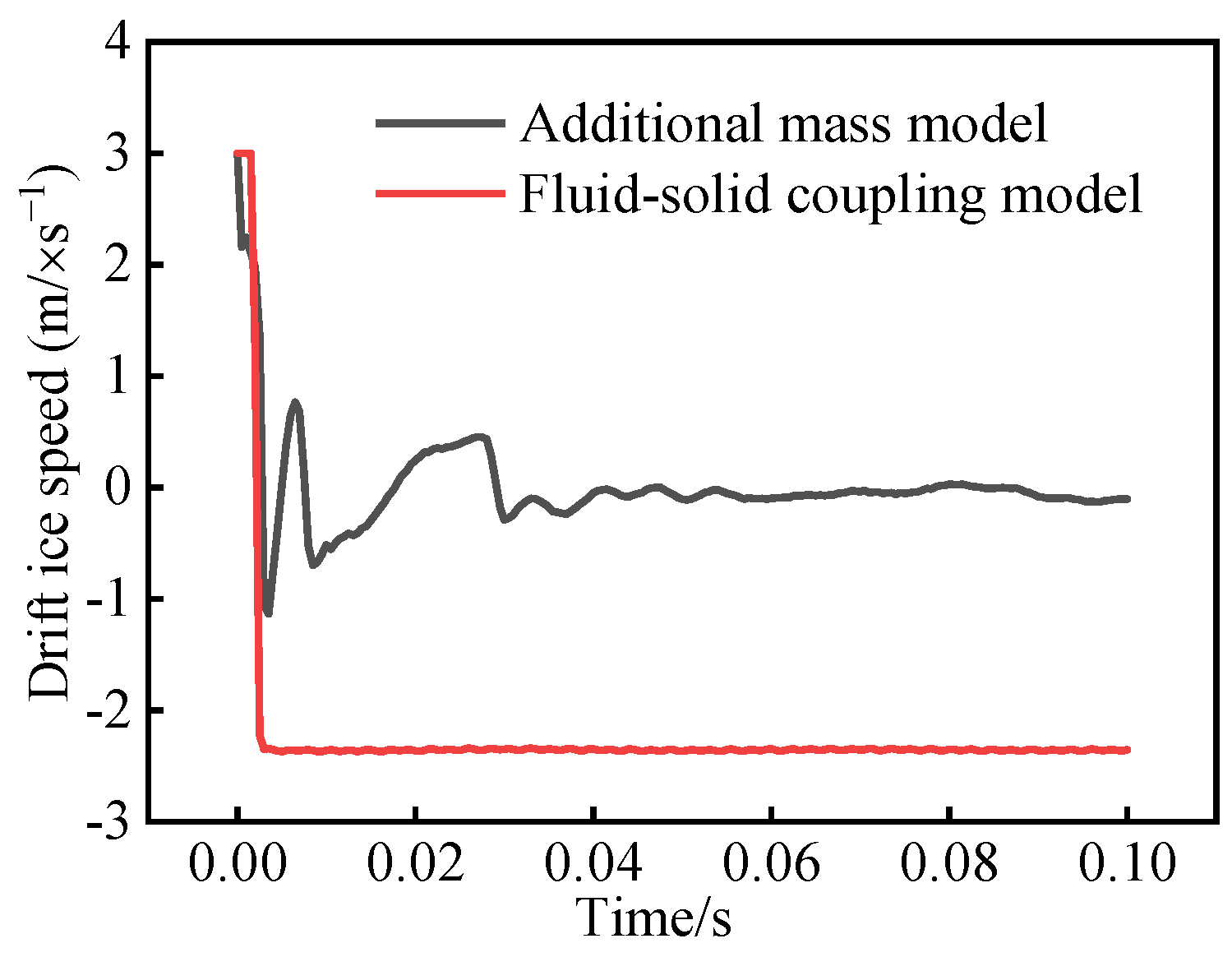
- Through comparative analysis of the water medium under typical working conditions by the additional mass method and fluid–solid coupling method, it was found that a high-pressure field will be formed by extrusion of the water medium during drift ice movement. This will have an impact on the tunnel lining during the impact process, and, through analysis of drift ice velocity under different tunnel sections, it was found that water medium has an obvious influence on drift ice movement. This should be fully considered in numerical simulations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zuo, Q.T.; Zhang, Z.; Ma, J.; Li, J. Solutions to Difficult Problems Caused by the Complexity of Human–Water Relationship in the Yellow River Basin: Based on the Perspective of Human–Water Relationship Discipline. Water 2022, 14, 2868. [Google Scholar] [CrossRef]
- Wang, T.; Yu, H.J.; Guo, X.L.; Liu, J.F.; Chen, Y.Z.; Yu, Y.T. Numerical modeling of typical ice processes in the Inner Mongolia reach of the Yellow River. J. Hydraul. Eng. 2021, 52, 535–545. [Google Scholar]
- Gong, L.; Gong, X.L.; Liang, Y. Experimental study and microscopic analysis on frost resistance of iron ore tailings recycled aggregate concrete. Adv. Mater. Sci. Eng. 2022. [Google Scholar] [CrossRef]
- Yang, Q.G.; Zhang, C.J.; Yan, T.Y. Integrated research and application of construction and safe operation of long-distance water transfer projects. Chin. J. Geotech. Eng. 2022, 44, 1188–1210. [Google Scholar]
- Jin, C.L.; Guan, Q.Y.; Gong, L. Evaluation of Regional Water Environmental Carrying Capacity and Diagnosis of Obstacle Factors Based on UMT Model. Water 2022, 14, 2621. [Google Scholar] [CrossRef]
- Xie, X.S.; Xie, X.H.; Wang, X.D. Influences of aquiclude on external water pressures on linings of dee buried tunnels. Chin. J. Geotech. Eng. 2020, 42 (Suppl. S2), 146–150. [Google Scholar]
- Simanjuntak, Y.; Marence, M.; Mynett, A.; Schleiss, A. Mechanical-Hydraulic Interaction in the Cracking Process of Pressure Tunnel Linings. Int. J. Hydropower Dams. 2013, 20, 112–119. [Google Scholar]
- Mehrdad, K.; Abdorreza, K.; Mohammad, N.; Moses, K. Investigating the effects of transient flow in concrete-lined pressure tunnels, and developing a new analytical formula for pressure wave velocity. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2019, 91, 1. [Google Scholar]
- Pachoud, A.; Manso, A.; Schleiss, J. Stress intensity factors for axial semi-elliptical surface cracks and embedded elliptical cracks at longitudinal butt welded joints of steel-lined pressure tunnels and shafts considering weld shape. Eng. Fract. Mech. 2017, 179, 93–119. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, Z.Q.; Ringsberg, J.W.; Gang, C. Nonlinear viscoelastic-plastic material modelling for the behave our of ice in ice-structure interactions. Ocean. Eng. 2019, 173, 284–297. [Google Scholar] [CrossRef]
- Li, F.; Mihkey, K.; Pentti, K. Finite element based meta-modeling of ship-ice interaction at shoulder and mid ship areas for ship performance simulation. Mar. Struct. 2020, 71, 102736. [Google Scholar] [CrossRef]
- Gong, L.; Jia, Z.Y.; Li, Y.Q. Impact of drift ice on concrete lining of open water conveyance channel. Trans. Chin. Soc. Agric. Eng. 2021, 37, 163–172. [Google Scholar]
- Kim, J.H.; Kim, Y. Numerical simulation of concrete abrasion induced by unbreakable ice floes. Int. J. Nav. Arc-Hitecture Ocean Eng. 2018, 11, 59–69. [Google Scholar] [CrossRef]
- Hendrikse, H.; Nord, T.S. Dynamic response of an offshore structure interacting with an ice floe failing in crushing. Mar. Struct. 2019, 65, 271–290. [Google Scholar] [CrossRef]
- Wang, C.H.; Wang, J.A.; Wang, C. Research on vertical movement of cylindrical structure out of water and breaking through ice layer basedon S-ALE method. Chin. J. Theor. Appl. Mech. 2021, 53, 3110–3123. [Google Scholar]
- Yu, Z.L.; Amdahl, J. A numerical solver for coupled dynamic simulation of glacial ice impacts considering hydrodynamic-ice-structure interaction. Ocean. Eng. 2021, 226, 108827. [Google Scholar] [CrossRef]
- Wang, C.; Yang, B.; Zhang, Y. Numerical Simulation and Analysis of Cylindrical Ice Impacting Problem. J. Shanghai Jiaotong Univ. 2022, 56, 368. [Google Scholar]
- Istrati, D.; Hasanpour, A.; Buckle, I. Numerical Investigation of Tsunami-Borne Debris Damming Loads on a Coastal Bridge. In Proceedings of the 17th World Conf Earthq Eng, Sendai, Japan, 27 September–2 October 2021. [Google Scholar]
- Pasculli, A.; Minatti, L.; Sciarra, N. SPH modeling of fast muddy debris flow: Numerical and experimental comparison of certain commonly utilized approaches. Ital. J. Geosci. 2013, 132, 350–365. [Google Scholar] [CrossRef] [Green Version]
- Hasanpour, A.; Istrati, D.; Buckle, I. Coupled SPH–FEM Modeling of Tsunami-Borne Large Debris Flow and Impact on Coastal Structures. J. Mar. Sci. Eng. 2021, 9, 1068. [Google Scholar] [CrossRef]
- Hasanpour, A.; Istrati, D.; Buckle, I. Multi-Physics Modeling of Tsunami Debris Impact on Bridge Decks. In Proceedings of the 3rd International Conference on Natural Hazards & Infrastructure 2022, Athens, Greece, 5–7 July 2022. [Google Scholar]
- Istrati, D.; Hasanpour, A. Advanced numerical modelling of large debris impact on piers during extreme flood events. In Proceedings of the 7th IAHR Europe Congress, Athens, Greece, 7–9 September 2022. [Google Scholar]
- Niu, J. Study on the Interaction between River Ice and Bridge Piers in Alpine Regions. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2018. [Google Scholar]
- Meng, Y.; Yi, J.W. Dynamic behavior of concrete cylinder specimens under low velocity impact. J. Vib. Shock. 2011, 30, 205–210. [Google Scholar]
- Liu, D.L. Numerical Simulation of Crushed Ice Resistance of Ship in Arctic. Master’s Thesis, Dalian University of Technology, Dalian, China, 2018. [Google Scholar]
- Zhang, J.; Wang, P.Z.; Liu, H.D. The Influence of Water Medium on the Structure Response of Ship Ice Collision. Ship Eng. 2019, 41, 12–15. [Google Scholar]
- Petersen, M.J. Dynamic of Ship Collisions. Ocean Eng. 1982, 8, 295–329. [Google Scholar] [CrossRef]
- Wang, H.; Gong, L.; Wang, Z.H. Dynamic response of drift ice-water tunnel collision based on different colliasion models. J. Water Resour. Water Eng. 2021, 32, 164–171. [Google Scholar]
- Li, T. Study on Numerical Simulation of Ship-Bridge Collision under Fluid-Structure Interaction. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2020. [Google Scholar]
- Lei, F. Dynamic Response Research of Submarine Flexible Structures with Fluic-Solid Interaction. Master’s Thesis, Wuhan Ligong University, Wuhan, China, 2011. [Google Scholar]
- Hallquist, J.O. LS-Dyna Theory Manual; Livermore Software Technology Corporation: San Francisco, CA, USA, 2006. [Google Scholar]
- Zhao, X.; Wang, X.; Zhang, Y.Z. Research on Similarity Law of Physical Model Experiments for ice Cover Thickening in the Conveyance Channel. South-North Water Transf. Water Sci. Technol. 2012, 10, 12–15. [Google Scholar]
- Xu, G.B.; Li, D.R.; Huang, Y. Laboratory study of problems in ice mechanics encountered in the Middle Route of South-to-North Water Transfer Project. Adv. Water Sci. 2010, 21, 808–815. [Google Scholar]
- Liu, J.J.; Xia, J.S.; Jin, Y. Numerical simulation of dynamic response of collision between ship and floating ice under ice-water coupling effect. J. Ship Mech. 2020, 24, 651–661. [Google Scholar]
- Jones, S.J.; Chew, H. Effect of sample and grain size on the compressive strength of ice. Ann. Glaciol. 1983, 4, 129–132. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.C. Study on Section form selection and structure Analysis of small Cross-section Water conveyance Tunnel. China Waterw. 2022, 22, 89–91. [Google Scholar]

| Parameters | Values |
|---|---|
| Density (kg·m−3) | 910 |
| Modulus of elasticity/GPa | Related to strain rate |
| Poisson’s ratio | 0.3 |
| Parameters | Values |
|---|---|
| Mass density/(kg·m−3) | 2500 |
| Maximum strain increment | 0 |
| Rate effect switch | 1 |
| Pre-existing damage | 0 |
| Erosion coefficient | 1.1 |
| Coefficient recovery parameter | 10 |
| Blocking options | 0 |
| Compression strength/MPa | 29 |
| Aggregate size/m | 0.02 |
| Parameters | Water | Air |
|---|---|---|
| Density/(kg/m3) | 1.1845 | 998.21 |
| Cutting stress/(Pa) | −10 | −1 × 105 |
| Viscosity coefficient | 1.7456 × 10−5 | 8.684 × 10−4 |
| Constant C | 1647 | |
| Constant S1 | 1.921 | |
| Constant S2 | −0.096 | |
| Constant C4 | 0.4 | |
| Constant C5 | 0.4 | |
| Constant | 0.35 | |
| Initial internal energy(E0/J) | 2.53 × 105 | 2.895 × 105 |
| Initial internal energy/V0 | 1.0 | 1.0 |
| Mesh Serial Number | A1 | A2 | A3 | Experimental Value |
|---|---|---|---|---|
| mesh size | 0.05 × 0.05 × 0.05 m3 | 0.08 × 0.08 × 0.08 m3 | 0.10 × 0.10 × 0.10 m3 | |
| Peak equivalent stress (×106 Pa) | 2.475 (2.1%) | 2.916 (−15%) | 3.211 (−27%) | 2.528 |
| X-direction displacement peak (×10−5 m) | 5.216 (0%) | 5.913(−13%) | 6.295 (−21%) | 5.216 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, L.; Dong, Z.; Jin, C.; Jia, Z.; Yang, T. Flow–Solid Coupling Analysis of Ice–Concrete Collision Nonlinear Problems in the Yellow River Basin. Water 2023, 15, 643. https://doi.org/10.3390/w15040643
Gong L, Dong Z, Jin C, Jia Z, Yang T. Flow–Solid Coupling Analysis of Ice–Concrete Collision Nonlinear Problems in the Yellow River Basin. Water. 2023; 15(4):643. https://doi.org/10.3390/w15040643
Chicago/Turabian StyleGong, Li, Zhouquan Dong, Chunling Jin, Zhiyuan Jia, and Tengteng Yang. 2023. "Flow–Solid Coupling Analysis of Ice–Concrete Collision Nonlinear Problems in the Yellow River Basin" Water 15, no. 4: 643. https://doi.org/10.3390/w15040643






