Comparison of Machine Learning Algorithms for Merging Gridded Satellite and Earth-Observed Precipitation Data
Abstract
:1. Introduction
2. Methods
2.1. Machine Learning Algorithms for Spatial Interpolation
2.1.1. Linear Regression
2.1.2. Multivariate Adaptive Regression Splines
2.1.3. Multivariate Adaptive Polynomial Splines
2.1.4. Random Forests
2.1.5. Gradient Boosting Machines
2.1.6. Extreme Gradient Boosting
2.1.7. Feed-Forward Neural Networks
2.1.8. Feed-Forward Neural Networks with Bayesian Regularization
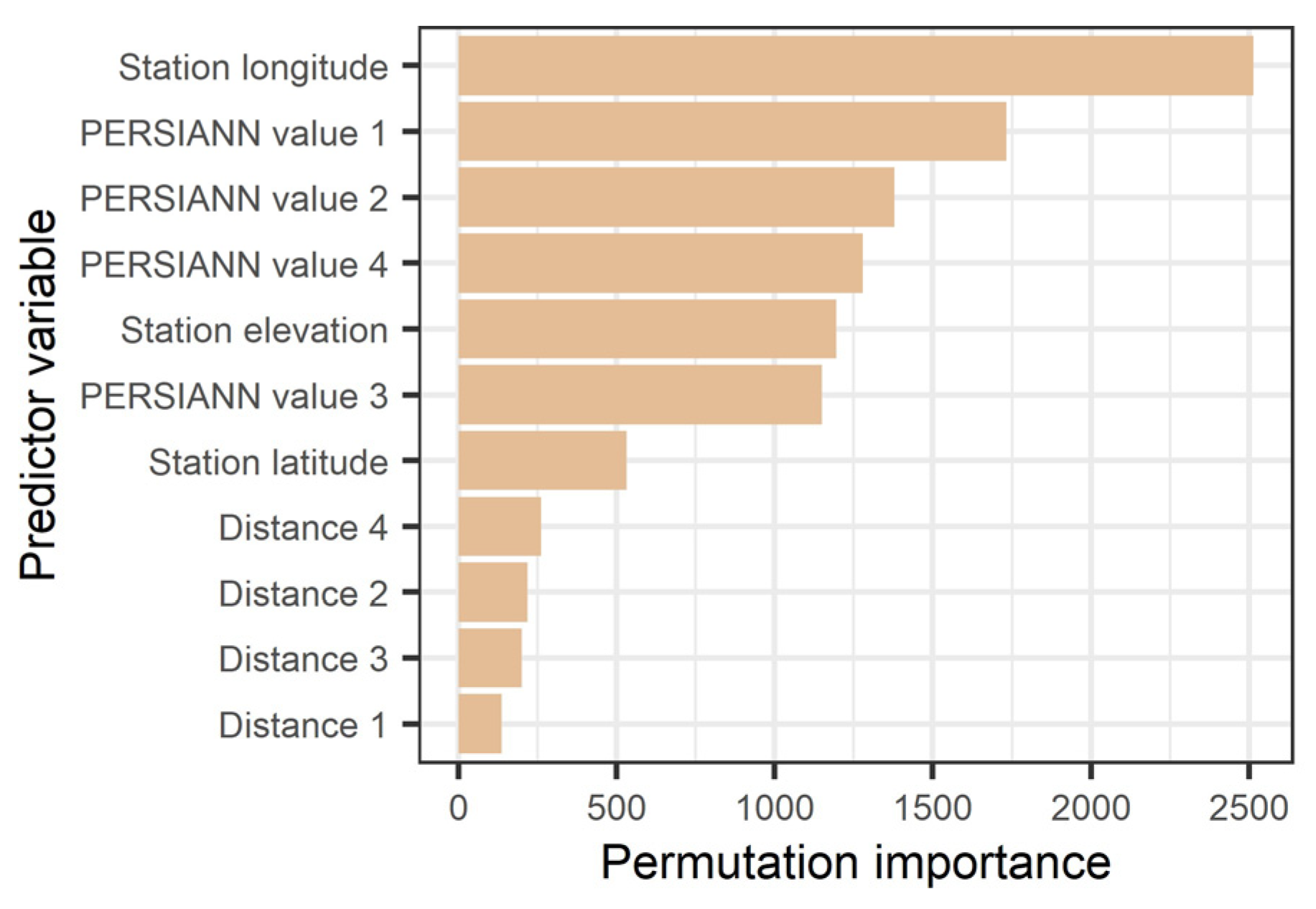
2.2. Variable Importance Metric
3. Data and Application
3.1. Data
3.1.1. Earth-Observed Precipitation Data
3.1.2. Satellite Precipitation Data
3.1.3. Elevation Data
3.2. Validation Setting and Predictor Variables
- Stations with missing monthly precipitation values do not need to be excluded from the dataset, and missing values do not need to be filled. Instead, a varying number of stations are included in the procedure for each time point in the period investigated. In brief, we kept a dataset with the maximum possible size, and we did not add uncertainties to the procedure by filling in the missing values.
- The cross-validation is totally random with respect to both space and time. This is a standard procedure in the validation of precipitation products that combine satellite and earth-observed data.
- In the setting proposed, it is possible to create a corrected precipitation gridded dataset because, after fitting the regression algorithm, it is possible to directly interpolate in the space conditional upon the predictor variables that are known.
- There is no need to first interpolate the station data to grid points and then verify the algorithms based on the earth-observed data previously interpolated. This procedure is common in the field, but it creates additional uncertainties.
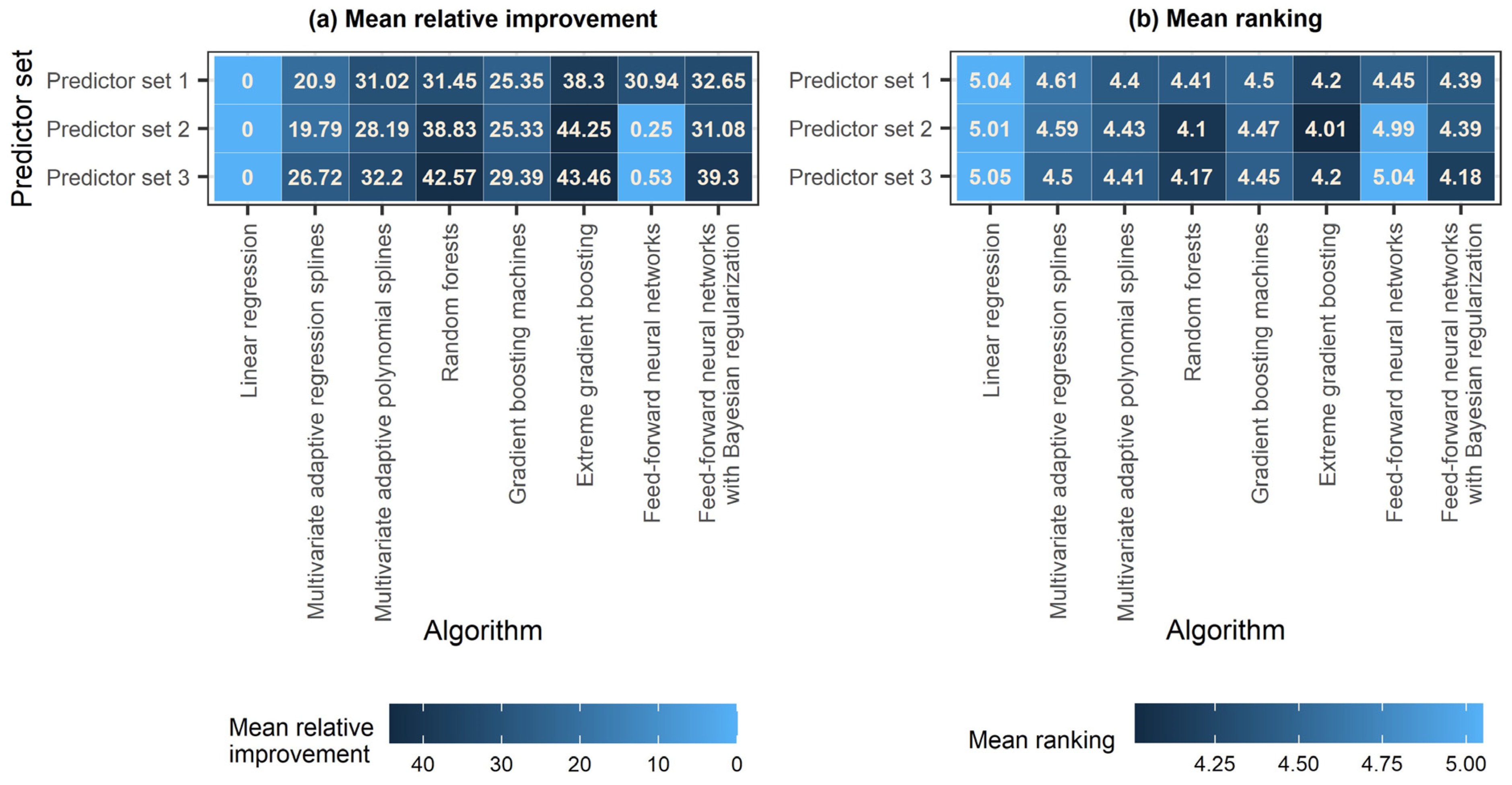
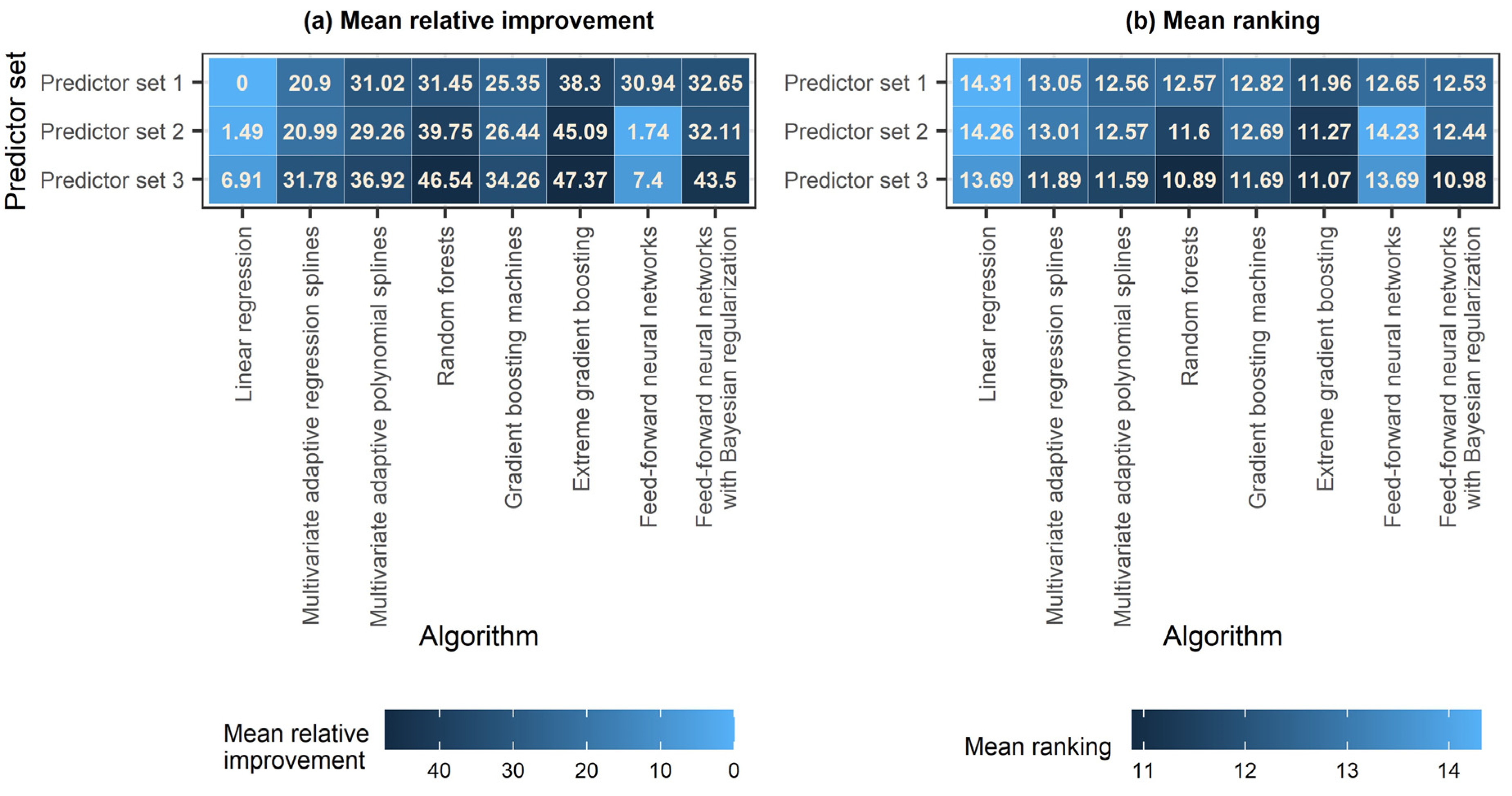
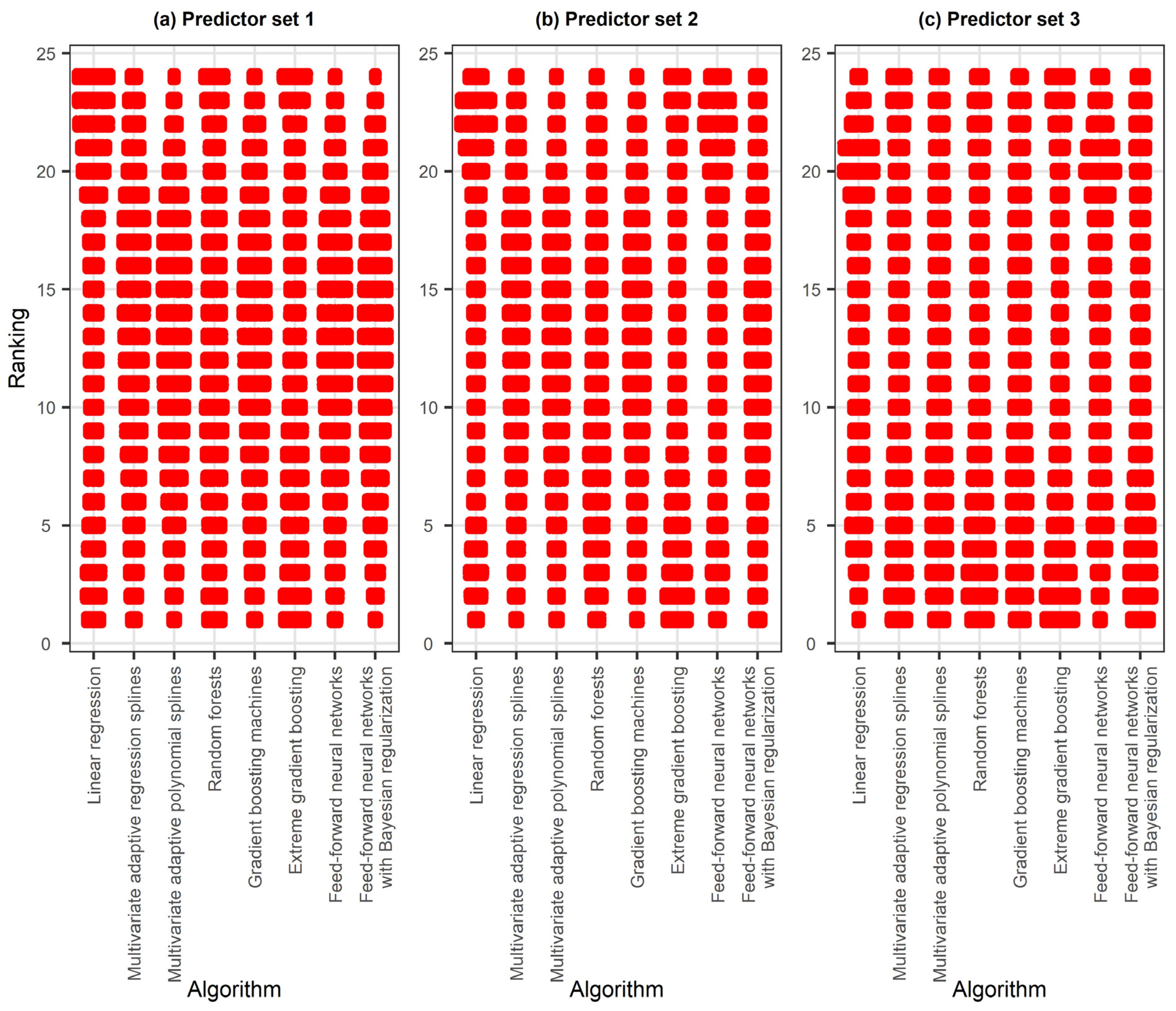
3.3. Performance Metrics and Assessment
4. Results
4.1. Regression Setting Exploration
4.2. Comparison of the Algorithms
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Blöschl, G.; Bierkens, M.F.P.; Chambel, A.; Cudennec, C.; Destouni, G.; Fiori, A.; Kirchner, J.W.; McDonnell, J.J.; Savenije, H.H.G.; Sivapalan, M.; et al. Twenty-three unsolved problems in hydrology (UPH)–A community perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K.-L. A review of global precipitation data sets: Data sources, estimation, and intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Mega, T.; Ushio, T.; Matsuda, T.; Kubota, T.; Kachi, M.; Oki, R. Gauge-adjusted global satellite mapping of precipitation. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1928–1935. [Google Scholar] [CrossRef]
- Salmani-Dehaghi, N.; Samani, N. Development of bias-correction PERSIANN-CDR models for the simulation and completion of precipitation time series. Atmos. Environ. 2021, 246, 117981. [Google Scholar] [CrossRef]
- Li, W.; Jiang, Q.; He, X.; Sun, H.; Sun, W.; Scaioni, M.; Chen, S.; Li, X.; Gao, J.; Hong, Y.; et al. Effective multi-satellite precipitation fusion procedure conditioned by gauge background fields over the Chinese mainland. J. Hydrol. 2022, 610, 127783. [Google Scholar] [CrossRef]
- Tang, T.; Chen, T.; Gui, G. A comparative evaluation of gauge-satellite-based merging products over multiregional complex terrain basin. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5275–5287. [Google Scholar] [CrossRef]
- Bivand, R.S.; Pebesma, E.; Gómez-Rubio, V. Applied Spatial Data Analysis with R, 2nd ed.; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. Spatial interpolation methods applied in the environmental sciences: A review. Environ. Model. Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Heuvelink, G.B.M.; Webster, R. Spatial statistics and soil mapping: A blossoming partnership under pressure. Spat. Stat. 2022, 50, 100639. [Google Scholar] [CrossRef]
- Kopczewska, K. Spatial machine learning: New opportunities for regional science. Ann. Reg. Sci. 2022, 68, 713–755. [Google Scholar] [CrossRef]
- Hu, Q.; Li, Z.; Wang, L.; Huang, Y.; Wang, Y.; Li, L. Rainfall spatial estimations: A review from spatial interpolation to multi-source data merging. Water 2019, 11, 579. [Google Scholar] [CrossRef]
- Abdollahipour, A.; Ahmadi, H.; Aminnejad, B. A review of downscaling methods of satellite-based precipitation estimates. Earth Sci. Inform. 2022, 15, 1–20. [Google Scholar] [CrossRef]
- He, X.; Chaney, N.W.; Schleiss, M.; Sheffield, J. Spatial downscaling of precipitation using adaptable random forests. Water Resour. Res. 2016, 52, 8217–8237. [Google Scholar] [CrossRef]
- Meyer, H.; Kühnlein, M.; Appelhans, T.; Nauss, T. Comparison of four machine learning algorithms for their applicability in satellite-based optical rainfall retrievals. Atmos. Res. 2016, 169, 424–433. [Google Scholar] [CrossRef]
- Tao, Y.; Gao, X.; Hsu, K.; Sorooshian, S.; Ihler, A. A deep neural network modeling framework to reduce bias in satellite precipitation products. J. Hydrometeorol. 2016, 17, 931–945. [Google Scholar] [CrossRef]
- Yang, Z.; Hsu, K.; Sorooshian, S.; Xu, X.; Braithwaite, D.; Verbist, K.M.J. Bias adjustment of satellite-based precipitation estimation using gauge observations: A case study in Chile. J. Geophys. Res. Atmos. 2016, 121, 3790–3806. [Google Scholar] [CrossRef]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Beck, H.E.; McNamara, I.; Ribbe, L.; Nauditt, A.; Birkel, C.; Verbist, K.; Giraldo-Osorio, J.D.; Thinh, N.X.; et al. RF-MEP: A novel random forest method for merging gridded precipitation products and ground-based measurements. Remote Sens. Environ. 2020, 239, 111606. [Google Scholar] [CrossRef]
- Chen, H.; Chandrasekar, V.; Cifelli, R.; Xie, P. A machine learning system for precipitation estimation using satellite and ground radar network observations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 982–994. [Google Scholar] [CrossRef]
- Chen, S.; Xiong, L.; Ma, Q.; Kim, J.-S.; Chen, J.; Xu, C.-Y. Improving daily spatial precipitation estimates by merging gauge observation with multiple satellite-based precipitation products based on the geographically weighted ridge regression method. J. Hydrol. 2020, 589, 125156. [Google Scholar] [CrossRef]
- Rata, M.; Douaoui, A.; Larid, M.; Douaik, A. Comparison of geostatistical interpolation methods to map annual rainfall in the Chéliff watershed, Algeria. Theor. Appl. Climatol. 2020, 141, 1009–1024. [Google Scholar] [CrossRef]
- Chen, C.; Hu, B.; Li, Y. Easy-to-use spatial random-forest-based downscaling-calibration method for producing precipitation data with high resolution and high accuracy. Hydrol. Earth Syst. Sci. 2021, 25, 5667–5682. [Google Scholar] [CrossRef]
- Nguyen, G.V.; Le, X.-H.; Van, L.N.; Jung, S.; Yeon, M.; Lee, G. Application of random forest algorithm for merging multiple satellite precipitation products across South Korea. Remote Sens. 2021, 13, 4033. [Google Scholar] [CrossRef]
- Shen, Z.; Yong, B. Downscaling the GPM-based satellite precipitation retrievals using gradient boosting decision tree approach over Mainland China. J. Hydrol. 2021, 602, 126803. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.; Zheng, D.; Zhang, K.; Ma, Q.; Zhao, Y.; Ge, Y. Merging multiple satellite-based precipitation products and gauge observations using a novel double machine learning approach. J. Hydrol. 2021, 594, 125969. [Google Scholar] [CrossRef]
- Chen, H.; Sun, L.; Cifelli, R.; Xie, P. Deep learning for bias correction of satellite retrievals of orographic precipitation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4104611. [Google Scholar] [CrossRef]
- Fernandez-Palomino, C.A.; Hattermann, F.F.; Krysanova, V.; Lobanova, A.; Vega-Jácome, F.; Lavado, W.; Santini, W.; Aybar, C.; Bronstert, A. A novel high-resolution gridded precipitation dataset for Peruvian and Ecuadorian watersheds: Development and hydrological evaluation. J. Hydrometeorol. 2022, 23, 309–336. [Google Scholar] [CrossRef]
- Lin, Q.; Peng, T.; Wu, Z.; Guo, J.; Chang, W.; Xu, Z. Performance evaluation, error decomposition and tree-based machine learning error correction of GPM IMERG and TRMM 3B42 products in the Three Gorges reservoir area. Atmos. Res. 2022, 268, 105988. [Google Scholar] [CrossRef]
- Yang, X.; Yang, S.; Tan, M.L.; Pan, H.; Zhang, H.; Wang, G.; He, R.; Wang, Z. Correcting the bias of daily satellite precipitation estimates in tropical regions using deep neural network. J. Hydrol. 2022, 608, 127656. [Google Scholar] [CrossRef]
- Zandi, O.; Zahraie, B.; Nasseri, M.; Behrangi, A. Stacking machine learning models versus a locally weighted linear model to generate high-resolution monthly precipitation over a topographically complex area. Atmos. Res. 2022, 272, 106159. [Google Scholar] [CrossRef]
- Militino, A.F.; Ugarte, M.D.; Pérez-Goya, U. Machine learning procedures for daily interpolation of rainfall in Navarre (Spain). In Trends in Mathematical, Information and Data Sciences; Springer: New York, NY, USA, 2023; Volume 445, pp. 399–413. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D.; Potter, A.; Daniell, J.J. Application of machine learning methods to spatial interpolation of environmental variables. Environ. Model. Softw. 2011, 26, 1647–1659. [Google Scholar] [CrossRef]
- Baratto, P.F.B.; Cecílio, R.A.; de Sousa Teixeira, D.B.; Zanetti, S.S.; Xavier, A.C. Random forest for spatialization of daily evapotranspiration (ET0) in watersheds in the Atlantic Forest. Environ. Monit. Assess. 2022, 194, 449. [Google Scholar] [CrossRef] [PubMed]
- Sekulić, A.; Kilibarda, M.; Protić, D.; Tadić, M.P.; Bajat, B. Spatio-temporal regression kriging model of mean daily temperature for Croatia. Theor. Appl. Climatol. 2020, 140, 101–114. [Google Scholar] [CrossRef]
- Sekulić, A.; Kilibarda, M.; Protić, D.; Bajat, B. A high-resolution daily gridded meteorological dataset for Serbia made by random forest spatial interpolation. Sci. Data 2021, 8, 123. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Tantanee, S. How to explain and predict the shape parameter of the generalized extreme value distribution of streamflow extremes using a big dataset. J. Hydrol. 2019, 574, 628–645. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H. Time series features for supporting hydrometeorological explorations and predictions in ungauged locations using large datasets. Water 2022, 14, 1657. [Google Scholar] [CrossRef]
- Wadoux, A.M.J.-C.; Minasny, B.; McBratney, A.B. Machine learning for digital soil mapping: Applications, challenges and suggested solutions. Earth-Sci. Rev. 2020, 210, 103359. [Google Scholar] [CrossRef]
- Chen, S.; Arrouays, D.; Leatitia Mulder, V.; Poggio, L.; Minasny, B.; Roudier, P.; Libohova, Z.; Lagacherie, P.; Shi, Z.; Hannam, J.; et al. Digital mapping of GlobalSoilMap soil properties at a broad scale: A review. Geoderma 2022, 409, 115567. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.M.; Gräler, B. Random Forest as a generic framework for predictive modeling of spatial and spatio-temporal variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef]
- Saha, A.; Basu, S.; Datta, A. Random forests for spatially dependent data. J. Am. Stat. Assoc. 2021. [Google Scholar] [CrossRef]
- Behrens, T.; Schmidt, K.; Viscarra Rossel, R.A.; Gries, P.; Scholten, T.; MacMillan, R.A. Spatial modelling with Euclidean distance fields and machine learning. Eur. J. Soil Sci. 2018, 69, 757–770. [Google Scholar] [CrossRef]
- Sekulić, A.; Kilibarda, M.; Heuvelink, G.B.M.; Nikolić, M.; Bajat, B. Random forest spatial interpolation. Remote Sens. 2020, 12, 1687. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Niang Gadiaga, A.; Linard, C.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E.; Kalogirou, S. Geographical random forests: A spatial extension of the random forest algorithm to address spatial heterogeneity in remote sensing and population modelling. Geocarto Int. 2021, 36, 121–136. [Google Scholar] [CrossRef]
- Georganos, S.; Kalogirou, S. A forest of forests: A spatially weighted and computationally efficient formulation of geographical random forests. ISPRS Int. J. Geo-Inf. 2022, 11, 471. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Langousis, A.; Jayawardena, A.W.; Sivakumar, B.; Mamassis, N.; Montanari, A.; Koutsoyiannis, D. Probabilistic hydrological post-processing at scale: Why and how to apply machine-learning quantile regression algorithms. Water 2019, 11, 2126. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. Super ensemble learning for daily streamflow forecasting: Large-scale demonstration and comparison with multiple machine learning algorithms. Neural Comput. Appl. 2021, 33, 3053–3068. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T. Computer Age Statistical Inference; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Friedman, J.H. Fast MARS. Technical Report 110. Available online: https://statistics.stanford.edu/sites/g/files/sbiybj6031/f/LCS%20110.pdf (accessed on 17 December 2022).
- Kooperberg, C.; Bose, S.; Stone, C.J. Polychotomous regression. J. Am. Stat. Assoc. 1997, 92, 117–127. [Google Scholar] [CrossRef]
- Stone, C.J.; Hansen, M.H.; Kooperberg, C.; Truong, Y.K. Polynomial splines and their tensor products in extended linear modeling. Ann. Stat. 1997, 25, 1371–1470. [Google Scholar] [CrossRef]
- Kooperberg, C. polspline: Polynomial Spline Routines. R Package Version 1.1.20. 2022. Available online: https://CRAN.R-project.org/package=polspline (accessed on 17 December 2022).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Mayr, A.; Binder, H.; Gefeller, O.; Schmid, M. The evolution of boosting algorithms: From machine learning to statistical modelling. Methods Inf. Med. 2014, 53, 419–427. [Google Scholar] [CrossRef] [PubMed]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G. Boosting algorithms in energy research: A systematic review. Neural Comput. Appl. 2021, 33, 14101–14117. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Breiman, L. Statistical modeling: The two cultures. Stat. Sci. 2001, 16, 199–215. [Google Scholar] [CrossRef]
- Shmueli, G. To explain or to predict? Stat. Sci. 2010, 25, 289–310. [Google Scholar] [CrossRef]
- Peterson, T.C.; Vose, R.S. An overview of the Global Historical Climatology Network temperature database. Bull. Am. Meteorol. Soc. 1997, 78, 2837–2849. [Google Scholar] [CrossRef]
- Hsu, K.-L.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. Climatol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Nguyen, P.; Ombadi, M.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Braithwaite, D.; Ashouri, H.; Rose Thorstensen, A. The PERSIANN family of global satellite precipitation data: A review and evaluation of products. Hydrol. Earth Syst. Sci. 2018, 22, 5801–5816. [Google Scholar] [CrossRef]
- Nguyen, P.; Shearer, E.J.; Tran, H.; Ombadi, M.; Hayatbini, N.; Palacios, T.; Huynh, P.; Braithwaite, D.; Updegraff, G.; Hsu, K.; et al. The CHRS data portal, an easily accessible public repository for PERSIANN global satellite precipitation data. Sci. Data 2019, 6, 180296. [Google Scholar] [CrossRef] [PubMed]
- Hollister, J.W. elevatr: Access Elevation Data from Various APIs. R package version 0.4.2. 2022. Available online: https://CRAN.R-project.org/package=elevatr (accessed on 17 December 2022).
- Xiong, L.; Li, S.; Tang, G.; Strobl, J. Geomorphometry and terrain analysis: Data, methods, platforms and applications. Earth-Sci. Rev. 2022, 233, 104191. [Google Scholar] [CrossRef]
- Meyer, H.; Pebesma, E. Predicting into unknown space? Estimating the area of applicability of spatial prediction models. Methods Ecol. Evol. 2021, 12, 1620–1633. [Google Scholar] [CrossRef]
- Meyer, H.; Pebesma, E. Machine learning-based global maps of ecological variables and the challenge of assessing them. Nat. Commun. 2022, 13, 2208. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Kounadi, O.; Zurita-Milla, R. Incorporating spatial autocorrelation in machine learning models using spatial lag and eigenvector spatial filtering features. ISPRS Int. J. Geo-Inf. 2022, 11, 242. [Google Scholar] [CrossRef]
- Talebi, H.; Peeters, L.J.M.; Otto, A.; Tolosana-Delgado, R. A truly spatial random forests algorithm for geoscience data analysis and modelling. Math. Geosci. 2022, 54, 1–22. [Google Scholar] [CrossRef]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Gneiting, T. Making and evaluating point forecasts. J. Am. Stat. Assoc. 2011, 106, 746–762. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H. A review of machine learning concepts and methods for addressing challenges in probabilistic hydrological post-processing and forecasting. Front. Water 2022, 4, 961954. [Google Scholar] [CrossRef]
- Davies, M.M.; van der Laan, M.J. Optimal spatial prediction using ensemble machine learning. Int. J. Biostat. 2016, 12, 179–201. [Google Scholar] [CrossRef]
- Egaña, A.; Navarro, F.; Maleki, M.; Grandón, F.; Carter, F.; Soto, F. Ensemble spatial interpolation: A new approach to natural or anthropogenic variable assessment. Nat. Resour. Res. 2021, 30, 3777–3793. [Google Scholar] [CrossRef]
- Petropoulos, F.; Svetunkov, I. A simple combination of univariate models. Int. J. Forecast. 2020, 36, 110–115. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H. Hydrological time series forecasting using simple combinations: Big data testing and investigations on one-year ahead river flow predictability. J. Hydrol. 2020, 590, 125205. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Burnetas, A.; Langousis, A. Hydrological post-processing using stacked generalization of quantile regression algorithms: Large-scale application over CONUS. J. Hydrol. 2019, 577, 123957. [Google Scholar] [CrossRef]
- Montero-Manso, P.; Athanasopoulos, G.; Hyndman, R.J.; Talagala, T.S. FFORMA: Feature-based forecast model averaging. Int. J. Forecast. 2020, 36, 86–92. [Google Scholar] [CrossRef]
- Talagala, T.S.; Li, F.; Kang, Y. FFORMPP: Feature-based forecast model performance prediction. Int. J. Forecast. 2021, 38, 920–943. [Google Scholar] [CrossRef]
- Fulcher, B.D.; Little, M.A.; Jones, N.S. Highly comparative time-series analysis: The empirical structure of time series and their methods. J. R. Soc. Interface 2013, 10, 20130048. [Google Scholar] [CrossRef]
- Kang, Y.; Hyndman, R.J.; Smith-Miles, K. Visualising forecasting algorithm performance using time series instance spaces. Int. J. Forecast. 2017, 33, 345–358. [Google Scholar] [CrossRef]
- Linardatos, P.; Papastefanopoulos, V.; Kotsiantis, S. Explainable AI: A review of machine learning interpretability methods. Entropy 2021, 23, 18. [Google Scholar] [CrossRef]
- Belle, V.; Papantonis, I. Principles and practice of explainable machine learning. Front. Big Data 2021, 4, 688969. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Pechlivanidis, I.G.; Grimaldi, S.; Volpi, E. Massive feature extraction for explaining and foretelling hydroclimatic time series forecastability at the global scale. Geosci. Front. 2022, 13, 101349. [Google Scholar] [CrossRef]
- Fouedjio, F.; Klump, J. Exploring prediction uncertainty of spatial data in geostatistical and machine learning approaches. Environ. Earth Sci. 2019, 78, 38. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org (accessed on 17 December 2022).
- Kuhn, M. caret: Classification and Regression Training; R Package Version 6.0-93. 2022. Available online: https://CRAN.R-project.org/package=caret (accessed on 17 December 2022).
- Dowle, M.; Srinivasan, A. data.table: Extension of ‘data.frame’. R Package Version 1.14.4. 2022. Available online: https://CRAN.R-project.org/package=data.table (accessed on 17 December 2022).
- Pedersen, T.L. ggforce: Accelerating ‘ggplot2’. R Package Version 0.4.1. 2022. Available online: https://cran.r-project.org/package=ggforce (accessed on 17 December 2022).
- Pierce, D. ncdf4: Interface to Unidata netCDF (Version 4 or Earlier) Format Data Files. R Package Version 1.19. 2021. Available online: https://CRAN.R-project.org/package=ncdf4 (accessed on 17 December 2022).
- Bivand, R.S.; Keitt, T.; Rowlingson, B. rgdal: Bindings for the ‘Geospatial’ Data Abstraction Library. R Package Version 1.5-32. 2022. Available online: https://CRAN.R-project.org/package=rgdal (accessed on 17 December 2022).
- Pebesma, E. Simple features for R: Standardized support for spatial vector data. R J. 2018, 10, 439–446. [Google Scholar] [CrossRef] [Green Version]
- Pebesma, E. sf: Simple Features for R. R Package Version 1.0-8. 2022. Available online: https://CRAN.R-project.org/package=sf (accessed on 17 December 2022).
- Bivand, R.S. spdep: Spatial Dependence: Weighting Schemes, Statistics. R Package Version 1.2-7. 2022. Available online: https://CRAN.R-project.org/package=spdep (accessed on 17 December 2022).
- Bivand, R.S.; Wong, D.W.S. Comparing implementations of global and local indicators of spatial association. TEST 2018, 27, 716–748. [Google Scholar] [CrossRef]
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.D.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J.; et al. Welcome to the tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Wickham, H. tidyverse: Easily Install and Load the ‘Tidyverse’. R Package Version 1.3.2. 2022. Available online: https://CRAN.R-project.org/package=tidyverse (accessed on 17 December 2022).
- Rodriguez, P.P.; Gianola, D. brnn: Bayesian Regularization for Feed-Forward Neural Networks. R Package Version 0.9.2. 2022. Available online: https://CRAN.R-project.org/package=brnn (accessed on 17 December 2022).
- Milborrow, S. earth: Multivariate Adaptive Regression Splines. R Package Version 5.3.1. 2021. Available online: https://CRAN.R-project.org/package=earth (accessed on 17 December 2022).
- Greenwell, B.; Boehmke, B.; Cunningham, J. gbm: Generalized Boosted Regression Models. R Package Version 2.1.8.1. 2022. Available online: https://CRAN.R-project.org/package=gbm (accessed on 17 December 2022).
- Ripley, B.D. nnet: Feed-Forward Neural Networks and Multinomial Log-Linear Models. R Package Version 7.3-18. 2022. Available online: https://CRAN.R-project.org/package=nnet (accessed on 17 December 2022).
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002; ISBN 0-387-95457-0. [Google Scholar]
- Wright, M.N. ranger: A Fast Implementation of Random Forests. R Package Version 0.14.1. 2022. Available online: https://CRAN.R-project.org/package=ranger (accessed on 17 December 2022).
- Wright, M.N.; Ziegler, A. ranger: A fast implementation of random forests for high dimensional data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. xgboost: Extreme Gradient Boosting. R Package Version 1.6.0.1. 2022. Available online: https://CRAN.R-project.org/package=xgboost (accessed on 17 December 2022).
- Tyralis, H.; Papacharalampous, G. A review of probabilistic forecasting and prediction with machine learning. arXiv 2022, arXiv:2209.08307. Available online: https://arxiv.org/abs/2209.08307 (accessed on 17 December 2022).
- Tyralis, H.; Papacharalampous, G. scoringfunctions: A Collection of Scoring Functions for Assessing Point Forecasts. R Package Version 0.0.5. 2022. Available online: https://CRAN.R-project.org/package=scoringfunctions (accessed on 17 December 2022).
- Wickham, H.; Hester, J.; Chang, W.; Bryan, J. devtools: Tools to Make developing R Packages Easier. R Package Version 2.4.5. 2022. Available online: https://CRAN.R-project.org/package=devtools (accessed on 17 December 2022).
- Xie, Y. knitr: A Comprehensive Tool for Reproducible Research in R. In Implementing Reproducible Computational Research; Stodden, V., Leisch, F., Peng, R.D., Eds.; Chapman and Hall/CRC: London, UK, 2014. [Google Scholar]
- Xie, Y. Dynamic Documents with R and Knitr, 2nd ed.; Chapman and Hall/CRC: London, UK, 2015. [Google Scholar]
- Xie, Y. knitr: A General-Purpose Package for Dynamic Report Generation in R. R Package Version 1.40. 2022. Available online: https://CRAN.R-project.org/package=knitr (accessed on 17 December 2022).
- Allaire, J.J.; Xie, Y.; McPherson, J.; Luraschi, J.; Ushey, K.; Atkins, A.; Wickham, H.; Cheng, J.; Chang, W.; Iannone, R.; et al. rmarkdown: Dynamic Documents for R. R Package Version 2.17. 2022. Available online: https://CRAN.R-project.org/package=rmarkdown (accessed on 17 December 2022).
- Xie, Y.; Allaire, J.J.; Grolemund, G. R Markdown: The Definitive Guide; Chapman and Hall/CRC: London, UK, 2018; ISBN 9781138359338. Available online: https://bookdown.org/yihui/rmarkdown (accessed on 17 December 2022).
- Xie, Y.; Dervieux, C.; Riederer, E. R Markdown Cookbook; Chapman and Hall/CRC: London, UK, 2020; ISBN 9780367563837. Available online: https://bookdown.org/yihui/rmarkdown-cookbook (accessed on 17 December 2022).
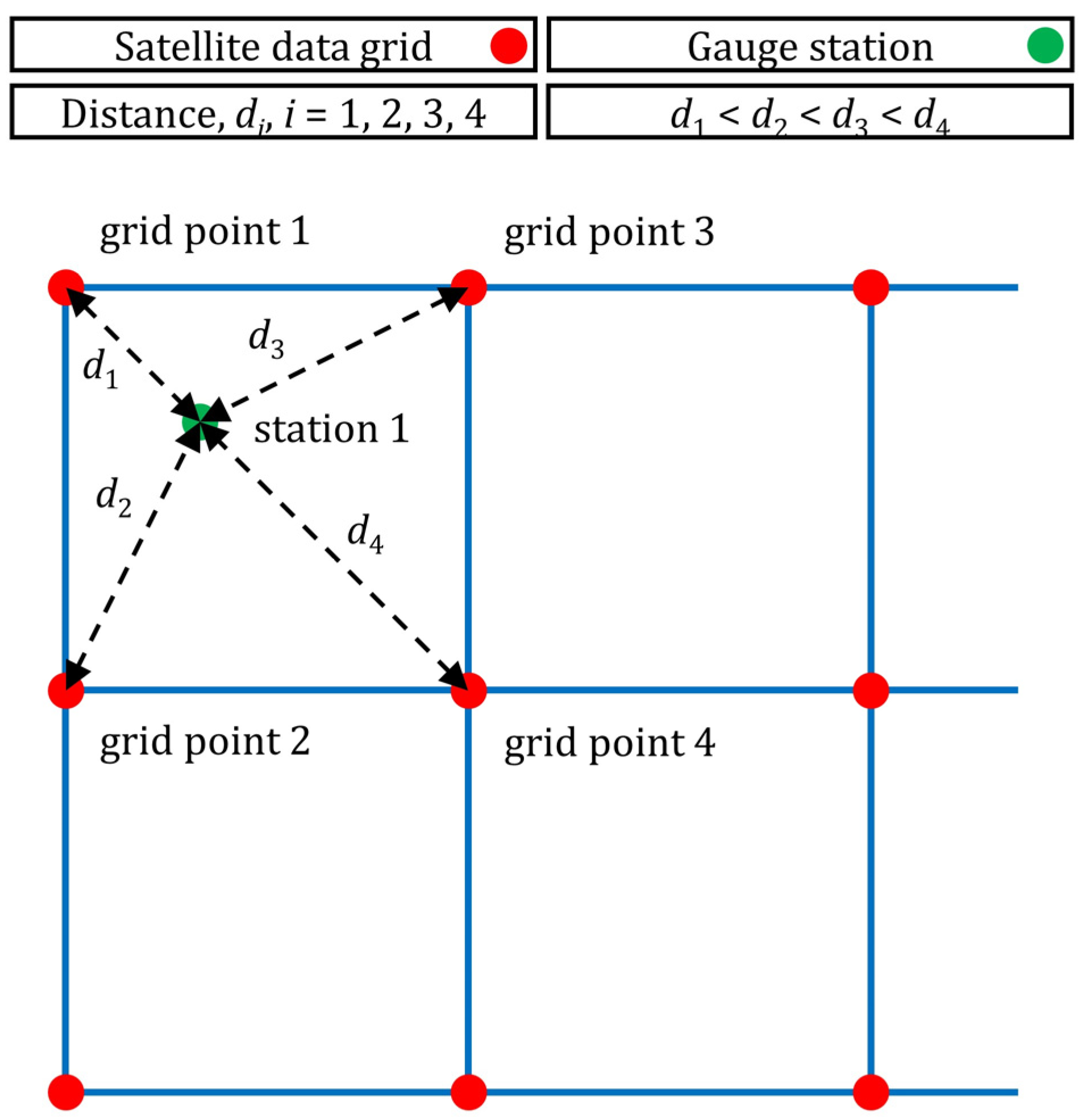
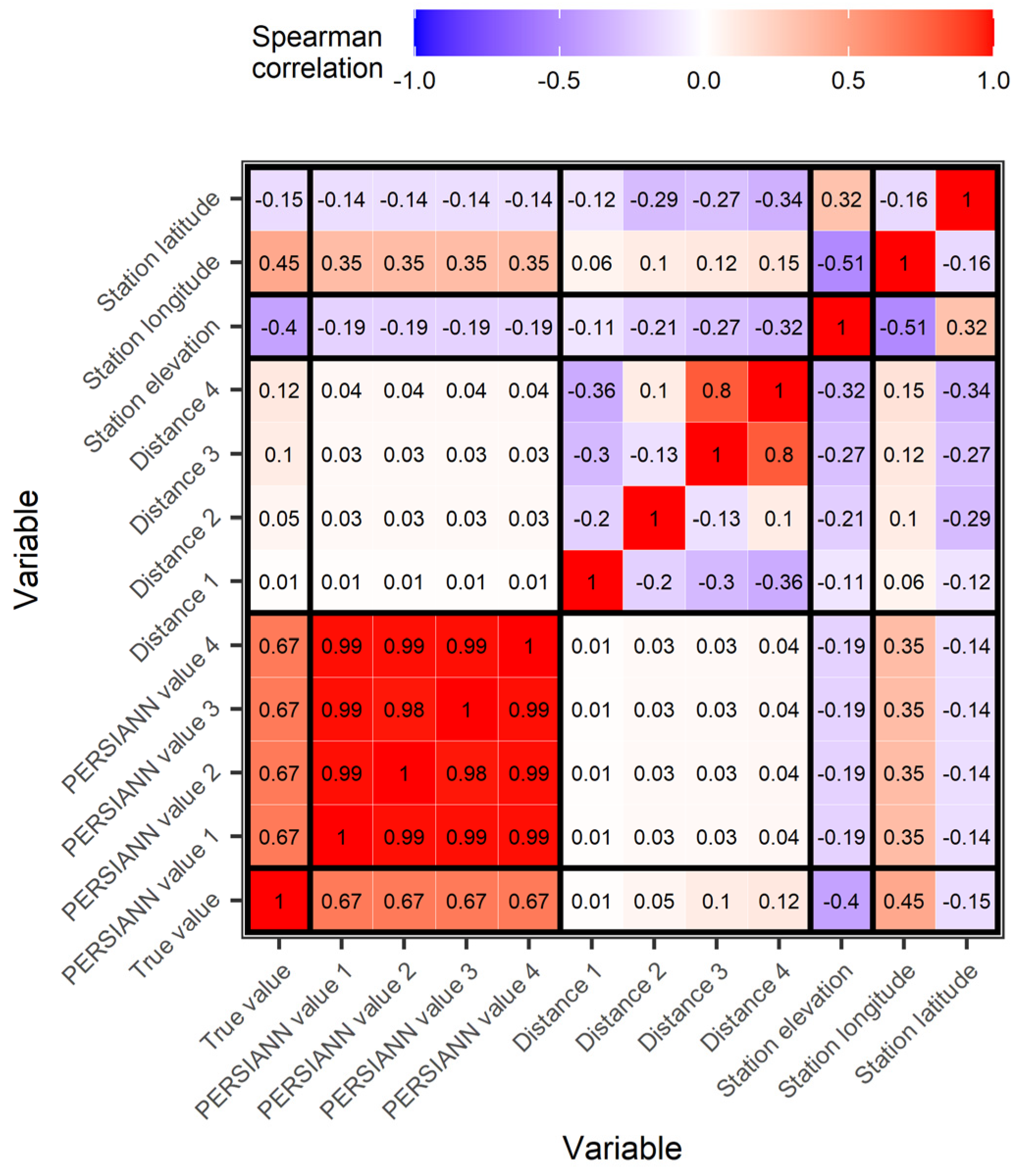
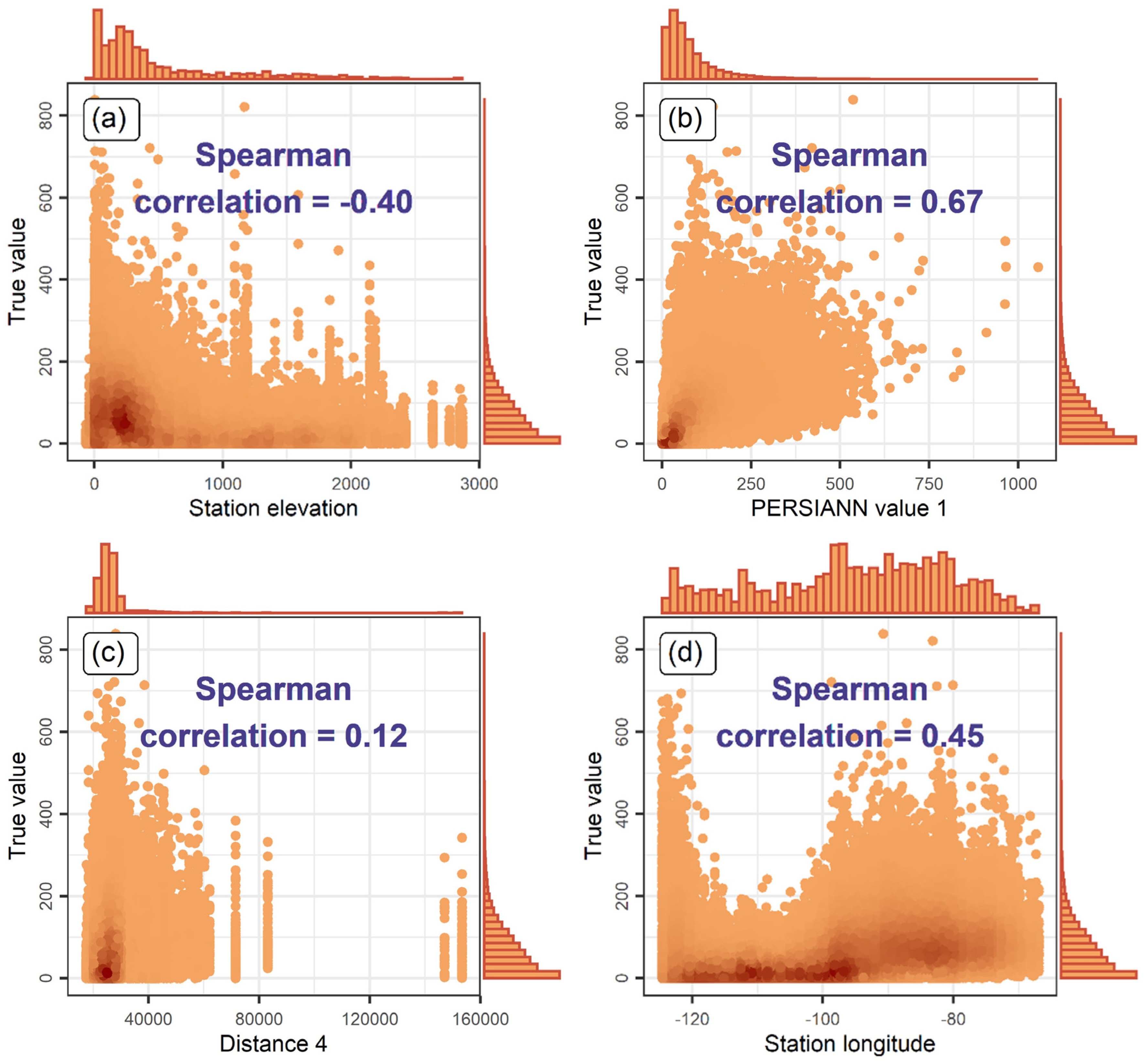

| Study | Time Scale | Spatial Scale | Algorithms |
|---|---|---|---|
| He et al. [13] | Hourly | South-western, central, north-eastern and south-eastern United States | Random forests |
| Meyer et al. [14] | Daily | Germany | Random forests, artificial neural networks, support vector regression |
| Tao et al. [15] | Daily | Central United States | Deep learning |
| Yang et al. [16] | Daily | Chile | Quantile mapping |
| Baez-Villanueva et al. [17] | Daily | Chile | Random forests |
| Chen et al. [18] | Daily | Dallas–Fort Worth in the United States | Deep learning |
| Chen et al. [19] | Daily | Xijiang basin in China | Geographically weighted ridge regression |
| Rata et al. [20] | Annual | Chéliff watershed in Algeria | Kriging |
| Chen et al. [21] | Monthly | Sichuan Province in China | Artificial neural networks, geographically weighted regression, kriging, random forests |
| Nguyen et al. [22] | Daily | South Korea | Random forests |
| Shen and Yong [23] | Annual | China | Gradient boosting decision trees, random forests, support vector regression |
| Zhang et al. [24] | Daily | China | Artificial neural networks, extreme learning machines, random forests, support vector regression |
| Chen et al. [25] | Daily | Coastal mountain region in the western United States | Deep learning |
| Fernandez-Palomino et al. [26] | Daily | Ecuador and Peru | Random forests |
| Lin et al. [27] | Daily | Three Gorges Reservoir area in China | Adaptive boosting decision trees, decision trees, random forests |
| Yang et al. [28] | Daily | Kelantan river basin in Malaysia | Deep learning |
| Zandi et al. [29] | Monthly | Alborz and Zagros mountain ranges in Iran | Artificial neural networks, locally weighted linear regression, random forests, stacked generalization, support vector regression |
| Militino et al. [30] | Daily | Navarre in Spain | K-nearest neighbors, random forests, artificial neural networks |
| Present study | Monthly | Contiguous United States | Linear regression, multivariate adaptive regression splines, multivariate adaptive polynomial splines, random forests, gradient boosting machines, extreme gradient boosting, feed-forward neural networks, feed-forward neural networks with Bayesian regularization |
| Predictor Variable | Predictor Set 1 | Predictor Set 2 | Predictor Set 3 |
|---|---|---|---|
| PERSIANN value 1 | ✔ | ✔ | ✔ |
| PERSIANN value 2 | ✔ | ✔ | ✔ |
| PERSIANN value 3 | ✔ | ✔ | ✔ |
| PERSIANN value 4 | ✔ | ✔ | ✔ |
| Distance 1 | × | ✔ | ✔ |
| Distance 2 | × | ✔ | ✔ |
| Distance 3 | × | ✔ | ✔ |
| Distance 4 | × | ✔ | ✔ |
| Station elevation | ✔ | ✔ | ✔ |
| Station longitude | × | × | ✔ |
| Station latitude | × | × | ✔ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papacharalampous, G.; Tyralis, H.; Doulamis, A.; Doulamis, N. Comparison of Machine Learning Algorithms for Merging Gridded Satellite and Earth-Observed Precipitation Data. Water 2023, 15, 634. https://doi.org/10.3390/w15040634
Papacharalampous G, Tyralis H, Doulamis A, Doulamis N. Comparison of Machine Learning Algorithms for Merging Gridded Satellite and Earth-Observed Precipitation Data. Water. 2023; 15(4):634. https://doi.org/10.3390/w15040634
Chicago/Turabian StylePapacharalampous, Georgia, Hristos Tyralis, Anastasios Doulamis, and Nikolaos Doulamis. 2023. "Comparison of Machine Learning Algorithms for Merging Gridded Satellite and Earth-Observed Precipitation Data" Water 15, no. 4: 634. https://doi.org/10.3390/w15040634






