An Interpretable Recurrent Neural Network for Waterflooding Reservoir Flow Disequilibrium Analysis
Abstract
:1. Introduction
2. Methodology
2.1. Material Balance Equation of the Waterflooding Reservoir
2.2. Development of the Interpretable Recurrent Neural Network
| Algorithm 1: The training pseudocode for IRNN. | |
| Input:WIRs, water injection rates; BHPI and BHPP, BHP data of the injectors and producers, respectively Output: Estimated liquid production rates, | |
| 1 | / Start training / |
| 2 | While stop criteria is not met |
| 3 | / Drainage module computation / |
| Calculate the fluid change rate among the drainage volume, according to Equation (9); | |
| 4 | / Inflow module computation / |
| Calculate the total inflow rates for Q producers, according to Equation (12); | |
| 5 | / Modeled liquid production rates computation / |
| Calculate the modeled liquid production rates, , according to Equation (13); | |
| 6 | / Loss evaluation / |
| Compute the total loss of IRNN, , using Equation (14); | |
| 7 | / Model parameters optimization / |
| Optimize weight matrices and the independent variables of Equation (10). | |
| 8 | End while |
| 9 | / End training / |
3. Results and Discussion
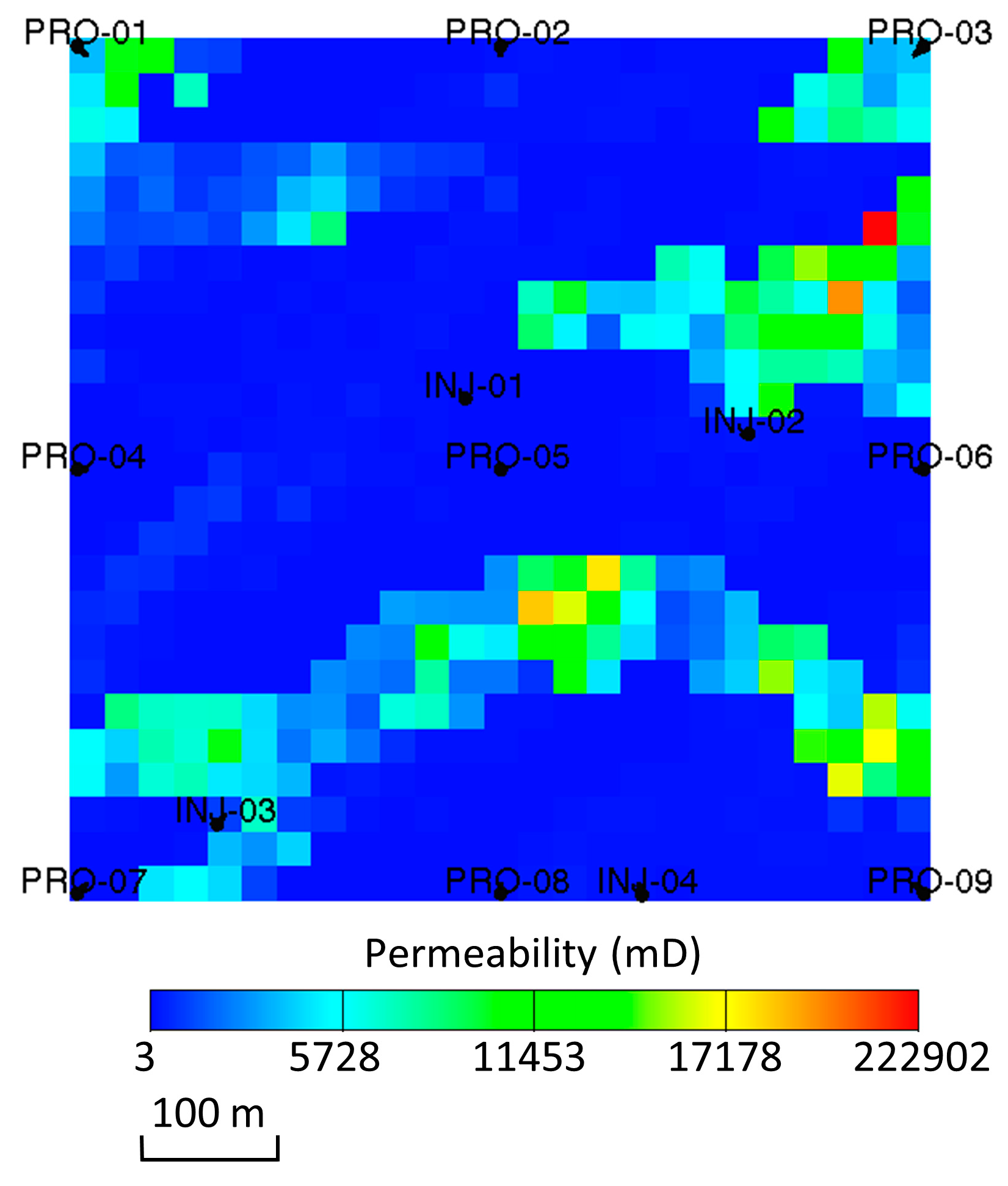
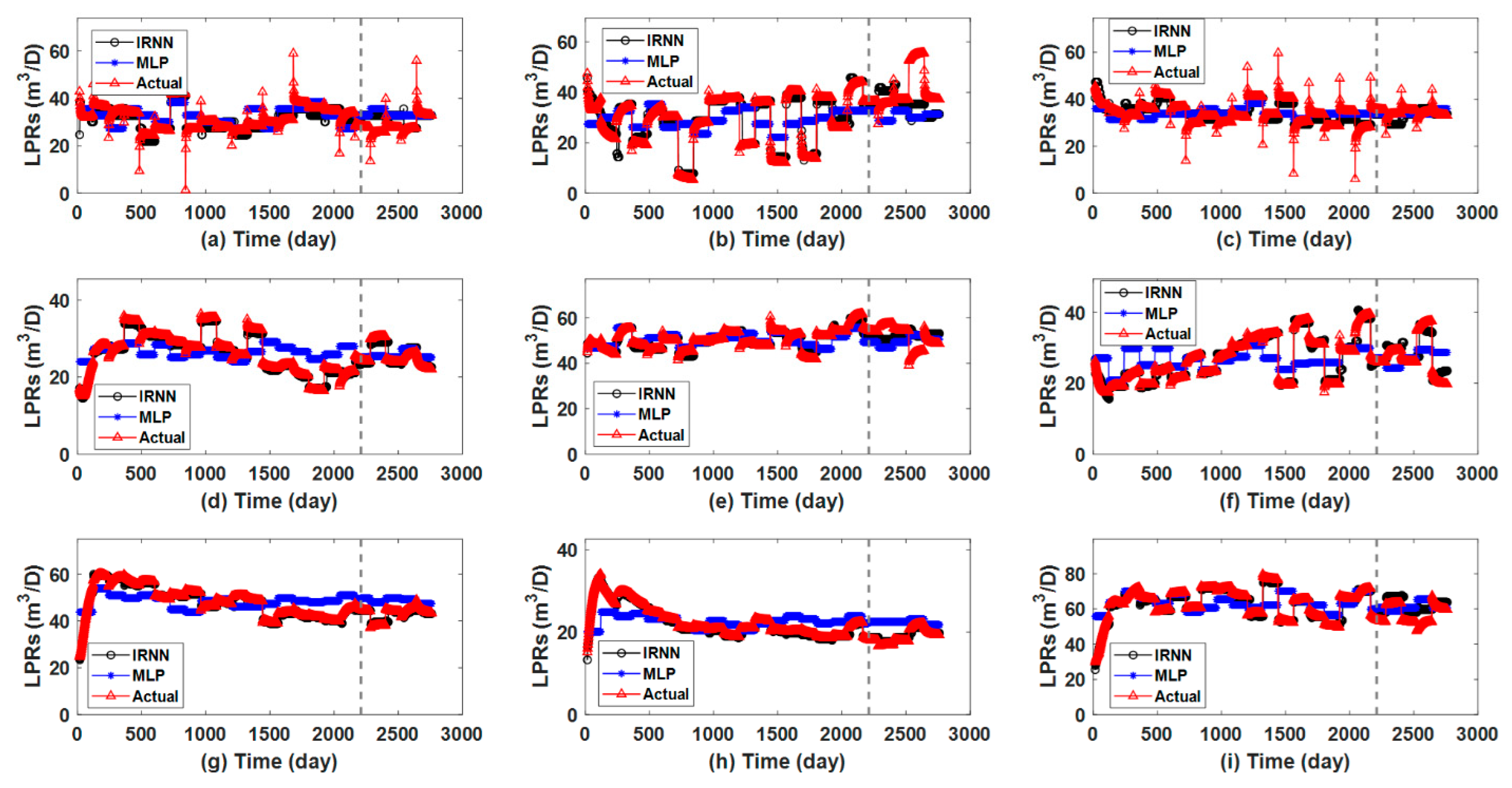
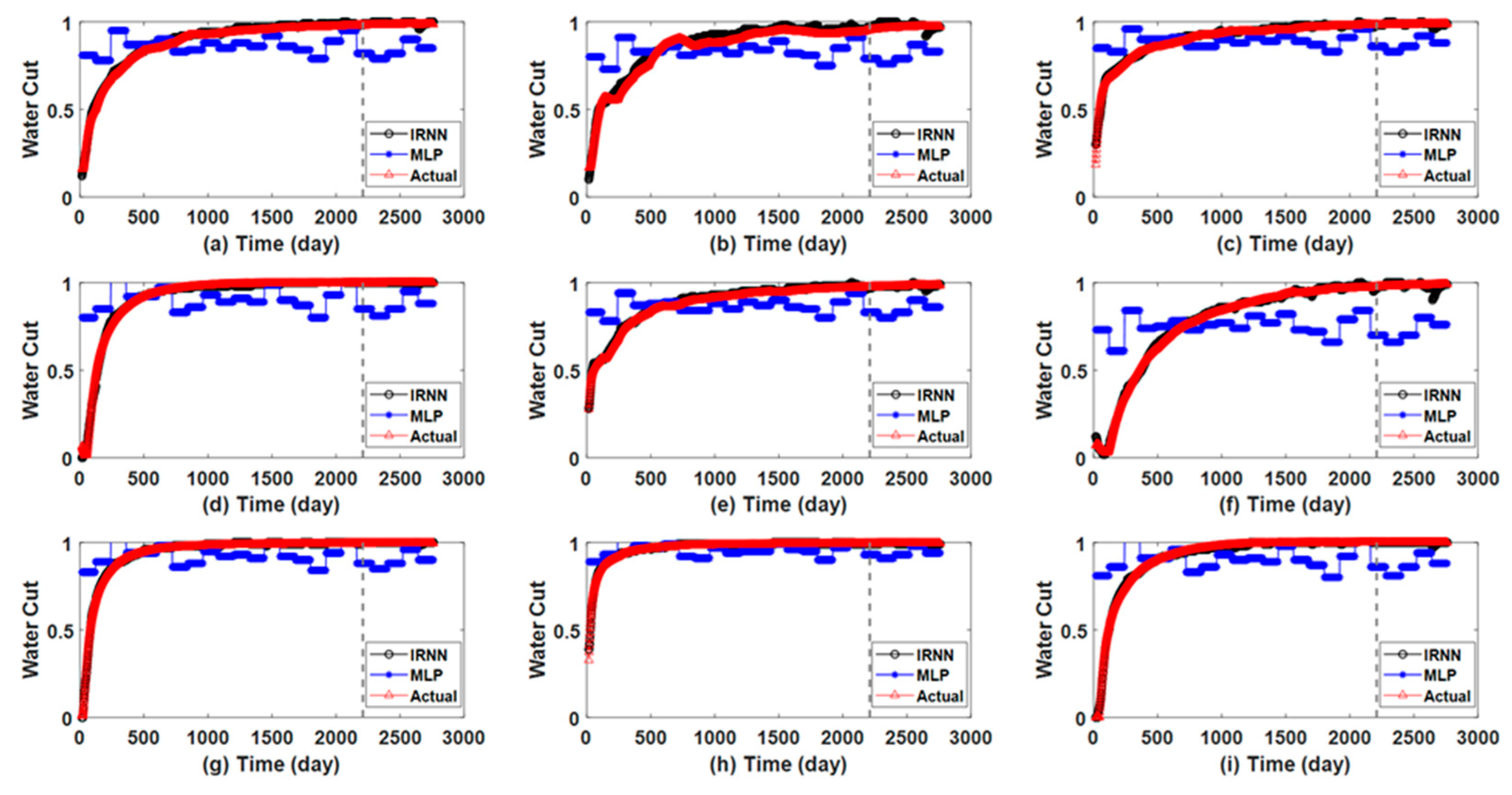
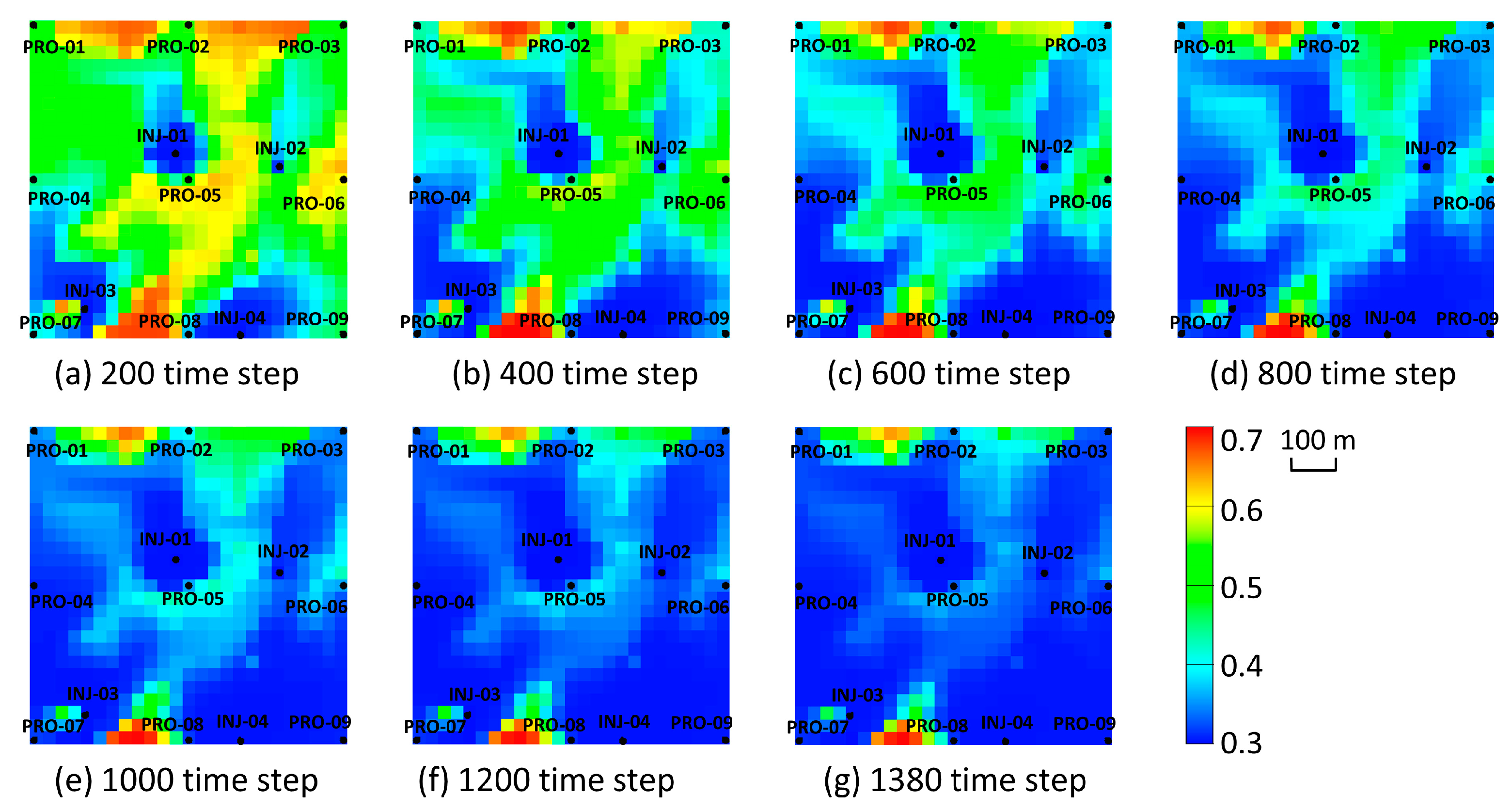
3.1. Three-Channel Model
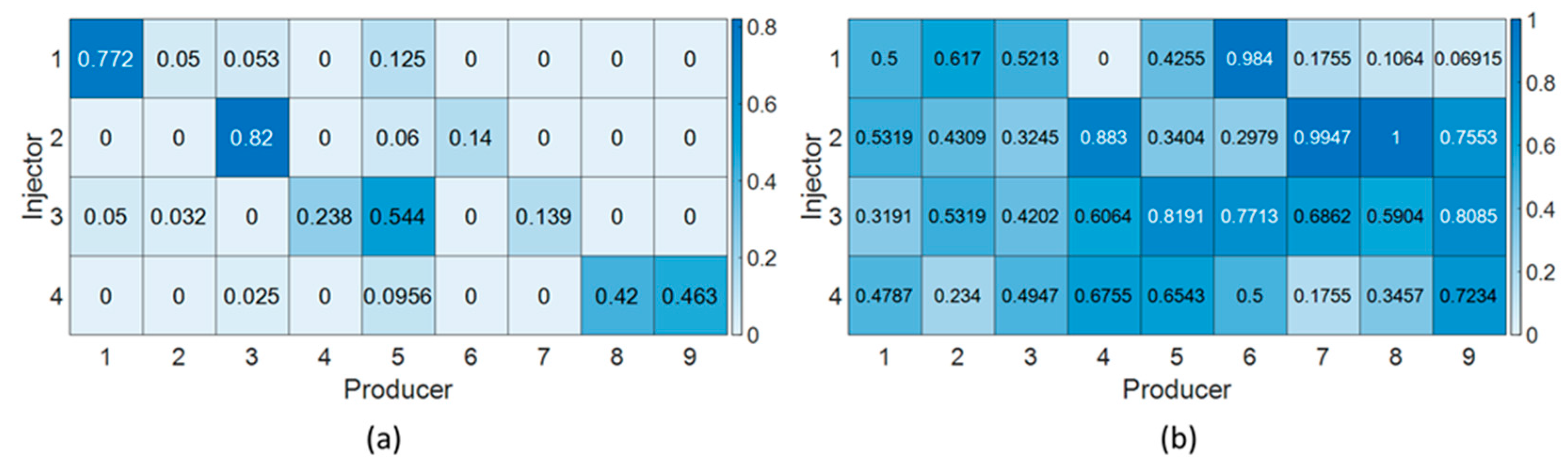
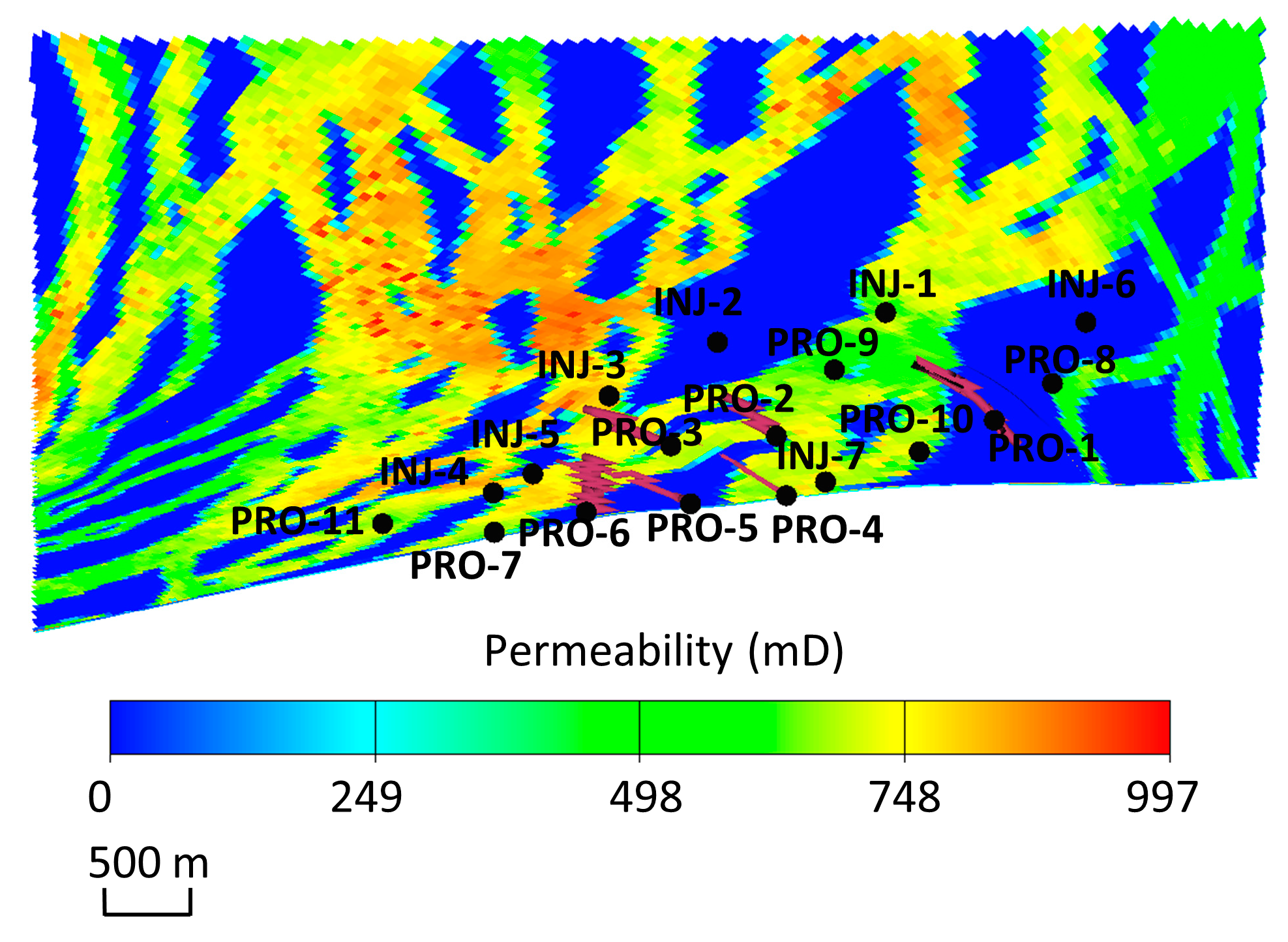
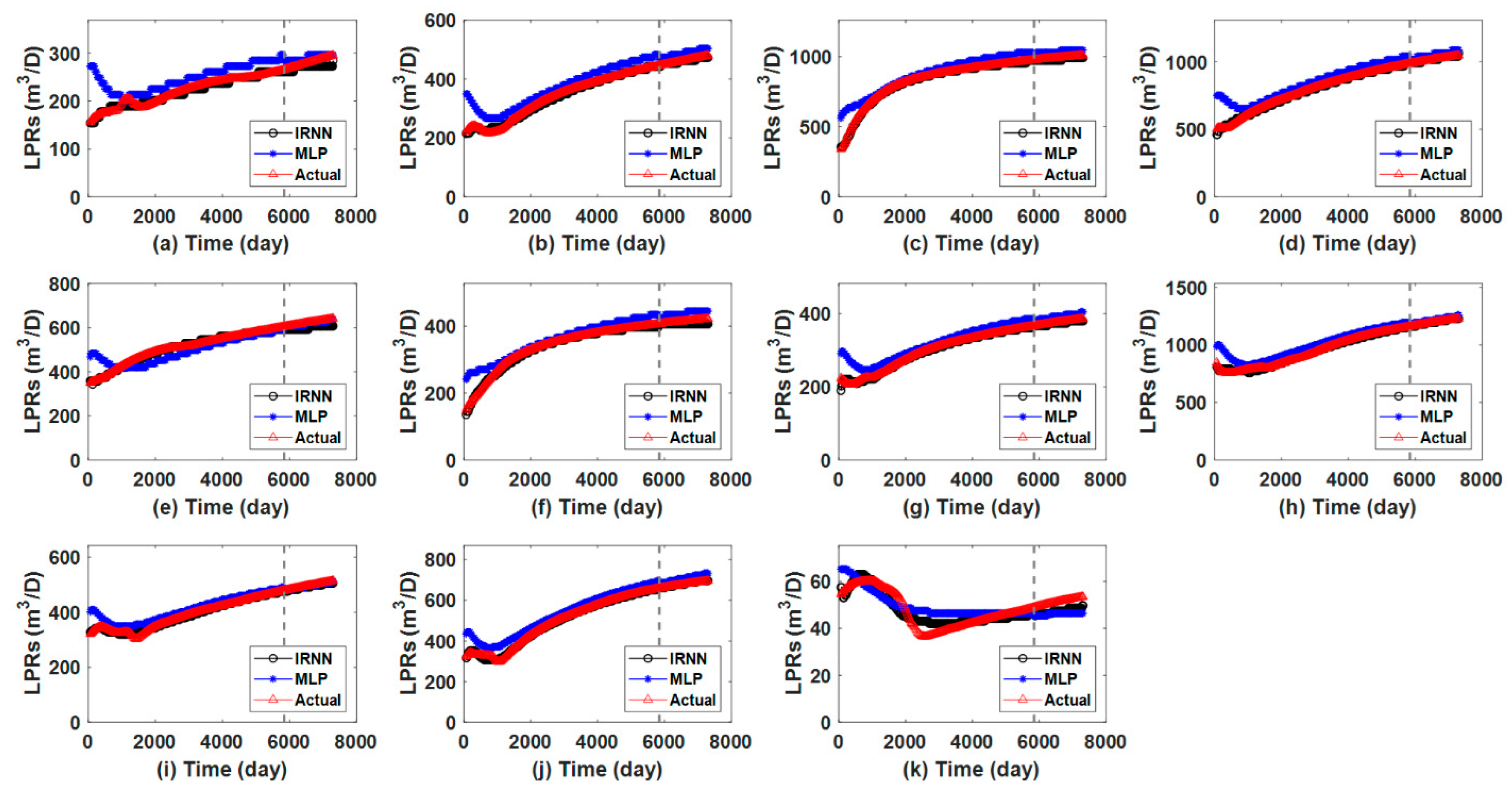
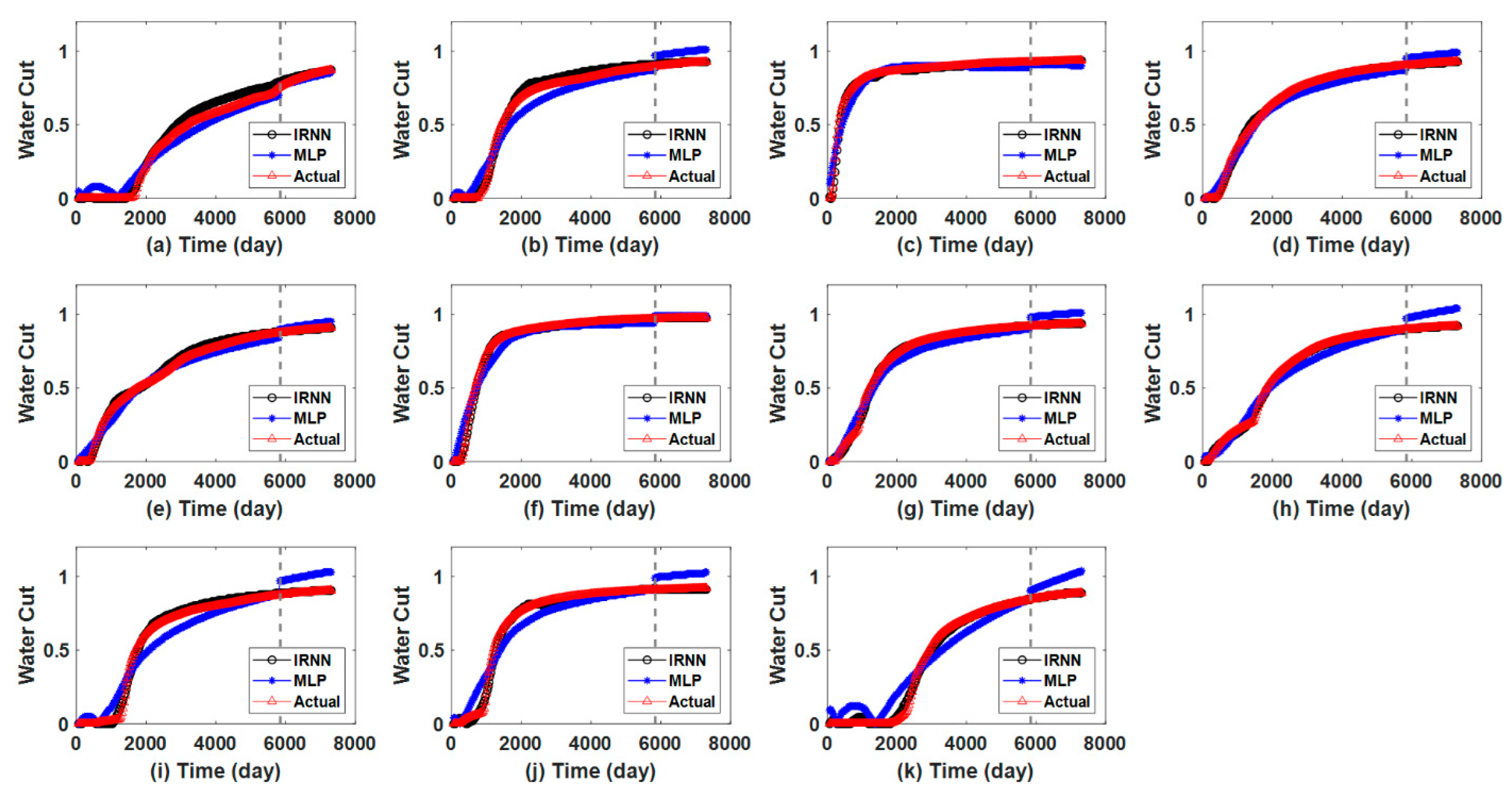
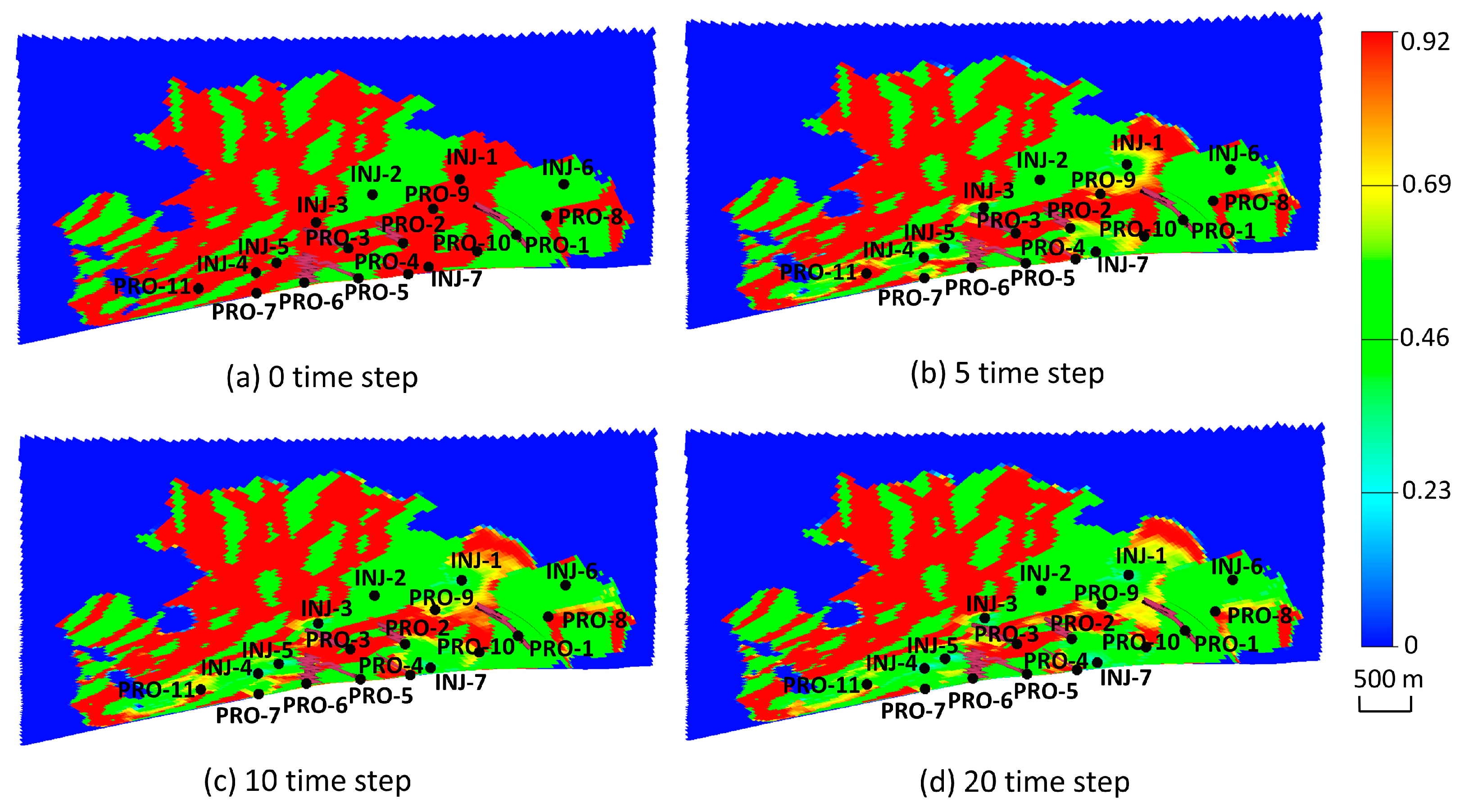
3.2. Olympus Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, J.; Zhan, S.; Wang, W.; Su, Y.; Wang, H. Molecular dynamics simulations of two-phase flow of n-alkanes with water in quartz nanopores. Chem. Eng. J. 2022, 430, 132800. [Google Scholar] [CrossRef]
- Li, W.; Nan, Y.; Wen, X.; Wang, W.; Jin, Z. Effects of Salinity and N-, S-, and O-Bearing Polar Components on Light Oil–Brine Interfacial Properties from Molecular Perspectives. J. Phys. Chem. C 2019, 123, 23520–23528. [Google Scholar] [CrossRef]
- Sheng, G.; Su, Y.; Wang, W. A new fractal approach for describing induced-fracture porosity/permeability/ compressibility in stimulated unconventional reservoirs. J. Pet. Sci. Eng. 2019, 179, 855–866. [Google Scholar] [CrossRef]
- Wang, W.; Fan, D.; Sheng, G.; Chen, Z.; Su, Y. A review of analytical and semi-analytical fluid flow models for ultra-tight hydrocarbon reservoirs. Fuel 2019, 256, 115737. [Google Scholar] [CrossRef]
- Cai, J.; Jin, T.; Kou, J.; Zou, S.; Xiao, J.; Meng, Q. Lucas–Washburn Equation-Based Modeling of Capillary-Driven Flow in Porous Systems. Langmuir 2021, 37, 1623–1636. [Google Scholar] [CrossRef]
- Chen, G.; Li, Y.; Zhang, K.; Xue, X.; Wang, J.; Luo, Q.; Yao, C.; Yao, J. Efficient hierarchical surrogate-assisted differential evolution for high-dimensional expensive optimization. Inf. Sci. 2021, 542, 228–246. [Google Scholar] [CrossRef]
- Yousef, A.A.; Gentil, P.H.; Jensen, J.L.; Lake, L.W. A Capacitance Model To Infer Interwell Connectivity From Production and Injection Rate Fluctuations. SPE Reserv. Eval. Eng. 2006, 9, 630–646. [Google Scholar] [CrossRef]
- Naudomsup, N.; Lake, L.W. Extension of Capacitance/Resistance Model to Tracer Flow for Determining Reservoir Properties. SPE Reserv. Eval. Eng. 2018, 22, 266–281. [Google Scholar] [CrossRef]
- Temizel, C.; Artun, E.; Yang, Z. Improving Oil-Rate Estimate in Capacitance/Resistance Modeling Using the Y-Function Method for Reservoirs Under Waterflood. SPE Reserv. Eval. Eng. 2019, 22, 1161–1171. [Google Scholar] [CrossRef]
- Gubanova, A.; Orlov, D.; Koroteev, D.; Shmidt, S. Proxy Capacitance-Resistance Modeling for Well Production Forecasts in Case of Well Treatments. SPE J. 2022, 27, 3474–3488. [Google Scholar] [CrossRef]
- Arouri, Y.; Lake, L.W.; Sayyafzadeh, M. Bilevel Optimization of Well Placement and Control Settings Assisted by Capacitance-Resistance Models. SPE J. 2022, 27, 3829–3848. [Google Scholar] [CrossRef]
- Zhao, H.; Kang, Z.; Zhang, X.; Sun, H.; Cao, L.; Reynolds, A.C. INSIM: A Data-Driven Model for History Matching and Prediction for Waterflooding Monitoring and Management with a Field Application. In Proceedings of the SPE Reservoir Simulation Symposium, Houston, TX, USA, 23 February 2015. [Google Scholar]
- Guo, Z.; Chen, C.; Gao, G.; Vink, J. Enhancing the Performance of the Distributed Gauss-Newton Optimization Method by Reducing the Effect of Numerical Noise and Truncation Error With Support-Vector Regression. SPE J. 2018, 23, 2428–2443. [Google Scholar] [CrossRef]
- Zhang, Y.; He, J.; Yang, C.; Xie, J.; Fitzmorris, R.; Wen, X.-H. A Physics-Based Data-Driven Model for History Matching, Prediction, and Characterization of Unconventional Reservoirs. SPE J. 2018, 23, 1105–1125. [Google Scholar] [CrossRef]
- Guo, Z.; Reynolds, A.C. INSIM-FT-3D: A Three-Dimensional Data-Driven Model for History Matching and Waterflooding Optimization. In Proceedings of the SPE Reservoir Simulation Conference, Society of Petroleum Engineers, Galveston, TX, USA, 20–22 February 2019; p. SPE–193841-MS. [Google Scholar]
- Li, Y.; Onur, M. INSIM-BHP: A physics-based data-driven reservoir model for history matching and forecasting with bottomhole pressure and production rate data under waterflooding. J. Comput. Phys. 2023, 473, 111714. [Google Scholar] [CrossRef]
- Artun, E. Characterizing interwell connectivity in waterflooded reservoirs using data-driven and reduced-physics models: A comparative study. Neural Comput. Appl. 2017, 28, 1729–1743. [Google Scholar] [CrossRef]
- Jensen, J. Comment on “Characterizing interwell connectivity in waterflooded reservoirs using data-driven and reduced-physics models: A comparative study” by E. Artun DOI 10.1007/s00521-015-2152-0. Neural Comput. Appl. 2016, 28, 1–2. [Google Scholar] [CrossRef]
- Mo, S.; Zhu, Y.; Zabaras, N.; Shi, X.; Wu, J. Deep Convolutional Encoder-Decoder Networks for Uncertainty Quantification of Dynamic Multiphase Flow in Heterogeneous Media. Water Resour. Res. 2019, 55, 703–728. [Google Scholar] [CrossRef]
- Carpenter, C. Machine Learning Improves Accuracy of Virtual Flowmetering and Back-Allocation. J. Pet. Technol. 2019, 71, 77–78. [Google Scholar] [CrossRef]
- Zhang, Z.; He, X.; AlSinan, M.; Kwak, H.; Hoteit, H. Robust Method for Reservoir Simulation History Matching Using Bayesian Inversion and Long-Short-Term Memory Network-Based Proxy. SPE J. 2022, 1–25. [Google Scholar] [CrossRef]
- Chakraborty, R.; Pal, N.R. Feature Selection Using a Neural Framework With Controlled Redundancy. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 35–50. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, K.; Xue, X.; Zhang, L.; Yao, J.; Sun, H.; Fan, L.; Yang, Y. Surrogate-assisted evolutionary algorithm with dimensionality reduction method for water flooding production optimization. J. Pet. Sci. Eng. 2020, 185, 106633. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, K.; Zhang, L.; Xue, X.; Ji, D.; Yao, C.; Yao, J.; Yang, Y. Global and Local Surrogate-Model-Assisted Differential Evolution for Waterflooding Production Optimization. SPE J. 2020, 25, 105–118. [Google Scholar] [CrossRef]
- Fonseca, R.-M.; Rossa, E.; Emerick, A.; Hanea, R.G.; Jansen, J.-D. Overview Of The Olympus Field Development Optimization Challenge. In Proceedings of the 16th European Conference on the Mathematics of Oil Recovery, ECMOR 2018, Barcelona, Spain, 3–6 September 2018. [Google Scholar]


| Hyperparameter | IRNN |
|---|---|
| Hidden nodes of GRU block | 15 |
| Hidden nodes of queries, keys, and values of self-attention block | 10 |
| Hidden nodes of fully connected layer | 15 |
| Batch size | 10 |
| Initial learning rate | 0.03 |
| Coefficient of regularization item | 0.02 |
| Reservoir Properties | Values |
|---|---|
| Model scale | 25 × 25 × 1 |
| Grid size | 100 × 100 × 10 ft |
| Depth | 4800 ft |
| Initial pressure | 4000 psi |
| Initial temperature | 100 °C |
| Pore compressibility | 6.9 × 10−5 psi−1 |
| Porosity | 0.20 |
| Initial oil saturation | 0.80 |
| Oil density | 900 kg/m3 |
| Oil viscosity | 2.2 cP |
| Water density | 1000 kg/m3 |
| Water viscosity | 0.5 cP |
| MLP | IRNN | |
|---|---|---|
| History matching error of LPRs | 0.0933 | 0.0124 |
| Prediction error of LPRs | 0.2465 | 0.0203 |
| History matching error of water cut | 0.0242 | 0.0017 |
| Prediction error of water cut | 0.0225 | 4.9051 × 10−4 |
| Training time of LPRs | 24.1563 s | 208.9531 s |
| Training time of water cut | 16.3875 s | 170.5313 s |
| MLP | IRNN | |
|---|---|---|
| History matching error of LPRs | 0.0272 | 0.0066 |
| Prediction error of LPRs | 0.0320 | 1.4986 × 10−4 |
| History matching error of water cut | 0.0137 | 0.0012 |
| Prediction error of water cut | 0.0054 | 1.4271 × 10−4 |
| Training time of LPRs | 3.9843 s | 71.5156 s |
| Training time of water cut | 3.0625 s | 64.9062 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Shen, W.; Zhang, H.; Zhang, K.; Wang, J.; Zhang, L. An Interpretable Recurrent Neural Network for Waterflooding Reservoir Flow Disequilibrium Analysis. Water 2023, 15, 623. https://doi.org/10.3390/w15040623
Jiang Y, Shen W, Zhang H, Zhang K, Wang J, Zhang L. An Interpretable Recurrent Neural Network for Waterflooding Reservoir Flow Disequilibrium Analysis. Water. 2023; 15(4):623. https://doi.org/10.3390/w15040623
Chicago/Turabian StyleJiang, Yunqi, Wenjuan Shen, Huaqing Zhang, Kai Zhang, Jian Wang, and Liming Zhang. 2023. "An Interpretable Recurrent Neural Network for Waterflooding Reservoir Flow Disequilibrium Analysis" Water 15, no. 4: 623. https://doi.org/10.3390/w15040623





