Credal-Decision-Tree-Based Ensembles for Spatial Prediction of Landslides
Abstract
:1. Introduction
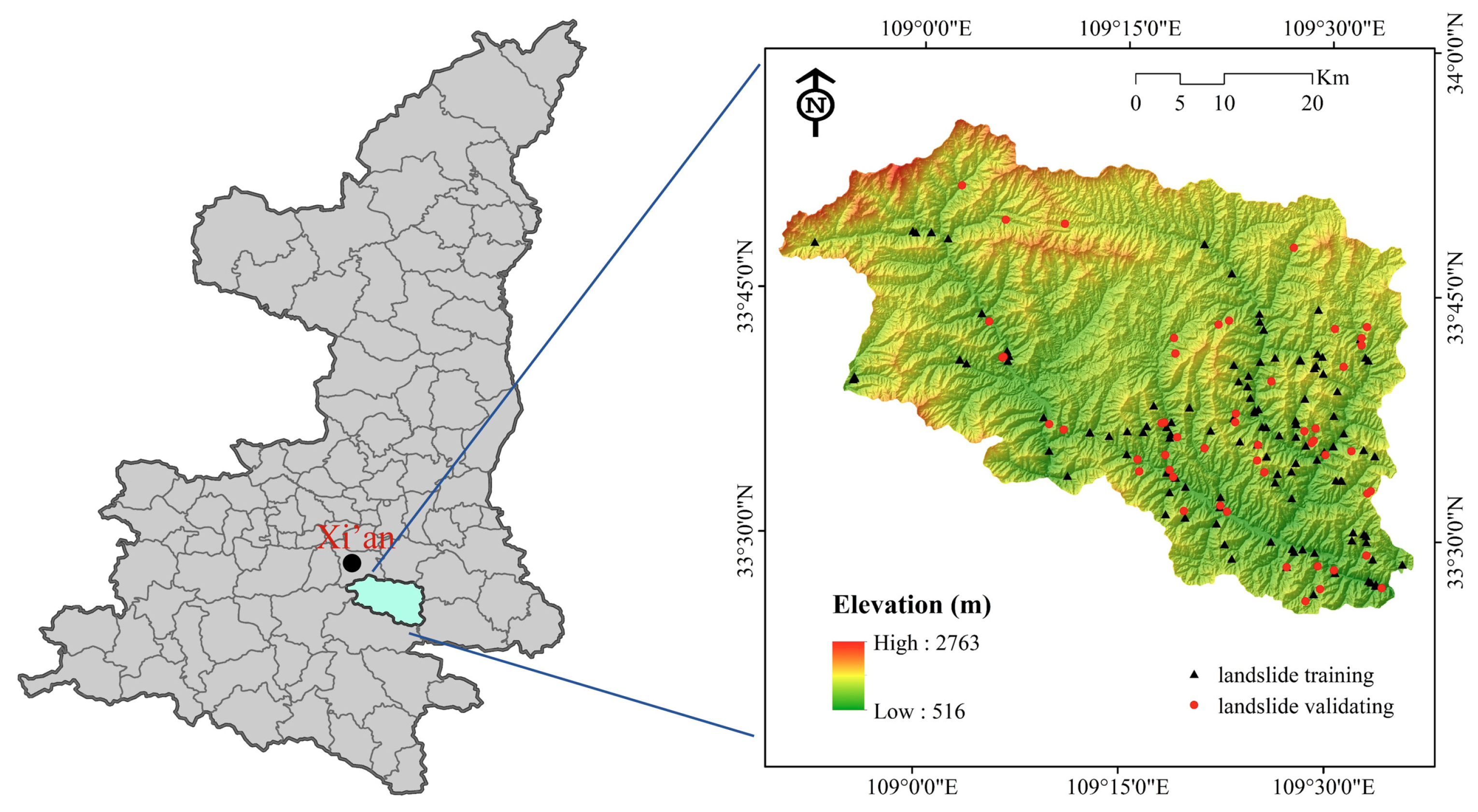
2. Study Area
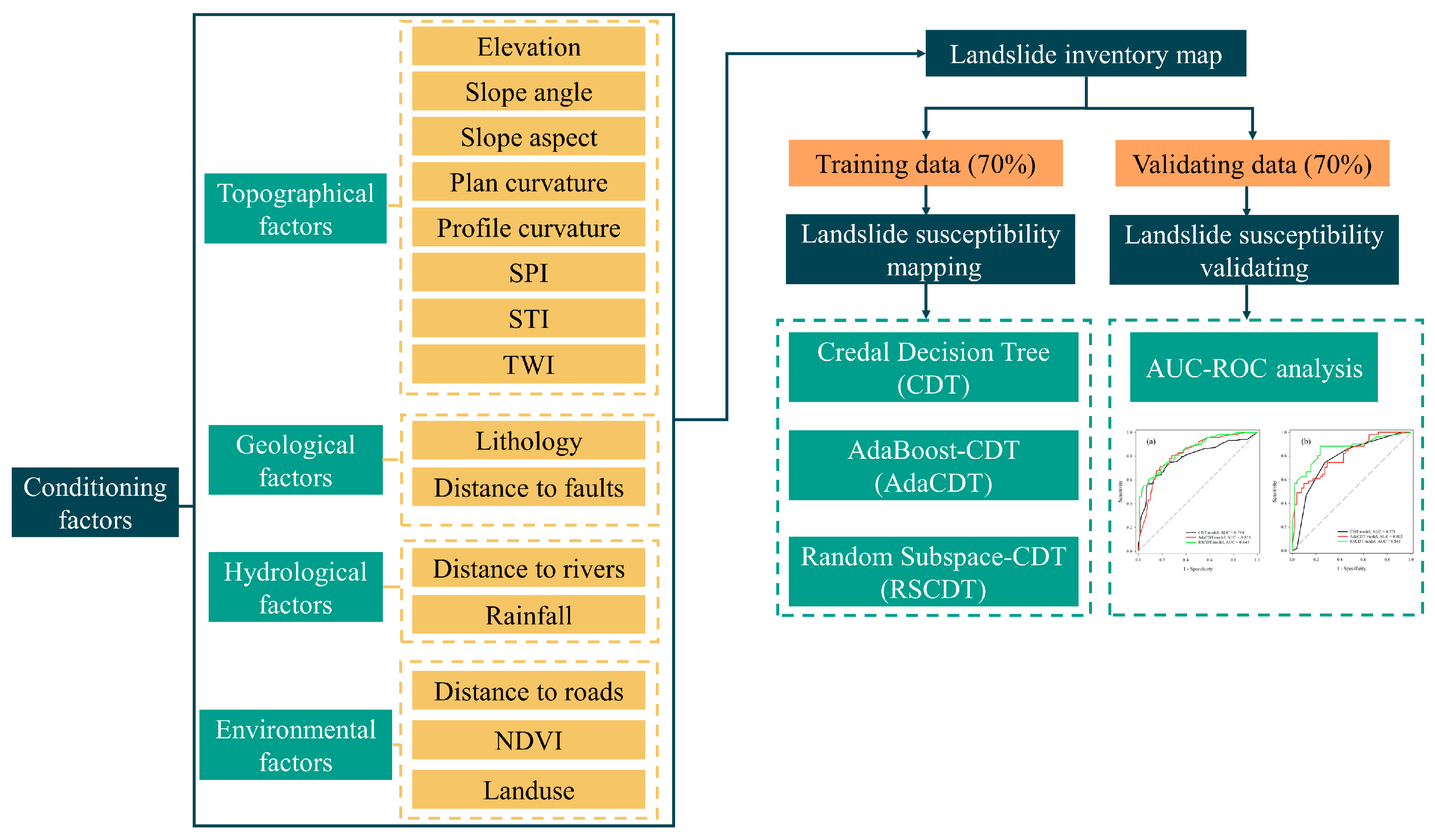
3. Methodology
3.1. Landslide Inventory Map
3.2. Landslide Conditioning Factors
3.3. Modeling Approaches
3.3.1. Credal Decision Tree
3.3.2. AdaBoost
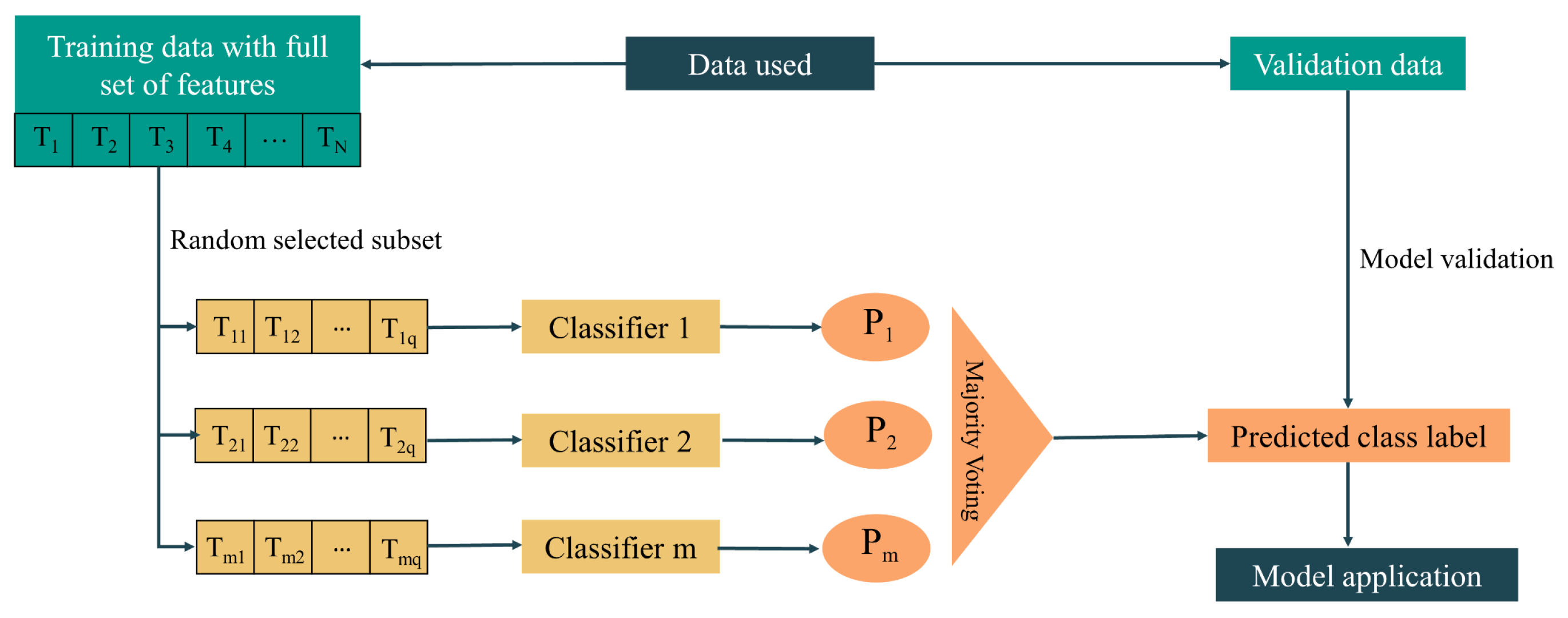
3.3.3. Random Subspace (RS)
4. Results
4.1. Correlation Analysis between Landslide and Conditioning Factors Using Frequency Ratio Method
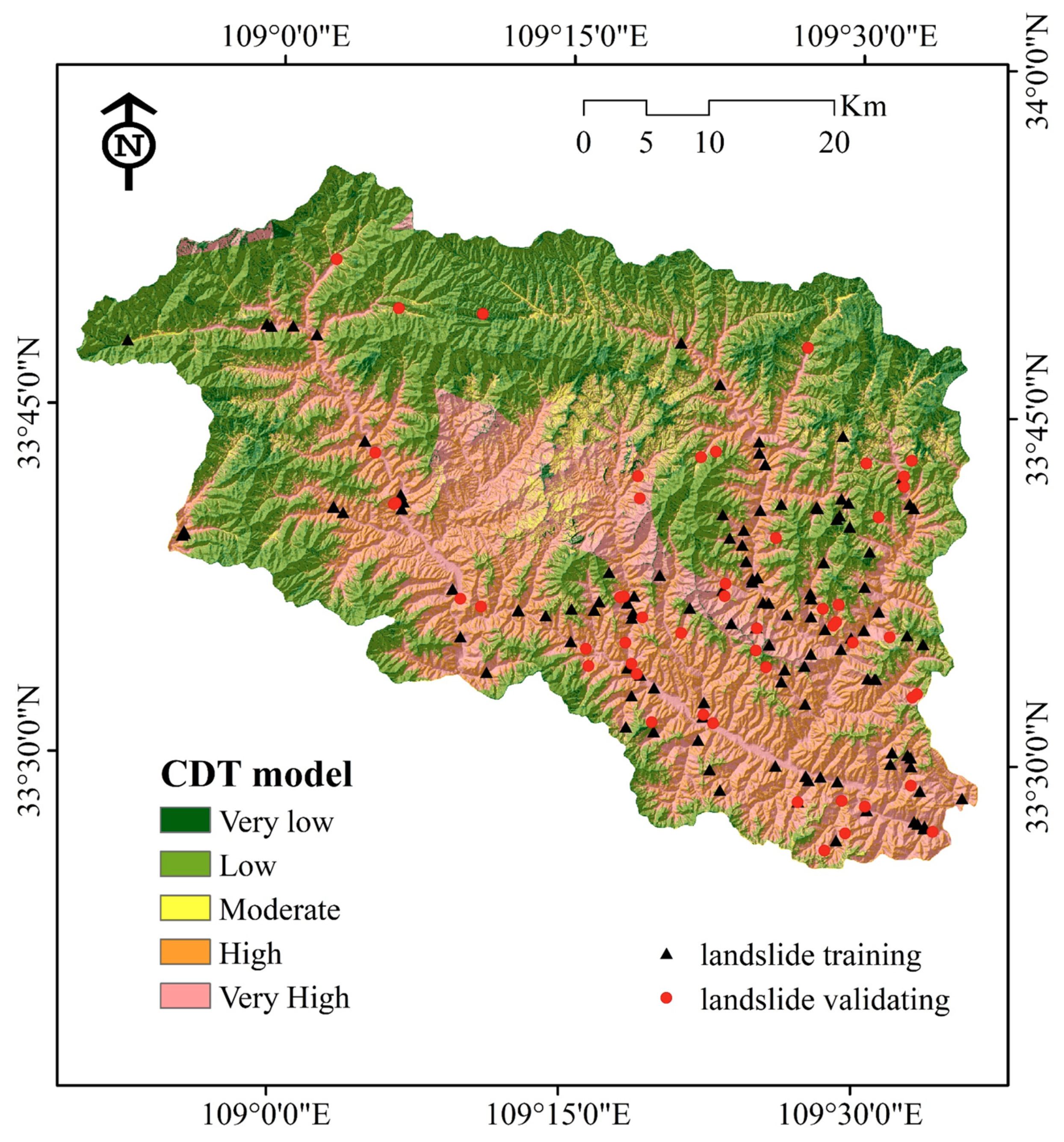
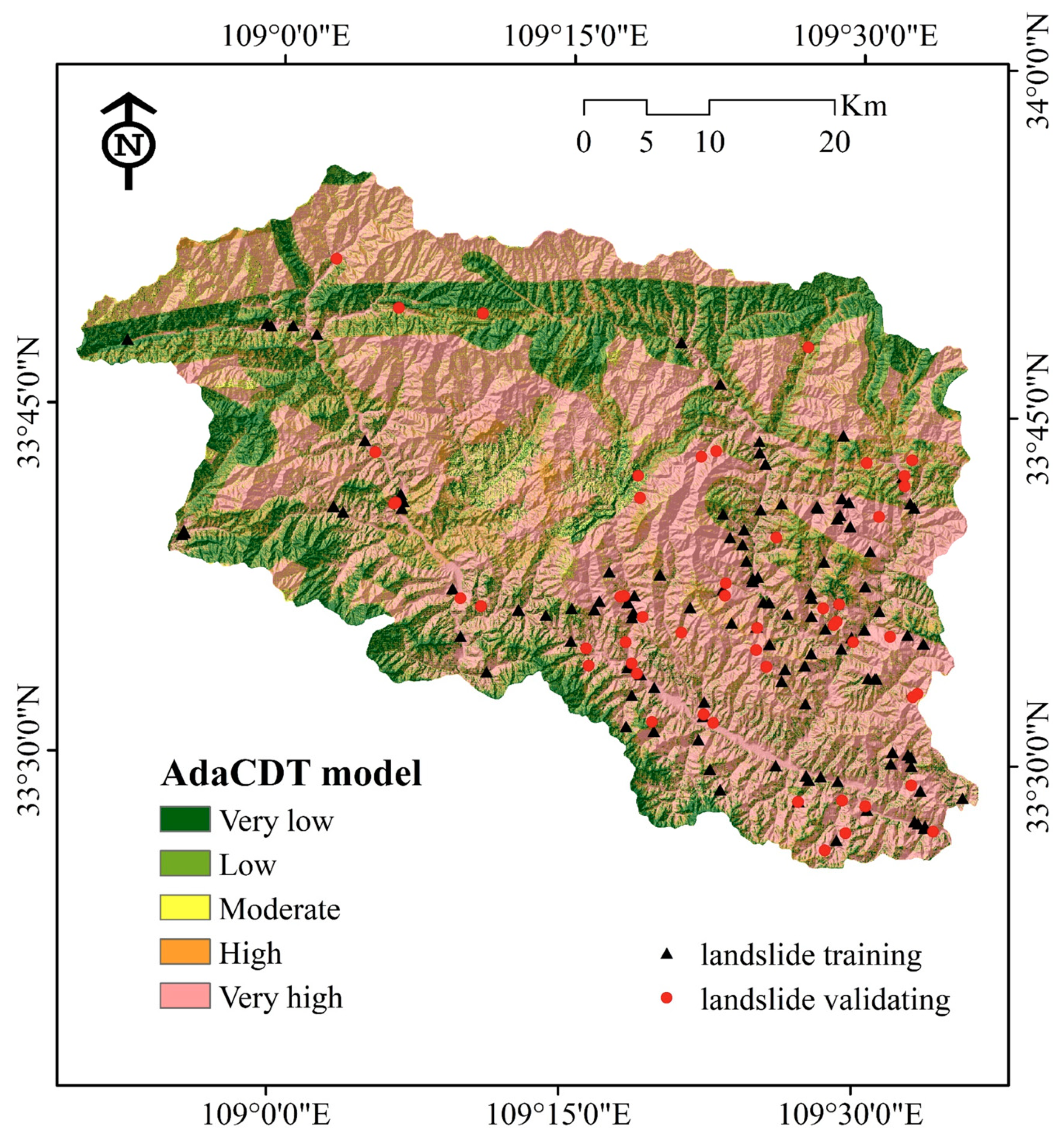
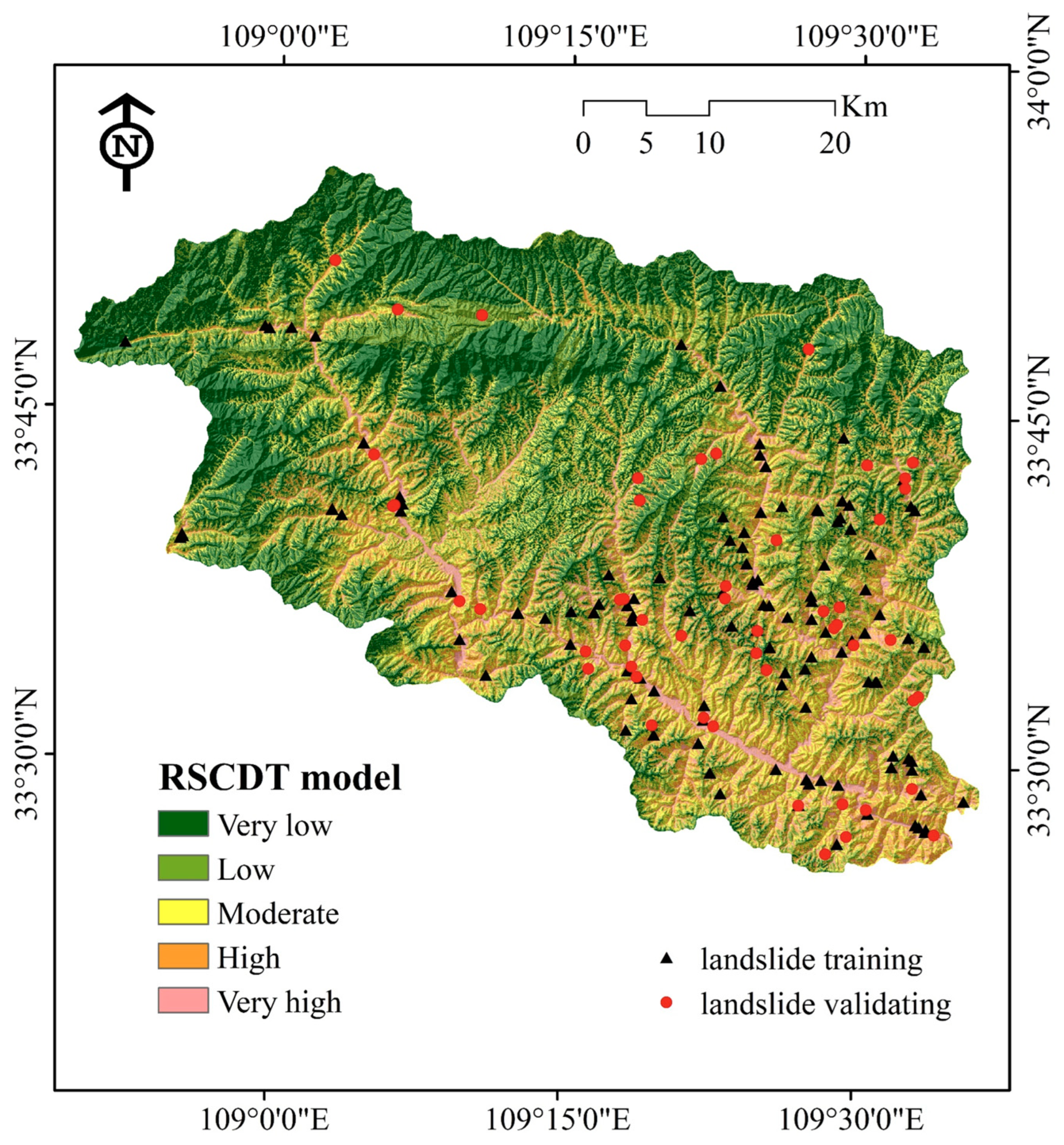
4.2. Application of Landslide Susceptibility Models
4.3. Model Performance and Validation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, G.; Lei, X.; Chen, W.; Shahabi, H.; Shirzadi, A. Hybrid Computational Intelligence Methods for Landslide Susceptibility Mapping. Symmetry 2020, 12, 325. [Google Scholar] [CrossRef]
- Kamran, C.; Ramesh, P.R.; Syed, I.A.; Alamgir, A.K.; Bahram, G.; William, T.D.; Pradeep, K.G. Spatial-temporal dynamics of runoff generation areas in a small agricultural watershed in southern Ontario. J. Water Resour. Prot. 2015, 7, 27. [Google Scholar] [CrossRef]
- Bacha, A.S.; Shafique, M.; van der Werff, H. Landslide inventory and susceptibility modelling using geospatial tools, in Hunza-Nagar valley, northern Pakistan. J. Mt. Sci. 2018, 15, 1354–1370. [Google Scholar] [CrossRef]
- Hong, H.; Ilia, I.; Tsangaratos, P.; Chen, W.; Xu, C. A hybrid fuzzy weight of evidence method in landslide susceptibility analysis on the Wuyuan area, China. Geomorphology 2017, 290, 1–16. [Google Scholar] [CrossRef]
- Li, L.; Lan, H.; Guo, C.; Zhang, Y.; Li, Q.; Wu, Y. A modified frequency ratio method for landslide susceptibility assessment. Landslides 2017, 14, 727–741. [Google Scholar] [CrossRef]
- Ramesh, V.; Anbazhagan, S. Landslide susceptibility mapping along Kolli hills Ghat road section (India) using frequency ratio, relative effect and fuzzy logic models. Environ. Earth Sci. 2015, 73, 8009–8021. [Google Scholar] [CrossRef]
- Akinci, H.; Zeybek, M. Comparing classical statistic and machine learning models in landslide susceptibility mapping in Ardanuc (Artvin), Turkey. Nat. Hazards 2021, 108, 1515–1543. [Google Scholar] [CrossRef]
- Lian Zhipeng, X.Y.; Sheng, F. Landslide susceptibility assessment based on multi-model fusion method: A case study in Wufeng County, Hubei Province. Bull. Geol. Sci. Technol. 2020, 39, 178–186. [Google Scholar] [CrossRef]
- Bourenane, H.; Bouhadad, Y.; Guettouche, M.S.; Braham, M. GIS-based landslide susceptibility zonation using bivariate statistical and expert approaches in the city of Constantine (Northeast Algeria). Bull. Eng. Geol. Environ. 2015, 74, 337–355. [Google Scholar] [CrossRef]
- Daniel, M.T.; Ng, T.F.; Kadir, M.F.A.; Pereira, J.J. Landslide Susceptibility Modeling Using a Hybrid Bivariate Statistical and Expert Consultation Approach in Canada Hill, Sarawak, Malaysia. Front. Earth Sci. 2021, 9, 616225. [Google Scholar] [CrossRef]
- Benchelha, S.; Aoudjehane, H.C.; Hakdaoui, M.; El Hamdouni, R.; Mansouri, H.; Benchelha, T.; Layelmam, M.; Alaoui, M. Landslide susceptibility mapping in the commune of Oudka, Taounate Province, North Morocco: A comparative analysis of logistic regression, multivariate adaptive regression spline, and artificial neural network models. Environ. Eng. Geosci. 2020, 26, 185–200. [Google Scholar] [CrossRef]
- Chu, L.; Wang, L.-J.; Jiang, J.; Liu, X.; Sawada, K.; Zhang, J. Comparison of landslide susceptibility maps using random forest and multivariate adaptive regression spline models in combination with catchment map units. Geosci. J. 2019, 23, 341–355. [Google Scholar] [CrossRef]
- Ashournejad, Q.; Hosseini, A.; Pradhan, B.; Hosseini, S.J. Hazard zoning for spatial planning using GIS-based landslide susceptibility assessment: A new hybrid integrated data-driven and knowledge-based model. Arab. J. Geosci. 2019, 12, 126. [Google Scholar] [CrossRef]
- Sheikh, V.; Kornejady, A.; Ownegh, M. Application of the coupled TOPSIS–Mahalanobis distance for multi-hazard-based management of the target districts of the Golestan Province, Iran. Nat. Hazards 2019, 96, 1335–1365. [Google Scholar] [CrossRef]
- Quan, H.-C.; Lee, B.-G. GIS-based landslide susceptibility mapping using analytic hierarchy process and artificial neural network in Jeju (Korea). KSCE J. Civ. Eng. 2012, 16, 1258–1266. [Google Scholar] [CrossRef]
- Wu, Y.; Li, W.; Liu, P.; Bai, H.; Wang, Q.; He, J.; Liu, Y.; Sun, S. Application of analytic hierarchy process model for landslide susceptibility mapping in the Gangu County, Gansu Province, China. Environ. Earth Sci. 2016, 75, 422. [Google Scholar] [CrossRef]
- Pham, B.T.; Pradhan, B.; Bui, D.T.; Prakash, I.; Dholakia, M.B. A comparative study of different machine learning methods for landslide susceptibility assessment: A case study of Uttarakhand area (India). Environ. Model. Softw. 2016, 84, 240–250. [Google Scholar] [CrossRef]
- Wang, G.; Chen, X.; Chen, W. Spatial prediction of landslide susceptibility based on GIS and discriminant functions. ISPRS Int. J. Geo Inf. 2020, 9, 144. [Google Scholar] [CrossRef]
- Arabameri, A.; Saha, S.; Roy, J.; Chen, W.; Blaschke, T.; Bui, D.T. Landslide Susceptibility Evaluation and Management Using Different Machine Learning Methods in The Gallicash River Watershed, Iran. Remote. Sens. 2020, 12, 475. [Google Scholar] [CrossRef]
- Abedini, M.; Ghasemian, B.; Shirzadi, A.; Shahabi, H.; Chapi, K.; Pham, B.T.; Bin Ahmad, B.; Tien Bui, D. A novel hybrid approach of Bayesian Logistic Regression and its ensembles for landslide susceptibility assessment. Geocarto Int. 2019, 34, 1427–1457. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Zandi, D.; Shahabi, H.; Chapi, K.; Shirzadi, A.; Al-Ansari, N.; Singh, S.K.; Dou, J.; Nguyen, H. Comparison of support vector machine, Bayesian logistic regression, and alternating decision tree algorithms for shallow landslide susceptibility mapping along a mountainous road in the west of Iran. Appl. Sci. 2020, 10, 5047. [Google Scholar] [CrossRef]
- Huang Faming, L.J.; Junyu, W.; Daxiong, M.; Mingqiang, S. Modelling rules of landslide susceptibility prediction considering the suitability of linear environmental factors and different machine learning models. Bull. Geol. Sci. Technol. 2022, 41, 44–59. [Google Scholar] [CrossRef]
- Bui, D.T.; Shahabi, H.; Omidvar, E.; Shirzadi, A.; Geertsema, M.; Clague, J.J.; Khosravi, K.; Pradhan, B.; Pham, B.T.; Chapi, K.; et al. Shallow landslide prediction using a novel hybrid functional machine learning algorithm. Remote Sens. 2019, 11, 931. [Google Scholar] [CrossRef]
- Zheng Yingkai, C.J.; Chengbin, W. Application of certainty factor and random forests model in landslide susceptibility evaluation in Mangshi City, Yunnan Province. Bull. Geol. Sci. Technol. 2022, 39, 131–144. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Tran, T.-T.-T.; Bui, D.T. Landslide susceptibility modeling using Reduced Error Pruning Trees and different ensemble techniques: Hybrid machine learning approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Khosravi, K.; Chapi, K.; Trinh, P.T.; Ngo, T.Q.; Hosseini, S.V.; Bui, D.T. A comparison of Support Vector Machines and Bayesian algorithms for landslide susceptibility modelling. Geocarto Int. 2019, 34, 1385–1407. [Google Scholar] [CrossRef]
- Althuwaynee, O.F.; Pradhan, B.; Ahmad, N. Landslide susceptibility mapping using decision-tree based CHi-squared automatic interaction detection (CHAID) and Logistic regression (LR) integration. IOP Conf. Series Earth Environ. Sci. 2014, 20, 12032. [Google Scholar] [CrossRef]
- Huang, C.; Li, F.; Wei, L.; Hu, X.; Yang, Y. Landslide susceptibility modeling using a deep random neural network. Appl. Sci. 2022, 12, 12887. [Google Scholar] [CrossRef]
- Lian, C.; Zeng, Z.; Yao, W.; Tang, H. Multiple neural networks switched prediction for landslide displacement. Eng. Geol. 2015, 186, 91–99. [Google Scholar] [CrossRef]
- Akinci, H. Assessment of rainfall-induced landslide susceptibility in Artvin, Turkey using machine learning techniques. J. Afr. Earth Sci. 2022, 191, 104535. [Google Scholar] [CrossRef]
- Yang Can, L.L.; Yili, Z.; Wenqing, Z.; Shaohe, Z. Machine learning based on landslide susceptibility assessment with Bayesian optimized the hyperparameters. Bull. Geol. Sci. Technol. 2022, 41, 228–238. (In Chinese) [Google Scholar] [CrossRef]
- Cai, Z.; Xu, W.; Meng, Y.; Shi, C.; Wang, R. Prediction of landslide displacement based on GA-LSSVM with multiple factors. Bull. Eng. Geol. Environ. 2016, 75, 637–646. [Google Scholar] [CrossRef]
- Cao, Y.; Yin, K.; Zhou, C.; Ahmed, B. Establishment of landslide groundwater level prediction model based on GA-SVM and influencing factor analysis. Sensors 2020, 20, 845. [Google Scholar] [CrossRef] [PubMed]
- Tutsoy, O. COVID-19 Epidemic and Opening of the Schools: Artificial Intelligence-Based Long-Term Adaptive Policy Making to Control the Pandemic Diseases. IEEE Access 2021, 9, 68461–68471. [Google Scholar] [CrossRef]
- Tutsoy, O.; Tanrikulu, M.Y. Priority and age specific vaccination algorithm for the pandemic diseases: A comprehensive parametric prediction model. BMC Med. Inform. Decis. Mak. 2022, 22, 4. [Google Scholar] [CrossRef] [PubMed]
- Pham, B.T.; Bui, D.T.; Prakash, I. Bagging based Support Vector Machines for spatial prediction of landslides. Environ. Earth Sci. 2018, 77, 146. [Google Scholar] [CrossRef]
- Bui, D.T.; Shirzadi, A.; Shahabi, H.; Geertsema, M.; Omidvar, E.; Clague, J.J.; Thai Pham, B.; Dou, J.; Asl, D.T.; Bin Ahmad, B.; et al. New Ensemble Models for Shallow Landslide Susceptibility Modeling in a Semi-Arid Watershed. Forests 2019, 10, 743. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, W. GIS-Based Evaluation of Landslide Susceptibility Models Using Certainty Factors and Functional Trees-Based Ensemble Techniques. Appl. Sci. 2020, 10, 16. [Google Scholar] [CrossRef]
- Wu, Y.; Ke, Y.; Chen, Z.; Liang, S.; Zhao, H.; Hong, H. Application of alternating decision tree with AdaBoost and bagging ensembles for landslide susceptibility mapping. Catena 2020, 187, 104396. [Google Scholar] [CrossRef]
- Huang Faming, H.S.; Xueya, Y.; Ming, L.; Junyu, W.; Wenbin, L.; Zizheng, G.; Wenyan, F. Landslide susceptibility prediction and identification of its main environmental factors based on machine learning models. Bull. Geol. Sci. Technol. 2022, 41, 79–90. [Google Scholar] [CrossRef]
- Halil, A.; Mustafa, Z.; Sedat, D. Evaluation of Landslide Susceptibility of Şavşat District of Artvin Province (Turkey) Using Machine Learning Techniques. In Landslides; Yuanzhi, Z., Qiuming, C., Eds.; IntechOpen: Rijeka, Croatia, 2021; pp. 69–95. [Google Scholar]
- Azarafza, M.; Azarafza, M.; Akgün, H.; Atkinson, P.M.; Derakhshani, R. Deep learning-based landslide susceptibility mapping. Sci. Rep. 2021, 11, 24112. [Google Scholar] [CrossRef] [PubMed]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. Catena 2020, 186, 104249. [Google Scholar] [CrossRef]
- Habumugisha, J.M.; Chen, N.; Rahman, M.; Islam, M.; Ahmad, H.; Elbeltagi, A.; Sharma, G.; Liza, S.N.; Dewan, A. Landslide Susceptibility Mapping with Deep Learning Algorithms. Sustainability 2022, 14, 1734. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Wang, M.; Peng, L.; Hong, H. Comparative study of landslide susceptibility mapping with different recurrent neural networks. Comput. Geosci. 2020, 138, 104445. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Janizadeh, S.; Avand, M.; Chen, W.; Farzin, M.; Omidvar, E.; Shirzadi, A.; Shahabi, H.; Clague, J.J.; Jaafari, A.; et al. GIS-Based Gully Erosion Susceptibility Mapping: A Comparison of Computational Ensemble Data Mining Models. Appl. Sci. 2020, 10, 2039. [Google Scholar] [CrossRef]
- Bui, D.T.; Ho, T.-C.; Pradhan, B.; Pham, B.-T.; Nhu, V.-H.; Revhaug, I. GIS-based modeling of rainfall-induced landslides using data mining-based functional trees classifier with AdaBoost, Bagging, and MultiBoost ensemble frameworks. Environ. Earth Sci. 2016, 75, 1101. [Google Scholar] [CrossRef]
- Arabameri, A.; Chen, W.; Lombardo, L.; Blaschke, T.; Bui, D.T. Hybrid Computational Intelligence Models for Improvement Gully Erosion Assessment. Remote. Sens. 2020, 12, 140. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Bui, D.T. Spatial prediction of landslides using a hybrid machine learning approach based on Random Subspace and Classification and Regression Trees. Geomorphology 2018, 303, 256–270. [Google Scholar] [CrossRef]
- Akinci, H.; Kilicoglu, C.; Dogan, S. Random Forest-Based Landslide Susceptibility Mapping in Coastal Regions of Artvin, Turkey. ISPRS Int. J. Geo Inf. 2020, 9, 553. [Google Scholar] [CrossRef]
- Chen, W.; Sun, Z.; Han, J. Landslide Susceptibility Modeling Using Integrated Ensemble Weights of Evidence with Logistic Regression and Random Forest Models. Appl. Sci. 2019, 9, 171. [Google Scholar] [CrossRef] [Green Version]
- Riaz, M.T.; Basharat, M.; Hameed, N.; Shafique, M.; Luo, J. A Data-Driven Approach to Landslide-Susceptibility Mapping in Mountainous Terrain: Case Study from the Northwest Himalayas, Pakistan. Nat. Hazards Rev. 2018, 19, 05018007. [Google Scholar] [CrossRef]
- Katz, O.; Morgan, J.K.; Aharonov, E.; Dugan, B. Controls on the size and geometry of landslides: Insights from discrete element numerical simulations. Geomorphology 2014, 220, 104–113. [Google Scholar] [CrossRef]
- Chen Qian, Y.E.; Shaoping, H.; Xi, W. Susceptibility evaluation of geological disasters in southern Huanggang based on samples and factor optimization. Bull. Geol. Sci. Technol. 2020, 39, 175–185. [Google Scholar] [CrossRef]
- Ercanoglu, M.; Gokceoglu, C. Assessment of landslide susceptibility for a landslide-prone area (north of Yenice, NW Turkey) by fuzzy approach. Environ. Geol. 2002, 41, 720–730. [Google Scholar] [CrossRef]
- Ding, Q.; Chen, W.; Hong, H. Application of frequency ratio, weights of evidence and evidential belief function models in landslide susceptibility mapping. Geocarto Int. 2017, 32, 619–639. [Google Scholar] [CrossRef]
- Moore, I.D.; Gessler, P.; Nielsen, G.; Peterson, G. Terrain analysis for soil specific crop management. In Proceedings of the Proceedings of Soil Specific Crop Management: A Workshop on Research and Development Issues; Robert, P.C., Rust, R.H., Larson, W.E., Eds.; American Society of Agronomy: Madison, WI, USA, 1993; pp. 27–55. [Google Scholar]
- De Roo, A.P.J. Modelling runoff and sediment transport in catchments using GIS. Hydrol. Process. 1998, 12, 905–922. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Moore, I.D.; Turner, A.K.; Wilson, J.P.; Jenson, S.K.; Band, L.E. GIS and land-surface-subsurface process modeling. Environ. Model. GIS 1993, 20, 196–230. [Google Scholar]
- Mejía-Navarro, M.; Wohl, E.E. Geological hazard and risk evaluation using GIS: Methodology and model applied to Medellin, Colombia. Environ. Eng. Geosci. 1994, 31, 459–481. [Google Scholar] [CrossRef]
- Saha, A.K.; Gupta, R.P.; Arora, M.K. GIS-based landslide hazard zonation in the Bhagirathi (Ganga) Valley, Himalayas. Int. J. Remote Sens. 2002, 23, 357–369. [Google Scholar] [CrossRef]
- Fan Yajie, F.X.; Fang, C. County comprehensive geohazard modelling based on the grid maximum method. Bull. Geol. Sci. Technol. 2022, 41, 197–208. [Google Scholar] [CrossRef]
- Pachauri, A.K.; Gupta, P.V.; Chander, R. Landslide zoning in a part of the Garhwal Himalayas. Environ. Geol. 1998, 36, 325–334. [Google Scholar] [CrossRef]
- Gökceoglu, C.; Aksoy, H. Landslide susceptibility mapping of the slopes in the residual soils of the Mengen region (Turkey) by deterministic stability analyses and image processing techniques. Eng. Geol. 1996, 44, 147–161. [Google Scholar] [CrossRef]
- Nam, K.; Wang, F. An extreme rainfall-induced landslide susceptibility assessment using autoencoder combined with random forest in Shimane Prefecture, Japan. Geoenviron. Disasters 2020, 7, 6. [Google Scholar] [CrossRef]
- Akgun, A. A comparison of landslide susceptibility maps produced by logistic regression, multi-criteria decision, and likelihood ratio methods: A case study at İzmir, Turkey. Landslides 2012, 9, 93–106. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, L.; Xiao, T.; Li, X. Enhancement of slope stability by vegetation considering uncertainties in root distribution. Comput. Geotech. 2017, 85, 84–89. [Google Scholar] [CrossRef]
- Kim, J.H.; Fourcaud, T.; Jourdan, C.; Maeght, J.-L.; Mao, Z.; Metayer, J.; Meylan, L.; Pierret, A.; Rapidel, B.; Roupsard, O.; et al. Vegetation as a driver of temporal variations in slope stability: The impact of hydrological processes. Geophys. Res. Lett. 2017, 44, 4897–4907. [Google Scholar] [CrossRef]
- Turrini, M.C.; Visintainer, P. Proposal of a method to define areas of landslide hazard and application to an area of the Dolomites, Italy. Eng. Geol. 1998, 50, 255–265. [Google Scholar] [CrossRef]
- Abellán, J.; Moral, S. Building classification trees using the total uncertainty criterion. Int. J. Intell. Syst. 2003, 18, 1215–1225. [Google Scholar] [CrossRef]
- Dempster, A.P. Upper and Lower Probabilities Induced by a Multivalued Mapping. In Classic Works of the Dempster-Shafer Theory of Belief Functions; Yager, R.R., Liu, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 57–72. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Walley, P. Inferences from Multinomial Data: Learning about a Bag of Marbles. J. R. Stat. Soc. Ser. B Methodolog. 1996, 58, 3–57. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y.; Schapire, R.E. Experiments with a New Boosting Algorithm. In Proceedings of the International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Peng, T.; Chen, Y.; Chen, W. Landslide Susceptibility Modeling Using Remote Sensing Data and Random SubSpace-Based Functional Tree Classifier. Remote Sens. 2022, 14, 4803. [Google Scholar] [CrossRef]
- Zhao, C.H.; Zhang, B.L.; Zhang, X.Z.; Zhao, S.Q.; Li, H.X. Recognition of driving postures by combined features and random subspace ensemble of multilayer perceptron classifiers. Neural Comput. Applic. 2013, 22, 175–184. [Google Scholar] [CrossRef]
- Chen, W.; Hong, H.; Li, S.; Shahabi, H.; Wang, Y.; Wang, X.; Ahmad, B.B. Flood susceptibility modelling using novel hybrid approach of reduced-error pruning trees with bagging and random subspace ensembles. J. Hydrol. 2019, 575, 864–873. [Google Scholar] [CrossRef]






| Group | Code | Lithology | Geological Age |
|---|---|---|---|
| 1 | J2 | Monzonitic granite, quartz monzonite, granodiorite, quartz diorite | Middle Jurassic |
| 2 | T2, T3 | Quartz monzonite, monzonitic granite, granodiorite | Middle and late Triassic |
| 3 | C1, C2 | Lower: carbonaceous phyllite; middle: siltstone, gray-green phyllite; upper: medium-thin bedded limestone; carbonaceous slate with quartz sandstone, carbonaceous slate, slate-sandwiched sandstone, quartz conglomerate, and limestone, breccia limestone | Early and middle Carboniferous |
| 4 | D1, D2, D3 | Lower: sandstone sandwiches slate, sandy argillaceous limestone, and local siderite sandwiches; upper: slate and phyllite-sandwiched sandstone, dolomite, limestone, sandstone, siltstone with a small amount of slate, locally intercalated argillaceous limestone, slate mixed with fine sandstone | Devonian |
| 5 | S | Granite | Silurian |
| 6 | O | Quartz diorite, diorite, gabbro, gabbro-norite, alaskite | Ordovician |
| 7 | Є1 | Lower: black carbonaceous slate and siliceous rock; upper: variegated (dark gray, gray-purple, light gray, gray-white) limestone, dolomitic limestone; dolomite with flint | Cambrian |
| 8 | Z1, Z2 | Lower: conglomerate, sandstone, shale with limestone; upper: dolomite, marl with sandstone, shale | Early and middle Sinian |
| 9 | Pz2 | Lower: mainly metamorphic quartz sandstone, meta granulite with mica-quartz schist; upper: sandy conglomerate, meta-sandstone, mica-quartz schist with a few marble layers from bottom to top | Upper Paleozoic |
| 10 | Pt1, Qn | Biotite schist, graphite marble, clastic rock interbedded with basic lava, volcanic rock with marble, clastic rock with basic lava, volcanic rock with carbonaceous phyllite, marble, and siliceous rock | Lower Proterozoic, Qingbaikouan |
| Factors | Data Source | Format Resolution/Scale |
|---|---|---|
| Elevation, slope angle, slope aspect, plan curvature, profile curvature, SPI, STI, TWI, distance to faults, distance to roads, distance to rivers | ASTER GDEM | Raster, 30 m |
| NDVI | Landsat 8 operational land imager | Raster, 30 m |
| Lithology | Geological maps | Polygon, 1:200,000 |
| Rainfall | National Earth System Science Data Center | Raster, 30 m |
| Land use/cover | Land use/cover maps | Polygon, 1:100,000 |
| Factor | Subclass | No. of Class Pixels | No. of Landslide Pixel | FR Value |
|---|---|---|---|---|
| Elevation (m) | <1000 | 434680 | 66 | 3.39 |
| 1000–1200 | 582467 | 35 | 1.34 | |
| 1200–1400 | 684338 | 13 | 0.42 | |
| 1400–1600 | 497394 | 4 | 0.18 | |
| 1600–1800 | 252707 | 0 | 0.00 | |
| 1800–2000 | 114189 | 0 | 0.00 | |
| 2000–2200 | 47075 | 0 | 0.00 | |
| >2200 | 23672 | 0 | 0.00 | |
| Slope (°) | 0–10 | 134147 | 21 | 3.50 |
| 10–20 | 488228 | 36 | 1.65 | |
| 20–30 | 927360 | 32 | 0.77 | |
| 30–40 | 794942 | 23 | 0.65 | |
| 40–50 | 269518 | 3 | 0.25 | |
| 50–60 | 21531 | 3 | 3.11 | |
| 60–70 | 777 | 0 | 0.00 | |
| 7–74 | 19 | 0 | 0.00 | |
| Aspect | Flat | 162829 | 8 | 1.10 |
| North | 295253 | 19 | 1.44 | |
| Northeast | 355388 | 15 | 0.94 | |
| East | 376859 | 21 | 1.25 | |
| Southeast | 306409 | 23 | 1.68 | |
| South | 321254 | 10 | 0.70 | |
| Southwest | 338043 | 17 | 1.12 | |
| West | 318849 | 5 | 0.35 | |
| Northwest | 161638 | 5 | 0.69 | |
| Plan curvature | (−11.48)–(−0.55) | 517544 | 20 | 0.86 |
| (−0.55)–0.51 | 1520401 | 82 | 1.21 | |
| 0.51–15.57 | 598577 | 16 | 0.60 | |
| Profile curvature | (−18.32)–(−0.98) | 400907 | 12 | 0.67 |
| (−0.98)–0.65 | 1632087 | 74 | 1.01 | |
| 0.65–19.48 | 603528 | 32 | 1.18 | |
| SPI | 0–20 | 29795 | 12 | 9.00 |
| 20–40 | 6605 | 2 | 6.77 | |
| 40–60 | 9282 | 2 | 4.81 | |
| 60–80 | 8520 | 3 | 7.87 | |
| >80 | 2582320 | 99 | 0.86 | |
| STI | 0–10 | 1467316 | 82 | 1.25 |
| 10–20 | 1148396 | 36 | 0.70 | |
| 20–30 | 19775 | 0 | 0.00 | |
| 30–40 | 841 | 0 | 0.00 | |
| >40 | 194 | 0 | 0.00 | |
| TWI | 0–5 | 1294286 | 27 | 0.47 |
| 5–6 | 714821 | 28 | 0.88 | |
| 6–7 | 284237 | 25 | 1.97 | |
| 7–8 | 126771 | 10 | 1.76 | |
| >8 | 216407 | 28 | 2.89 | |
| Lithology | Group 1 | 123884 | 1 | 0.18 |
| Group 2 | 639471 | 3 | 0.10 | |
| Group 3 | 31452 | 2 | 1.42 | |
| Group 4 | 1311573 | 110 | 1.87 | |
| Group 5 | 4482 | 0 | 0.00 | |
| Group 6 | 89099 | 0 | 0.00 | |
| Group 7 | 21375 | 1 | 1.05 | |
| Group 8 | 2655 | 0 | 0.00 | |
| Group 9 | 10151 | 1 | 2.20 | |
| Group 10 | 402380 | 0 | 0.00 | |
| Distance to faults (m) | 0–1000 | 684637 | 42 | 1.37 |
| 1000–2000 | 518613 | 16 | 0.69 | |
| 2000–3000 | 416778 | 19 | 1.02 | |
| 3000–4000 | 310547 | 17 | 1.22 | |
| >4000 | 705947 | 24 | 0.76 | |
| Distance to rivers (m) | 0–200 | 803551 | 67 | 1.86 |
| 200–400 | 656896 | 17 | 0.58 | |
| 400–600 | 454343 | 10 | 0.49 | |
| 600–800 | 279554 | 6 | 0.48 | |
| >800 | 442178 | 18 | 0.91 | |
| Rainfall (mm/yr) | 653–673 | 93654 | 0 | 0.00 |
| 673–693 | 466030 | 5 | 0.24 | |
| 693–713 | 573189 | 32 | 1.25 | |
| 713–733 | 724650 | 47 | 1.45 | |
| 733–764 | 778999 | 34 | 0.98 | |
| Distance to roads (m) | 0–400 | 803551 | 47 | 1.31 |
| 400–800 | 656896 | 8 | 0.27 | |
| 800–1200 | 454343 | 6 | 0.30 | |
| 1200–1600 | 279554 | 5 | 0.40 | |
| >1600 | 442178 | 52 | 2.63 | |
| NDVI | (−0.13)–0.28 | 57074 | 17 | 6.66 |
| 0.28–0.41 | 169814 | 43 | 5.66 | |
| 0.41–0.48 | 513496 | 22 | 0.96 | |
| 0.48–0.54 | 989002 | 21 | 0.47 | |
| 0.54–0.65 | 907136 | 15 | 0.37 | |
| Land use/cover | Farmland | 531645 | 46 | 1.93 |
| Garden land | 1231021 | 34 | 0.62 | |
| Forestland | 861886 | 34 | 0.88 | |
| Commercial land | 9889 | 4 | 9.04 | |
| Industrial and mining storage land | 2081 | 0 | 0.00 |
| Class | CDT | AdaCDT | RSCDT |
|---|---|---|---|
| Very low | 44.92 | 15.84 | 35.45 |
| Low | 4.26 | 15.94 | 24.43 |
| Moderate | 15.70 | 7.80 | 19.65 |
| High | 20.08 | 11.10 | 14.88 |
| Very high | 15.05 | 49.33 | 5.59 |
| Models | AUC | Standard Error | 95% Confidence Interval |
|---|---|---|---|
| CDT | 0.788 | 0.0304 | 0.728–0.847 |
| AdaCDT | 0.821 | 0.0274 | 0.767–0.875 |
| RSCDT | 0.847 | 0.0245 | 0.799–0.895 |
| Models | AUC | Standard Error | 95% Confidence Interval |
|---|---|---|---|
| CDT | 0.771 | 0.0467 | 0.680–0.863 |
| AdaCDT | 0.802 | 0.0426 | 0.719–0.886 |
| RSCDT | 0.861 | 0.0375 | 0.788–0.935 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gui, J.; Pérez-Rey, I.; Yao, M.; Zhao, F.; Chen, W. Credal-Decision-Tree-Based Ensembles for Spatial Prediction of Landslides. Water 2023, 15, 605. https://doi.org/10.3390/w15030605
Gui J, Pérez-Rey I, Yao M, Zhao F, Chen W. Credal-Decision-Tree-Based Ensembles for Spatial Prediction of Landslides. Water. 2023; 15(3):605. https://doi.org/10.3390/w15030605
Chicago/Turabian StyleGui, Jingyun, Ignacio Pérez-Rey, Miao Yao, Fasuo Zhao, and Wei Chen. 2023. "Credal-Decision-Tree-Based Ensembles for Spatial Prediction of Landslides" Water 15, no. 3: 605. https://doi.org/10.3390/w15030605








